Καταλανικό στερεό

Καταλανικό στερεό
αγγλικά : Catalan solid
γαλλικά : Solide de Catalan
γερμανικά : Catalanischer Körper

Στη γεωμετρία, Καταλανικό στερεό ονομάζεται το δυϊκό πολύεδρο ενός στερεού του Αρχιμήδη, έτσι είναι γνωστό και ως Αρχιμήδειο δυϊκό. Τα Καταλανικά στερεά πήραν το όνομά τους από τον Βέλγο μαθηματικό Ευγένιο Καταλάν, που τα περιέγραψε πρώτος το 1865.

Περιγραφή

Τα καταλανικά στερεά είναι όλα κυρτά και έχουν μεταβατικότητα εδρών και όχι κορυφών. Αυτό οφείλεται στο γεγονός ότι τα δυϊκά τους, τα στερεά του Αρχιμήδη, έχουν μεταβατικότητα κορυφών και όχι εδρών. Σε αντίθεση με τα Πλατωνικά στερεά και τα στερεά του Αρχιμήδη, οι έδρες των Καταλανικών στερεών είναι μη κανονικά πολύγωνα. Ωστόσο, το σχήμα κορυφής των Καταλανικών στερεών είναι κανονικό και έχουν σταθερές δίεδρες γωνίες. Λόγω της μεταβατικότητας των εδρών τους, τα Καταλανικά στερεά είναι ισόεδρα.

Επιπλέον, δύο από τα Καταλανικά στερεά έχουν μεταβατικότητα ακμών, το ρομβικό δωδεκάεδρο και το ρομβικό τριακοντάεδρο. Αυτά είναι τα δυϊκά των δύο ψευδοκανονικών στερεών του Αρχιμήδη (κυβοκτάεδρο και εικοσιδωδεκάεδρο αντίστοιχα).

Ακριβώς όπως τα πρίσματα και τα αντιπρίσματα που δεν θεωρούνται γενικά στερεά του Αρχιμήδη, έτσι και οι διπυραμίδες και τα τραπεζόεδρα δεν θεωρούνται γενικά Καταλανικά στερεά, παρά το γεγονός ότι έχουν μεταβατικότητα εδρών.[1]

Δύο από τα Καταλανικά στερεά είναι χειρικά, το πενταγωνικό εικοσιτετράεδρο και το πενταγωνικό εξηκοντάεδρο, που είναι τα αντίστοιχα δυϊκά του χειρικού πεπλατυσμένου κύβου και του πεπλατυσμένου δωδεκαέδρου. Το καθένα από αυτά εμφανίζεται με δύο εναντιόμορφα. Επειδή δεν καταμετρώνται ξεχωριστά τα εναντιόμορφα τραπεζόεδρα και διπυραμίδες, έτσι υπάρχουν συνολικά 13 Καταλανικά στερεά.

ΑΑ	Αρχιμήδειο στερεό	Καταλανικό στερεό
1	κόλουρο τετράεδρο	τριάκις τετράεδρο
2	κόλουρος κύβος	τριάκις οκτάεδρο
3	κόλουρο κυβοκτάεδρο	δισδυάκις δωδεκάεδρο
4	κόλουρο οκτάεδρο	τετράκις εξάεδρο
5	κόλουρο δωδεκάεδρο	τριάκις εικοσάεδρο
6	κόλουρο εικοσιδωδεκάεδρο	δισδυάκις τριακοντάεδρο
7	κόλουρο εικοσάεδρο	Πεντάκις δωδεκάεδρο
8	κυβοκτάεδρο	ρομβικό δωδεκάεδρο
9	εικοσιδωδεκάεδρο	ρομβικό τριακοντάεδρο
10	ρομβοκυβοκτάεδρο	δελτοειδές εικοσιτετράεδρο
11	ρομβοεικοσιδωδεκάεδρο	δελτοειδές εξηκοντάεδρο
12	πεπλατυσμένος κύβος	πενταγωνικό εικοσιτετράεδρο
13	πεπλατυσμένο δωδεκάεδρο	πενταγωνικό εξηκοντάεδρο

Συμμετρία

Τα καταλανικά στερεά, μαζί με τα δυϊκά τους Αρχιμήδεια στερεά, μπορούν να ομαδοποιηθούν ως προς τη συμμετρία τους (τετραεδρική, οκταεδρική και εικοσαεδρική). Υπάρχουν έξι μορφές ανά συμμετρία, ενώ η αυτοσυμμετρική τετραεδρική ομάδα έχει μόνο τρεις μοναδιαίες μορφές και δύο από αυτά αναπαράγονται με οκταεδρική συμμετρία.

Τετραεδρική συμμετρία Αρχιμήδεια Καταλανικά

Οκταεδρική συμμετρία Αρχιμήδεια Καταλανικά

Εικοσαεδρική συμμετρία

Αρχιμήδεια
Καταλανικά

Κατάλογος

Ονομασία (ονομασία δυϊκού) ονομασία Conway	Εικόνες	Ορθές προβολές	Πολύγωνο έδρας	Έδρες	Ακμές	Κορυφές	Συμ.
τριάκις τετράεδρο (κόλουρο τετράεδρο) "kT"			Ισοσκελές V3.6.6	12	18	8	Td
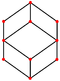ρομβικό δωδεκάεδρο (κυβοκτάεδρο) "jC"			Ρόμβος V3.4.3.4	12	24	14	Oh
τριάκις οκτάεδρο (κόλουρος κύβος) "kO"			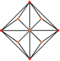Ισοσκελές V3.8.8	24	36	14	Oh
τετράκις εξάεδρο (κόλουρο οκτάεδρο) "kC"			Ισοσκελές V4.6.6	24	36	14	Oh
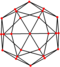δελτοειδές εικοσιτετράεδρο (ρομβοκυβοκτάεδρο) "oC"			Δελτοειδές V3.4.4.4	24	48	26	Oh
δισδυάκις δωδεκάεδρο (κόλουρο κυβοκτάεδρο) "mC"			Σκαληνό V4.6.8	48	72	26	Oh
πενταγωνικό εικοσιτετράεδρο (πεπλατυσμένος κύβος) "gC"			Πεντάγωνο V3.3.3.3.4	24	60	38	O
ρομβικό τριακοντάεδρο (εικοσιδωδεκάεδρο) "jD"			Ρόμβος V3.5.3.5	30	60	32	Ih
τριάκις εικοσάεδρο (κόλουρο δωδεκάεδρο) "kI"			Ισοσκελές V3.10.10	60	90	32	Ih
πεντάκις δωδεκάεδρο (κόλουρο εικοσάεδρο) "kD"			Ισοσκελές V5.6.6	60	90	32	Ih
δελτοειδές εξηκοντάεδρο (ρομβοεικοσιδωδεκάεδρο) "oD"			Δελτοειδές V3.4.5.4	60	120	62	Ih
δισδυάκις τριακοντάεδρο (κόλουρο εικοσιδωδεκάεδρο) "mD"			Σκαληνό V4.6.10	120	180	62	Ih
πενταγωνικό εξηκοντάεδρο (πεπλατυσμένο δωδεκάεδρο) "gD"			Πεντάγωνο V3.3.3.3.5	60	150	92	I

Δείτε επίσης

Στερεό του Αρχιμήδη
Στερεό του Τζόνσον

Παραπομπές

Pugh (1976), Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms.

Πηγές

Catalan, Eugène (1865). Mémoire sur la Théorie des Polyèdres. 41. Paris: J. l'École Polytechnique. σελίδες 1–71.
Holden, Alan (1991). Shapes, Space, and Symmetry. New York: Dover Publications Inc.
Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
Wenninger, Magnus (1983), Dual Models (The thirteen semiregular convex polyhedra and their duals), Cambridge University Press, ISBN 978-0-521-54325-5
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of DesignFree registration required. Dover Publications Inc. ISBN 0-486-23729-X. (Section 3-9)

Εξωτερικοί σύνδεσμοι

Weisstein, Eric W., "Catalan Solids" από το MathWorld.
Weisstein, Eric W., "Isohedron" από το MathWorld.

γεωμετρικά στερεά
Πολύεδρα
1–10 έδρες

Μονόεδρο Δίεδρο Τρίεδρο Τετράεδρο Πεντάεδρο Εξάεδρο Επτάεδρο Οκτάεδρο Εννεάεδρο Δεκάεδρο

11–20 έδρες
Ενδεκάεδρο Δωδεκάεδρο Τριδεκάεδρο Τετραδεκάεδρο Πενταδεκάεδρο Εξαδεκάεδρο Επταδεκάεδρο Οκταδεκάεδρο Εννεαδεκάεδρο Εικοσάεδρο
Άλλα πολύεδρα
Εικοσιδωδεκάεδρο Τριακοντάεδρο Τετρακοντάεδρο Εξηκοντάεδρο Εννενηκοντάεδρο Απειρόεδρο

Εγκυκλοπαίδεια Μαθηματικών

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License