Στη στερεομετρία, το ρομβοκυβοκτάεδρο (ή μικρό ρομβοκυβοκτάεδρο) είναι ένα κυρτό ημικανονικό πολύεδρο, που ανήκει στα στερεά του Αρχιμήδη. Διαθέτει 26 έδρες: 8 ισόπλευρα τρίγωνα και 18 τετράγωνα. Έχει 24 κορυφές και 48 ακμές.
Η διαμόρφωση κορυφής του είναι (3.4.4.4), δηλαδή σε κάθε κορυφή του ενώνονται ένα τρίγωνο με τρία τετράγωνα. Συνολικά, 6 από τα 18 τετράγωνα ενώνονται με τρίγωνα μόνο στις κορυφές τους, ενώ τα υπόλοιπα 12 τετράγωνα μοιράζονται τις πλευρές τους με τρίγωνα.
| Ρομβοκυβοκτάεδρο | |
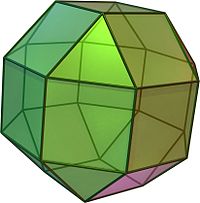 (κινούμενο μοντέλο) |
|
| Τύπος | Στερεό του Αρχιμήδη |
| Έδρες | 26 8 τρίγωνα 18 τετράγωνα |
| Ακμές | 48 |
| Κορυφές | 24 |
| Διαμόρφωση κορυφής |  (3.4.4.4) |
| Ομάδα συμμετρίας | οκταεδρική (Oh) |
| Δυϊκό |  Δελτοειδές εικοσιτετράεδρο |
| Ανάπτυγμα | 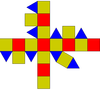 |
Δώδεκα από τις τετραγωνικές έδρες του πολυέδρου είναι συνεπίπεδες με τις 12 έδρες του ρομβικού δωδεκαέδρου, το οποίο είναι δυϊκό του κυβοκτάεδρου, εξού και το όνομα ρομβοκυβοκτάεδρο.
Γεωμετρικά χαρακτηριστικά ρομβοκυβοκτάεδρου
Αν θεωρήσουμε \( {\displaystyle \alpha \,\!} \) το μήκος της ακμής του στερεού, τότε ισχύουν τα εξής:
| Ακτίνα περιγεγραμμένης σφαίρας (απόσταση κορυφών από το κέντρο) |
\( {\displaystyle R={\frac {1}{2}}{\sqrt {5+2{\sqrt {2}}}}\alpha \approx 1,399\alpha } \) |
| Απόσταση ακμών από το κέντρο | \( {\displaystyle \rho ={\frac {1}{2}}{\sqrt {4+2{\sqrt {2}}}}\alpha \approx 1,307\alpha } \) |
| Απόσταση τριγωνικών εδρών από το κέντρο | \( {\displaystyle r_{3}={\frac {1}{2}}{\sqrt {{\frac {1}{3}}\left(11+6{\sqrt {2}}\right)}}\alpha \approx 1,274\alpha } \) |
| Απόσταση τετραγωνικών εδρών από το κέντρο | \({\displaystyle r_{4}={\frac {1}{2}}\left(1+{\sqrt {2}}\right)\alpha \approx 1,207\alpha } \) |
| Συνολική επιφάνεια | \( {\displaystyle S=\left(18+2{\sqrt {3}}\right)\alpha ^{2}\approx 21,464\alpha ^{2}} \) |
| Όγκος | \( {\displaystyle V={\frac {1}{3}}\left(12+10{\sqrt {2}}\right)\alpha ^{3}\approx 8,714\alpha ^{3}} \) |
Κατασκευαστικά, το ρομβοκυβοκτάεδρο μπορεί να προέλθει από τον κύβο, εάν αποκοπούν όλες οι ακμές του, έτσι ώστε στη θέση των ακμών του αρχικού κύβου να σχηματιστούν νέα τετράγωνα, ενώ στις κορυφές του να σχηματιστούν τρίγωνα. Με τον ίδιο τρόπο μπορεί να προέλθει και από το δυϊκό πολύεδρο του κύβου, το οκτάεδρο.
Ένας άλλος τρόπος κατασκευής του ρομβοκυβοκτάεδρου είναι να λάβουμε έναν κύβο και να απομακρύνουμε προς τα έξω (σε σχέση με το κέντρο του) όλες τις έδρες του κατά ορισμένη απόσταση (διατηρώντας το μέγεθος και τον προσανατολισμό τους), να κάνουμε το ίδιο και με ένα οκτάεδρο (που έχει το ίδιο κέντρο και την ίδια ακμή με τον κύβο) και, τέλος, να καλύψουμε τα κενά που θα δημιουργηθούν με τετράγωνα. Έτσι το καινούριο στερεό (το ρομβοκυβοκτάεδρο) θα έχει ως έδρες τα 6 τετράγωνα του κύβου, τα 8 τρίγωνα του οκταέδρου και τα 12 νέα τετράγωνα που θα δημιουργηθούν (σύνολο εδρών: 26).
 Κύβος |
 Ρομβοκυβοκτάεδρο |
 Οκτάεδρο |
Πηγές - Παραπομπές
Weisstein, Eric W., Small Rhombicuboctahedron (Αγγλικά)
γεωμετρικά στερεά
τυπικά γεωμετρικά στερεά
κύβος παραλληλεπίπεδο πυραμίδα (κυκλικός) κύλινδρος κώνος σφαίρα
Πλατωνικά στερεά
τετράεδρο κύβος οκτάεδρο δωδεκάεδρο εικοσάεδρο
στερεά του Αρχιμήδη
κόλουρο τετράεδρο κυβοκτάεδρο κόλουρος κύβος κόλουρο οκτάεδρο ρομβοκυβοκτάεδρο κόλουρο κυβοκτάεδρο πεπλατυσμένος κύβος εικοσιδωδεκάεδρο κόλουρο δωδεκάεδρο κόλουρο εικοσάεδρο ρομβοεικοσιδωδεκάεδρο κόλουρο εικοσιδωδεκάεδρο πεπλατυσμένο δωδεκάεδρο
Καταλανικά στερεά
τριάκις τετράεδρο ρομβικό δωδεκάεδρο τριάκις οκτάεδρο τετράκις εξάεδρο δελτοειδές εικοσιτετράεδρο δισδυάκις δωδεκάεδρο πενταγωνικό εικοσιτετράεδρο ρομβικό τριακοντάεδρο τριάκις εικοσάεδρο πεντάκις δωδεκάεδρο δελτοειδές εξηκοντάεδρο δισδυάκις τριακοντάεδρο πενταγωνικό εξηκοντάεδρο
άλλα στερεά
πρίσμα κύλινδρος ελλειψοειδή ωοειδές δίσκος τόρος σχήμα εκ περιστροφής αντιπρίσμα
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License


