Bosonic string theory is the original version of string theory, developed in the late 1960s. It is so called because it only contains bosons in the spectrum.
In the 1980s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory (supersymmetric string theory) became the real focus. Nevertheless, bosonic string theory remains a very useful model to understand many general features of perturbative string theory, and many theoretical difficulties of superstrings can actually already be found in the context of bosonic strings.
Problems
Although bosonic string theory has many attractive features, it falls short as a viable physical model in two significant areas.
First, it predicts only the existence of bosons whereas many physical particles are fermions.
Second, it predicts the existence of a mode of the string with imaginary mass, implying that the theory has an instability to a process known as "tachyon condensation".
In addition, bosonic string theory in a general spacetime dimension displays inconsistencies due to the conformal anomaly. But, as was first noticed by Claud Lovelace,[1] in a spacetime of 26 dimensions (25 dimensions of space and one of time), the critical dimension for the theory, the anomaly cancels. This high dimensionality is not necessarily a problem for string theory, because it can be formulated in such a way that along the 22 excess dimensions spacetime is folded up to form a small torus or other compact manifold. This would leave only the familiar four dimensions of spacetime visible to low energy experiments. The existence of a critical dimension where the anomaly cancels is a general feature of all string theories.
Types of bosonic strings
There are four possible bosonic string theories, depending on whether open strings are allowed and whether strings have a specified orientation. Recall that a theory of open strings also must include closed strings; open strings can be thought as having their endpoints fixed on a D25-brane that fills all of spacetime. A specific orientation of the string means that only interaction corresponding to an orientable worldsheet are allowed (e.g., two strings can only merge with equal orientation). A sketch of the spectra of the four possible theories is as follows:
| Bosonic string theory | Non-positive M^{2} states |
|---|---|
| Open and closed, oriented | tachyon, graviton, dilaton, massless antisymmetric tensor |
| Open and closed, unoriented | tachyon, graviton, dilaton |
| Closed, oriented | tachyon, graviton, dilaton, antisymmetric tensor, U(1) vector boson |
| Closed, unoriented | tachyon, graviton, dilaton |
Note that all four theories have a negative energy tachyon ( M^{2}=-{\frac {1}{\alpha '}} ) and a massless graviton.
The rest of this article applies to the closed, oriented theory, corresponding to borderless, orientable worldsheets.
Mathematics
Path integral perturbation theory
Bosonic string theory can be said[2] to be defined by the path integral quantization of the Polyakov action:
I_{0}[g,X]={\frac {T}{8\pi }}\int _{M}d^{2}\xi {\sqrt {g}}g^{mn}\partial _{m}x^{\mu }\partial _{n}x^{\nu }G_{\mu \nu }(x)
{\displaystyle x^{\mu }(\xi )} is the field on the worldsheet describing the embedding of the string in 25+1 spacetime; in the Polyakov formulation, g {\displaystyle g} g is not to be understood as the induced metric from the embedding, but as an independent dynamical field. G is the metric on the target spacetime, which is usually taken to be the Minkowski metric in the perturbative theory. Under a Wick rotation, this is brought to a Euclidean metric G_{\mu \nu }=\delta _{\mu \nu } . M is the worldsheet as a topological manifold parametrized by the \xi coordinates. T is the string tension and related to the Regge slope as T={\frac {1}{2\pi \alpha '}} .
I_{0} has diffeomorphism and Weyl invariance. Weyl symmetry is broken upon quantization (Conformal anomaly) and therefore this action has to be supplemented with a counterterm, along with a hypothetical purely topological term, proportional to the Euler characteristic:
I=I_{0}+\lambda \chi (M)+\mu _{0}^{2}\int _{M}d^{2}\xi {\sqrt {g}}
The explicit breaking of Weyl invariance by the counterterm can be cancelled away in the critical dimension 26.
Physical quantities are then constructed from the (Euclidean) partition function and N-point function:
Z=\sum _{h=0}^{\infty }\int {\frac {{\mathcal {D}}g_{mn}{\mathcal {D}}X^{\mu }}{\mathcal {N}}}\exp(-I[g,X])
\left\langle V_{i_{1}}(k_{1}^{\mu })\cdots V_{i_{p}}(k_{p}^{\mu })\right\rangle =\sum _{h=0}^{\infty }\int {\frac {{\mathcal {D}}g_{mn}{\mathcal {D}}X^{\mu }}{\mathcal {N}}}\exp(-I[g,X])V_{i_{1}}(k_{1}^{\mu })\cdots V_{i_{p}}(k_{p}^{\mu })
The perturbative series is expressed as a sum over topologies, indexed by the genus.
The discrete sum is a sum over possible topologies, which for euclidean bosonic orientable closed strings are compact orientable Riemannian surfaces and are thus identified by a genus h. A normalization factor {\mathcal {N}} is introduced to compensate overcounting from symmetries. While the computation of the partition function corresponds to the cosmological constant, the N-point function, including p vertex operators, describes the scattering amplitude of strings.
The symmetry group of the action actually reduces drastically the integration space to a finite dimensional manifold. The g path-integral in the partition function is a priori a sum over possible Riemannian structures; however, quotienting with respect to Weyl transformations allows us to only consider conformal structures, that is, equivalence classes of metrics under the identifications of metrics related by
g'(\xi )=e^{\sigma (\xi )}g(\xi )
Since the world-sheet is two dimensional, there is a 1-1 correspondence between conformal structures and complex structures. One still has to quotient away diffeomorphisms. This leaves us with an integration over the space of all possible complex structures modulo diffeomorphisms, which is simply the moduli space of the given topological surface, and is in fact a finite-dimensional complex manifold. The fundamental problem of perturbative bosonic strings therefore becomes the parametrization of Moduli space, which is non-trivial for genus h\geq 4 .
h = 0
At tree-level, corresponding to genus 0, the cosmological constant vanishes: Z_{0}=0.
The four-point function for the scattering of four tachyons is the Shapiro-Virasoro amplitude:
A_{4}\propto (2\pi )^{26}\delta ^{26}(k){\frac {\Gamma (-1-s/2)\Gamma (-1-t/2)\Gamma (-1-u/2)}{\Gamma (2+s/2)\Gamma (2+t/2)\Gamma (2+u/2)}}
Where k is the total momentum and s, t, u are the Mandelstam variables.
h = 1
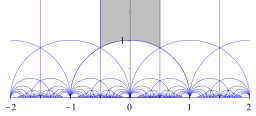
Fundamental domain for the modular group.
The shaded region is a possible fundamental domain for the modular group.
Genus 1 is the torus, and corresponds to the one-loop level. The partition function amounts to:
Z_{1}=\int _{{\mathcal {M}}_{1}}{\frac {d^{2}\tau }{8\pi ^{2}\tau _{2}^{2}}}{\frac {1}{(4\pi ^{2}\tau _{2})^{12}}}\left|\eta (\tau )\right|^{-48}
\tau is a complex number with positive imaginary part \tau _{2} ; {\mathcal {M}}_{1} , holomorphic to the moduli space of the torus, is any fundamental domain for the modular group PSL(2,\mathbb {Z} ) acting on the upper half-plane, for example { \left\{\tau _{2}>0,|\tau |^{2}>1,-{\frac {1}{2}}<\tau _{1}<{\frac {1}{2}}\right\} . \eta (\tau ) is the Dedekind eta function. The integrand is of course invariant under the modular group: the measure {\frac {d^{2}\tau }{\tau _{2}^{2}}} is simply the Poincaré metric which has PSL(2,R) as isometry group; the rest of the integrand is also invariant by virtue of \tau _{2}\rightarrow |c\tau +d|^{2}\tau _{2} and the fact that \eta (\tau ) is a modular form of weight 1/2.
This integral diverges. This is due to the presence of the tachyon and is related to the instability of the perturbative vacuum.
See also
Nambu–Goto action
Polyakov action
Notes
Lovelace, Claud (1971), "Pomeron form factors and dual Regge cuts", Physics Letters, B34 (6): 500–506, Bibcode:1971PhLB...34..500L, doi:10.1016/0370-2693(71)90665-4.
D'Hoker, Phong
References
D'Hoker, Eric & Phong, D. H. (Oct 1988). "The geometry of string perturbation theory". Reviews of Modern Physics. American Physical Society. 60 (4): 917–1065. Bibcode:1988RvMP...60..917D. doi:10.1103/RevModPhys.60.917. Cite uses deprecated parameter |lastauthoramp= (help)
Belavin, A.A. & Knizhnik, V.G. (Feb 1986). "Complex geometry and the theory of quantum strings". ZhETF. 91 (2): 364–390. Bibcode:1986ZhETF..91..364B.
String theory
Background
Strings History of string theory
First superstring revolution Second superstring revolution String theory landscape
Calabi-Yau-alternate
Theory
Nambu–Goto action Polyakov action Bosonic string theory Superstring theory
Type I string Type II string
Type IIA string Type IIB string Heterotic string N=2 superstring F-theory String field theory Matrix string theory Non-critical string theory Non-linear sigma model Tachyon condensation RNS formalism GS formalism
String duality
T-duality S-duality U-duality Montonen–Olive duality
Particles and fields
Graviton Dilaton Tachyon Ramond–Ramond field Kalb–Ramond field Magnetic monopole Dual graviton Dual photon
Branes
D-brane NS5-brane M2-brane M5-brane S-brane Black brane Black holes Black string Brane cosmology Quiver diagram Hanany–Witten transition
Conformal field theory
Virasoro algebra Mirror symmetry Conformal anomaly Conformal algebra Superconformal algebra Vertex operator algebra Loop algebra Kac–Moody algebra Wess–Zumino–Witten model
Gauge theory
Anomalies Instantons Chern–Simons form Bogomol'nyi–Prasad–Sommerfield bound Exceptional Lie groups (G2, F4, E6, E7, E8) ADE classification Dirac string p-form electrodynamics
Geometry
Kaluza–Klein theory Compactification Why 10 dimensions? Kähler manifold Ricci-flat manifold
Calabi–Yau manifold Hyperkähler manifold
K3 surface G2 manifold Spin(7)-manifold Generalized complex manifold Orbifold Conifold Orientifold Moduli space Hořava–Witten domain wall K-theory (physics) Twisted K-theory
Supergravity Superspace Lie superalgebra Lie supergroup
Holography
Holographic principle AdS/CFT correspondence
M-theory
Matrix theory Introduction to M-theory
String theorists
Aganagić Arkani-Hamed Atiyah Banks Berenstein Bousso Cleaver Curtright Dijkgraaf Distler Douglas Duff Ferrara Fischler Friedan Gates Gliozzi Gopakumar Green Greene Gross Gubser Gukov Guth Hanson Harvey Hořava Gibbons Kachru Kaku Kallosh Kaluza Kapustin Klebanov Knizhnik Kontsevich Klein Linde Maldacena Mandelstam Marolf Martinec Minwalla Moore Motl Mukhi Myers Nanopoulos Năstase Nekrasov Neveu Nielsen van Nieuwenhuizen Novikov Olive Ooguri Ovrut Polchinski Polyakov Rajaraman Ramond Randall Randjbar-Daemi Roček Rohm Scherk Schwarz Seiberg Sen Shenker Siegel Silverstein Sơn Staudacher Steinhardt Strominger Sundrum Susskind 't Hooft Townsend Trivedi Turok Vafa Veneziano Verlinde Verlinde Wess Witten Yau Yoneya Zamolodchikov Zamolodchikov Zaslow Zumino Zwiebach
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License