“...the first man in history to whom specific mathematical discoveries have been attributed.” Boyer in A History of Mathematics

Thales in a stamp together with the amber or ilektron that is able to attract other objects if charged

Philosophy among the Greeks is believed to have begun in the Ionian city of Miletus, the richest and most powerful Greek city on the coast of Asia Minor. Miletus was on the edge of interacting cultures: Greek, Mesopotamian and Egyptian, and was adjacent to the rich kingdom of Lydia. Its people travelled, giving them an awareness of conflicting ideas, which encouraged thinking. And among the aristocrats of Miletus was an independence of thought that was a part of an effort toward individual excellence that had been encouraged as justification for their privileges.

Thales of Miletus (Θαλής ο Μιλήσιος)(from 640-610 to ca 548-545 ) BC, son of Examyas of Miletus and Cleobuline, took his name from Thallath, the Chaldean goddess personifying the sea. Thales had traveled widely in quest of knowledge, visiting Crete, Phoenicia, and Egypt. Thales was supposedly of Phoenician descent but he was actually probably a Carian or Cretan and thoroughly merged into Ionian culture. The Phoenician link (according to Herodotus) might be because he brought Phoenician navigational techniques into Miletus. ”Καλλίμαχος δ΄ αὐτὸν οἶδεν εὑρετὴν τῆς ἄρκτου τῆς μικρᾶς λέγων ἐν τοῖς Ἰάμβοις οὕτως καὶ τῆς ἁμάξης ἐλέγετο σταθμήσασθαι τοὺς ἀστερίσχους, ᾗ πλέουσι Φοίνικες. “ The Milesians were great traders by sea and land and therefore interested in navigation. Thales showed how a ship could be steered by observing Ursa Minor (which can be better used than Ursa Major as it is closer to the North Pole its position in the sky changes less). There are arguments that Phoenicians would not tell their navigation knowledge to foreigners and thus Thales must have been of Phoenician descent (like others such as Zeno of Citium). Thales is also said to have tried to revise the calendar.

Herodotus, the Father of History, tells us that once upon a time--which time, as the modern computator shows us, was about the year 590 B.C. --a war had risen between the Lydians and the Medes and continued five years. "In these years the Medes often discomfited the Lydians and the Lydians often discomfited the Medes (and among other things they fought a battle by night); and yet they still carried on the war with equally balanced fortitude. In the sixth year a battle took place in which it happened, when the fight had begun, that suddenly the day became night. And this change of the day Thales, the Milesian, had foretold to the Ionians, laying down as a limit this very year in which the change took place. The Lydians, however, and the Medes, when they saw that it had become night instead of day, ceased from their fighting and were much more eager, both of them, that peace should be made between them."
Henry Smith Williams, The Beginnings of Greek Science

He studied astronomy in Babylonia, and after his return to Miletus gained great fame by predicting an eclipse of the sun (28.5. 585 BC, Julian Calendar or 22. 5. 584 BC Gregorian Calendar Famous Eclipse ) . Today this seems unlikely as the Astronomy as we assume at that time was not developed to be accurate enough to predict such phenomena. Some say that he was just lucky since the Chaldeans told him that every 54 years and 34 days (Saros Cycles) there is a eclipse of the sun but solar eclipses occur only in narrow regions on earth, unlike lunar eclipses that are visible everywhere.

When he (Croesus) reached the river Halys, he transported his army across it, as I maintain, by the bridges which exist there at the present day; but, according to the general belief of the Greeks, by the aid of Thales the Milesian. The tale is that Croesus was in doubt how he should get his army across, as the bridges were not made at that time, and that Thales, who happened to be in the camp, divided the stream and caused it to flow on both sides of the army instead of on the left only. This he effected thus:—Beginning some distance above the camp, he dug a deep channel, which he brought round in a semicircle, so that it might pass to rearward of the camp; and that thus the river, diverted from its natural course into the new channel at the point where this left the stream, might flow by the station of the army, and afterwards fall again into the ancient bed. In this way the river was split into two streams, which were both easily fordable. It is said by some that the water was entirely drained off from the natural bed of the river. But I am of a different opinion; for I do not see how, in that case, they could have crossed it on their return.
Herodotus, History I

He was first noted as an inventor and an engineer, and it is said that for king Croesus of Lydia he made the river Halys passable by diverting its waters. Thales was also interested in heavenly bodies.

Socrates. I will illustrate my meaning, Theodorus, by the jest which the clever witty Thracian handmaid is said to have made about Thales, when he fell into a well as he was looking up at the stars. She said, that he was so eager to know what was going on in heaven, that he could not see what was before his feet. This is a jest which is equally applicable to all philosophers. For the philosopher is wholly unacquainted with his next-door neighbour; he is ignorant, not only of what he is doing, but he hardly knows whether he is a man or an animal; he is searching into the essence of man, and busy in enquiring what belongs to such a nature to do or suffer different from any other;-I think that you understand me, Theodorus? Plato Theaetetus

A story about Thales says he was once was so intent in his observations of the heavens, he fell into a well. One maid servant named Thratta laughed at him and said: ”How canst thou know what is doing in the heavens, when thy seest not what is at thy feet.” In his travels, he might have come into contact with the astronomical data that Babylonians had accumulated across the centuries, but he also made his own observations of the stars. He supposedly paid and got all the olive presses in Miletus after he found that the olive harvest would be exceptional in the coming year in order to demonstrate that he was a practical person and that he could easy gain money with his knowledge. The question of course is how true this story is. How could Thales predict the harvest by astronomical (or astrological) methods.

To Thales the primary question was not what do we know, but how do we know it.
Aristotle (ca 330 BC) Mathematical Intelligencer v. 6, no. 3, 1984.

He is also credited with the discovery of the electrical properties of amber (or “electron” from which also the name electricity was derived). He was one of the Seven Sages of Greece, according to Pausanias, authored the "maxims useful for the life of men (10.24.1)" inscribed on the temple at Delphi. These maxims, such as "know thyself" and "nothing overmuch," were used by Plato to argue that Thales and the other Seven Wise Men were enthusiasts of the Spartan culture.

The common tale among the Greeks was that Thales accompanied Croesus as a military engineer in his campaigns. The Ionians, noted engineers, were employed by the eastern kings, and Thales supposedly diverted the Halys river for his employer. The Ionian philosophers sought the material principle (arche) of things, and the mode of their origin and disappearance.

It is known that Thales was asked by his mother Kleobulina to get married. He was not very interested and his reply was: O Mother I am too young to marry. This he repeated for many years until some day, when his mother again asked him to marry he replied:
Mother now it is too late! When he was asked why he has no children his reply was: “Because I love children!” (Diogenes Laertios)

He divided tha year in 365 days according to Dioegenes Laertios who also has written that Thales died in the stadium looking some athletic game. When the visitors left they found that Thales remained there looking as sleeping. He was actually dead. Thales died in the 58^th Olympiad period (548-545 BC)

According to Proclus to Thales we owe several propositions later included by Euclid in his Elements. Thales is probably the first Greek mathematician to demonstrate or prove that:

• The angle in semicircle = 90 degrees, Java Applet (German Site)
• A circle is bisected by a diameter
• The pairs of vertical angles formed by two intersecting lines are equal
• The base angles of isosceles triangle are equal
• If two triangles are such that two angles and a side of one are equal respectively to two angles and a side of the other, then the triangles are congruent.

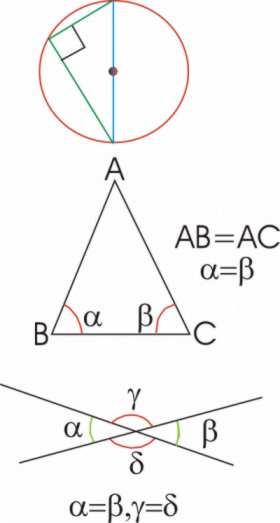
Andrew Wisner says in “The Return of Odysseus and the Elements of Euclid”:

Proclus writes of Thales that "He is said to have been the first to prove (apodeiksai) that a circle is bisected by its diameter." A second theorem which Thales is said to have proven is more complicated, and the attribution, if correct, implies that Thales was in command of some sort of deductive method as well as the diagrammatic procedure of superposition. Diogenes Laertius cites Pamphile, who claims that Thales, "was the first to inscribe a right- angled triangle in a circle, whereupon he sacrificed an ox." The implication seems to be that Thales understood the general proposition that the angle inscribed on the semi-circle is always right, which implies, in turn, that he knew among other things that the angles of a triangle are together equal to two right angles, from which fact he could have deduced the theorem suggested by Pamphile's remark. The accuracy of the remark has been called into question on two grounds: first that Pamphile may have this story confused with a similar one which Apollodorus tells about Pythagoras; and second that it is anachronistic in that the proposition about the angle sum of triangles has traditionally been attributes to Pythagoras or the more or less nebulous "Pythagoreans" and in either case would not have been available to Thales. However the case may be, it is clear that by the middle of the sixth century in Ionia the Greeks had begun to formulate general geometrical propositions, and had developed a notion of proof which was diagrammatic if not yet deductive.

...τὴν βακτηρίαν στήσας ἐπι τῷ πέρατι τῆς σκιᾶς ἣν ἡ πυραμὶς ἐποίει, γενομένων τῇ ἐπαφῇ τῆς ἀκτῖνος δυοῖν πριγώνων, ἔδειξας ὃν ἡ σκιὰ πρὸς τὴν σκιὰν λόγον εἶχε, τὴν πυραμίδα πρὸς τὴν βακτηρίαν ἔχουσαν. Plutarch

Thales was able to determine the height of a pyramid by measuring the length of its shadow at a particular time of day (Heath pp. 128-139). The simplest way probably would be to measure the shadow of the pyramid at the time of day when an objects shadow was the same length as the height of the object. Thales may have been able to observe that at a certain position of the sun an objects height is equal to the length of its shadow. This is true for all objects at the same time of day, regardless of their size.

Thales has chosen Water for the Primordial Substance the so-called “Arche”, Anaximenes of Miletus Air to describe the One Life which animates it and Heraclitus of Ephesus maintained that the one Principle underlying all physical phenomena is Fire.

Thales said that Water is the most beautiful Substance probably influenced by his Egyptian teachers who in desert like regions knew how important water is.

Aristotle writes about Thales:

Of the first philosophers, then, most thought the principles which were of the nature of matter were the only principles of all things. That of which all things that are consist, the first from which they come to be, the last into which they are resolved (the substance remaining, but changing in its modifications), this they say is the element and this the principle of things, and therefore they think nothing is either generated or destroyed, since this sort of entity is always conserved, as we say Socrates neither comes to be absolutely when he comes to be beautiful or musical, nor ceases to be when loses these characteristics, because the substratum, Socrates himself remains. just so they say nothing else comes to be or ceases to be; for there must be some entity-either one or more than one-from which all other things come to be, it being conserved.

Yet they do not all agree as to the number and the nature of these principles. Thales, the founder of this type of philosophy, says the principle is water (for which reason he declared that the earth rests on water), getting the notion perhaps from seeing that the nutriment of all things is moist, and that heat itself is generated from the moist and kept alive by it (and that from which they come to be is a principle of all things). He got his notion from this fact, and from the fact that the seeds of all things have a moist nature, and that water is the origin of the nature of moist things.

Some think that even the ancients who lived long before the present generation, and first framed accounts of the gods, had a similar view of nature; for they made Ocean and Tethys the parents of creation, and described the oath of the gods as being by water, to which they give the name of Styx; for what is oldest is most honourable, and the most honourable thing is that by which one swears. It may perhaps be uncertain whether this opinion about nature is primitive and ancient, but Thales at any rate is said to have declared himself thus about the first cause. Hippo no one would think fit to include among these thinkers, because of the paltriness of his thought. Metaphysics, I. 3 ; 983 b 6

and F. Nietzsche says:

Greek philosophy seems to begin with a preposterous fancy, with the proposition that water is the origin and mother-womb of all things. Is it really necessary to stop there and become serious? Yes, and for three reasons: firstly, because the preposition does enunciate something about the origin of things; secondly, because it does so without figure and fable; thirdly and lastly, because it contained, although only in the chrysalis state, the idea everything is one. ... That which drove him to this generalization was a metaphysical dogma, which had its origin in a mystic intuition and which together with the ever renewed endeavors to express it better, we find in all philosophies- the proposition: everything is one!

These words of Nietzsche explain why somebody ironically said that even if Thales would use syrup instead water for the primordial substance he still would be considered as one of the first scientists.

Except some first observations of electrical effects he also showed the influence of a Magnet has to a piece of iron, showing that everything has some “soul”, “is filled with Gods” according to Aristotle's De Anima (On the Soul):

And Thales, according to what is related of him, seems to have regarded the soul as something endowed with the power of motion, if indeed he said that the loadstone has a soul because it moves iron.
On the Soul, i. 2; 405 a 19.

Thales was one of the first Greek Scientists who initiated with others in the Ionian Islands the “Revolution of Wisdom”.

Total Solar Eclipse of Thales , http://aa.usno.navy.mil/data/docs/JulianDate.html

Plutarch, Solon (and why Thales avoided marriage and children):

Solon went, they say, to Thales at Miletus, and wondered that Thales took no care to get him a wife and children. To this, Thales made no answer for the present; but, a few days after, procured a stranger to pretend that he had left Athens ten days ago; and Solon inquiring what news there, the man, according to his instructions, replied, "None but a young man's funeral, which the whole city attended; for he was the son, they said, of an honorable man, the most virtuous of the citizens, who was not then at home, but had been traveling a long time." Solon replied, "What a miserable man is he! But what was his name?" "I have heard it," says the man, "but have now forgotten it, only there was great talk of his wisdom and his justice." Thus Solon was drawn on by every answer, and his fears heightened, till at last, being extremely concerned, he mentioned his own name, and asked the stranger if that young man was called Solon's son; and the stranger assenting, he began to beat his head, and to do and say all that is usual with men in transports of grief. But Thales took his hand, and, with a smile, said, "These things, Solon, keep me from marriage and rearing children, which are too great for even your constancy to support; however, be not concerned at the report, for it is a fiction."

Aristotle, Politics Book I:

There is the anecdote of Thales the Milesian and his financial device, which involves a principle of universal application, but is attributed to him on account of his reputation for wisdom. He was reproached for his poverty, which was supposed to show that philosophy was of no use. According to the story, he knew by his skill in the stars while it was yet winter that there would be a great harvest of olives in the coming year; so, having a little money, he gave deposits for the use of all the olive-presses in Chios and Miletus, which he hired at a low price because no one bid against him. When the harvest-time came, and many were wanted all at once and of a sudden, he let them out at any rate which he pleased, and made a quantity of money. Thus he showed the world that philosophers can easily be rich if they like, but that their ambition is of another sort. He is supposed to have given a striking proof of his wisdom, but, as I was saying, his device for getting wealth is of universal application, and is nothing but the creation of a monopoly. It is an art often practiced by cities when they are want of money; they make a monopoly of provisions.

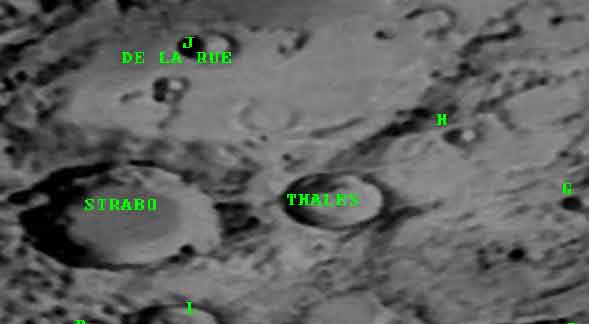
Lunar Crater Thales

LINKS

Thales Fragments and Commentary (Many Interesting Ideas of Thales from Text Fragments!)

Herodotos's Report on Thales' Eclipse by Thomas Worthen, Electronic Antiquity, May 1997.

Other Milesians

Hylozoism