Σταυροειδής καμπύλη
αγγλικά : Cruciform curve
γαλλικά :
γερμανικά :
Η σταυροειδής καμπύλη, είναι μια Τεταρτοβάθμια επίπεδη που δίνεται από την εξίσωση
x^{2}y^{2}-b^{2}x^{2}-a^{2}y^{2}=0\,
όπου a και b είναι δύο παράμετροι που καθορίζουν το σχήμα της καμπύλης. Η σταυροειδής καμπύλη σχετίζεται με έναν τυπικό τετραγωνικό μετασχηματισμό, x ↦ 1 / x, y ↦ 1 / y με την έλλειψη a2x2 + b2y2 = 1 και επομένως είναι μια ρητή επίπεδη αλγεβρική καμπύλη του γένους μηδέν. Η σταυροειδής καμπύλη έχει τρία διπλά σημεία στο πραγματικό προβολικό επίπεδο, σε x = 0 και y = 0, x = 0 και z = 0, και y = 0 και z = 0. [6]
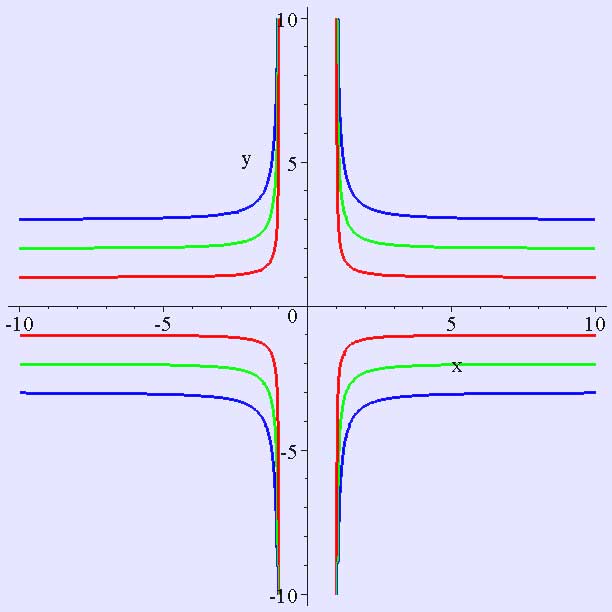
Γράφημα μιας σταυροειδούς καμπύλης, με παράμετρους (b, a) να είναι (1,1), (2,1), (3,1) με κόκκινο, πράσινο και μπλε χρώμα αντίστοιχα
Επειδή η καμπύλη είναι ρητή μπορεί να παραμεριστεί από ρητές συναρτήσεις. Για παράδειγμα, εάν a = 1 και b = 2, τότε
x = -\frac{t^2-2t+5}{t^2-2t-3},\quad y = \frac{t^2-2t+5}{2t-2}
παραμετροποιεί τα σημεία στην καμπύλη εκτόε από τις εξαιρετικές περιπτώσεις όπου ο παρονομαστής είναι μηδέν.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

