Οµάδα των πλεξίδων
αγγλικά : braid group
γαλλικά :
γερμανικά : Zopfgruppe
Η πρώτη μελέτη των πλεξίδων έγινε το 1925 όταν μια κλωστοϋφαντουργία ζήτησε απο τον μαθηματικό Emil Artin να μοντελοποιήσει το πλέξιμο των κλωστών. Ο Artin διαπίστωσε ότι οι πλεξίδες με σταθερό αριθμό n κλωστών συνιστούν ομάδα, την οποία ονόμασε ομάδα πλεξίδων Bn.
Οι πλεξίδες μελετώνται στο μαθηματικό πεδίο της τοπολογίας. Οι ομάδες πλεξίδων ορίστηκαν για πρώτη φορά στο άρθρο Theory of Braids το 1925 από τον Emil Artin. Υπήρχε μια παρόμοια κατασκευή το 1891 σε ένα έργο του Adolf Hurwitz.
Τα 24 στοιχεία μιας ομάδας μετάθεσης σε 4 στοιχεία ως πλεξίδες
Η ομάδα πλεξίδων \( B_{n} \) είναι η ομάδα της οποίας τα στοιχεία είναι πλεξίδες με n κλωστες. Η ομαδική πράξη είναι η συνένωση πλεξίδων και το ουδέτερο στοιχείο είναι η n-πλεξίδα χωρίς διασταυρώσεις.
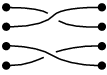
Έστω n = 4; η γενίκευση σε άλλες τιμές του n θα είναι απλή. Σκεφτείτε δύο σύνολα τεσσάρων αντικειμένων που βρίσκονται σε ένα τραπέζι, με τα αντικείμενα σε κάθε σύνολο να είναι διατεταγμένα σε κάθετη γραμμή, και έτσι ώστε το ένα σύνολο να κάθεται δίπλα στο άλλο. (Στις παρακάτω εικόνες, αυτές είναι οι μαύρες κουκκίδες.) Χρησιμοποιώντας τέσσερα σκέλη, κάθε στοιχείο του πρώτου συνόλου συνδέεται με νήμα με ένα στοιχείο του δεύτερου συνόλου έτσι ώστε να προκύπτει αντιστοίχιση ένας προς έναν. Μια τέτοια σύνδεση ονομάζεται πλεξίδα. Συχνά κάποια σκέλη θα πρέπει να περάσουν πάνω ή κάτω από άλλα, και αυτό είναι σημαντικό: οι ακόλουθες δύο συνδέσεις είναι διαφορετικές πλεξίδες:
Το 
είναι διαφορετικό από το 
Από την άλλη πλευρά, δύο τέτοιες συνδέσεις που μπορούν να γίνουν οι ίδιες "τραβώντας τα νήματα" θεωρούνται η ίδια πλεξίδα:
Το είναι το ίδιο με 
Όλα τα σκέλη πρέπει να κινηθούν από αριστερά προς τα δεξιά, κόμβοι όπως τα παρακάτω δεν θεωρούνται πλεξίδες:
δεν είναι πλεξίδα
Δύο πλεξίδες μπορούν να συντεθούν σχεδιάζοντας το πρώτο δίπλα στο δεύτερο, προσδιορίζοντας τα τέσσερα αντικείμενα στη μέση και συνδέοντας τα αντίστοιχα σκέλη:
με 
αποδίδει 
Ενα άλλο παράδειγμα:
με 
αποδίδει 
Η σύνθεση των πλεξίδων σ και τ γράφεται ως στ.
Το σύνολο όλων των πλεξίδων σε τέσσερα σκέλη συμβολίζεται με B4. Η παραπάνω σύνθεση πλεξίδων είναι πράγματι μια πράξη ομάδα;. Το στοιχείο ταυτότητας είναι η πλεξίδα που αποτελείται από τέσσερις παράλληλ ες κλψστες και το αντίστροφο μιας πλεξίδας αποτελείται από εκείνη την πλεξίδα που «αναιρεί» ό, τι έκανε η πρώτη πλεξίδα, το οποίο επιτυγχάνεται με την ανατροπή ενός διαγράμματος όπως αυτό που βρίσκεται πάνω σε κάθετη γραμμή μέσω του κέντρου του. (Τα δύο πρώτα παραδείγματα πλεξίδων είναι αντίστροφα μεταξύ τους.)
Ένας άλλος τομέας έντονης έρευνας που περιλαμβάνει ομάδες πλεξίδας και συναφείς τοπολογικές έννοιες στο πλαίσιο της κβαντικής φυσικής είναι στη θεωρία και υποθετική πειραματική εφαρμογή των λεγόμενων ανυονίων. Αυτά μπορεί να αποτελέσουν τη βάση για κβαντικό υπολογισμό με διόρθωση σφαλμάτων και έτσι η αφηρημένη μελέτη των ομαδων πλεξίδων είναι επί του παρόντος θεμελιώδους σημασίας στην κβαντική πληροφορική.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License
