.

Das Pentagramm, Pentagon und irrationale Zahlen

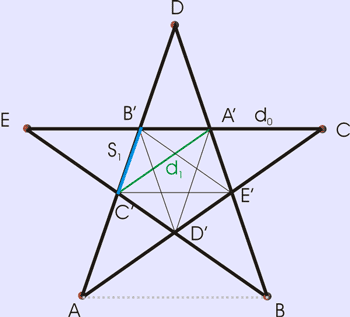
$Graphic4$

AB = BA', BE' = A'D

EB/BA' = BA'/DB' = DB'/B'C' = 1.618033989.... (golden ratio)

The Pythagoreans used the Pentagon star (Pentagram) formed by the five diagonals of a regular Pentagon as a symbol of their school. It was probably this reason that they studied its geometrical properties and that they discovered that this symbol contradicts their idea that everything can be expressed by integer numbers or ratio of integer numbers. Pentagram is a greek word for “pente grammes”, i.e. five lines. Sometimes it is called also a pentalpha, as it looks consisting of 5 rotated “A” symbols.

Agrippa von Nettesheim (Heinrich Cornelius ) (1486 – 1535) , De occulta philosophia

Hippasus of Metapont (around 450 BC) provided a proof of the irrationality of the ratio (diagonal of a Pentagon / side of the Pentagon).

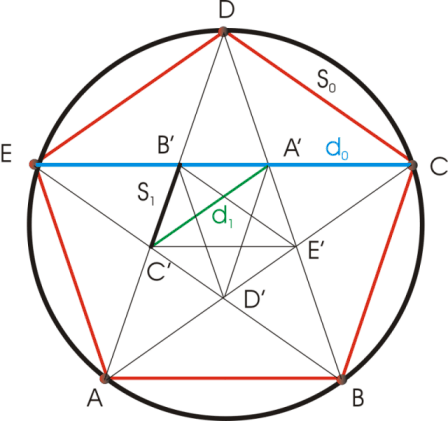
$Graphic1$

Consider the Pentagon ABCDE, the length of each side is s₀and the length of the each diagonal (e.g. EC) d₀. Consider that all sides of CDED' are of equal length and all the four sides of AC'A'D also.

Hippasos used a geometric analog of Euclid's algorithm to show that the ratio d₀/s₀ is an irrational number. From the Pentagon ABCDE and the diagonals a smaller pentagon A'B'C'D'E' can be formed with diagonal d₁ and side s_{1 ,}and from this a smaller pentagon can be again constructed with a diagonal d₂ and side s₂ and so forth. One can find the following relations between the sides and the diagonals of these pentagons:

d₀-s₀ = d₁ < s₀, s₀ – d₁ = s₁ < d₁,

d₁-s₁ = d₂ < s₁, s1 – d₂ = s₂ < d₂,

d₂-s₂ = d₃ < s₂, s2 – d₃ = s₃ < d₃,

and so forth.

Hippasos showed that the Euclid algorithm will never stop! Therefore it is impossible to expressed the ratio d₀ /s₀ as a ratio of integers. It is incredible but the golden ratio phi = 1.618033989.... is the most irrational among all irrational numbers: The most irrational number (American Mathematical Society)

Euclid's Elements Book 4, Proposition 11 (To inscribe an equilateral and equiangular pentagon in a given circle.)

Ptolemy provided in his Almagest a ruler and compass construction method for the pentagon with a simplicity of 16.

Mathematical Properties of the Regular Pentagon

Fibonacci Numbers

Did the ancient Greeks new the Fibonacci numbers? Euclid in Book 6, Proposition 30 shows how to divide a line in mean and extreme ratio which we would call "finding the golden section point on the line". I have no direct information of a text by the ancient Greeks which discusses the Fibonacci numbers but I found the following information interesting ( Source ) :

Epidaurus Theater: The place for the spectators was divided into two tiers: the first one had 34 rows of places, the second one 21. The angle between theatron and scene divides a circumference of the basis of an amphitheater in ratio: 137°,5 : 222°,5 = 0.618.

Dionysus Theater Athens: Three tiers. The first tier has 13 sectors, the second one 21 sectors.

Now 13, 21 and 34 are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...) with the property that the ratio a_n+1/a_n converges to phi.

LINKS

Thrace, Cherronesos, circa 400-350 BC, AR Hemidrachm. Lion / Pentagram and VE monogram

"Pentagon" and "pentagram"

Triangular, Quadratic and Pentagonal Numbers

Visual Explanations and the Pentagon (PDF File)

The Pythagorean Pentacle (Strange Theories)and more strange stories: Coins with Pentagrams and the fact that the Pentagram of the Greeks is always with the two vertices on the top!

Inscribing a regular pentagon in a circle – and proving it

Phillip S. Jones, Irrationals or Incommensurables. I. Their discovery, and a "Logical Scandal". Mathematics Teacher 49, 123-27 (1956)

Ancient Greece

Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images