.
Griechische Mathematik: Geometrische Zahlen
- Triangular number and sums
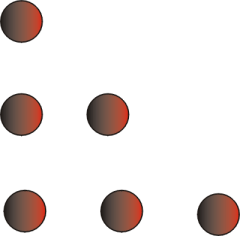
Triangular numbers are so called because they can be arranged in a triangular array of dots (elements).
Consider the sum 1+2+3+...+n = n(n+1)/2. This sum can be considered as the number of elements of a triangular number, see example with n = 3.
For n =4 we have a special number for the Pythagoreans, the Tetraktys, that has 10 elements.
I swear by the discoverer of the Tetraktys,Which is the spring of all our wisdom, The perennial root of Nature's fount. (Iambl., VP, 29.162)
- The sums of the uneven numbers, as reported by Aristotle in Metaphysics, give us the series of squared numbers:
1 + 3 = 22 , 1 + 3 + 5 = 32, 1 + 3 + 5 + 7 = 42, etc.
- Any pair of adjacent triangular numbers add to a square number
1 + 3 = 4, 3 + 6 = 9, 6 + 10 = 16, 45 + 55 = 100
The Pythagoreans were the first people to discover this relationship.
- According to Plutarch the square of the nth triangular number equals the sum of the first n cubes.
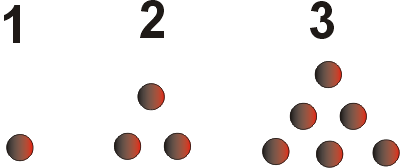
The image shows the first 3 triangular elements with 1,3 and 6 elements and their square are 1, 9 and 36 respectively. We have:
12 = 13, 32 = 13 + 23, 62 = 13+23+33 , etc.
This is equivalent to say that 13+23+...+ n3 = (n(n+1)/2)2

Square numbers are so called because they can be arranged as a square array of dots.
The first four perfect numbers are: 6, 28, 496, 8128. Euclid was able to find that each of these numbers is of the form 2n(2n+1- 1), where 2n+1-1 is prime. Euclid proved that all numbers of this form were perfect. The Pythagoreans knew that 1 + 2 + 4 + ... + 2k = 2k+1 - 1.
Euclid's perfect numbers are triangular.
- Odd Square number relation to Triangular number
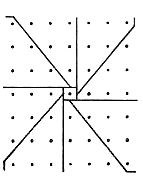
Divide the quadratic number in triangular numbers. We obtain (2n+1)2 = 8n(n+1)/2 + 1
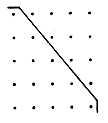
Divide the quadratic number in two triangular numbers. n(n-1)/2 + n(n+1)/2 = n2. This is a graphic explanation why any pair of adjacent triangular numbers add to a square number.
- Pythagorean Numbers
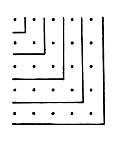
Subtracting two quadratic numbers (n+1) and n we obtain, see figure above , (2n+1) = (n+1)2 - n2
Assume that there is a n for which 2n+1 = m2 (i.e. 2n+1 is a quadrat) and m is odd. Then n = (m2-1)/2, n+1 = (m2+1)/2 or
m2 + ( (m2-1)/2)2 = ((m2-1)/2)2.
We have therefore a method to produce integer solutions forming a Pythagorean triple.
Every perfect number is triangular. The number 666, also known as the Number of the Beast, is a triangular number.
- Pentagonal Numbers

LINKS
Triangular Numbers 1 and Triangular Numbers 2
Formulas and their geometric interpretation
Polygonal numbers Patterns of prime distribution
References
There exist triangular numbers that are also square
-
Eric W. Weisstein. "Figurate Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FigurateNumber.html
-
Eric W. Weisstein. "Triangular Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/TriangularNumber.html
What is a number? (From Rational , Irrational to Surreal Numbers)
| Ancient Greece
Science, Technology , Medicine , Warfare, , Biographies , Life , Cities/Places/Maps , Arts , Literature , Philosophy ,Olympics, Mythology , History , Images Medieval Greece / Byzantine Empire Science, Technology, Arts, , Warfare , Literature, Biographies, Icons, History Modern Greece Cities, Islands, Regions, Fauna/Flora ,Biographies , History , Warfare, Science/Technology, Literature, Music , Arts , Film/Actors , Sport , Fashion --- |

