.
Ψύξη Ντόπλερ
αγγλικά : Bose–Einstein condensate
γαλλικά : Condensat de Bose-Einstein
γερμανικά : Bose-Einstein-Kondensat
Το συμπύκνωμα Μπόζε-Αϊνστάιν (Bose-Einstein Condensate, BEC) είναι η κατάσταση της ύλης που δημιουργείται όταν μποζόνια περιοριστούν από ένα εξωτερικό δυναμικό και ψυχθούν σε θερμοκρασίες πολύ κοντά στο απόλυτο μηδέν (0 Κ). Σε τέτοιες συνθήκες υψηλής ψύξης, ένα σημαντικό ποσοστό των ατόμων (μποζονίων) βρίσκονται στη θεμελιώδη κατάσταση του εξωτερικού δυναμικού, με αποτέλεσμα να εμφανίζονται κβαντικά φαινόμενα στο μακροσκοπικό αυτό επίπεδο.
Η πρόβλεψη για τη δημιουργία του συμπυκνώματος έγινε πρώτη φορά από τον Μπόζε το 1925. Χρειάστηκαν 70 χρόνια για να πραγματοποιηθεί η συμπύκνωση ΒΕΣ το 1995 από τους Έρικ Κορνέλ και Καρλ Βίμαν στο Εργαστήριο NIST του Πανεπιστημίου Μπόλντερ στο Κολοράντο, ψύχοντας άτομα Ρουβιδίου στους 170° nanoKelvin. Μοιράστηκαν το βραβείο Νόμπελ 2001 μαζί με τον Βόλφγκανγκ Κέτερλε (Wolfgang Ketterle) του MIT για την ανακάλυψή τους.[1]
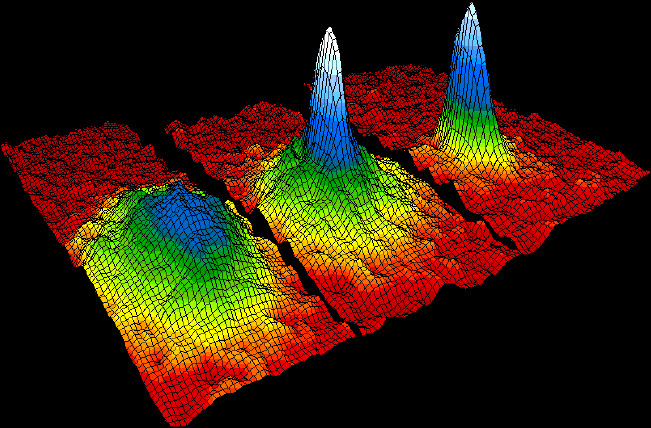
Διανομή ταχυτήτων (τρεις εικόνες) για ένα αέριο από άτομα ρουβιδίου, επιβεβαιώνοντας την ανακάλυψη μια νέας φάσης της ύλης, του συμπυκνώματος Bose-Einstein. Αριστερά: Λίγο πριν την εμφάνιση του συμπυκνώματος Bose–Einstein. Κέντρο: Λίγο μετά την εμφάνιση του συμπυκνώματος Bose–Einstein. Δεξιά: μετά την περαιτέρω εξάτμιση, αφήνοντας ένα δείγμα σχεδόν καθαρού συμπυκνώματος. Από την εργασία των Cornell και Carl Wieman που τους χάρισε το Νόμπελ[1]
Περιγραφή
Τα συμπυκνώματα είναι ρευστά σε εξαιρετικά χαμηλές θερμοκρασίες που παρουσιάζουν ιδιότητες που δεν είναι ακόμα πλήρως κατανοητές, όπως η υπερρευστότητα και η υπεραγωγιμότητα. Τα φαινόμενα αυτά είναι κβαντικής φύσης και οφείλονται στο ότι τα ρευστά αυτά βρίσκονται στην κατάσταση ελάχιστης ενέργειας από την οποία δε μπορούν να μεταβούν σε κατάσταση χαμηλότερης ενέργειας. Τέτοιο φαινόμενο είναι και η ΒΕΣ.
Θεωρία
Η στατιστική κατανομή των μποζονίων που βρίσκονται στην θεμελιώδη τους κατάσταση περιγράφεται από την στατιστική Bose-Einstein. Κάτω από μια κρίσιμη θερμοκρασία, σημαντικός αριθμός μποζονίων θα βρεθούν στη θεμελιώδη τους κατάσταση. Η θερμοκρασία αυτή είναι για αδρανές αέριο στις 3 διαστάσεις χωρίς εσωτερικούς βαθμούς ελευθερίας είναι:
T_c=\left(\frac{n}{\zeta(3/2)}\right)^{2/3}\frac{h^2}{2\pi m k_B}
όπου:
\,T_c κρίσιμη θερμοκρασία,
\,n πυκνότητα σωματιδίων,
\,m μάζα κάθε μποζονίου,
\,h Σταθερά του Πλανκ,
\,k_B Σταθερά του Μπόλτζμαν
\,\zeta η συνάρτηση Ζ του Ρίμαν: \,\zeta(3/2)\approx 2.6124. [2]
Η υπόθεση του Αϊνστάιν
Έστω ένας αριθμός Ν σωματιδίων που δεν αντιδρούν μεταξύ τους και βρίσκονται σε μία από τις 2 διαθέσιμες κβαντικές καταστάσεις \scriptstyle |1\rangle και \scriptstyle |0\rangle. Αν οι δυο αυτές καταστάσεις έχουν την ίδια ενέργεια, τότε έχουν την ίδια πιθανότητα.
Ο αριθμός των διαφορετικών καταστάσεων του συστήματος είναι \scriptstyle 2^N . Σχεδόν τα μισά σωματίδια στον πληθυσμό επομένως είναι στην κατάσταση \scriptstyle |1\rangle και τα υπόλοιπα στην \scriptstyle |0\rangle . Αν όμως τα σωματίδια είναι μη-διακρίσιμα (όπως είναι τα μποζόνια), υπάρχουν μόνο N+1 διαφορετικές καταστάσεις του συστήματος, Κ σωματίδια στην κατάσταση \scriptstyle |0\rangle και Ν-Κ στην κατάσταση \( \scriptstyle |1\rangle.
Ας υποθέσουμε τώρα ότι η κατάσταση \scriptstyle |1\rangle έχει μεγαλύτερη ενέργεια από την \scriptstyle |0\rangle κατά Ε. Στην θερμοκρασία Τ ενα σωματίδιο θα έχει μικρότερη πιθανότητα να είναι στην κατάσταση \scriptstyle |1\rangle κατά \scriptstyle \exp(-E/T) . Στην περίπτωση που είναι διακριτά τα σωματίδια, η κατανομή τους θα τείνει ελαφρά προς την κατάσταση \scriptstyle |0\rangle δεν θα είναι πλέον μοιρασμένα ίσα τα σωματίδια στις δύο καταστάσεις. Στην περίπτωση μη-διακριτών σωματιδίων, δεν υπάρχει απαίτηση για ισοκατανομή, οπότε το πιο πιθανό είναι όλα τα σωματίδια να πέσουν στην ενεργειακή κατάσταση \scriptstyle |0\rangle.
Σ' αυτή την περίπτωση, για κάθε Κ υπάρχει μία κατάσταση που έχει τη δική της πιθανότητα:
\, P(K)= C e^{-KE/T} = C p^K
Για μεγάλα Ν, η σταθερά κανονικοποίησης C = (1-p).
Η αναμενόμενη τιμή συνολικού αριθμού σωματιδίων στην θεμελιώδη κατάσταση είναι το όριο \scriptstyle N\rightarrow \( \infty είναι ίσο με\( \scriptstyle \sum_{n>0} C n p^n=p/1-p . Για μεγάλο Ν, πλησιάζει μια σταθερά. Αυτή θα είναι ένα μικρό ποσοστό του συνολικού αριθμού σωματιδίων. Επομένως όσο μικρή και αν είναι η ενεργειακή διαφορά, πάντα μια συλλογή αρκετών μποζονίων σε θερμική ισορροπία θα καταλαμβάνουν τη θεμελιώδη στάθμη και πολύ λίγα θα βρίσκονται σε διεγερμένες στάθμες.
Στην περίπτωση που έχουμε νέφος σωματιδίων με διαφορετικές ορμές \scriptstyle |k\rangle, αν ο αριθμός των σωματιδίων είναι μεγαλύτερος από τον αριθμό των διαθέσιμων ενεργειακά καταστάσεων ο αριθμός αυτός των καταστάσεων μειώνεται όσο αυξάνεται ο αριθμός των σωματιδίων. Αν η πυκνότητα γίνει μεγαλύτερη από κάποια τιμή, περισσότερα από 1 σωματίδια θα καταλάβουν την ίδια κβαντική κατάσταση. Από αυτή την τιμή και άνω, κάθε καινούριο σωματίδιο θα καταλαμβάνει την θεμελιώδη στάθμη.
Η θερμοκρασία μετάπτωσης είναι:
\, N = V \int {d^3k \over (2\pi)^3} {p(k)\over 1-p(k)} = V \int {d^3k \over (2\pi)^3} {1 \over e^{k^2\over 2mT}-1} ,
όπου:
\, p(k)= e^{-k^2\over 2mT}
Εξωτερικοί σύνδεσμοι
Cretan Matter-Waves / Bose-Einstein Condensation group
Αναφορές
Levi, Barbara Goss (2001). «Cornell, Ketterle, and Wieman Share Nobel Prize for Bose–Einstein Condensates». Search & Discovery. Physics Today online. Αρχειοθετήθηκε από το πρωτότυπο στις 24 October 2007. Ανακτήθηκε στις 26 January 2008.
sequence A078434 in OEIS
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License