Προσοφθάλμιος φακός

 

Προσοφθάλμιος φακός

αγγλικά : Eyepiece
γαλλικά : Oculaire
γερμανικά : Okular

Ένα προσοφθάλμιο, ή προσοφθάλμιος φακός, είναι ένα σύστημα φακών το οποίο είναι προσαρμοσμένο σε μία ποικιλία οπτικών οργάνων, όπως το τηλεσκόπιο και το μικροσκόπιο. Ονομάζεται έτσι, επειδή συνήθως, είναι ο φακός που βρίσκεται πιο κοντά στο μάτι, όταν κάποιος κοιτάζει μέσα από το οπτικό όργανο. Ο αντικειμενικός φακός ή το κάτοπτρο, συλλέγει το φως και το εστιάζει δημιουργώντας ένα είδωλο. Το προσοφθάλμιο λοιπόν, δεν «βλέπει» ένα πραγματικό αντικείμενο, αλλά το ενδιάμεσο είδωλο του αντικειμένου όπως σχηματίζεται από το αντικειμενικό σύστημα φακών που προηγείται. Ο προσοφθάλμιος φακός τοποθετείται κοντά στο σημείο εστίασης του αντικειμενικού παράγοντας ένα φανταστικό, μεγεθυμένο είδωλο του αντικειμένου, τοποθετημένο συνήθως κοντά στο άπειρο, ούτως ώστε ο παρατηρητής να μπορεί να το δει χωρίς να χρειάζεται να προσαρμόσει (να εστιάσει δηλαδή το βλέμμα του κοντά). Η συνολική μεγέθυνση εξαρτάται απο την εστιακή απόσταση του προσοφθάλμιου φακού.

Kellner 25mm eyepiece

Ένα προσοφθάλμιο αποτελείται από πολλά “οπτικά στοιχεία” καλυμμένα με ένα περίβλημα, με ένα κυλινδρικό τμήμα στο ένα άκρο. Ο κύλινδρος είναι σχεδιασμένος έτσι ώστε να ταιριάζει με ένα ειδικό άνοιγμα του οπτικού οργάνου με το οποίο συνδέεται. Το είδωλο εστιάζεται μετακινώντας το προσοφθάλμιο πλησιέστερα ή μακρύτερα από τον αντικειμενικό φακό. Τα περισσότερα οπτικά όργανα έχουν ένα μηχανισμό εστίασης που επιτρέπει την κίνηση της ατράκτου στην οποία είναι συναρμολογημένο το προσοφθάλμιο, χωρίς να χρειάζεται ο άμεσος χειρισμός του προσοφθαλμίου.

Εικόνα μέσα από προσοφθάλμιο φακό Kellner 25mm.

Τα κιάλια έχουν συνήθως μόνιμα τοποθετημένους τους προσοφθάλμιους φακούς, με αποτέλεσμα η μεγέθυνση και το οπτικό πεδίο να είναι προκαθορισμένα. Τα τηλεσκόπια και τα μικροσκόπια, ωστόσο, έχουν συνήθως τη δυνατότητα να εναλλάσσουν τους προσοφθάλμιους φακούς. Με την εναλλαγή του προσοφθάλμιου, ο χρήστης μπορεί να προσαρμόσει το τι απεικονίζεται. Για παράδειγμα, οι προσοφθάλμιοι συχνά εναλλάσονται έτσι ώστε να αυξηθεί ή να μειωθεί η μεγέθυνση ενος τηλεσκοπίου. Επιπλέον οι προσοφθάλμιοι προσφέρουν μια ποικιλία βάθους πεδίου, και διαφορετικές αποστάσεις παρατήρησης, υπο την έννοια της βέλτισης αποστασης παρατήρησης απο τον χρήστη. Σύγχρονα ερευνητικά τηλεσκόπια δεν χρησιμοποιούν προσοφθάλμια. Αντί αυτού, έχουν υψηλής ποιότητας αισθητήρες CCD τοποθετημένους στην εστία του αντικειμενικού συστήματος, και τα είδωλα παρατηρούνται μέσω της οθόνης ενός ηλεκτρονικoύ υπολογιστή. Μερικοί ερασιτέχνες αστρονόμοι χρησιμοποιούν τα τηλεσκόπιά τους με τον ίδιο τρόπο, αλλά η άμεση οπτική θέαση με προσοφθάλμια είναι μακράν η πιο κοινή.

Χαρακτηριστικά προσοφθάλμιων φακών

Κατά τη σύγκριση προσοφθάλμιων φακών, υπάρχουν πολλά χαρακτηριστικά που παρουσιάζουν ενδιαφέρον για ένα χρήστη ενός οπτικού οργάνου, ούτως ώστε να αποφασίσει ποιο ταιριάζει στις ανάγκες του.

Θέση της κόρης εισόδου

Τα προσοφθάλμια είναι οπτικά συστήματα όπου η κόρη εισόδου βρίσκεται πάντα έξω από το σύστημα. Είναι σχεδιασμένα για βέλτιστη απόδοση σε μία συγκεκριμένη απόσταση από αυτή την κόρη εισόδου (δηλ. με τα ελάχιστα σφάλματα απεικόνισης για την απόσταση αυτή). Σε ένα διαθλαστικό αστρονομικό τηλεσκόπιο η κόρη εισόδου ταυτίζεται με τον αντικειμενικό φακό. Αυτό μπορεί να βρίσκεται αρκετά μέτρα μακριά από το προσοφθάλμιο. Σε ένα προσοφθάλμιο μικροσκοπίου η κόρη εισόδου είναι κοντά στο πίσω εστιακό επίπεδο του αντικειμενικού συστήματος, μόνο μερικά εκατοστά από το προσοφθάλμιο. Οι προσοφθάλμιοι φακοί μικροσκοπίου μπορεί να είναι διορθωμένοι διαφορετικά από αυτούς ενός τηλεσκοπίου, ωστόσο οι περισσότεροι είναι επίσης κατάλληλοι για χρήση σε τηλεσκόπιο.

Στοιχεία και ομάδες

Στοιχεία είναι οι ξεχωριστοί φακοί, οι οποίοι μπορεί να είναι απλοί μονοί φακοί, διπλοί, ή τριπλοί . Όταν οι φακοί είναι κολλημένοι μεταξύ τους σε ζεύγη ή τριάδες, τα συνδυαζόμενα στοιχεία ονομάζονται ομάδες φακών. Τα πρώτα προσοφθάλμια είχαν μόνο ένα στοιχείο, το οποίο έδινε πολύ παραμορφωμένες εικόνες με έντονο χρωματικό σφάλμα. Τα σχέδια δύο και τριών στοιχείων εφευρέθηκαν αμέσως μετά, και γρήγορα έγιναν πρότυπο λόγω της βελτιωμένης ποιότητας εικόνας. Σήμερα, οι οπτικοί σχεδιαστές, με τη βοήθεια υπολογιστικών λογισμικών σχεδίασης, έχουν σχεδιάσει προσοφθάλμια με επτά ή οκτώ στοιχεία που δίνουν ιδιαίτερα ευρείες και μεγάλης οξύτητας εικόνες.

Εσωτερικές ανακλάσεις και σκέδαση

Οι εσωτερικές ανακλάσεις, συχνά ονομάζονται σκεδάσεις του φωτός που διέρχεται μέσα από ένα προσοφθάλμιο και μειώνουν την αντίθεση της εικόνας που προβάλλεται από αυτό. Το φαινόμενο αυτό σε μεγάλο βαθμό, προκαλεί την εμφάνιση ειδώλων που χαρακτηρίζονται ως “φαντασμάτα”. Για πολλά χρόνια, γινόταν χρήση απλών σχεδίων προσοφθαλμίων με τον ελάχιστο αριθμό εσωτερικών επιφανειών (αέρας – γυαλί) για να αποφευχθεί αυτό το πρόβλημα. Μία λύση για τη σκέδαση είναι να επικαλυφθούν οι επιφάνειες των στοιχείων με λεπτές επιστρώσεις φίλμ. Αυτές οι λεπτές επιστρώσεις έχουν πάχος μόνο ένα ή δύο μήκη κύματος, και έχουν σκοπό τη μείωση των ανακλάσεων και της σκέδασης αλλάζοντας την διάθλαση του φωτός που περνούσε απο ένα στοιχείο. Ορισμένες επιστρώσεις μπορούν επίσης να απορροφούν το φως που δεν διέρχεται από το φακό κατά την ολική ανάκλαση, όπου η γωνία του προσπίπτοντος φωτός στο φίλμ είναι μικρή.

Χρωματικά σφάλματα

Τα χρωματικά σφάλματα (διαμήκη ή εγκάρσια) προκαλούνται λόγω της διαφορετικής διάθλασης του φωτός σε γυάλινες επιφάνειες για διαφορετικά μήκη κύματος. Το μπλε φως, διερχόμενο από ένα προσοφθάλμιο, δεν θα εστιαστεί στο ίδιο επίπεδο με το κόκκινο φως. Το φαινόμενο αυτό δημιουργεί ένα χρωματικό δακτύλιο γύρω από σημειακές πηγές φωτός και έχει ως αποτέλεσμα τη θόλωση του ειδώλου. Μείωση του χρωματικού σφάλματος μπορεί να επιτευχθεί με τη χρήση πολλών φακών κατασκευασμένων από διαφορετικούς τύπους γυαλιού. Οι αχρωματικοί φακοί είναι ομάδες φακών που εστιάζουν στο ίδιο επίπεδο δύο διαφορετικά μήκη κύματος φωτός (συνήθως το μπλε και το κόκκινο) και εμφανίζουν μειωμένα χρωματικά σφάλματα. Μπορεί επίσης να χρησιμοποιηθεί γυαλί χαμηλής διασποράς για τη μείωση των χρωματικών σφαλμάτων. Το διαμήκες χρωματικό σφάλμα έχει σημαντική επίδραση στα τηλεσκόπια εξαιτίας των μεγάλων εστιακών αποστάσεων τους. Στα μικροσκόπια, τα οποία έχουν αντικειμενικούς φακούς με μικρές εστιακές αποστάσεις, το φαινόμενο αυτό έχει μικρότερη επίδραση.

Εστιακή απόσταση

Η εστιακή απόσταση ενός προσοφθάλμιου είναι η απόσταση από το κύριο επίπεδο του προσοφθάλμιου φακού όπου παράλληλες ακτίνες φωτός συγκλίνουν σε ένα μόνο σημείο. Η εστιακή απόσταση ενός προσοφθάλμιου φακού, σε συνδυασμό με την εστιακή απόσταση του αντικειμενικού φακού του τηλεσκοπίου ή μικροσκοπίου, με το οποίο είναι συνδεδεμένο, καθορίζει τη μεγέθυνση, η οποία συνήθως εκφράζεται σε χιλιοστά. Ωστόσο, κατά την εναλλαγή προσοφθάλμιων σε ένα συγκεκριμένο οπτικό όργανο, ορισμένοι χρήστες προτιμούν να αναφέρονται για την ταυτοποίηση κάθε προσοφθαλμίου στη μεγέθυνση που προκαλεί.

Σε ένα τηλεσκόπιο, η γωνιακή μεγέθυνση ΜΑ που προκαλείται από το συνδυασμό ενός συγκεκριμένου προσοφθαλμίου με ένα αντικειμενικό φακό υπολογίζεται από τον παρακάτω τύπο:

\( {\mathrm {MA}}={\frac {f_{O}}{f_{E}}} \)

όπου :

f\( f_{O} \) η εστιακή απόσταση του αντικειμενικού συστήματος
\( f_{E} \) η εστιακή απόσταση του προσοφθαλμίου

Επομένως η μεγέθυνση αυξάνεται όσο η εστιακή απόσταση του προσοφθαλμίου μικραίνει ή η εστιακή απόσταση του αντικειμενικού μεγαλώνει. Για παράδειγμα, ένα προσοφθάλμιο με εστιακή απόσταση 25 mm σε ένα τηλεσκόπιο με αντικειμενικό σύστημα εστιακής απόστασης 1200 mm θα μεγεθύνει τα αντικείμενα 48 φορές. Ένα προσοφθάλμιο με εστιακή απόσταση 4 mm στο ίδιο τηλεσκόπιο θα μεγεθύνει 300 φορές. Οι ερασιτέχνες αστρονόμοι συνήθως αναφέρονται στα προσοφθάλμια των τηλεσκοπίων χρησιμοποιώντας τις εστιακές αποστάσεις τους σε χιλιοστά. Αυτές κυμαίνονται τυπικά από περίπου 3 mm έως 50 mm. Μερικοί αστρονόμοι, ωστόσο, χρησιμοποιούν την προκύπτουσα μεγέθυνση παρά την εστιακή απόσταση. Συχνά είναι πιο βολικό να αναφέρονται στη μεγέθυνση στις αναφορές παρατήρησης, καθώς αυτή δίνει μία πιο άμεση εντύπωση της εικόνας που είδε ο παρατηρητής. Λόγω όμως της εξάρτησής της από τις ιδιότητες του συγκεκριμένου τηλεσκοπίου που χρησιμοποιείται, η μεγέθυνση από μόνη της δεν έχει νόημα για την περιγραφή ενός τηλεσκοπικού προσοφθαλμίου.

\( {\mathrm {MA}}={\frac {DD_{{{\mathrm {EG}}}}}{f_{G}f_{E}}} \)

Σε ένα μικροσκόπιο ο αντίστοιχος τύπος είναι:

\( {\mathrm {MA}}={\frac {DD_{{{\mathrm {EO}}}}}{f_{O}f_{E}}}={\frac {D}{f_{E}}}\times {\frac {D_{{{\mathrm {EO}}}}}{f_{O}}} \)

όπου D είναι η τυπική ελάχιστη απόσταση ευκρινούς όρασης (συνήθως 250 mm), \( D_{{\mathrm {EO}}} \) είναι η απόσταση μεταξύ του πίσω εστιακού επιπέδου του αντικειμενικού συστήματος και του πίσω εστιακού επιπέδου του προσοφθάλμιου φακού (επονομαζόμενο μήκος του σωλήνα), συνήθως 160 mm για ένα σύγχρονο οπτικό όργανο. \( f_{O} \) είναι η εστιακή απόσταση του αντικειμενικού συστήματος, \( f_{E} \)είναι η εστιακή απόσταση του προσοφθαλμίου

Κατά συνθήκη, οι προσοφθάλμιοι μικροσκοπίου συνήθως προσδιορίζονται από την ισχύ, αντί της εστιακής απόστασης. Η ισχύς του προσοφθαλμίου μικροσκοπίου \( P_{{\mathrm {E}}} \) και η ισχύς του αντικειμενικού συστήματος μικροσκοπίου \( P_{{\mathrm {O}}} \) ορίζονται από τις σχέσεις:

\( P_{{\mathrm {E}}}={\frac {D}{f_{E}}},\qquad P_{{\mathrm {O}}}={\frac {D_{{{\mathrm {EO}}}}}{f_{O}}} \)

έτσι από την προηγούμενη σχέση για τη γωνιακή μεγέθυνση ενός μικροσκοπίου έχουμε:

\( {\mathrm {MA}}=P_{{\mathrm {E}}}\times P_{{\mathrm {O}}} \)

Η συνολική γωνιακή μεγέθυνση μίας εικόνας μικροσκοπίου υπολογίζεται απλά πολλαπλασιάζοντας την ισχύ του προσοφθαλμίου με την ισχύ του αντικειμενικού συστήματος. Για παράδειγμα, ένα προσοφθάλμιο 10× με αντικειμενικό 40× θα μεγεθύνει την εικόνα 400 φορές. Αυτός ο ορισμός της ισχύος ενός φακού πηγάζει από τον διαχωρισμό της γωνιακής μεγέθυνσης του οπτικού οργάνου σε ξεχωριστούς όρους για το προσοφθάλμιο και τον αντικειμενικό φακό. Ιστορικά, ο Abbe περιέγραψε τα προσοφθάλμια μικροσκοπίου με διαφορετικό τρόπο, από την άποψη της γωνιακής μεγέθυνσης του προσοφθαλμίου και της «αρχικής μεγέθυνσης» του αντικειμενικού φακού. Ενώ αυτό ήταν βολικό για τον σχεδιαστή των οπτικών συστημάτων, αποδείχθηκε ότι ήταν λιγότερο βολικό από τη σκοπιά της πρακτικής μικροσκοπίας και έτσι στη συνέχεια εγκαταλείφθηκε. Η ευρέως αποδεκτή τυπική ελάχιστη απόσταση εστίασης του ανθρώπινου οφθαλμού D {\displaystyle D} D είναι 250 mm και η ισχύς του προσοφθαλμίου προσδιορίζεται χρησιμοποιώντας την τιμή αυτή. Τα προσοφθάλμα έχουν συνήθως ισχύ 8×, 10×, 15× και 20×. Όταν χρειάζεται, η εστιακή απόσταση του προσοφθαλμίου (σε mm) μπορεί να προσδιοριστεί διαιρώντας τα 250 mm με την ισχύ του προσοφθαλμίου. Τα σύγχρονα οπτικά όργανα χρησιμοποιούν συχνά αντικειμενικούς φακούς διορθωμένους για ένα άπειρο μήκος σωλήνα, αντί των 160mm, τοποθετώντας ένα βοηθητικό διορθωτικό φακό μέσα στο σωλήνα.

Θέση του εστιακού επιπέδου

Θέση μικρομετρικής κλίμακας σε προσοφθάλμιο

Σε ορισμένους τύπους προσοφθαλμίων, όπως τα προσοφθάλμια Ramsden (περιγράφονται λεπτομερέστερα παρακάτω), ο προσοφθάλμιος φακός συμπεριφέρεται ως μεγεθυντικός φακός, και το εστιακό του επίπεδο βρίσκεται έξω από το προσοφθάλμιο μπροστά από τον φακό-πεδίου (ο πρώτος φακός του προσοφθαλμίου, από τη μεριά του αντικειμενικού συστήματος). Αυτό το επίπεδο είναι συνεπώς προσβάσιμο ως τοποθεσία για την τοποθέτηση ενός σταυρονήματος ή μίας μικρομετρικής κλίμακας. Στο προσοφθάλμιο του Κρίστιαν Χόυχενς, το εστιακό επίπεδο βρίσκεται ανάμεσα στο φακό-ματιού (ο φακός του προσοφθαλμίου που βρίσκεται πλησιέστερα του οφθαλμού) και τον φακό-πεδίου, μέσα στο προσοφθάλμιο, και έτσι δεν είναι προσβάσιμο.

Οπτικό πεδίο

Προσομοίωση θέασης μέσα από ένα τηλεσκόπιο χρησιμοποιώντας διαφορετικά προσοφθάλμια. Στην κεντρική εικόνα έχει χρησιμοποιηθεί προσοφθάλμιο με την ίδια εστιακή απόσταση με αυτό της αριστερής, αλλά με μεγαλύτερο φαινόμενο οπτικό πεδίο, δίνοντας μία μεγαλύτερη εικόνα που απεικονίζει περισσότερο χώρο. Στη δεξιά εικόνα το προσοφθάλμιο έχει μικρότερη εστιακή απόσταση σε σχέση με την αριστερή, δίνοντας το ίδιο πραγματικό οπτικό πεδίο αλλά με μεγαλύτερη μεγέθυνση.

Το οπτικό πεδίο (Field Of View - FOV), περιγράφει την περιοχή ενός αντικειμένου - στόχου (μετρημένη ως γωνία από τη θέση της παρατήρησης) που μπορεί να θεαθεί όταν παρατηρούμε μέσα από ένα προσοφθάλμιο. Το παρατηρούμενο οπτικό πεδίο μέσα από ένα προσοφθάλμιο ποικίλλει, εξαρτώμενο από τη μεγέθυνση που επιτυγχάνεται όταν προσαρμόζεται σε ένα συγκεκριμένο τηλεσκόπιο ή μικροσκόπιο, καθώς επίσης και από τις ιδιότητες του προσοφθαλμίου αυτού καθεαυτού. Τα προσοφθάλμια διαφοροποιούνται από το διάφραγμα πεδίου τους (field stop), το οποίο είναι το στενότερο άνοιγμα από το οποίο μπορεί να περάσει το φως κατά την είσοδό του στο προσοφθάλμιο και να φτάσει στον φακό πεδίου του προσοφθαλμίου. Λόγω των επιπτώσεων αυτών των μεταβλητών, ο όρος «οπτικό πεδίο» αναφέρεται σχεδόν πάντοτε με μία από τις παρακάτω δύο έννοιες:

Πραγματικό οπτικό πεδίο

Πραγματικό οπτικό πεδίο ονομάζουμε το γωνιακό μέγεθος της ποσότητας του ουρανού που μπορεί να θεαθεί μέσα από ένα προσοφθάλμιο, όταν χρησιμοποιείται σε ένα συγκεκριμένο τηλεσκόπιο, παράγοντας μία συγκεκριμένη μεγέθυνση. Είναι συνήθως μεταξύ 0.1 και 2 μοιρών.

Φαινόμενο οπτικό πεδίο

αυτό είναι μία μέτρηση του γωνιακού μεγέθους της παρατηρούμενης εικόνας μέσα από το προσοφθάλμιο, με άλλα λόγια, το πόσο μεγάλη εμφανίζεται η εικόνα (όπως διακρίνεται από τη μεγέθυνση). Το μέγεθος αυτό είναι σταθερό για δεδομένο προσοφθάλμιο σταθερής εστιακής απόστασης, και μπορεί να χρησιμοποιηθεί για να υπολογιστεί το πραγματικό οπτικό πεδίο του προσοφθαλμίου όταν χρησιμοποιηθεί με ένα συγκεκριμένο τηλεσκόπιο. Η μέτρηση κυμαίνεται από 30 έως 110 μοίρες. Συνήθως οι χρήστες ενός προσοφθαλμίου θέλουν να υπολογίζουν το πραγματικό οπτικό πεδίο, γιατί δείχνει πόσος ουρανός θα είναι ορατός όταν το χρησιμοποιήσουν στο τηλεσκόπιο τους.

Το ποια θα είναι η μέθοδος υπολογισμού του πραγματικού οπτικού πεδίου εξαρτάται από το αν το φαινόμενο οπτικό πεδίο είναι γνωστό. Εάν το φαινόμενο οπτικό πεδίο είναι γνωστό, το πραγματικό οπτικό πεδίο μπορεί να υπολογιστεί από την ακόλουθη κατά προσέγγιση σχέση:

\( FOV_{C}={\frac {FOV_{P}}{mag}} \)

ή

\( FOV_{C}={\frac {FOV_{P}}{({\frac {f_{T}}{f_{E}}})}} \)

όπου :

\( FOV_{C} \)είναι το πραγματικό οπτικό πεδίο
\( FOV_{P} \) είναι το φαινόμενο οπτικό πεδίο
\( mag \) είναι η μεγέθυνση του τηλεσκοπίου
\( f_{T} \) είναι η εστιακή απόσταση του αντικειμενικού συστήματος του τηλεσκοπίου
\( f_{E} \) είναι η εστιακή απόσταση του προσοφθάλμιου φακού του τηλεσκοπίου

Η εστιακή απόσταση του αντικειμενικού συστήματος του τηλεσκοπίου ισούται με το γινόμενο της διαμέτρου του επί τον αριθμό f# . Αντιπροσωπεύει την απόσταση στην οποία το κάτοπτρο ή ο αντικειμενικός φακός θα προκαλέσει το φως (που μπαίνει παράλληλα) να συγκλίνει σε ένα σημείο.

Ο τύπος είναι ακριβής με σφάλμα 4% για φαινόμενο οπτικό πεδίο έως 40°, και έχει σφάλμα 10% για φαινόμενο οπτικό πεδίο 60°.

Εάν το φαινόμενο οπτικό πεδίο είναι άγνωστο, το πραγματικό οπτικό πεδίο μπορεί να υπολογιστεί κατά προσέγγιση από τη σχέση:

\( FOV_{C}={\frac {57.3d}{f_{T}}} \)

όπου :

\( FOV_{C} \) είναι το πραγματικό οπτικό πεδίο (σε μοίρες)
\( d \)είναι η διάμετρος του διαφράγματος πεδίου (field stop) του προσοφθαλμίου (σε mm)
\( f_{T} \) είναι η εστιακή απόσταση του τηλεσκοπίου (σε mm)

Ο δεύτερος τύπος είναι στην πραγματικότητα πιο ακριβής, αλλά το μέγεθος του διαφράγματος πεδίου (field stop) δεν καθορίζεται συνήθως από τους περισσότερους κατασκευαστές. Ο πρώτος τύπος δεν θα είναι ακριβής, εάν το πεδίο δεν είναι επίπεδο, ή είναι μεγαλύτερο από 60°, το οποίο είναι σύνηθες για τα περισσότερα προσοφθάλμια ευρέως πεδίου. Οι παραπάνω σχέσεις είναι προσεγγιστικές. Το πρότυπο ISO 14132-1:2002 καθορίζει το πώς το ακριβές φαινόμενο γωνιακό οπτικό πεδίο (AAOV) υπολογίζεται από το πραγματικό γωνιακό οπτικό πεδίο (AOV) .

\( tan{\frac {AAOV}{2}}=mag\times tan{\frac {AOV}{2}} \)

Εάν χρησιμοποιηθεί πριν από το προσοφθάλμιο ένας αποκλίνων φακός για να αυξήσει τη μεγέθυνση (φακός Barlow), το οπτικό πεδίο μπορεί να περιοριστεί ελαφρώς σε σχέση με τη χρήση μόνο του προσοφθαλμίου. Αυτό συμβαίνει διότι αν ο φακός πριν από το προσοφθάλμιο έχει στενότερο διάφραγμα πεδίου από αυτό του προσοφθαλμίου, θα λειτουργεί σαν εμπόδιο και θα δίνει μικρότερο διάφραγμα πεδίου στο προσοφθάλμιο. Η ακριβής σχέση είναι:

\( {AAOV}=2\times arctan{\frac {0.5d}{f_{E}}} \)

Προσοφθάλμιο τύπου Plössl με μεγάλο φαινόμενο οπτικό πεδίο.

Αυτή η σχέση μας λέει επίσης ότι για ένα προσοφθάλμιο με δεδομένο φαινόμενο οπτικό πεδίο, η διάμετρος του κυλίνδρου θα καθορίζει τη μέγιστη δυνατή εστιακή απόσταση για το συγκεκριμένο προσοφθάλμιο. Αυτό συμβαίνει επειδή το διάφραγμα πεδίου δεν μπορεί να είναι μεγαλύτερο από τον ίδιο τον κύλινδρο. Για παράδειγμα, ένα προσοφθάλμιο Plossl με φαινόμενο οπτικό πεδίο 45° σε ένα κύλινδρο 1,25 ιντσών θα αποδώσει μέγιστη εστιακή απόσταση 35mm..[1] Για μεγαλύτερη εστιακή απόσταση θα χρειαστεί μεγαλύτερος κύλινδρος αλλιώς το πεδίο θα περιορίζεται από τον κύλινδρο, καθιστώντας ουσιαστικά το οπτικό πεδίο μικρότερο από 45°.

Διάμετρος κυλίνδρου

Τα προσοφθάλμια τηλεσκοπίων και μικροσκοπίων είναι συνήθως εναλλάξιμα για να μπορεί ο χρήστης να αυξάνει ή να μειώνει τη μεγέθυνση του οπτικού οργάνου, αλλά και να επιλέγει το προσοφθάλμιο με τα συγκεκριμένα χαρακτηριστικά και επιδόσεις που του ταιριάζει. Για να είναι αυτό δυνατό, τα προσοφθάλμια κατασκευάζονται με συγκεκριμένες διαμέτρους κυλίνδρου.

Προσοφθάλμιοι φακοί τηλεσκοπίου

Υπάρχουν τρεις τυποποιημένες διάμετροι κυλίνδρου για τηλεσκόπια. Τα μεγέθη κυλίνδρου (συνήθως εκφράζεται σε ίντσες) είναι: 0.965 ίντσες (24,5 mm) - Αυτή είναι η μικρότερη τυποποιημένη διάμετρος κυλίνδρου και συναντάται συνήθως κοινά χαμηλού κόστους τηλεσκόπια. Πολλά από αυτά τα προσοφθάλμια, αυτού του είδους των τηλεσκοπίων, είναι από πλαστικό, ενώ μερικά έχουν ακόμη και πλαστικούς φακούς. Προσοφθάλμια τηλεσκοπίου υψηλής ποιότητας με αυτό το μέγεθος κυλίνδρου δεν κατασκευάζονται πλέον, παρά μόνο τα προσοφθάλμια Kellner.

1 ¼ ίντσες (31,75 mm) – Αυτή η διάμετρος κυλίνδρου είναι η πιο δημοφιλής. Το ανώτερο όριο εστιακής απόστασης για τα προσοφθάλμια με 1¼ ίντσες διάμετρο κυλίνδρου, είναι περίπου 32mm. Για μεγαλύτερες εστιακές αποστάσεις, τα άκρα του ίδιου του κυλίνδρου εισέρχονται στο πεδίο περιορίζοντας το μέγεθός του. Για εστιακές αποστάσεις μεγαλύτερες από 32mm, το διαθέσιμο οπτικό πεδίο πέφτει κάτω από τις 50°, το οποίο οι περισσότεροι ερασιτέχνες θεωρούν ότι είναι το ελάχιστο αποδεκτό εύρος. Αυτά τα μεγέθη κυλίνδρου σπειρώνονται για να μπορούν να προσαρμόζονται πάνω τους φίλτρα διαμέτρου 30mm. 2 ίντσες (50,8 mm) - Το μεγαλύτερο μέγεθος κυλίνδρου στα προσοφθάλμια 2 ιντσών βοηθάει στη αύξηση του ορίου των εστιακών αποστάσεων. Το ανώτατο όριο εστιακής απόστασης με 2 ιντσών προσοφθάλμια είναι περίπου 55mm. Το αντίτιμο είναι ότι αυτά τα προσοφθάλμια είναι συνήθως πιο ακριβά, δεν ταιριάζουν σε ορισμένα τηλεσκόπια, και μπορεί να έχουν βάρος ικανό να ανατρέψει το τηλεσκόπιο. Αυτά τα μεγέθη κυλίνδρου σπειρώνονται για να μπορούν να προσαρμόζονται πάνω τους φίλτρα διαμέτρου 48mm (ή σπανιότερα 49mm).
Προσοφθάλμιοι φακοί μικροσκοπίου
Διαφορετικά μεγέθη κυλίνδρου :(από αριστερά προς τα δεξιά) 2 ίντσες (51 mm), 1¼ ίντσες (32 mm), και 0.965 ίντσες (24.5 mm).

Τα προσοφθάλμια για μικροσκόπια έχουν συγκεκριμένες διαμέτρους κυλίνδρου , μετρούμενες σε χιλιοστά: 23,2mm και 30mm, έτσι είναι ελαφρώς μικρότερα από τους κυλίνδρους των τηλεσκοπίων.
Απόσταση παρατήρησης

Το μάτι πρέπει να βρίσκεται σε μια ορισμένη απόσταση πίσω από το φακό του ματιού ενός προσοφθαλμίου για να μπορεί να δει τα είδωλα σωστά μέσα από αυτό. Η απόσταση αυτή ονομάζεται απόσταση παρατήρησης. Μεγαλύτερη απόσταση παρατήρησης σημαίνει ότι η βέλτιστη θέση είναι μακρύτερα από το προσοφθάλμιο, πράγμα που καθιστά την παρατήρηση ευκολότερη. Ωστόσο, εάν η απόσταση παρατήρησης είναι πολύ μεγάλη μπορεί να είναι δύσκολο για κάποιον να κρατήσει το μάτι του στη σωστή θέση για πολύ ώρα. Για το λόγο αυτό, κάποιοι προσοφθάλμιοι φακοί με μεγάλη απόσταση παρατήρησης έχουν βοηθητικές προεκτάσεις πίσω από το φακό ματιού για να βοηθούν τον παρατηρητή να διατηρεί τη σωστή θέση. Η οφθαλμική κόρη θα πρέπει να συμπίπτει με την κόρη εξόδου που αποτελεί το είδωλο της κόρης εισόδου. Στην περίπτωση ενός τηλεσκοπίου η κόρη εισόδου αντιστοιχεί στον αντικειμενικό φακό.

Η απόσταση παρατήρησης τυπικά κυμαίνεται από περίπου 2mm έως 20mm, ανάλογα με την κατασκευή του προσοφθαλμίου. Προσοφθάλμια μεγάλης εστιακής απόστασης συνήθως έχουν αρκετή απόσταση παρατήρησης, όμως τα προσοφθάλμια μικρής εστιακής απόστασης είναι πιο προβληματικά. Μέχρι πρόσφατα, αλλά ακόμα και τώρα αρκετά συχνά, τα προσοφθάλμια μικρής εστιακής απόστασης είχαν μικρή απόσταση παρατήρησης. Οι οδηγίες καλής σχεδίασης προτείνουν τουλάχιστον 5-6mm απόσταση από το φακό ματιού για να χωράνε οι βλεφαρίδες του παρατηρητή και να αποφεύγεται η κόπωση του χρήση. Ωστόσο, σύγχρονα σχέδια με πολλά στοιχεία φακών, μπορούν να διορθώσουν αυτό το πρόβλημα, έτσι ώστε η παρατήρηση με ισχυρά οπτικά όργανα να γίνεται πιο άνετη. Αυτό ισχύει ιδιαίτερα για όσους φορούν γυαλιά, για τους οποίους μπορεί να χρειαστεί έως 20 mm απόσταση παρατήρησης για να φιλοξενήσει τα γυαλιά τους.

1-Πραγματικό είδωλο, 2-Διάφραγμα πεδίου, 3-Απόσταση παρατήρησης 4-Κόρη
Σχέδια προσοφθαλμίων

Η τεχνολογία έχει εξελιχθεί με την πάροδο του χρόνου και υπάρχει μία ποικιλία από σχέδια προσοφθαλμίων για χρήση σε τηλεσκόπια, μικροσκόπια, διόπτρες όπλων και άλλα οπτικά όργανα. Μερικά από αυτά τα σχέδια περιγράφονται λεπτομερέστερα παρακάτω.

Αποκλίνων φακός ή προσοφθάλμιος του Γαλιλαίου
Αποκλίνων φακός.

Ένας απλός αποκλίνων φακός τοποθετείται πριν από το εστιακό επίπεδο του αντικειμενικού φακού δίνοντας στον παρατηρητή ένα ορθό είδωλο με περιορισμένη όμως μεγέθυνση. Αυτό το είδος του προσοφθάλμιου φακού χρησιμοποιήθηκε στα πρώτα διαθλαστικά τηλεσκόπια που εμφανίστηκαν στην Ολλανδία περίπου το 1608. Χρησιμοποιήθηκε επίσης το 1609 στα σχέδια τηλεσκοπίου του Γαλιλαίου, από όπου και πήρε η συγκεκριμένη διάταξη το όνομα «προσοφθάλμιο του Γαλιλαίου». Αυτός ο τύπος προσοφθαλμίου εξακολουθεί να χρησιμοποιείται σε πολύ φθηνά τηλεσκόπια, κιάλια και κιάλια όπερας.

Συγκλίνων φακός
Συγκλίνων φακός.

Ένας απλός συγκλίνων φακός τοποθετείται μετά το εστιακό επίπεδο του αντικειμενικού φακού δίνοντας στον παρατηρητή ένα μεγεθυμένο ανεστραμμένο είδωλο. Αυτή η πρώιμη διάταξη χρησιμοποιήθηκε στα πρώτα τηλεσκόπια από την Ολλανδία και είχαν προταθεί ως ένας τρόπος επίτευξης πολύ ευρύτερου οπτικού πεδίου και μεγαλύτερης μεγέθυνσης στα τηλεσκόπια του βιβλίου του Johannes Kepler, Dioptrice. Αυτή η πρώιμη διάταξη χρησιμοποιήθηκε στο μικροσκόπιο του Zaccharias Janssen 1590, και προτάθηκε το 1611 στο βιβλίο του Johannes Kepler, Dioptrice, ως ένας τρόπος επίτευξης πολύ ευρύτερου οπτικού πεδίου και μεγαλύτερης μεγέθυνσης στα τηλεσκόπια. Καθώς ο φακός τοποθετείται μετά το εστιακό επίπεδο του αντικειμενικού φακού, είναι δυνατή επίσης η χρήση μίας μικρομετρικής κλίμακας στο εστιακό επίπεδο (χρήσιμη για τον προσδιορισμό του γωνιακού μεγέθους ή και της απόστασης μεταξύ των αντικειμένων που παρατηρούνται).
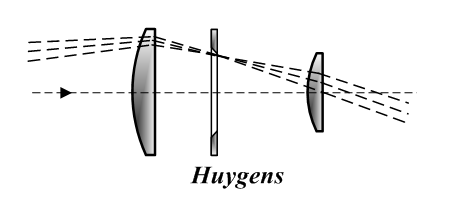
Προσοφθάλμιο Huygens

Σχέδιο προσοφθαλμίου Huygens.

Το προσοφθάλμιο του Huygens αποτελείται από δύο επιπεδόκυρτους φακούς με τις επίπεδες πλευρές προς τον οφθαλμό, χωριζόμενες μεταξύ τους από ένα διάκενο αέρα. Οι φακοί ονομάζονται φακός-ματιού και φακός-πεδίου. Το εστιακό επίπεδο του αντικειμενικού φακού βρίσκεται μεταξύ των δύο φακών. Εφευρέθηκε από τον Christiaan Huygens στα τέλη της δεκαετίας του 1660 και ήταν το πρώτο σύνθετο (πολλών φακών) προσοφθάλμιο..[2] Ο Christian Huygens ανακάλυψε ότι δύο φακοί που χωρίζονται με αέρα μπορούν να χρησιμοποιηθούν σαν προσοφθάλμιο με μηδενικό εγκάρσιο χρωματικό σφάλμα. Εάν και οι δύο φακοί είναι κατασκευασμένοι από γυαλί με ίδιο δείκτης διάθλασης, για να χρησιμοποιηθούν από ένα μη προσαρμοσμένο μάτι (χαλαρό, που εστιάζει στο άπειρο) σε ένα τηλεσκόπιο με αντικειμενικό φακό απείρως μεγάλης εστιακής απόστασης, τότε η μεταξύ τους απόσταση θα δίνεται από τη σχέση:

\( d={\frac {1}{2}}(f_{A}+f_{B}) \)

όπου \( f_{A} \) και \( f_{B} \) είναι οι εστιακές αποστάσεις των δύο φακών του προσοφθαλμίου

Αυτά τα προσοφθάλμια λειτουργούν καλά σε τηλεσκόπια με αντικειμενικό φακό πολύ μεγάλης εστιακής απόστασης (στον καιρό του Huygens τα χρησιμοποιούσαν σε διαθλαστικά τηλεσκόπια με ένα αντικειμενικό -όχι αχρωματικό φακό- μεγάλης εστιακής απόστασης, συμπεριλαμβανομένων των πολύ μεγάλης εστιακής απόστασης εναέριων τηλεσκοπίων). Αυτή η οπτική διάταξη θεωρείται πλέον ξεπερασμένη, καθώς στα σημερινά τηλεσκόπια, με μικρότερη εστιακή απόσταση αντικειμενικού φακού, το προσοφθάλμιο αυτό πάσχει από μικρη απόσταση παρατήρησης, μεγάλη παραμόρφωση του ειδώλου, χρωματικό σφάλμα και ένα πολύ στενό φαινόμενο οπτικό πεδίο. Δεδομένου ότι αυτά τα προσοφθάλμια είναι φθηνά στην κατασκευή, βρίσκονται συχνά σε φθηνά τηλεσκόπια και μικροσκόπια.[3]

Επειδή τα προσοφθάλμια Huygens δεν περιέχουν κόλλα για να κρατάει τα στοιχεία του φακού, οι χρήστες τηλεσκοπίων μερικές φορές τα χρησιμοποιούν για “ηλιακή προβολή”, π.χ. για να προβάλλουν μία εικόνα του ήλιου επάνω σε μία οθόνη. Για αυτή τη χρήση, άλλα προσοφθάλμια, με κολλημένα μεταξύ τους στοιχεία, μπορεί να καταστραφούν από την υπερθέρμασνη από το συγκεντρωμένο φως του ήλιου.

Προσοφθάλμιο Ramsden

Σχέδιο προσοφθαλμίου Ramsden.

Το προσοφθάλμιο Ramsden αποτελείται από δύο επιπεδόκυρτους φακούς κατασκευασμένους από το ίδιο γυαλί και με παρόμοιες εστιακές αποστάσεις, οι οποίοι βρίσκονται σε απόσταση μικρότερη από την εστιακή απόσταση του φακού-ματιού. Το προσοφθάλμιο αυτό σχεδιάστηκε από τον κατασκευαστή αστρονομικών και επιστημονικών οργάνων Τζέσσι Ράμσντεν (Jesse Ramsden) το 1782. Η απόσταση μεταξύ των δύο φακών ποικίλει μεταξύ των διαφόρων σχεδίων, αλλά τυπικά είναι κάπου μεταξύ 7/10 και 7/8 της εστιακής απόστασης του φακού-ματιού. Για μικρές αποστάσεις υπάρχει εγκάρσιο χρωματικό σφάλμα ενώ για μεγάλες αποστάσεις υπάρχει ο κίνδυνος, ο φακός-πεδίου να “αγγίξει” το εστιακό επίπεδο του φακού-ματιού, όταν χρησιμοποιείται από έναν παρατηρητή ο οποίος παρατηρεί ένα κοντινό φανταστικό είδωλο, όπως ένας μυωπικός παρατηρητής, ή ένα νεαρό άτομο το οποίο μπορεί να προσαρμόσει σε ένα κοντινό φανταστικό είδωλο. Αυτό είναι ένα σοβαρό πρόβλημα όταν χρησιμοποιείται σε οπτικό όργανο με μικρόμετρο (που είναι τοποθετημένο στο εστιακό επίπεδο του φακού-ματιού), καθώς μπορεί ο φακός πεδίου να “συγκρουστεί” με το μικρόμετρο και να οδηγήσει σε βλάβη του οργάνου. Η απόσταση μίας ακριβώς εστιακής απόστασης, επίσης δεν συνιστάται, δεδομένου ότι εστιάζει έντονα στη σκόνη του φακού-πεδίου. Οι δύο καμπύλες επιφάνειες είναι στραμμένες προς τα μέσα. Έτσι το εστιακό επίπεδο βρίσκεται έξω από το προσοφθάλμιο, επομένως είναι προσβάσιμο ώστε να τοποθετηθεί ένα σταυρόνημα, ή μία μικρομετρική κλίμακα. Επειδή χρειάζεται ακριβώς μία εστιακή απόσταση του φακού-πεδίου ως απόσταση μεταξύ των δύο φακών του προσοφθαλμίου για να διορθωθεί το εγκάρσιο χρωματικό σφάλμα, δεν είναι δυνατό να διορθωθεί εντελώς από τα χρωματικά σφάλματα αυτό το σχέδιο προσοφθαλμίου. Είναι λίγο καλύτερο από το προσοφθάλμιο του Huygens, αλλά εξακολουθεί να μη φτάνει τα σημερινά πρότυπα. Εξακολουθεί βέβαια, να είναι κατάλληλο για χρήση με οπτικά όργανα που λειτουργούν με κοντινές μονοχρωματικές πηγές φωτός, π.χ. πολωσίμετρα.
Προσοφθάλμιο Kellner ή «Αχρωματικός» προσοφθάλμιος φακός
Σχέδιο προσοφθαλμίου Kellner.

Σε ένα προσοφθάλμιο Kellner, αντί για τον επιπεδόκυρτο φακό-ματιού που χρησιμοποιείται στο προσοφθάλμιο Ramsden, υπάρχει ένας αχρωματικός φακός (διπλός) για να διορθώσει το απομένον εγκάρσιο χρωματικό σφάλμα. Ο Carl Kellner σχεδίασε αυτό το πρώτο σύγχρονο αχρωματικό προσοφθάλμιο το 1849,[4] το οποίο ονομάζεται επίσης και «αχρωματικός Ramsden». Οι προσοφθάλμιοι Kellner είναι ένα σχέδιο τριών φακών. Είναι φθηνοί και έχουν αρκετά καλή εικόνα μέχρι μία μεσαία μεγέθυνση, και είναι κατά πολύ ανώτεροι από τους προσοφθάλμιους Huygens ή Ramsden. Η απόσταση παρατήρησης είναι καλύτερη από αυτή του Huygens και χειρότερη από τα προσοφθάλμια Ramsden. .[5] Το μεγαλύτερο πρόβλημα των προσοφθαλμίων Kellner ήταν οι εσωτερικές ανακλάσεις, οι οποίες αντιμετωπίζονται σήμερα με ειδικές αντι-ανακλαστικές επιστρώσεις, οι οποίες τα καθιστούν οικονομικές λύσεις για μικρού και μεσαίου ανοίγματος τηλεσκόπια, δίνοντας τυπικό οπτικό πεδίο 40 έως 50 μοίρες.
Προσοφθάλμιο Plössl ή «Συμμετρικό» προσοφθάλμιο
Σχέδιο προσοφθαλμίου Plössl.

Το προσοφθάλμιο Plössl αποτελείται από δύο διπλούς φακούς, και σχεδιάστηκε από τον Georg Simon Plössl το 1860. Δεδομένου ότι τα δύο αυτά ζεύγη μπορούν να είναι πανομοιότυπα, το προσοφθάλμιο αυτό ονομάζεται και «συμμετρικό προσοφθάλμιο». .[6] Ο σύνθετος προσοφθάλμιος φακός Plössl, παρέχει ένα μεγάλο (>50ο) φαινόμενο οπτικό πεδίο. Αυτό τον καθιστά ιδανικό για πολλά είδη παρατηρήσεων, όπως ουράνια και πλανητική παρατήρηση. Το βασικό μειονέκτημα του προσοφθαλμίου Plössl είναι η μικρή απαιτούμενη απόσταση παρατήρησης σε σύγκριση με ένα ορθοσκοπικό, δεδομένου ότι η απόσταση παρατήρησης στο προσοφθάλμιο Plössl περιορίζεται περίπου στο 70-80 % της εστιακής απόστασης. Η απόσταση παρατήρησης είναι πιο κρίσιμη σε περιπτώσεις μικρής εστιακής απόστασης, μικρότερης των 10mm, οπότε και η παρατήρηση μπορεί να γίνει άβολη, ειδικά για αυτούς που φοράνε γυαλιά. Το προσοφθάλμιο Plössl ήταν ένα άγνωστο σχέδιο μέχρι το 1980, οπότε οι κατασκευαστές αστρονομικού εξοπλισμού άρχισαν να πωλούν επανασχεδιασμένες εκδόσεις του..[7] Σήμερα είναι ένα πολύ δημοφιλές προσοφθάλμιο στην αγορά της ερασιτεχνικής αστρονομίας [8], όπου το όνομα Plössl καλύπτει ένα φάσμα προσοφθαλμίων με τουλάχιστον τέσσερα οπτικά στοιχεία. Αυτό το προσοφθάλμιο είναι από τα πιο ακριβά στην κατασκευή, λόγω της ποιότητας του γυαλιού που απαιτεί, αλλά και της ανάγκης για πολύ καλή ένωση κυρτών και κοίλων φακών, για να αποφευχθούν οι εσωτερικές ανακλάσεις. Εξαιτίας αυτού, η ποιότητα μεταξύ διαφορετικών προσοφθαλμίων Plössl ποικίλλει. Υπάρχουν τεράστιες διαφορές μεταξύ των φθηνών προσοφθαλμίων Plössl με απλές αντιανακλαστικές επιστρώσεις και αυτών με άρτια κατασκευή.
Ορθοσκοπικό προσοφθάλμιο ή προσοφθάλμιο «Abbe»
Σχέδιο ορθοσκοπικού προσοφθαλμίου.

Το τεσσάρων στοιχείων ορθογραφικό προσοφθάλμιο αποτελείται από έναν επιπεδόκυρτο φακό-ματιού και μία αμφίκυρτη τριπλέτα (τρεις φακοί κολλημένοι μεταξύ τους) στο ρόλο ενός αχρωματικού φακού-πεδίου. Αυτό δίνει στον προσοφθάλμιο μια σχεδόν τέλεια ποιότητα ειδώλου και καλή απαιτούμενη απόσταση παρατήρησης, αλλά ένα στενό φαινόμενο οπτικό πεδίο (περίπου 40°-45°). Εφευρέθηκε από τον :Ernst Abbe το 1880.[9] Λέγεται «ορθοσκοπικό» ή «ορθογραφικό», λόγω της μικρής παραμόρφωσης που προσφέρει, και μερικές φορές αποκαλείται «ορθό» ή «Abbe». Μέχρι την έλευση των πολλαπλών επιστρώσεων και της δημοτικότητας του Plössl, το ορθοσκοπικό προσοφθάλμιο ήταν το πιο δημοφιλές σχέδιο για προσοφθάλμια τηλεσκοπίου. Ακόμα και σήμερα αυτά τα προσοφθάλμια θεωρούνται καλά για πλανητικές και σεληνιακές παρατηρήσεις. Εξαιτίας της χαμηλής παραμόρφωσης που παρέχουν και της προκαλούμενης υποκειμενικής οπτικής παραμόρφωσης (globe effect), είναι λιγότερο κατάλληλα για εφαρμογές που απαιτούν υπερβολική οριζόντια περιστροφή του οργάνου.
Μονοκεντρικό προσοφθάλμιο
Σχέδιο μονοκεντρικού προσοφθαλμίου.

Ένας μονοκεντρικός προσοφθάλμιος είναι ένας αχρωματικός τριπλός φακός (τριπλέτα) με δύο κομμάτια στεφανύαλου (με μικρό δείκτη διάθλασης και μικρή διασπορά) στις δύο πλευρές ενός πυριτίαλου (με μεγάλο δείκτη διάθλασης και μεγάλη διασπορά). Τα στοιχεία έχουν μεγάλο πάχος και κυρτότητα, και οι επιφάνειές τους έχουν ένα κοινό κέντρο, δίνοντάς του το όνομα «μονοκεντρικό» . Εφευρέθηκε από τον Adolf Steinheil περίπου το 1883.[10] Αυτό το σχέδιο προσοφθαλμίου, όπως τα σχέδια προσοφθάλμιων του Robert Tolles, Charles S. Hastings, και Ε. Wilfred Taylor,[11] είναι απαλλαγμένο από τις αντανακλάσεις που προκαλούν “παραμένοντα είδωλα” και δίνει ένα φωτεινό, με μεγάλη αντίθεση είδωλο, κάτι το οποίο το έκανε πολύ ελκυστικό όταν εφευρέθηκε (πριν τις αντιανακλαστικές επιστρώσεις).[12] Έχει ένα στενό οπτικό πεδίο, περίπου 25°[13] και είναι δημοφιλές για πλανητικές παρατηρήσεις.[14]

Το 2013, ανακοινώθηκε η κατασκευή ενός μονοκεντρικού φακού φωτογραφικής μηχανής. Ο όγκος του φακού αυτού είναι μόνο το ένα δέκατο του όγκου ενός συμβατικού ευρυγώνιου φακού. Το σύστημα αποτελείται από δύο θολωτούς γυάλινους φλοιούς που ενώνονται μεταξύ τους έτσι ώστε οι κοίλες επιφάνειές τους να είναι προς τα μέσα, δημιουργώντας έναν μονό φακό που μοιάζει με ένα μία απόλυτα στρογγυλή γυάλινη μπίλια. Τέτοιοι φακοί έχουν ένα ευρύ οπτικό πεδίο και συλλαμβάνουν εικόνες υψηλής ανάλυσης. Επιπλέον, οι φακοί αυτοί παράγουν λιγότερη παραμόρφωση από τους παραδοσιακούς ευρυγώνιους φακούς “μάτι του ψαριού” (fish-eye). Μία συστοιχία οπτικών ινών, συνδέει την πίσω κυρτή επιφάνεια του φακού με τον αισθητήρα της κάμερας. Το σύστημα μπορεί και εστιάζει αντικείμενα σε απόσταση από 0.5 έως 500 μέτρα με υψηλή ανάλυση.[15]
Προσοφθάλμιο Erfle
Σχέδιο προσοφθαλμίου Erfle.

Το προσοφθάλμιο Erfle είναι ένα προσοφθάλμιο 5 στοιχείων, που αποτελείται από δύο αχρωματικούς φακούς με επιπλέον φακούς ανάμεσά τους. Εφευρέθηκαν από τον Heinrich Erfle το 1921 κατά τη διάρκεια του πρώτου παγκοσμίου πολέμου για στρατιωτικούς σκοπούς. Είναι μια λογική εξέλιξη των προσοφθαλμίων τεσσάρων στοιχείων, όπως του Plössls, για να επιτευχθούν ευρύτερα πεδία. Τα προσοφθάλμια Erfle έχουν σχεδιαστεί να έχουν ευρύ οπτικό πεδίο (περίπου 60º), αλλά δεν μπορούν να έχουν μεγάλη ισχύ επειδή πάσχουν από αστιγματισμό και “παραμένοντα είδωλα”. Ωστόσο, εάν έχουν επιστρώσεις και μικρή ισχύ (εστιακά μήκη 20 mm και άνω) είναι αποδεκτά, και στα 40 mm μπορούν να είναι εξαιρετικά. Τα προσοφθάλμια Erfles είναι πολύ δημοφιλή επειδή έχουν μεγάλους φακούς-ματιού, καλή απόσταση παρατήρησης και είναι πολύ άνετα στη χρήση.

Προσοφθάλμιο König
Σχέδιο προσοφθαλμίου König.

Το προσοφθάλμιο König έχει έναν κυρτό μηνίσκο διπλό φακό και έναν επιπεδόκυρτο (η αναφερόμενη επίπεδη επιφάνεια είναι λίγο κυρτή) μονό φακό. Οι έντονα κυρτές επιφάνειες του διπλού και του μονού φακού είναι σχεδόν σε επαφή. Ο διπλός φακός έχει την κοίλη επιφάνειά του στραμμένη προς την πηγή φωτός και ο μονός έχει τη σχεδόν επίπεδη (ελαφρώς κυρτή) επιφάνειά του στραμμένη προς το μάτι. Σχεδιάστηκε το 1915 από τον Γερμανό οπτικό Albert König (1871-1946) ως ένας απλοποιημένο προσοφθάλμιο Abbe. Ο σχεδιασμός επιτρέπει την υψηλή μεγέθυνση με εξαιρετικά μεγάλη απόσταση παρατήρησης (η μεγαλύτερη απόσταση παρατήρησης αναλογικά με την εστιακή απόσταση οποιουδήποτε σχεδίου προσοφθαλμίου πριν από το προσοφθάλμιο Nagler, το 1979). Το οπτικό πεδίο των περίπου 55° το καθιστά σε επιδόσεις παρόμοιο με το προσοφθάλμιο Plossl, με το πλεονέκτημα ότι απαιτεί έναν λιγότερο φακό. Σύγχρονες εκδόσεις του Königs χρησιμοποιούν βελτιωμένο γυαλί, ή προσθέτουν περισσότερους φακούς, ομαδοποιημένους σε διάφορους συνδυασμούς διπλών και μονών φακών. Η πιο συνήθης παραλλαγή είναι η πρόσθεση ενός συγκλίνοντα κυρτού μηνίσκου φακού πριν από τον διπλό, με την κοίλη επιφάνειά του προς την πηγή του φωτός και την κυρτή επιφάνεια στραμμένη προς το διπλό φακό. Τα σύγχρονα βελτιωμένα σχέδια προσοφθαλμίου Königs έχουν συνήθως οπτικό πεδίο 60° -70°.
Προσοφθάλμιο RKE
Σχέδιο προσοφθαλμίου RKE.

Το προσοφθάλμιο RKE έχει έναν αχρωματικό φακό-πεδίου και έναν αμφίκυρτο φακό-ματιού και αποτελεί μία ανεστραμμένη παραλλαγή του προσοφθαλμίου Kellner ή μία παραλλαγή του προσοφθαλμίου König με μεγαλύτερη απόσταση μεταξύ των φακών. Σχεδιάστηκε από τον Dr. David Rank για την Edmund Scientific Corporation, που το εμπορεύτηκε ολόκληρη τη δεκαετία του 1960 και στις αρχές της δεκαετίας του 1970. Αυτό το σχέδιο παρέχει ελαφρώς ευρύτερο οπτικό πεδίο από την κλασική σχεδίαση του προσοφθαλμίου Kellner.

Προσοφθάλμια Nagler
Σχέδιο προσοφθαλμίου Nagler τύπου 2.

Το προσοφθάλμιο Nagler εφευρέθηκε από τον Albert Nagler και κατοχυρώθηκε με δίπλωμα ευρεσιτεχνίας το 1979. Είναι ένα σχέδιο βελτιστοποιημένο για αστρονομικά τηλεσκόπια, ώστε να παρέχει ένα εξαιρετικά ευρύ οπτικό πεδίο (82°), και που έχει καλή διόρθωση του αστιγματισμού και άλλων σφαλμάτων. Το Ethos, ένα σχέδιο που παρουσιάστηκε το 2007, με ένα εξαιρετικά ευρύ οπτικό πεδίο, αναπτύχθηκε κυρίως από τον Paul Dellechiaie υπό την καθοδήγηση του Albert Nagler στο Tele Vue Optics και παράγει φαινόμενο οπτικό πεδίο 100° -110° AFOV.[16] [17] Αυτό επιτυγχάνεται με τη χρήση γυαλιού με υψηλό δείκτη διάθλασης και μέχρι και οκτώ οπτικά στοιχεία σε τέσσερις ή πέντε ομάδες. Υπάρχουν πέντε παρόμοια σχέδια που ονομάζονται Nagler: Nagler τύπου 2, Nagler τύπου 4, Nagler τύπου 5, και Nagler τύπου 6. Ένα νεότερο σχέδιο, το Delos, είναι ένα τροποποιημένο σχέδιο Ethos με οπτικό πεδίο “μόνο” 72°, αλλά με μεγάλη απόσταση παρατήρησης (20mm).
Σχέδια προσοφθαλμίων τύπου Nagler.

Ο αριθμός των στοιχείων στα προσοφθάλμια Nagler, τα κάνει να φαίνονται πολύπλοκα, αλλά η ιδέα του σχεδιασμού είναι αρκετά απλή. Κάθε Nagler έχει έναν αποκλίνοντα διπλό φακό πεδίου, ο οποίος αυξάνει τη μεγέθυνση, και ακολουθείται από πολλές ομάδες από συγκλίνοντες φακούς. Οι συγκλίνουσες ομάδες, που θεωρούνται ξεχωριστές από την πρώτη αποκλίνουσα ομάδα, συνδυάζονται για να έχουν μεγάλη εστιακή απόσταση, και σχηματίζουν έναν συγκλίνοντα φακό. Αυτό επιτρέπει στο σχέδιο να επωφελείται από τις καλές ιδιότητες των φακών χαμηλής ισχύος. Στην πραγματικότητα, ένα προσοφθάλμιο Nagler είναι μια έκδοση ενός φακού Barlow σε συνδυασμό με ένα μεγάλης εστιακής απόστασης προσοφθάλμιο. Αυτό το σχέδιο έχει αντιγραφεί ευρέως σε άλλα προσοφθάλμια ευρέως πεδίου ή με μεγάλη απόσταση παρατήρησης. Το κύριο μειονέκτημα των προσοφθάλμιων Nagler είναι το βάρος τους. Οι εκδόσεις με μεγάλη εστιακή απόσταση υπερβαίνουν το 0,5 kg, το οποίο είναι αρκετό για να προκαλέσει ανισορροπία σε μικρά τηλεσκόπια. Ένα άλλο μειονέκτημα είναι το υψηλό κόστος αγοράς, με τις υψηλές τιμές των Nagler να είναι συγκρίσιμες με το κόστος ενός μικρού τηλεσκοπίου. Ως εκ τούτου, αυτά τα προσοφθάλμια θεωρούνται από πολλούς ερασιτέχνες αστρονόμους ως πολυτέλεια.[18]
Παραπομπές

Clark, Roger N. (1990). Visual astronomy of the deep sky. Cambridge: Cambridge University Press. σελ. 29. ISBN 0521361559.
Philip S. Harrington, "Star Ware", page 181
copes/eyepieces.htm astro-tom.com -Huygens[νεκρός σύνδεσμος]
Jack Kramer. «The Good Old Plossl Eyepiece». The Lake County Astronomical Society (Lake County, Illinois). Ανακτήθηκε στις 25 Δεκεμβρίου 2009.
«"Military handbook MIL-HDBK-141", chapter 14» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 6 Αυγούστου 2010. Ανακτήθηκε στις 10 Μαΐου 2015.
Steven R. Coe, Nebulae and how to observe them, p. 9.
Philip S. Harrington, Star Ware: The Amateur Astronomer's Guide, page 183
John W. McAnally, Jupiter and How to Observe It - Page 156
«astro-tom.com -Huygens». Αρχειοθετήθηκε από το πρωτότυπο στις 22 Απριλίου 2015. Ανακτήθηκε στις 10 Μαΐου 2015.
Comments on Gary Seronik's TMB Monocentric Eyepiece test report Sky & Telescope August 2004 pp98-102 by Chris Lord
Handbook of Optical Systems, Survey of Optical Instruments by Herbert Gross, Hannfried Zügge, Fritz Blechinger, Bertram Achtner, page 110
"Demystifying Multicoatings" by Rodger Gordon Αρχειοθετήθηκε 2008-05-18 στο Wayback Machine. (Originally appeared in TPO Volume 8, Issue 4. 1997)
Martin Mobberley, "Astronomical Equipment for Amateurs", page 71
Gerald North, "Advanced Amateur Astronomy", page 36
Tiny round wide-angle lens outperforms its bigger brothers
http://www.televue.com/engine/TV3_page.asp?id=20&Tab=_dev
Daniel Mounsey, Cloudynights review of Ethos, www.cloudynights.com

Martin C. Cohen . Televue: A Historical Perspective, company7.com

[1]
Hecht, Eugene, Optics, 4nd Ed, Addison Wesley, 2002
A. E. Conrady, Applied Optics and Optical Design, Volume I. Oxford 1929.
R. Kingslake, Lens Design Fundamentals. Academic Press 1978.
H. Rutten and M. van Venrooij, Telescope Optics. Willmann-Bell 1988, 1989. ISBN 0-943396-18-2.
P. S. Harrington, Star Ware: An Amateur Astronomer's Guide to Choosing, Buying, and Using Telescopes and Accessories: Fourth Edition. John Wiley & Sons, Inc.

Εξωτερικοί Σύνδεσμοι

EYEPIECE EVOLUTION
A. Nagler - United States Patent US4286844
A. Nagler - United States Patent US4747675
A. Nagler - United States Patent US4525035
A. Nagler - Finder scope for use with astronomical telescopes
The evolution of the astronomical eyepiece, in-depth discussion of various design and theoretical background
John Savard's Eyepiece Page, a list of eyepieces with some details of their construction.
Peoria Astronomical Society Eyepiece page, a list of eyepieces with some details of their construction.
Astro-Tom.com Eyepiece Article, a list of eyepieces with some details of their construction.
Eyepiece Simulator, demonstrates the effect of eyepieces
United States Patent Office: Ultra wide ocular NAGLER.[νεκρός σύνδεσμος]
Basic guide to eyepieces, covers the relationship between focal length of eyepiece and telescope.
Guide to different eyepieces with descriptions of their use.

Εγκυκλοπαίδεια Φυσικής

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org και el.wiktionary.org/. Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License