Μέθοδος των εικονικών φορτίων
αγγλικά : Method of image charges
γαλλικά :
γερμανικά :
Η Μέθοδος των εικονικών φορτίων (επίσης γνωστή ως μέθοδος κατοπτρικών φορτίων ) είναι ένα βασικό εργαλείο επίλυσης προβλημάτων στην ηλεκτροστατική. Το όνομα προέρχεται από την αντικατάσταση ορισμένων στοιχείων στην αρχική διάταξη με φανταστικά φορτία, τα οποία αναπαράγουν τις οριακές συνθήκες του προβλήματος (βλ. Συνθήκες ορίου Dirichlet ή συνθήκες ορίου Neumann).
Η εγκυρότητα της Μεθόδου των εικονικών φορτίων βασίζεται σε συνέπεια του θεώρηματος μοναδικότητας, το οποίο δηλώνει ότι το ηλεκτρικό δυναμικό σε έναν όγκο V καθορίζεται μοναδικά εάν είναι γνωστή τόσο η πυκνότητα φόρτισης σε ολόκληρη την περιοχή όσο και η τιμή του ηλεκτρικού δυναμικού σε όλα τα όρια . Εναλλακτικά, η εφαρμογή αυτού του επακόλουθου στη διαφορική μορφή του νόμου Gauss δείχνει ότι σε έναν τόμο V που περιβάλλεται από αγωγούς και περιέχει μια καθορισμένη πυκνότητα φορτίου ρ, το ηλεκτρικό πεδίο προσδιορίζεται μοναδικά εάν δοθεί το συνολικό φορτίο σε κάθε αγωγό. Διαθέτοντας γνώση είτε του ηλεκτρικού δυναμικού είτε του ηλεκτρικού πεδίου και των αντίστοιχων οριακών συνθηκών μπορούμε να ανταλλάξουμε την κατανομή φορτίου που εξετάζουμε για μία με μια διαμόρφωση που είναι πιο εύκολο να αναλυθεί, αρκεί να ικανοποιεί την εξίσωση του Poisson στην περιοχή ενδιαφέροντος και να υποθέτει τις σωστές τιμές στα όρια.
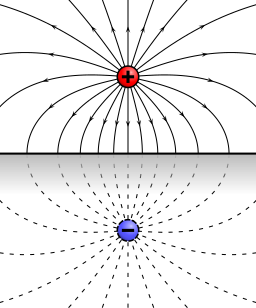
Το απλούστερο παράδειγμα της μεθόδου των εικονικών φορτίων είναι αυτή σημειακού φορτίου q, που βρίσκεται στο (0, 0, a) πάνω από μια άπειρη γειωμένη (δηλαδή: V = 0 ) αγώγιμη πλάκα στο επίπεδο xy. Για να απλοποιήσουμε αυτό το πρόβλημα, προσθέτουμε ενα κατοπτρικό φορτίο –q, που βρίσκεται στο (0, 0, - a) . Αυτή η διάταξη θα παράγει το ίδιο ηλεκτρικό πεδίο σε οποιοδήποτε σημείο για το οποίο z> 0 (δηλαδή πάνω από την αγώγιμη πλάκα) και ικανοποιεί την οριακή συνθήκη ότι το δυναμικό κατά μήκος της πλάκας πρέπει να είναι μηδέν. Αυτή η κατάσταση είναι ισοδύναμη με την αρχική και έτσι η δύναμη στο πραγματικό φορτίο μπορεί τώρα να υπολογιστεί με το νόμο του Coulomb μεταξύ των δύο σημειακών φορτίων.
Το δυναμικό σε οποιοδήποτε σημείο του διαστήματος, λόγω αυτών των δύο σημειακών φορτίων + q στο + a και -q at -a στον άξονα z, δίνεται σε κυλινδρικές συντεταγμένες ως
V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}}+{\frac {-q}{{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}}\right)\,
Η πυκνότητα επιφανειακού φορτίου στο γειωμένο επίπεδο δίνεται συνεπώς από
\sigma =-\epsilon _{0}{\frac {\partial V}{\partial z}}{\Bigg |}_{{z=0}}={\frac {-qa}{2\pi \left(\rho ^{2}+a^{2}\right)^{{3/2}}}}
Επιπλέον, το συνολικό φορτίο που προκαλείται στο αγώγιμο επίπεδο θα είναι το ολοκλήρωμα της πυκνότητας φόρτισης σε ολόκληρο το επίπεδο, οπότε:
{\begin{aligned}Q_{t}&=\int _{0}^{{2\pi }}\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta \\[6pt]&={\frac {-qa}{2\pi }}\int _{0}^{{2\pi }}d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{{3/2}}}}\\[6pt]&=-q\end{aligned}}
Το συνολικό φορτίο που προκαλείται στο επίπεδο αποδεικνύεται οτί είναι απλά –q. Αυτό μπορεί επίσης να φανεί από τον νόμο του Gauss, δεδομένου ότι το δίπολο πεδίο μειώνεται με τον κύβο της απόστασης σε μεγάλες αποστάσεις, και συνεπώς η συνολική ροή του πεδίου σε μια απείρως μεγάλη σφαίρα εξαφανίζεται.
Επειδή τα ηλεκτρικά πεδία ικανοποιούν την αρχή της υπέρθεσης, ένα αγώγιμο επίπεδο κάτω από πολλαπλά σημειακά φορτία μπορεί να υπολογιστεί με την βοήθεια κατοπτρικά φορτίων για κάθε πραγματικό φορτίο.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org και el.wiktionary.org/. Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License