Αεροτομή
αγγλικά : Airfoil
γαλλικά :
γερμανικά :
Μια αεροτομή είναι μορφή πτέρυγας, λεπίδας (ενός έλικα, ενός στροφείου ή ενός στροβίλου) ή ιστίου.
Ένα σώμα σχήματος αεροτομής που κινείται μέσα σε ένα ρευστό παράγει αεροδυναμική δύναμη. Η συνιστώσα αυτής της δύναμης η κάθετη προς την κατεύθυνση της κίνησης ονομάζεται άντωση. Η συνιστώσα η παράλληλη προς την κατεύθυνση της κίνησης ονομάζεται οπισθέλκουσα. Οι αεροτομές που χρησιμοποιούνται σε αεροσκάφη υποηχητικής πτήσης έχουν χαρακτηριστικό σχήμα με στρογγυλεμένο πρόσθιο άκρο, και οξεία άκρη, και συχνά διαθέτουν συμμετρική καμπυλότητα των άνω και κάτω επιφανειών. Φύλλα παρόμοιας λειτουργίας σχεδιασμένα για το νερό ονομάζονται υδροτομές.
Παραδείγματα αεροτομών στη φύση και σε διάφορα οχήματα. Αν και δεν πρόκειται για αεροτομή με την αυστηρή έννοια, τα πτερύγια των δελφινιών υπακούν στους ίδιους νόμους σε διαφορετικό μέσο.
Η άντωση μιας αεροτομής είναι κατά κύριο λόγο αποτέλεσμα της γωνίας προσβολής και του σχήματος της. Όταν στρέφεται υπό κατάλληλη γωνία, η αεροτομή αποκλίνει τον εισερχόμενο αέρα (για αεροσκάφη σταθερής πτέρυγας, μια κινούμενη προς τα κάτω δύναμη), με αποτέλεσμα να ασκείται δύναμη στην αεροτομή προς την αντίθετη κατεύθυνση της απόκλισης. Αυτή η δύναμη είναι γνωστή ως αεροδυναμική δύναμη και μπορεί να αναλυθεί σε δύο συνιστώσες: άντωση και οπισθέλκουσα. Τα περισσότερα σχήματα αεροτομών χρειάζονται θετική γωνία προσβολής για να δημιουργήσουν άντωση, αλλά οι καμπύλες αεροτομές μπορούν να δημιουργήσουν άντωση με μηδενική γωνία προσβολής. Αυτή η «περιστροφή» του αέρα στην περιοχή της αεροτομής δημιουργεί καμπύλες ροές, με αποτέλεσμα τη χαμηλότερη πίεση στη μία πλευρά και την υψηλότερη πίεση στην άλλη. Αυτή η διαφορά πίεσης συνοδεύεται από διαφορά ταχύτητας, μέσω του Νόμου του Μπερνούλι, έτσι ώστε το προκύπτον πεδίο ροής γύρω από την αεροτομή να έχει υψηλότερη μέση ταχύτητα στην άνω επιφάνεια από ότι στην κάτω επιφάνεια. Η δύναμη άντωσης μπορεί να σχετίζεται άμεσα με τη μέση διαφορά ταχύτητας άνω/κάτω μέρους χωρίς υπολογισμό της πίεσης χρησιμοποιώντας την έννοια της κυκλοφορίας και το θεώρημα Κούτα-Γιουκόφσκι.[1][2][3][4]
Επισκόπηση
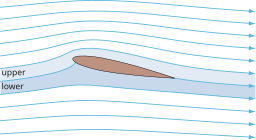
Ροές αέρα γύρω από αεροτομή NACA 0012 με μέτρια γωνία προσβολής
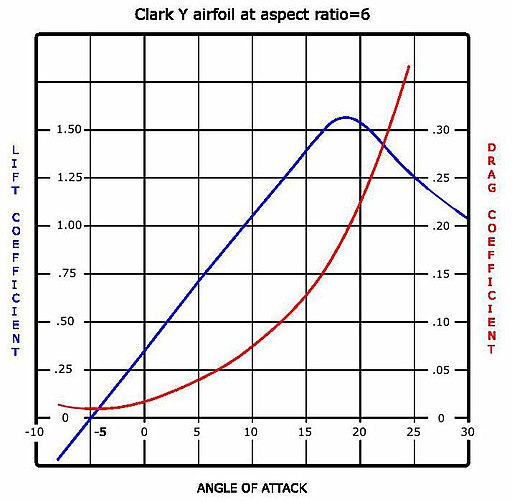
Καμπύλες άντωσης και οπισθέλκουσας για μια συνηθισμένη αεροτομή
Τα πτερύγια ενός αεροσκάφους σταθερών πτερύγων, οριζόντιοι και κάθετοι σταθεροποιητές κατασκευάζονται με διατομές σε σχήμα αεροτομής, όπως και τα πτερύγια του στροφείου του ελικοπτέρου. Οι αεροτομές βρίσκονται επίσης σε έλικες, ανεμιστήρες, συμπιεστές και στροβίλους. Τα ιστία είναι επίσης αεροτομές και οι υποθαλάσσιες επιφάνειες των πλοίων, όπως η καρίνα, είναι παρόμοιες σε διατομή και λειτουργούν σύμφωνα με τις ίδιες αρχές με τις αεροτομές. Τα υδρόβια και πτηνά όντα και ακόμη και πολλά φυτά και άμισχοι οργανισμοί χρησιμοποιούν αεροτομές/υδροτομές: συνηθισμένα παραδείγματα είναι τα φτερά των πουλιών και τα σώματα των ψαριών. Μια πτέρυγα σχήματος αεροτομής μπορεί να δημιουργήσει καθοδική δύναμη σε αυτοκίνητο ή άλλο μηχανοκίνητο όχημα, βελτιώνοντας την πρόσφυση.
Οποιοδήποτε αντικείμενο με γωνία προσβολής μέσα σε κινούμενο ρευστό, όπως μία επίπεδη πλάκα, ένα κτίριο ή ένα κατάστρωμα γέφυρας, θα παράγει αεροδυναμική δύναμη (η οποία ονομάζεται άντωση) κάθετη προς τη ροή. Οι αεροτομές είναι πιο αποτελεσματικά ανυψωτικά σχήματα, ικανά να παράγουν περισσότερη άντωση (μέχρι ένα σημείο) και να παράγουν άντωση με λιγότερη οπισθέλκουσα.
Στα δεξιά παρουσιάζεται μια καμπύλη άντωσης και οπισθέλκουσας που λαμβάνεται από δοκιμή σε αεροδυναμική σήραγγα. Η καμπύλη αντιπροσωπεύει μια αεροτομή με θετική καμπύλη, ώστε να δημιουργείται άντωση υπό μηδενική γωνία προσβολής. Με μεγαλύτερη γωνία προσβολής, η άντωση αυξάνεται με μία σχεδόν γραμμική σχέση, που ονομάζεται κλίση της καμπύλης ανύψωσης. Στις περίπου 18 μοίρες αυτή αεροτομή σταματά, και η άντωση μειώνεται τάχιστα πέρα από αυτό. Η πτώση της άντωσης μπορεί να εξηγηθεί από τη δράση της οριακής στρώσης της ανώτερης επιφάνειας, η οποία διαχωρίζει και πυκνώνει σε μεγάλο βαθμό πάνω από την ανώτερη επιφάνεια κατά και πέρα από τη γωνία διακοπής. Η μετατόπιση του πυκνού οριακού στρώματος αλλάζει το αποτελεσματικό τμήμα της αεροτομής, μειώνοντας ιδίως την αποτελεσματική καμπύλη του, η οποία τροποποιεί το συνολικό πεδίο ροής έτσι ώστε να μειώνεται η κυκλοφορία και η άντωση. Το παχύτερο οριακό στρώμα προκαλεί επίσης μεγάλη αύξηση της οπισθέλκουσας πίεσης, έτσι ώστε η συνολική οπισθέλκουσα να αυξάνεται απότομα κοντά στο σημείο απώλειας της ισορροπίας.
Ο σχεδιασμός αεροτομών είναι μια σημαντική πτυχή της αεροδυναμικής. Διαφορετικές αεροτομές εξυπηρετούν διαφορετικές καταστάσεις πτήσης. Οι ασύμμετρες αεροτομές μπορούν να δημιουργήσουν άντωση με μηδενική γωνία προσβολής, ενώ μια συμμετρική αεροτομή ταιριάζει καλύτερα σε πτήσεις συχνής αντιστροφής όπως σε ένα αεροβατικό αεροπλάνο. Στην περιοχή των πηδαλίων κλίσης και κοντά σε ένα ακροπτερύγιο μπορεί να χρησιμοποιηθεί μια συμμετρική αεροτομή για να αυξήσει το εύρος των γωνιών προσβολής για να αποφευχθεί η περιστροφή. Έτσι μπορεί να χρησιμοποιηθεί ένα μεγάλο εύρος γωνιών χωρίς διαχωρισμό οριακών στρωμάτων. Οι υποηχητικές αεροτομές έχουν μια κυρτή αιχμή, η οποία σε φυσικές καταστάσεις δεν είναι ευαίσθητη στη γωνία προσβολής. Ωστόσο, η διατομή δεν είναι αυστηρά κυκλική: η ακτίνα καμπυλότητας αυξάνεται πριν επιτευχθεί το μέγιστο πάχος ώστε να ελαχιστοποιηθεί η πιθανότητα διαχωρισμού οριακών στρωμάτων. Αυτό επιμηκύνει το πτερύγιο και μετακινεί το σημείο μέγιστου πάχους πίσω από την πρόσθια άκρη.
Οι υπερηχητικές αεροτομές είναι πολύ πιο γωνιακές σε σχήμα και μπορούν να έχουν μια πολύ αιχμηρή αιχμή, η οποία είναι πολύ ευαίσθητη στη γωνία προσβολής. Μια υπερκρίσιμη αεροτομή έχει το μέγιστο πάχος της κοντά στην αιχμή που έχει μεγάλο μήκος για να προσβάλει αργά την υπερηχητική ροή στις υποηχητικές ταχύτητες. Γενικά, τέτοιες διηχητικές αεροτομές καθώς και οι υπερηχητικές αεροτομές έχουν μικρή καμπύλη για να μειωθεί η απόκλιση οπισθέλκουσας. Οι σύγχρονες πτέρυγες αεροσκαφών μπορεί να έχουν διαφορετικά τμήματα αεροτομής κατά μήκος του εύρους των πτερύγων, με τη καθεμία βελτιστοποιημένη για τις συνθήκες σε κάθε τμήμα της πτέρυγας.
Οι κινητές συσκευές μεγάλης άντωσης και τα πτερύγια τοποθετούνται σε αεροτομές σχεδόν σε κάθε αεροσκάφος. Ένα πτερύγιο της ακμής λειτουργεί παρόμοια με ένα πηδάλιο κλίσης. Ωστόσο, σε αντίθεση με ένα πηδάλιο κλίσης, μπορεί να αποσπαστεί εν μέρει στην πτέρυγα αν δεν χρησιμοποιηθεί.
Μια πτέρυγα ελασματώδους ροής έχει μέγιστο πάχος στη μέση γραμμή καμπύλης. Η ανάλυση των εξισώσεων Νάβιερ-Στόουκς σε γραμμική κατάσταση δείχνει ότι μια αρνητική κλίση πίεσης κατά μήκος της ροής έχει το ίδιο αποτέλεσμα με τη μείωση της ταχύτητας. Έτσι με τη μέγιστη καμπύλη στη μέση, είναι δυνατή η διατήρηση μιας ελασματοειδούς ροής πάνω από το μεγαλύτερο μέρος της πτέρυγας σε υψηλότερη ταχύτητα πλεύσης. Ωστόσο, οποιαδήποτε επιφανειακή μόλυνση θα διαταράξει τη ελασματώδη ροή, καθιστώντας την τυρβώδη. Για παράδειγμα, με σταγόνες βροχής στην πτέρυγα, η ροή θα είναι τυρβώδης. Υπό ορισμένες συνθήκες, τα υπολείμματα των εντόμων σε κάποια πτέρυγα θα προκαλέσουν επίσης απώλεια μικρών περιοχών ελασματώδους ροής.[5] Πριν από την έρευνα της NASA στη δεκαετία του 1970 και του 1980, η κοινότητα του αεροναυπηγικού σχεδιασμού αντιλήφθηκε μέσα από τις προσπάθειες εφαρμογής στην εποχή του Β΄ Παγκοσμίου Πολέμου ότι τα σχέδια της πτέρυγας με ελασματώδη ροή δεν ήταν πρακτικά χρησιμοποιώντας κοινές κατασκευαστικές ανεκτικότητες και επιφανειακές ατέλειες. Αυτή η πεποίθηση άλλαξε αφού αναπτύχθηκαν νέες μέθοδοι κατασκευής με σύνθετα υλικά (π.χ. ίνες γραφίτη) και εισήχθησαν μηχανικές μέθοδοι. Η έρευνα της NASA τη δεκαετία του 1980 αποκάλυψε την πρακτικότητα και τη χρησιμότητα του σχεδιασμού πτερύγων με ελασματώδη ροή και άνοιξε το δρόμο για εφαρμογές ελασματώδους ροής σε σύγχρονες πρακτικές επιφάνειες αεροσκαφών, από υποηχητικά αεροσκάφη γενικής αεροπορίας έως μεγάλα μεταγωγικά υπερηχητικά αεροσκάφη.[6]
Έχουν δημιουργηθεί σχεδιαγράμματα για τον καθορισμό των αεροτομών - ένα παράδειγμα είναι το σύστημα NACA. Χρησιμοποιούνται επίσης διάφορα συστήματα δημιουργίας αεροτομών. Ένα παράδειγμα αεροτομής γενικού σκοπού που βρίσκει ευρεία εφαρμογή και προηγήθηκε του συστήματος NACA είναι το Clark-Y. Σήμερα, οι αεροτομές μπορούν να σχεδιαστούν για συγκεκριμένες λειτουργίες χρησιμοποιώντας αντίστροφα προγράμματα σχεδιασμού όπως τα PROFOIL, XFOIL και AeroFoil.[7]
Ορολογία αεροτομών
Ονοματολογία των αεροτομών
Παρακάτω παρουσιάζονται διάφοροι ορισμοί σχετικά με τις αεροτομές:[8]
Η επιφάνεια αναρρόφησης (ή αλλιώς άνω επιφάνεια) συσχετίζεται με υψηλότερη ταχύτητα και χαμηλότερη στατική πίεση.
Η επιφάνεια πίεσης (ή αλλιώς κατώτερη επιφάνεια) έχει συγκριτικά υψηλότερη στατική πίεση από την επιφάνεια αναρρόφησης. Η κλίση της πίεσης μεταξύ αυτών των δύο επιφανειών συμβάλλει στη δύναμη άντωσης που δημιουργείται για μια δεδομένη αεροτομή.
Η γεωμετρία της αεροτομής περιγράφεται με διάφορους όρους:
Η αιχμή είναι το σημείο στο μπροστινό μέρος της αεροτομής που έχει μέγιστη καμπυλότητα (ελάχιστη ακτίνα).[9]
Η οπίσθια άκρη ορίζεται ως το σημείο μέγιστης καμπυλότητας στο πίσω μέρος της αεροτομής.
Η χορδή είναι η ευθεία που συνδέει την αιχμή με το οπίσθιο άκρο. Το μήκος της χορδής, ή απλά χορδή, c c, είναι το μήκος του άξονα της χορδής, το οποίο αποτελεί διάσταση αναφοράς για το τμήμα της αεροτομής.
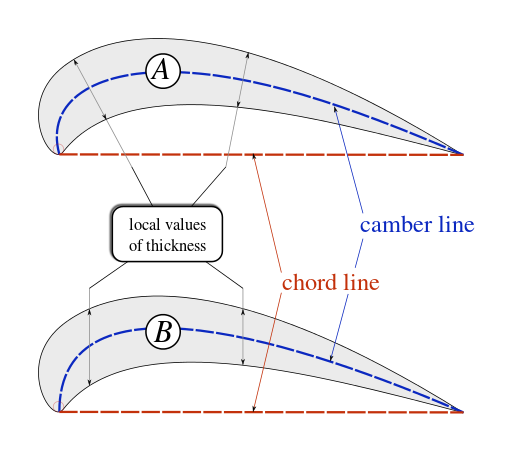
Διαφορετικοί ορισμοί του πάχους της αεροτομής
Αεροτομή για ακροπτέρυγα (PSU 90-125WL)
Το σχήμα της αεροτομής ορίζεται με τις ακόλουθες γεωμετρικές παραμέτρους:
Η μέση γραμμή καμπύλης ή μέση γραμμή είναι ο τόπος συνάντησης των σημείων στο μέσο μεταξύ της άνω και της κάτω επιφάνειας. Το σχήμα της εξαρτάται από την κατανομή του πάχους κατά μήκος της χορδής.
Το πάχος μιας αεροτομής ποικίλλει κατά μήκος της χορδής. Μπορεί να μετρηθεί με δύο τρόπους:
Το πάχος που μετράται κάθετα στη γραμμή της καμπύλης.[10][11] Αυτός ο τρόπος αναφέρεται μερικές φορές ως «αμερικανική σύμβαση».[10]
Το πάχος που μετράται κάθετα στη γραμμή της χορδής.[12] Αυτός ο τρόπος αναφέρεται μερικές φορές ως «βρετανική σύμβαση».
Ορισμένες σημαντικές παράμετροι για την περιγραφή ενός σχήματος αεροτομής είναι η καμπυλότητα και το πάχος της.
Τέλος, οι σημαντικές έννοιες που χρησιμοποιούνται για να περιγράψουν τη συμπεριφορά της αεροτομής όταν κινείται μέσα σε ένα ρευστό είναι:
Το αεροδυναμικό κέντρο, το οποίο είναι το μήκος της χορδής με το οποίο η ροπή ανύψωσης είναι ανεξάρτητη από το συντελεστή άντωσης και τη γωνία προσβολής.
Το κέντρο πίεσης, το οποίο είναι θέση της χορδή, για την οποία η ροπή ανύψωσης είναι μηδέν.
Θεωρία λεπτών αεροτομών
Τμήμα αεροτομής εκτίθεται στην κορυφή ενός αεροσκάφους Denney Kitfox, κατασκευασμένο το 1991.
Αεροτομή ελικοπτέρων Kamov Ka-26
Η θεωρία λεπτών αεροτομών είναι μια απλή θεωρία των αεροτομών που σχετίζεται με τη γωνία προσβολής για την ανύψωση σε ασυμπίεστες ροές. Επινοήθηκε από τον Γερμανοαμερικανό μαθηματικό Μαξ Μουνκ και επανακαθορίστηκε από τον Βρετανό αεροδυναμικό Χέρμαν Γκλάουερτ και άλλους[13] τη δεκαετία του 1920. Η θεωρία ιδανικοποιεί τη ροή γύρω από μια αεροτομή ως δισδιάστατη ροή γύρω από μια λεπτή αεροτομή. Μπορεί να θεωρηθεί ως αεροτομή με μηδενικό πάχος και άπειρο άνοιγμα πτερύγων.
Η θεωρία λεπτών αεροτομών ήταν ιδιαίτερα σημαντική στην εποχή της, διότι παρείχε μια καλή θεωρητική βάση για τις ακόλουθες σημαντικές ιδιότητες των αεροτομών σε δισδιάστατη ροή:[14][15]
σε μία συμμετρική αεροτομή, το κέντρο πίεσης και το αεροδυναμικό κέντρο βρίσκονται ακριβώς στο ένα τέταρτο της χορδής πίσω από το πρόσθιο άκρο.
σε μια κυρτή αεροτομή, το αεροδυναμικό κέντρο βρίσκεται ακριβώς στο ένα τέταρτο της χορδής πίσω από την αιχμή.
Η κλίση του συντελεστή ανύψωσης προς τη γωνία προσβολής είναι {\displaystyle 2\pi \!} μονάδες ανά ακτίνιο.
Ως συνέπεια του (3), ο συντελεστής ανύψωσης τμήματος μιας συμμετρικής αεροτομής με άπειρο άνοιγμα πτερύγων είναι:
{\displaystyle \ c_{l}=2\pi \alpha }
όπου {\displaystyle c_{l}\!} είναι ο συντελεστής ανύψωσης τμήματος,
{\displaystyle \alpha \!} είναι η γωνία προσβολής σε ακτίνια, μετρημένη σε σχέση με τον άξονα της χορδής.
(Η παραπάνω εξίσωση ισχύει και για κυρτές αεροτομές όπου {\displaystyle \alpha \!} είναι η γωνία προσβολής μετρημένη σε σχέση με τον άξονα μηδενικής ανύψωσης αντί της χορδής.)
Επίσης ως συνέπεια του (3), ο συντελεστής ανύψωσης τμήματος κυρτής αεροτομής με άπειρο άνοιγμα πτερύγων είναι:
{\displaystyle \ c_{l}=c_{l_{0}}+2\pi \alpha }
όπου {\displaystyle \ c_{l_{0}}} είναι ο συντελεστής ανύψωσης του τμήματος όταν η γωνία προσβολής ισούται με μηδέν.
Η θεωρία λεπτών αεροτομών δεν εφαρμόζεται για κατάσταση έλλειψης ισορροπίας της αεροτομής, η οποία συμβαίνει συνήθως σε γωνίες μεταξύ 10° και 15° σε κανονικές αεροτομές.[16] Στα μέσα προς τέλη της δεκαετίας του 2000, ωστόσο, μια θεωρία που πρόβλεπε την εφόρμηση της αιχμής προτάθηκε από τον Γουάλας Τζ. Μόρις στη διδακτορική του διατριβή.[17] Οι επακόλουθες βελτιώσεις του Μόρις περιέχουν τις λεπτομέρειες σχετικά με την τρέχουσα κατάσταση των θεωρητικών γνώσεων σχετικά με το φαινόμενο της έλλειψης ισορροπίας στην αιχμή.[18][19] Η θεωρία του Morris προβλέπει την κρίσιμη γωνία προσβολής στην εκκίνηση του σημείου αιχμής ως την κατάσταση στην οποία προβλέπεται η καθολική ζώνη διαχωρισμού στη λύση για την εσωτερική ροή.[20] Η θεωρία του Morris καταδεικνύει ότι μια υποηχητική ροή γύρω από μια λεπτή αεροτομή μπορεί να περιγραφεί με όρους εξωτερικής περιοχής, γύρω από το μεγαλύτερο μέρος της χορδής της αεροτομής, και μιας εσωτερικής περιοχής, γύρω από την κορυφή, που ταιριάζουν ασυμπτωτικά μεταξύ τους. Καθώς η ροή στην εξωτερική περιοχή κυριαρχείται από την κλασσική θεωρία των λεπτών αεροτομών, οι εξισώσεις του Μόρις παρουσιάζουν πολλά συστατικά της θεωρίας της αεροτομής.
Απόδειξη της θεωρίας λεπτών αεροτομών
Από πάνω προς τα κάτω:
• Αεροτομή ελασματώδους ροής για τηλεχειριζόμενο park flyer
• Αεροτομή ελασματώδους ροής για τηλεχειριζόμενο pylon racer
• Αεροτομή ελασματώδους ροής για επανδρωμένο ελικοφόρο αεροσκάφος
• Ελασματώδης ροή σε αεροτομή αεριωθούμενου αεροσκάφους
• Σταθερή αεροτομή που χρησιμοποιείται σε ιπτάμενες πτέρυγες
• Αεροτομή φορτωμένη στο οπίσθιο μέρος της η οποία δίνει τη δυνατότητα για μεγάλο κύριο ιστό και μεταγενέστερη έλλειψη ισορροπίας
• Διηχητική υπερκρίσιμη αεροοτομή
• Υπερηχητική αεροτομή αιχμής
ελασματώδης ροή
τυρβώδης ροή
υποηχητική ροή
όγκος υπερηχητικής ροής
Η αεροτομή μοντελοποιείται ως μια λεπτή γραμμή μέσης ανύψωσης (γραμμή καμπύλης). Η μέση γραμμή, y(x), θεωρείται ότι παράγει την κατανομή του στροβιλισμού {\displaystyle \gamma (s)} κατά μήκος της γραμμής, s. Σύμφωνα με τη συνθήκη Κούτα, η στροβιλότητα είναι μηδενική στο πίσω άκρο. Δεδομένου ότι η αεροτομή είναι λεπτή, το x (θέση χορδής) μπορεί να χρησιμοποιηθεί αντί του s, και όλες οι γωνίες μπορούν να προσεγγιστούν ως μικρές.
Από τον νόμο Μπιό-Σαβάρ, αυτή η στροβιλότητα παράγει ένα πεδίο ροής w ( x ) {\displaystyle w(x)} {\displaystyle w(x)} όπου
{\displaystyle w(x)={\frac {1}{(2\pi )}}\int _{0}^{c}{\frac {\gamma (x')}{(x-x')}}dx'}
x είναι η θέση όπου παράγεται η επαγόμενη ταχύτητα, x' είναι η θέση του στοιχείου στροβίλου που παράγει την ταχύτητα και c είναι το μήκος της χορδής της αεροτομής.
Δεδομένου ότι δεν υπάρχει κανονική ροή στην κυρτή επιφάνεια της αεροτομής, το {\displaystyle w(x)} εξισορροπεί από το στοιχείο της κύριας ροής V , το οποίο είναι τοπικά κανονικό ως προς την πλάκα – η κύρια ροή είναι τοπικά κεκλιμένη στην πλάκα υπό γωνία {\displaystyle \alpha -dy/dx} . Έτσι:
{\displaystyle V\;(\alpha -dy/dx)=w(x)={\frac {1}{(2\pi )}}\int _{0}^{c}{\frac {\gamma (x')}{(x-x')}}dx'}
Αυτή η εξίσωση με το ολοκλήρωμα μπορεί να λυθεί ως {\displaystyle \gamma (x)} , μετά την αντικατάσταση του x με
{\displaystyle \ x=c\cdot {\frac {1-\cos(\theta )}{2}}} ,
ως σειρά Φουριέ στο {\displaystyle A_{n}\sin(n\theta )} με τροποποιημένο κύριο όρο {\displaystyle A_{0}(1+\cos(\theta ))/\sin(\theta )}
Έτσι
{\displaystyle {\frac {\gamma (\theta )}{(2V)}}=A_{0}{\frac {(1+\cos(\theta ))}{\sin(\theta )}}+\sum A_{n}\;\sin(n\theta ))}
(Αυτοί οι όροι είναι γνωστοί ως ολοκλήρωμα Γκλάουερτ).
Οι συντελεστές δίδονται από
{\displaystyle A_{0}=\alpha -{\frac {1}{\pi }}\int _{0}^{\pi }({\frac {dy}{dx}})\;d\theta }
και
{\displaystyle A_{n}={\frac {2}{\pi }}\int _{0}^{\pi }({\frac {dy}{dx}})\cos(n\theta )\;d\theta }
Από το θεώρημα Κούτα-Γιοκόφσκι, η συνολική δύναμη ανύψωσης F είναι ανάλογη προς
{\displaystyle \rho V\int _{0}^{c}\gamma (x)\;dx}
και η ροπή Μ στην αιχμή του
{\displaystyle \rho V\int _{0}^{c}x\;\gamma (x)\;dx}
Ο υπολογιζόμενος συντελεστής ανύψωσης εξαρτάται μόνο από τους δύο πρώτους όρους της σειράς Φουριέ, όπως
\displaystyle \ C_{L}=2\pi (A_{0}+A_{1}/2)}
Η ροπή M για την αιχμή εξαρτάται μόνο από τα {\displaystyle A_{0},A_{1}} και {\displaystyle A_{2}} , ως
{\displaystyle \ C_{M}=-0.5\pi (A_{0}+A_{1}-A_{2}/2)}
Συνεπώς η ροπή για το 1/4 της χορδής θα είναι,
{\displaystyle \ C_{M}(1/4c)=-\pi /4(A_{1}-A_{2})}.
Από αυτό προκύπτει ότι το κέντρο πίεσης βρίσκεται πίσω από το σημείο του ενός τετάρτου της χορδής στο 0.25 c, ως
{\displaystyle \ \Delta x/c=\pi /4((A_{1}-A_{2})/C_{L})}
Το αεροδυναμικό κέντρο, AC, βρίσκεται στο σημείο του ενός τετάρτου. Το AC είναι το σημείο όπου η ροπή M' δεν διαφέρει ανάλογα με τη γωνία προσβολής, λ.χ.,
{\displaystyle {\frac {\partial (C_{M'})}{\partial (C_{L})}}=0}
Παραπομπές
Halliday, David; Resnick, Robert, Fundamentals of Physics 3rd Edition, John Wiley & Sons, σελ. 378
«Lift from Flow Turning». www.grc.nasa.gov. NASA Glenn Research Center. Αρχειοθετήθηκε από το πρωτότυπο στις 5 Ιουλίου 2011. Ανακτήθηκε στις 23 Μαρτίου 2018.
Weltner, Klaus; Ingelman-Sundberg, Martin, Physics of Flight – reviewed
"...if a streamline is curved, there must be a pressure gradient across the streamline..."Babinsky, Holger (November 2003), «How do wings work?», Physics Education, doi:10.1088/0031-9120/38/6/001
Croom, C. C.; Holmes, B. J. (1 Απριλίου 1985). Flight evaluation of an insect contamination protection system for laminar flow wings.
Holmes, B. J.; Obara, C. J.; Yip, L. P. (1984-06-01). Natural laminar flow experiments on modern airplane surfaces.
Torenbeek, Egbert (1982). Synthesis of Subsonic Airplane Design. Dordrecht: Springer Science & Business Media. σελ. 438. ISBN 9789024727247.
Hurt, H. H., Jr. (Ιανουαρίου 1965) [1960]. Aerodynamics for Naval Aviators. U.S. Government Printing Office, Washington, D.C.: U.S. Navy, Aviation Training Division. σελίδες 21–22. NAVWEPS 00-80T-80.
Houghton, E.L.; Carpenter, P.W. (2003). Butterworth Heinmann, επιμ. Aerodynamics for Engineering Students (5th έκδοση). σελ. 18. ISBN 0-7506-5111-3.
Houghton, E. L.; Carpenter, P.W. (2003). Butterworth Heinmann, επιμ. Aerodynamics for Engineering Students (5η έκδοση). σελ. 17. ISBN 0-7506-5111-3.
Phillips, Warren F. (2010). Mechanics of Flight (2η έκδοση). Wiley & Sons. σελ. 27. ISBN 978-0-470-53975-0.
Bertin, John J.; Cummings, Russel M. (2009). Pearson Prentice Hall, επιμ. Aerodynamics for Engineers (5η έκδοση). σελ. 199. ISBN 978-0-13-227268-1.
Abbott, Ira H., and Von Doenhoff, Albert E. (1959), Theory of Wing Sections, Section 4.2, Dover Publications Inc., New York, Standard Book Number 486-60586-8
Abbott, Ira H., and Von Doenhoff, Albert E. (1959), Theory of Wing Sections, Section 4.3
Clancy, L.J. (1975), Aerodynamics, Sections 8.1 to 8.8, Pitman Publishing Limited, London. (ISBN 0-273-01120-0)
«Lift Coefficient & Thin Airfoil Theory». www.aerospaceweb.org. Ανακτήθηκε στις 25 Μαρτίου 2018.
Morris, Wallace J., II (2009). «A universal prediction of stall onset for airfoils at a wide range of Reynolds number flows». Ph.D. Thesis.
Morris, Wallace J.; Rusak, Zvi (October 2013). «Stall onset on aerofoils at low to moderately high Reynolds number flows». Journal of Fluid Mechanics 733: 439–472. doi:10.1017/jfm.2013.440. ISSN 0022-1120. Bibcode: 2013JFM...733..439M.
Traub, Lance W. (2016-03-24). «Semi-Empirical Prediction of Airfoil Hysteresis» (στα αγγλικά). Aerospace 3 (2): 9. doi:10.3390/aerospace3020009.
Ramesh, Kiran; Gopalarathnam, Ashok; Granlund, Kenneth; Ol, Michael V.; Edwards, Jack R. (July 2014). «Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding». Journal of Fluid Mechanics 751: 500–538. doi:10.1017/jfm.2014.297. ISSN 0022-1120. Bibcode: 2014JFM...751..500R.
Βιβλιογραφία
Anderson, John, D (2007). Fundamentals of Aerodynamics. McGraw-Hill.
Desktopaero
Batchelor, George. K (1967). An Introduction to Fluid Dynamics. Cambridge: Cambridge UP. σελ. 467–471.
Εξωτερικοί σύνδεσμοι
Βάση δεδομένων σχετικά με αεροτομές
Εφαρμογή αναφοράς αεροτομών και υδροτομών
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License