Τυχαίος περίπατος
αγγλικά : Random walk
γαλλικά : Marche aléatoire
γερμανικά : Random walk
Στα μαθηματικά, ενας Τυχαίος περίπατος είναι ένα μαθηματικό αντικείμενο, γνωστό ως στοχαστική ή τυχαία διαδικασία, που περιγράφει μια διαδρομή που αποτελείται από μια σειρά τυχαίων βημάτων σε κάποιο μαθηματικό χώρο, όπως οι ακέραιοι.
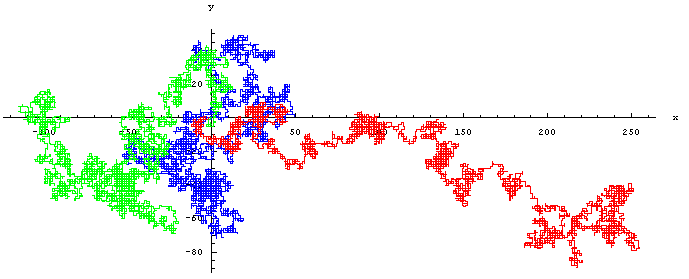
Τρεις ισοτροπικοί (ανεξάρτητοι) τυχαίοι περίπατοι στο πλέγμα ℤ2. 10.000 βήματα.
Για μια σειρά φυσικών φαινομένων έχουν υποβληθεί προσπάθειες περιγραφής με τυχαίους περίπατους , ιδίως στη φυσική και στη χημεία, επιστήμη υλικών, βιολογία και διάφορα άλλα πεδία. Τα παρακάτω είναι μερικές συγκεκριμένες εφαρμογές τυχαίαου περίπατου:
Στα χρηματοοικονομικά, η «υπόθεση τυχαίας περίπατος» χρησιμοποιείται για τη μοντελοποίηση των τιμών των μετοχών και άλλων παραγόντων. Οι εμπειρικές μελέτες διαπίστωσαν κάποιες αποκλίσεις από αυτό το θεωρητικό μοντέλο, ειδικά σε βραχυπρόθεσμους και μακροπρόθεσμους συσχετισμούς.
Στη γενετική του πληθυσμού, ο τυχαίος περίπατος περιγράφει τις στατιστικές ιδιότητες της γενετικής μετατόπισης
Στη φυσική, οι τυχαίοι περίπατοι χρησιμοποιούνται ως απλοποιημένα μοντέλα φυσικής κίνησης και διάχυσης Brown, όπως η τυχαία κίνηση μορίων σε υγρά και αέρια. . Επίσης στη φυσική, οι τυχαίοι περίπατοι και μερικοί από τους αυτοαπασχολούμενους περιπάτους παίζουν ρόλο στη θεωρία κβαντικών πεδίων.
Στη μαθηματική οικολογία, χρησιμοποιούνται τυχαίοι περίπατοι για την περιγραφή μεμονωμένων κινήσεων των ζώων, για την εμπειρική υποστήριξη διαδικασιών βιοδιάχυσης και περιστασιακά για τη μοντελοποίηση της δυναμικής του πληθυσμού.
Στη φυσική του πολυμερούς, ο τυχαίος περίπατος περιγράφει μια ιδανική αλυσίδα. Είναι το απλούστερο μοντέλο για τη μελέτη πολυμερών.
Σε άλλα πεδία των μαθηματικών, χρησιμοποιείται ο τυχαίοσ περίπατοσ για τον υπολογισμό λύσεων στην εξίσωση του Laplace, για την εκτίμηση του αρμονικού μέτρου και για διάφορες κατασκευές στην ανάλυση και το συνδυασμό.
Στην επιστήμη των υπολογιστών, χρησιμοποιούνται τυχαίες διαδρομές για την εκτίμηση του μεγέθους του Διαδικτύου. Στο συνέδριο World Wide Web-2006, οι Bar-Yossef et al. δημοσίευσε τα ευρήματά τους και τους αλγόριθμους για το ίδιο.
Στην τμηματοποίηση εικόνας, χρησιμοποιούνται τυχαίοι περιπάτουι για τον προσδιορισμό των ετικετών (δηλαδή, "αντικείμενο" ή "υπόβαθρου") για συσχέτιση με κάθε εικονοστοιχείο. Αυτός ο αλγόριθμος αναφέρεται συνήθως ως ο αλγόριθμος τμηματοποίησης τυχαίου περίπατου.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License