.
Στα μαθηματικά, οι τριγωνομετρικές συναρτήσεις είναι συναρτήσεις γωνιών, δηλαδή συναρτήσεις των οποίων το όρισμα είναι γωνία. Πολλές φορές το όρισμα των τριγωνομετρικών συναρτήσεων δεν είναι άμεσα αντιληπτό ως γωνία, οπότε ονομάζεται (φάση). Είναι σημαντικές στη μελέτη τριγώνων και την μοντελοποίηση περιοδικών φαινομένων, μεταξύ άλλων. Οι τριγωνομετρικές συναρτήσεις ορίζονται συνήθως ως λόγος των δυο πλευρών ενός ορθογωνίου τριγώνου που περιέχει τη δεδομένη γωνία, και μπορούν ισοδύναμα να οριστούν ως το μήκος διαφόρων ευθύγραμμων τμημάτων σε ένα μοναδιαίο κύκλο. Νεώτεροι ορισμοί εκφράζουν τις τριγωνομετρικές συναρτήσεις ως εκθετικές συναρτήσεις μιγαδικών αριθμών. Επιπλέον οι τριγωνομετρικές συναρτήσεις μπορούν να εκφρασθούν και σαν αθροίσματα απειροσειρών που επιτρέπουν τον αριθμητικό υπολογισμό της τιμής τους.
Στη σύγχρονη τριγωνομετρία, υπάρχουν έξι βασικές τριγωνομετρικές συναρτήσεις, που παρουσιάζονται εδώ μαζί με τις εξισώσεις που τις συσχετίζουν μεταξύ τους. Ειδικά στην περίπτωση των τελευταίων τεσσάρων, αυτές οι σχέσεις συχνά δίνονται ως ορισμοί των συναρτήσεων αυτών, αλλά μπορούν να οριστούν εξίσου καλά γεωμετρικά ή με άλλα μέσα, και στη συνέχεια να αποδειχθούν οι σχέσεις αυτές.
Οι τριγωνομετρικοί αριθμοί και τριγωνομετρία
Σχήμα 1
Χρησιμοποιώντας τις πλευρές ενός ορθογωνίου τριγώνου, μπορούν να οριστούν οι τρεις βασικές τριγωνομετρικές συναρτήσεις, η εφαπτομένη, το ημίτονο και το συνημίτονο. Επιπλέον μπορεί να οριστεί και η συνάρτηση συνεφαπτομένη. Αυτές οι συναρτήσεις ορίζονται ως προς μια οξεία γωνία θ του τριγώνου. Η θ συνήθως μετριέται σε ακτίνια ή μοίρες. Αν η γωνία δε μετριέται σε ακτίνια, τότε η γωνία γράφεται μαζί με τις μονάδες μέτρησης.
Ένα ορθογώνιο τρίγωνο έχει δύο κάθετες μεταξύ τους πλευρές και μια υποτείνουσα. Οι κάθετες είναι αυτές που σχηματίζουν μεταξύ τους ορθή γωνία, ενώ η υποτείνουσα είναι η τρίτη πλευρά που σχηματίζει οξείες γωνίες με τις υπόλοιπες δύο πλευρές. Στο Σχήμα 1, οι κάθετες είναι οι πλευρές c και b, ενώ η υποτείνουσα είναι η a.
Με βάση μια οξεία γωνία σε ένα ορθογώνιο τρίγωνο, ορίζουμε ως προσκείμενη (κάθετη) πλευρά την πλευρά του τριγώνου που είναι ταυτόχρονα και πλευρά της γωνίας. Επιπλέον, ως απέναντι (κάθετη) πλευρά της γωνίας ορίζουμε την άλλη κάθετη πλευρά του τριγώνου. Στο συγκεκριμένο σχήμα προσκείμενη πλευρά είναι η b, και απέναντι πλευρά η c.
Οι τρεις τριγωνομετρικές συναρτήσεις ορίζονται ως συναρτήσεις μόνο της γωνίας θ, γιατί αποδεικνύεται ότι η τιμή τους δεν εξαρτάται από το μήκος των πλευρών, αλλά μόνο από τη γωνία θ. Το πεδίο ορισμού των συναρτήσεων όπως ορίζονται με βάση ορθογώνιο τρίγωνο είναι από μηδέν μέχρι π/2 ακτίνια, δηλαδή η γωνία θ πρέπει να είναι οξεία.
Εφαπτομένη
Σε ένα ορθογώνιο τρίγωνο ορίζεται ως εφαπτομένη της γωνίας θ του τριγώνου το πηλίκο της απέναντι κάθετης πλευράς διά την προσκείμενη κάθετη πλευρά. Συμβολίζεται με εφθ, στα ελληνικά ή tanθ διεθνώς. Η εφαπτομένη, όπως έχει οριστεί εδώ, μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του μηδενός.
Ημίτονο
Κύριο λήμμα: Ημίτονο
Σε ένα ορθογώνιο τρίγωνο ορίζεται ως ημίτονο της γωνίας θ του τριγώνου το πηλίκο της απέναντι κάθετης πλευράς διά την υποτείνουσα. Συμβολίζεται με ημθ, στα ελληνικά ή sinθ διεθνώς. Το ημίτονο, όπως έχει οριστεί εδώ, μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του μηδενός και μικρότερη του ενός. Η απέναντι πλευρά είναι πάντα μικρότερη της υποτείνουσας, άρα το κλάσμα πάντα μικρότερο του ενός. Το όνομα της συνάρτησης οφείλεται σε ένα πολύ σημαντικό ορθογώνιο τρίγωνο, το ορθογώνιο τρίγωνο με γωνίες 90, 60 και 30 μοιρών στις γωνίες. Το ημίτονο των 30 μοιρών είναι 1/2, δηλαδή η απέναντι πλευρά είναι το μισό του τόνου, όπου με τον όρο τόνος εννοείται το μήκος της υποτείνουσας.
Συνημίτονο
Κύριο λήμμα: Συνημίτονο
Σε ένα ορθογώνιο τρίγωνο ορίζεται ως συνημίτονο της γωνίας θ του τριγώνου το πηλίκο της προσκείμενης κάθετης πλευράς διά την υποτείνουσα. Συμβολίζεται με συνθ, στα ελληνικά ή cosθ διεθνώς. Το συνημίτονο, όπως έχει οριστεί εδώ, μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του μηδενός και μικρότερη του ενός. Η προσκείμενη πλευρά είναι πάντα μικρότερη της υποτείνουσας, άρα το κλάσμα πάντα μικρότερο του ενός. Το όνομά του οφείλεται στο όνομα του ημιτόνου, συνημίτονο είναι ο τριγωνομετρικός αριθμός που συνοδεύει το ημίτονο. Γενικά κάθε τριγωνομετρικός αριθμός συνοδεύεται από κάποιον άλλον, και το όνομά του προκύπτει από την προσθήκη του προθέματος συν πριν από το όνομά του.
Συνεφαπτομένη
Σε ένα ορθογώνιο τρίγωνο ορίζεται ως συνεφαπτομένη της γωνίας θ του τριγώνου το πηλίκο της προσκείμενης πλευράς δια την απέναντι πλευρά. Συμβολίζεται με σφθ, στα ελληνικά ή cotθ διεθνώς. Η συνεφαπτομένη, όπως έχει οριστεί εδώ, μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του μηδενός.
Επιπλέον ορίζονται και οι εξής τριγωνομετρικοί αριθμοί:
Τέμνουσα(sec): Το κλάσμα 1/cosθ.
Συντέμνουσα(csc): Το κλάσμα 1/sinθ.
Παρατηρούμε ότι δεδομένου των συναρτήσεων ημίτονο και συνημίτονο. Αν ορίσουμε έναν άλλο τριγωνομετρικό αριθμό με μία σχέση που περιλαμβάνει ημίτονα και συνημίτονα, ο αντίστοιχος συν- τριγωνομετρικός αριθμός προκύπτει, αν στη σχέση αντιμεταθέσουμε τα ημίτονα και τα συνημίτονα.
Από το πυθαγόρειο θεώρημα στο ορθογώνιο τρίγωνο προκύπτει η βασική τριγωνομετρική ταυτότητα ότι sin2x+cos2x=1.
Γενίκευση των τριγωνομετρικών συναρτήσεων (στους πραγματικούς αριθμούς)
Τριγωνομετρικός κύκλος
Οι τριγωνομετρικές συναρτήσεις μπορούν να γενικευθούν μέσω του καρτεσιανού συστήματος συντεταγμένων. Έστω ένα ορθοκανονικό σύστημα συντεταγμένων και πάνω σε αυτό μοναδιαίος κύκλος με κέντρο την αρχή των αξόνων. Θεωρούμε τη γωνία θ ως τη γωνία του θετικού ημιάξονα x'x και της θέσης που θα λάβει ο θετικός ημιάξονας x'x, αν περιστραφεί κατά τη θετική φορά, για να διαγράψει γωνία θ. Ως θετική φορά θεωρείται η φορά κατά την οποία η μεταβλητή πλευρά αρχίζει την πορεία της στο πρώτο τεταρτημόριο, δηλαδή κατά την αντίθετη φορά των δεικτών του ρολογιού. Τότε η μεταβλητή πλευρά της γωνίας τέμνει το μοναδιαίο κύκλο σε ένα σημείο. Έστω οι συντεταγμένες του χ, ψ. Το τόξο που αντιστοιχεί στη γωνία προφανώς είναι του ίδιου μεγέθους με τη γωνία. Επειδή ο κύκλος είναι μοναδιαίος, δηλαδή έχει ακτίνα ίση με τη μονάδα, το μήκος του τόξου ισούται με το μέτρο της γωνίας (σε ακτίνια).
Τότε μπορούμε να ορίσουμε εκ νέου τους τριγωνομετρικούς αριθμούς, ώστε σαν πεδίο ορισμού να δέχονται οποιονδήποτε πραγματικό αριθμό, δηλαδή η γωνία θ δεν είναι ανάγκη πλέον να είναι οξεία, μπορεί να είναι οποιαδήποτε. Αν η γωνία θ είναι μεγαλύτερη από μία πλήρη γωνία, τότε η μεταβλητή πλευρά εκτελεί μια πλήρη περιστροφή και συνεχίζει. Αν η γωνία θ είναι αρνητική, τότε η περιστροφή θεωρείται κατά την αρνητική φορά. Με αυτήν τη γενίκευση οι τριγωνομετρικές συναρτήσεις έχουν ως ανεξάρτητη μεταβλητή οποιονδήποτε πραγματικό αριθμό και όχι υποχρεωτικά γωνία. Γι' αυτό η ανεξάρτητη μεταβλητή των τριγωνομετρικών συναρτήσεων ονομάζεται φάση.

Ορισμός των τριγωνομετρικών συναρτήσεων
Ορίζουμε ως ημίτονο την τεταγμένη ψ του σημείου και ως συνημίτονο την τετμημένη χ. Έτσι, οι συναρτήσεις αυτές πλέον μπορούν να λάβουν οποιαδήποτε τιμή μεταξύ του ένα και του πλην ένα.
Για τους υπόλοιπους τριγωνομετρικούς αριθμούς χρησιμοποιούμε τη σχέση τους με το ημίτονο και το συνημίτονο. Έτσι:
tanθ=sinθ/cosθ
cotθ=cosθ/sinθ
secθ=1/cosθ
cscθ=1/sinθ
Γεωμετρική ερμηνεία των τριγωνομετρικών αριθμών
Γεωμετρικά στο καρτεσιανό επίπεδο αυτοί οι αριθμοί αντιστοιχούν σε ευθύγραμμα τμήματα, ενώ η τιμή τους είναι ίση με το μήκος τους (κατά απόλυτη τιμή). Πιο συγκεκριμένα:
Το ημίτονο ισούται με την απόσταση στον άξονα y'y.
Το συνημίτονο ισούται με την απόσταση στον άξονα x'x.
Η εφαπτομένη ισούται με την τεταγμένη της τομής της μεταβλητής πλευράς με τον άξονα των εφαπτόμενων. Ο άξονας αυτός προκύπτει από τη μετατόπιση του άξονα y'y κατά μία μονάδα στον άξονα x'x. Εφάπτεται στο μοναδιαίο κύκλο στο σημείο (1,0).
Η συνεφαπτομένη ισούται με την τετμημένη της τομής της μεταβλητής πλευράς με τον άξονα των συνεφαπτόμενων. Ο άξονας αυτός προκύπτει από τη μετατόπιση του άξονα x'x κατά μία μονάδα στον άξονα y'y. Εφάπτεται στο μοναδιαίο κύκλο στο σημείο (0,1).
Θεωρούμε την εφαπτομένη ευθεία στο μοναδιαίο κύκλο στο σημείο τομής του κύκλου με τη μεταβλητή πλευρά. Τότε αυτή έχει σημείο τομής με τον άξονα x'x (άξονας των συνημιτόνων) και τον άξονα y'y (άξονας των ημιτόνων).
Η τέμνουσα ισούται με την τετμημένη του σημείου τομής με τον άξονα των συνημιτόνων.
Η συντέμνουσα ισούται με την τεταγμένη του σημείου τομής με τον άξονα των ημιτόνων.
Θεωρήσουμε το ορθογώνιο τρίγωνο, που προκύπτει από τη γωνία θ, και το κάθετο στον άξονα x'x ευθύγραμμο τμήμα από το σημείο τομής της μεταβλητής πλευράς με τον τριγωνομετρικό κύκλο. Τότε αν η γωνία θ είναι οξεία, με βάση του ορισμούς του ημιτόνου και του συνημιτόνου στο ορθογώνιο τρίγωνο ισχύει ότι ημθ=ψ/1=ψ και συνθ=χ/1=χ. Έτσι, αποδείχθηκε ότι οι τριγωνομετρικοί αριθμοί που ορίστηκαν με βάση τον τριγωνομετρικό κύκλο είναι γενίκευση των τριγωνομετρικών αριθμών που ορίστηκαν με βάση το ορθογώνιο τρίγωνο.
Χρήσιμες τριγωνομετρικές ταυτότητες
| Συνάρτηση | Συμβολισμός | Διεθνής συμβολισμός |
Ταυτότητες |
|---|---|---|---|
| Ημίτονο | ημ | sin | \( \eta \mu ~ \theta = \sigma \upsilon \nu ~ \left(\frac{\pi}{2} - \theta \right) = \frac{1}{\csc \theta}\,\) |
| Συνημίτονο | συν | cos | \( \sigma \upsilon \nu ~ \theta = \eta \mu ~ \left(\frac{\pi}{2} - \theta \right) = \frac{1}{\sec \theta}\,\) |
| Εφαπτομένη | εφ | tan (or tg) |
\(\epsilon \phi ~ \theta = \frac{\eta \mu ~ \theta}{\sigma \upsilon \nu ~ \theta} = \sigma \phi ~ \left(\frac{\pi}{2} - \theta \right) = \frac{1}{\sigma \phi ~ \theta} \, \) |
| Συνεφαπτομένη | σφ | cot (or ctg or ctn) |
\( \sigma \phi ~ \theta = \frac{\sigma \upsilon \nu ~ \theta}{\eta \mu ~ \theta} = \epsilon \phi ~ \left(\frac{\pi}{2} - \theta \right) = \frac{1}{\epsilon \phi ~ \theta} \,\) |
| Συντέμνουσα | στεμ | csc (or cosec) |
\(\csc \theta = \sec \left(\frac{\pi}{2} - \theta \right) =\frac{1}{\eta \mu ~ \theta} \, \) |
| Τέμνουσα | τεμ | sec | \( \sec \theta = \csc \left(\frac{\pi}{2} - \theta \right) =\frac{1}{\sigma \upsilon \nu ~ \theta} \,\) |
Μελέτη των τριγωνομετρικών συναρτήσεων
Οι τριγωνομετρικοί αριθμοί είναι πραγματικές συναρτήσεις πραγματικής μεταβλητής. Η φάση είναι πραγματικός αριθμός, αντιστοιχίζεται πρώτα στην αντίστοιχη γωνία με μέτρο την ανεξάρτητη μεταβλητή σε ακτίνια και έπειτα στον αντίστοιχο τριγωνομετρικό αριθμό. Για παράδειγμα sin5=sin(5rad). Από τη μελέτη τους ως συναρτήσεις προκύπτουν τα παρακάτω:
Ημίτονο
Κύριο λήμμα: ημίτονο
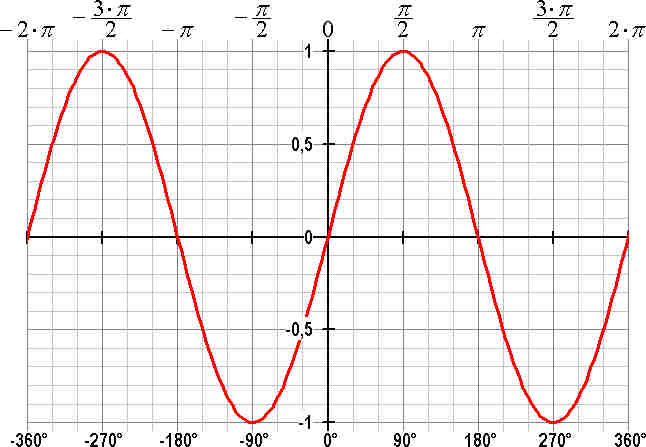
Η γραφική παράσταση του ημιτόνου.
Πεδίο ορισμού της συνάρτησης ημίτονο είναι οι πραγματικοί αριθμοί. Σύνολο τιμών είναι το σύνολο [-1,1], ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=2π. Είναι παραγωγίσιμη με (sinx)'=cosx. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα [0,2π) ως αντιπροσωπευτικό) η συνάρτηση ημίτονο είναι γνησίως αύξουσα και κοίλη στο [0,π/2], γνησίως φθίνουσα και κοίλη στο [π/2,π], γνησίως φθίνουσα και κυρτή στο [π,3π/2], γνησίως αύξουσα και κυρτή στο [3π/2,2π). Παρουσιάζει μέγιστο την τιμή 1 στο π/2, ελάχιστο την τιμή -1 στο 3π/2 και δύο σημεία καμπής, ένα στο 0 και ένα στο π.
Συνημίτονο
Πεδίο ορισμού της συνάρτησης συνημίτονο είναι οι πραγματικοί αριθμοί. Σύνολο τιμών είναι το σύνολο [-1,1], ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=2π. Είναι παραγωγίσιμη με (cosx)'=-sinx. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα [0,2π) ως αντιπροσωπευτικό) η συνάρτηση συνημίτονο είναι γνήσια φθίνουσα και κοίλη στο [0,π/2], γνήσια φθίνουσα και κυρτή στο [π/2,π], γνήσια αύξουσα και κυρτή στο [π,3π/2], γνήσια αύξουσα και κοίλη στο [3π/2,2π). Παρουσιάζει μέγιστο την τιμή 1 στο 0, ελάχιστο την τιμή -1 στο π και δύο σημεία καμπής, ένα στο π/2 και ένα στο 3π/2.

Η δημιουργία της γραφικής παράστασης του συνημιτόνου. Χρησιμοποιείται ο ακόμη πιο γενικευμένος ορισμός με το μιγαδικό εψιλοτικό μετασχηματισμό.
Εφαπτομένη

Η γραφική παράσταση της συνάρτησης της εφαπτομένης φαίνεται παρακάτω. (προσοχή η γωνία μετριέται σε μοίρες!)
Πεδίο ορισμού της συνάρτησης εφαπτομένη είναι οι πραγματικοί αριθμοί, εξαιρουμένων αυτών που μηδενίζουν τη συνάρτηση συνημίτονο, δηλαδή των αριθμών της μορφής x=κπ +π/2, όπου κ ακέραιος αριθμός. Σύνολο τιμών είναι το σύνολο όλοι οι πραγματικοί αριθμοί, ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=π. Είναι παραγωγίσιμη με (tanx)'=1/cos2x=sec2x. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα (-π/2,π/2) ως αντιπροσωπευτικό) η συνάρτηση εφαπτομένη είναι γνήσια αύξουσα και κοίλη στο (-π/2,0], γνήσια αύξουσα και κυρτή στο [0,π/2). Παρουσιάζει σημείο καμπής στο μηδέν και κατακόρυφες ασύμπτωτες τις ευθείες x=-π/2, x=π/2.
Γεωμετρικά, όταν η φάση είναι μηδέν, η γωνία θ είναι μηδενική, τότε προφανώς και η εφαπτομένη της θ θα είναι μηδενική, αφού η υποτείνουσα του τριγώνου θα είναι παράλληλη στον άξονα x, δηλαδή θα έχει μηδενική κλίση και η απέναντι κάθετη πλευρά θα είναι κι αυτή μηδενική, δηλαδή Δy=0. Η εφαπτομένη της γωνίας θ απειρίζεται όταν θ=90ο, αφού σ'αυτήν την περίπτωση, η απόσταση Δy είναι άπειρη και η κλίση της υποτείνουσας είναι κάθετη προς τον άξονα x.
Συνεφαπτομένη
Πεδίο ορισμού της συνάρτησης συνεφαπτομένη είναι οι πραγματικοί αριθμοί, εξαιρουμένων αυτών που μηδενίζουν τη συνάρτηση ημίτονο, δηλαδή των αριθμών της μορφής x=κπ, όπου κ ακέραιος αριθμός. Σύνολο τιμών είναι το σύνολο όλοι οι πραγματικοί αριθμοί, ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=π. Είναι παραγωγίσιμη με (cotx)'=-1/sin2x=csc2x. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα (0,π) ως αντιπροσωπευτικό) η συνάρτηση συνεφαπτομένη είναι γνήσια φθίνουσα και κυρτή στο (0,π/2], γνήσια φθίνουσα και κοίλη στο [π/2,π). Παρουσιάζει σημείο καμπής στο π/2 και κατακόρυφες ασύμπτωτες τις ευθείες x=0, x=π.
Τέμνουσα
Πεδίο ορισμού της συνάρτησης τέμνουσα είναι οι πραγματικοί αριθμοί, εξαιρουμένων αυτών που μηδενίζουν τη συνάρτηση συνημίτονο, δηλαδή των αριθμών της μορφής x=κπ+π/2, όπου κ ακέραιος αριθμός. Σύνολο τιμών είναι το σύνολο των πραγματικών αριθμών εξαιρουμένου του τμήματος (-1,1), ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=2π. Είναι παραγωγίσιμη με (secx)'=sinx/cos2x=tanx/cosx. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα (-π/2,π/2)U(π/2,3π/2) ως αντιπροσωπευτικό) η συνάρτηση τέμνουσα είναι γνήσια φθίνουσα και κυρτή στο (-π/2,0], γνήσια αύξουσα και κυρτή στο [0,π/2), γνήσια αύξουσα και κοίλη στο (π/2,π], γνήσια φθίνουσα και κοίλη στο [π,3π/2). Παρουσιάζει τοπικό ελάχιστο με τιμή 1 στο 0, τοπικό μέγιστο με τιμή -1 στο π και κατακόρυφες ασύμπτωτες τις ευθείες y=π/2, y=3π/2.
Συντέμνουσα

Γραφική παράσταση της συντέμνουσας
Πεδίο ορισμού της συνάρτησης συντέμνουσα είναι οι πραγματικοί αριθμοί, εξαιρουμένων αυτών που μηδενίζουν τη συνάρτηση ημίτονο, δηλαδή των αριθμών της μορφής x=κπ, όπου κ ακέραιος αριθμός. Σύνολο τιμών είναι το σύνολο των πραγματικών αριθμών εξαιρουμένου του τμήματος (-1,1), ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=2π. Είναι παραγωγίσιμη με (cscx)'=-cosx/sin2x=-cotx/sinx. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα (0,π)U(π,2π) ως αντιπροσωπευτικό) η συνάρτηση συντέμνουσα είναι γνήσια φθίνουσα και κυρτή στο (0,π/2], γνήσια αύξουσα και κυρτή στο [π/2,π), γνήσια αύξουσα και κοίλη στο (π,3π/2], γνήσια φθίνουσα και κοίλη στο [3π/2,2π). Παρουσιάζει τοπικό ελάχιστο με τιμή 1 στο π/2, τοπικό μέγιστο με τιμή -1 στο 3π/2 και κατακόρυφες ασύμπτωτες τις ευθείες y=0, y=π.
Αρμονική συνάρτηση
Οι συναρτήσεις ημίτονο και συνημίτονο είναι οι ίδιες συναρτήσεις, η μία είναι αποτέλεσμα της μετατόπισης της άλλης.
Παρατηρήθηκε ότι ισχύει cosx=sin(x+π/2). Επιπλέον, στη μοντελοποίηση πολλών φυσικών φαινομένων, όπως η απλή αρμονική ταλάντωση εμφανίζονται συναρτήσεις της μορφής sin(x+α), όπου α μπορεί να είναι οποιαδήποτε γωνία (σε ακτίνια). Έτσι, μπορεί να οριστεί μια τριγωνομετρική συνάρτηση, η αρμονική συνάρτηση, η οποία είναι της παραμετρικής μορφής sin(x+α). Ουσιαστικά η αρμονική συνάρτηση είναι η συνάρτηση ημίτονο μετατοπισμένη στον άξονα x'x κατά -α μονάδες.
Πεδίο ορισμού της αρμονικής συνάρτησης είναι οι πραγματικοί αριθμοί. Σύνολο τιμών είναι το σύνολο [-1,1], ενώ η συνάρτηση δεν είναι ένα προς ένα, ως περιοδική, με περίοδο Τ=2π. Είναι παραγωγίσιμη με (sin(x+α))'=sin(x+α+π/2), δηλαδή η παράγωγός της αρμονικής συνάρτησης είναι αρμονική συνάρτηση. Σε διάστημα μιας περιόδου (θεωρείται το διάστημα [-α,2π-α) ως αντιπροσωπευτικό) η συνάρτηση ημίτονο είναι γνήσια αύξουσα και κοίλη στο [-α,π/2-α], γνήσια φθίνουσα και κοίλη στο [π/2-α,π-α], γνήσια φθίνουσα και κυρτή στο [π-α,3π/2-α], γνήσια αύξουσα και κυρτή στο [3π/2-α,2π-α). Παρουσιάζει μέγιστο την τιμή 1 στο π/2-α, ελάχιστο την τιμή -1 στο 3π/2-α και δύο σημεία καμπής, ένα στο -α και ένα στο π-α.
Η αρμονική συνάρτηση έχει άπειρα σημεία συμμετρίας, όλες τις ρίζες της. Επιπλέον έχει άπειρους κατακόρυφους άξονες συμμετρίας, όλες τις κατακόρυφες ευθείες που διέρχονται από τα μέγιστα και τα ελάχιστά της.
Με βάση τον ορισμό της αρμονικής συνάρτησης προκύπτει ότι οι συναρτήσεις sinx, cosx, -sinx, -cosx, είναι περιπτώσεις της αρμονικής συνάρτησης. Επιπλέον, η αρμονική συνάρτηση μπορεί να οριστεί ως cos(x+α). Ανεξάρτητα ποια τριγωνομετρική συνάρτηση θα χρησιμοποιηθεί ως βάση για τον ορισμό της το νόημα είναι ότι οι συναρτήσεις ημίτονο και συνημίτονο, όπως και άλλες παρόμοιες συναρτήσεις, είναι παραμετρικές μορφές της ίδιας συνάρτησης.
Αντίστροφες τριγωνομετρικές συναρτήσεις
Για κάθε τριγωνομετρική συνάρτηση ορίζεται αντίστοιχη αντίστροφη τριγωνομετρική συνάρτηση. Οι αντίστροφες τριγωνομετρικές συναρτήσεις, ορίζονται με βάση τμήμα του πεδίου ορισμού των τριγωνομετρικών, στο οποίο αυτές είναι ένα προς ένα. Προφανώς αυτό το τμήμα είναι τμήμα περιόδου. Για παράδειγμα η συνάρτηση ημίτονο είναι ένα προς ένα στο [-π/2,π/2], και με βάση αυτό ορίζεται η αντίστροφη της. Ονομάζονται και τόξο της τριγωνομετρικής συνάρτησης που αντιστοιχούν, γιατί αντιστοιχούν το δοσμένο τριγωνομετρικό αριθμό σε αντίστοιχη γωνία, άρα και στο μήκος του αντίστοιχου τόξου του μοναδιαίου κύκλου. Η γωνία στην οποία αντιστοιχούν οι αντίστροφες πάντα εντός μιας πλήρης περιστροφής. Συνήθως οι αντίστροφες τριγωνομετρικές συναρτήσεις αντιστοιχούν σε θετικές γωνίες, εκτός αν προκύπτει ασυνεχής η αντίστροφη συνάρτηση, ή δεν είναι δυνατό να οριστεί πλήρως η αντίστροφη, οπότε αντιστοιχούν και σε αρνητικές γωνίες.
Αντίστροφη συνάρτηση του ημιτόνου
Γραφική παράσταση του τόξου ημιτόνου
Θεωρούμε τη συνάρτηση ημίτονο στο [-π/2,π/2], όπου είναι ένα προς ένα. Η αντίστροφη συνάρτηση ονομάζεται τόξο ημιτόνου και συμβολίζεται με arc sin x.
Πεδίο ορισμού του τόξου ημιτόνου είναι το [-1,1]. Σύνολο τιμών είναι το σύνολο [-π/2,π/2], ενώ η συνάρτηση είναι ένα προς ένα, ως αντίστροφη. Είναι παραγωγίσιμη με \( (\arcsin(x))' = \frac{1}{\sqrt{1-x^2}} \).Η συνάρτηση τόξο ημιτόνου είναι γνήσια αύξουσα και κοίλη στο [-1,0], γνήσια αύξουσα και κυρτή στο [0,1]. Παρουσιάζει μέγιστο την τιμή π/2 στο 1, ελάχιστο την τιμή -π/2 στο -1 και σημείο καμπής στο 0.
Αντίστροφη συνάρτηση του συνημιτόνου
Θεωρούμε τη συνάρτηση συνημίτονο στο [0,π], όπου είναι ένα προς ένα. Η αντίστροφη συνάρτηση ονομάζεται τόξο συνημιτόνου και συμβολίζεται με arc cos x.
Πεδίο ορισμού του τόξου συνημιτόνου είναι το [-1,1]. Σύνολο τιμών είναι το σύνολο [0,π], ενώ η συνάρτηση είναι ένα προς ένα, ως αντίστροφη. Είναι παραγωγίσιμη με \( (\arccos(x))' = -\frac{1}{\sqrt{1-x^2}} \). Η συνάρτηση τόξο συνημιτόνου είναι γνήσια φθίνουσα και κυρτή στο [-1,0], γνήσια φθίνουσα και κοίλη στο [0,1]. Παρουσιάζει μέγιστο την τιμή π στο -1, ελάχιστο την τιμή 0 στο 1 και σημείο καμπής στο 0.
Υπερβολικές τριγωνομετρικές συναρτήσεις
Κύριο λήμμα: Υπερβολικές συναρτήσεις
Ορισμός υπερβολικών τριγωνομετρικών συναρτήσεων
Ορίζονται με βάση την εκθετική συνάρτηση \( e^x \). Ουσιαστικά είναι η περιττή και άρτια συνάρτηση των οποίων το άθροισμα ισούται με τη συνάρτηση \( e^x \). Ορίζεται:
Υπερβολικό ημίτονο
\( \sinh x = \frac{e^x - e^{-x}}{2} = -i \sin ix \! \)
Υπερβολικό συνημίτονο
\( \cosh x = \frac{e^{x} + e^{-x}}{2} = \cos ix \!\)
Υπερβολική εφαπτομένη
\( \tanh x = \frac{\sinh x}{\cosh x} = \frac {\frac {e^x - e^{-x}} {2}} {\frac {e^x + e^{-x}} {2}} = \frac {e^x - e^{-x}} {e^x + e^{-x}} = \frac{e^{2x} - 1} {e^{2x} + 1} = -i \tan ix \!\)
Υπερβολική συνεφαπτομένη
\( \coth x = \frac{\cosh x}{\sinh x} = \frac {\frac {e^x + e^{-x}} {2}} {\frac {e^x - e^{-x}} {2}} = \frac {e^x + e^{-x}} {e^x - e^{-x}} = \frac{e^{2x} + 1} {e^{2x} - 1} = i \cot ix \!\)
Υπερβολική τέμνουσα
\( \operatorname{sech} x = \frac{1}{\cosh x} = \frac {2} {e^x + e^{-x}} = \sec {ix} \!\)
υπερβολική συντέμνουσα
\( \operatorname{cosech} x = \frac{1}{\sinh x} = \frac {2} {e^x - e^{-x}} = i\,\csc\,ix \!\)
Σύγκριση υπερβολικών (τριγωνομετρικών) συναρτήσεων και (κυκλικών) τριγωνομετρικών συναρτήσεων
Σύγκριση κυκλικών και υπερβολικών τριγωνομετρικών συναρτήσεων. Προσέξτε ότι η ανεξάρτητη μεταβλητή είναι το εμβαδόν του γραμμοσκιασμένου χωρίου.
Παρατηρούμε ότι οι τριγωνομετρικές συναρτήσεις έχουν άμεση σχέση με τις κωνικές τομές. Πιο συγκεκριμένα οι απλές ή κυκλικές τριγωνομετρικές συναρτήσεις αντιστοιχούν σε κύκλο (και κατ' επέκταση σε έλλειψη), ενώ οι υπερβολικές συναρτήσεις στην ισοσκελή υπερβολή (και κατ' επέκταση στις υπερβολές). Αυτό γίνεται αντιληπτό από τις βασικές σχέσεις που συνδέουν τα ημίτονα και τα συνημίτονα:
- cos2x+sin2x=1 Συνδέουν τα ημίτονα και τα συνημίτονα στις απλές τριγωνομετρικές συναρτήσεις. Το σημείο (cos2x,sin2x) ανήκει σε κύκλο ακτίνας 1. Είναι ο μοναδιαίος κύκλος.
- cosh2x-sinh2x=1 Συνδέουν τα ημίτονα και συνημίτονα στις υπερβολικές τριγωνομετρικές συναρτήσεις. Το σημείο (cosh2x,sinh2x) ανήκει στο δεξιό κλάδο ισοσκελούς υπερβολής.
Στο καρτεσιανό σύστημα συντεταγμένων θεωρούμε ένα μοναδιαίο κύκλο και μια ισοσκελής υπερβολή με εξισώσεις x2+y2=1 και x2-y2=1 αντίστοιχα. Θεωρούμε και έναν μεταβλητό ημιάξονα Οz. Έστω το εμβαδόν που περικλείεται από τον ημιάξονα, τον άξονα x'x και το μοναδιαίο κύκλο Εc, και το σημείο τομής του ημιάξονα με τον κύκλο Μc. Έστω, επίσης, το εμβαδόν που περικλείεται από τον ημιάξονα, τον άξονα x'x και την υπερβολή Eh και το σημείο Μh. Αποδεικνύεται ότι όταν το εμβαδόν Ε είναι θ/2, τότε το σημείο Μ έχει συντεταγμένες (συνημίτονο,ημίτονο). Δηλαδή η ανεξάρτητη μεταβλητή των τριγωνομετρικών συναρτήσεων είναι το εμβαδόν (για την ακρίβεια είναι ολοκλήρωμα).
Όμως στις κυκλικες τριγωνομετρικές συναρτήσεις οι ορισμοί βασίζονται στη γωνία και όχι το εμβαδόν. Το φαινομενικό παράδοξο λύνεται από τον τύπο Ε=θ/2, που δίνει το εμβαδόν κυκλικού τομέα συναρτήσει της γωνίας θ (μετρημένη σε ακτίνια.
Γενίκευση των τριγωνομετρικών συναρτήσεων (στους μιγαδικούς αριθμούς)
Η γενίκευση αυτή δε μπορεί να γίνει άμεσα, επειδή δεν υπάρχουν (αντιληπτές) μιγαδικές γωνίες ή εμβαδά. Αρχικά, αποδείχθηκαν ποιες σειρές Taylor αντιστοιχούν στο ημίτονο, το συνημίτονο, το υπερβολικό ημίτονο και το υπερβολικό συνημίτονο. Επαναθεωρώντας τους ορισμούς του ημιτόνου και του συνημιτόνου, μπορούμε να τα ορίσουμε ως σειρές Taylor, δηλαδή ως πολυώνυμα άπειρων όρων. Έτσι, μπορούμε να χρησιμοποιήσουμε ως ανεξάρτητη μεταβλητή οποιονδήποτε μιγαδικό αριθμό. Επίσης, αποδείχθηκαν με βάση αυτές τις σειρές και οι εξής σχέσεις:
Η δημιουργία της γραφικής παράστασης του ημιτόνου. Χρησιμοποιείται ο ακόμη πιο γενικευμένος ορισμός με το μιγαδικό εψιλοτικό μετασχηματισμό.
- eix=cosx+isinx
- eiπ+1=0
- sinx=(eix-e-ix)/2i
- cosx=(eix+e-ix)/2
Στην περίπτωση της πρώτης εξίσωσης, αν θεωρήσουμε την ανεξάρτητη μεταβλητή στον πραγματικό άξονα και την εξαρτημένη στο μιγαδικό επίπεδο, τότε η τρισδιάστατη γραφική παράσταση είναι έλικας.
Κατηγοριοποίηση των τριγωνομετρικών συναρτήσεων
Κυκλικές τριγωνομετρικές συναρτήσεις
Βασικές:
ημίτονο (sinx)
συνημίτονο (cosx) και
εφαπτομένη (tanx)
Δευτερεύουσες:
συνεφαπτομένη (cotx)
τέμνουσα (secx)
συντέμνουσα (cscx)
Αντίστροφες κυκλικών τριγωνομετρικών συναρτήσεων
τόξο ημιτόνου (arcsinx)
τόξο συνημιτόνου (arccosx)
τόξο εφαπτομένης (arctanx)
τόξο συνεφαπτομένης (arccotx)
τόξο τέμνουσας (arcsecx)
τόξο συντέμνουσας (arccscx)
Υπερβολικές τριγωνομετρικές συναρτήσεις
υπερβολικό ημίτονο (sinhx)
υπερβολικό συνημίτονο (coshx)
υπερβολική εφαπτομένη (tanhx)
υπερβολική συνεφαπτομένη (cothx)
υπερβολική τέμνουσα (sechx)
υπερβολική συντέμνουσα (cschx)
Αντίστροφες υπερβολικές συναρτήσεις
αντίστροφη υπερβολικού ημιτόνου (sinhx)−1
αντίστροφη υπερβολικού συνημιτόνου (coshx)−1
αντίστροφη υπερβολικής εφαπτομένης (tanhx)−1
αντίστροφη υπερβολικής συνεφαπτομένης (cothx)−1
αντίστροφη υπερβολικής τέμνουσας (sechx)−1
αντίστροφη υπερβολικής συντέμνουσας (cschx)−1
Χρησιμότητα τριγωνομετρικών συναρτήσεων
Οι τριγωνομετρικές συναρτήσεις έχουν οριστεί τουλάχιστον τρεις φορές, ενώ υπάρχουν τουλάχιστον είκοσι τέσσερις διαφορετικές τριγωνομετρικές συναρτήσεις (υπάρχουν και μερικές που συναντώνται σπάνια και δεν αναφέρονται στο άρθρο). Ο λόγος της μεγάλης ανάπτυξης της μελέτης τους είναι η χρησιμότητά τους στη μηχανική, τη φυσική και άλλες επιστήμες. Ακολουθούν μερικά παραδείγματα:
Συνδέουν τα μήκη των πλευρών των τριγώνων με τις γωνίες τους.
Αυτές οι συναρτήσεις χρησιμοποιούνται στη μοντελοποίηση περιοδικών φαινομένων, όπως η ταλάντωση, το κύμα, το ηλεκτρικό ρεύμα, τις τηλεπικοινωνίες και άλλα.
Εμφανίζονται πολλές φορές στη επίλυση των διαφορικών εξισώσεων.
Χρησιμοποιούνται στον απειροστικό λογισμό, συνήθως στον υπολογισμό ολοκληρωμάτων.
Συνδέουν το ορθοκανονικό σύστημα συντεταγμένων με το πολικό σύστημα συντεταγμένων.
Με βάση αυτές εκφράζονται οι παραμετρικές εξισώσεις των κωνικών τομών.
Συνδέουν τις εκθετικές εκφράσεις με το μιγαδικό επίπεδο.
Δείτε επίσης
ανάλυση Φουριέ
ορθογώνιο τρίγωνο
τριγωνομετρία
υπερβολικές συναρτήσεις
Σύνδεσμοι σε καταλόγους καθιερωμένων όρων
NDL: 00570156
Στο λήμμα αυτό έχει ενσωματωθεί κείμενο από το λήμμα Trigonometric functions της Αγγλικής Βικιπαίδειας, η οποία διανέμεται υπό την GNU FDL και την CC-BY-SA 3.0. (ιστορικό/συντάκτες).
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

