.
Το συνημίτονο είναι ένας σημαντικός τριγωνομετρικός αριθμός, συμβολίζεται με συνθ ή διεθνώς με cosθ. Υπάρχουν τρεις ορισμοί που αποδίδουν το συνημίτονο, όπου ο ένας είναι γενίκευση του άλλου:
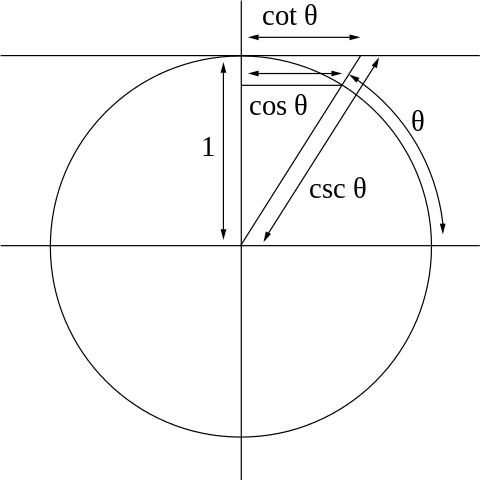
Με βάση το ορθογώνιο τρίγωνο: Σε ένα ορθογώνιο τρίγωνο ορίζεται ως συνημίτονο μίας από τις οξείες γωνίες του τριγώνου το πηλίκο της προσκείμενης κάθετης πλευράς δια την υποτείνουσα. Το συνημίτονο, όπως έχει οριστεί εδώ, μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του μηδενός και μικρότερη του ενός. Η προσκείμενη πλευρά είναι πάντα μικρότερη της υποτείνουσας, άρα το κλάσμα πάντα μικρότερο του ενός. Το όνομα της συνάρτησης οφείλεται στο ημίτονο, είναι ο συνοδευτικός τριγωνομετρικός αριθμός ως προς τη συμπληρωματικότητα των γωνιών, δηλαδή το συνημίτονο μιας γωνίας ισούται με το ημίτονο της συμπληρωματικής της.
Με βάση τον τριγωνομετρικό κύκλο: cosθ=x, όπου x η τετμημένη του σημείου τομής της πλευράς της γωνίας θ και του τριγωνομετρικού κύκλου
Ως ανάπτυγμα σειράς Taylor: cosx=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+...
Η συνάρτηση συνημίτονο όπως ορίστηκε παραπάνω αναφέρεται στο κυκλικό συνημίτονο. Το υπερβολικό συνημίτονο είναι άλλη συνάρτηση. Το συνημίτονο είναι μία μορφή της αρμονικής συνάρτησης.
Ως συνάρτηση το συνημίτονο είναι περιοδική με περίοδο Τ=2π και άρτια.
Χαρακτηριστικά της συνάρτησης συνημίτονο
Γραφική παράσταση της περιόδου [0,2π] της συνάρτησης συνημίτονο.
Πεδίο ορισμού
Συνήθως χρησιμοποιούμε το δεύτερο ορισμό με πεδίο ορισμού το σύνολο των πραγματικών αριθμών.
Συνέχεια-Παραγωγισιμότητα
Η συνάρτηση συνημίτονο είναι συνεχής σε όλο το πεδίο ορισμού της, όπως και παραγωγίσιμη. Επιπλέον, κάθε της παράγωγος είναι παραγωγίσιμη. Ισχύει (cosx)'=-sinx=cos(x+\frac{\pi}{2}), ενώ για τη νιοστή παράγωγο (cosx)^{(\nu)}=cos(x-\frac{\nu\pi}{2}).
Μονοτονία
Σε διάστημα μιας περιόδου (χρησιμοποιείται το τμήμα [0,2π) ως αντιπροσωπευτικό):
Στο [0,π] είναι γνησίως φθίνουσα. Στο [π,2π] είναι γνησίως αύξουσα.
Ακρότατα-Ασύμπτωτες
Η συνάρτηση συνημίτονο δεν έχει σύμπτωτες. Στο διάστημα μιας περιόδου εμφανίζει ένα ελάχιστο, στο π το -1, και ένα μέγιστο, στο 0 (ή το 2π) το 1.
Σύνολο τιμών-Γνωστές τιμές-Ρίζες
Το σύνολο τιμών της εκθετικής συνάρτησης είναι το [-1,1]. Αυτό συνήθως συμβολίζεται από τους μαθηματικούς με |sinx|\le 1, αν και αυτός ο τύπος φράζει τη συνάρτηση χωρίς να προσδιορίζει ακριβώς το σύνολο τιμών. Η συνάρτηση συνημίτονο έχει άπειρες ρίζες της μορφής κπ+π/2, όπου κ ακέραιος αριθμός.
Κοιλοκυρτότητα
Η συνάρτηση ημίτονο είναι κοίλη στο [0,π/2] και κυρτή στο [π/2,3π/2] και κοίλη ξανά στο [3π/2,2π]. Παρουσιάζει σημείο καμπής στα π/2, 3π/2.
Συμμετρίες
Η συνάρτηση συνημίτονο είναι συμμετρική ως προς τον άξονα y'y. Όμως, όπως αρμονική συνάρτηση έχει άπειρους κατακόρυφους άξονες συμμετρίας και σημεία συμμετρίας, τις ρίζες τις.
Δείτε επίσης
Ημίτονο
Πηγές
Το άρθρο βασίστηκε στη διαδικασία της μαθηματικής ανάλυσης συνάρτησης που αναγράφεται στο βιβλίο Μαθηματικά θετικής και τεχνολογικής κατεύθυνσης, ISBN 960-06-0703-6 ΟΕΔΒ εκδόσεις 2008, παράγραφος 2.10, σελίδα 287
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

