Θεωρία κόμβων
αγγλικά : Knot theory
γαλλικά :
γερμανικά :
Στην τοπολογία, η θεωρία κόμβων είναι ο κλάδος που μελετά τους κόμβους. Παρόλο που η αρχική έμπνευση για την έννοια του κόμβου προέρχεται από τους κόμπους που απαντώνται στην καθημερινή ζωή, όπως αυτοί που δημιουργούνται με σχοινιά και κορδόνια, ο μαθηματικός κόμβος διαφέρει στο ότι τα άκρα του είναι ενωμένα και δεν μπορεί να "λυθεί". Σε μαθηματική γλώσσα, ο κόμβος είναι μια ενσωμάτωση ενός κύκλου στον τρισδιάστατο Ευκλείδειο χώρο, R3 (στην τοπολογία, ο όρος "κύκλος" δεν αναφέρεται στην κλασική γεωμετρική έννοια, αλλά σε όλους τους ομοιομορφισμούς του κλασικού σχήματος). Δύο μαθηματικοί κόμβοι είναι ισοδύναμοι αν ο ένας μπορεί να μετασχηματιστεί στον άλλον μέσω μιας παραμόρφωσης του R3 στον εαυτό του (γνωστή ως πλήρης ισοτοπία). Αυτοί οι μετασχηματισμοί αντιστοιχούν σε χειρισμούς μιας χορδής δεμένης σε κόμπο, χωρίς η χορδή να κόβεται ή να περνά μέσα από τον εαυτό της.
Οι κόμβοι μπορούν να περιγραφούν με διάφορους τρόπους αλλά, ανάλογα με τη μέθοδο, κάθε κόμβος μπορεί να αντιπροσωπεύεται από περισσότερες από μία περιγραφές. Για παράδειγμα, μια συνήθης μέθοδος περιγραφής ενός κόμβου είναι ένα γραμμικό διάγραμμα που ονομάζεται διάγραμμα κόμβου. Σε ένα διάγραμμα κόμβου κάθε κύκλος μπορεί να απεικονισθεί με πολλούς διαφορετικούς τρόπους. Συνεπώς, ένα θεμελιώδες πρόβλημα της θεωρίας κόμβων είναι η απόδειξη ότι δύο διαφορετικές περιγραφές αντιπροσωπεύουν τον ίδιο κόμβο. Υπάρχει πλήρης αλγοριθμική λύση σε αυτό το πρόβλημα, με άγνωστη υπολογιστική πολυπλοκότητα. Στην πράξη, οι κόμβοι συχνά διακρίνονται με χρήση της αναλλοίωτης κόμβου, μιας "ποσότητας" που παραμένει σταθερή όταν υπολογίζεται για διαφορετικές περιγραφές ενός κόμβου. Σημαντικές αναλλοίωτες είναι τα πολυώνυμα κόμβων, οι ομάδες κόμβων και οι υπερβολικές αναλλοίωτες.
Το αρχικό κίνητρο για τους μαθηματικούς που θεμελίωσαν τη θεωρία κόμβων ήταν η δημιουργία ενός πίνακα κόμβων και συνδέσμων, δηλαδή κόμβων αποτελούμενων από πολλά μεμονωμένα στοιχεία πεπλεγμένα μεταξύ τους. Από την εποχή που ξεκίνησε η ανάπτυξη της θεωρίας κόμβων, τον 19ο αιώνα, έως σήμερα έχουν πινακογραφηθεί πάνω από έξι δισεκατομμύρια κόμβοι και σύνδεσμοι.
Για να κερδίσουν περαιτέρω γνώσεις, οι μαθηματικοί έχουν ερμηνεύσει τον όρο κόμβο με διαφορετικές έννοιες. Οι κόμβοι μπορούν να θεωρηθούν και σε άλλουςτρισδιάστατους χώρους και σε άλλα αντικείμενα μπορούν να χρησιμοποιηθούν όπως οι κύκλοι: Δες κόμβος(μαθηματικά). Μεγαλύτερων διαστάσεων κόμβοι είναι ν-διαστάσεων σφαίρα σε μ-Διάστασης ευκλείδειο χώρο.
Ιστορία
Κύριο λήμμα: Ιστορία της θεωρίας κόμβων
Intricate Celtic knotwork in the 1200 year old Book of Kells
Οι αρχαιολόγοι έχουν ανακαλύψει ότι το δέσιμο των κόμπων χρονολογείται από τα προϊστορικά χρόνια. Εκτός από τις χρήσεις του ως καταγραφή πληροφοριών και δέσιμο αντικειμένων μαζί, οι κόμβοι ενδιαφέρουν τους ανθρώπους για την αισθητική τους και τον πνευματικό συμβολισμό τους. Οι κόμβοι εμφανίζονται σε διάφορες μορφές της κινέζικης τέχνης που χρονολογούνται πριν από αρκετούς αιώνες Π.Χ (Δες Κινέζικο Δέσιμο). Οι ατελείωτοι κόμποι εμφανίστηκαν στο θιβετιανό βουδισμό, ενώ τα Μπορομέο δακτυλίδια εμφανίστηκαν σε διάφορους πολιτισμούς, και αποτυπώνουν τη δύναμη της ενότητας. Οι Σέλτικ μοναχοί δημιούργησαν Book of Kells πάμπολλες ολόκληρες σελίδες με πολύπλοκους Κέλτικους κόμπους.
Η μαθηματική θεωρία των κόμβων αναπτύχθηκε για πρώτη φορά το 1771 από τον Alexandre-Théophile Vandermonde που επισήμανε ρητά τη σημασία των τοπολογικών χαρακτηριστικών καθώς συζητούσε για τις ιδιότητες των κόμβων που σχετίζονται με τη γεωμετρική τους θέση. Η μαθηματική μελέτη των κόμβων άρχισε το 19ου αιώνα με τον Gauss, που όρισε τη σύνδεση των ολοκληρωμάτων (Silver 2006). Στη δεκαετία του 1860, η θεωρία του Lord Kelvin ότι τα άτομα, αποτελούν κόμβοι μέσα σε αιθέρα οδήγησε τον Peter Guthrie Tait στο να δημιουργήσει την πρώτη ολοκληρωμένη ταξινόμηση των κόμβων σε καταλόγους. Το 1885, δημοσιεύτηκε ένας κατάλογος κόμβων με πάνω από δέκα διελεύσεις, και έγινε γνωστός ως Tait conjectures. Αυτή η καταγραφή κινητοποίησε τους πρώιμους θεωρητικούς ερευνητές των κόμβων , αλλά τελικά η θεωρία των κόμβων έγινε μέρος της αναδυόμενης τοπολογίας.
The first knot tabulator, Peter Guthrie Tait
Οι εξής μαθηματικοί που ασχολούνταν με την τοπολογία στις αρχές του 20ου αιώνα —Max Dehn, J. W. Alexander, και άλλοι— μελέτησαν τους κόμβους από την οπτική γωνία των ομάδων κόμβων και από τη θεωρία της αναλλοίωτης [[ομολογίας (μαθηματική)|ομολογία], όπως Alexander polynomial. Αυτή πρέπει να ήταν η κύρια προσέγγιση της θεωρίας των κόμβων μέχρι τη στιγμή που μία σειρά ανακαλύψεων τη μετατρέπουν σε θέμα .
Στο τέλος της δεκαετίας του 1970 ο William Thurston εισήγαγε την υπερβολική γεωμετρία στη μελέτη των κόμβων με το hyperbolization theorem. Πολλοί κόμβοι υπερβολικοί κόμβοι αποδείχθηκαν, με τη χρήση της γεωμετρίας στον ορισμό των νέων και ισχυρότερων αμετάβλητων κόμβων . Η ανακάλυψη Jones polynomial του Vaughan Jones το 1984 (Sossinsky 2002, σελίδες 71–89), και οι μετέπειτα εισφορές των Edward Witten, Maxim Kontsevich, και άλλων, αποκάλυψε μία βαθιά σύνδεση μεταξύ της θεωρία των κόμβων και άλλων μαθηματικών μεθόδων στη στατιστική μηχανική και στη κβαντική θεωρία πεδίου. Μία πληθώρα σταθερών κόμβων έχει εφευρεθεί από τότε, που άρχισαν να χρησιμοποιούν εξελιγμένα εργαλεία όπως οι κβαντικές ομάδες και Floer homology.
Τις τελευταίες δεκαετίες του 20ου αιώνα, οι επιστήμονες άρχισαν να ενδιαφέρονται για τη μελέτη των θεωρία φυσικών κόμβων με σκοπό να κατανοήσουν το φαινόμενο των κόμβων στο DNA και σε άλλα πολυμερή. Η θεωρία των κόμβων μπορεί να χρησιμοποιηθεί για να αποδειχτεί αν ένα μόριο είναι χειρικό ("μπορείς να το χειριστείς") ή όχι (Simon 1986). Χορδές και με τα δύο άκρα σταθερά , έχουν χρησιμοποιηθεί αποτελεσματικά στη μελέτη της δράσης της τοποισομέρισης στο DNA (Flapan 2000). Η θεωρία των κόμβων είναι ζωτικής σημασίας για την κατασκευή κβαντικών υπολογιστών,μέσω του μοντέλου τοπολογικού κβαντικού υπολογισμού (Collins 2006).
Ισοδύναμα για τους κόμβους
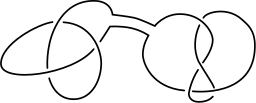
Στα αριστερά, ο μη κόμβος, και ο ισοδύναμος του. Μπορεί να είναι πιο δύσκολο να προσδιορίσεις ένα οποιοδήποτε σύμπλεγμα κόμβων, όπως δεξιά της εικόνας. Στα αριστερά, ο μη κόμβος, και ο ισοδύναμος του. Μπορεί να είναι πιο δύσκολο να προσδιορίσεις ένα οποιοδήποτε σύμπλεγμα κόμβων, όπως δεξιά της εικόνας.
Στα αριστερά, ο μη κόμβος, και ο ισοδύναμος του. Μπορεί να είναι πιο δύσκολο να προσδιορίσεις ένα οποιοδήποτε σύμπλεγμα κόμβων, όπως δεξιά της εικόνας.
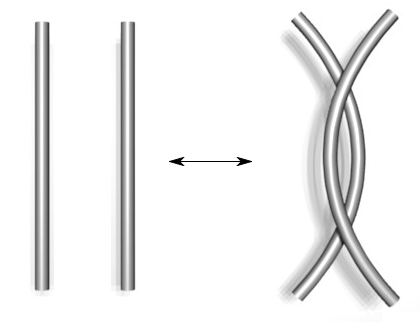
Ένας κόμβος δημιουργείται, αρχικά σε μία -διάσταση με ένα ευθύγραμμο τμήμα, που τυλίγεται αυθαίρετα, και στη συνέχεια ενώνονται τα δύο ελεύθερα άκρα του και σχηματίζει κάτι που μοιάζει με βράχο (Adams 2004)(Sossinsky 2002). Απλά , δεν μπορούμε να πούμε ότι ο κόμβος είναι K μονομορφισμός και μία συνεχής συνάρτηση \( K:[0,1]\to {\mathbb {R}}^{3} \) με \( {\displaystyle K(0)=K(1)} \). Όταν οι μαθηματικοί που ασχολούνταν με την τοπολογία, θεώρησαν τους κόμβους και άλλους πολύπλοκους σχηματισμούς όπως links και braids, θεώρησαν και το χώρο γύρω από τον κόμβο ως ένα παχύρρευστο υγρό. Αν ο κόμβος μπορεί να πιεστεί ομαλά μέσα στο υγρό , χωρίς να τέμνει τον ίδιο ,και μπορεί να συμπιεστεί με άλλον κόμβο, τότε οι δύο κόμβοι θεωρούνται ισοδύναμοι. Η ιδέα των ισοδύναμων κόμβων είναι για να δοθεί ένας ακριβής ορισμός για το πότε πρέπει δύο κόμβοι να θεωρούνται ίδιοι ακόμη και όταν βρίσκονται σε διαφορετικά διαστήματα. Ένας μαθηματικός ορισμός είναι ότι δύο κόμβοι \( K_{1},K_{2} \) είναι ισοδύναμοι αν \( K_{1} \) μπορεί να μετασχηματιστεί σε \( K_{2} \) μέσω ενός μονομορφισμούκαι μίας συνεχής συνάρτησης \( F:[0,1]\times [0,1]\to {\mathbb {R}}^{3} \) όπου \( F(0,x)=K_{1}(x),F(1,x)=K_{2}(x) \) ,και αυτό είναι γνωστό ως περιβάλλων ισοτοπία.
Το βασικό πρόβλημα της θεωρίας των κόμβων, αναγνώριση προβλημάτων, είναι το να προσδιορίσεις δύο ισοδύναμους κόμβους. Οι Αλγόριθμοι υπάρχουν για να λύσουν αυτό το πρόβλημα, με τον πρώτο να δίνεται από τον Wolfgang Haken στο τέλος της δεκαετίας του 1960 (Hass 1998). Παρόλα αυτά, οι αλγόριθμοι αυτοί μπορεί να είναι πολλοί χρονοβόροι , και το μείζων θέμα της θεωρίας είναι να καταλάβουμε πόσο δύσκολο είναι αυτό το πρόβλημα στην πραγματικότητα (Hass 1998). Η ειδική περίπτωση της αναγνώρισης των μη κόμβων, ονομάζεται μη κομβικό πρόβλημα, και έχει ιδιαίτερο ενδιαφέρον (Hoste 2005).
Διαγράμματα Κόμβων
Ένας χρήσιμος τρόπος για να απεικονίσεις και να χειριστείς τους κόμβους είναι να τους προβάλεις πάνω σε ένα επίπεδο —και σκεφτείτε τον κόμβο ως μία σκιά στον τοίχο. Μία μικρή αλλαγή στην κατεύθυνση της προβολής θα εξασφαλίσει ότι αυτός είναι 1 προς 1 εκτός από τα διπλά σημεία, που ονομάζονται διασταυρώσεις, όπου η "σκιά" των κόμβων διασχίζει τα ίδια μία φορά εγκάρσια (Rolfsen 1976). Κάθε διασταύρωση , είναι ικανή να δημιουργήσει έναν γνήσιο κόμβο, όπου το πάνω μέρος του θα πρέπει να διακρίνεται από το κάτω. Αυτό συχνά γίνεται με τη δημιουργία ενός σχίσματος που είναι προς τα κάτω. Το διάγραμμα που προκύπτει είναι μία immersed plane curve με τα αντίστοιχα στοιχεία της να είναι πάνω και κάτω από τις αντίστοιχες διασταυρώσεις . (Αυτά τα διαγράμματα ονομάζονται Διαγράμματα κόμβων όταν αντιπροσωπεύουν Κόμβους σύνδεση διαγραμμάτων όταν αντιπροσωπεύουν σύνδεση.) Αναλογικά,κόμβοι σε επιφάνεια 4-χώρων μπορούν να είναι συναφή με μία βυθισμένη επιφάνεια 3-χώρων.
Ένα μειωμένο διάγραμμα είναι ένα διάγραμμα κόμβου στο οποίο δεν υπάρχουν αναγώγιμες διασταυρώσεις ( μηδαμινές ή αφαιρούμενες διασταυρώσεις), στο οποίο δηλαδή όλες οι αναγώγιμες διασταυρώσεις έχουν αφαιρεθεί.(Weisstein, ReducedKnotDiagram)(Weisstein, ReducibleCrossing)
Κινήσεις Reidemeister
Κύριο λήμμα: κινήσεις Reidemeister
Το 1927, δουλεύοντας με αυτό το διάγραμμα των κόμβων ο, J. W. Alexander και G. B. Briggs, και ανεξάρτητα ο Kurt Reidemeister, έδειξαν ότι τα δύο διαγράμματα των κόμβων ανήκουν στον ίδιο κόμβο και μπορούν να συσχετιστούν με τη βοήθεια μιας σειράς τριών ειδών κινήσεων ,όπως φαίνεται παρακάτω. Αυτοί οι χειρισμοί, τώρα ονομάζονται κινήσεις Reidemeister είναι:
Στρίψε και ξέστριψε ως προς οποιαδήποτε κατεύθυνση.
Μετακινήστε το ένα σκέλος πάνω στο άλλο.
Μετακινήστε το ένα σκέλος πάνω ή κάτω από μία διασταύρωση.
Reidemeister moves
Η απόδειξη ότι τα διαγράμματα των ισοδύναμων κόμβων από τις Κινήσεις Reidemeister βασίζονται πάνω σε μία ανάλυση δηλαδή συμβαίνει κάτω από την επίπεδη προβολή της κίνησης, παίρνει δηλαδή τον ένα κόμβο πάνω στον άλλο . Η κίνηση μπορεί να οριστεί έτσι ώστε τον περισσότερο χρόνο η προβολή να είναι ένα διάγραμμα κόμβου , εκτός βέβαια αν είναι πεπερασμένη και αυτό συμβαίνει όταν επέρχεται ένα "γεγονός" ή μία "καταστροφή" , όπως όταν διασταυρώνονται δύο ή περισσότερα σκέλη σε ένα σημείο ή όταν πολλά σκέλη γίνονται εφαπτομένη σε ένα σημείο . Μια προσεκτική παρατήρηση θα δείξει ότι τα πολύπλοκα γεγονότα μπορούν να εξαλείφουν, αφήνοντας μόνο απλούστερα : (1) ένας "κόμβος" μπορεί να ρυθμιστεί ή να διαμορφωθεί; (2) δύο σκέλη μετατρέπονται σε μία εφαπτομένη σε ένα σημείο, από το οποίο στη συνέχεια διέρχεται; και (3) τρία σκέλη διασταυρώνονται σε ένα σημείο. Αυτές είναι τις κινήσεις Reidemeister (Sossinsky 2002, ch. 3) (Lickorish 1997, ch. 1).
Αναλλοίωτοι κόμβοι
Πρότυπο:Κύριο μέρος Ένας αναλλοίωτος κόμβος είναι μια "ποσότητα" η οποία είναι ίδια με τον ισοδύναμο κόμβο (Adams 2004)(Lickorish 1997)(Rolfsen 1976).Για παράδειγμα,εάν ο αναλλοίωτος κόμβος υπολογίζεται από ένα διάγραμμα,θα πρέπει να δώσει την ίδια τιμή για δύο διαγράμματα κόμβων που αντιπροσωπεύουν τον ισοδύναμο κόμβο.Ένας αναλλοίωτος κόμβος μπορεί να πάρει την ίδια τιμή για δύο διαφορετικούς κόμβους,έτσι από μόνος του είναι ικανός να αναγνωρίσει όλους τους κόμβους.Ένας στοιχειώδες αναλλοίωτος κόμβος είναι τρίχρωμος.
Ο "κλασικός" αναλλοίωτος κόμβος περιλαμβάνει την ομάδα κόμβων, η οποία είναι η βασική ομάδα του συμπληρωματικού κόμβου, και το πολυώνυμο Alexander, το οποίο μπορεί να υπολογιστεί από τον αναλλοίωτο κόμβο του Alexander,μια μονάδα που κατασκευάζεται από το άπειρο κυκλικό κάλυμμα ου συμπληρωματικού κόμβου (Lickorish 1997)(Rolfsen 1976).Στα τέλη του 20 αιώνα,αναλλοίωτοι κόμβοι όπως οι κόμβοι "κβαντικών" πολυώνυμων, οι αναλλοίωτοι του Vasilliev και οι υπερβολικοί αναλλοίωτοι κόμβοι ανακαλύφθηκαν.Αυτοί οι προαναφερθείς αναλλοίωτοι κόμβοι είναι μόνο η κορυφή του παγόβουνου της σύγχρονης θεωρίας κόμβων.
Πολυώνυμα κόμβων
Κύριο λήμμα: Πολυώνυμα Κόμβων
Ένα πολυώνυμο κόμβου είναι ένας αναλλοίωτος κόμβος που είναι πολυώνυμο.Πολύ γνωστά παραδείγματα περιλαμβάνουν τα πολυώνυμα του Jones και του Alexander.Μια παραλλαγή του πολυωνύμου Alexander,το πολυώνυμο Alexander–Conway,είναι ένα πολυώνυμο ως προς την μεταβλητή "z" με ακεραίους συντελεστές (Lickorish 1997).
Το πολυώνυμο Alexander-Conmway στην πραγματικότητα ορίζεται με βάση τον σύνδεσμο,στην οποία περιέχονται από ένας ή περισσότεροι κόμβοι μπλεγμένοι μεταξύ τους.Οι έννοιες εξηγούνται και παραπάνω για τους κόμβους ,π.χ διαγράμματα και κινήσεις Reidemeister,περιέχουν τον σύνδεσμο αυτόν.
Σκεφτείτε ένα προσανατολισμένο διάγραμμα με σύνδεσμο, δηλαδή ένα στο οποίο κάθε συνιστώσα του συνδέσμου έχει μια προτιμώμενη κατεύθυνση που υποδεικνύεται με ένα βέλος. Για μια δεδομένη διάβαση του διαγράμματος,έστω τα ω L_{+},L_{-},L_{0} \), τα προσανατολισμένα διαγράμματα που προκύπτουν από την αλλαγή του διαγράμματος όπως φαίνεται στην εικόνα:

Το αρχικό διάγραμμα μπορεί να είναι το \( L_{+} \) or \( L_{-}, \) το οποίο εξαρτάται από την διαμόρφωση της διέλευσης του. Τότε το πολυώνυμο των Alexander–Conway,C(z),ορίζεται αναδρομικά από τους κανόνες:
C(O) = 1 (οπού το Ο είναι το διάγραμμα του μη-κόμβου)
\( C(L_{+})=C(L_{-})+zC(L_{0}). \)
Ο δεύτερος κανόνας συχνά αναφέρεται ως σχέση κουβάρι. Για να ελέγξουμε ότι αυτοί οι κανόνες μας δίνουν έναν αναλλοίωτο κόμβο που περνάει από ένα προσανατολισμένο σύνδεσμο,πρέπει κανείς να προσδιορίσει ότι το πολυώνυμο δεν αλλάζει στο πλαίσιο των τριών κινήσεων του Reidemeister. Πολλά σημαντικά πολυώνυμα κόμβων μπορούν να οριστούν με αυτό τον τρόπο.
Το ακόλουθο είναι ένα τυπικό παράδειγμα υπολογισμού,χρησιμοποιώντας μια σχέση κουβάρι.Που υπολογίζει το πολυώνυμο Alexander-Conway του τριφυλλοειδούς κόμβου. Οι κίτρινες κηλίδες μας δείχνουν που εφαρμόζεται η σχέση.
δίνει τον μη-κόμβο και την σχέση Hopf. Εφαρμόζοντας την σχέση στον δεσμό Hopf,όπου ενδεικνύεται,
δίνει μια σχέση που παραμορφώνεται σε ένα κόμβο με 0 διαβάσεις(στην πραγματικότητα μας δίνει την αποσύνδεση των δύο κόμβων) και ένα μη-κόμβο. Η αποσύνδεση των κόμβων θέλει λίγο υπουλότητα:
γεγονός που συνεπάγεται ότι C(η αποσύνδεση των δύο κόμβων) = 0, δεδομένου ότι τα δύο πολυώνυμα περιέχουν τον μη-κόμβο επομένως είναι ίσα .
Περιλαμβάνοντας όλα αυτά μαζί προκύπτει ότι:
C(τριφύλλι) = 1 + z (0 + z) = 1 + z2.
Εφόσον το πολυώνυμο Alexander-Conway είναι ένας αναλλοίωτος κόμβος, αυτό δείχνει ότι το τριφύλλι δεν είναι ισοδύναμο με τον μη-κόμβο. Έτσι στην πραγματικότητα το τριφύλλι είναι "δεμένο".
-
Το αριστερόστροφο τριφύλλι κόμβος.
Στην πραγματικότητα ,υπάρχουν δύο κόμβοι τριφύλλια, που ονομάζονται αριστερόστροφα και δεξιόστροφα τριφύλλια, τα οποία είναι κατοπτρική εικόνα μεταξύ τους (κάντε ένα σχέδιο του τριφυλλιού που δίνεται πάνω και αλλάξτε κάθε διέλευση προς την άλλη πλευρά για να πάρετε την κατοπτρική εικόνα). Τα τριφύλλια δεν είναι ισοδύναμα μεταξύ τους, πράγμα που σημαίνει ότι δεν είναι και αμφίχειρες(δηλαδή γυρνώντας το σχήμα αριστερόστροφα ή δεξιόστροφα να καταλήξουμε στο ίδιο αποτέλεσμα). Αυτό αποδείχτηκε από τον Max Dehn, πριν την ανακάλυψη των πολυωνύμων κόμβων,χρησιμοποιώντας θεωρητικές μεθόδους (Dehn 1914). Αλλά το πολυώνυμο Alexander-Conway του κάθε είδους τριφυλλιού είναι το ίδιο, όπως μπορεί να φανεί με τον υπολογισμό μέσω της μετάβασης της κατοπτρικής εικόνας. Το πολυώνυμο Jones μπορεί να αναγνωριστεί από τα αριστερόστροφα και δεξιόστροφα τριφύλλια κόμβοι (Lickorish 1997).
Υπερβολικοί αναλλοίωτοι κόμβοι
Ο William Thurston απέδειξε ότι πολύ κόμβοι είναι υπερβολικοί, που σημαίνει ότι ο συμπληρωματικός κόμβος, δηλαδή το σύνολο των σημείων σε ένα χώρο 3-διαστάσεων που δεν περιλαμβάνονται στο κόμβο, παραδέχονται μια γεωμετρική δομή, συγκεκριμένα μια δομή της υπερβολικής γεωμετρίας. Η υπερβολική δομή εξαρτάται μόνο από τον κόμβο, έτσι ώστε οποιαδήποτε ποσότητα και να υπολογίζεται από την υπερβολική δομή να είναι ένας αναλλοίωτος κόμβος (Adams 2004).
Τα δαχτυλίδια του Borromean είναι ένας σύνδεσμος με την ιδιότητα ότι αν αφαιρέσουμε ένα δαχτυλίδι αποσυνδέονται και τα υπόλοιπα.
Η προβολική όψη του SnapPea: η συμπλήρωση των δαχτυλιδιών Borromean από την οπτική ενός κατοίκου που μένει κοντά στα κόκκινο συστατικό (κόκκινο δαχτυλίδι).
Η γεωμετρία μας επιτρέπει αν δούμε πως μοιάζει το εσωτερικό ενός συμπληρωματικού κόμβου ή συνδέσμου, θα μπορούσε να παρομοιαστεί με τις ακτίνες του φωτός που ταξιδεύουν κατά μήκος του γεωδαιτικού της γεωμετρίας.Ένα παράδειγμα μας παρέχετε από την εικόνα που δείχνει το συμπλήρωμα των δαχτυλιδιών του Borromean. Οι κάτοικοι αυτού του συμπληρωματικού συνδέσμου βλέπουν τον χώρο από κοντά από το κόκκινο συστατικό. Οι σφαίρες στην εικόνα είναι οπτικές της χώρο σφαιρικής γειτονιάς του συνδέσμου. Με την πύκνωση του συνδέσμου με ένα τυποποιημένο τρόπο,λαμβάνονται οι χώρο σφαιρικές γειτονιές του συνδέσμου. Ακόμη και αν το όριο της γειτονίας είναι ένας τόρος,όταν βλέπουμε μέσα από το συμπληρωματικός σύνδεσμο,μοιάζει με σφαίρα. Κάθε συστατικό στοιχείο του συνδέσμου εμφανίζεται να έχει άπειρους τομείς (ενός χρώματος),καθώς υπάρχουν άπειρες ακτίνες φωτός που φτάνουν από τον παρατηρητή στο συστατικό στοιχείο του συνδέσμου. Το θεμελιώδες παραλληλόγραμμο(που εμφανίζεται στη εικόνα),δημιουργεί σχηματισμούς που μοιάζουν με πλακάκια τόσο οριζόντια όσο και κάθετα και μας δείχνει πως επεκτείνετε το σχέδιο των σφαιρών στο άπειρο.
Αυτό το μοτίβο,το χώρο σφαιρικό μοτίβο,είναι από μόνο του ένα χρήσιμο αναλλοίωτο κομβικό. Άλλα αναλλοίωτα υπερβολικά κομβικά περιλαμβάνουν ένα θεμελιώδες παραλληλόγραμμο, το μήκος του μικρότερου γεωδαιτικού και τον όγκο. Η σύγχρονες προσπάθειες πινακοποίηση των κόμβων και των συνδέσμων έχουν χρησιμοποίηση αυτές της σταθερές αποτελεσματικά. Οι γρήγοροι υπολογιστές και οι έξυπνες μέθοδοι έχουν κάνει τον υπολογισμό αυτών των αναλλοίωτων κόμβων,στην πράξη,μια πολύ εύκολη υπόθεση (Adams, Hildebrand & Weeks 1991).
Υψηλότερες διαστάσεις
Ένας κόμβος στις 3-διαστάσεις μπορεί να λυθεί όταν τοποθετηθεί στις 4-διαστάσεις. Αυτό γίνεται αλλάζοντας της διαβάσεις. Υποθέστε ότι το ένα νήμα είναι πίσω από ένα άλλο όπως φαίνεται από μια συγκεκριμένη οπτική γωνιά. Τοποθετήστε τον κόμβο στις 4 διαστάσεις, πιάστε το μπροστινό σκέλος (το μπροστινό σκέλος δεν έχει εμπόδιο εκεί), ύστερα μετακινήστε το προς τα εμπρός, και αφήστε το να πέσει πίσω, τώρα μπροστά έχουμε το πίσω σκέλος του κόμβου.Η ανάλογη διαδικασία για ένα επίπεδο θα ήταν να αφαιρέσουμε μια χορδή από την επιφάνεια,όπως και για τη σφαίρα να αφαιρέσουμε ένα σημείο από το εσωτερικό της.
Κανονικά, στις 4 διαστάσεις, κάθε μη-τεμνόμενος κλειστός βρόχος μιας μονοδιάστατης χορδής είναι ισοδύναμη με έναν μη-κόμβο. Αρχικά τοποθετήστε τον βρόχο μέσα σε ένα υποχώρο 3-διαστάσεων, πράγμα το οποίο γίνεται κάθε φορά, αν και πολύ σύνθετο για να εξηγηθεί.
Σφαίρες κόμβοι υψηλότερων διαστάσεων
Από την στιγμή που ένας κόμβος μπορεί να θεωρηθεί τοπολογικά μια σφαίρα 1-διάστασης, η επόμενη γενίκευση είναι να θεωρήσουμε μια μια σφαίρα 2-διαστάσεων να ενσωματώνετε μέσα σε μια σφαίρα 4-διαστάσεων. Σε μια τέτοια ενσωμάτωση ο κόμβος λύνεται αν υπάρχει ένας ομοιομορφισμός της σφαίρας 4 διαστάσεων στον εαυτό της, μεταμορφώνοντας έτσι την 2-σφαίρα σε μια "στρόγγυλη" σφαίρα 2 διαστάσεων. Αιωρούμενοι κόμβοι και περιστρεφόμενοι κόμβοι είναι κλασικές περιπτώσεις τέτοιων 2-σφαιρών κόμβων. Η μαθηματική τεχνική που ονομάζεται "γενική τοποθεσία" συνεπάγεται ότι για μια δοσμένη ν-σφαίρα μέσα στην κ-σφαίρα, αν το κ είναι αρκετά μεγάλο (βέβαια αυτό εξαρτάται και από το ν), η σφαίρα θα πρέπει να πάψει να είναι κόμβος. Γενικά, η τμηματικά συνεχής ν-σφαίρα δημιουργεί κόμβους μόνο (ν + 2)-διάστημα (Zeeman 1963), αν και πλέον αυτό δεν είναι προϋπόθεση για τις σφαίρες ομαλών κόμβων.}}, αν και αυτό δεν είναι πλέον προϋπόθεση για να υπάρξουν σφαίρες με ομαλούς κόμβους. Βασικά, υπάρχουν (4κ − 1)-σφαίρες με ομαλούς κόμβους σε 6κ-διάστημα, π.χ υπάρχει μια 3-σφαίρα με ομαλούς κόμβους στο 6-διάστημα (Haefliger 1962)(Levine 1965).Έτσι διαδικασία μετατροπής σε διανύσματα ενός ομαλού κόμβου μπορεί να είναι αυθαίρετα μεγάλη όταν δεν διορθώνεται η διάσταση της σφαίρας κόμβου, ωστόσο οποιαδήποτε ομαλή κ-σφαίρα μέσα σε μια ν-σφαίρα ,αν ισχύει 2ν − 3κ − 3 > 0 μπορεί να πάψει να είναι κόμβος. Η έννοια ενός κόμβου έχει έχει πολύ μεγαλύτερη γενίκευση στα μαθηματικά, δείτε: μαθηματικοί κόμβοι, κατάταξη ισότοπης εμβυθίσεως.
Κάθε κόμβος στο Sν είναι ένας σύνδεσμος μιας πραγματική αλγεβρική δομή με μοναδικότητα στο Rν+1 (Akbulut & King 1981).
Ένας ν-κόμβος είναι μια μοναδική Sn εμβύθιση στο Sμ. Ένας ν-σύνδεσμος είναι κ-αντιγραφές του Sν το οποίο βρίσκεται εμβυθισμένος στο Sμ, όπου κ είναι πραγματικός αριθμός. Οι δύο περιπτώσεις μ = ν + 2 περίπτωση και η μ > ν + 2 περίπτωση είναι ορισμένες καλά.Η ν > 1 περίπτωση έχει διαφορετικές βλέψεις από την ν = 1 περίπτωση και είναι ένα πολύ ενδιαφέρον πεδίο που αξίζει να ασχοληθεί κανείς .[1] [2]
Πρόσθεση κόμβων
Κύριο λήμμα: Άθροισμα κόμβων
Δύο κόμβοι μπορούν να προστεθούν, κόβοντας και τους δύο κόμβους και ενώνοντας τα ζεύγη των ακρών τους . Η διαδικασία αυτή ονομάζεται άθροισμα κόμβων, ή μερικές φορές συνδεδεμένο άθροισμα ή σύνθεση των δύο κόμβων. Αυτό μπορεί να οριστεί επίσημα ως εξής (Adams 2004): Να θεωρήσουμε μία επίπεδη προβολή του κάθε κόμβου και να υποθέσουμε ότι αυτές οι προβολές είναι ξένες μεταξύ τους. Στη συνέχεια, βρίσκουμε ένα ορθογώνιο στο επίπεδο, όπου ένα ζευγάρι από αντίθετες πλευρές είναι κατά μήκος του κάθε κόμβου ενώ το υπόλοιπο μέρος του ορθογωνίου δεν συνδέεται από τους κόμβους. Προκειμένου να δημιουργηθεί ένας νέος κόμβος, διαγράφουμε το πρώτο ζεύγος των αντίθετων πλευρών και το παρακείμενο του άλλου ζεύγους των αντίθετων πλευρών . Ο κόμβος που προκύπτει είναι το άθροισμα των δύο αρχικών κόμβων. Με ανάλογο τρόπο , δύο διαφορετικοί κόμβοι (αλλά όχι περισσότεροι) μπορούν να προκύψουν. Αυτή η ασάφεια που αφορά το άθροισμα των κόμβων, μπορεί να εξαλειφθεί προσανατολισμό, π.χ. έχει μία προτεινόμενη κατεύθυνση διασχίζοντας κατά μήκος τον κόμβο, και απαιτώντας το άθροισμα των τόξων των κόμβων να είναι προσανατολισμένο με σταθερό προσανατολισμό το όριο του ορθογωνίου.
Το άθροισμα κόμβων είναι ένας προσανατολισμένος κόμβος αντιμεταθετικός και συνειρμικός. Κόμβος είναι πρώτος Αν αυτός είναι μη τετριμμένος και δεν μπορεί να γραφεί ως άθροισμα δύο μη τετριμμένων κόμβων. Ένας κόμβος που μπορεί να γραφεί ως άθροισμα είναι σύνθετος. Υπάρχει μία πρώτη αποσύνθεση για τους κόμβους, ανάλογα με τον πρώτο και τους σύνθετους αριθμούς (Schubert 1949). Για τον προσανατολισμό των κόμβων, αυτή η αποσύνθεση είναι επίσης μοναδική. Για Μεγαλύτερες-Διαστάσεις κόμβων, μπορούν επίσης να προστεθούν , αλλά υπάρχουν μερικές διαφορές . Παρόλο που δεν μπορεί να προκύψει ένας μη κόμβος σε τρεις διαστάσεις προσθέτοντας δύο μη τετριμμένους κόμβους ,μπορεί να προκύψει σε μεγαλύτερες διαστάσεις, τουλάχιστον όταν θεωρηθούν λείοι κόμβοι μέσα σε συνδιάσταση τουλάχιστον 3.
Ταξινόμηση Κόμβων
Δείτε επίσης: List of prime knots και Knot tabulation
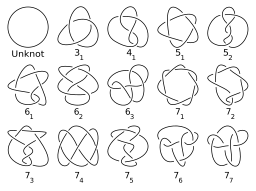
Ένας πίνακας πρώτων κόμβων μέχρι εφτά διασταυρώσεων. Οι κόμβοι σημειώνονται με τον συμβολισμό Alexander–Briggs
Παραδοσιακά, οι κόμβοι ταξινομούνταν ανάλογα με τους αριθμούς διασταύρωσης. Οι πίνακες κόμβων γενικά περιλαμβάνουν μόνο πρώτους κόμβους και μόνο μία είσοδο για τον κόμβο και την κατοπτρική του εικόνα (ακόμα και αν διαφέρουν) (Hoste, Thistlethwaite & Weeks 1998). Ο αριθμός των τετριμένων κόμβων ενός δοσμένου αριθμού διασταύρωσης αναπτύσσεται γρήγορα, καθιστώντας την ταξινόμηση δύσκολη, από υπολογιστικής πλευράς (Hoste 2005, σελ. 20). Παρόλα αυτά οι επιτυχημένες προσπάθειες απαριθμούνται σε περισσότερες από 6 δισεκατομμύρια κόμβους και συνδέσμους (Hoste 2005, σελ. 28). Η ακολουθία των αριθμών των πρώτων κόμβων ενός δοσμένου αριθμού διασταύρωσης, μέχρι τον αριθμό διασταύρωσης 16, είναι η εξής: 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705... (ακολουθία A002863 στην OEIS). Παρ’ όλο που τα εκθετικά άνω και κάτω φράγματα είναι γνωστά, δεν έχεις αποδειχθεί αν αυτή η ακολουθία είναι γνησίως αύξουσα (Adams 2004).
Στους πρώτους πίνακες κόμβων από τους Tait, Little, και Kirkman χρησιμοποιούνταν διαγράμματα κόμβων, ενώ ο Tait είχε χρησιμοποιήσει επίσης έναν πρώιμο συμβολισμό του συμβολισμού Dowker. Διαφορετικοί συμβολισμοί εφευρέθηκαν για τους κόμβους, οι οποίοι καθιστούσαν ευκολότερη την ταξινόμηση τους (Hoste 2005).
Στους πρώιμους πίνακες δοκιμάστηκε να καταγραφούν όλοι οι κόμβοι το πολύ 10 διασταυρώσεων και όλοι οι εναλλασσόμενοι κόμβοι 11 διασταυρώσεων (Hoste, Thistlethwaite & Weeks 1998). Η ανάπτυξη της θεωρίας κόμβων χάρις τους Alexander, Reidemeister, Seifert, και άλλων διευκόλυνε το έργο της επαλήθευσης και οι πίνακες κόμβων μέχρι και 9 διασταυρώσεων δημοσιεύτηκαν από τους Alexander–Briggs και Reidemeister στα τέλη του 1920.
Η πρώτη σημαντική επαλήθευση αυτής της δουλειάς έγινε στην δεκαετία του 1960 από τον John Horton Conway, ο οποίος δεν ανέπτυξε μόνο έναν συμβολισμό αλλά και το Πολυώνυμο Alexander–Conway επίσης (Conway 1970)(Doll & Hoste 1991). Αυτό επαλήθευσε τη λίστα κόμβων το πολύ 11 διασταυρώσεων και μία νέα λίστα συνδέσμων μέχρι και 10 διασταυρώσεων. Ο Conway βρήκε έναν αριθμό παραλείψεων, αλλά μόνο μία επικάλυψη στον μικρό πίνακα–Tait. Παρόλα αυτά δεν εντόπισε τις επικαλύψεις που αποκαλούνται Ζεύγος Perko, το οποίο βρέθηκε το 1974 από τον Kenneth Perko (Perko 1974). Αυτό το διάσημο λάθος πολλαπλασιάστηκε όταν ο Dale Rolfsen πρόσθεσε έναν πίνακα κόμβων στο επηρεασμένο κείμενο του βασισμένο στη δουλειά του Conway. Η μοναδική διατριβή του Conway στη θεωρία κόμβων επίσης περιέχει τυπογραφικές επικαλύψεις στους μη-εναλλασσόμενους 11-διασταυρώσεων κόμβους και παραλείπει 4 παραδείγματα, από τα οποία 2 έχουν συμπεριληφθεί στην διατριβή του D. Lombardero το 1968 στο Princeton και 2 ακόμα που ανακαλύφθηκαν από τον A. Caudron. Λιγότερο γνωστή είναι η επικάλυψη που έκανε στον πίνακα συνδέσμων 10 διασταυρώσεων: 2.-2.-20.20 που είναι ο κατοπτρισμός του 8*-20:-20.
Στα τέλη του 1990s οι Hoste, Thistlethwaite, και Weeks ταξινόμησαν όλους τους κόμβους μέχρι και 16 διασταυρώσεων (Hoste, Thistlethwaite & Weeks 1998). Το 2003 οι Rankin, Flint, και Schermann, ταξινόμησαν τους εναλλασσόμενους κόμβους μέχρι και 22 διασταυρώσεων(Hoste 2005).
Συμβολισμός Alexander–Briggs
Αυτός είναι ο πιο συνηθισμένος συμβολισμός, λόγω της διατριβής του J. W. Alexander και του G. Briggs το 1927 που αργότερα επεκτάθηκε από τον Dale Rolfsen στον πίνακα κόμβων του (δείτε την εικόνα παραπάνω και τη Λίστα πρώτων κόμβων). Ο συμβολισμός απλώς ταξινομεί τους κόμβους σύμφωνα με τον αριθμό διασταυρώσεων τους. Οι αριθμοί διασταύρωσης γράφονται με έναν δείκτη , που υποδηλώνει την τάξη του ανάμεσα σε όλους τους κόμβους αυτού του αριθμού διασταύρωσης. Αυτή η τάξη είναι αυθαίρετη απότε δεν έχει ιδιαίτερη σημασία (παρ'όλα αυτά σε κάθε αριθμό διασταύρωσης ο κόμβος twist ακολουθεί μετά τον σπειροειδή κόμβο). Οι σύνδεσμοι γράφονται ανά αριθμό διασταύρωσης με έναν εκθέτη, που υποδηλώνει τον αριθμό των συνιστωσών και έναν δείκτη, που υποδηλώνει την τάξη ανάμεσα σε όλους τους συνδέσμους με τον ίδιο αριθμό συνιστοσών και διασταυρώσεων. Έτσι ο κόμβος trefoil συμβολίζεται ως 31 και ο σύνδεσμος Hopf ως 22
1.
Συμβολισμός Dowker
Ένα διάγραμμα κόμβων με διασταυρώσεις σημειωμένες με τον συμβολισμό Dowker
Ο συμβολισμός Dowker, ονομαζόμενος επίσης και συμβολισμός ή κώδικας Dowker–Thistlethwaite, για έναν κόμβο είναι μία πεπερασμένη ακολουθία άρτιων ακεραίων. Οι αριθμοί προκύπτουν ακολουθώντας τους κόμβους και σημειώνοντας τις διασταυρώσει με διαδοχικούς ακεραίους. Καθώς κάθε διασταύρωση συναντιέται δύο φορές δημιουργείται ένα ζεύγος άρτιων ακεραίων και περιττών ακεραίων. Ένα κατάλληλο πρόσημο δίνετε για δηλώσει την άνω και την κάτω διασταύρωση. Για παράδειγμα, ο κόμβος του διαγράμματος έχει διασταυρώσεις σημειωμένες με τα ζεύγη (1,6) (3,−12) (5,2) (7,8) (9,−4) και (11,−10). Οπότε ο συμβολισμός Dowker σύμφωνα με αυτή τη σήμανση είναι η ακολουθία: 6 −12 2 8 −4 −10. Το διάγραμμα ενός κόμβου έχει περισσότερους από έναν συμβολισμούς Dowker και υπάρχει μία κατανοητή ασάφεια όταν ανακατασκευάζεται ένας κόμβος από έναν συμβολισμό Dowker.
Συμβολισμός Conway
Ο συμβολισμός Conway για κόμβους και συνδέσμους, ονομαζόμενος από τονJohn Horton Conway, είναι βασισμένος στη θεωρία διαπλοκών (Conway 1970). Το πλεονέκτημα αυτού του συμβολισμού είναι ότι αναπαριστά κάποια χαρακτηριστικά των κόμβων και των συνδέσμων.
Ο συμβολισμός περιγράφει πως θα κατασκευαστεί ένα συγκεκριμένο διάγραμμα του συνδέσμου. Ξεκινάμε με ένα “βασικό πολύεδρο”, ένα 4-δύναμο ενωμένο επίπεδο γράφημα χωρίς digon περιοχές. Ένα τέτοιο πολύγωνο σημειώνεται πρώτα από τον αριθμό των κορυφών και στη συνέχεια από έναν αριθμό αστερίσκων, ο οποίος καθορίζει την θέση του πολυέδρου στη λίστα των βασικών πολυέδρων. Για παράδειγμα, το 10** δηλώνει το δεύτερο πολύεδρο με 10 κορυφές στη λίστα του Conway.
Κάθε κορυφή έπειτα έχει μία αλγεβρική διαπλοκή υποκατεστημένη σ’ αυτή (κάθε κορυφή είναι προσανατολισμένη έτσι ώστε να μην είναι αυθαίρετη η επιλογή της αντικατάστασης). Κάθε τέτοια διαπλοκή έχει ένα συμβολισμό που αποτελείται από αριθμούς και + ή − σύμβολα.
Ένα παράδειγμα είναι το 1*2 −3 2. To 1* δηλώνει το μόνο βασικό πολύεδρο με μία κορυφή. Το 2 −3 2 είναι μία ακολουθία που περιγράφει το συνεχές κλάσμα που σχετίζεται με μία ρητή διαπλοκή. Κάποιος μπορεί να εισαγάγει αυτή τη διαπλοκή στην κορυφή του βασικού πολυέδρου 1*.
Ένα πιο περίπλοκο παράδειγμα είναι το 8*3.1.2 0.1.1.1.1.1 Εδώ το 8* επίσης αναφέρεται στο βασικό πολύεδρο με 8 κορυφές. Οι τελείες χωρίζουν τον συμβολισμό για κάθε διαπλοκή.
Οποιοσδήποτε σύνδεσμος δέχεται τέτοια επεξήγηση και είναι ξεκάθαρο πως αυτός είναι ένας πολύ συμπαγής συμβολισμός, ακόμα και για πολύ μεγάλους αριθμούς διασταύρωσης. Υπάρχουν κάποιες συντομεύσεις που συχνά χρησιμοποιούνται. Το τελευταίο παράδειγμα συχνά γράφεται ως 8*3:2 0, όπου οι αριθμοί ένα παραλείπονται και γράφεται ο αριθμός των αναμενόμενων τελειών στο τέλος. Για έναν αλγεβρικό κόμβο, όπως στο πρώτο παράδειγμα, το 1* συχνά παραλείπεται.
Η πρωτοποριακή εργασία του Conway στο θέμα των λιστών βασικών πολυέδρων μέχρι 10 κορυφών, τα οποία χρησιμοποιεί για να ταξινομήσει τους συνδέσμους καθιερώθηκε για τους συνδέσμους. Για περεταίρω ταξινόμηση πολυέδρων περισσότερων κορυφών, δεν υπάρχουν τυπικοί τρόποι διαθέσιμοι.
Κώδικας Gauss
Ο κώδικας Gauss, που είναι παρόμοιος με το συμβολισμό Dowker, αναπαρηστά έναν κόμβο με μία ακολουθία ακεραίων. Παρόλα αυτά, αντί της αναπαράστασης κάθε διασταύρωσης από δύο διαφορετικούς αριθμούς, οι διασταυρώσεις σημειώνονται με ένα μόνο αριθμό. Όταν έχουμε άνω διασταύρωση, σημειώνεται ένας θετικός αριθμός και όταν είναι κάτω ένας αρνητικός αριθμός.
Για παράδειγμα, ο κόμβος trefoil με τον κώδικα Gauss δίνεται ως: 1,−2,3,−1,2,−3
Ο κώδικας Gauss έχει περιορισμένη ικανότητα ταυτοποίησης των κόμβων, λόγω μερικών προβλημάτων. Το αρχικό σημείο σε έναν κόμβο, από το οποίο ξεκινάμε να αναζητούμε τις διασταυρώσεις είναι αυθαίρετο και δεν υπάρχει τρόπος να καθοριστεί προς πια διεύθυνση θα αναζητηθούν. Επίσης ο κώδικας Gauss δεν μπορεί να υποδηλώσει την διεύθυνση που θα ακολουθηθεί σε κάθε διασταύρωση, το οποίο είναι απαραίτητο για να μπορεί να ταυτοποιηθεί ο κόμβος έναντι του αναστρόφου του. Για παράδειγμα, ο κώδικας Gauss για τους κόμβους trefoil δεν προσδιορίζει αν μελετούνται δεξιόστροφα ή αριστερόστροφα.
Αυτό το τελευταίο ζήτημα συχνά λύνεται με τον επεκταμένο κώδικα Gauss. Με αυτή την τροποποίηση, το θετικό/αρνητικό σύμβολο στην δεύτερη περίπτωση κάθε αριθμού επιλέγεται ώστε να αντιπροσωπεύει την διεύθυνση που θα ακολουθηθεί σε κάθε διασταύρωση, αντί του άνω /κάτω συμβόλου της διασταύρωσης, το οποίο γίνεται ξεκάθαρο στην πρώτη περίπτωση του αριθμού. Σε μία διασταύρωση που μελετάτε δεξιόστροφα δίνεται ένας θετικός αριθμός και σε μία που μελετάτε αριστερόστροφα δίνεται ένας αρνητικός αριθμός.
Δείτε επίσης
Αναφορές
Adams, Colin (2004), The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, American Mathematical Society, ISBN 0-8218-3678-1
Adams, Colin; Hildebrand, Martin; Weeks, Jeffrey (1991), «Hyperbolic invariants of knots and links», Transactions of the American Mathematical Society 326 (1): 1–56, doi:10.1090/s0002-9947-1991-0994161-2
Akbulut, Selman; King, Henry C. (1981), «All knots are algebraic», Comm. Math. Helv. 56 (3): 339–351, doi:10.1007/BF02566217
Bar-Natan, Dror (1995), «On the Vassiliev knot invariants», Topology 34 (2): 423–472, doi:10.1016/0040-9383(95)93237-2
Collins, Graham (April 2006), «Computing with Quantum Knots», Scientific American 294 (4): 56, doi:10.1038/scientificamerican0406-56
Conway, John Horton (1970), «An enumeration of knots and links, and some of their algebraic properties», Computational Problems in Abstract Algebra, Pergamon, σελ. 329–358, ISBN 0080129757, OCLC 322649
Doll, Helmut; Hoste, Jim (1991), «A tabulation of oriented links. With microfiche supplement», Math. Comp. 57 (196): 747–761, doi:10.1090/S0025-5718-1991-1094946-4
Flapan, Erica (2000), «When topology meets chemistry: A topological look at molecular chirality», Outlooks (Cambridge University Press), ISBN 0-521-66254-0
Haefliger, André (1962), «Knotted (4k − 1)-spheres in 6k-space», Annals of Mathematics. Second Series 75 (3): 452–466
Hass, Joel (1998), «Algorithms for recognizing knots and 3-manifolds», Chaos, Solitons and Fractals (Elsevier) 9 (4–5): 569–581, doi:10.1016/S0960-0779(97)00109-4
Hoste, Jim; Thistlethwaite, Morwen; Weeks, Jeffrey (1998), «The First 1,701,935 Knots», Math. Intelligencer (Springer) 20 (4): 33–48, doi:10.1007/BF03025227
Hoste, Jim (2005), «The enumeration and classification of knots and links», Handbook of Knot Theory, Amsterdam: Elsevier
Levine, Jerome (1965), «A classification of differentiable knots», Annals of Mathematics. Second Series 1982: 15–50
Kontsevich, Maxim (1993), «Vassiliev's knot invariants», I. M. Gelfand Seminar, Adv. Soviet Math., 2 (Providence, RI: Amer. Math. Soc.) 16: 137–150
Lickorish, W. B. Raymond (1997), An Introduction to Knot Theory, Graduate Texts in Mathematics, Springer-Verlag, ISBN 0-387-98254-X
Perko, Kenneth (1974), «On the classification of knots», Proceedings of the American Mathematical Society 45 (2): 262–6
Rolfsen, Dale (1976), Knots and Links, Publish or Perish, ISBN 0-914098-16-0
Schubert, Horst (1949), «Die eindeutige Zerlegbarkeit eines Knotens in Primknoten», Heidelberger Akad. Wiss. Math.-Nat. Kl. (3): 57–104
Silver, Dan (2006), «Knot theory's odd origins», American Scientist 94 (2): 158–165, doi:10.1511/2006.2.158
Simon, Jonathan (1986), «Topological chirality of certain molecules», Topology 25 (2): 229–235, doi:10.1016/0040-9383(86)90041-8
Sossinsky, Alexei (2002), Knots, mathematics with a twist, Harvard University Press, ISBN 0-674-00944-4
Turaev, V. G. (1994), «Quantum invariants of knots and 3-manifolds», De Gruyter Studies in Mathematics (Berlin: Walter de Gruyter & Co.) 18, ISBN 3-11-013704-6
Weisstein, Eric W. «Reduced Knot Diagram». MathWorld. Wolfram. Ανακτήθηκε στις 8 Μαΐου 2013.
Weisstein, Eric W. «Reducible Crossing». MathWorld. Wolfram. Ανακτήθηκε στις 8 Μαΐου 2013.
Witten, Edward (1989), «Quantum field theory and the Jones polynomial», Comm. Math. Phys. 121 (3): 351–399, doi:10.1007/BF01217730
Zeeman, E. C. (1963), «Unknotting combinatorial balls», Annals of Mathematics. Second Series 78 (3): 501–526
Παραπομπές
Levine, J.; Orr, K (2000), «A survey of applications of surgery to knot and link theory», Surveys on Surgery Theory: Papers Dedicated to C.T.C. Wall, Annals of mathematics studies, 1, Princeton University Press, CiteSeerX: 10.1.1.64.4359, ISBN 0691049386 — An introductory article to high dimensional knots and links for the advanced readers
Ogasa, Eiji, Introduction to high dimensional knots — An introductory article to high dimensional knots and links for the beginners
Εξωτερικοί σύνδεσμοι
wiktionary logo
Το Βικιλεξικό έχει σχετικό λήμμα:
θεωρία κόμβων
Ιστορία
Thomson, Sir William (1867), «On Vortex Atoms», Proceedings of the Royal Society of Edinburgh VI: 94–105
Silliman, Robert H. (December 1963), «William Thomson: Smoke Rings and Nineteenth-Century Atomism», Isis 54 (4): 461–474, doi:10.1086/349764
Movie of a modern recreation of Tait's smoke ring experiment
History of knot theory (on the home page of Andrew Ranicki)
Πίνακες κόμβων και λογισμικά
KnotInfo: Table of Knot Invariants and Knot Theory Resources
Πρότυπο:Knot Atlas — detailed info on individual knots in knot tables
KnotPlot — software to investigate geometric properties of knots
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License