Τετραγωνισμός του τετραγώνου
αγγλικά : Squaring the square
γαλλικά :
γερμανικά :
Ο Τετραγωνισμός του τετραγώνου είναι το πρόβλημα της τοποθέτησης ενός ακέραιου τετραγώνου χρησιμοποιώντας μόνο άλλα ακέραια τετράγωνα. (Ένα ακέραιο τετράγωνο είναι ένα τετράγωνο του οποίου οι πλευρές έχουν ακέραιο μήκος.) Το όνομα επινοήθηκε σε μια χιουμοριστική αναλογία με το τετραγωνισμό του κύκλου. Ο Τετραγωνισμός του τετραγώνου είναι μια εύκολη εργασία, εκτός εάν έχουν οριστεί πρόσθετες συνθήκες. Ο πιο μελετημένος περιορισμός είναι ότι το τετράγωνο είναι τέλεια, που σημαίνει ότι τα μεγέθη των μικρότερων τετραγώνων είναι όλα διαφορετικά. Ένα σχετικό πρόβλημα είναιο Τετραγωνισμός του του επιπέδου, το οποίο μπορεί να γίνει ακόμη και με τον περιορισμό ότι κάθε φυσικός αριθμός εμφανίζεται ακριβώς μία φορά ως μέγεθος ενός τετραγώνου στα πλακάκια. Η τάξη ενός Ο Τετραγωνισμένου τετραγώνου είναι ο αριθμός των τετραγωνικών συστατικών του.
Το πρώτο τέλειο τετραγωνισμένου τετράγωνο που ανακαλύφθηκε, με πλευρά 4205 και τάξη 55. Κάθε αριθμός δηλώνει το πλευρικό μήκος του τετραγώνου του.
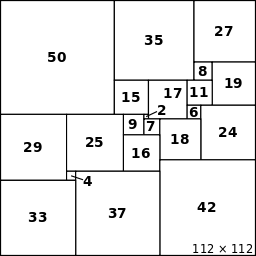
Το 1978, ο A. J. W. Duijvestijn ανακάλυψε ένα απλό τέλειο τετραγωνισμένο τετράγωνο με πλευρά 112 με τον μικρότερο αριθμό τετραγώνων χρησιμοποιώντας μια αναζήτηση υπολογιστή. Ο τετραγωνισμός γίνεται με 21 τετράγωνα και έχει αποδειχθεί ότι είναι ελάχιστος. Αυτό το τετράγωνο τετράγωνο αποτελεί το λογότυπο της Trinity Mathematical Society.
Ο κυβισμός του κύβου είναι το ανάλογο σε τρεις διαστάσεις του τετραγωνισμού του τετραγώνου: δηλαδή, δεδομένου ενός κύβου Γ, το πρόβλημα της διαίρεσής του σε πολύ λιγότερους μικρότερους διαφορετικους κύβους .
Σε αντίθεση με την περίπτωση του τετραγωνισμού του τετραγώνου, ενός σκληρού αλλά επιλύσιμου προβλήματος, δεν υπάρχει τέλειος κυβικοποιήμένος κύβος και, γενικότερα, καμία τομή ενός ορθογώνιου κυβοειδούς C σε έναν πεπερασμένο αριθμό άνισων κύβων.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License