Συστήματα ριζών

Συστήματα ριζών
αγγλικά : Root system
γαλλικά :
γερμανικά :

Στα μαθηματικά, ένα σύστημα ριζών είναι μια διαμόρφωση από διανύσματα σε έναν Ευκλείδειο χώρο όπου ικανοποιούνται οι βασικές γεωμετρικές ιδιότητες. H έννοια είναι εδραιωτική στις ομάδες Lie και στην Άλγεβρα Lie. Από τότε που οι ομάδες Lie (και κάποια ανάλογη όπως αλγεβρική ομάδα) και Άλγεβρα Lie έγιναν σημαντικές σε πολλούς τομείς των μαθηματικών κατά τη διάρκεια του εικοστού αιώνα, η προφανής ειδική φύση των συστημάτων ριζών διαψεύδει τον αριθμό των περιοχών όπου αυτά εφαρμόζονται. Ακόμη, το σχέδιο ταξινόμησης των συστημάτων ριζών , από τα διαγράμματα Dynkin, συμβαίνει στο κομμάτι των μαθηματικών που δεν έχει καμία φανερή σύνδεση στη θεωρία Lie (όπως θεωρία μοναδικότητας). Τέλος, τα συστήματα ριζών είναι σημαντικά για τους δικούς τους λόγους, όπως στη θεωρία γραφημάτων στη μελέτη των ιδιοδιανυσμάτων.

Ορισμοί και πρώτα παραδείγματα
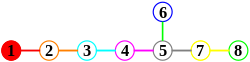
Tα έξι διανύσματα του συστήματος ριζών A2.

Σαν πρώτο παράδειγμα, θεωρούμε τα έξι διανύσματα στο δισδιάστατο Ευκλείδειο χώρο, R2, όπως φαίνεται στην εικόνα στα δεξιά; και τα ονομάζουμε ρίζες. Αυτά τα διανύσματα ορίζουν όλο το χώρο. Αν θεωρήσουμε τη κάθετη γραμμή σε κάθε ρίζα, έστω β, τότε η ανακλαστική ιδιότητα του R2 στέλνει κάθε ρίζα, έστω α, σε άλλη ρίζα. Επίσης, η ρίζα στην οποία στάλθηκε η ισότητα β + n α, όπου n ακέραιος (σ' αυτή την περίπτωση, n είναι ίσο 1). Αυτά τα έξι διανύσματα ικανοποιούν τον ακόλουθο ορισμό, και ακόμη αποτελούν ένα σύστημα ριζών, το γνωστό A2.
Ορισμός

Έστω V ότι είναι ένας πεπερασμένης διάστασης Ευκλείδειος διανυσματικός χώρος, με το γνωστό Ευκλείδειο εσωτερικό γινόμενο που ορίζεται ως εξής \( {\displaystyle (\cdot ,\cdot )} \). Ένα σύστημα ριζών στο V είναι ένα πεπερασμένο σύνολο Φ από μη μηδενικά διανύσματα που λέγονται ( ρίζες) που ικανοποιούν τις παρακάτω ιδιότητες :

Ο χώρος ριζών V.

Το μόνα πολλαπλάσια μιας ρίζας x ∈ Φ που ανήκει στο Φ είναι το ίδιο το x και το –x.
Για κάθε ρίζα x ∈ Φ, το σύνολο Φ είναι μια αντανάκλαση μέσου του υπερεπιπέδου που είναι κάθετο στο x.
(Ακεραιότητα) Αν x και y είναι ρίζες του Φ, τότε η προβολή του y πάνω στη γραμμή μέσω του x είναι μισό ακέραιο πολλαπλάσιο του x.

Ένας ισοδύναμος τρόπος για να γράψουμε τις καταστάσεις 3 και 4 είναι ο παρακάτω:

Για κάθε δυο ρίζες x and y, το σύνολο Φ περιέχει το στοιχείο \( {\displaystyle \sigma _{x}(y)=y-2{\frac {(x,y)}{(x,x)}}x\in \Phi .} \)
Για κάθε δυο ρίζες x and y,ο αριθμός \( {\displaystyle \langle y,x\rangle :=2{\frac {(x,y)}{(x,x)}}} \) είναι ακέραιος.

Συστήματα ριζών τάξης 2

Σύστημα ριζών \*} {\displaystyle A_{1}\times A_{1}} \)	Σύστημα ριζών \({\displaystyle D_{2}} \)
Σύστημα ριζών \( {\displaystyle A_{2}} \)	Σύστημα ριζών \( {\displaystyle G_{2}} \)
Σύστημα ριζών \( {\displaystyle B_{2}} \)	Σύστημα ριζών \( {\displaystyle C_{2}} \)

Η τάξη ενός συστήματος ριζών Φ είναι η διάσταση του χώρου V. Δυο συστήματα ριζών θεωρώντας τον Ευκλείδειο χώρο στον οποίον αυτά επεκτείνονται σαν ένα ορθογώνιο υποχώρο του γνωστού Ευκλείδειου χώρου. Ένα σύστημα ριζών το οποίο δεν προκύπτει από τον παραπάνω συνδυασμό , όπως τα συστήματα A₂, B₂,και G₂ όπως φαίνονται δεξιά, λέγεται ανάγωγο.

Δυο συστήματα ριζών (E1, Φ1) και (E2, Φ2) ονομάζονται ισόμορφα αν υπάρχει μια αντιστρέψιμη μεταφόρα E1 → E2 η οποία στέλνει το Φ1 στο Φ2 τέτοια ώστε για κάθε ζεύγος ριζών, ο αριθμός \( {\displaystyle \langle x,y\rangle } \) να διατηρείται.

Το σύνολο των ισομετριών των V που παράγεται από τις απεικονίσεις μέσω υπερεπιπέδων που συνδέονται με τις ρίζες του Φ ονομάζεται ομάδα Weyl του Φ. Αφού το Φ, είναι πεπερασμένο τότε και η ομάδα Weyl είναι πάντα πεπερασμένη.

Δυο παραδείγματα τάξης

Υπάρχει μόνο ένα σύστημα ριζών τάξης 1,που περιέχει δυο μη μηδενικά διανύσματα \( {\displaystyle \{\alpha ,-\alpha \}} \). Αυτό το σύστημα ριζών ονομάζεται \( {\displaystyle A_{1}} \).

Στη τάξη δυο υπάρχουν τέσσερις δυνατότητες, που ανταποκρίνονται στο \( {\displaystyle \sigma _{\alpha }(\beta )=\beta +n\alpha } \), όπου \( {\displaystyle n=0,1,2,3} \). Να σημειώσουμε ότι το σύστημα ριζών που παράγει ένα πλέγμα δεν είναι μοναδικό : \( {\displaystyle A_{1}\times A_{1}} \) και \( {\displaystyle B_{2}} \) παράγουν ένα τετράγωνο πλέγμα ενώ \( {\displaystyle A_{2}} \) και \( {\displaystyle G_{2}} \) παράγουν ένα εξάγωνο πλέγμα, μόνο δυο από τους πέντε δυνατούς τύπους των δισδιάστατων πλεγμάτων.

Αν Φ είναι ένα σύστημα ριζών του V, και U είναι ένας υποχώρος του V τέτοιος ώστε Ψ = Φ ∩ U, then Ψ είναι ένα σύστημα ριζών του U. Έτσι, εξαντλώντας όλες τις περιπτώσεις των τεσσάρων συστημάτων ριζών τάξης 2 βλέπουμε τις γεωμετρικές δυνατότητες για οποιεσδήποτε δυο ρίζες επιλεγμένες από ένα σύστημα ριζών τυχαίας τάξης. Συγκεκριμένα, δυο τέτοιες ρίζες αντιστοιχούν στις γωνίες των 0, 30, 45, 60, 90, 120, 135, 150, ή 180 μοιρών.

Ιστορικό

Η λογική ενός συστήματος ριζών εισήχθηκε από τον Wilhelm Killing γύρω στο 1889 στη Γερμανία^[1]).^[2]. Τα χρησιμοποίησε στη προσπάθειά του να ορίσει την απλή άλγεβρα Lie στο τομέα των μαθηματικών τωνμιγαδικών αριθμών. Όμως έκανε ένα λάθος στον όρισμό του , ταξινομώντας δυο συστήματα ριζών τάξης 4 όταν στην πραγματικότητα υπάρχει μόνο 1 , γνωστό ως F₄. Ο Cartan αργότερα διόρθωσε αυτό το λάθος, δείχνοντας οτι τα δυο συστήματα ριζών του Killing είναι ισόμορφα.^[3]

Ο Killing ανακάλυψε τη δομή της άλγεβρας Lie L, θεωρώντας (όπως ονομάζεται σήμερα) μια Cartan υποάλγεβρα \( {\displaystyle {\mathfrak {h}}} \). Έπειτα μελέτησε τις ρίζες του χαρακτηριστικού πολυωνύμου \( {\displaystyle \det(\mathrm {ad} _{L}x-t)} \), όπου \( {\displaystyle x\in {\mathfrak {h}}} \). Εδώ μια ρίζα θεωρείται ως μια συνάρτηση του \( {\displaystyle {\mathfrak {h}}} \), ή στη πραγματικότητα ένα στοιχείο του διπλού διανυσματικού χώρου \( {\displaystyle {\mathfrak {h}}^{*}} \). Αυτό το ζεύγος λύσεων του συστήματος ριζών μέσα στο \( {\displaystyle {\mathfrak {h}}^{*}} \), όπως ορίστηκε παραπάνω, όπου το εσωτερικό γινόμενο είναι ο τύπος του Κilling.
Πρώτες συνέπειες των αξιωμάτων των συστημάτων ριζών
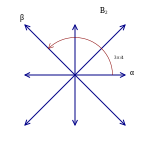
H κατάσταση ακεραιότητας για το <β, α> εκπληρώνεται μόνο για το β σε μία από τις κάθετες γραμμές, ενώ η κατάσταση ακεραιότητας για το <α, β> εκπληρώνεται μόνο για το β σε έναν από τους κόκκινους κύκλους. Οποιοδήποτε β κάθετο στο α (στον άξονα Y) τετριμμένα εκπληρώνει και τα δυο με το 0, αλλά δεν ορίζει ένα ανάγωγο σύστημα ριζών.
Η αντανάκλαση υπολοίπων, για ένα δοσμένο α υπάρχουν μόνο 5 μη-τετριμμένες πιθανότητες για το β, και 3 πιθανές γωνίες μεταξύ α και β σε ένα σύνολο απλών ριζών. Οι δείκτες γραμμάτων ανταποκρίνονται σε εκείνα τα συστήματα ριζών για τα οποία το δοθέν β μπορεί να θεωρηθεί σαν η πρώτη ρίζα και το α σαν η δεύτερη ρίζα. (ή στο F4 οι 2 μεσαίες ρίζες)

Το συνημίτονο της γωνίας μεταξύ των δυο ριζών περιορίζεται να είναι ακέραιο πολλαπλάσιο της τετραγωνικής ρίζας ενός ακεραίου. Αυτό είναι διότι \( {\displaystyle \langle \beta ,\alpha \rangle } \) και \( {\displaystyle \langle \alpha ,\beta \rangle } \)είναι και οι δυο ακέραιοι, από υπόθεση, και

\( {\displaystyle \langle \beta ,\alpha \rangle \langle \alpha ,\beta \rangle =2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\cdot 2{\frac {(\alpha ,\beta )}{(\beta ,\beta )}}=4{\frac {(\alpha ,\beta )^{2}}{\vert \alpha \vert ^{2}\vert \beta \vert ^{2}}}=4\cos ^{2}(\theta )=(2\cos(\theta ))^{2}\in \mathbb {Z} .} \)

Από τότε που \( {\displaystyle 2\cos(\theta )\in [-2,2]} \),οι μόνες πιθανές αξίες για τα \( {\displaystyle \cos(\theta )} \) είναι \( {\displaystyle 0,\pm {\tfrac {1}{2}},\pm {\tfrac {\sqrt {2}}{2}},\pm {\tfrac {\sqrt {3}}{2}},\pm {\tfrac {\sqrt {4}}{2}}=\pm 1} \), ανταποκρίνονται στις γωνίες των 90°, 60° ή 120°, 45° ή 135°, 30° ή 150°, και 0 ή 180°. Η περίπτωση 2 λέει ότι μόνο αυτά που δεν είναι πολλαπλάσια του α εκτός των 1 και -1 μπορεί να είναι ρίζες, έτσι 0 ή 180°, που αντιστοιχούν στα 2α ή −2α, αποκλείονται.
Θετικές και απλές ρίζες

Δοθέντος ενός συστήματος ριζών Φ μπορούμε πάντα να διαλέξουμε (με πολλούς τρόπους) ένα σύνολο θετικών ριζών. Αυτό είναι ένα υποσύνολο \( {\displaystyle \Phi ^{+}} \) του Φ όπως παρακάτω

Για κάθε ρίζα \( {\displaystyle \alpha \in \Phi } \) ακριβώς μια από τις ρίζες \( \alpha \) , – \( \alpha \) περιέχεται στο \( {\displaystyle \Phi ^{+}} \).
Για κάθε δυο διακεκριμένες \( {\displaystyle \alpha ,\beta \in \Phi ^{+}} \) όπως \( {\displaystyle \alpha +\beta } \) είναι μια ρίζα, \( {\displaystyle \alpha +\beta \in \Phi ^{+}} \).

Αν ένα σύνολο θετικών ριζών Φ + {\displaystyle \Phi ^{+}} {\displaystyle \Phi ^{+}} που επιλέχτηκε,είναι στοιχεία του − Φ + {\displaystyle -\Phi ^{+}} {\displaystyle -\Phi ^{+}} ονομάζονται αρνητικές ρίζες.

Ένα στοιχείο του \( {\displaystyle \Phi ^{+}} \) λέγεται απλή ρίζα αν δεν μπορεί να γραφεί ως άθροισμα δυο στοιχείων του Φ + {\displaystyle \Phi ^{+}} {\displaystyle \Phi ^{+}}. Το σύνολο Δ {\displaystyle \Delta } \Delta των απλών ριζών είναι μια βάση του V {\displaystyle V} V με την ιδιότητα ότι κάθε διάνυσμα του Φ {\displaystyle \Phi } \Phi είναι ένας γραμμικός συνδυασμός από στοιχεία του Δ {\displaystyle \Delta } \Delta με όλους τους συντελεστές μη αρνητικούς, ή μη θετικούς. Για κάθε επιλογή θετικών ριζών , το αντίστοιχο σύνολο απλών ριζών είναι το μοναδικό σύνολο ριζών όπου οι θετικές ρίζες είναι ακριβώς εκείνες που μπορεί να εκφραστούν ως ένα συνδυασμό αυτών με μη αρνητικούς παράγοντες,και αυτοί οι συνδυασμοί είναι μοναδικοί .

Το διατεταγμένο σύνολο ριζών

Διάγραμμα Hasse του E6 διατεταγμένο σύνολο ριζών με ετικέτες στις άκρες που δηλώνουν τη θέση των επιπλέον απλών ριζών

Το σύνολο των θετικών ριζών ορίζεται από τη σχέση \( {\displaystyle \alpha \leq \beta } \) αν και μόνο αν \( {\displaystyle \beta -\alpha } \) είναι ένας μη αρνητικός γραμμικός συνδυασμός απλών ριζών. Αυτό το διατεταγμένο σύνολο έχει βαθμό deg ⁡ \( {\displaystyle \operatorname {deg} {\big (}\sum _{\alpha \in \Delta }\lambda _{\alpha }\alpha {\big )}=\sum _{\alpha \in \Delta }\lambda _{\alpha }} \), και έχει πολλές αξιοσημείωτες συνδυαστικές ιδιότητες, μία από τις οποίες είναι ότι μπορεί κανείς να προσδιορίσει τους βαθμούς των θεμελιωδών αναλλοίωτων του αντίστοιχου συνόλου Weyl από αυτό το διατεταγμένο σύνολο.[4]

Το γράφημα Hasse είναι μια οπτικοποίηση του ορισμού του διατεταγμένου συνόλου.

Ορισμός των συστημάτων ριζών από τα διαγράμματα Dynkin

Εικόνες από όλα τα ανάγωγα διαγράμματα Dynkin

Ανάγωγα συστήματα ριζών αντιστοιχούν σε ορισμένα γραφήματα, τα διαγράμματα Dynkin που πήραν το όνομά τους από τον Eugene Dynkin. Ο ορισμός αυτών των γραφικών είναι ένας απλός τρόπος συνδυαστικής, και επάγει έναν ορισμό των ανάγωγων συστημάτων ριζών.

Δοθέντος ενός συστήματος ριζών, επιλέγοντας ένα σύνολο Δ απλών ριζών όπως προηγουμένως. Οι κορυφές που σχετίζονται με το διάγραμμα Dynkin αντιστοιχούν στα διανύσματα του Δ. Μια άκρη που σχεδιάζεται μεταξύ κάθε μη ορθογώνιου ζεύγους από διανύσματα: είναι μια μόνο ακμή χωρίς διεύθυνση εφόσον σχηματίζουν μια γωνία των \( {\displaystyle 2\pi /3} \) ακτίνια, μια διπλή ακμή με διεύθυνση αν σχηματίζουν γωνία \( {\displaystyle 3\pi /4} \) ακτίνια, και μια τριπλή ακμή αν σχηματίζουν γωνία \( {\displaystyle 5\pi /6} \) ακτίνια. Ο όρος "ακμή με διεύθυνση" σημαίνει ότι οι διπλές και οι τριπλές ακμές σημειώνονται με μια γωνία με κατεύθυνση προς το πλησιέστερο διάνυσμα.

Παρόλο που ένα δοσμένο σύστημα ριζών έχει περισσότερα από ένα σύνολα από απλές ρίζες, η ομάδα Weyl δρα σημαντικά σε τέτοιες επιλογές. Συνεπώς, το διάγραμμα Dynkin είναι ανεξάρτητο της επιλογής των απλών ριζών; είναι καθορισμένο από το ίδιο το σύστημα ριζών. Αντίθετα, δοθέντων δυο συστημάτων ριζών με το ίδιο διάγραμμα Dynkin, το ένα μπορεί να ταιριάξει ρίζες, ξεκινώντας με τις ρίζες της βάσης , και αποδεικνύοντας ότι τα συστήματα είναι στη πραγματικότητα τα ίδια.

Έτσι το πρόβλημα ορισμού των συστημάτων ριζών ανάγεται στο πρόβλημα ορισμού πιθανών διαγραμμάτων Dynkin . Τα συστήματα ριζών είναι ανάγωγα αν και μόνο αν τα διαγράμματά τους Dynkin συνδέονται. Τα διαγράμματα Dynkin κωδικοποιούν το εσωτερικό γινόμενο E με τους όρους της βάσης Δ, και η συνθήκη ότι το εσωτερικό γινόμενο πρέπει να είναι θετικά ορισμένο φανερώνει ότι έχουμε ότι χρειάζεται για τον επιθυμητό ορισμό.

Iδιότητες των ανάγωγων συστημάτων ριζών

\( \Phi \)	\( {\displaystyle |\Phi |}\)	\( {\displaystyle |\Phi ^{<}|} \)	I	D	\( displaystyle |W|} \)
An (n ≥ 1)	n(n + 1)			n + 1	(n + 1)!
Bn (n ≥ 2)	2n2	2n	2	2	2n n!
Cn (n ≥ 3)	2n2	2n(n − 1)	2	2	2n n!
Dn (n ≥ 4)	2n(n − 1)			4	2n − 1 n!
E6	72			3	51840
E7	126			2	2903040
E8	240			1	696729600
F4	48	24	4	1	1152
G2	12	6	3	1	12

Τα ανάγωγα συστήματα ριζών ονομάζονται σύμφωνα με την αντίστοιχη σχέση τους με τα διαγράμματα Dynkin. Υπάρχουν τέσσερις οικογένειες ορισμών (An, Bn, Cn,και Dn, που λέγονται τα κλασσικά συστήματα ριζών) και πέντε διακεκριμένες περιπτώσεις (τα διακεκριμένα συστήματα ριζών ).[5] Ο δείκτης δείχνει τη τάξη του συστήματος ριζών.

Σε ένα ανάγωγο σύστημα ριζών μπορεί να υπάρχουν το πολύ δυο μεταβλητές για το μήκος (α, α)1/2, αντιστοιχίζοντας τις κοντές και μακρές ρίζες. Αν όλες οι ρίζες έχουν το ίδιο μήκος και πάρθηκαν να είναι μακρές από τον ορισμό το σύστημα ριζών λέγεται απλά δεμένο; αυτό συμβαίνει στις περιπτώσεις A, D και E. Οποιεσδήποτε δυο ρίζες του ίδιου μήκους ανήκουν στην ίδια τροχιά της ομάδας Weyl. Στις μη-απλά δεμένες περιπτώσεις B, C, G και F, το πλέγμα της ρίζας αποτελείται από τις βραχείς ρίζες και οι μακρές ρίζες αποτελούν ένα υποπλέγμα, αμετάβλητες κάτω από την ομάδα Weyl , ίσες με r2/2 φορές το μιγαδικό , όπου r το μήκος μιας μακράς ρίζας.

Στο πίνακα στα δεξιά, |Φ < | δηλώνει το πλήθος των βραχέων ριζών, το I δηλώνει το περιεχόμενο στο πλέγμα ριζών του υποπλέγματος των μακρών ριζών , το D δηλώνει τον καθοριστικό πίνακα Cartan, και το |W| δηλώνει τη διάταξη της ομάδας Weyl.

Ρητή κατασκευή ανάγωγων συστημάτων ριζών

An

A₃

	e1	e2	e3	e4
α1	1	−1	0	0
α2	0	1	−1	0
α3	0	0	1	−1

Έστω V είναι ο υποχώρος του Rⁿ⁺¹ στον οποίο οι συντεταγμένες έχουν άθροισμα 0, και έστω Φ είναι το σύνολο των διανυσμάτων τουV μήκους √2 και τα οποία είναι ακέραια διανύσματα, δηλαδή έχουν ακέραιες συντεταγμένες στο Rⁿ⁺¹. ¨Ενα τέτοιο διάνυσμα πρέπει να έχει όλες τις συντεταγμένες του εκτός δυο ίσες με το 0, μια συντεταγμένη ίση με 1, και μια ίση με -1, έτσι ώστε να υπάρχουν n² + n ρίζες συνολικά. Μια επιλογή απλών ριζών που εκφράζεται ως βασική βάση είναι: α_i = e_i – e_i+1, για 1 ≤ i ≤ n.

Η αντανάκλαση σ_i μέσω του υπερεπιπέδου κάθετη στο α_i είναι ίδια σαν τη μετάθεση των παρακείμενων i-οστών and (i + 1)-οστών συντεταγμένων. Τέτοιες μεταθέσεις παράγουν ολόκληρη την ομάδα μεταθέσεων. Για γειτονικές απλές ρίζες, σ_i(α_i+1) = α_i+1 + α_i = σ_i+1(α_i) = α_i + α_i+1, δηλαδή, η αντανάκλαση είναι ισοδύναμη με την προσθήκη ενός πολλαπλάσιου του  1; αλλά αντανάκλαση μιας απλής ρίζας κάθετη σε μια μη γειτονική απλή ρίζα την αφήνει αμετάβλητη, που διαφέρουν κατά ένα πολλαπλάσιο του 0.

.
Bn

B₄

1	-1	0	0
0	1	-1	0
0	0	1	-1
0	0	0	1

Έστω V = Rn, και έστω Φ που περιέχει όλα τα ακέραια διανύσματα στο V μήκους 1 ή √2. Το συνολικό πλήθος ριζών είναι 2n2. Μια επιλογή απλών ριζών είναι: αi = ei – ei+1, για 1 ≤ i ≤ n – 1 (για τη παραπάνω επιλογή απλών ριζών για το An-1), και η πιο βραχέα ρίζα αn = en.

Η αντανάκλαση σn μέσω του υπερεπιπέδου που είναι κάθετο στη βραχέα ρίζα αn είναι φυσικά απλή άρνηση της nοστης συντεταγμένης. Για τη μακρά απλή ρίζα αn-1, σn-1(αn) = αn + αn-1, αλλά για την αντανάκλαση κάθετη στη βραχέα ρίζα , σn(αn-1) = αn-1 + 2αn, με διαφορά πολλαπλάσιου 2 αντί για 1.

B1 είναι ισόμορφο στο A1 μέσω μετατόπισης κατά √2, και επομένως δεν είναι ένα ξεχωριστό σύστημα ριζών.
Cn

C₄

1	-1	0	0
0	1	-1	0
0	0	1	-1
0	0	0	2

Έστω V = Rn, και έστω Φ να αποτελείται από όλα τα ακέραια διανύσματα του V μήκους √2 μαζί με όλα τα διανύσματα τύπου 2λ, όπου λ είναι ένα ακέραιο διάνυσμα μήκους 1. Το συνολικό πλήθος των ριζών είναι 2n2. Μια επιλογή απλών ριζών είναι: αi = ei – ei+1, για 1 ≤ i ≤ n – 1 (η παραπάνω επιλογή απλών ριζών για το An-1), και η πιο μακρά ρίζα αn = 2en. Η αντανάκλαση σn(αn-1) = αn-1 + αn, αλλά σn-1(αn) = αn + 2αn-1.

C2 είναι ισόμορφο με το B2 μέσω μετατόπισης κατά √2 και μιας 45 μοιρών περιστροφής, και γι' αυτό δεν είναι ένα ξεχωριστό σύστημα ριζών.

Σύστημα ριζών B₃, C₃, και A₃=D₃ όπως φαίνεται μέσω ενός κύβου και ενός οκτάεδρου

D₄

1	-1	0	0
0	1	-1	0
0	0	1	-1
0	0	1	1

Έστω V = Rⁿ, και έστω Φ να περιέχει όλα τα ακέραια διανύσματα του V μήκους √2. Το συνολικό πλήθος των ριζών είναι 2n(n – 1). Μια επιλογή απλών ριζών είναι: α_i = e_i – e_i+1, για 1 ≤ i < n (η παραπάνω επιλογή απλών ριζών για A_n-1) συν α_n = e_n + e_n-1.

Η αντανάκλαση μέσω του υπερεπιπέδου κάθετο στο α_n είναι η ίδια αν μεταφέρουμε και αναιρέσουμε τις παρακάτω n-οστές and (n – 1)-οστές συντεταγμένες. Οποιαδήποτε απλή ρίζα και η αντανάκλασή της που είναι κάθετη σε μια άλλη απλή ρίζα διαφέρουν κατά ένα πολλαπλάσιο του 0 ή του 1 της δεύτερης ρίζας, όχι όμως κατά μεγαλύτερο πολλαπλάσιο.

D₃ μειώνεται στο A₃, και γι' αυτό δεν είναι ένα ξεχωριστό σύστημα ριζών.

D₄ έχει επιπλέον συμμετρία που ονομάζεται τριαδικότητα.

72 κορυφές του 122 αντιπροσωπεύουν τα διανύσματα ρίζες του E6 (Οι πράσινοι κόμβοι είναι διπλάσιοι σε αυτό το E6 Coxeter επίπεδο )	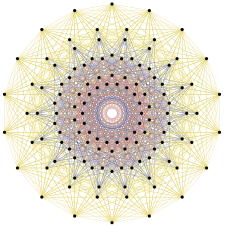126 κορυφές του 231 αντιπροσωπεύουν τα διανύσματα ρίζες του E7	240 κορυφές του 421 αντιπροσωπεύουν τα διανύσματα ρίζες του E8

• Το E₈ σύστημα ριζών είναι ένα σύνολο διανυσμάτων στο root R⁸ το οποίο είναι ανάλογο στο ακόλουθο σύνολο:

D₈ ∪ { ½( ∑_i=1⁸ ε_ie_i) : ε_i = ±1, ε₁•••ε₈ = +1}.

Το σύστημα ριζών έχει 240 ρίζες. Το σύνολο που μόλις ταξινομήθηκε είναι σύνολο διανυσμάτων μήκους √2 στο E8 πλέγμα Γ₈, το οποίο είναι το σύνολο των σημείων στο R⁸ τέτοια ώστε:

1. όλες οι συντεταγμένες να είναι ακέραιες ή όλες να είναι στο μισό ακέραιες (μία μίξη από ακέραιες και μίσες ακέραιες δεν επιτρέπεται), και
2. το άθροισμα οκτώ συντεταγμένων να είναι ένας άρτιος ακέραιος.

Έτσι,

E₈ = {α ∈ Z⁸ ∪ (Z+½)⁸ : |α|² = ∑α_i² = 2, ∑α_i ∈ 2Z}.

• Το σύστημα ριζών E₇

είναι το σύνολο των διανυσμάτων στο E₈ που είναι κάθετα σε μια σταθερή ρίζα στο E₈. Το σύστημα ριζών E₇ έχει 126 ρίζες.

• Το σύστημα ριζών E₆ δεν είναι το σύνολο των διανυσμάτων στο E₇ που είναι κάθετα σε μια σταθερή ρίζα στο E₇, στην πραγματικότητα, ένα λαμβάνει το D₆ αυτό το δρόμο.

Όμως, E6 είναι το υποσύστημα του E8 κάθετο σε δυο κατάλληλες διαλεγμένες ρίζες του E8. Το σύστημα ριζών E6 έχει 72 ρίζες.

Απλές ρίζες στο E₈ άρτιες συντεταγμένες:

1	-1	0	0	0	0	0	0
0	1	-1	0	0	0	0	0
0	0	1	-1	0	0	0	0
0	0	0	1	-1	0	0	0
0	0	0	0	1	-1	0	0
0	0	0	0	0	1	-1	0
0	0	0	0	0	1	1	0
-½	-½	-½	-½	-½	-½	-½	-½

Μια εναλλακτική περιγραφή του πλέγματος του E₈ που είναι καμιά φορά βολική είναι ότι το σύνολο Γ'₈ όλων των σημείων του R⁸ τέτοια ώστε

• όλες οι συντεταγμένες είναι ακέραιες και το άθροισμα των συντεταγμένων είναι άρτιο , ή
• όλες οι συντεταγμένες είναι κατά το ήμισυ ακέραιες και το άθροισμά τους είναι περιττό.

Τα πλέγματα Γ₈ και Γ'₈ είναι ισόμορφα· μπορεί κανείς να περάσει από το ένα στο άλλο αλλάζοντας τα πρόσημα από οποιουσδήποτε περιττούς αριθμούς των συντεταγμένων. Το πλέγμαΓ₈ μερικές φορές λέγεται άρτιο σύστημα συντεταγμένων για το E₈ ενώ το πλέγμα Γ'₈ λέγεται περιττό σύστημα συντεταγμένων.

Μια επιλογή απλών ριζών για το E₈ στο άρτιο σύστημα συντεταγμένων με τις σειρές διατεταγμένες (μη-κανονικά) στα διαγράμματα Dynkin είναι:

α_i = e_i – e_i+1, για 1 ≤ i ≤ 6, και

α₇ = e₇ + e₆

(η παραπάνω επιλογή απλών ριζών για το D₇) μαζί με

α8 = β0 = − \( {\displaystyle -\textstyle {\frac {1}{2}}(\textstyle \sum _{i=1}^{8}e_{i})} \) = (-½,-½,-½,-½,-½,-½,-½,-½).

Απλές ρίζες στο E₈: περιττές συντεταγμένες

1	-1	0	0	0	0	0	0
0	1	-1	0	0	0	0	0
0	0	1	-1	0	0	0	0
0	0	0	1	-1	0	0	0
0	0	0	0	1	-1	0	0
0	0	0	0	0	1	-1	0
0	0	0	0	0	0	1	-1
-½	-½	-½	-½	-½	½	½	½

Μια επιλογή απλών ριζών για το E₈ στο περιττό σύστημα συντεταγμένων με τις σειρές διατεταγμένες (μη-κανονικά) στα διαγράμματα Dynkin είναι:

α_i = e_i – e_i+1, για 1 ≤ i ≤ 7

(η παραπάνω επιλογή απλών ριζών για το A₇) μαζί με

α₈ = β₅, όπου
β_j =\( {\displaystyle \textstyle {\frac {1}{2}}(-\textstyle \sum _{i=1}^{j}e_{i}+\textstyle \sum _{i=j+1}^{8}e_{i})}. \)

(Χρησιμοποιώντας το β₃ θα δώσει ένα ισόμορφο αποτέλεσμα. Χρησιμοποιώντας το β_1,7 ή το β_2,6 θα δώσουν απλά το A₈ ή το D₈. Όσο για το β₄, η συντεταγμένη του έχει άθροισμα 0, και το ίδιο ισχύει και για το α_1...7, έτσι ορίζουν μόνο το 7-διάστατο υποχώρο για τον οποίο κάθε συντεταγμένη αθροίζει στο 0; στη πραγματικότητα –2β₄ έχει συντεταγμένες τις (1,2,3,4,3,2,1) στη βάση (α_i).)

Διαγράφοντας το α₁ και μετά το α₂ δίνει το σύνολο των απλών ριζών για τα E₇ και E₆. Από τότε που η καθετότητα στο α₁ σημαίνει ότι οι πρώτες δυο συντεταγμένες είναι ίσες, E₇ είναι τότε το υποσύνολο του E₈ όπου οι δυο πρώτες συντεταγμένες είναι ίσες, και όμοια E₆ είναι το υποσύνολο του E₈ όπου οι πρώτες τρεις συντεταγμένες είναι ίσες. Αυτό διευκολύνει πολύ τους ορισμούς του E₇ και E₆ όπως:

E₇ = {α ∈ Z⁷ ∪ (Z+½)⁷ : ∑α_i² + α₁² = 2, ∑α_i + α₁ ∈ 2Z},

E₆ = {α ∈ Z⁶ ∪ (Z+½)⁶ : ∑α_i² + 2α₁² = 2, ∑α_i + 2α₁ ∈ 2Z}

F4

F₄

1	-1	0	0
0	1	-1	0
0	0	1	0
-½	-½	-½	-½

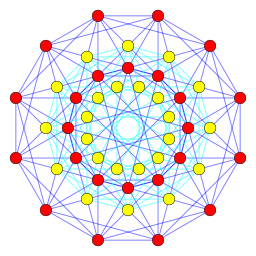
48 ρίζες διανύσματα του F4, ορισμένα από τις κορυφές των 24-κελιών και των διπλών τους, όπως φαίνεται στο Coxeter επίπεδο

Για το F₄, έστω V = R⁴, και έστω Φ να δηλώνει το σύνολο των διανυσμάτων α μήκους 1 ή √2 τέτοια ώστε οι συντεταγμένες του 2α είναι όλες ακέραιες και είτε είναι όλες άρτιες είτε όλες περιττές . Υπάρχουν 48 ρίζες σε αυτό το σύστημα. Μια επιλογή απλών ριζών είναι: η επιλογή απλών ριζών που δίνεται παραπάνω για το B₃,συν το α₄ = – \( {\displaystyle \textstyle {\frac {1}{2}}\sum _{i=1}^{4}e_{i}} \).
G2

Απλές ρίζες στο G₂

1	-1	0
-1	2	-1

Το σύστημα ριζών G₂ έχει 12 ρίζες, οι οποίες σχηματίζουν κορυφές ενός εξαγώνου S

Μια επιλογή απλών ριζών είναι: (α₁, β = α₂ – α₁) όπου α_i = e_i – e_i+1 για i = 1, 2 είναι η παραπάνω επιλογή απλών ριζών για το A₂.

Συστήματα ριζών και θεωρία Lie

Ανάγωγα συστήματα ριζών ορίζουν έναν αριθμό από σχετικά αντικείμενα στη θεωρία Lie, συγκεκριμένα τα

απλά Lie σύνολα (βλέπε τη λίστα απλών συνόλων Lie), συμπεριλαμβανομένου τα εξής
απλές μιγαδικές ομάδες Lie;
τις σχετικές τους απλές μιγαδικές άλγεβρες Lie; και
τις απλά συνδεδεμένες μιγαδικές ομάδες Lie τα οποία είναι απλά υπόλοιπα.

Σε αυτήν την περίπτωση, οι ρίζες είναι μη μηδενικές. Στην περίπτωση που έχουμε μια απλά συνδεδεμένη απλή συμπαγή ομάδα Lie G με μέγιστη βάση στήλης T, το πλέγμα ριζών μπορεί φυσικά να αναγνωριστεί με το Hom(T, T) και το πλέγμα των συζυγών ριζών με το Hom(T, T), όπου T είναι η κυκλική ομάδα; βλέπε Adams (1983).

Παραπομπές

Killing (1889)
Bourbaki (1998), p.270
Coleman, p.34
Humphreys (1992), Theorem 3.20
Hall, Brian C. (2003), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 0-387-40122-9.

Εγκυκλοπαίδεια Μαθηματικών

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License