Συνάρτηση Griewank
αγγλικά : Griewank function
γαλλικά :
γερμανικά :
Στα μαθηματικά, η συνάρτηση Griewank χρησιμοποιείται συχνά στη δοκιμή βελτιστοποίησης, ορίζεται ως εξής
1+{\frac {1}{4000}}\sum _{{i=1}}^{n}x_{i}^{2}-\prod _{{i=1}}^{n}\cos \left({\frac {x_{i}}{{\sqrt {i}}}}\right)
Οι ακόλουθες παράγραφοι εμφανίζουν τις ειδικές περιπτώσεις της συνάρτησης Griewank πρώτης, δεύτερης και τρίτης τάξης, και τις γραφικές παραστάσεις τους.
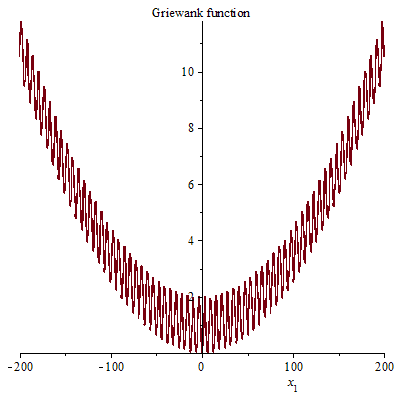
Συνάρτηση Griewank πρώτης τάξης
{\displaystyle g:=1+(1/4000)\cdot x_{1}^{2}-\cos(x_{1})}
Η συνάρτηση Griewank πρώτης τάξης έχει πολλαπλά μέγιστα και ελάχιστα. [2]
Έστω η παράγωγος της συνάρτησης Griewank είναι μηδέν:
{\displaystyle {\frac {1}{2000}}\cdot x_{1}+\sin(x_{1})=0}
Βρείτε τις ρίζες του στο διάστημα [−100..100] με αριθμητική μέθοδο,
Στο διάστημα [−10000.10000], η συνάρτηση Griewank έχει 6365 κρίσιμα σημεία.
Συνάρτηση Griewank δεύτερης τάξης
2ης τάξης Griewank 3D τρισδιάστατη γράφημα
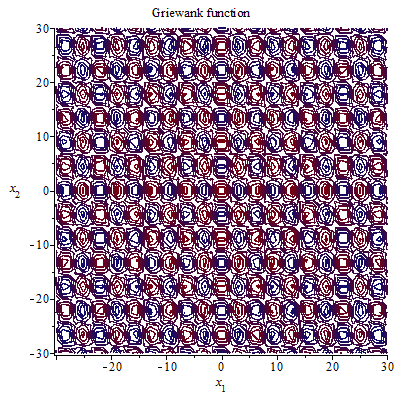
γράφημα περιγράμματος συνάρτησης 2ης τάξης Griewank
1+{\frac {1}{4000}}x_{1}^{2}+{\frac {1}{4000}}x_{2}^{2}-\cos(x_{1})\cos \left({\frac 12}x_{2}{\sqrt {2}}\right)
Συνάρτηση τρίτης τάξης Griewank
συνάρτηση Griewank τρίτης τάξης
\( \left\{1+{\frac {1}{4000}}\,x_{1}^{2}+{\frac {1}{4000}}\,x_{2}^{2}+{\frac {1}{4000}}\,{x_{{{3}}}}^{{2}}-\cos(x_{1})\cos \left({\frac 12}x_{2}{\sqrt {2}}\right)\cos \left({\frac 13}x_{3}{\sqrt {3}}\right)\right\}
βιβλιογραφικές αναφορές
Griewank, A. O. "Generalized Decent for Global Optimization." J. Opt. Th. Appl. 34, 11–39, 1981
Locatelli, M. "A Note on the Griewank Test Function." J. Global Opt. 25, 169–174, 2003
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License