Στερεό του Τζόνσον

Στερεό του Τζόνσον
αγγλικά :
γαλλικά :
γερμανικά :

Στη γεωμετρία, το στερεό του Τζόνσον είναι ένα αυστηρώς κυρτό πολύεδρο που η κάθε έδρα του είναι κανονικό πολύγωνο, και δεν είναι ομοιόμορφο, π.χ., δεν είναι Πλατωνικό στερεό, ούτε Αρχιμήδειο στερεό, ούτε πρίσμα ή αντιπρίσμα. Δεν υπάρχει απαίτηση η κάθε έδρα του να είναι ιδίου είδους πολύγωνο, ή γύρω από κάθε κορυφή του να εντάσσονται ιδίου είδους πολύγωνα. Ένα παράδειγμα στερεού Τζόνσον είναι η πυραμίδα με βάση τετραγωνική και πλευρές ισόπλευρα τρίγωνα (τετραγωνική πυραμίδα, J1), δηλαδή, έχει μία έδρα τετράγωνο και τέσσερις έδρες τρίγωνα.

Όπως σε κάθε αυστηρώς κυρτό στερεό, συναντώνται σε κάθε κορυφή τουλάχιστον τρεις έδρες, και το σύνολο των γωνιών τους είναι μικρότερο από 360 μοίρες. Δεδομένου ότι ένα κανονικό πολύγωνο έχει γωνίες τουλάχιστον 60 μοιρών, συνεπάγεται ότι το πολύ πέντε έδρες συναντώνται σε κάθε κορυφή (π.χ., η πενταγωνική πυραμίδα, J2).

Αν και δεν υπάρχει προφανής περιορισμός στο ότι το κάθε δεδομένο κανονικό πολύγωνο να μην μπορεί να είναι έδρα ενός στερεού του Τζόνσον, αποδεικνύεται ότι οι όψεις των στερεών του Τζόνσον έχουν πάντοτε 3, 4, 5, 6, 8, ή 10 πλευρές.

Το 1966, ο μαθηματικός Νόρμαν Τζόνσον δημοσίευσε μια λίστα που περιελάμβανε όλα αυτά τα 92 στερεά, τα οποία αρίθμησε και τους έδωσε ονόματα. Δεν απέδειξε ότι υπήρχαν μόνο 92, αλλά έκανε την εικασία ότι δεν υπάρχουν άλλα. Το 1969, ο μαθηματικός Βίκτορ Ζαλγκαλλέρ απέδειξε ότι ο κατάλογος του Τζόνσον ήταν πλήρης.

Το στερεό του Τζόνσον επιμήκης τετραγωνικός γυροδιτρούλος (J37), που ονομάζεται επίσης ψευδο-ρομβικυβοκτάεδρο,[1] είναι μοναδικό στο να είναι τοπικά ομοιόμορφο στις κορυφές: υπάρχουν 4 έδρες σε κάθε κορυφή, και η διάταξή τους είναι πάντα η ίδια: 3 τετράγωνα και 1 τρίγωνο. Ωστόσο, δεν είναι μεταβατικές οι κορυφές του, καθώς έχει διαφορετική ισομετρία σε διάφορες από τις κορυφές, καθιστώντας το έτσι, στερεό του Τζόνσον αντί για στερεό του Αρχιμήδη.

Jn	'Ονομα	Εικόνα	Κατηγορία	E	K	F	F3	F4	F5	F6	F8	F10	Συμμετρία
1	Tετραγωνική πυραμίδα		Πυραμίδα	5	8	5	4	1	0	0	0	0	C4v
2	Πενταγωνική πυραμίδα		Πυραμίδα	6	10	6	5	0	1	0	0	0	C5v
3	Τριγωνικός θόλος		Θόλος	9	15	8	4	3	0	1	0	0	C3v
4	Τετραγωνικός θόλος		Θόλος	12	20	10	4	5	0	0	1	0	C4v
5	Πενταγωνικός θόλος		Θόλος	15	25	12	5	5	1	0	0	1	C5v
6	Πενταγωνική ροτόντα		Ροτόντα	20	35	17	10	0	6	0	0	1	C5v

Jn	Ονομα	Εικόνα	Κατηγορία	E	K	F	F3	F4	F5	Συμμετρία
7	Επιμήκης τριγωνική πυραμίδα		Επιμήκης πυραμίδα	7	12	7	4	3	0	C3v
8	Επιμήκης τετραγωνική πυραμίδα		Επιμήκης πυραμίδα	9	16	9	4	5	0	C4v
9	Επιμήκης πενταγωνική πυραμίδα		Επιμήκης πυραμίδα	11	20	11	5	5	1	C5v
10	Γυροεπιμήκης τετραγωνική πυραμίδα		Γυροεπιμήκης πυραμίδα	9	20	13	12	1	0	C4v
11	Γυροεπιμήκης πενταγωνική πυραμίδα		Γυροεπιμήκης πυραμίδα	11	25	16	15	0	1	C5v
12	Τριγωνική Διπυραμίδα		Διπυραμίδα	5	9	6	6	0	0	D3h
13	Πενταγωνική Διπυραμίδα		Διπυραμίδα	7	15	10	10	0	0	D5h
14	Επιμήκης τριγωνική Διπυραμίδα		Επιμήκης Διπυραμίδα	8	15	9	6	3	0	D3h
15	Επιμήκης τετραγωνική Διπυραμίδα		Επιμήκης Διπυραμίδα	10	20	12	8	4	0	D4h
16	Επιμήκης πενταγωνική Διπυραμίδα		Επιμήκης Διπυραμίδα	12	25	15	10	5	0	D5h
17	Γυροεπιμήκης τετραγωνική Διπυραμίδα			10	24	16	16	0	0	D4d

Jn	Ονομα	Εικόνα	Κατηγορία	E	K	F	F3	F4	F5	F6	F8	F10	Συμμετρία
18	Επιμήκης τριγωνικός θόλος			15	27	14	4	9	0	1	0	0	C3v
19	Επιμήκης τετραγωνικός θόλος			20	36	18	4	13	0	0	1	0	C4v
20	Επιμήκης πενταγωνικός θόλος		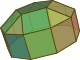	25	45	22	5	15	1	0	0	1	C5v
21	Επιμήκης πενταγωνική ροτόντα			30	55	27	10	10	6	0	0	1	C5v
22	Γυροεπιμήκης τριγωνικός θόλος			15	33	20	16	3	0	1	0	0	C3v
23	Γυροεπιμήκης τετραγωνικός θόλος			20	44	26	20	5	0	0	1	0	C4v
24	Γυροεπιμήκης πενταγωνικός θόλος			25	55	32	25	5	1	0	0	1	C5v
25	Γυροεπιμήκης πενταγωνική ροτόντα			30	65	37	30	0	6	0	0	1	C5v
26	Γυροδικόρυφο			8	14	8	4	4	0	0	0	0	D2d
27	Τριγωνικός ορθοδιθόλος			12	24	14	8	6	0	0	0	0	D3h
28	Τετραγωνικός ορθοδιθόλος			16	32	18	8	10	0	0	0	0	D4h
29	Τετραγωνικός γυροδιθόλος			16	32	18	8	10	0	0	0	0	D4d
30	Πενταγωνικός ορθοδιθόλος			20	40	22	10	10	2	0	0	0	D5h
31	Πενταγωνικός γυροδιθόλος			20	40	22	10	10	2	0	0	0	D5d
32	Πενταγωνική ορθοθολοροτόντα			25	50	27	15	5	7	0	0	0	C5v
33	Πενταγωνική γυροθολοροτόντα			25	50	27	15	5	7	0	0	0	C5v
34	Πενταγωνική ορθοδιροτόντα			30	60	32	20	0	12	0	0	0	D5h
35	Επιμήκης τριγωνική ορθοδιροτόντα			18	36	20	8	12	0	0	0	0	D3h
36	Επιμήκης τριγωνικός γυροδιθόλος			18	36	20	8	12	0	0	0	0	D3d
37	Επιμήκης τετραγωνικός γυροδιθόλος			24	48	26	8	18	0	0	0	0	D4d
38	Επιμήκης πενταγωνικός ορθοδιθόλος			30	60	32	10	20	2	0	0	0	D5h
39	Επιμήκης πενταγωνικός γυροδιθόλος			30	60	32	10	20	2	0	0	0	D5d
40	Επιμήκης πενταγωνική ορθοθολοροτόντα			35	70	37	15	15	7	0	0	0	C5v
41	Επιμήκης πενταγωνική γυροθολοροτόντα			35	70	37	15	15	7	0	0	0	C5v
42	Επιμήκης πενταγωνική ορθοδιροτόντα			40	80	42	20	10	12	0	0	0	D5h
43	Επιμήκης πενταγωνική γυροδιροτόντα			40	80	42	20	10	12	0	0	0	D5d
44	Γυροεπιμήκης τριγωνικός διθόλος			18	42	26	20	6	0	0	0	0	D3
45	Γυροεπιμήκης τετραγωνικός διθόλος			24	56	34	24	10	0	0	0	0	D4
46	Γυροεπιμήκης πενταγωνικός διθόλος			30	70	42	30	10	2	0	0	0	D5
47	Γυροεπιμήκης πενταγωνική θολοροτόντα			35	80	47	35	5	7	0	0	0	C5
48	Γυροεπιμήκης πενταγωνική διροτόντα			40	90	52	40	0	12	0	0	0	D5

Jn	Ονομα	Εικόνα	E	K	F	F3	F4	F5	F6	Συμμετρία
49	Επαυξημένο τριγωνικό πρίσμα		7	13	8	6	2	0	0	C2v
50	Διεπαυξημένο τριγωνικό πρίσμα		8	17	11	10	1	0	0	C2v
51	Τριεπαυξημένο τριγωνικό πρίσμα		9	21	14	14	0	0	0	D3h
52	Επαυξημένο πενταγωνικό πρίσμα		11	19	10	4	4	2	0	C2v
53	Διεπαυξημένο πενταγωνικό πρίσμα		12	23	13	8	3	2	0	C2v
54	Επαυξημένο εξαγωνικό πρίσμα		13	22	11	4	5	0	2	C2v
55	Παραδιεπαυξημένο εξαγωνικό πρίσμα		14	26	14	8	4	0	2	D2h
56	Μεταδιεπαυξημένο εξαγωνικό πρίσμα		14	26	14	8	4	0	2	C2v
57	Τριεπαυξημένο εξαγωνικό πρίσμα		15	30	17	12	3	0	2	D3h

Jn	Ονομα	Εικόνα	Κατηγορία	E	K	F	F3	F4	F5	Συμμετρία
58	Επαυξημένο δωδεκάεδρο			21	35	16	5	0	11	C5v
59	Παραδιεπαυξημένο δωδεκάεδρο			22	40	20	10	0	10	D5d
60	Μεταδιεπαυξημένο δωδεκάεδρο			22	40	20	10	0	10	C2v
61	Τριεπαυξημένο δωδεκάεδρο			23	45	24	15	0	9	C3v
62	Μεταδιελαττωμένο εικοσάεδρο		κομμένα εικοσάεδρο	10	20	12	10	0	2	C2v
63	Τριελαττωμένο εικοσάεδρο		κομμένα εικοσάεδρο	9	15	8	5	0	3	C3v
64	Επαυξημένο τριελαττωμένο εικοσάεδρο		-	10	18	10	7	0	3	C3v

Jn	Ονομα	Εικόνα	Κατηγορία	E	K	F	F3	F4	F5	F6	F8	F10	Συμμετρία
65	Επαυξημένο κολοβό τετράεδρο			15	27	14	8	3	0	3	0	0	C3v
66	Επαυξημένος κολοβός κύβος			28	48	22	12	5	0	0	5	0	C4v
67	Διεπαυξημένος κολοβός κύβος			32	60	30	16	10	0	0	4	0	D4h
68	Επαυξημένο κολοβό δωδεκάεδρο			65	105	42	25	5	1	0	0	11	C5v
69	Παραδιεπαυξημένο κολοβό δωδεκάεδρο			70	120	52	30	10	2	0	0	10	D5d
70	Μεταδιεπαυξημένο κολοβό δωδεκάεδρο			70	120	52	30	10	2	0	0	10	C2v
71	Τριεπαυξημένο κολοβό δωδεκάεδρο			75	135	62	35	15	3	0	0	9	C3v
72	Gyrate rhombicosidodecahedron			60	120	62	20	30	12	0	0	0	C5v
73	Parabigyrate rhombicosidodecahedro			60	120	62	20	30	12	0	0	0	D5d
74	Metabigyrate rhombicosidodecahedron			60	120	62	20	30	12	0	0	0	C2v
75	Trigyrate rhombicosidodecahedron			60	120	62	20	30	12	0	0	0	C3v
76	Ελαττωμένο Ρομβοεικοσιδωδεκάεδρο			55	105	52	15	25	11	0	0	1	C5v
77	Paragyrate diminished rhombicosidodecahedron			55	105	52	15	25	11	0	0	1	C5v
78	Metagyrate diminished rhombicosidodecahedron			55	105	52	15	25	11	0	0	1	Cs
79	Bigyrate diminished rhombicosidodecahedronr			55	105	52	15	25	11	0	0	1	Cs
80	Παραδιελαττωμένο Ρομβοεικοσιδωδεκάεδρο			50	90	42	10	20	10	0	0	2	D5d
81	Μεταδιελαττωμένο Ρομβοεικοσιδωδεκάεδρο			50	90	42	10	20	10	0	0	2	C2v
82	Gyrate bidiminished rhombicosidodecahedron			50	90	42	10	20	10	0	0	2	C2v
83	Τριδιελαττωμένο Ρομβοεικοσιδωδεκάεδρο			45	75	32	5	15	9	0	0	3	C3v

Jn	Ονομα	Εικόνα	E	K	F	F3	F4	F5	F6	Συμμετρία
84	Κολοβό δισφηνοειδές		8	18	12	12	0	0	0	D2d
85	Πεπλατυσμένο τετραγωνικό αντίπρισμα		16	40	26	24	2	0	0	D4d
86	Σφηνοκορώνα		10	22	14	12	2	0	0	C2v
87	Επαυξημένη σφηνοκορώνα		11	26	17	16	1	0	0	Cs
88	Σφηνομεγακορώνα		12	28	18	16	2	0	0	C2v
89	Ηβησφηνομεγακορώνα		14	33	21	18	3	0	0	C2v
90	Disphenocingulum		16	38	24	20	4	0	0	D2d
91	Bilunabirotunda		14	26	14	8	2	4	0	D2h
92	Τριγωνική ηβησφηνοροτόντα		18	36	20	13	3	3	1	C3v

Παραπομπές

«Virtual polyhedra: Pseudo-rhombicuboctahedra». George Hart's website.

Πηγές

Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 3 Further Convex polyhedra

Εργασία που περιέχει την αρχική αρίθμηση των 92 στερεών και την εικασία ότι δεν υπάρχουν άλλα:

(Αγγλικά) Johnson, Norman W. (1966). «Convex Solids with Regular Faces». Canadian Journal of Mathematics 18: 169–200. doi:10.4153/cjm-1966-021-8. ISSN 0008-414X. Zbl 0132.14603.

Η πρώτη απόδειξη ότι υπάρχουν μόνο 92 στερεά του Τζόνσον:

(Αγγλικά) Zalgaller, Victor A. (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. Zbl 0177.24802.
(Ρωσικά) Zalgaller, Victor A. (1967). «Convex Polyhedra with Regular Faces». Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova 2: 1–221. ISSN 0373-2703. Zbl 0165.56302.

Εξωτερικοί σύνδεσμοι

Weisstein, Eric W., "Johnson Solid" από το MathWorld.

Εγκυκλοπαίδεια Μαθηματικών

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License