Πολυώνυμα Chebyshev
αγγλικά : Chebyshev polynomials
γαλλικά :
γερμανικά :
Τα πολυώνυμα Chebyshev είναι δύο ακολουθίες πολυωνύμων T_{n}(x) και U_{n}(x) που σχετίζονται με τις συναρτήσης του ημίτονου και συνημίτονου ). Μπορούν να οριστούν διάφοροι τρόποι με το ίδιο τελικό αποτέλεσμα. σε αυτό το άρθρο τα πολυώνυμα ορίζονται ξεκινώντας με τριγωνομετρικές συναρτήσεις,
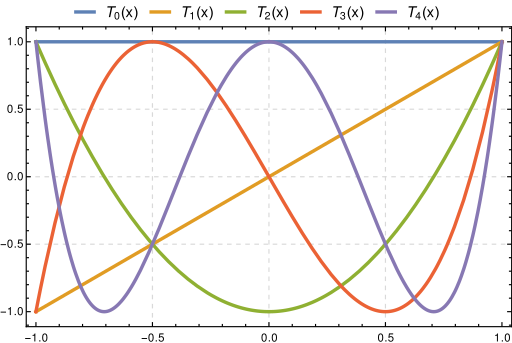
Τα πολυώνυμα Chebyshev του πρώτου είδους λαμβάνονται από τις εξής σχέσεις
{\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2x\,T_{n}(x)-T_{n-1}(x)~.\end{aligned}}}
Τα πολυώνυμα Chebyshev του δεύτερου είδους λαμβάνονται από τις εξής σχέσεις
{\displaystyle {\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{n+1}(x)&=2x\,U_{n}(x)-U_{n-1}(x)~.\end{aligned}}}
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License