.
Παραλληλόγραμμο στην Ευκλείδεια γεωμετρία είναι ένα τετράπλευρο που έχει τις απέναντι πλευρές του παράλληλες.
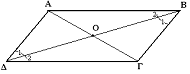
Σε κάθε παραλληλόγραμμο οι απέναντι πλευρές είναι ίσες, οι απέναντι γωνίες είναι ίσες και οι διαγώνιοι διχοτομούνται..
Το σημείο τομής των διαγωνίων του λέγεται κέντρο του παραλληλογράμμου. Η απόσταση δύο απέναντι πλευρών παραλληλογράμμου λέγεται ύψος του ενώ οι απέναντι πλευρές λέγονται βάσεις ως προς το ύψος αυτό (κάθε παραλληλόγραμμο έχει δύο ύψη).
Ειδικές περιπτώσεις παραλληλογράμμου είναι το ορθογώνιο, ο ρόμβος και το τετράγωνο.
Ιδιότητες
- Σε κάθε παραλληλόγραμμο οι απέναντι πλευρές είναι ίσες και οι απέναντι γωνίες είναι ίσες.
- Σε κάθε παραλληλόγραμμο οι διαγώνιοι διχοτομούνται.
Απόδειξη: Τα τρίγωνα ΟΑΒ και ΟΓΔ στο σχήμα είναι ίσα επειδή έχουν δύο ίσες γωνίες και την περιεχόμενη πλευρά τους ίση, συνεπώς ΟΒ = ΟΔ και ΑΟ = ΟΓ.
- Το κέντρο ενός παραλληλογράμμου είναι κέντρο συμμετρίας του.
- Κριτήρια παραλληλογράμμου: Ένα τετράπλευρο είναι παραλληλόγραμμο αν και μόνο αν ισχύει μία από τις παρακάτω προτάσεις:
- Οι απέναντι πλευρές είναι ίσες ανά δύο.
- Δύο απέναντι πλευρές είναι ίσες και παράλληλες.
- Οι απέναντι γωνίες είναι ίσες ανά δύο.
- Οι διαγώνιοί του διχοτομούνται.
Εμβαδόν
Το Εμβαδόν του παραλληλογράμμου βρίσκεται πολλαπλασιάζοντας τη βάση του σχήματος με το ύψος (Εμ. = Β x Υ).
Δείτε επίσης
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

