.
Τραπέζιο στην ευκλείδεια γεωμετρία είναι το κυρτό τετράπλευρο που έχει δύο πλευρές παράλληλες. Οι παράλληλες αυτές πλευρές λέγονται βάσεις και η απόστασή τους ύψος του τραπεζίου. Τέλος το ευθύγραμμο τμήμα που ενώνει τα μέσα των μη παράλληλων πλευρών του λέγεται διάμεσος του τραπεζίου· πρόκειται για το τμήμα της μεσοπαράλληλης των βάσεων που αποκόπτουν οι μη παράλληλες πλευρές. Ειδική περίπτωση τραπεζίου είναι το ισοσκελές τραπέζιο.
Ιδιότητες
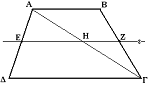
Η διάμεσος ενός τραπεζίου είναι παράλληλη προς τις βάσεις του και ίση με το ημιάθροισμά τους.
Η διάμεσος ενός τραπεζίου είναι παράλληλη προς τις βάσεις του και ίση με το ημιάθροισμά τους.
Απόδειξη: Ας είναι ΑΒΓΔ ένα τραπέζιο με βάσεις ΑΒ, ΓΔ και ΑΓ η διαγώνιος. Από το μέσο Ε της ΑΔ φέρνουμε ευθεία ε παράλληλα προς την ΔΓ. Στο τρίγωνο ΑΔΓ η ε διέρχεται από το μέσο της πλευράς ΑΔ και είναι παράλληλη στην πλευρά ΓΔ, άρα περνάει από το μέσο της τρίτης πλευράς ΑΓ, ας το πούμε Η, και έτσι τα ΕΗ, ΓΔ/2 είναι ίσα και παράλληλα. Όμοια, στο τρίγωνο ΑΒΓ το Η είναι μέσο της ΑΓ και η ΗΖ παράλληλη στην ΑΒ, άρα το Ζ θα είναι το μέσο της ΒΓ και έτσι τα ΖΗ, ΑΒ/2 ειναι ίσα και παράλληλα. Συνεπώς η ΕΖ θα είναι η διάμεσος του τραπεζίου και θα ισχύει
\Epsilon\Zeta = \Epsilon\Eta+\Eta\Zeta||=\frac{\Gamma\Delta+\Alpha\Beta}{2}
Η διάμεσος τραπεζίου διέρχεται από τα μέσα των διαγωνίων και τους αποκόπτει τμήμα ίσο με την ημιδιαφορά των βάσεων.
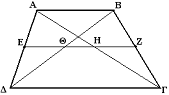
Η διάμεσος ενός τραπεζίου διέρχεται από τα μέσα των διαγωνίων του και το τμήμα που αποκόπτεται από αυτές ισούται με την ημιδιαφορά των βάσεων.
Απόδειξη: Για τους ίδιους λόγους όπως στην προηγούμενη ιδιότητα, το Θ είναι το μέσον της ΒΔ. Είναι:
\Theta\Eta = \Epsilon\Eta-\Eta\Theta=\frac{\Gamma\Delta-\Alpha\Beta}{2}
Το ΘΗ είναι παράλληλο με τις βάσεις ως τμήμα της διαμέσου του τραπεζίου.
Τετράπλευρο
Παραλληλόγραμμο
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

