Ορθογώνιο τρίγωνο
αγγλικά : Right triangle
γαλλικά :
γερμανικά :
Ορθογώνιο τρίγωνο στη γεωμετρία είναι τρίγωνο του οποίου μία γωνία είναι ορθή. Οι πλευρές που περιέχουν την ορθή γωνία λέγονται κάθετες πλευρές και η απέναντί της λέγεται υποτείνουσα του ορθογώνιου τριγώνου.
Το ορθογώνιο τρίγωνο στην ευκλείδεια γεωμετρία
Κριτήρια ισότητας ορθογώνιων τριγώνων
Κριτήριο πλευράς-πλευράς.
Κριτήριο πλευράς-προσκείμενης οξείας.
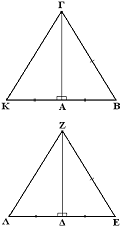
Κριτήριο πλευράς-πλευράς: Αν δύο ορθογώνια τρίγωνα έχουν δύο αντίστοιχες πλευρές τους ίσες μία προς μία τότε είναι ίσα.
Απόδειξη: Διακρίνουμε δύο περιπτώσεις: Έχουν δύο κάθετες πλευρές ίσες. Στην περίπτωση αυτή θα είναι ίσα από το κριτήριο πλευράς-γωνίας-πλευράς, με δύο πλευρές ίσες μία προς μία και την περιεχόμενη γωνία ίση ως ορθή. Έχουν μία κάθετη πλευρά ίση και την υποτείνουσα. Αρκεί να δείξουμε ότι οι αντίστοιχες περιεχόμενες (οξείες) γωνίες θα είναι ίσες και τότε από το κριτήριο πλευράς-γωνίας-πλευράς θα είναι ίσα. Έστω λοιπόν δύο ορθογώνια τρίγωνα ΑΒΓ και ΔΕΖ, τέτοια ώστε Α = Δ = ορθή γωνία, ΑΒ = ΔΕ και ΒΓ = ΕΖ (η ορθή γωνία σε κάθε τρίγωνο δεν μπορεί να είναι περιεχόμενη της κάθετης και της υποτείνουσας). Αρκεί να δείξουμε ότι Β = Ε (ισότητα γωνιών). Στις προεκτάσεις των ΑΒ και ΔΕ προς τα Α και Δ, παίρνουμε σημεία Κ και Λ τέτοια ώστε ΑΚ = ΑΒ και ΔΛ = ΔΕ αντίστοιχα. Από το κριτήριο πλευράς-γωνίας-πλευράς έχουμε τις ισότητες του ΑΒΓ με το ΑΚΓ και του ΔΕΖ με το ΔΛΖ. Συνεπώς έχουμε ΚΓ = ΒΓ = ΕΖ = ΛΖ. Από το κριτήριο πλευράς-πλευράς-πλευράς τότε τα τρίγωνα ΓΚΒ και ΖΛΕ είναι ίσα, από όπου έχουμε Β = Ε (ισότητα γωνιών).
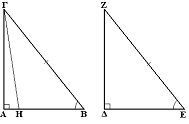
Κριτήριο πλευράς-προσκείμενης οξείας: Αν δύο ορθογώνια τρίγωνα έχουν μία πλευρά και την προσκείμενη οξεία γωνία ίσα τότε είναι ίσα.
Απόδειξη: Διακρίνουμε πάλι δύο περιπτώσεις: Έχουν μία κάθετη πλευρά και την προσκείμενη οξεία γωνία ίσα. Θα είναι ίσα από το κριτήριο γωνίας-πλευράς-γωνίας, με δύο γωνίες ίσες μία προς μία (η οξεία και η ορθή) και την περιεχόμενη κάθετη πλευρά ίση. Έχουν μία οξεία γωνία ίση και την υποτείνουσα. Έστω δύο τρίγωνα ΑΒΓ και ΔΕΖ με Α = Δ = ορθή γωνία, ΒΓ = ΕΖ και Β = Ε (ισότητα γωνιών). Αρκεί να δείξουμε ότι ΑΒ = ΔΕ. Θα το δείξουμε με απαγωγή σε άτοπο: Υποθέτουμε ότι ΑΒ > ΔΕ. Θα υπάρχει τότε στην ΑΒ σημείο Η για το οποίο ΒΗ = ΔΕ. Τότε από το κριτήριο πλευράς-γωνίας-πλευράς τα τρίγωνα ΗΒΓ και ΔΕΖ πρέπει να είναι ίσα και να είναι Η = Δ = ορθή γωνία. Αυτό είναι άτοπο αφού από σημείο ευθείας περνά μόνο μία κάθετη στην ευθεία.
Ιδιότητες
Οι οξείες γωνίες ορθογώνιου τριγώνου είναι συμπληρωματικές.
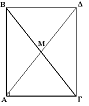
Η διάμεσος της ορθής γωνίας.
Η διάμεσος ορθογωνίου τριγώνου που άγεται από την κορυφή της ορθής γωνίας ισούται με το μισό της υποτείνουσας και αντίστροφα.
Απόδειξη ευθέος: Ας είναι ΑΒΓ ένα ορθογώνιο τρίγωνο με την Α ορθή, και Μ το μέσο της υποτείνουσας. Αν Δ είναι το συμμετρικό του Α ως προς το Μ, τότε το ΑΒΔΓ θα είναι ορθογώνιο παραλληλόγραμμο, ως τετράπλευρο με διχοτομούμενες διαγωνίους και μία ορθή γωνία. Άρα έχουμε ΑΔ = ΒΓ, άρα 2ΑΜ = ΒΓ, άρα ΑΜ = ΒΓ/2.
Απόδειξη αντίστροφου: Ας είναι ΑΒΓ ένα τρίγωνο με διάμεσο ΑΜ τέτοια ώστε ΑΜ = ΒΓ/2. Αν Δ είναι το συμμετρικό του Α ως προς το Μ, τότε το ΑΒΔΓ είναι ορθογώνιο αφού οι διαγώνιοί του διχοτομούνται και είναι
ίσες.
Μία κάθετη πλευρά ενός ορθογώνιου τριγώνου είναι το μισό της υποτείνουσας αν και μόνο αν η απέναντι γωνία του ισούται με 30°.
Μετρικές σχέσεις ορθογωνίου τριγώνου
{\displaystyle {\widehat {\mathrm {B} \mathrm {A} \Gamma }}=90^{o}\ \ \kappa \alpha \iota \ \ {\widehat {\mathrm {A} \Delta \Gamma }}=90^{o}(\mathrm {A} \Delta } : ύψος)
{\displaystyle \mathrm {A} \mathrm {B} ^{2}=\mathrm {B} \Delta \cdot \mathrm {B} \Gamma }
{\displaystyle \mathrm {A} \Gamma ^{2}=\Gamma \Delta \cdot \mathrm {B} \Gamma }
ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ: {\displaystyle \mathrm {B} \Gamma ^{2}=\mathrm {A} \Gamma ^{2}+\mathrm {A} \mathrm {B} ^{2}}
{\displaystyle \mathrm {A} \Delta ^{2}=\mathrm {B} \Delta \cdot \Delta \Gamma }
{\displaystyle \mathrm {A} \mathrm {B} \cdot \mathrm {A} \Gamma =\mathrm {B} \Gamma \cdot \mathrm {A} \Delta }
{\displaystyle {\frac {1}{\mathrm {A} \mathrm {B} ^{2}}}+{\frac {1}{\mathrm {A} \Gamma ^{2}}}={\frac {1}{\mathrm {A} \Delta ^{2}}}}
Δείτε ακόμη
Τριγωνομετρία
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License