Καμπύλη του Ευδόξου
αγγλικά : Kampyle of Eudoxus
γαλλικά :
γερμανικά :
Η Καμπύλη του Ευδόξου είναι μια καμπύλη με καρτεσιανή εξίσωση
{\displaystyle x^{4}=a^{2}(x^{2}+y^{2}),}
από την οποία αποκλείεται η λύση x = y = 0
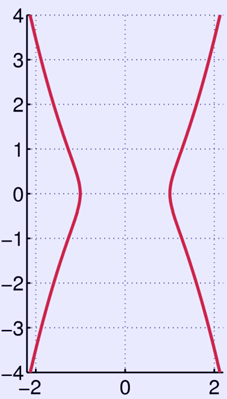
Καμπύλη του Ευδόξου, a = 1
Εναλλακτικές παραμετρικοποιήσεις
Στις πολικές συντεταγμένες, το καμπύλη έχει την εξίσωση
{\displaystyle r=a\sec ^{2}\theta .}
Ομοίως, έχει μια παραμετρική αναπαράσταση
{ {\displaystyle x=a\sec(t),\quad y=a\tan(t)\sec(t).}
Ιστορία
Αυτή η τεταρτική καμπύλη μελετήθηκε από τον Έλληνα αστρονόμο και μαθηματικό Εύδοξο της Κνίδου (περ. 408 π.Χ. - περίπου 347 π.Χ.) σε σχέση με το κλασικό πρόβλημα του διπλασιασμού του κύβου.
Είναι συμμετρική και στους δύο άξονες x και y. Διασχίζει τον άξονα x στο (± a, 0). Έχει σημεία καμπής στο
{\displaystyle \left(\pm a{\frac {\sqrt {6}}{2}},\pm a{\frac {\sqrt {3}}{2}}\right)}
(τέσσερις καμπές, μία σε κάθε τεταρτημόριο). Το πάνω μισό της καμπύλης είναι ασυμπτωματικό σε {\displaystyle x^{2}/a-a/2} as x\to \infty , και μπορεί να γραφτεί ως
{\displaystyle y={\frac {x^{2}}{a}}{\sqrt {1-{\frac {a^{2}}{x^{2}}}}}={\frac {x^{2}}{a}}-{\frac {a}{2}}\sum _{n=0}^{\infty }C_{n}\left({\frac {a}{2x}}\right)^{2n},}
όπου
C_n = \frac1{n+1} \binom{2n}{n}
is the n-οστός καταλανικός αριθμός.
βιβλιογραφικές αναφορές
J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 141–142. ISBN 0-486-60288-5.
External links
O'Connor, John J.; Robertson, Edmund F., "Kampyle of Eudoxus", MacTutor History of Mathematics archive, University of St Andrews.
Weisstein, Eric W. "Kampyle of Eudoxus". MathWorld.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

