Καμπύλη Κάππα
αγγλικά : Kappa curve
γαλλικά :
γερμανικά :
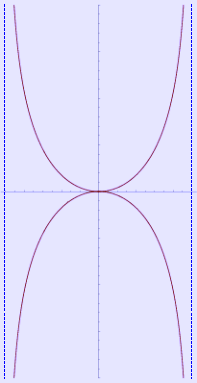
Στη γεωμετρία, η καμπύλη κάππα ή η καμπύλη του Γκούτσεβεν είναι μια δισδιάστατη αλγεβρική καμπύλη που μοιάζει με το ελληνικό γράμμα ϰ (κάπα). Η καμπύλη κάππα μελετήθηκε για πρώτη φορά από τον Gérard van Gutschoven γύρω στο 1662. Στην ιστορία των μαθηματικών, είναι γνωστή ως ένα από τα πρώτα παραδείγματα της εφαρμογής των βασικών λογιστικών μεθόδων του Isaac Barrow για τον προσδιορισμό της εφαπτομένης μιας καμπύλης. Οι Isaac Newton και Johann Bernoulli συνέχισαν τις μελέτες αυτής της καμπύλης .
Χρησιμοποιώντας το καρτεσιανό σύστημα συντεταγμένων μπορεί να εκφραστεί ως
{\displaystyle x^{2}(x^{2}+y^{2})=a^{2}y^{2}}
ή, χρησιμοποιώντας παραμετρικές εξισώσεις,
{\displaystyle {\begin{aligned}x&=a\sin t,\\y&=a\sin t\tan t.\end{aligned}}}
Στις πολικές συντεταγμένες η εξίσωση της είναι ακόμα πιο απλή:
{\displaystyle r=a\tan \theta .}
Έχει δύο κατακόρυφα ασυμπτωματικές στο x=\pm a, που εμφανίζονται ως διακεκομμένες μπλε γραμμές στο πιο κάτω σχήμα
Η καμπυλότητα της καμπύλης κάππα:
{\displaystyle \varkappa (\theta )={\frac {8(3-\sin ^{2}\theta )\sin ^{4}\theta }{a(\sin ^{2}(2\theta )+4)^{\frac {3}{2}}}}.}
Εφαπτομενική γωνία:
{\displaystyle \phi (\theta )=-\arctan \left({\tfrac {1}{2}}\sin(2\theta )\right).}
Εφαπτόμενες μέσω απειροστών
Οι εφαπτόμενες γραμμές της καμπύλης κάππα μπορούν επίσης να προσδιοριστούν γεωμετρικά χρησιμοποιώντας διαφορικά και τους στοιχειώδεις κανόνες της απειροστικής αριθμητικής. Ας υποθέσουμε ότι τα x και y είναι μεταβλητές, ενώ το a θεωρείται σταθερά. Από τον ορισμό της καμπύλης κάππα,
x^{2}(x^{2}+y^{2})-a^{2}y^{2}=0
Τώρα, μια απειροστή αλλαγή στην τοποθεσία μας πρέπει επίσης να αλλάξει την αξία της αριστεράς πλευράς, έτσι
d(x^{2}(x^{2}+y^{2})-a^{2}y^{2})=0
Διανομή του διαφορικού και εφαρμογή κατάλληλων κανόνων,
d(x^{2}(x^{2}+y^{2}))-d(a^{2}y^{2})=0
(2xdx)(x^{2}+y^{2})+x^{2}(2xdx+2ydy)-a^{2}2ydy=0
(4x^{3}+2xy^{2})dx+(2yx^{2}-2a^{2}y)dy=0
x(2x^{2}+y^{2})dx+y(x^{2}-a^{2})dy=0
{\frac {x(2x^{2}+y^{2})}{y(a^{2}-x^{2})}}={\frac {dy}{dx}}
Παράγωγος
άν χρησιμοποιούμε τη σύγχρονη έννοια μιας λειτουργικής σχέσης y (x) και εφαρμόζουμε πεπλεγμένη διαφοροποίηση, η κλίση μιας εφαπτομένης γραμμής στην καμπύλη κάππα σε ένα σημείο (x, y) είναι:
2x(x^{2}+y^{2})+x^{2}(2x+2y{\frac {dy}{dx}})=2a^{2}y{\frac {dy}{dx}}
2x(x^{2}+y^{2})+x^{2}(2x+2y{\frac {dy}{dx}})=2a^{2}y{\frac {dy}{dx}}
2x^{3}+2xy^{2}+2x^{3}=2a^{2}y{\frac {dy}{dx}}-2x^{2}y{\frac {dy}{dx}}
4x^{3}+2xy^{2}=(2a^{2}y-2x^{2}y){\frac {dy}{dx}}
{\frac {2x^{3}+xy^{2}}{a^{2}y-x^{2}y}}={\frac {dy}{dx}}
Εξωτερικοί σύνδεσμοι
Weisstein, Eric W. "Kappa curve". MathWorld.
A Java applet for playing with the curve
O'Connor, John J.; Robertson, Edmund F., "Kappa Curve", MacTutor History of Mathematics archive, University of St Andrews.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

