Ιπποπέδη
αγγλικά : Hippopede
γαλλικά : Ηippopède
γερμανικά :
Στη γεωμετρία, η Ιπποπέδη (από την Αρχαία Ελληνική ἱπποπέδη ) είναι μια καμπύλη επιπέδου που καθορίζεται από μια εξίσωση της μορφής
(x^{2}+y^{2})^{2}=cx^{2}+dy^{2},
όπου θεωρείται ότι τα c> 0 και c> d αφού οι υπόλοιπες περιπτώσεις είτε μειώνονται σε ένα σημείο είτε μπορούν να τοποθετηθούν στη δεδομένη μορφή με περιστροφή. Οι Ιπποπέδη είναι δικυκλική ρητή αλγεβρική καμπύλη τετάρτου βαθμού και συμμετρική σε σχέση με τους άξονες x και y.
Ειδικές περιπτώσεις
Όταν d> 0 η καμπύλη έχει οβάλ μορφή και είναι συχνά γνωστή ως ωοειδές του Booth, και όταν d <0 η καμπύλη μοιάζει με ένα σχήμα οκτώ πλαγιασμενο, ή λεμνισκάτη, και είναι συχνά γνωστό ως λεμνισκάτη, του Booth, απο τον μαθηματικό Τζέιμς Μπουθ του 19οθ αιώνα που την μελέτησε. Η Ιπποπέδη διερευνήθηκε επίσης από τον Πρόκλο (για τον οποίο μερικές φορές ονομάζονται Ιπποπέδη του Πρόκλου ) και τον Εύδοξο )
Για d = −c, η ιπποπέδη αντιστοιχεί στη λεμνισκάτη του Bernoulli.
Ορισμός ως σπειροειδή τμήματα
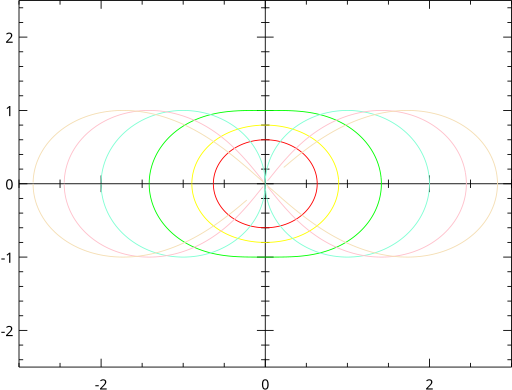
Ιπποπέδη , a = 1, b = 0.1, 0.2, 0.5, 1.0, 1.5, και 2.0.
Ιπποπέδη b = 1, a = 0.1, 0.2, 0.5, 1.0, 1.5, και 2.0.
Η Ιπποπέδη μπορεί να οριστεί ως η καμπύλη που σχηματίζεται από τη διασταύρωση ενός τόρου και ενός επιπέδου, όπου το επίπεδο είναι παράλληλο με τον άξονα του τόρου και εφαπτόμενο σε αυτόν στον εσωτερικό κύκλο. Έτσι είναι ένα σπειροειδές τμήμα το οποίο με τη σειρά του είναι ένας τύπος τορικού τμήματος.
Εάν ένας κύκλος με ακτίνα a περιστρέφεται γύρω από έναν άξονα σε απόσταση b από το κέντρο του, τότε η εξίσωση του προκύπτοντος ιπποπόδου σε πολικές συντεταγμένες
{\displaystyle r^{2}=4b(a-b\sin ^{2}\theta )}
ή σε καρτεσιανές συντεταγμένες
(x^{2}+y^{2})^{2}+4b(b-a)(x^{2}+y^{2})=4b^{2}x^{2}.
όταν a> b ο τόρος τέμνεται, δεν μοιάζει με τη συνηθισμένη εικόνα ενός τόρου.
Βιβλιογραφικές αναφορές
Lawrence JD. (1972) Catalog of Special Plane Curves, Dover. Pp. 145–146.
Booth J. A Treatise on Some New Geometrical Methods, Longmans, Green, Reader, and Dyer, London, Vol. I (1873) and Vol. II (1877).
Weisstein, Eric W. "Hippopede". MathWorld.
"Hippopede" at 2dcurves.com
"Courbes de Booth" at Encyclopédie des Formes Mathématiques Remarquables
External links
"The Hippopede of Proclus" at The National Curve Bank
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License