Γωνία
αγγλικά : Angle
γαλλικά : Angle
γερμανικά : Winkel
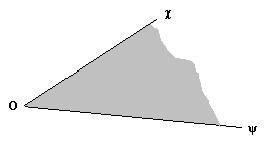
Στην ευκλείδεια γεωμετρία, επίπεδη γωνία ή απλά γωνία είναι το γεωμετρικό σχήμα που αποτελείται από δύο ημιευθείες με κοινή αρχή. Ο αυστηρός μαθηματικός ορισμός της επίπεδης γωνίας είναι «Το κοινό σύνολο σημείων που ανήκουν σε δύο συνεπίπεδα ημιεπίπεδα». Αν οι ευθείες που ορίζουν τα ημιεπίπεδα τέμνονται σε κάποιο σημείο, τότε αυτό ονομάζεται «κορυφή». Σε κάθε μία από τις δύο ευθείες ανήκει μόνο ένα μέρος της στη γωνία, το μέρος που ανήκει είναι μία ημιευθεία με αρχή την κορυφή της γωνίας. Οι ημιευθείες λέγονται «πλευρές» της γωνίας. Στο σχήμα, Ο είναι η κορυφή και Οχ, Οψ οι δύο πλευρές. Το σύνολο των σημείων της γωνίας που δεν ανήκουν στις πλευρές λέγεται «εσωτερικό» της γωνίας, ενώ το σύνολο των σημείων του επιπέδου που δεν ανήκουν στη γωνία εξωτερικό.
Γωνία ορισμένη από τις ημιευθείες Οχ και Οψ.
Στην επίπεδη γεωμετρία, μια γωνία σχηματίζεται από δυο ημιευθείες, οι οποίες ονομάζονται πλευρές της γωνίας, και έχουν κοινή αρχή, η οποία ονομάζεται κορυφή της γωνίας.[1] Οι γωνίες σχηματίζονται από δυο ημιευθείες που βρίσκονται στο ίδιο επίπεδο, αλλά αυτό το επίπεδο δεν χρειάζεται απαραίτητα να είναι ένα ευκλείδειο επίπεδο. Οι γωνίες σχηματίζονται επίσης με τη συνάντηση δυο επιπέδων, τόσο στο ευκλείδιο, όσο και σε άλλα διαστήματα. Αυτές οι γωνίες μεταξύ επιπέδων ονομάζονται «δίεδρες γωνίες». Ως γωνίες που σχηματίζονται με τη συνάντηση δύο καμπυλών ορίζονται οι γωνίες που σχηματίζουν οι εφαπτόμενες ημιευθείες που συναντιώνται στο σημείο τομής των δύο αυτών καμπυλών. Όμοιοι ορισμοί χρησιμοποιούνται και για τον τρισδιάστατο χώρο. Για παράδειγμα, μια «σφαιρική γωνία» σχηματίζεται από δυο μεγάλους κύκλους σε μια σφαίρα και είναι η δίεδρη γωνία ανάμεσα στα επίπεδα που ορίζονται από τους δυο μεγάλους κύκλους.
Διχοτόμος μίας γωνίας χΟψ ονομάζεται μία ημιευθεία Οδ που έχει αρχή την κορυφή της γωνίας, βρίσκεται στο εσωτερικό της και είναι τέτοια ώστε να χωρίζει τη γωνία σε δύο ίσες γωνίες χΟδ και δΟψ. Στα πλαίσια της Ευκλείδειας γεωμετρίας, η διχοτόμος μίας γωνίας είναι αξιωματικά μοναδική.
Ειδικές περιπτώσεις
Μία γωνία στην οποία οι πλευρές είναι αντικείμενες ημιευθείες λέγεται ευθεία γωνία. Με άλλα λόγια κάθε ευθεία με ένα σημείο της μπορεί να θεωρηθεί ως ευθεία γωνία.
Κάθε γωνία μικρότερη από την ευθεία λέγεται κυρτή γωνία
Κάθε γωνία μεγαλύτερη από την ευθεία λέγεται μη κυρτή γωνία ή γωνία ανάκλασης.
Ορθή είναι μία γωνία που προκύπτει από τη διχοτόμηση μίας ευθείας γωνίας. Προφανώς, όλες οι ορθές είναι ίσες μεταξύ τους.
Κάθε γωνία μικρότερη από την ορθή λέγεται οξεία γωνία.
Κάθε κυρτή γωνία μεγαλύτερη από την ορθή λέγεται αμβλεία γωνία.
Μια γωνία το εσωτερικό της οποίας δεν περιέχει κανένα σημείο λέγεται μηδενική γωνία, ενώ μια γωνία το εσωτερικό της οποίας περιέχει όλο το επίπεδο εκτός των πλευρών της λέγεται πλήρης γωνία ή περιγώνια. Κάθε ημιευθεία μπορεί να ιδωθεί ως μηδενική ή πλήρης γωνία, ανάλογα με το πώς εκλαμβάνουμε το εσωτερικό της.
Κάθε γωνία, το μέτρο της οποίας δεν είναι ακέραιο πολλαπλάσιο του μέτρου της ορθής, καλείται λοξή γωνία (oblique angle).
Σύγκριση γωνιών και πράξεις
Ας είναι χΟψ και κΑλ δύο γωνίες. Ταυτίζουμε την Οχ με την Ακ, ώστε η Αλ να βρίσκεται προς το μέρος της Οψ.
Αν οι Οψ και Αλ συμπίπτουν τότε λέμε ότι η γωνία χΟψ είναι ίση με την κΑλ και γράφουμε χΟψ = κΑλ.
Αν η Αλ βρίσκεται στο εσωτερικό της χΟψ τότε λέμε ότι η χΟψ είναι μεγαλύτερη από την κΑλ και γράφουμε χΟψ > κΑλ.
Αν η Αλ βρίσκεται στο εξωτερικό της χΟψ τότε λέμε ότι η χΟψ είναι μικρότερη από την κΑλ και γράφουμε χΟψ < κΑλ.
Δύο γωνίες που έχουν κοινή αρχή, μία κοινή πλευρά και κανένα κοινό εσωτερικό σημείο, λέγονται διαδοχικές ή εφεξής γωνίες.
Ας είναι χΟψ και κΑλ δύο γωνίες. Ταυτίζουμε την Οψ με την Ακ, έτσι ώστε οι δύο γωνίες να είναι διαδοχικές. Λέμε άθροισμα των γωνιών χΟψ και κΑλ τη γωνία χΑλ και γράφουμε χΑλ = χΟψ + κΑλ.
Αν χΟψ > κΑλ, ταυτίζουμε την Οχ με την Ακ έτσι ώστε η Αλ να βρίσκεται στο εσωτερικό της χΟψ. Λέμε διαφορά της κΑλ από την χΟψ τη γωνία λΑψ και γράφουμε λΑψ = χΟψ - κΑλ.
Ας είναι χΟψ μια γωνία και ν ένας φυσικός αριθμός. Αν κΑλ είναι μια γωνία για την οποία \( {\displaystyle \kappa A\lambda =\underbrace {\chi O\psi +\cdots +\chi O\psi } _{\nu }} , τότε λέμε ότι η κΑλ είναι το ν-πλάσιο γινόμενο της χΟψ και γράφουμε {\displaystyle \kappa A\lambda =\nu \cdot \chi O\psi } . Γράφουμε επίσης {\displaystyle \chi O\psi ={\frac {1}{\nu }}\cdot \kappa A\lambda } και λέμε ότι η χΟψ είναι το υπο-ν-πλάσιο γινόμενο της κΑλ. Τέλος, αν μ είναι ένας φυσικός αριθμός και εΒζ είναι μια γωνία έτσι ώστε {\displaystyle \epsilon B\zeta =\mu \cdot \chi O\psi } , τότε γράφουμε {\displaystyle \epsilon B\zeta ={\frac {\mu }{\nu }}\cdot \kappa A\lambda } , και λέμε ότι η εΒζ είναι το γινόμενο ρητού αριθμού με γωνία.
Ως μέτρηση μιας γωνίας χΟψ εννοούμε την σύγκρισή της με μια άλλη γωνία, ας πούμε κΑλ, την οποία θεωρούμε αυθαίρετα μοναδιαία. Αν ισχύει {\displaystyle \chi O\psi ={\frac {\mu }{\nu }}\cdot \kappa A\lambda } , λέμε ότι το μέτρο ή το άνοιγμα της χΟψ ως προς την κΑλ είναι {\displaystyle {\frac {\mu }{\nu }}} . Το μέτρο μιας γωνίας συνδέεται και με το μέτρο τόξου σε κύκλο.
Συνοπτικά
| Τύπος | οξεία | ορθή | αμβλεία | ευθεία | ανάκλασης | περιγώνια | ||||
| Μονάδες | Διάστημα | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Στροφή | (0, 14) | 14 | (14, 12) | 12 | (12, 1) | 1 | ||||
| Ακτίνια | (0, 12π) | 12π | (12π, π) | π | (π, 2π) | 2π | ||||
| Μοίρες | (0, 90)° | 90° | (90, 180)° | 180° | (180, 360)° | 360° | ||||
| Βαθμοί | (0, 100)g | 100g | (100, 200)g | 200g | (200, 400)g | 400g | ||||
Ειδικά ζεύγη γωνιών
Αριστερά: Οι κατακορυφήν γωνίες είναι ίσες. Δεξιά: Οι διχοτόμοι δύο διαδοχικών παραπληρωματικών γωνιών είναι κάθετες μεταξύ τους.
Δυο γωνίες στις οποίες οι πλευρές της μιας είναι οι αντικείμενες ημιευθείες των πλευρών της άλλης, λέγονται κατακορυφήν. Δυο γωνίες με άθροισμα μια ευθεία γωνία, λέγονται παραπληρωματικές και δυο γωνίες με άθροισμα μια ορθή γωνία, λέγονται συμπληρωματικές.
Στα πλαίσια της ευκλείδειας γεωμετρίας ισχύουν τα παρακάτω:
Οι κατακορυφήν γωνίες είναι ίσες.
Οι διχοτόμοι δυο κατακορυφήν γωνιών είναι αντικείμενες ημιευθείες.
Αν δύο διαδοχικές γωνίες είναι παραπληρωματικές, τότε έχουν τις μη κοινές πλευρές τους αντικείμενες ημιευθείες, και αντίστροφα.
Οι διχοτόμοι δύο διαδοχικών παραπληρωματικών γωνιών είναι κάθετες μεταξύ τους.
Γωνίες εντός, εκτός, εναλλάξ και επί τα αυτά ευθειών.
Ας είναι φ και χ δύο ευθείες οι οποίες τέμνονται από τρίτη ευθεία ψ στα σημεία αντίστοιχα Α και Β. Σχηματίζονται οχτώ γωνίες, όπως φαίνεται στο σχήμα αριστερά. Οι γωνίες Α1, Α2, Β3 και Β4 λέγονται εκτός των φ και χ. Οι Α3, Α4, Β1 και Β2 λέγονται εντός των φ και χ. Επίσης οι Α1 και Β3 λέμε ότι είναι γωνίες εναλλάξ της ψ. Το ίδιο και για τις Α2 και Β4. Τέλος λέμε ότι οι Α2 και Β2 είναι επί τα αυτά μέρη της ψ.
Ιδιότητες
Αν δύο παράλληλες ευθείες τέμνονται από τρίτη, τότε:
σχηματίζουν τις εντός εναλλάξ γωνίες ίσες
σχηματίζουν τις εντός-εκτός και επί τα αυτά γωνίες ίσες
σχηματίζουν τις εντός και επί τα αυτά γωνίες παραπληρωματικές
Δύο γωνίες που έχουν πλευρές παράλληλες μία προς μία είναι ίσες ή παραπληρωματικές.
Γωνίες με παράλληλες πλευρές.
Απόδειξη: Έστω γωνίες φ και ω με πλευρές παράλληλες. Διακρίνουμε σε τρεις περιπτώσεις:
Αν φ < 90° και ω < 90° τότε είναι ίσες ως εντός εκτός επί τα αυτά με γωνία ρ, όπως φαίνεται στο αντίστοιχο σχήμα (αριστερά επάνω).
Αν φ > 90° και ω < 90°, όπως στο αντίστοιχο σχήμα (αριστερά κάτω) τότε είναι ίσες ως παραπληρωματικές ίσων γωνιών, από την προηγούμενη περίπτωση.
Αν φ > 90° και ω > 90° τότε είναι παραπληρωματικές ως ίσες προς παραπληρωματικές. Στο αντίστοιχο σχήμα (δεξιά) φερειπείν έχουμε φ = ρ και ω + ρ = 180°.
Δύο γωνίες που έχουν πλευρές κάθετες μία προς μία είναι ίσες ή παραπληρωματικές.
Γωνίες με κάθετες πλευρές.
Απόδειξη: Έστω φ και ω δύο γωνίες με πλευρές κάθετες μία προς μία. Διακρίνουμε σε τρεις περιπτώσεις:
Αν φ < 90° και ω < 90° τότε από την κορυφή της ω φέρνουμε ημιευθείες παράλληλες αντίστοιχα στις πλευρές της φ, όπως φαίνεται στο αντίστοιχο σχήμα (επάνω). Η γωνία κΒι που σχηματίζεται θα είναι ίση με τη φ, σύμφωνα με την προηγούμενη ιδιότητα. Επίσης, επειδή η Βι είναι παράλληλη στην Αε και η Αε είναι κάθετη στην Βη, οι Βι, Βη είναι κάθετες, δηλαδή η γωνία ιΒη θα είναι ορθή. Όμοια, είναι και η κΒθ ορθή. Έχουμε τις ακόλουοθες διαδοχικά ισότητες γωνιών:
κΒθ = ιΒη
κΒη + ηΒθ = ιΒκ + κΒη
ηΒθ = ιΒκ
ω = φ
Αν φ > 90° και ω > 90° τότε είναι ίσες ως παραπληρωματικές οξειών γωνιών με κάθετες πλευρές.
Αν φ < 90° και ω > 90° τότε, όπως φαίνεται στο αντίστοιχο σχήμα (κάτω), η εφεξής παραπληρωματική της ω είναι οξεία και έχει κάθετες πλευρές με τη φ, άρα είναι ίση της φ. Δηλαδή:
ηΒθ + θΒη' = 180°
ω + φ = 180°
Σχετική βιβλιογραφία
Baynes, Thomas Spencer, επιμ.. (1878), «Angle», Encyclopædia Britannica, 9th ed., Vol. II, New York: Charles Scribner's Sons.
Chisholm, Hugh; Phillips, Walter Alison, επιμ.. (1911), «Angle», Encyclopædia Britannica, 11th ed., Vol. II, Cambridge: Cambridge University Press.
Heiberg, Johan Ludvig (1908). Heath, T. L., επιμ. Euclid. The Thirteen Books of Euclid's Elements. 1. Cambridge: Cambridge University Press..
Δείτε επίσης
Γωνία
Κύκλος
Ωρική γωνία
Δίεδρη γωνία
Στερεά γωνία
Παρατηρήσεις, υποσημειώσεις και αναφορές
Sidorov, L.A. (2001), «Angle», στο: Hazewinkel, Michiel, επιμ., Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License