Ελκυστής
αγγλικά : Attractor
γαλλικά :
γερμανικά :
Ενας ελκυστής είναι ένας όρος από τη θεωρία των δυναμικών συστημάτων και περιγράφει ένα υποσύνολο ενός χώρου φάσεων (δηλαδή έναν ορισμένο αριθμό καταστάσεων) προς το οποίο ένα δυναμικό σύστημα κινείται με την πάροδο του χρόνου και που κάτω από η δυναμική αυτού του συστήματος δεν εγκαταλείπεται πλέον. Αυτό σημαίνει ότι ένα σύνολο μεταβλητών προσεγγίζει μια συγκεκριμένη τιμή, μια καμπύλη ή κάτι πιο περίπλοκο (δηλ. Μια περιοχή στον n-διάστατο χώρο) με την πάροδο του χρόνου (ασυμπτωτικά) και στη συνέχεια παραμένει κοντά στον εν λόγω ελκυστή για την περαιτέρω πορεία του χρόνου.
Ένας ελκυστής εμφανίζεται ως μια σαφώς αναγνωρίσιμη δομή. Συνηθισμένα, θα μπορούσε κανείς να μιλήσει για ένα είδος «σταθερής κατάστασης» ενός συστήματος (όπου περιοδικές, δηλαδή επαναλαμβανόμενες καταστάσεις τύπου κύματος ή άλλα αναγνωρίσιμα μοτίβα μπορούν επίσης να εννοηθούν), δηλαδή μια κατάσταση στην οποία κινείται ένα σύστημα.
Γνωστά παραδείγματα είναι ο ελκυστής Lorenz, ο ελκυστής Rössler και τα μηδενικά μιας παραγωγίσιμης συνάρτησης, που είναι ελκυστές της σχετικής μεθόδου Newton.
Το αντίθετο ενός ελκυστής ονομάζεται απωθητής ή αρνητικός ελκυστής . Οι όροι χρησιμοποιούνται στη φυσική και τη βιολογία.
Παράξενος ελκυστής
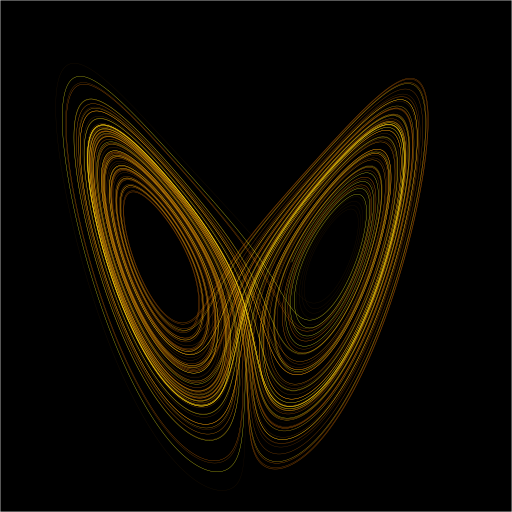
Μια γραφική παράσταση του παράξενου ελκυστήρα του Lorenz για τιμές ρ = 28, σ = 10, β = 8/3
Ένας ελκυστής ονομάζεται παράξενος εάν έχει δομή φράκταλ. Αυτό συμβαίνει συχνά όταν η δυναμική του είναι χαοτική, αλλά υπάρχουν επίσης παράξενοι μη χαοτικοί ελκυστές. Εάν ένας παράξενος ελκυστής είναι χαοτικός, παρουσιάζεται μια ευαίσθητη εξάρτηση από τις αρχικές συνθήκες, τότε δύο αυθαίρετα κοντά εναλλακτικά αρχικά σημεία στον ελκυστή, μετά από οποιονδήποτε αριθμό επαναλήψεων, θα οδηγήσουν σε σημεία που είναι αυθαίρετα μακριά (υπόκεινται στα όρια του ελκυστή ), και μετά από οποιονδήποτε άλλο αριθμό επαναλήψεων θα οδηγήσει σε σημεία που βρίσκονται αυθαίρετα κοντά μεταξύ τους. Έτσι, ένα δυναμικό σύστημα με χαοτικό ελκυστή είναι τοπικά ασταθές αλλά ολικά σταθερό: όταν κάποιες ακολουθίες έχουν εισέλθει στον ελκυστή, τα κοντινά σημεία αποκλίνουν το ένα από το άλλο αλλά ποτέ δεν απομακρύνονται από τον ελκυστή.
Ο όρος παράξενος ελκυστής επινοήθηκε από τον David Ruelle και τον Floris Takens για να περιγράψει τον ελκυστή που προέκυψε από μια σειρά διακλαδώσεων ενός συστήματος που περιγράφει τη ροή του υγρού. Οι παράξενοι ελκυστές είναι συχνά παραγωγίσιμοι σε μερικές κατευθύνσεις, αλλά μερικοί είναι σαν σκόνη Cantor και συνεπώς δεν είναι παραγωγίσιμοι. Παράξενοι ελκυστές μπορεί επίσης να βρεθούν παρουσία θορύβου, όπου μπορεί να αποδειχθεί ότι υποστηρίζουν αμετάβλητα τυχαία μέτρα πιθανότητας τύπου Sinai-Ruelle – Bowen.
Παραδείγματα περίεργων ελκυστών περιλαμβάνουν τον ελκυστή διπλής κύλισης, τον ελκυστή Hénon, τον ελκυστή Rössler και τον ελκυστή Lorenz.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License