Εικοσάγωνο
αγγλικά : Icosagon
γαλλικά :
γερμανικά :
Στη γεωμετρία το εικοσάγωνο είναι ένα οποιοδήποτε πολύγωνο σχήμα με είκοσι πλευρές και είκοσι κορυφές. Οι εσωτερικές γωνίες οποιουδήποτε εικοσαγώνου έχουν άθροισμα 3.240 μοίρες (°), ενώ το σχήμα έχει 170 διαγωνίους.
Πίνακας περιεχομένων
Κανονικό εικοσάγωνο
Συνήθως ο όρος εικοσάγωνο αναφέρεται σε ένα κανονικό εικοσάγωνο, στο οποίο όλες οι πλευρές και όλες οι γωνίες είναι ίσες μεταξύ τους. Σε ένα τέτοιο εικοσάγωνο, οι εσωτερικές γωνίες είναι ίσες με 162° η καθεμιά, ώστε η κάθε εξωτερική γωνία είναι ίση με 18°. Το σύμβολο Schläfli του κανονικού εικοσαγώνου είναι {20}.
Το εμβαδό (E) ενός κανονικού εικοσαγώνου με μήκος πλευράς α δίνεται από τη σχέση:
\( {\displaystyle E={5}a^{2}(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {5}}}})\simeq 31,5687a^{2}.}
Εκφραζόμενο με την ακτίνα R του περιγεγραμμένου κύκλου, το παραπάνω εμβαδό δίνεται από τη σχέση:
\( {\displaystyle E={\frac {5R^{2}}{2}}({\sqrt {5}}-1);}
Το κανονικό εικοσάγωνο καταλαμβάνει το 98,36% περίπου του εμβαδού του δίσκου του περιγεγραμμένου κύκλου.
Κατασκευή
Το κανονικό εικοσάγωνο είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη, είτε με διχοτόμηση πλευρών ενός κανονικού δεκαγώνου (ή διπλή διχοτόμηση των πλευρών κανονικού πενταγώνου), είτε με ανεξάρτητο τρόπο:

Κατασκευή ενός κανονικού εικοσαγώνου

Κατασκευή ενός κανονικού δεκαγώνου
Εφαρμογές
H «παχιά» σβάστικα ως ορθογώνιο εικοσάγωνο
Το «Globe», το υπαίθριο κυκλικό θέατρο του θιάσου του Σαίξπηρ στην Αγγλία, ανακαλύφθηκε ότι είχε κτίσθεί πάνω σε εικοσάγωνα θεμέλια, από μια μερική ανασκαφή[1] το 1989.
Ως σχήμα με εμβαδό, η σβάστικα είναι ένα μη κανονικό και μη κυρτό ορθογώνιο εικοσάγωνο, έχοντας εσωτερικές γωνίες 90 και 270 μοιρών.[2]
4.5.20 vertex.png Το κανονικό εικοσάγωνο μαζί με ένα τετράγωνο και ένα κανονικό πεντάγωνο μπορούν επαναλαμβανόμενα να καλύψουν πλήρως ένα επίπεδο.
Διαμερισμός
Εικοσάγωνο διαμερισμένο σε 180 ρόμβους (δεν υπάρχει μη ευθύγραμμο τμήμα στο σχήμα!)
Κατά τον Κόξετερ κάθε «ζωνόγωνο» (ένα 2m-γωνο του οποίου οι απέναντι πλευρές είναι ίσες και παράλληλες) μπορεί να διαμερισθεί σε m(m-1)/2 παραλληλόγραμμα.[3] Αυτό ισχύει και στην ειδικότερη περίπτωση των κανονικών πολυγώνων με άρτιο αριθμό πλευρών, οπότε τα παραλληλόγραμμα είναι όλα τους ρόμβοι. Για το εικοσάγωνο, m = 10 και μπορεί να διαμερισθεί σε 45 ρόμβους, από τους οποίους οι 5 είναι τετράγωνα. Αυτός ο μερισμός βασίζεται σε προβολή ως πολύγωνο Πέτρι ενός δεκαδιάστατου υπερκύβου. Υπάρχουν περαιτέρω διαμερισμοί, όπως σε 180 παραλληλόγραμμα.
Διαμερισμοί σε 45 ρόμβους 10-cube.svg
 Δεκαδιάστατος υπερκύβος |
 |
 |
 |
 |
Σχετιζόμενα πολύγωνα
Το αστεροειδές πολύγωνο με είκοσι πλευρές ονομάζεταιεικοσάγραμμα. Υπάρχουν τρεις κανονικές μορφές του, που συμβολίζονται με τα σύμβολο Schläfli {20/3}, {20/7} και {20/9}. Επίσης υπάρχουν πέντε κανονικά αστεροειδή σχήματα (σύνθετα) με την ίδια διάταξη κορυφών: τα 2{10}, 4{5}, 5{4}, 2{10/3}, 4{5/2} και
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Μορφή | Κυρτό πολύγωνο | Σύνθετο | Αστεροειδές πολύγωνο | Σύνθετο | |
| Σχήμα |  {20/1} = {20} |
 {20/2} = 2{10} |
 {20/3} |
 {20/4} = 4{5} |
 {20/5} = 5{4} |
| Εσωτερική γωνία | 162° | 144° | 126° | 108° | 90° |
| n | 6 | 7 | 8 | 9 | 10 |
| Μορφή | Σύνθετο | Αστεροειδές πολύγωνο | Σύνθετο | Αστεροειδές πολύγωνο | Σύνθετο |
| Σχήμα |  {20/6} = 2{10/3} |
 {20/7} |
 {20/8} = 4{5/2} |
 {20/9} |
 {20/10} = 10{2} |
| Εσωτερική γωνία | 72° | 54° | 36° | 18° | 0° |
Παραπέρα τομές του κανονικού δεκαγώνου και δεκαγράμματος μπορούν να δώσουν ισογώνιες ενδιάμεσες μορφές εικοσαγράμματος με ισαπέχουσες κορυφές.[4]
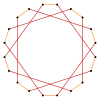
Κάθε κανονικό εικοσάγραμμα, {20/9}, μπορεί να θεωρηθεί ως ένα ημιδιχοτομημένο (quasitruncated) δεκάγωνο: t{10/9}={20/9}. Παρόμοια ένα δεκάγραμμα, που συμβολίζεται με {10/3}, έχει μια ημιδιχοτόμηση t{10/7}={20/7}, και τέλος μία απλή διχοτόμηση ενός δεκαγράμματος δίνει t{10/3}={20/3}.
Τα εικοσαγράμματα ως διχοτομήσεις κανονικών δεκαγώνων και δεκαγράμμων, {10}, {10/3} Ημικανονικό
| Ημικανονικό | Quasiregular | ||||
|---|---|---|---|---|---|
 t{10}={20} |
 |
 |
 |
 |
 t{10/9}={20/9} |
 t{10/3}={20/3} |
 |
 |
 |
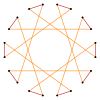 |
 t{10/7}={20/7} |
Παραπομπές
Muriel Pritchett, University of Georgia "To Span the Globe" Αρχειοθετήθηκε 2010-06-10 στο Wayback Machine., βλ. και Editor's Note, ανακτήθηκε στις 10 Ιανουαρίου 2016
Weisstein, Eric W., "Icosagon" από το MathWorld.
H.S. MacDonald Coxeter: Mathematical recreations and Essays, 13η έκδ, σελ. 141
The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History (1994), «Metamorphoses of polygons», Branko Grünbaum
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

