Αστροειδής
αγγλικά : Astroid
γαλλικά : Astroïde
γερμανικά : Astroide
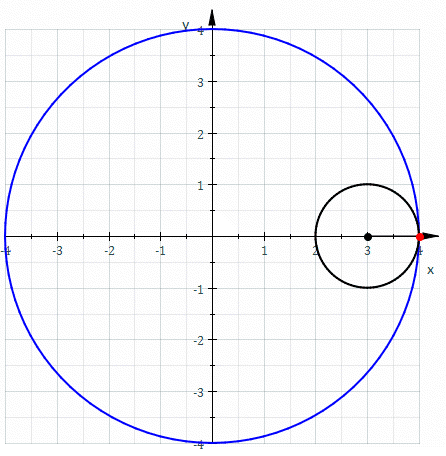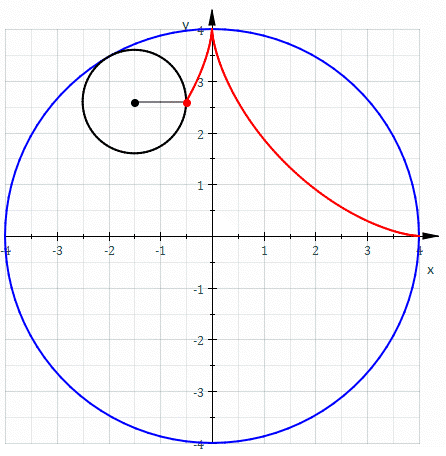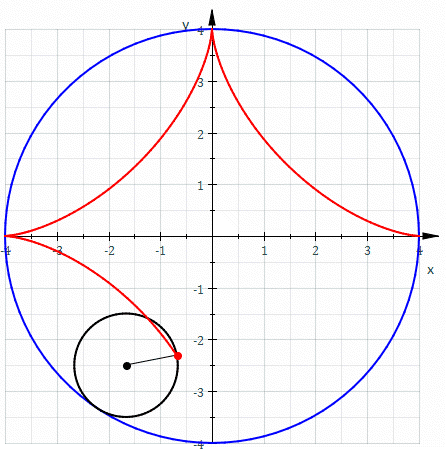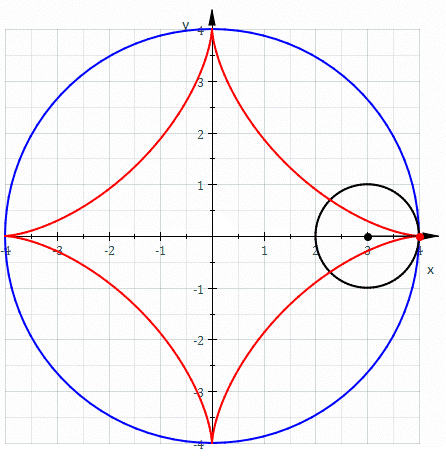
Η αστροειδής είναι μια συγκεκριμένη μαθηματική καμπύλη (που ανήκει στην οικογένεια των υποκυκλοειδών) με τέσσερις ακμές. Συγκεκριμένα, είναι ο γεωμετρικός τόπος ενός σημείου σε ένα κύκλο καθώς αυτός κυλά μέσα σε ένα άλλο σταθερό κύκλο με τετραπλάσια ακτίνα.[1] Ισοδύναμα, είναι επίσης ο γεωμετρικός τόπος ενός σημείου σε ένα κύκλο καθώς αυτός κυλά μέσα σε ένα μεγαλύτερο κύκλο με ακτίνα 4/3 φορές μεγαλύτερη. Μπορεί επίσης να οριστεί ως το περίγραμμα που προκύπτει όταν σε δύο ορθογώνιους άξονες κυλάμε ένα ευθύγραμμο τμήμα σταθερού μήκουε έτσι ώστε τα άκρα του να είναι πάντα στους άξονες.
Το σύγχρονο όνομα προέρχεται από την ελληνική λέξη για το "αστέρι" και στο παρελθόν είχε και διαφορετικά ονόματα [2][3].
Εξισώσεις
Αν η ακτίνα του μεγάλου σταθερού κύκλο είναι α, τότε η εξίσωση δίνεται από[4]
{\displaystyle |x|^{\frac {2}{3}}+|y|^{\frac {2}{3}}=a^{\frac {2}{3}}}
Οι παραμετρικές εξισώσεις είναι
{\displaystyle x=a\cos ^{3}t={a \over 4}(3\cos t+\cos 3t),}
{\displaystyle y=a\sin ^{3}t={a \over 4}(3\sin t-\sin 3t).}
Η πολική εξίσωση είναι[5]
{\displaystyle r={\frac {a}{(\cos ^{2/3}\theta +\sin ^{2/3}\theta )^{3/2}}}.}
Με απλές αλγεβρικές πράξεις μπορούμε να δούμε ότι η εξίσωσή της μπορεί να γραφεί ως:
{\displaystyle (x^{2}+y^{2}-a^{2})^{3}+27a^{2}x^{2}y^{2}=0.\,}
το οποίο σημείναι ότι η αστροειδής είναι μια πραγματική αλγεβρική καμπύλη του βαθμού έξι.
Μετρικές ιδιότητες
Περιοχή που περικλείεται[6]
\( } {\displaystyle {\frac {3}{8}}\pi a^{2}}
Μήκος της καμπύλης
{\displaystyle 6a}
Παραπομπές
Yates
J. J. v. Littrow (1838). «§99. Die Astrois». Kurze Anleitung zur gesammten Mathematik. Wien. σελ. 299.
Loria, Gino (1902). Spezielle algebraische und transscendente ebene kurven. Theorie und Geschichte. Leipzig. σελ. 224.
Yates, for section
Mathworld
Yates, for section
Εξωτερικοί σύνδεσμοι
"Astroid" στο MacTutor History of Mathematics archive
"Astroid" Η Εγκυκλοπαίδεια των Aξιόλογων Μαθηματικών Μορφών
Άρθρο για 2dcurves.com
Visual Dictionary Of spacial plane curves, Xah Λι
Μπάρες της Αστροειδούς από Sándor Καμπάι, παρουσίαση με Wolfram Mathematica.
Η αστροειδής καμπύλη, MathStudies Blog.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License