.
Popular Scientific Recreations, Gaston Tissandier

POPULAR
SCIENTIFIC RECREATIONS
IN
NATURAL PHILOSOPHY, ASTRONOMY, GEOLOGY, CHEMISTRY,
ETC., ETC., ETC.
Translated and Enlarged from “Les Récréations Scientifiques”
OF
GASTON TISSANDIER.
(Editor of “La Nature.”)

PROFUSELY ILLUSTRATED.
London:
WARD, LOCK, AND CO., WARWICK HOUSE,
SALISBURY SQUARE, E.C.
NEW YORK: 10, BOND STREET.

PREFACE.

A learned mathematician of the seventeenth century, Ozanam by name, a member of the Academy of Sciences and author of several distinguished works, did not think it derogatory to his dignity to write, under the title of “Mathematical and Physical Recreations,” a book designed for the amusement of youth, in which science lends itself to every pastime, even jugglery and tricks of legerdemain.
“Jeux d’esprit” says Ozanam, “are for all seasons and all ages; they instruct the young, they amuse the old, they are welcomed by the rich, and are not above the reach of the poor.”
The object of the book now presented to the reader is also to instruct while it amuses, but we have not thought proper to make use, as Ozanam did, of any physical feats, so called amusing. Such do not constitute experiments, and are but ingenious deceptions, intended to disguise the true mode of operation, and we have not desired to make use of or popularise such methods. We wish, on the contrary, that every game we describe, every pastime or amusement of which we give the exposition, should be rigorously based on the scientific method, and looked upon as a genuine exercise in physics, chemistry, mechanics, or natural science. It does not appear to us desirable to teach deception, even in play.
Science in the open air, in the fields, in the sunshine, is our first study; we point out how, in the country, it is possible, pleasantly and unceasingly, to occupy one’s leisure in observing nature, in capturing insects or aquatic animals, or in noting atmospheric phenomena.
We next teach a complete course of physics without any apparatus, and point out the methods for studying the different phenomena[Pg v] of heat, light, optics, and electricity, by means of a simple water-bottle, tumbler, stick of sealing-wax, and other ordinary objects, such as everyone has at hand. A series of chemical experiments, performed by means of some phials and inexpensive appliances, completes that part of the book relating to the physical sciences.
Another kind of recreation, both intelligent and useful, consists in collecting the ingenious inventions which are constantly being supplied to our requirements by the applied sciences, and learning how to use them. We have collected a number of mechanical inventions and appliances, with which most ingenious and skilful people will wish to supply themselves, from Edison’s electric pen, or the chromograph, which will produce a large number of copies of a letter, drawing, etc., to the more complicated, but not less valuable contrivances, for making science useful in the house.
Having described some scientific toys for the young, we have endeavoured to point out those interesting to persons of riper years, and have grouped together curious systems of locomotion, and ingenious mechanical appliances, such as small steam-boats, ice-boats, swimming apparatus, etc., under proper heads.
In addition to the foregoing subjects, we have included some of the experimental details of Chemical Science, with illustrations. We have added a chapter upon Aërial Navigation and Ballooning, with anecdotes of some of our celebrated aëronauts. We have also enlarged upon Light, Sound, Heat, Physical Geography, Mineralogy, Geology, Electrical Appliances, the Electric Light, and most of the latest adaptations of electricity.
It will be seen, therefore, that the present work is not only intended for the young; everyone, it is hoped, will find in it something interesting and also profitable, which, if not desired for self-instruction, may at any rate be turned to account as a means of teaching others that science, which is universal, can, when rightly apprehended, preside even over our pleasures and amusements.
The Editor.


CONTENTS.
| CHAPTER I.—INTRODUCTORY. | |
| PAGE | |
| Science and Recreation—The Book of Nature—The Senses—Natural History—Natural Philosophy—Matter—Objects—Properties of Matter | 1 |
| CHAPTER II.—OPEN-AIR SCIENCE. | |
| Science in the Open Air—Aphides—Evaporation by Leaves—An Aquarium—The Cataleptic Fowl—Needle Points and Thorns—Microscopic Aquarium—Cape Grisnez—Crystals—Ice on the Gas Lamps | 6 |
| CHAPTER III.—PHYSICS. | |
| Physics—The Meaning of Physics—Forces of Nature—Gravity—Cohesion—Chemical Attraction—Centre of Gravity—Experiments—Automaton Tumblers | 22 |
| CHAPTER IV.—PHYSICS (Continued). | |
| Some Properties of Solid Bodies—Inertia—Motion—Friction—The Pendulum—Equilibrium | 35 |
| CHAPTER V.—GASES. | |
| Gases and Liquids—Pressure of the Air—Experiments | 44 |
| CHAPTER VI.—WATER. | |
| About Water—Hydrostatics and Hydraulics—Law of Archimedes—The Bramah Press—The Syphon | 59 |
| CHAPTER VII.—HEAT. | |
| Heat—What it is—Theory of Heat—The Thermometer—Expansion by Heat—Ebullition and Distillation | 72 |
| CHAPTER VIII.—HEAT (Continued). | |
| Specific Heat—Fusion—Latent Heat—Conduction and Convection of Heat—Calorescence | 88 |
| CHAPTER IX.—LIGHT. | |
| Light and its Sources—What is Light?—Velocity of Light—Reflection and Refraction—Relative Value of Lights | 93 |
| CHAPTER X.—LIGHT (Continued). | |
| Vision and Optical Illusions—The Eye Described—Accommodation of the Eye—Chromatic Aberration—Spinning Tops | 102 |
| CHAPTER XI.—OPTICS. | |
| Optical Illusions—Zollner’s Designs—The Thaumatrope—Phenokistoscope—The Zootrope—The Praxinoscope—The Dazzling Top | 116 |
| CHAPTER XII.—OPTICS (Continued). | |
| Optical Illusions Continued—Experiments—The Talking Head—Ghost Illusions | 129[Pg vii] |
| CHAPTER XIII.—OPTICS (Continued). | |
| Vision—The Eye—The Stereoscope—Spectrum Analysis—The Spectroscope—The Telescope and Microscope—Photography—Dissolving Views—Luminous Paint | 140 |
| CHAPTER XIV.—SPECTRAL ILLUSIONS. | |
| A Spectre Visible—Curious Illusions—Ghosts | 161 |
| CHAPTER XV.—ACOUSTICS. | |
| The Ear and Hearing—Physiology of Hearing and Sound—Sound as Compared with Light—What is Sound?—Velocity of Sound—Conductibility—The Harmonograph | 166 |
| CHAPTER XVI.—ACOUSTICS (Continued). | |
| The Topophone—The Megaphone—The Autophone—The Audiphone—The Telephone—The Phonograph—The Microphone | 180 |
| CHAPTER XVII.—ACOUSTICS (Continued). | |
| The Tuning-Fork—The Syren—Sound Figures—Singing Flames | 193 |
| CHAPTER XVIII.—ELECTRICITY. | |
| Derivation of Electricity—Sealing Wax Experiment—The Electrophorus—Leyden Jar—Positive and Negative—The Electroscope—Electric Machines | 197 |
| CHAPTER XIX. | |
| Velocity of Electricity—Experiments—The Electric Egg—Force of the Electric Spark | 212 |
| CHAPTER XX.—GALVANISM. | |
| Galvani’s Discovery—The Frogs Electrified—Experiments—Volta’s Pile—The Test—Its Usefulness—Faraday’s “Researches.” | 217 |
| CHAPTER XXI.—MAGNETISM. | |
| The Loadstone—Magnetic Curves—The Magnetic Needle—The Mariner’s Compass—Magneto-Electricity | 254 |
| CHAPTER XXII.—APPLIED ELECTRICITY. | |
| Sundry Electrical Appliances—Mr. Edison’s Inventions—The Electric Light—The Gyroscope—A New Electrophorus—Electric Toys | 262 |
| CHAPTER XXIII.—AERONAUTICS. | |
| Pressure of Air in Bodies—Early Attempts to fly in the Air—Discovery of Hydrogen—The Montgolfier Balloons—First Experiments in Paris—Noted Ascents | 293 |
| CHAPTER XXIV.—CHEMISTRY. | |
| What Chemistry is—The Elements—Metallic and Non-Metallic—Atomic Weight—Acids—Alkalis—Bases—Salts—Chemical Combination and Study | 307 |
| CHAPTER XXV.—CHEMISTRY (Continued). | |
| Chemistry without a Laboratory | 313 |
| CHAPTER XXVI.—CHEMISTRY (Continued). | |
| Chemistry and Alchemy—Chemical Combinations—The Atmospheric Air | 336 |
| CHAPTER XXVII.—THE ELEMENTS. | |
| Non-Metallic Elements | 348 |
| CHAPTER XXVIII.—NON-METALLIC ELEMENTS (Continued). | |
| Chlorine—Bromine—Iodine—Fluorine—Carbon—Sulphur—Phosphorus—Silicon—Boron—Tellurium—Arsenic | 366 |
| CHAPTER XXIX.—THE METALS. | |
| What Metals are—Characteristics and General Properties of Metals—Classification—Specific [Pg viii]Gravity—Descriptions | 386 |
| CHAPTER XXX.—ORGANIC CHEMISTRY. | |
| Radicals—Acids—Bases—Neutrals | 410 |
| CHAPTER XXXI.—MINERALOGY AND CRYSTALLOGRAPHY. | |
| The Minerals—Characteristics—Crystals and their Forms—Descriptions of Minerals | 424 |
| CHAPTER XXXII.—NEW LOCOMOTIVE APPLIANCES. | |
| The Kite—The Aerophane—Ice Yachts—Sailing Trucks—Water Velocipedes | 448 |
| CHAPTER XXXIII.—ASTRONOMY. | |
| Introductory—History of Astronomy—Nomenclature | 466 |
| CHAPTER XXXIV.—ANGLES AND MEASUREMENT OF ANGLES. | |
| The Quadrant—Transit Instrument—Clocks—Stellar Time—Solar Time—“Mean Time” | 474 |
| CHAPTER XXXV.—THE SOLAR SYSTEM. | |
| Gravitation—The Planets—Size and Measurement of the Planets—Satellites—Falling Stars—Comets—Aerolites | 486 |
| CHAPTER XXXVI.—THE SUN. | |
| Motion of the Sun—The Seasons—Character of the Sun—Sun-Spots—Zodiacal Light | 496 |
| CHAPTER XXXVII.—THE EARTH. | |
| Form of the Earth—Motion of the Globe—Rate and Manner of Progression—Latitude and Longitude—The Seasons | 504 |
| CHAPTER XXXVIII.—THE MOON. | |
| What is it Like?—Moon Superstitions—Description of the Moon—Phases—Tides—Eclipses | 510 |
| CHAPTER XXXIX.—THE STARS. | |
| The Planets and Asteroids | 521 |
| CHAPTER XL.—THE FIXED STARS. | |
| Fixed-Stars—Magnitude of the Stars—Constellations—Descriptions of the Zodiacal Constellations—Northern and Southern Star Groups—Distance of Stars | 535 |
| CHAPTER XLI.—THE STARS (Continued). | |
| Double and Multiple Stars—Coloured and Variable Stars—Clusters, Groups, and Nebulæ—The Galaxy, or Milky Way—How to Find out the Principal Stars | 546 |
| CHAPTER XLII.—NEW ASTRONOMICAL APPLIANCES. | |
| A Celestial Indicator—Astronomical or Cosmographical Clock—A Simple Globe—A Solar Chronometer | 557 |
| CHAPTER XLIII.—PHYSICAL GEOGRAPHY AND GEOLOGY. | |
| Geography and Geology—The Earth’s Crust—Origin of the Earth—Denudation and Excavation by Water—Rocks, Gravel, and Sand—Classes of Rocks | 564 |
| CHAPTER XLIV.—GEOLOGY. | |
| Crust of the Earth—Geological Systems—Eozoic, Primary, Secondary, Tertiary, Pre-Historic Formations | 573 |
| CHAPTER XLV.—GEOLOGY (Continued). | |
| The Mesozoic System—The Triassic, Oolitic, and Cretaceous Formations—The Eocene, Miocene, and Pliocene—The Glacial Period—Pre-Historic Man | 584 |
| CHAPTER XLVI.—PHYSICAL GEOGRAPHY. | |
| Igneous Rocks—Land and Water—Springs, Wells, and Geysers—Snow and Ice—Their Effects | 601[Pg ix] |
| CHAPTER XLVII.—THE SEA AND THE SKY. | |
| The Sea—Salt Water—Waves and their Effects—Under Water—The Floor of the Ocean | 610 |
| CHAPTER XLVIII.—PHYSICAL GEOGRAPHY. METEOROLOGY. | |
| The Atmosphere—Winds and Air Currents—Wind Pressure—Storms—Rain-clouds—Water-Spouts—Atmospherical Phenomena | 628 |
| CHAPTER XLIX.—PHYSICAL GEOGRAPHY. METEOROLOGY (Continued). | |
| Atmospheric Phenomena—Thunder and Lightning—Aurora Borealis—The Rainbow—Mock-Suns and Mock-Moons—Halos—Fata Morgana—Reflection and Refraction—Mirage—Spectre of the Brocken | 642 |
| CHAPTER L.—PHYSICAL GEOGRAPHY. CLIMATOLOGY. | |
| Weather; Climate, and Temperature—Isothermal Lines—Isobars, Weather Forecasts, and Signs of the Sky | 651 |
| CHAPTER LI.—BIOLOGY. PART I.: BOTANY. | |
| Plants and Animals—Structure of Plants—Flowering Plants—The Stem—The Leaves—Forms of Leaves | 658 |
| CHAPTER LII.—FLOWERING PLANTS. | |
| Organs of Increase and Reproduction—The Flower—The Calyx—The Corolla—The Stamen—The Pistil | 675 |
| CHAPTER LIII.—FLOWERING PLANTS (Continued). | |
| The Floral Axis—Inflorescence—Fruit—Seed—Nutrition of Plants—Absorbtion of Constituents | 679 |
| CHAPTER LIV.—ZOOLOGY. | |
| Classification of Animals—Vertebrates and Invertebrates—Protozoa—Hydrozoa—Actinozoa | 700 |
| CHAPTER LV.—ECHINODERMATA—ANNULOSA—ENTOZOA—INSECTA. | |
| Sea-Urchins—Star-Fishes—Feathery Stars—Sea-Cucumbers—Worms—Leeches—Rotifers—Tape Worms—Insects | 712 |
| CHAPTER LVI.—THE ANALYSIS OF CHANCE AND MATHEMATICAL GAMES. | |
| Magic Squares—The Sixteen Puzzle—Solitaire—Equivalents | 726 |
| CHAPTER LVII.—GAMES (Continued). | |
| The Magic Top—The Gyroscope and Scientific Games | 740 |
| CHAPTER LVIII.—SCIENCE AT HOME. | |
| Scientific Objects for the Household | 747 |
| CHAPTER LIX.—DOMESTIC SCIENCE. | |
| Science and Domestic Economy | 757 |
| CHAPTER LX.—CURIOUS INVENTIONS. | |
| Some Curious Modes of Transit | 770 |

SCIENTIFIC RECREATIONS.
CHAPTER I.—INTRODUCTORY.
SCIENCE AND RECREATION—THE BOOK OF NATURE—THE SENSES—NATURAL HISTORY—NATURAL PHILOSOPHY—MATTER—OBJECTS—PROPERTIES OF MATTER.

It may at the first glance appear paradoxical to combine Science and Recreation, but we hope to show that true scientific recreation is anything but the dry bones of learning. To those who study science with us, we will point out first how easy and pleasant it is to watch the sky and the plants and Nature generally in the open air. Then we will carry our readers along with us, and by means of illustrations and diagrams instruct them pleasantly in the reasons for things. “How?” and “Why?” will be questions fully answered. Not only will the usual scientific courses be touched upon, but we will show how Science is applied to Domestic Economy. We will have Chemistry put before us without needing a laboratory, and we will experiment in Physics without elaborate apparatus. We will have, in short, a complete Encyclopædia of Science free from dryness and technicalities—an amusing volume suited to old and young who wish to find out what is going on around them in their daily life in earth and sea and sky.
Bernard Palissy used to say that he wished “no other book than the earth and the sky,” and that “it was given to all to read this wonderful book.”
It is indeed by the study of the material world that discoveries are accomplished. Let an attentive observer watch a ray of light passing from the air into water, and he will see it deviate from the straight line by refraction; let him seek the origin of a sound, and he will discover that it results[Pg 2] from a shock or a vibration. This is physical science in its infancy. It is said that Newton was led to discover the laws of universal gravitation by beholding an apple fall to the ground, and that Montgolfier first dreamt of air-balloons while watching fogs floating in the atmosphere. The idea of the inner chamber of the eye may, in like manner, be developed in the mind of any observer, who, seated beneath the shade of a tree, looks fixedly at the round form of the sun through the openings in the leaves.

Every one, of course, may not possess the ambition to make such[Pg 3] discoveries, but there is no one who cannot compel himself to learn to enjoy the pleasure that can be derived from the observation of Nature.
It must not be imagined that in order to cultivate science it is absolutely necessary to have laboratories and scientific work-rooms. The book of which Palissy spoke is ever present; its pages are always open, wherever we turn our eyes or direct our steps. So we may hope to introduce all our friends to a pleasant and lasting acquaintance with Dame Nature.
“But what is Nature?” We are fond of admiring Nature, and the effects of certain causes in the world, and we want to know why things are so. Very well—so you shall; and as to the question “What is Nature?” we will endeavour to answer you at once.
Nature is the united totality of all that the various Senses can perceive. In fact, all that cannot be made by man is termed “Nature”; i.e., God’s creation.
From the earliest ages man has sought to read the open leaves of the Book of Nature, and even now, with all our attainments, we cannot grasp all, or nearly all. One discovery only leads up to another. Cause and Effect are followed up step by step till we lose ourselves in the search. Every effect must have a cause. One thing depends upon another in the world, and it does not need Divine revelation to tell us that. Nothing happens by “mere chance.” “Chance!” said a Professor to us at the University, “Chance!—Remember, there is no such thing in the world as chance.”
Between our minds or consciousness and Nature are our Senses. We feel, we see, we hear, we taste, we smell,—so it is only through the Senses that we can come to any knowledge of the outer world. These attributes, or Senses, act directly upon a certain “primary faculty” called Consciousness, and thus we are enabled to understand what is going on around us. The more this great existing faculty is educated and trained, the more useful it will become. So if we accustom our minds to observation of Nature, we shall find out certain causes and effects, and discover Objects. Now an Object is a thing perceptible both to feeling and sight, and an Object occupies space. Therefore there are objects Artificial as well as Natural. The former are created by man from one or more Natural products. Natural Objects are those such as trees, rocks, plants, and animals. We may also class the heavenly bodies, etc., as Objects, though we cannot touch them, but we can feel their effects, and see them. The Phenomena of Nature include those results which are perceptible by only one sense, as thunder; light and sound may also be classed as Phenomena.
Take a familiar instance. A stone is a Natural Object. We take it up, open our fingers, and it falls. The motion of that object is a Phenomenon. We know it falls because we see it fall, and it possesses what we term weight; but we cannot tell why it possesses weight.
[Professor Huxley says: “Stones do not fall to the ground in consequence of a law of nature,” for a law is not a cause. “A law of nature[Pg 4] merely tells us what we may expect natural objects will do under certain circumstances.”]
A cause of a Phenomenon being independent of human will is called a Force, and the stone falls by the force of Gravitation, or that natural law which compels every material object to approach every other material object.
A single Force may produce a great number of Phenomena.
Nature being revealed to us by Objects, and by means of Phenomena, we have got already two Branches of Science extending from such Roots; viz., Natural History, the Science of Objects; and Natural Philosophy, the Science of Phenomena.
Both of these Branches have been subdivided thus:
| ⌈Zoology, referring to Animals | Biology. | |
| Natural History | ⎢Botany, referring to Plants | |
| ⎢Mineralogy | referring to Minerals, etc. | |
| ⌊Geology | ||
| ⌈Physics. Phenomena without essential change of the Objects. | ||
| Natural Philosophy | ⎢Chemistry. Phenomena with change of the Objects. | |
| ⌊Physiology. Phenomena of animated Objects. | ||
These two great divisions comprehend, in their extended senses, all that is known respecting the material world.
We have spoken of Objects. Objects occupy Space. What is Space? Space is magnitude which can be conceived as extending in three directions—Length, Breadth, and Depth. Matter occupies portions of Space, which is infinite. Matter, when finite, is termed a body or object. The general properties of Matter are Magnitude, Form, Impenetrability, Inertia, Divisibility, Porosity, Elasticity, Compressibility, Expansibility.
Matter is present in Nature in three conditions. We find it as a Solid, a Liquid, and a Gas. We shall explain the various properties of Solids, Liquids, and Gases in their proper places (in Physics). To test the actual existence of Matter in one or other of these forms our Senses help us. We can touch a Solid, or taste it and see it. But touch is the test. We have said that Matter possesses certain properties. We will examine these briefly. The two which belong to all material bodies are Impenetrability and Magnitude. You cannot, strictly speaking, penetrate Matter. You can find the form of an object by touch or sight, but you cannot penetrate it. You will think you can drive a nail or a screw into a board, but you cannot; you only displace the fibres of the wood by the screw. Take water as a very common instance. Water is Matter, for it occupies a certain space. Water is impenetrable, for if you put your hand or foot into a basin full of it, it will overflow, thus proving that you displace, and do not penetrate it. It is almost impossible to compress water.
Divisibility is another quality of Matter; and when we attempt to show how far Matter can be divided, the brain refuses to grasp the infinity. A pin’s head is a small object, but it is gigantic compared to some[Pg 5] animals, of which millions would occupy a space no larger than the head of a pin. These tiny animals must contain organs and veins, etc., and those veins are full of blood globules. Professor Tyndall informs us that a drop of blood contains three millions of red globules. So these infinitesimally small animals must have millions of globules in their blood also. Thus we see to what an extent, far beyond our Senses’ power to grasp, Matter can be divided.
But there is something even more astonishing than this. It is stated that there are more animals in the milt of a single codfish than there are men in the world; and that one grain of sand is larger than four millions of these animals! each of which must be possessed of life germs of an equal amount, which would grow up as it grew to maturity. This carries us back again, and
Or take other interesting facts. One hundred threads of the silkworm must be placed side by side to make up the thickness of a line (—) about 1/25th of an inch; and metals can be drawn out to such exceeding fineness that twelve hundred of the fine wires will occupy only the space of one hundred silkworms’ threads, or one millimetre.
Porosity is another attribute of Matter, for in all Matter there are pores, or spaces, between the particles. Sometimes such openings are plainly visible; in very “solid” bodies they are, to a great extent, indistinguishable. But we know that the spaces exist, because we can compress the particles together.
Inertia is also a general property of Matter, and the meaning of the term is “inactivity,” or passiveness—a want of power in an object to move, or when moving, to stop of itself. It will come to rest apparently by itself, but the resistance of the air and the friction of the ground, or the attraction of the earth, will really occasion the stoppage of the object. We will speak more fully of Inertia presently. Elasticity and Expansibility are evident in fluids and gases.
We have thus introduced our readers to some of the most evident facts connected with Matter. The various Forces and Phenomena of attraction will be fully considered farther on; at present we are about to show our readers how they may first profitably study Science in the open air for themselves, and we will give them our experience of the Book of Nature.

CHAPTER II.
SCIENCE IN THE OPEN AIR—APHIDES—EVAPORATION BY LEAVES—AN AQUARIUM—THE CATALEPTIC FOWL—NEEDLE POINTS AND THORNS—MICROSCOPIC AQUARIUM—CAPE GRISNEZ—CRYSTALS—ICE ON THE GAS LAMPS.

Some years ago we were staying in Normandy, not far from the town of C——, enjoying, in the midst of most cordial hospitality, the peacefulness of country life; and my kind hosts, with me, took great pleasure in having what we called “a course of science in the open air.” The recollections of that time are some of the pleasantest in the whole course of my life, because all our leisure was intelligently occupied. Each of us set himself to provide the subject of some curious observation or instructive experiment; one made[Pg 7] a collection of insects, another studied botany. In the daytime we might have been seen examining, under a magnifying glass, the branch of a rose-tree, from which the ants were endeavouring to extract the aphides1 (fig. 1). At night we admired through the telescope the stars and planets that were visible; or if the sky was not clear, we examined under a strong magnifier grains of pollen from flowers, or the infusoria in a drop of stagnant water. Frequently some very insignificant object became the occasion for some scientific discussion, which terminated with an experimental verification.

of water by leaves.
I recollect that one day one of us remarked that after a week of dry weather a stream of water had nearly dried up, although sheltered by thick trees, which necessarily impeded the calorific action of the sun; and he expressed surprise at the rapid evaporation. An agriculturist among the company, however, drew his attention to the fact that the roots of the trees were buried in the course of the stream, and that, far from preventing the evaporation of the water, the leaves had contributed to accelerate it. As the first speaker was not convinced, the agriculturist, on our return to the house, prepared an experiment represented in fig. 2. He placed the branch of a tree covered with foliage in a U-shaped tube, the two branches of unequal diameter, and filled with water. He placed the vegetable stem in the water, and secured it to the tube by means of a cork covered with a piece of india-rubber, and tied tightly to make it hermetically closed.
At the commencement of the experiment the water was level with A in the larger branch of the tube, and level with B in the smaller, rising by capillarity to a higher point in the more slender of the two. The evaporation of the water caused by the leaves was so active that in a very short time we beheld the water sink to the points C and C′.

Thus did the excellent method of seeking the cause of phenomena by experiments often lead us to interesting results. We had among us many children and young people who had reached the age of ardent curiosity. We took pleasure in pointing out to them the means of studying natural science; and we were not long before feeling convinced that our lessons out in the fields had much greater success than those given between the four walls of a class-room. Insects were collected, and preserved by being carefully placed in a small bottle, into which was let fall a drop of sulphuret of carbon;2 the insect was immediately asphyxiated, and we[Pg 9] thus avoided the cruelty of passing a pin through a living body. Having chased butterflies and insects, we next desired to study the aquatic creatures which swarmed in the pools of the neighbourhood. For this purpose I constructed a fishing-net fitted to an iron ring, and firmly secured to a wooden handle. When this was plunged under the water and drawn quickly out again, it came back full of slime. In the midst of this muddy substance one generally succeeded in finding the hydrophilus, tadpoles, coleoptera, many curious kinds of caddis-worms, tritons, and sometimes frogs, completely astounded by the rapidity of their capture. All these creatures were transported in a bottle to the house, and I then constructed, at small expense, a glass aquarium, by means of the bell of a melon-glass turned upside down, thus forming a transparent receptacle of considerable size. Four wooden stakes were then fixed in the ground, and a plank with a circular hole nailed on the top, in which the glass bell was placed. I next scattered some large pebbles and shells at the bottom of the vase to form a stony bed, poured in some water, placed a few reeds and water plants among the pebbles, and then[Pg 10] threw a handful of water lentils on the surface; thus a comfortable home was contrived for all the captured animals.3 The aquarium, when placed under the shade of a fine tree in a rustic spot abounding with field flowers, became a favourite rendezvous, and we often took pleasure in watching the antics of the little inmates (fig. 3). Sometimes we beheld very sanguinary scenes; the voracious hydrophilus would seize a poor defenceless tadpole, and rend him in pieces for a meal without any compunction. The more robust tritons defended themselves better, but sometimes they also succumbed in the struggle.


The success of the aquarium was so complete that one of us resolved to continue this museum in miniature, and one day provided himself with an insects palace, which nearly made us forget the tadpoles and tritons. It was a charming little cage, having the form of a house, covered with a roof;[Pg 11] wires placed at equal distances forming the sides. In it was a large cricket beside a leaf of lettuce, which served as his food (fig. 4). The little creature moved up and down his prison, which was suspended from the branch of a tree, and when one approached him very closely gave vent to his lively chirps.

The menagerie was soon further augmented by a hitherto unthought-of object; namely, a frogs’ ladder. It was made with much skill. A large bottle served for the base of the structure. The ladder which was fixed in it was composed of the twigs of very small branches, recently cut from a tree, and undivested of their bark, which gave to the little edifice a more picturesque and rustic appearance. The pieces of wood, cleverly fixed into two posts, conducted the green frogs (tree-frogs) on to a platform, whence they ascended the steps of a genuine ladder. There they could disport themselves at pleasure, or climb up further to a branch of birch-tree placed upright in the centre of the bottle (fig. 5). A net with fine meshes prevented the little animals from escaping. We gave the tree-frogs flies for their food, and sometimes they caught them with remarkable dexterity. I have often seen a frog when at liberty watching a fly, on which it pounces as a cat does on a bird (fig. 6). The observations that we made on the[Pg 12] animals of our menagerie led us to undertake others of a very different nature; I recollect particularly a case of catalepsy produced in a cock. I will describe this remarkable experiment, certainly one of the most curious we ever performed.

We place a cock on a table of dark colour, rest its beak on the surface, where it is firmly held, and with a piece of chalk slowly draw a white line in continuation from the beak, as shown in our engraving. If the crest is thick, it is necessary to draw it back, so that the animal may follow with his eyes the tracing of the line. When the line has reached a length of about two feet the cock has become cataleptic. He is absolutely motionless,[Pg 13] his eyes are fixed, and he will remain from thirty to sixty seconds in the same posture in which he had at first only been held by force. His head remains resting on the table in the position shown in fig. 7. This experiment, which we have successfully performed on different animals, can also be accomplished by drawing a straight line with a piece of chalk on a slate. M. Azam declares that the same result is also produced by drawing a black line on a table of white wood. According to M. Balbiani, German students had formerly a great predilection for this experiment, which they always performed with marked success. Hens do not, when operated on, fall into a cataleptic condition so easily as cocks; but they may often be rendered motionless by holding their heads fixed in the same position for several minutes. The facts we have just cited come properly under the little studied phenomena, designated by M. Braid in 1843 by the title of Hypnotism. MM. Littré and Ch. Robin have given a description of the hypnotic condition in their Dictionnaire de Médecine.


If any shining object, such as a lancet, or a disc of silver-paper gummed to a plate, is placed at about the distance of a foot from the eyes of a person, slightly above the head, and the patient regards this object fixedly, and without interruption for twenty or thirty minutes, he will become gradually motionless, and in a great number of cases will fall into a condition of torpor and genuine sleep. Dr. Braid affirms that under such circumstances he has been able to perform surgical operations, without the patient having any consciousness of pain. Later also, M. Azam has proved the complete insensibility to pricking on the part of individuals whom he has rendered cataleptic by the fixing of a brilliant object. The[Pg 14] experiment of the cataleptic cock was first described under the name of Experimentum Mirabile, by P. Kircher, in his Ars Magna, published at Rome in 1646. It evidently belongs to the class of experiments which were performed at the Salpêtrière asylum at Paris, by M. Charcot, on patients suffering from special disorders. It must now be evident to our readers that our scientific occupations were sufficiently varied, and that we easily found around us many objects of study. When the weather was wet and cloudy we remained indoors, and devoted ourselves to microscopical examinations. Everything that came under our hands, insects, vegetables, etc., were worthy of observation. One day, while engaged over a microscopical preparation, I was making use of one of those steel points generally employed in such purposes, when happening to pass it accidentally beneath the microscope, I was astonished to see how rough and uneven it appeared when highly magnified. The idea then occurred to me to have recourse to something still more pointed, and I was thus led to make comparisons between the different objects represented in figs. 8 and 9. It will here be seen how very coarse is the product of our industry when compared with the product of Nature. No. 1 of fig. 8 represents the point of a pin that has already been used, magnified 500 diameters. The point is evidently slightly blunted and flattened. The malleable metal has yielded a little under the pressure necessary to make it pass through a material. No. 2 is a little more pointed; it is a needle. This, too, will be seen to be defective when regarded by the aid of the microscope. On the other hand, what fineness and delicacy do the rose thorn and wasp’s sting[Pg 15] present when examined under the same magnifier! (See the two points in fig. 9.)
An examination of this exact drawing has led me to make a calculation which leads to rather curious results: at a half millimetre from the point, the diameters of the four objects represented are in thousandths of a millimetre respectively, 3·4; 2·2; 1·1; 0·38. The corresponding sections in millionths of a square millimetre are: 907·92; 380·13; 95·03; 11·34; or, in round numbers, 908; 380; 95; 11.
If one bears in mind, which is much below the truth, that the pressure exercised on the point must be proportional to the section, and admitting that a pressure of 11 centigrams suffices to thrust in the sting of a wasp half a millimetre, it will require more than 9 grams of pressure to thrust in a needle to the same extent. In fact, this latter figure is much too small, for we have not taken into account the advantage resulting from the elongated shape of the rose thorn, which renders it more favourable for penetration than a needle through a drop of tallow.
It would be easy to extend observations of this kind to a number of other objects, and the remarks I have just made on natural and artificial points will apply incontestably to textures for example. There is no doubt that the thread of a spider’s web would far surpass the thread of the finest lace, and that art will always find itself completely distanced by nature.
We amused ourselves frequently by examining the infusoria which are so easily procured by taking from some stagnant water the mucilage adhering to the vegetation on the banks, or attached to the lower part of water lentils. In this way we easily captured infusoria, which, when placed under a strong magnifier, presented the most remarkable spectacle that one can imagine. They are animalcules, having the form of transparent tulips attached to a long stem. They form bunches which expand and lengthen; then, suddenly, they are seen to contract with such considerable rapidity that the eye can scarcely follow the movement, and all the stems and flower-bells are folded up into the form of a ball. Then, in another moment, the stems lengthen, and the tulip-bells open once more. One can easily encourage the production of infusoria by constructing a small microscopic aquarium, in which one arranges the centre in a manner favourable to the development of the lowest organisms. It suffices to put a few leaves (a piece of parsley answers the purpose perfectly)4 in a small vase containing water (fig. 10), over which a glass cover is placed, and it is then exposed to the rays of the sun. In two or three days’ time, a drop of this water seen under the microscope will exhibit infusoria. After a certain time, too, the different species will begin to show themselves. Microscopical observations can be made on a number of different objects. Expose to the air some flour moistened by water, and before long a mouldiness will form on it; it is the penicillium glaucum, and when examined under a magnifier of 200 to 300 diameters, cells are dis[Pg 16]tinguishable, branching out from an organism remarkable for its simplicity. We often amused ourselves by examining, almost at hazard, everything that came within our reach, and sometimes we were led to make very instructive investigations. When the sky was clear, and the weather favourable to walking, we encouraged our young people to run about in the fields and chase butterflies. The capture of butterflies is accomplished, as every one knows, by means of a gauze net, with which we provided the children, and the operation of chasing afforded them some very salutary exercise. It sometimes happens that butterflies abound in such numbers, that it is comparatively easy to capture them. During the month of June 1879, a large part of Western Europe was thronged with swarms of Vanessa algina butterflies, in such numbers that their appearance was regarded as an important event, and attracted the lively attention of all entomologists (fig. 11). This passage of butterflies provided the occasion for many interesting studies on the part of naturalists.



We cannot point out too strongly to our readers that the essential condi[Pg 17]tion for the student of natural science, is the possession of that sacred fire which imparts the energy and perseverance necessary for acquiring and enlarging collections. It is also necessary that the investigator should furnish himself with certain indispensable tools. For collecting plants, the botanist should be armed with a pickaxe set in a thoroughly strong handle, a trowel, of which there is a variety of shapes, and a knife with a sharp blade. A botanical case must also be included, for carrying the plants. The geologist, or mineralogist, needs no more elaborate instruments; a hammer, a chisel, and a pickaxe with a sharp point for breaking the rocks, and a bag for carrying[Pg 18] the specimens, will complete his outfit. We amused ourselves by having these instruments made by the blacksmith, sometimes even by manufacturing them ourselves; they were simple, but solid, and admirably adapted to the requirements of research. Often we directed our walks to the seashore, where we liked to collect shells on the sandy beach, or fossils among the cliffs and rocks. I recollect, in a walk I had taken some years previously along the foot of the cliffs of Cape Blanc-Nez, near Calais, having found an impression of an ammonite of remarkable size, which has often excited the admiration of amateurs; this ammonite measured no less than twelve inches in diameter. The rocks of Cape Grisnez, not far from Boulogne, also afford the geologian the opportunity of a number of curious investigations. In the Ardennes and the Alps I have frequently procured some fine mineral specimens; in the first locality crystallized pyrites, in the second, fine fragments of rock crystal (fig. 12). I did not fail to recount these successful expeditions to the young people who accompanied me, and their ardour was thereby inflamed by the hope that they also should find something valuable. It often happened when the sun was powerful, and the air extremely calm, that my young companions and I remarked some very beautiful effects of mirage on the beach, due to the heating of the lower strata of the atmosphere. The trees and houses appeared to be raised above a sheet of silver, in which their reflections were visible as in a sheet of tranquil water. It can hardly be believed how frequently the atmosphere affords interesting spectacles[Pg 19] which pass unperceived before the eyes of those who know not how to observe. I recollect having once beheld at Jersey a magnificent phenomenon of this nature, on the 24th June, 1877, at eight o’clock in the evening: it was a column of light which rose above the sinking sun like a sheaf of fire. I was walking on the St. Helier pier, where there were also many promenaders, but there were not more than two or three who regarded with me this mighty spectacle. Columns and crosses of light are much more frequent than is commonly supposed, but they often pass unperceived before indifferent spectators. We will describe an example of this phenomenon observed at Havre on the 7th May, 1877. The sun formed the centre of the cross, which was of a yellow, golden colour. This cross had four branches. The upper branch was much more brilliant than the others; its height was about 15°. The lower branch was smaller, as seen in the sketch on page 2, taken from nature by Monsieur Albert Tissandier. The two horizontal branches were at times scarcely visible, and merged in a streak of reddish-yellow colour, which covered a large part of the horizon. A mass of cloud, which the setting sun tinged with a deep violet colour, formed the foreground of the picture. The atmosphere over the sea was very foggy. The phenomenon did not last more than a quarter of an hour, but the conclusion of the spectacle was signalized by an interesting circumstance. The two horizontal branches, and the lower branch of the luminous cross, completely disappeared, whilst the upper branch remained alone for some minutes longer. It had now the appearance of a vertical column rising from the sun, like that which Cassini studied on the 21st May, 1672, and that which M. Renon5 and M. A. Guillemin observed on the 12th July, 1876.6 Vertical columns, which, it is well known, are extremely rare phenomena, may therefore indicate the existence of a luminous cross, which certain atmospheric conditions have rendered but partially visible.
How often one sees along the roads little whirlwinds of dust raised by the wind accomplishing a rotatory movement, thus producing the imitation of a waterspout! How often halos encompass with a circle of fire the sun or the stars! How often we see the rainbow develop its iridescent beauties in the midst of a body of air traversed by bright raindrops! And there is not one of these great natural manifestations which may not give rise to instructive observations, and become the object of study and research. Thus, in walks and travels alike, the study of Science may always be exercised; and this method of study and instruction in the open air contributes both to health of body and of mind. As we consider the spectacles which Nature spreads before us,—from the insect crawling on the blade of grass, to the celestial bodies moving in the dome of the heavens,—we feel a vivifying and salutary influence awaken in the mind. The habit[Pg 20] of observation, too, may be everywhere exercised—even in towns, where Nature still asserts herself; as, for example, in displays of meteorological phenomena. We will give an example of such.

The extraordinary abundance of snow which fell in Paris for more than ten consecutive hours, commencing on the afternoon of Wednesday, January 22nd, 1880, will always be looked upon as memorable among the meteorological events of the city of Paris. It was stated that in the centre of Paris, the thickness of the snow that had fallen at different times exceeded fourteen inches. The snow had been preceded by a fall of small transparent
icicles, of rather more than a millimetre in diameter, some having crystalline facets. They formed on the surface of the ground a very slippery glazed frost. On the evening of the 22nd January, flakes of snow began to hover in the atmosphere like voluminous masses of wool. The greater part of the gas-lamps were ornamented by frozen stalactites, which continually attracted the attention of passers-by. The formation of these stalactites, of which we give a specimen (fig. 13), is easy of explanation. The snow falling on the glass of the lamp became heated by the flame of gas, melted, and trickled down, freezing anew into the shape of a stalactite below the lamp, at a temperature of 0° centigrade. Not only can meteorology be studied in towns, but certain other branches of natural science—entomology, for[Pg 21] example. We will quote what a young student in science, M. A. Dubois, says on this very subject: “Coleoptera,” he declares, “are to be met with everywhere, and I think it may be useful to notice this fact, supporting it by examples. I desire to prove that there are in the midst of our large towns spots that remain unexplored, where some fine captures are to be made. Let us visit, at certain times, the approaches to the quays, even at low tide, and we shall be surprised to find there species which we have searched for far and near.” This opinion is confirmed by the enumeration of several interesting captures.
Was not the great Bacon right when he said, “For the keen observer, nothing in Nature is mute”?

CHAPTER III.
PHYSICS—THE MEANING OF PHYSICS—FORCES OF NATURE—GRAVITY—COHESION—CHEMICAL ATTRACTION—CENTRE OF GRAVITY—EXPERIMENTS—AUTOMATON TUMBLERS.
Having now introduced our readers to Science which they can find for themselves in the open air, and the pursuit of which will both instruct and amuse, we will proceed to investigate the Branch of Science called Physics.
Physics may be briefly described as the Branch of Natural Science which treats of such phenomena as are unaccompanied by any important changes in the objects wherein such phenomena are observed.
For instance, the sounding of a bell or the falling of a stone are physical phenomena, for the objects which cause the sound, or the fall, undergo no change. Heat is set free when coal burns. This disengagement of heat is a physical phenomenon; but the change during combustion which coal undergoes is a chemical phenomenon. So the objects may be the same, but the circumstances in which they are placed, and the forces which act upon them, may change their appearance or position.
This brings us at once to the Forces of Nature, which are three in number; viz., Gravity, Cohesion, and Affinity, or Chemical Attraction. The phenomena connected with the last-named forms the Science of Chemistry. We give these three Forces these names. But first we must see what is Force, for this is very important. Force is a CAUSE—the cause of Motion or of Rest. This may appear paradoxical, but a little reflection will prove it. It requires force to set any object in motion, and this body would never stop unless some other force or forces prevented its movement beyond a certain point. Force is therefore the cause of a change of “state” in matter.
We have said there are three forces in nature. The first is Gravity, or the attraction of particles at a distance from each other. We may say that Gravity, or Gravitation, is the mutual attraction between different portions of matter acting at all distances,—the force of attraction being, of course, in proportion to the mass of the bodies respectively. The greatest body is the Earth, so far as our purposes are concerned. So the attraction of the Earth is Gravity, or what we call Weight.
We can easily prove this. We know if we jump from a chair we shall come to the floor; and if there were nothing between us and the actual ground sufficient to sustain the force of the attracting power of the earth, we should[Pg 23] fall to the earth’s surface. In a teacup the spoon will attract air bubbles, and large air bubbles will attract small ones, till we find a small mass of bubbles formed in the centre of the cup of tea. Divide this bubble, and the component parts will rush to the sides of the cup. This form of attraction is illustrated by the accompanying diagrams.

Suppose two balls of equal magnitude, A and B (fig. 14). These being of equal magnitude, attract each other with equal force, and will meet, if not opposed, at a point (M) half-way between the two. But they do not meet, because the attraction of the earth is greater than the attraction they relatively and collectively exercise towards each other. But if the size of the balls be different, the attraction of the greater will be more evident, as shown below, where the points of meeting are indicated respectively (figs. 15 and 16). These experiments will illustrate the phenomena of falling bodies. Gravity is the cause of this, because every object on the surface of the earth is very much smaller than the earth itself, and therefore all bodies fall towards the centre of the earth. A certain time is thus occupied, and we can find the velocity or rapidity of a falling body very easily. On the earth a body, if let fall, will pass through a space sixteen feet in the first second; and as the attraction of the earth still continues and is exercised upon a body already in rapid motion, this rate of progress must be proportionately increased. Just as when steam is kept up in an engine running down hill, the velocity of the train will rapidly increase as it descends the gradient.

A body falling, then, descends sixteen feet in the first second, and for every succeeding second it assumes a greater velocity. The distance the body travels has been calculated, and the space it passes through has been found to increase in proportion to the square of the time it takes to fall. For instance, suppose you drop a stone from the top of a cliff to the beach, and it occupies two seconds in falling, if you multiply 2 × 2, and the result by sixteen, you will find how high the cliff is: in this (supposed) case it is (omitting decimals) sixty-four feet high. The depth of a well can also be ascertained in the same way, leaving out the effect of air resistance.
But if we go up into the air, the force of gravity will be diminished. The attraction will be less, because we are more distant from the centre of the earth. This decrease is scarcely, if at all, perceptible, even on very high mountains, because their size is not great in comparison with the mass of the earth’s surface. The rule for this is that gravity decreases in proportion to the square of the distance. So that if at a certain distance from the earth’s surface the force of attraction be 1, if the distance be doubled the attraction will be only one quarter as much as before—not one-half.
Gravity has exactly the same influence upon all bodies, and the force of the attraction is in proportion to the mass. All bodies of equal mass will fall in the same time in a given distance. Two coins (or a coin and a feather in vacuo) will fall together. But in the air the feather will remain far behind the coin, because nearly all the atoms of the former are resisted by the air, while in the coin only some particles are exposed to the resistance, the density of the latter preventing the air from reaching more than a few atoms, comparatively speaking. The theory of weight and gravitation, and experiments relating to the falling of bodies, may be easily demonstrated with ordinary objects that we have at hand. I take a halfpenny and a piece of paper, which I cut in the shape of the coin, and holding them side by side, I drop them simultaneously; the halfpenny reaches the ground some time before the paper, a result quite in accordance with the laws of gravitation, as one must bear in mind the presence of air, and the different resistance it offers to two bodies differing in density. I next place the paper disc on the upper surface of the piece of money, and then drop them simultaneously. The two objects now reach the ground at the same time, the paper, in contact with the halfpenny, being preserved from the action of the air. This experiment is so well known that we need not further discuss it; but it must be plainly evident that it is capable of development in experiments on phenomena relating to falling bodies.7 When a body influenced by the action of a force acts, in its turn, upon another, the latter reacts in an opposite manner upon the first, and with the same intensity.
The Attraction of Cohesion is the attraction of particles of bodies to[Pg 25] each other at very small distances apart. Cohesion has received various names in order to express its various degrees. For instance, we say a body is tough or brittle, or soft or hard, according to the degrees of cohesion the particles exercise. We know if we break a glass we destroy the cohesion; the particles cannot be reunited. Most Liquid particles can be united, but not all. Oil will not mix with water.
The force of cohesion depends upon heat. Heat expands everything, and the cohesion diminishes as temperature increases.
There are some objects or substances upon the earth the particles of which adhere much more closely than others, and can only, with very great difficulty, be separated. These are termed Solids. There are other substances whose particles can easily be divided, or their position altered. These are called Fluids. A third class seem to have little or no cohesion at all. These are termed Gases.
Adhesion is also a form of attraction, and is cohesion existing on the surfaces of two bodies. When a fluid adheres to a solid we say the solid is wet. We turn this natural adhesion to our own purposes in many ways,—we whitewash our walls, and paint our houses; we paste our papers together, etc.
On the other hand, many fluids will hot adhere. Oil and water have already been instanced. Mercury will not stick to a glass tube, nor will the oiled glass tube retain any water. We can show the attraction and repulsion in the following manner:—Let one glass tube be dipped into water and another into mercury, you will see that the water will ascend slightly at the side, owing to the attraction of the glass, while the mercury will be higher in the centre, for it possesses no attraction for the glass (fig. 17). If small, or what are termed capillary (or hair) tubes, be used (fig. 18), the water will rise up in the one tube, while in the other the mercury will remain lower than the mercury outside the tube. (See Capillarity.)

Chemical Attraction is the force by which two different bodies unite to form a new and different body from either. This force will be fully considered in Chemistry, in a future part.
It is needless for us to dwell upon the uses of these Forces of Nature. Gravity and Cohesion being left out of our world, we can imagine the result. The earth and sun and planets would wander aimlessly about; we should float away into space, and everything would fall to pieces, while our bodies would dissolve into their component parts.
The Balance and Centre of Gravity.—We have spoken at some length about Gravity, and now we must say something respecting that point called[Pg 26] the Centre of Gravity, and the Balance, and upon the latter we have a few remarks to make first, for a well-adjusted balance is a most useful thing, and we will show you how to make one, and then proceed to our illustrations of the Centre of Gravity, and explain it.

All those who cultivate experimental science are aware that it is useful to unite with theoretical ideas that manual dexterity which is acquired by the student accustoming himself to practical operations. One cannot too strongly urge both chemists and physicists to exercise themselves in the construction of the appliances they require, and also to modify those already existing, which may be adapted to their wants. In a large number of cases it is possible to manufacture, at small expense, delicate instruments, capable of rendering the same service as the most elaborate apparatus. Important scientific labours have often been undertaken by men whose laboratories were most simple, who, by means of skill and perseverance, knew how to do great things with small resources. A delicate balance, for instance, indispensable alike to chemist and physicist, can be manufactured at little cost in different ways. A thin platinum wire and a piece of wood is all that is needed to make a balance capable of weighing a milligram; and to make a very sensitive hydrostatic balance, little is required besides a glass balloon. Fig. 19 represents a small torsion balance of extreme simplicity. A thin platinum wire is stretched horizontally through two staples, from the wooden supports, A B, which are fixed in a deal board. A very thin, delicate lever, C D, cut in wood, or made with a wisp of straw, is fixed in the centre of the platinum wire by means of a small clip, which secures it firmly. This lever is placed in such a manner that it is raised perceptibly out of the horizontal line. At D is fixed a paper scale, on which is put the weight of a centigram. The lever is lowered to a certain point, slightly twisting the platinum wire. Near the end of the lever a piece of wood, F, is fixed, on which is marked the extreme point of its movements. Ten equi-distant divisions are marked between these two points, which represent the distance traversed by the lever under the weight of the milligram. If a smaller weight than a centigram is placed on the paper scale the lever falls, and balances itself[Pg 27] after a few oscillations. If it falls four divisions, it is evident that the substance weighs four milligrams. Taking a rather thicker platinum wire, to which a shorter lever must be adapted, one can weigh the decigram, and so on. It would be an easy matter, also, to make, on the same model, balances for weighing considerable weights. The platinum wire should be replaced by iron wires of larger diameter, firmly stretched, and the lever should be made of a piece of very resisting wood. One can also, by adaptation, find the exact value of the most trifling weights. By lengthening a very fine platinum wire several yards, and adapting a long, slender lever, it will not be impossible to ascertain the tenth of a milligram. In this latter case the balance can be set when it is wanted.

Fig. 20 represents Nicholson’s Areometer, which any one may construct for himself, and which, as it is here represented, constitutes another kind of balance. A glass balloon, filled with air, is hermetically closed with a cork, through which is passed a cylinder of wood, surmounted by a wooden disc, D. The apparatus is terminated at its lower end by a small tray, C, on which one can put pieces of lead in variable quantities. It is then plunged into a glass filled with water. The pieces of lead on the tray, C, are added by degrees, until the stem of the areometer rises almost entirely above the level of the water; it is next passed through a ring, which keeps it in position, and which is fastened to the upper part of the glass by means of four iron wires in the shape of a cross. The stem is divided in such a way that the space comprised in each division represents the volume of a cubic centimetre. Thus arranged, the apparatus constitutes a balance. The object to be weighed is placed on the disc, D, and the areometer sinks in the water, oscillates, and then remains in equilibrium. If the stem sinks five divisions, it is evident that the weight of the object corresponds to that of five cubic centimetres of displaced water, or five grams.
It is obvious, therefore, from the preceding examples, that it is not impossible to construct a weighing apparatus with ordinary and very inexpensive objects. We can, in the same way, show that it is possible to perform instructive experiments with no appliances at all, or, at any rate, with common things, such as everyone has at hand. The lamented Balard, whose loss science has had recently to deplore, excelled in chemical experiments without a laboratory; fragments of broken glass or earthenware[Pg 28] were used by him for improvising retorts, bottles and vases for forming precipitates, and carrying on many important operations.
Scheele also operated in like manner; he knew how to make great discoveries with the humblest appliances and most slender resources. One cannot too earnestly endeavour to imitate such leaders, both in teaching others and instructing oneself.
The laws relating to the weight of bodies, the centre of gravity, and stable or unstable equilibrium, may be easily taught and demonstrated by means of a number of very familiar objects. By putting into the hands of a child a box of soldiers cut in elder-wood, the end of each fixed into half a bullet, we provide him with the means of making some easy experiments on the centre of gravity. According to some authorities on equilibrium, it is not impossible, with a little patience and delicacy of manipulation, to keep an egg balanced on one of its ends. This experiment should be performed on a perfectly horizontal surface, a marble chimney-piece, for example. If one can succeed in keeping the egg up, it is, according to the most elementary principles of physics, because the vertical line of the centre of gravity passes through the point of contact between the end of the egg and the surface on which it rests.

Fig. 21 reproduces a curious experiment in equilibrium, which is performed with great facility. Two forks are stuck into a cork, and the cork is placed on the brim of the neck of a bottle. The forks and the cork form a whole, of which the centre of gravity is fixed over the point of support. We can bend the bottle, empty it even, if it contains fluid, without the little construction over its mouth being in the least disturbed[Pg 29] from its balance. The vertical line of the centre of gravity passes through the point of support, and the forks oscillate with the cork, which serves as their support, thus forming a movable structure, but much more stable than one is inclined to suppose. This curious experiment is often performed by conjurors, who inform their audience, that they will undertake to empty the bottle without disturbing the cork. If a woodcock has been served for dinner, or any other bird with a long beak, take off the head at the extreme end of the neck; then split a cork so that you can insert into it the neck of the bird, which must be tightly clipped to keep it in place; two forks are then fixed into the cork, exactly as in the preceding example, and into the bottom of the cork a pin is inserted. This little contrivance is next placed on a piece of money, which has been put on the opening of the neck of the bottle, and when it is fairly balanced, we give it a rotatory movement, by pushing one of the forks as rapidly as we please, but as much as possible without any jerk (fig. 22). We then see the two forks, and the cork surmounted by the woodcock’s head, turning on the slender pivot of a pin. Nothing can be more comical than to witness the long beak of the bird turning round and round, successively facing all the company assembled round the table, sometimes with a little oscillation, which gives it an almost lifelike appearance. This rotatory movement will last some time, and wagers are often laid as to which of the company the beak will point at when it[Pg 30] stops. In laboratories, wooden cylinders are often to be seen which will ascend an inclined plane without any impulsion. This appears very surprising at first, but astonishment ceases when we perceive that the centre of gravity is close to the end of the cylinder, because of a piece of lead, which has been fixed in it.


Fig. 23 gives a very exact representation of a plaything which was sold extensively on the Boulevards at Paris at the beginning of the New Year. This little contrivance, which has been known for some time, is one of the most charming applications of the principles relating to the centre of gravity. With a little skill, any one may construct it for himself. It consists of two little puppets, which turn round axles adapted to two parallel tubes containing mercury. When we place the little contrivance in the position of fig. 24, the mercury being at a, the two dolls remain motionless, but if we lower the doll S, so that it stands on the second step (No. 2) of the flight, as indicated in fig. 25, the mercury descends to b at the other end of the tube; the centre of gravity is suddenly displaced; the doll R then accomplishes a rotatory movement, as shown by the arrow in fig. 25, and finally alights on step No. 3. The same movement is also effected by the doll S, and so on, as many times as there are steps. The dolls may be replaced by a hollow cylinder of cartridge paper closed at both ends, and containing a marble; the cylinder, when placed vertically on an inclined[Pg 31] plane, descends in the same way as the puppets. The laws of equilibrium and displacement of the centre of gravity, are rigorously observed by jugglers, who achieve many wonderful feats, generally facilitated by the rotatory motion given to the bodies on which they operate, which brings into play the centrifugal force. The juggler who balances on his forehead a slender rod, on the end of which a plate turns round, would never succeed in the experiment if the plate did not turn on its axis with great rapidity. But by quick rotation the centre of gravity is kept near the point of support. We need hardly remark, too, that it is the motion of a top that tends to keep it in a vertical position.


Many experiments in mechanical physics may occur to one’s mind. To conclude the enumeration of those we have collected on the subject, I will describe the method of lifting a glass bottle full of water by means of a simple wisp of straw. The straw is bent before being passed into the bottle of water, so that, when it is lifted, the centre of gravity is displaced,[Pg 32] and brought directly under the point of suspension. Fig. 26 shows the method of operation very plainly. It is well to have at hand several pieces of straw perfectly intact, and free from cracks, in case the experiment does not succeed with the first attempt.
Having now seen how this point we call the centre of gravity acts, we may briefly explain it.

The centre of gravity of a body is that point in which the sum of the forces of gravity, acting upon all the particles, may be said to be united. We know the attraction of the earth causes bodies to have a property we call Weight. This property of weight presses upon every particle of the body, and acts upon them as parallel forces. For if a stone be broken all the portions will equal the weight of the stone; and if some of them be suspended, it will be seen that they hang parallel to each other, so we may call these weights parallel forces united in the whole stone, and equal to a single resultant. Now, to find the centre of gravity, we must suspend the body, and it will hang in a certain direction. Draw a line from the point of suspension, and suspend the body again: a line drawn from that point of suspension will pass through the same place as the former line did, and so on. That point is the centre of gravity of that suspended body. If the form of it be regular, like a ball or cylinder, the centre of gravity is the same as the mathematically central point. In such forms as pyramids it will be found near the largest[Pg 33] mass; viz., at the bases, about one-fourth of the distance between the apex and the centre of gravity of the base.
When the centre of gravity of any body is supported, that body cannot fall. So the well-known leaning towers are perfectly safe, because their lines of direction fall within the bases. The centre of gravity is in the centre of the leaning figure. The line of direction drawn vertically from that point falls within the base; but if the tower were built up higher, so that the centre of gravity were higher, then the structure would fall, because the line of direction would fall without the base.
We see that animals (and men) are continually altering the position of the centre of gravity; for if a man bears a load he will lean forward, and if he takes up a can of water in one hand he will extend the other to preserve his balance or equilibrium.

The experiment shown in the accompanying illustration is apparently very difficult, but it will be found easy enough in practice if the hand be steady. Take a key, and by means of a crooked nail, or “holdfast,” attach it to a bar of wood by a string tied tightly round the bar, as in the picture. To the other extremity of the bar attach a weight, and then drive a large-headed nail into the table. It will be found that the key will balance, and even move upon the head of the nail, without falling. The weight is under the table, and the centre of gravity is exactly beneath the point of suspension.
Another simple experiment may prove amusing. Into a piece of wood insert the points of two knives, and at the centre of the end of the bar insert a needle between the knife handles. The wood and the knives may then be balanced on another needle fixed in a cork at A.

We may conclude this chapter by summing up in a few words what the Centre of Gravity is. We can define it as “that point in a body upon which the body, acted on solely by the force of gravity, will balance itself in all positions.” Such a point exists in every body, and equally in a number of bodies fastened tightly together. The Centre of Gravity has by some writers been denominated the Centre of Parallel Forces, or the Centre of Magnitude, but the Centre of Gravity is the most usual and best understood term.

CHAPTER IV.
SOME PROPERTIES OF SOLID BODIES—INERTIA—MOTION—FRICTION—THE PENDULUM—EQUILIBRIUM.
Those who have followed us through the preceding pages have now, we hope, some ideas upon Gravity and the Forces of Nature. In speaking of Forces we said “Force was a cause of Motion.” Let us now consider Inertia, and Motion with its accompanying opponent, Friction.

Inertia is the passiveness of Matter. This perfect indifference to either rest or motion makes the great distinction between living and lifeless matter. Inertia, or Vis Inertia, is this passiveness. Now, to overcome this indifference we must use force, and when we have applied force to matter we set it in motion; that is, we move it. When we move it we find a certain resistance which is always proportionate to the force applied. In mechanics this is termed Action, and Reaction, which are always equal forces acting in opposite directions. This is Newton’s law, and may be explained by a “weight” on a table, which presses against the table with the same force with which[Pg 36] the table presses against the “weight”; or when you strike a ball, it strikes the hand with the same force.
We can communicate motion by elasticity. For instance, if we place a number of coins upon a table touching each other and in a straight line, and strike the last coin of the line by pushing another sharply against it, the piece at the opposite extremity will slip out of its place from the effect of the shock transmitted by the coin at the other end (fig. 29).

When two forces act upon a body at the same time, it takes a direction intermediate. This is known as the resultant. The enormous forces exercised[Pg 37] by the heavenly bodies will be treated of later. We will first consider Inertia.
There are several experiments relating to the subject of Inertia which may be performed. I once witnessed one quite accidentally when taking a walk.

I was one day passing the Observatory at Paris, when I noticed a number of people collected round a professor, who after executing several juggling tricks, proceeded to perform the curious experiment I am about to describe. He took a broomstick and placed it horizontally, passing the ends through two paper rings. He then asked two children to hold the paper rings by means of two razors, so that the rings rested on the blade. This done, the operator took a stout stick, and, with all his strength, struck the broomstick in the centre; it was broken into shivers, but the paper rings were not torn in the least, or even cut by the razors! One of my friends, M. M——, a painter, showed me how to perform this experiment as represented in the illustration (fig. 30). A needle is fixed at each end of the broomstick, and these needles are made to rest on two glasses, placed on chairs; the needles alone must be in contact with the glasses. If the broomstick is then struck violently with another stout stick, the former will be broken, but the glasses will remain intact. The experiment answers all the better the more energetic the action. It is explained by the resistance of[Pg 38] inertia in the broomstick. The shock suddenly given, the impulse has not time to pass on from the particles directly affected to the adjacent particles; the former separate before the movement can be transmitted to the glasses serving as supports.8

The experiment represented in fig. 31 is of the same nature. A wooden ball is suspended from the ceiling by a rather slender thread, and a similar thread is attached to the lower end of the ball. If the lower thread is pulled forcibly it will break, as shown in the illustration; the movement communicated to it has not time to pass into the ball; if, on the contrary, it is pulled very gradually and without any shock, the upper thread instead will break, because in this case it supports the weight of the ball. Motion is not imparted simultaneously to all parts of a body, but only to the particles first exposed to a blow, for instance. One might multiply examples of this. If a bullet be shot from a gun, it will make a round hole in a piece of wood or glass, whilst if thrown by the hand,—that is to say, with much less force,[Pg 39]— it will shiver the wood or the pane of glass to pieces. When the celerity of the motive force is very great, the particles directly affected are disturbed so quickly that they separate from the adjacent particles before there is time for the movement to be communicated to the latter.
It is possible, for the same reason, to extract from a pile of money a piece placed in the middle of the pile without overturning the others. It suffices to move them forcibly and quickly with a flat wooden ruler. The experiment succeeds very well also if performed with draughtsmen piled up on the draught-board (fig. 32).

Fig. 33 represents another experiment which belongs to the laws of resisting force. A sixpence is placed on a table covered with a cloth or napkin. It is covered with a glass, turned over so that its brim rests on two penny pieces. The problem to be solved is how to extract the sixpence from underneath the glass without touching it, or slipping anything beneath it. To do this it is necessary to scratch the cloth with the nail of the forefinger; the elasticity of the material communicates the movement to the sixpence, which slowly moves in the direction of the finger, until it finally comes out completely from beneath the glass.
We may give another experiment concerning Inertia. Take a strip of paper, and upon it place a coin, on a marble chimney-piece, as in the illustration. If, holding the paper in the left hand, you strike it rapidly and[Pg 40] forcibly, you will be enabled to draw away the paper without causing the coin (say a five-shilling-piece) to fall down (fig. 34).
It is not impossible to draw away a napkin laid as a tablecloth for one person’s dinner, without disturbing the various articles laid upon it. A quick motion is all that is necessary, keeping the napkin tightly extended by the hands at the same time. This latter experiment, however, is not recommended to boys home for the holidays, as they may unwillingly practise a feat analogous to that executed by Humpty-Dumpty, and find equal difficulty to match the pieces.

We will now examine the term Motion. A body is said to be in motion when it changes its position in relation to surrounding objects. To perceive motion the surrounding objects must be relatively at rest, for if they all hurried along at the same rate no motion would be perceptible. This is evident, for when we stand still trees and houses appear stationary, as do we ourselves, but we know we all are rushing round with the earth, though our relative positions are unchanged. Hence there is no absolute rest.
What are the causes of motion?—Gravity is one. The influence of heat, which is itself caused by the motion of atoms, the effects of electricity, etc., and finally, the power of force in men or animals—any of these causes will produce motion. But a body at rest cannot put itself in motion, nor can a body in motion stop itself, or change its condition of motion.
But you may say a body will stop itself. Your ball on the ground, or even upon ice, will eventually come to a stop. We fire a bullet, and it will stop in time. We reply it does not stop of itself, The resistance of the Air and Friction tend to bring the body in motion to a state of rest. In the case of a bullet gravity brings it down.
There is no need to insist upon the resistance offered by the air even when it is not rushing violently past to fill up a vacuum beyond us, and called a breeze, or high wind. But we may say something of Friction.
Friction is derived from the Latin frico, to rub, and expresses the resistance to motion which arises from uneven surfaces. It is a passive resistance, and depends upon the force which keeps the bodies together. Thus a train running upon a smooth iron rail would never be able to proceed but for friction, which gives the necessary purchase or grip to the wheel and rail in contact.
No surface is perfectly smooth, for we must push a body upon the smoothest surface we possess. Friction tends to resist motion always, and is the cause of a great loss of power in mechanics, though it is employed to stop motion by certain appliances, such as “brakes” and “drags,” for sliding friction is greater than rolling friction. But without friction most structures would fall to pieces, and all forward motion would cease. So though it is an inconvenient force to overcome, we could not do without it.
If a body is set in motion, we see that the tendency of it is to go on for ever. Such, indeed, is the case with the stars; but so long as we are within the influence of the earth’s attraction, we cannot expect such a result. We know now what motion is; we must also, to understand it perfectly, consider its direction and its velocity.
The line which indicates the way from the starting point to the end is the direction of the object in motion, and the rate it moves at its velocity. The latter is calculated at so many miles an hour, as a train; or so many feet in a second if the object be a shot, or other very rapidly-moving body. In equal velocity the same distance is traversed in the same time; and so if a train run a mile in a minute, we know it will travel sixty miles in an hour, and is therefore during that minute going at the rate of sixty miles an hour. We have already spoken of the velocity of a stone falling from a cliff as sixteen feet in a second, and a stone thrown into the air to rise sixteen feet will be a second in going up, and a second in descending. But the velocity will be accelerated in the descent after the first second of time, and retarded in the upward cast by gravity. So we have two terms—accelerated and retarded velocity—used to express an increased or decreased force of attraction.
Perpetual motion has often been sought, but never discovered, nor will it ever be till the elixir of life has been found. It is quite impossible to construct any machine that will work without friction; if any work be done energy will be expended and transformed into other energy, so the total must be diminished by so much as was employed to transform the remainder.[Pg 42] No body can give unlimited work, therefore the perpetual motion theory is untenable and impossible.

The pendulum is considered the nearest approach to perpetual motion. This is so well known that no description is needed, but we may say a few words concerning it. By the diagram, we see that if we lift the ball to b, and let it fall, it will descend to l, and pass it to a opposite, nearly as far from l as b is from it. So the oscillations will continue, each beat being less and less, till rest is reached by the action of gravity (page 23). Were it not for friction and the pressure of the air, the oscillations would continue for ever; as it is, it declines by shorter swings till it remains in equilibrium.
The seconds’ pendulum oscillates sixty times an hour, and must be of a certain length in certain places. In London it is 39·1393 inches, and furnishes a certain standard of length, and by an Act of Parliament the yard is divided into 36 parts, and 39·1393 such parts make the seconds’ pendulum in the latitude of London (in vacuo) in a temperature of 62°.

But the same pendulum will not perform the same number of oscillations in one minute in all parts of the globe. At the equator they will be[Pg 43] less, and at the pole more. Thus it was discovered that, as the movements of the pendulum are dependent upon the force of gravity, and as this force decreases the farther we get from the centre of the earth, the equator must be farther from the earth’s centre than the poles, and therefore the poles must be depressed. The decline of the pendulum at the equator is also, in a measure, due to Centrifugal Force.
Centrifugal Force, which means “flying from the centre,” is the force which causes an object to describe a circle with uniform velocity, and fly away from the centre; the force that counteracts it is called the centripetal force. A very simple experiment will illustrate it.

To represent its action, we shall have recourse to an ordinary glass tumbler placed on a round piece of cardboard, held firmly in place by cords. Some water is poured in the glass, and we then show that it can be swung to and fro and round without the water being spilt, even when the glass is upside down (fig. 36).
Another experiment on the same subject is as shown in the above illustration, by which a napkin ring can be kept in revolution around the forefinger, and by a continued force the ring may be even held suspended at the tip of the finger, apparently in the air, without support (fig. 37).
CHAPTER V.
GASES AND LIQUIDS—PRESSURE OF THE AIR—EXPERIMENTS.
We have more than once referred to the pressure of the air which exerts a great influence upon bodies in motion, but a few experiments will make this more obvious, and clearly demonstrate the fact. We have also told you some of the properties of Solids, such as Weight, Inertia, Friction, and Resistance, or Strength. Solids also, as we have seen, occupy space, and cannot be readily compressed, nor bent to other shapes. Now the subject of the Pressure of the Air leads us to the other forms of Matter; namely, Gases and Liquids, which will be found very interesting to study.

The force of air can very soon be shown as acting with considerable[Pg 45] pressure upon an egg in a glass. By blowing in a claret glass containing a hard-boiled egg, it is possible to cause the egg to jump out of the glass; and with practice and strength of lungs it is not impossible to make it pass from one glass to another, as per illustration (fig. 38).
The force of heated air ascending can also be ascertained by cutting up a card into a spiral, and holding it above the flame of a lamp (fig. 39). The spiral, if lightly poised, will turn round rapidly.
Now let us turn to a few experiments with the air, which is composed in two gases, Oxygen and Nitrogen, of which we shall hear more when we come to Chemistry.


It is not intended here to prosecute researches, but rather to sketch a programme for instruction, based on amusing experiments in Physics, performed without apparatus. The greater part of these experiments are probably well known, and we desire to say that we merely claim to have collected and arranged them for our descriptions. We must also add that we have performed and verified these experiments; the reader, therefore, can attempt them with every certainty of success. We will suppose that we are addressing a young auditory, and commence our course of Physics with some facts relating to the pressure of air. A wine glass, a plate, and water, will serve for our first experiments. Pour some water on the plate, light a piece of paper resting on a cork, and cover the flame with the glass[Pg 46] which I turn upside down (fig. 40). What follows?—The water rises in the glass. Why?—Because the burning of the paper having absorbed a part of the oxygen, and the volume of confined gas being diminished, the pressure of the outer air has driven back the fluid. I next fill a goblet with water up to the brim, and cover it with a sheet of paper which touches both the edge of the glass and the surface of the water. I turn the glass upside down, and the sheet of paper prevents the water running out, because it is held in place by atmospheric pressure (fig. 41). It sometimes happens that this experiment does not succeed till after a few attempts on the part of the operator; thus it is prudent to turn the glass over a basin, so that, in case of failure, the water is not spilt. Having obtained a vase and a bottle, both quite full of water, take the bottle, holding it round the neck so that the thumb can be used as a stopper, then turn it upside down, and pass the neck into the water in the vase. Remove your thumb, or stopper, keeping the bottle in a vertical position, and you will see that the water it contains does not escape, but remains in suspension. It is atmospheric pressure which produces this phenomenon. If, instead of water, we put milk in the bottle, or some other fluid denser than water, we shall see that the milk also remains suspended in the bottle, only there is a movement of the fluid in the neck of the bottle, and on careful examination we perceive very plainly that the milk descends to the bottom of the vase, and the water rises into the bottle. Here, again, it is atmo[Pg 47]spheric pressure which maintains the fluid in the bottle, but the milk descends, because fluids are superposed according to their order of density, and the densest liquid falls to the bottom.
This can be verified by means of the phial of the four elements, which is a plain, long, and narrow bottle, containing equal volumes of metallic mercury, salt water, alcohol, and oil. These four liquids will lie one on the top of the other without ever mixing, even if shaken.
Another experiment as to the pressure of the air may be made (fig. 42). Take a penny and press it against some oaken bookcase or press, rub the coin against the wood for a few seconds, then press it, and withdraw the fingers. The coin will continue to adhere to the wood. The reason of this is, because by the rubbing and the pressure you have dispersed the film of air which was between the penny and the wood, and under those conditions the pressure of the atmospheric air was sufficient to keep the penny in its place.

Or, again, let us now add a water-bottle and a hard-boiled egg to our appliances; we will make use of the air-pump, and easily perform another experiment. I light a piece of paper, and let it burn, plunging it into a water-bottle full of air. When the paper has been burning a few seconds I close the opening of the water-bottle by means of a hard-boiled egg, which I have previously divested of its shell, so that it forms a hermetic stopper. The burning of the paper has now caused a vacuum of air in the bottle, and[Pg 48] the egg is gradually thrust in by the atmospheric pressure outside. Fig. 43 exhibits it slowly lengthening and stretching out as it passes through the aperture; then it is suddenly thrust completely into the bottle with a little explosive sound, like that produced by striking a paper bag expanded with air. This is atmospheric pressure demonstrated in the clearest manner, and at little cost.

If it is desired to pursue a little further the experiments relating to atmospheric pressure, it will be easy enough to add to the before-mentioned appliances a closed glass-tube and some mercury, and one will then have the necessary elements for performing Torricelli’s and Pascal’s experiments, and explaining the theory of the barometer (page 52).
An amusing toy, well-known to schoolboys, called the “sucker,” may also be made the object of many dissertations on the vacuum and the pressure of air. It is composed of a round piece of soft leather, to the centre of which is attached a small cord. This leather is placed on the ground and pressed under foot, and when the cord is pulled it forms a cupping-glass, and is only separated with difficulty from the pavement.
Atmospheric air, in common with other gases, has a tendency to fill any space into which it may enter. The mutual attraction of particles of air is nil; on the contrary, they appear to have a tendency to fly away from each other; this property is called “repulsion.” Air also possesses an expansive[Pg 49] property—a tendency to press against all the sides of any vessel in which it may be enclosed. Of course the larger the vessel containing a given quantity of air, the less actual pressure it will exert on the sides of the vessel. The elasticity of air therefore decreases with increasing expansion, but it gains in elasticity or force when compressed.
There is a law in Physics which expresses the relation between expansion and elasticity of gases, which may be said to be as follows:—
The elasticity (of a gas) is in inverse ratio to the space it occupies, and therefore by compressing air into a small space we can obtain a great force, as in the air-gun and the pop-gun of our youthful days.

In the cut below we can illustrate the principle of the pop-gun. The chamber full of air is closed by a cork and by an air-tight piston (S) at p and p. When the piston is pushed into the chamber the air is compressed between it and the stopper, which at length flies out forcibly with a loud report

We have said that the tendency of air particles is to fly away from each other, and were it not for the earth’s attraction the air might be dispersed. The height of the atmosphere has been variously estimated from a height of[Pg 50] 45 miles to 212 miles in an attenuated form; but perhaps 100 miles high would be a fair estimate of the height to which our atmosphere extends.

The pressure of such an enormous body of gas is very great. It has been estimated that this pressure on the average human body amounts to fourteen tons, but being balanced by elastic fluids in the body, the inconvenience is not felt. The Weight of Air can easily be ascertained, though till the middle of the seventeenth century the air was believed to be without weight. The accompanying illustration will prove the weight of air. Take an ordinary balance; and suspend to one side a glass globe fitted with a stop-cock. From this globe extract the air by means of the air-pump, and weigh it. When the exact weight is ascertained turn the stop-cock, the air will rush in, and the globe will then pull down the balance, thus proving that air possesses weight. The experiments of Torricelli and Otto von Guerike, however, demonstrated that the air has weight and great pressure. Torricelli practically invented the barometer, but Otto von Guerike, by the cups known as Magdeburg Hemispheres, proved the pressure of the outward[Pg 51] air. This apparatus is well known, and consists of two hollow copper hemispheres which fit very closely. By means of the air-pump which he invented in 1650, Otto von Guerike exhausted the air from the closed hemispheres. So long as air remained in them, there was no great difficulty in separating them; but when it had been finally exhausted, the pressure of the surrounding atmosphere was so great that the hollow spheres could not be dragged asunder even by horses harnessed to rings which had been inserted in the globes.

The Air-Pump is a very useful machine, and we will now briefly explain its action. The inventor was, as remarked above, Otto von Guerike, of Magdeburg. The pump consists of a cylinder and piston and rod, with two valves opening upwards—one valve being in the bottom of the cylinder, the other in the piston. This pump is attached by a tube to a plate with a hole in it, one extremity of the tube being fixed in the centre of the plate, and the other at the valve at the bottom of the cylinder. A glass shade, called the receiver, is placed on the top of the plate, and of course this shade will be full of air (fig. 47).

When the receiver is in position, we begin to work the pump. We have said there are two valves. So when the piston is drawn up, the cylinder would be quite empty did not the valve at the bottom, opening upwards, admit some air from the glass shade through the tube to enter the cylinder. Now the lower part of the cylinder is full of air drawn from the glass shade. When we press the piston down again, we press against the air in it, which, being compressed, tries to escape. It cannot go back, because the valve at the bottom of the cylinder won’t open, so it escapes by the valve in the piston, and goes away. Thus a certain amount of air is got rid of at each stroke of the piston. Two cylinders and pistons can be used, and so by means of cog-wheels, etc., the air may be rapidly exhausted from the receiver. Many experiments are made with the assistance of the air-pump and receiver, though the air is never entirely exhausted from the glass.
The “Sprengel” air-pump is used to create an almost perfect vacuum, by putting a vessel to be exhausted in connection with the vacuum at the top of a tube of mercury thirty inches high. Some air will bubble out, and the mercury will fall. By filling up again and repeating the process, the air vessel will in time be completely exhausted. This is done by Mr. Sprengel’s pump, and a practically perfect vacuum is obtained, like the Torricellian vacuum.
The “Torricellian vacuum” is the empty space above the column of mercury in the barometer which we will proceed to describe. Air has a certain weight or pressure which is sufficient to raise a column of mercury thirty[Pg 52] inches. We will prove this by illustration. Take a bent tube and fill it with mercury; the liquid will stand equally high in both arms, in consequence of the ratio of equilibrium in fluids, of which we shall read more when we come to consider Water. So the two columns of mercury are in equilibrium. (See A.) Now stop the arm a with a cork, and take out half the mercury. It will remain in one arm only. Remove the cork, and the fluid will fall in both arms, and remain in equilibrio. If a long bent glass tube be used, the arms being thirty-six inches high, the mercury will fall to a point c, which measures 29·9 inches from the bottom. If the tube be a square inch in bore, we have 29·9 cubic inches of mercury, weighing 14⅘ lbs., balancing a column of air one square inch thick and as high as the atmosphere. So the mercury and the column of air must weigh the same. Thus every square inch on the earth supports a weight of (nearly) 15 lbs (figs. 48 and 50).

The barometer invented by Pascal, working on the investigations of Torricelli, is a very simple and useful instrument. Fill a tube with mercury from which all moisture has been expelled, and turn it over in a dish[Pg 53] of mercury; the mercury will rise to a certain height (30 inches), and no higher in vacuo. When the pressure of the air increases the mercury rises a little, and falls when the pressure is removed. Air charged with aqueous vapour is lighter than dry air, so a fall in the mercury indicates a certain amount of water-vapour in the air, which may condense and become rain. The action of mercury is therefore used as a weather-glass, by which an index-point shows the movements of the fluid, by means of a wheel over which a thread passes, sustaining a float and a counterpoise. When the mercury rises the float goes up, and the weight falls, and turns the wheel by means of the thread. The wheel having a pointer on the dial tells us how the mercury moves. This weather-glass is the usual syphon barometer with the float on the surface and a weight (fig. 50).
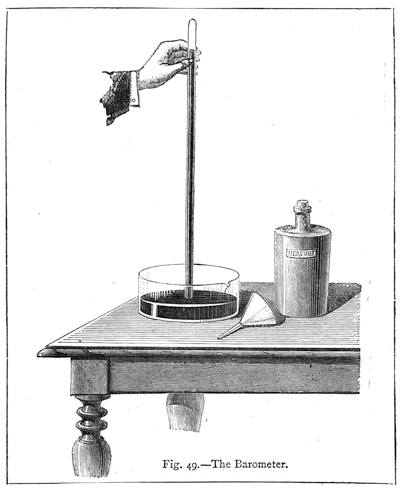

The Syphon Barometer is a bent tube like the one already shown, with one limb much shorter than the other.
The Aneroid Barometer, so called because it is “without moisture,” is now in common use. In these instruments the atmospheric pressure is held in equilibrium by an elastic metal spring or tube. A metal box, or tube, is freed from air, and then hermetically sealed. This box has a flexible side, the elasticity of which, and the pressure of the air on it, keep each other in equilibrium. Upon this elastic side the short arm of a lever is pressed, while the longer arm works an index-point, as in the circular barometer. When pressure increases the elastic box “gives”; when pressure diminishes it returns to its former place, and the index moves in the opposite direction. It is necessary to compare and “set” the aneroid with the mercurial barometer to ensure correctness. A curved tube is sometimes used, which coils and uncoils like a spring, according to the pressure on it.

There are other barometers, such as the Water Barometer, which can be fixed against the side of a house, and if the water be coloured, it will prove a useful indicator. As the name indicates, water[Pg 54] is used instead of mercury, but as the latter is thirteen-and-half times heavier than water, a much longer tube is necessary; viz., one about thirty-five feet in length. The construction is easy enough. A leaden pipe can be fixed against the house; on the top is a funnel furnished with a stop-cock, and placed in a vase of water. The lower part of the tube is bent, and a glass cylinder attached, with another stop-cock—the glass being about three feet long, and graduated. Fill the tube with water, shut the upper stop-cock, and open the lower one. The vacuum will be formed in the top of the tube, and the barometer will act on a larger scale than the mercury.
The Glycerine Barometer, invented by Mr. Jordan, and in use at the Times office, registers as more than one inch movements which on the mercurial thermometer are only one-tenth of an inch, and so are very distinctly visible. The specific gravity of pure glycerine is less than one-tenth that of mercury, so the mean height of the glycerine column is twenty-seven feet at sea level. The glycerine has, however, a tendency to absorb moisture from the air, but Mr. Jordan, by putting some petroleum oil upon the glycerine, neutralized that tendency, and the atmospheric pressure remains the same. A full description of this instrument was given in the Times of 25th October, 1880.

The uses of the barometer are various. It is employed to calculate the heights of mountains; for if a barometer at sea level stand at 30", it will[Pg 55] be lower on a mountain top, because the amount of air at an elevation of ten thousand feet is less than at the level of the sea, and consequently exercises less pressure, and the mercury descends. [The pressure is on the bulb of mercury at the bottom, not on the top, remember.]
The pressure of the air at the tops of mountains sometimes decreases very much, and it is not sufficiently dense for perfect respiration, as many people find. Some climbers suffer from bleeding at the nose, etc., at great altitudes. This is occasioned by the action of the heart, which pumps with great force, and the outward pressure upon the little veins being so much less than usual, they give way.

Many important instruments depend upon atmospheric pressure. The most important of these is the pump, which will carry us to the consideration of water and Fluids generally. The fire-engine is another example, but we will now proceed to explain the diving-bell already referred to.
Fig. 52 represents the experiment of the diving-bell, which is so simple, and is explained below. It belongs to the same category of experiments as those relating to the pressure of air and compression of gas. Two or three flies have been introduced into the glass, and they prove by their buzzing about that they are quite at their ease in the rather confined space.
The Diving-Bell in a crude form appears to have been used as early as 1538. It was used by two Greeks in the presence of the Emperor Charles V., and numerous spectators. In the year 1720 Doctor Halley improved the diving-bell, which was a wooden box or chamber open at the bottom. Air casks were used to keep the inmate supplied with air. The modern diving-bell was used by Smeaton in 1788, and was made of cast iron. It sinks by its own weight. The pressure of the air inside is sufficient to keep the water out. Air being easily compressed, it is always pumped in to keep the hollow iron “bell” full, and to supply the workmen. There are inventions now in use by which the diver carries a supply of air with him on his back, and by turning a tap can supply himself for a long time at a distance from the place of descent, and thus is able to dispense with the air-tube from the boat at the surface. This apparatus was exhibited at the Crystal Palace some years ago.

The Pump.
We have seen in the case of the Water Barometer that the pressure of the air will sustain a column of water about thirty feet high. So the distance between the lower valve and the reservoir or cistern must not be more than thirty-two feet, practically the distance is about twenty-five feet in pumps.
We can see by the illustration that the working is much the same as in the air-pump. The suction pipe B is closed by the valve C, the cylinder D and spout E are above, the piston rod F lifts the air-tight piston in which is a valve H. When the piston is raised the valve C opens and admits the water into the cylinder. When the piston is depressed the valve C is closed, the water already in forces H open, and passing through the piston, reaches the cylinder and the spout (fig. 55).
The hand fire-engine depends upon the action of compressed air, which is so compressed by pumping water into the air chamber a. The tube is closed at g, and the pumps e e drive water into the air chamber. At length the tap is opened, and the air drives the water out as it is continually supplied (fig. 54).
Compressed air was also used for driving the boring machines in the Mount Cenis tunnel. In this case also the air was compressed by water, and then let loose, like steam, to drive a machine furnished with boring instruments.

A pretty little toy may be made, and at the same time exemplify an interesting fact in Physics. It is called the ludion, and it “lies in a nut shell” in every sense. When the kernel has been extracted from the shell, fasten the portions together with sealing wax, so that no water can enter. At one end O, as in the illustration, leave a small hole about as large as a pin’s head; fasten two threads to the sealing wax, and to the threads a wooden doll. Let a weight be attached to his waist. When the figure is in equilibrium, and will float, put it into a jar of water, and tie a piece of bladder over the top. If this covering be pressed with the finger, the doll will descend and remount when the finger is removed. By quick successive pressure the figure may be made to execute a pas seul. The reason of the movement is because the slight cushion of air in the upper part of the vase is compressed, and the little water thus caused to enter the nut shell makes it heavier, and it descends with the figure (fig. 56).
We have now seen that air is a gas, that it exercises pressure, that it possesses weight. We know it can be applied to many useful purposes, and that the air machines and inventions—such as the air-pump and the “Pneumatic Despatch”—are in daily use in our laboratories, our steam engines, our condensed milk manufactories, and in many other industries, and for our social benefit. Compressed air is a powerful motor for boring machinery in tunnels where steam cannot be used, even if water could be supplied, for smoke or fire would suffocate the workers. To air we owe our life and our happiness on earth.
Pneumatics, then, deals with the mechanical properties of elastic fluids[Pg 58] represented by air. A gas is an elastic fluid, and differs very considerably, from water; for a gas will fill a large or small space with equal convenience, like the genii which came out of the bottle and obligingly retired into it again to please the fisherman. We have seen that the pressure of the air is 14⅘ per square inch at a temperature of 32°. It is not so easy to determine the pressure of air at various times as that of water. We can always tell the pressure of a column of water when we find the height of the column, as it is the weight of so many cubic inches of the liquid. But the pressure of the atmosphere per square inch at any point is equal to the weight of a vertical column of air one inch square, reaching from that point to the limit of the atmosphere above it. Still the density is not the same at all points, so we have to calculate. The average pressure at sea level is 14·7 per square inch, and sustains a column of mercury 1 square inch in thickness, 29·92, or say 30 inches high. These are the data upon which the barometer is based, as we have seen.

In our article upon “Chemistry” we will speak more fully of the atmosphere and of its constituents, etc.
CHAPTER VI.
ABOUT WATER—HYDROSTATICS AND HYDRAULICS—LAW OF ARCHIMEDES—THE BRAMAH PRESS—THE SYPHON.
At present we will pass from Air to Water, from Pneumatics to Hydrostatics and Hydraulics. We must remember that Hydrostatics and Hydraulics are very different. The former treats of the weight and pressure of liquids when they are at rest, the latter treats of them in motion. We will now speak of the properties of Liquids, of which Water may be taken as the most familiar example.
We have already seen that Matter exists in the form of Solids, Liquids, and Gases, and of course Water is one form of Matter. It occupies a certain space, is slightly compressible; it possesses weight, and exercises force when in motion. It is a fluid, but also a liquid. There are fluids not liquid, such as air or steam, to take equally familiar examples. These are elastic fluids and compressible, while water is inelastic, and termed incompressible.
The chemical composition of water will be considered hereafter, but at present we may state that water is composed of oxygen and hydrogen, and proportions of eight of the former to one of the latter by weight; in volume the hydrogen is as two to one.
From these facts, as regards water, we learn that volume and weight are very different things,—that equal volumes of various things may have different weights, and that volume (or bulk) by no means indicates weight Equal volumes of feathers and sand will weigh very differently.
[The old “catch” question of the “difference in weight between a pound of lead and a pound of feathers” here comes to the mind. The answer generally given is that “feathers make the heavier ‘pound’ because they are weighed by avoirdupois, and lead by troy weight.” This is an error. They are both weighed in the same way, and pound for pound are the same weight, though different in volume.]
Fluids in equilibrium have all their particles at the same distance from the centre of the earth, and although within small distances liquids appear perfectly level (in a direct line), they must, as the sea does, conform to the shape of the earth, though in small levels the space is too limited to admit of any deviation from the plane at right angle to the direction of gravity.
Liquids always fall to a perfectly level surface, and water will seek to find its original level, whether it be in one side of a bent tube, in a watering pot and its spout, or as a fountain. The surface of the water will be on the same level in the arms of a bent tube, and the fountain will rise to a height[Pg 60] corresponding with the elevation of the parent spring whence it issues. The waterworks companies first pump the water to a high reservoir, and then it rises equally high in our high-level cisterns.
As an example of the force of water, a pretty little experiment may be easily tried, and, as many of our readers have seen in a shop in the Strand in London, it always is attractive. A good-sized glass shade should be procured and placed over a water tap and basin, as per the illustration herewith. Within the glass put a number of balls of cork or other light material. Let a stop-cock, with a small aperture, be fixed upon the tube leading into the glass. Another tube to carry away the water should, of course, be provided, but it may be used over again. When the tap is properly fixed, if the pressure of the water be sufficient, it will rush out with some force, and catching the balls as they fall to the bottom of the glass shade bear them up as a juggler would throw oranges from hand to hand. If coloured balls be used the effect may be enhanced, and much variety imparted to the experiment, which is very easy to make.

Water exercises an enormous pressure, but the pressure does not depend upon the amount of water in the vessel. It depends upon the vessel’s height, and the dimensions of the base. This has been proved by filling vessels whose bases and heights are equal, but whose shapes are different, each holding a different quantity of water. The pressure at the bottom of each[Pg 61] vessel is the same, and depends upon the depth of the water. If we subject a portion of the liquid surface to certain force, this pressure will be dispersed equally in all directions, and from an acquaintance with this fact the Hydraulic Press was brought into notice. If a vessel with a horizontal bottom be filled with water to a depth of one foot, every square foot will sustain a pressure of 62·37 lbs., and each square inch of 0·433 lbs.

We will now explain the principle of this Water Press. In the small diagram, the letters A B represent the bottom of a cylinder which has a piston fitted in it (P). Into the opposite side a pipe is let in, which leads from a force-pump D, which is fitted with a valve E, opening upwards. When the piston in D is pulled up water enters through the valve; when the piston is forced down the valve shuts, and the water rushes into the chamber A B. The pressure pushes up the large piston with a force multiplied as many times as the area of the small piston is contained in the large one. So if the large one be ten times as great as the small one, and the latter be forced down with a 10 lb. pressure, the pressure on the large one will be 100 lbs., and so on.

The accompanying illustration shows the form of the Hydraulic or Bramah Press. A B C D is a strong frame, F the force-pump worked by means of a lever fixed at G, and H is the counterprise. E is the stop-cock to admit the water (fig. 63).

The principles of hydrostatics will be easily explained. The Lectures of M. Aimé Schuster, Professor and Librarian at Metz, have taught us in a very simple manner the principle of Archimedes, in which it is laid down that “a body immersed in a liquid loses a portion of its weight equal to the weight of the liquid displaced by it.” We take[Pg 62] a body of as irregular form as we please; a stone, for example. A thread is attached to the stone, and it is then placed in a glass of water full up to the brim. The water overflows; a volume of the liquid equal to that of the stone runs over. The glass thus partially emptied is then dried, and placed on the scale of a balance, beneath which we suspend the stone; equilibrium is established by placing some pieces of lead in the other scale. We then take a vase full of water, into which we plunge the stone suspended from the scale, supporting the vase by means of bricks. The equilibrium is now broken; to re-establish it, it is necessary to fill up with water the glass placed on the scale; that is to say, we put back in the glass the weight of a volume of water precisely equal to that of the stone.

If it is desired to investigate the principles relating to connected vessels, springs of water, artesian wells, etc., two funnels, connected by means of an india-rubber tube of certain length, will serve for the demonstration; and by placing the first funnel at a higher level, and pouring in water abundantly, we shall see that it overflows from the second.
A disc of cardboard and a lamp-glass will be all that is required to show the upward pressure of liquids. I apply to the opening of the lamp-glass a round piece of cardboard, which I hold in place by means of a string; the tube thus closed I plunge into a vessel filled with water. The piece of cardboard is held by the pressure of the water upwards. To separate it[Pg 63] from the opening it suffices to pour some water into the tube up to the level of the water outside (fig. 64). The outer pressure exercised on the disc, as well as the pressure beneath, is now equal to the weight of a body of water having for its base the surface of the opening of the tube, its depth being the distance from the cardboard to the level of the water.
Syringes, pumps, etc., are the effects of atmospheric pressure. Balloons rise in the air by means of the pressure of gas; a balloon being a body plunged in gas, is consequently submitted to the same laws as a body plunged in water.
Boats float because of the pressure of liquid, and water spurts from a fountain for the same reason. I recollect having read a very useful application of the principles of fluid pressure.

A horse was laden with two tubs for carrying a supply of water, and in the bottom of the tubs a valve was fixed. When the horse entered the stream the tubs were partly immersed; the water then exercised its upward pressure, the valve opened, and the tubs slowly filled. When they were nearly full the horse turned round and came out of the water; the pressure had ceased.
Thus the action of the water first opened the valve, and then closed it.
The particular phenomena observable in the water level in narrow spaces, as of a fine glass tube, or the level of two adjoining waves, capillary[Pg 64] phenomena, etc., do not need any special appliance for demonstration, and it is the same with the convexity or concavity of meniscuses.
Fig. 65 represents a pretty experiment in connection with these phenomena. I take a glass, which I fill up to the brim, taking care that the meniscus be concave, and near it I place a pile of pennies. I then ask my young friends how many pennies can be thrown into the glass without the water overflowing. Everyone who is not familiar with the experiment will answer that it will only be possible to put in one or two, whereas it is possible to put in a considerable number, even ten or twelve. As the pennies are carefully and slowly dropped in, the surface of the liquid will be seen to become more and more convex, and one is surprised to what an extent this convexity increases before the water overflows.

The common syphon may be mentioned here. It consists of a bent tube with limbs of unequal length. We give an illustration of the syphon (fig. 66). The shorter leg being put into the mixture, the air is exhausted from the tube at o, the aperture at g being closed with the finger. When the finger is removed the liquid will run out. If the water were equally high in both legs the pressure of the atmosphere would hold the fluid in equilibrium, but one leg being longer, the column of water in it preponderates, and as it falls, the pressure on the water in the vessel keeps up the supply.
Apropos of the syphon, we may mention a very simple application of the principle. Cut off a strip of cloth, and arrange it so that one end shall remain in a glass of water while the other hangs down, as in the illustration. In a short time the water from the upper glass will have passed through the cloth-fibres to the lower one (fig. 67).
This attribute of porous substances is called capillarity, and shows itself by capillary attraction in very fine pores or tubes. The same phenomenon is exhibited in blotting paper, sugar, wood, sand, and lamp-wicks, all of which give familiar instances of capillarity. The cook makes use of this property by using thin paper to absorb grease from the surface of soups.
Capillarity (referred to on page 25) is the term used to define capillary force, and is derived from the word capillus, a hair; and so very small bore tubes are called capillary tubes. We know that when we plunge a glass tube into water the liquid will rise up in it, and the narrower the tube the higher the water will go; moreover, the water inside will be higher than at the outside. This is in accordance with a well-known law of adhesion, which induces concave or convex surfaces9 in the liquids in the tubes, according as the tube is wetted with the liquid or not. For instance, water, as we[Pg 65] have said, will be higher in the tube, and concave in form; but mercury will be depressed below the outside level, and convex, because mercury will not adhere to glass. When the force of cohesion to the sides of the tube is more than twice as great as the adhesion of the particles of the liquid, it will rise up the sides, and if the forces be reversed, the rounded appearance will follow. This accounts for the convex appearance, or “meniscus,” in the column of mercury in a barometer.
Amongst the complicated experiments to demonstrate molecular attraction, the following is very simple and very pretty:—Take two small balls of cork, and having placed them in a basin half-filled with water, let them come close to each other. When they have approached within a certain distance they will rush together. If you fix one of them on the blade of your penknife, it will attract the other as a magnet, so that you can lead it round the basin (fig. 68). But if the balls of cork are covered with grease they will repel each other, which fact is accounted for by the form of the menisques, which are convex or concave, according as they are moistened, or preserved from action of the water by the grease.

This attribute is of great use in the animal and vegetable kingdoms. The rising of the sap is one instance of the latter.
Experience in hydrostatics can be easily applied to amusing little experiments. For instance, as regards the syphon, we may make an image[Pg 66] of Tantalus as per illustration (fig. 69). A wooden figure may be cut in a stooping posture, and placed in the centre of a wide vase, as if about to drink. If water be poured slowly into the vase it will never rise to the mouth of the figure, and the unhappy Tantalus will remain in expectancy. This result is obtained by the aid of a syphon hidden in the figure, the shorter limb of which is in the chest. The longer limb descends through a hole in the table, and carries off the water. These vases are called vases of Tantalus.
The principle of the syphon may also be adapted to our domestic filters. Charcoal, as we know, makes an excellent filter, and if we have a block of charcoal in one of those filters,—now so common,—we can fix a tube into it, and clear any water we may require. It sometimes (in the country) happens that drinking-water may become turgid, and in such a case the syphon filter will be found useful.

The old “deception” jugs have often puzzled people. We give an illustration of one, and also a sketch of the “deceptive” portion (figs. 70 and 71). This deception is very well managed, and will create much amusement if a jug can be procured; they were fashionable in the eighteenth century, and previously. A cursory inspection of these curious utensils will lead one to vote them utterly useless. They are, however, very quaint, and if not exactly useful are ornamental. They are so constructed, that if an inexperienced[Pg 67] person wish to pour out the wine or water contained in them, the liquid will run out through the holes cut in the jug.
To use them with safety it is necessary to put the spout A in one’s mouth, and close the opening B with the finger, and then by drawing in the breath, cause the water to mount to the lips by the tube which runs around the jug. The specimens herein delineated have been copied from some now existent in the museum of the Sèvres china manufactory.
The Buoyancy of Water is a very interesting subject, and a great deal may be written respecting it. The swimmer will tell us that it is easier to float in salt water than in fresh. He knows by experience how difficult it is to sink in the sea; and yet hundreds of people are drowned in the water, which, if they permitted it to exercise its power of buoyancy, would help to save life.

The sea-water holds a considerable quantity of salt in solution, and this adds to its resistance, or floating power. It is heavier than fresh water, and the Dead Sea is so salt that a man cannot possibly sink in it. This means that the man’s body, bulk for bulk, is much lighter than the water of the Dead Sea. A man will sink in fresh, or ordinary salt water if the air in his lungs be exhausted, because without the air he is much heavier than water, bulk for bulk. So if anything is weighed in water, it apparently loses in weight exactly equal to its own bulk of water.
Water is the means by which the Specific Gravity of liquids or solids is found, and by it we can determine the relative densities of matter in proportion. Air is the standard for gases and vapours. Let us examine this, and see what is meant by Specific Gravity.
We have already mentioned the difference existing between two equal volumes of different substances, and their weight, which proves that they may contain a different number of atoms in the same space. We also know, from the principle of Archimedes, that if a body be immersed in a fluid, a portion of its weight will be sustained by the fluid equal to the weight of the fluid displaced.

[This theorem is easily proved by filling a bucket with water, and moving it about in water, when it will be easy to lift; and likewise the human body may be easily sustained in water by a finger under the chin.]

The manner in which Archimedes discovered the displacement of liquids is well known, but is always interesting. King Hiero, of Syracuse, ordered a crown of gold to be made, and when it had been completed and delivered[Pg 69] to His Majesty, he had his doubts about the honesty of the goldsmith, and called to Archimedes to tell him whether or not the crown was of gold, pure and simple. Archimedes was puzzled, and went home deep in thought. Still considering the problem he went to the bath, and in his abstraction filled it to the brim. Stepping in he spilt a considerable quantity of water, and at once the idea struck him that any body put into water would displace its own weight of the liquid. He did not wait to dress, but ran half-naked to the palace, crying out, “Eureka, Eureka! I have found it, I have found it! “What had he found?—He had solved the problem.
He got a lump of gold the same weight as the crown, and immersed it in water. He found it weighed nineteen times as much as its own bulk of water. But when he weighed the kings crown he found it displaced more water than the pure gold had done, and consequently it had been adulterated by a lighter metal. He assumed that the alloy was silver, and by immersing lumps of silver and gold of equal weight with the crown, and weighing the water that overflowed from each dip, he was able to tell the king how far he had been cheated by the goldsmith.

It is by this method now that we can ascertain the specific gravity of bodies. One cubic inch of water weighs about half an ounce (or to be exact, 252½ grains). Take a piece of lead and weigh it in air; it weighs, say, eleven ounces. Then weigh it in a vase of water, and it will be only ten ounces in weight. So lead is eleven times heavier than water, or eleven ounces of lead occupy the same space as one ounce of water.

[The heavier a fluid is, or the greater its density, the greater will be the weight it will support. Therefore we can ascertain the purity or otherwise of certain liquids by using hydrometers, etc., which will float higher or lower in different liquids, and being gauged at the standard of purity, we can ascertain (for instance) how much water is in the milk when supplied from the dairy.]
But to return to Specific Gravity, which means the “Comparative[Pg 70] density of any substance relatively to water,” or as Professor Huxley says, “The weight of a volume of any liquid or solid in proportion to the weight of the same volume of water, at a known temperature and pressure.”
Water, therefore, is taken as the unit; so anything whose equal volume under the same circumstances is twice as heavy as the water, is declared to have its specific gravity 2; if three-and-a-half times it is 3·5, and so on. We append a few examples; so we see that things which possess a higher specific gravity than water sink, which comes to the same thing as saying they are heavier than water, and vice versâ.
To find the specific gravity of any solid body proceed as above, in the experiment of the lead. By weighing the substance in and out of water we find the weight of the water displaced; that is, the first weight less the second. Divide the weight in air by the remainder, and we shall find the specific gravity of the substance.

The following is a table of specific gravities of some very different substances, taking water as the unit.
| Substance. | Specific Gravity. |
Substance. | Specific Gravity. |
Substance. | Specific Gravity. |
|---|---|---|---|---|---|
| Platinum | 21·5 | Iron | 7·79 | Water | 1·000 |
| Gold | 19·5 | Tin | 7·29 | Sea Water | 1·026 |
| Mercury | 13·59 | Granite | 2·62 | Rain Water | 1·001 |
| Lead | 11·45 | Oak Wood | 0·77 | Ice | ·916 |
| Silver | 10·50 | Cork | 0·24 | Ether | 0·723 |
| Copper | 8·96 | Milk | 1·032 | Alcohol | 0·793 |
But we have by no means exhausted the uses of water. Hydrodynamics, which is the alternative term for hydraulics, includes the consideration of many forms of water-wheels, most of which, as mill-wheels, are[Pg 71] under-shot, or over-shot accordingly as the water passes horizontally over the floats, or acts beneath them. These wheels are used in relation to the fall of water. If there is plenty of water and a slight fall, the under-shot wheel is used. If there is a good fall less water will suffice, as the weight and momentum of the falling liquid upon the paddles will turn the wheel. Here is the Persian water-wheel, used for irrigation (fig. 75). The Archimedian Screw, called after its inventor, was one of the earliest modes of raising water. It consists of a cylinder somewhat inclined, and a tube bent like a screw within it. By turning the handle of the screw the water is drawn up and flows out from the top.

The Water Ram is a machine used for raising water to a great height by means of the momentum of falling water.
The Hydraulic Lift is familiar to us all, as it acts in our hotels, and we need only mention these appliances here; full descriptions will be found in Cyclopædias.
We have by no means exhausted the subject of Water in this chapter. Far from it. But when we come to Chemistry and Physical Geography we shall have more to tell, and our remarks as to the application of science to Domestic Economy, in accordance with our plan, will also lead us up to some of the uses of water. So for the present we will take our leave of water in a liquid form, and meet it again under the application of Heat, which subject will take us to Ice and Steam,—two very different conditions of water.
CHAPTER VII.
HEAT—WHAT IT IS—THEORY OF HEAT—THE THERMOMETER—EXPANSION BY HEAT—EBULLITION AND DISTILLATION—LATENT HEAT—SPECIFIC HEAT.
What is Heat?—We will consider this question, and endeavour to explain it before we speak of its effects on water and other matter.
Heat is now believed to be the effects of the rapid motion of all the particles of a body. It is quite certain that a heated body is no heavier than the same body before it was made “hot,” so the heat could not have gone into it, nor does the “heat” leave it when it has become what we call “cold,” which is a relative term. Heat is therefore believed to be a vibratory motion, or the effects of very rapid motion of matter.
The Science of Heat, as we may term it, is only in its infancy, or certainly has scarcely come of age. Formerly heat was considered a chemical agent, and was termed caloric, but now heat is found to be motion, which affects our nerves of feeling and sight; and, as Professor Stewart tells us, “a heated body gives a series of blows to the medium around it; and although these blows do not affect the ear, they affect the eye, and give us a sense of light.”
Although it is only within a comparatively few years that heat has been really looked upon as other than matter, many ancient philosophers regarded it as merely a quality of matter. They thought it the active principle of the universe. Epicurus declared that heat was an effluxion of minute spherical particles possessing rapid motion, and Lucretius maintained that the sun’s light and heat are the result of motion of primary particles. Fire was worshipped as the active agent of the universe, and Prometheus was fabled to have stolen fire from heaven to vivify mankind. The views of the ancients were more or less adopted in the Middle Ages; but John Locke recognized the theory of heat being a motion of matter. He says: “What in our sensation is heat, in the object is nothing but motion.”
Gradually two theories arose concerning heat;—one, the Material theory—the theory of Caloric or Phlogiston; the other, the Kinetic theory. Before the beginning of the present century the former theory was generally accepted, and the development of heat was accounted for by asserting that the friction or percussion altered the capacity for heat of the substances acted upon. The heat was squeezed out by the hammer, and the amount[Pg 73] of heat in the world was regarded as a certain quantity, which passed from one body to another, and that some substances contained, or could “store away,” more of the material called heat than other substances. Heat was the material of fire—the principle of it, or materia ignis; and by these theories Heat, or Caloric, was gradually adopted as a separate material agent—an invisible and subtle matter producing certain phenomena when liberated.
So the two theories concerning heat arose at the end of the last century. One, as we have said, is known as the Material, the other as the Kinetic theory. The latter is the theory of motion, so called from the Greek kinesis (motion), or sometimes known as the Dynamic theory of heat, from dunamis (force); or again as Thermo-dynamics.
But any possibility of producing a new supply of heat was denied by the materialists. They knew that some bodies possessed a greater capacity for heat than others; but Count Rumford, at Munich, in 1797, astonished an audience by making water boil without any fire! He had observed the great extent to which a cannon became heated while being bored in the gun factory, and influenced by those who maintained the material theory of heat, paid great attention to the evolution of heat. He accordingly endeavoured to produce heat by friction, and by means of horse power he caused a steel borer to work upon a cylinder of metal. The shavings were permitted to drop into a pan of water at 60° Fahrenheit. In an hour after the commencement of the operation the temperature of the water had risen to 107°: in another half-hour the heat of it was up to 142°: and in two hours had measured 170°. Upon this he says: “It is hardly necessary to add that anything which any insulated body or system of bodies can continue to furnish without limitation cannot possibly be a material substance, and it appears to me to be extremely difficult, if not quite impossible, to form any distinct idea of anything capable of being excited and communicated in these experiments except by motion.”
A few years later Sir Humphrey Davy made his conclusive experiments, and the Material theory of heat received its death-blow.
Sir Humphrey Davy—referring to the fact that water at a freezing temperature has “more heat in it” (as it was believed) than ice at the same temperature—said: “If I, by friction, liquify ice, a substance will be produced which contains a far greater absolute amount of heat than ice. In this case it cannot reasonably be affirmed that I merely render sensible heat which had been previously insensible in the frozen mass. Liquification will conclusively prove the generation of heat.
This reasoning could not be doubted. Sir Humphrey Davy made the experiment. He rubbed together two pieces of ice in the air, and in a vacuum surrounded by a freezing mixture. The ice became liquified, and so the generation of heat by “mechanical means” was proved. Its immateriality was demonstrated, but the Material theory was not even then abandoned by its adherents.
So things continued, until in 1842-3, Doctor Julius Meyer, of Heilbronn,[Pg 74] and Doctor Joule, of Manchester, separately, and by different means, arrived at the conclusion that a certain definite amount of mechanical work corresponds to a certain definite amount of Heat, and vice versâ. Thus was a great support afforded to the Dynamic theory. This fact Doctor Joule communicated to the Philosophical Magazine in 1843, and the conclusions he came to were—
1. “That the quantity of heat produced by the friction of bodies, whether solid or liquid, is always in proportion to the force expended;
2. “That the quantity of heat capable of increasing the temperature of a pound of water (weighed in vacuo and taken at between 55° and 60° Fahr.) by 1° Fahr., requires for its evolution the expenditure of a mechanical force represented by the fall of 772 lbs. through the space of one foot.”

This is the “mechanical equivalent of heat.” The first paper written by Mr. Joule demonstrated that the temperature of water rises when forced through narrow tubes; and to heat it one degree, the force of 770 foot pounds was necessary, which means that the 1 lb. of water falling 770 feet, got hotter by one degree when it reached the earth. He subsequently arrived at the more exact conclusions quoted above.
So heat is now known to be a series of vibrations, or vibratory motions, as sound vibrations, which we cannot hear nor see, but the effects of which are known to us as light and heat.
In considering heat we must put aside the idea of warmth and cold, for they are only different degrees of heat, not the absence of it.
The study of heat can be briefly undertaken without any complicated apparatus. If we desire a proof of the great conducting power of metals, let us place a fine piece of muslin tightly stretched over a lump of polished metal. On the muslin we put a burning ember, and excite combustion by blowing on it; the muslin is not burned in the least, the heat being entirely absorbed by the metal, which draws it through the material into itself. Fig. 76 represents a similar experiment: it consists of melting some tin on a playing card, held over the flame of a spirit lamp. The metal becomes completely melted without the card being burnt. It is through a similar effect that metals appear cold to us when we take them in our hands; by their conductibility they remove the heat from our hands, and give us the peculiar impression which we do not experience when in contact with substances that are bad conductors, such as wood, woollen materials, etc.

Fig. 77 shows the method of boiling water in paper. We make a small paper box, such as those made by school-boys, and suspend it by four threads to a piece of wood held horizontally at a suitable height. We fill this improvised vessel with water, and place it over the flame of a spirit lamp. The paper is not burnt, because the water absorbs all the heat into itself. After a few minutes the water begins to boil, sending forth clouds[Pg 76] of steam, but the paper remains intact. It is well to perform this operation over a plate, in case of accident, as the water may be spilt. We may also make use of an egg-shell as a little vessel in which to heat the water, by resting it on a wire ring over the flame of the spirit lamp.

Fig. 78 shows the arrangement of a very remarkable experiment, but little known, on the refreezing of ice. A block of ice is placed on the edge of two iron chairs, and is encircled by a piece of wire, to which is suspended the weight of say five pounds. The wire penetrates slowly, and in about an hour’s time has passed completely through the lump of ice, and the weight, with the piece of wire, falls to the ground. What happens then to the block of ice?—You imagine, doubtless, that it is cut in two. No such thing; it is intact, and in a single lump as it was previous to the experiment. In proportion as the wire was sunk through the mass, the slit has been closed again by refreezing. Ice or snow during the winter may serve for a number of experiments relating to heat. If we wish to demonstrate the influence of colours on radiation, we take two pieces of cloth of the same size,—one white, and the other black,—and place them both on the snow, if possible, when there is a gleam of sunlight. In a short time it will be found that the snow underneath the black cloth has melted to a much greater extent than that beneath the white cloth, because black absorbs heat more than white, which, on the contrary, has a tendency to reflect it. We perceive very plainly the[Pg 77] difference in temperature by touching the two cloths. The white cloth feels cold in comparison with the black cloth.
It is hardly necessary to point out experiments on the expansion of bodies. They can be performed in a number of different ways; by placing water in a narrow-necked bottle, and warming it over the fire, we can ascertain the expansion of liquids under the influence of heat. We may in this way construct a complete thermometer.
We may now consider the Sources of Heat, or causes of its development, which are various, and in many cases apparent. The first great source is the Sun, and it has been calculated that the heat received by the earth in one year is sufficient to melt an envelope of ice surrounding it one hundred and five feet thick. Of course the heat at the surface of the sun is enormously greater than this, about one-half being absorbed in the atmosphere before it reaches us at all. In fact, it is impossible to give you an idea of the enormous heat given out by the sun to the earth (which is a very small fraction indeed of the whole), stars, and planets, all of which give out heat. We know that heat is stored in the earth, and that it is in a very active condition we can perceive from the hot springs, lava, and flame which are continually erupting from the earth in various places. These sources of heat are beyond our control.
But apart from the extra- and intra-terrestrial sources of heat there are mechanical causes for its generation upon our globe, such as friction, percussion, or compression. The savage or the woodman can procure heat and fire by rubbing a pointed stick in a grooved log. The wooden “breaks” of a locomotive are often set on fire by friction of the wheels, so they require grease, and the wheels on the rails will develop heat and sparks. Our matches, and many other common instances of the generation of heat (and fire) by friction, will occur to every reader. Water may be heated by shaking it in a bottle, taking care to wrap something round it to keep the warmth of the hand from the glass. By percussion, such as hammering a nail or piece of iron, the solid bar may be made “red-hot”; and when cannon are bored at Woolwich the shavings of steel are too hot to hold even if soap-and-water has been playing upon the boring-machine.
The production of heat by chemical action is termed combustion, and this is the means by which all artificial heat for our daily wants is supplied. We can also produce heat by electricity. A familiar and not always pleasant instance of this is seen in the flash of lightning which will fuse metals, and experiment may do the same upon a smaller scale. These are, in brief, the Sources of Heat, and we may speak of its effects.
We may take it for granted that no matter from what source heat is derived, it exhibits the same phenomena in its relation to objects. One of the most usual of these phenomena is expansion. Let us take water, and see the effect of heat upon it.
We know that a certain weight of water under the same conditions[Pg 78] has always the same volume; and although the attributes of the liquid vary under different circumstances, under the same conditions its properties are exactly the same. Now, water expands very much when under the influence of heat, like all liquids; solids and gases also expand upon the application of heat.
We can easily establish these statements. A metallic ring when heated is larger than when cool. A small quantity of air in a bladder when heated will fill the bladder, and water will boil over the vessel, or expand into steam, and perhaps burst the boiler. So expansion is the tendency of what we term heat.
We make use of this quality of heat in the thermometer, by which we can measure the temperature not only of liquids or solids, but of the atmosphere. The reading of the thermometer varies in different countries, for the degrees are differently marked, but the construction of the instrument is the same. It is called thermometer from two Greek words signifying the measure of heat. It is a notable fact that Castelli, writing in 1638, says to Ferdinand Cæsarina: “I remembered an experiment which Signor Galileo had shown me more than thirty-five years ago. He took a glass bottle about the size of a hen’s egg, the neck of which was two palms long, and as narrow as a straw. Having well heated the bulb in his hands, he placed its mouth in a vessel containing water, and withdrawing the heat of his hand from the bulb, the water instantly rose in the neck more than a palm above the level of the water in the vessel.”
Here, then, we have an air-thermometer, but as it was affected by the pressure as well as the temperature of the atmosphere, it could not be relied upon as a “measurer of heat.” Until Torricelli propounded the principle of the barometer, this “weather-glass” of Galileo was used, for the philosopher divided the stem into divisions, and the air-thermometer served the purpose of our modern instruments.
The actual inventor of the thermometer is not known. It has been attributed to Galileo, to Drebbel, and to Robert Fludd. There is little doubt, however, that Galileo and Drebbel were both acquainted with it, but whether either claimed the honour of the invention, whether they discovered it independently, or together, we cannot say. Sanctorio, of Padua, and Drebbel have also been credited with the invention. We may add that the spirit thermometer was invented in 1655-1656. It was a rough form of our present thermometer, and roughly graduated. But it was hermetically closed to the air, and a great improvement on the old “weather-glass. Edmond Halley introduced mercury as the liquid for the instrument in 1680. Otto von Guerike first suggested the freezing point of water as the lowest limit, and Renaldini, in 1694, proposed that the boiling and freezing points of water should be the limit of the scale.
Let us now explain the construction and varied markings of the three kinds of thermometers in use. By noting the differences between the scales[Pg 79] every reader will be able to read the records from foreign countries noted upon the Centigrade and Réaumur instruments, which are all based upon the theory that heat expands liquids.

[We used to hear the expression, “Heat expands, and cold contracts,” but we trust that all our readers have now learnt that there is no such thing as cold. It is only a negative term. We feel things cold because they extract some warmth from our fingers, not because the substances have no heat.]
Thermometers are made of very fine bore glass tubes. One end has a bowl, or bulb, the other is at first open. By heating the bowl the air in the tube is driven away by the open end, which is quickly dipped in a bowl of mercury. The mercury will then occupy a certain space in the tube; and if it be heated till the liquid boils, all the air will be driven out by the mercurial vapour. By once again dipping the tube in the quicksilver the glass will be filled. Then, before it cools, close the open end of the tube, and the thermometer is so far made. Having now caught our thermometer we must proceed to mark it, which is an easy process. By plunging the mercury into pounded melting ice we can get the freezing point, and boiling water will give us the boiling point. The intermediate scale can be then indicated.
If mercury and glass expanded equally there would be no rise in the latter. Extreme delicacy of the thermometer can be arrived at by using a very fine tube, particularly if it be also flat.
The freezing point in Fahrenheit’s scale is 32°; in the Centigrade it is 0°, and the boiling point 100°. This was the scale adopted by Celsius, a Swede, and is much used. Réaumur called the freezing point 0°, and the boiling point 80°. There is another scale, almost obsolete,—that of Delisle, who called boiling point zero, and freezing point 150°.
There is no difficulty in converting degrees on one scale into degrees on the other. Fahrenheit made his zero at the greatest cold he could get; viz., snow and salt. The freezing point of water is 32° above his zero. Therefore 212-32 gives 180° the difference between the freezing and boiling points of water. So 180° Fahr. corresponds to 100° Cent., and to 80° Réaumur, reckoning from freezing point.
The following tables will explain the differences:—
| Table I. | |
|---|---|
| 1° Fahr. | = 0·55° Cent., or 0·44° Réaumur. |
| 1° Cent. | = ·80° Réaumur, or 1·80° Fahr. |
| 1° Réaumur | = 1·25° Cent., or 2·25° Fahr. |
| Table II. | |||
|---|---|---|---|
| Fahr. | Cent. | Réaumur. | |
| Boiling point | 212 | 100 | 80 |
| 194 | 90 | 72 | |
| 176 | 80 | 64 | |
| 158 | 70 | 56 | |
| 140 | 60 | 48 | |
| 122 | 50 | 40 | |
| 104 | 40 | 32 | |
| 86 | 30 | 24 | |
| 68 | 20 | 16 | |
| 50 | 10 | 8 | |
| Freezing point of water | 32 | 0 | 0 |
| 14 | -10 | -8 | |
| -4 | -20 | -16 | |
| Freezing point of Mercury | -40 | -40 | -32 |
Alcohol is used in thermometers in very cold districts, as it does not freeze even at a temperature of -132° Fahr.
We have now explained the way in which we can measure heat by the expansion of mercury in a tube. We can also find out that solids and gases expand also. Engineers always make allowances for the effects of winter and summer weather when building bridges; in summer the bridge gets longer, and unless due provision were made it would become strained and weakened. So there are compensating girders, and the structure remains safe.
The effects of expansion by heat are very great and very destructive at times. Instances of boilers bursting will occur to every reader. It is very important to be able to ascertain the extent to which solid bodies will expand. Such calculations have been made, and are in daily use.
We can crack a tumbler by pouring hot water into it, or by placing it on the “hob.” A few minutes’ consideration will assure us that the lower particles of the glass expanded before the rest, and cracked our tumbler. A gradual heating, particularly if the glass be thin, will ensure safety. Thick glass will crack sooner than thin.
Again, many people at railway stations have asked us, “Why don’t they join the rails together on this line?” We reply that if every length of rail were tightly fixed against its neighbour, the whole railway would be displaced. The iron expands and joins up close in hot weather. In wet weather, also, the wooden pegs and the sleepers swell with moisture, and get tightened up. Everyone knows how much more smoothly a train travels in warm, wet weather. This is due to the expansion of the iron and the swelling of the sleepers and pegs in the “chairs.” A railway 400 miles long expands 338[Pg 81] yards in summer,—that is the difference in length between the laid railroad in summer and in winter.
This can be proved. Iron expands 0·001235 of its length for every 180° Fahr. Divided by 180 it gives us the expansion for 1°, which is 0·00000686, taking the difference of winter and summer at 70° Fahr. Multiply these together, and the result (0·00048620 of its length) by the number of yards in 400 miles, and we find our answer 338 yards. Expansion acts in solids and most liquids by the destruction of cohesion between the particles. Gases, however, having much less cohesion amid the particles, will expand far more under a given heat than either solids or liquids, and liquids expand more than solids for the same reason, and more rapidly at a high temperature than at a low one.
We have spoken of expansion. We may give an instance in which the subsequent contraction of heated metal is useful. Walls sometimes get out of the perpendicular, and require pulling together. No force which can be conveniently applied would accomplish this so well as the cooling force due to the potential energy of iron. Rods are passed through the walls and braced up by nuts. The rods are then heated, and as they cool they contract and pull the walls with them.
When glass is suddenly cooled, the inner skin, as it were, presses with great force against the cooled surface, but as it is quite tight no explosion can follow. But break the tail, or scratch it with a diamond, and the strain is taken off. The glass drop crumbles with the effect of the explosion, as in the cases of Prince Rupert’s drops, and the Bologna flasks; the continuity is broken, and pulverization results.
But a very curious exception to the general laws of expansion is noticed in the case of nearly freezing water. We know water expands by heat, at first gradually, and then to an enormous extent in steam. But when cooling water, instead of getting more and more contracted, only contracts down to 39·2° Fahr., it then begins to expand, and at the moment it freezes into ice it expands very much—about one-twelfth of its volume, but according to Professor Huxley it weighs exactly the same, and the steam produced from that given quantity of water will weigh just exactly what the water and the ice produced by it weigh individually. At 39·2° Fahr. water is at its maximum density, or in other words, a vessel of a certain size will hold more water when it is at 39° Fahr. than at any other time. Whether the water be heated or cooled at this temperature, it expands to the boiling or freezing point when it becomes steam or ice, as the case may be.
Water, when heated, is lighter than cold water. You can prove this in filling a bath from two taps of hot and cold water at the same time. The cold falls to the bottom, and if you do not stir up the water when mixed you will have a hot surface and a cold foundation. The heat increases the volume of water, it becomes lighter, and comes uppermost.
Steam and Water and Ice are all the same things under different conditions, although to the eye they are so different. They are alike inasmuch[Pg 82] as a given weight of water will weigh as much when converted into ice or developed into steam. The half ounce of water will weigh half an ounce as ice or as steam, but the volume or bulk will vary greatly, as will be understood when we state that one cubic inch of water will produce 1,700 cubic inches of steam, and 1-1/11 cubic inch of ice; but at the same time each will yield, when decomposed, just the same amount of oxygen and hydrogen.
Let us now consider the Effects of Heat upon Water. We have all seen the vapour that hangs above a locomotive engine. We call it “steam.” It is not pure steam, for steam is really invisible. The visible vapour is steam on its way to become water again. On a very hot dry day we cannot distinguish the vapour at all.
The first effect of heat upon water is to expand it; and as the heat is applied we know that the water continues to expand and bubble up; and at last, when the temperature is as high as 212°, we say water “boils”—that is, at that heat it begins to pass away in vapour, and you will find that the temperature of the steam is the same as the boiling water. While undergoing this transformation, the water increases in volume to 1,700 times its original bulk, although it will weigh the same as the water. So steam has 1,700 less specific gravity than water.
It is perhaps scarcely necessary to remind our readers that water, when heated, assumes tremendous force. Air likewise expands with great violence, and the vessels containing either steam or air frequently burst, with destructive effects. Solid bodies also expand when heated, and the most useful and accurate observations have been made, so that the temperatures at which solid bodies expand are now exactly known. Air also expands by heat.
While speaking of Expansion by Heat, we may remark that a rapid movement is imparted to the air by Heat. In any ordinary room the air below is cool, while if we mount a ladder to hang up a picture, for instance, we shall find the air quite hot near the ceiling. This is quite in keeping with the effects of heat upon water. The hot particles rise to the top in a vessel, and thus a motion is conveyed to the water. So in our rooms. The heated air rushes up the chimney and causes a draught, and this produces motion, as we have seen by fig. 39, in which the cardboard spiral was set in motion by heated air. A balloon will ascend, because it is filled with heated air or gas; and we all have seen the paper balloons which will ascend if a sponge containing spirit of wine be set on fire underneath them.
Winds are also only currents of air produced by unequal temperature in different places. The heated air ascends, and the colder fluid rushes in sometimes with great velocity to fill the space. “Land” and “sea” breezes are constant; the cool air blows in from the sea during the day, and as the land cools more rapidly at night, the breeze passes out again. When we touch upon Meteorology, we will have more to say respecting Air Currents and the various Atmospheric Phenomena.
We know that water can be made to boil by heat, but it is not perhaps generally known that it will apparently boil by cold, and the experiment may[Pg 83] thus be made:—A flask half-full of water is maintained at ebullition for some minutes. It is removed from the source of heat, corked, inverted, and placed in one of the rings of a retort stand. If cold water is poured on the upturned bottom of the flask, the fluid will start into violent ebullition. The upper portion of the flask is filled with steam, which maintains a certain pressure on the water. By cooling the upper portion of the flask some of this is condensed, and the pressure reduced. The temperature at which water boils varies with the pressure. When it is reduced, water boils at a lower heat. By pouring the cold water over the flask we condense the steam so that the water is hot enough to boil at the reduced pressure. To assert that water boils by the application of cold is a chemical sophism.
Ebullition and Evaporation may be now considered, and these are the two principal modes by which liquids assume the gaseous condition. The difference is, when water boils we term it ebullition (from the Latin ebullio, I boil); evaporation means vapour given out by water not boiling (from evaporo, I disperse in vapour).
There are two operations based upon the properties which bodies possess of assuming the form of vapour under the influence of heat, which are called Distillation and Sublimation. These we will consider presently.
Ebullition then means a bubbling up or boiling; and when water is heated in an open vessel two forces oppose its conversion into vapour; viz., its own cohesive force and atmospheric pressure. At length, at 212° Fahr., the particles of water have gained by heat a force greater than the opposing forces; bubbles of vapour rise up from the bottom and go off in vapour. This is ebullition, and at that point the tension of the vapour is equal to the pressure of the atmosphere, for if not, the bubbles would not form. All this time of boiling, notwithstanding any increase of heat, the thermometer will not rise above 212° (Fahr.), for all the heat is employed in turning the water to steam.
We have said the ebullition takes place at 212° Fahr. (or 100° C.), but that is only at a certain level. If we ascend 600 feet high we shall find that water will boil at a less temperature; and on the top of a mountain (say Mont Blanc) water will boil at 185° Fahr.; so at an elevation of three miles water boils at a temperature less by 27° Fahr. An increase of pressure similarly will raise the boiling point of water. The heights of mountains are often ascertained by noticing the boiling point of water on their summits, the general rule being a fall of one degree for every 530 feet elevation at medium altitudes. We append a few instances taken at random:—
| Place. | Height above level of the sea—Feet. |
Barometer mean height. |
Boiling point of water, Fahr. |
|---|---|---|---|
| Quito | 9,541 | 20·75 | 194·2 |
| Mexico | 7,471 | 22·52 | 198·1 |
| St. Gothard | 6,808 | 23·07 | 199·2 |
| Garonne (Pyrenees) | 4,738 | 24·96 | 203·0 |
| Geneva | 1,221 | 28·54 | 209·5 |
| Paris (1st floor) | 213 | 29·69 | 211·5 |
| Sea level | 0 | 30·00 | 212·0 |
[The difference for a degree depends upon the height, varying between 510 and 590 feet, according to the elevation reached. The approximate height of a mountain can be found by multiplying 530 by the number of degrees between the boiling point and 212°. In some very elevated regions travellers have even failed to boil potatoes.]
The boiling point of liquid may be altered by mixing some substance with it; and although such a substance as sawdust would not alter the boiling point of water, yet if the foreign matter be dissolved in the liquid it will alter the boiling point. Even the air dissolved in liquids alters their boiling point, and water freed from air will not boil till it is raised to a temperature much higher than 212° Fahr. Water will boil at a higher temperature in a glass vessel than in metal, because there is a greater attraction between water and glass.
We said above that an increase of pressure will raise the boiling point of water. Under the pressure of one atmosphere—that is, when there is a pressure of 15 lbs. on the square inch—water boils at 212°. But under a pressure of two atmospheres, the boiling point rises to 234°, and of four atmospheres, 294°. So we see by increasing the pressure the water may be almost indefinitely heated, and it will not boil. We can understand that in a very deep vessel the layer of water at the bottom has to sustain the pressure of the water in addition to the weight of the atmosphere above it. The pressure of thirty-four feet of water is equal to the atmospheric pressure of 15 lbs. on the square inch, and thus at such a distance water must be heated to 234° before it will boil. Professor Bunsen founded his Theory of the Geysers upon this fact, for he maintained that water falling into the earth lost much air, and required with the super-incumbent pressure a very high temperature to boil it. When it did boil it generated steam so suddenly that it exploded upwards, throwing up vapour and the water with it, as water poured into a very hot basin will do.
Evaporation may now be considered, and is distinguished from Ebullition by the production of vapour on the surface of liquids, the latter term signifying the formation of vapour in the body of the liquid. Evaporation takes place at all temperatures, and from every liquid surface exposed to the air. We know what we call a “drying wind.” The air in fresh layers continually passing over the wet ground, takes up the moisture; like the east wind, for instance, which has great capabilities of that nature. Damp air can only take up a certain quantity, and when it contains as much water as corresponds to the temperature it can take no more, and is “saturated with moisture”; then evaporation ceases. Heat is a great cause of evaporation, and the greater the surface the more rapid the process, and in a vacuum more readily than in atmospheric air. Evaporation is resorted to very commonly to produce coolness; for instance, the universal fan, by increasing evaporation from a heated skin, generates a feeling of coolness; and we know the vaporization of ether will freeze into insensibility. When a fluid evaporates we can tell that the heat passes away at the same time, for we[Pg 85] cool water in porous jars, which permit some of it to pass off in vapour, the remainder being cooled.
Sir John Leslie invented a method of freezing water by rapid evaporation on sulphuric acid under the receiver of an air-pump, and water has been frozen even on a hot plate by these means. By pouring sulphurous acid and water on this plate, the acid evaporates so quickly that it produces sufficient cold to freeze the water it quitted into solid ice.
We leave the phenomena of clouds and watery vapour in the atmosphere for consideration on another opportunity, under the head of Meteorology, Rain, etc.

An experiment is often performed by which water is frozen in a vacuum. By putting a saucer full of water under the receiver of an air-pump it will first boil, and then become a solid mass of ice. It is not difficult to understand the cause of this. The water boils as soon as the air is removed; but in order to pass from the liquid to the gaseous state without the assistance of exterior heat, it gives out heat to the surroundings, and in so doing becomes ice itself. This fact Mr. Carré has made use of in the apparatus shown above (fig. 80). A small pump creates a vacuum in the water bottles, and ice is formed in them.
This apparatus might easily be adopted in country houses, and in places where ice is difficult to procure in summer. The only inconvenience attending it is the employment of sulphuric acid, of which a considerable quantity is[Pg 86] used to absorb the vapour from the water, as already referred to. If proper precautions are taken, however, there will be no danger in using the apparatus.
The mode of proceeding is as follows:—The bottle full of water is joined to the air-pump by a tube, and after a few strokes the water is seen in ebullition. The vapour thus disengaged traverses an intermediate reservoir filled with sulphuric acid, which absorbs it, and immediately condenses it, producing intense cold. In the centre of the liquid remaining in the carafe some needles of ice will be seen, which grow rapidly, and after a few more strokes of the pump the water will be found transformed into a mass of ice. This is very easy of accomplishment, and in less than a minute the carafe full of water will be found frozen.
The problem for the truly economical formation of ice by artificial means is one of those which have occupied chemists for a long time, but hitherto, notwithstanding all their efforts, no satisfactory conclusion has been arrived at. Nearly every arrangement possesses some drawback to its complete success, which greatly increases the cost of the ice, and causes inconvenience in its production. The usual mode in large towns is to collect the ice, in houses constructed for the purpose, during the winter, and this simple method is also the best, so far as at present has been ascertained.

In connection with vaporization we may now mention two processes referred to just now (page 83); viz., sublimation and distillation. The former is the means whereby we change solid bodies into vapour and condense the vapour into proper vessels. The condensed substances when deposited are called sublimates, and when we go into Chemistry we shall hear more of them. The mode of proceeding is to place the substance in a glass tube, and apply heat to it. Vapour will be formed, and will condense at the cool end of the tube. The sublimate of sulphur is called “Flowers of Sulphur,” and that of perchloride of mercury “Corrosive Sublimate.”
Distillation is a more useful process, or, at any rate, one more frequently employed, and is used to separate a volatile body from substances not volatile. A distilling apparatus (distillo, to drop) converts a liquid to vapour by means of heat, and then condenses it by cold in a separate vessel.
The distilling apparatus consists of three parts,—the vessel in which the liquid is heated (the still, or retort), the condenser, and the receiver. The simple retort and receiver are shown in fig. 81. But when very volatile vapours are dealt with, the arrangement shown on next page is used (fig. 82).[Pg 87] Then the vapour passes into the tube encased in a larger one, the intervening space being filled with cold water from the tap above (c), the warm water dropping from g. The vapours are thus condensed, and drop into the bottle (or receiver) B.

The apparatus for distilling spirits is shown below. The “still” A is fitted into a furnace, and communicates with a worm O in a metal cylinder filled with water, kept constantly renewed through the tube TT′. This spirit passes through the spiral, and being condensed, goes out into the receiver C.

There are even more simple apparatus for spirit distilling, but the diagram above will show the principle of all “stills.” In former days, in Ireland, whiskey was generally procured illegally by these means.
CHAPTER VIII.
SPECIFIC HEAT—FUSION—LATENT HEAT—CONDUCTION AND CONVECTION OF HEAT—CALORESCENCE.
We have considered the effects of heat upon water, and touched upon one or two kindred experiments. But we have some other subjects to discuss, two in particular; viz., Specific Heat, and Latent Heat.
The specific heat of any substance is “the number of units of heat required to raise one pound of such substance one degree.” We can explain this farther. When heat is communicated to a body it has two or three functions to perform. Some of it has to overcome the resistance of the air in expanding the body, more of it expands, and the remainder increases the temperature of the body. So some heat disappears as heat, and is turned into energy,—“molecular potential energy,”—as it is called, and the rest remains. Of course in objects the molecules vary very much in weight and in their mutual attraction, and the heat requisite to raise equal weights of different substances through the same number of degrees of temperature will vary. This is called capacity for heat, or specific heat. The capacity of different metals for heat can easily be shown. The specific heat of water is very high, because its capacity for heat is great. We can cool a hot iron in very little water, and it takes thirty times as much heat to raise a given weight of water a certain number of degrees, as it would to raise the same weight of mercury to the same temperature. Water has greater specific heat, generally speaking, than other bodies, and it is owing to this circumstance that the climate is so affected by ocean currents.
Nearly all substances can be melted by heat, if we go far enough, or frozen, if we could take the heat away. Solid can be made liquid, and these liquids can be made gases and fly off in vapour. Similarly, if we could only get heat away sufficiently from the atoms of a substance we could freeze it. We cannot freeze alcohol, nor make ice from air, nor can we liquify it, for we are unable to take away its heat sufficiently. But we can turn water into steam, and into ice; or ice into water, and then into steam. But there is one body we cannot melt by heat, that is carbon. In the hottest fire coal will not melt, it becomes soft. We call this melting fusion, and every body has its melting point, or fusing point, which is the same at all times if the air pressure be the same.
It is a curious fact that when a body is melting it rises to a certain temperature (its fusing point), and then gets no hotter, no matter whether or[Pg 89] not the fire be increased;—all the extra heat goes to melt the remainder of the substance. The heat only produces changes of state. So this heat above fusing point disappears apparently, and is called Latent Heat. This can easily be proved by melting ice. Ice melts at 32° Fahr., or 0° Cent., and at that temperature it will remain so long as any ice is left; but the water at 32°, into which the ice has melted, contains a great deal of latent heat, for it has melted the ice quickly, and yet the thermometer does not show it. It is just the same with boiling water.
When substances are fused they expand as a rule, but ice contracts; so does antimony. On the other hand, when water solidifies it does not contract as most things do. It expands, as many of us are aware, by finding our water pipes burst in the winter; and the geologist will tell us how the tiny trickling rills of water fall in between the cracks of rocks and there freeze. In freezing the drops expand and split the granite blocks. Type-metal expands also when it becomes solid, and leaves us a clear type; but copper contracts, and won’t do for moulding, so we have to stamp it when we want an impression on it.
There is no doubt that chemical combinations produce heat, as we can see every day in house-building operations, when water is poured upon lime; but there are also chemical combinations which produce cold. Fahrenheit produced his greatest cold by combining snow and salt, for in the act of combining, a great quantity of heat is swallowed up by reason of the heat becoming latent, as it will do when solid bodies become liquid. Such mixtures or combinations are used as Freezing Mixtures when it is necessary to produce intense cold artificially. Sulphate of Sodium and Hydrochloric acid will also produce great cold, and there are many other combinations equally or even more efficacious.
Heat is communicated to surrounding objects in three well-known ways—by conduction, by radiation, and by convection. Conduction of heat is easily understood, and is the propagation of heat through any body, and it varies very much according to the substance through which it passes. Some substances are better conductors of heat than others. Silver has a far greater conductivity than gold, and copper is a better heat-conductor than tin. Flannel is a non-conductor, or rather a bad conductor, for no substance can be termed actually a non-conductor. Flannel, we know, will keep ice from melting, and a sheep’s wool or a bird’s feathers are also bad conductors of heat; so Nature has provided these coverings to keep in the animal heat of the body. A good conductor of heat feels cold to the touch of our fingers, because it takes the heat from our hands. This can be tried by touching silver, lead, marble, wood, and wool. Each in turn will feel cold and less cold, because they respectively draw away, or conduct less and less heat from our bodies. So our clothes are made of bad-conducting substances. The bark of a tree is a bad conductor, and if you strip off this clothing the tree will die.
Solids conduct heat the better the more compact they are. Air being[Pg 90] a bad conductor it follows that the less tightly the molecules are packed the less conductibility there will be; and even a substance powdered will be a worse conductor than the same substance in solid form; and also more readily in the direction of the fibres than crossways.
Liquids do not possess great conductivity, but they, as well as gases, are influenced by convection, or the transport of heat from the bottom layers to the top (conveho, to carry up). We have already mentioned that the heated particles of water rise to the top because they expand, and so become lighter. This is convection of heat; and by it liquids and gases, though actually bad conductors, may become heated throughout to a uniform temperature. Of course the more easily expansible the body is the more rapidly will convection take place—so gases are more readily affected than liquids. Solids are not affected, because convection of heat depends upon molecular movement or mobility, and it is obvious that the particles of solid bodies are not mobile. Professor Balfour Stewart says with reference to this that “were there no gravity there would be no convection,” for the displacement of the light warm particles by the heavier cold ones is due to gravity. The instances of convection of heat in nature are numerous, and on a gigantic scale. The ocean currents, trade winds, lake freezing, etc., while the chimney draught already referred to, is another example; and in all these cases the particles of air or water are replaced by convection. In the case of the lake freezing the cold particles at the top sink, and the warmer ones ascend, until all the lake is at a temperature of 36·2°, or say 4° above freezing. At this temperature water assumes its maximum density, and then expands, as we have seen, instead of contracting. Ice is formed, and being thus lighter than water, floats; and so unites to cover in the water underneath, which is never frozen solid, because the cold of the atmosphere cannot reach it through the ice in time to solidify the whole mass.

Radiant heat is the motion of heat transmitted to the ether, and through it in the form of waves. The sun’s heat is radiant heat, and radiation may be defined as “The communication of the motion of heat from the articles of a heated substance to the ether.” The fire gives out radiant heat, and so does heated metal, and it is transmitted by an unseen medium. It is quite certain that the heat of a suspended red-hot poker is not communicated to the air, because it will cool equally in a vacuum. Sir Humphrey Davy proved that radiant heat could traverse a vacuum, for by putting tin reflectors in an exhausted receiver he found that a hot substance in the focus of one reflector caused an increase in the heat of the other. If we put a red-hot or a hot substance in one reflector, and tinder in the other, the latter will take fire. The velocity of heat rays is equal to that of light, 186,000 miles in a[Pg 91] second, and indeed, radiant heat is identical with light. Heat is reflected as is light, and is refracted in the same way as sound.
Some bodies allow the heat rays to pass through them, as air does, and as rock salt will do. White clothing is preferable in summer (and also in winter if we could only make people believe it). White garments radiate less heat in winter, and absorb less heat in summer. An old black kettle will boil water more quickly than a new bright one, but the latter will keep the water hotter for the longer time when not on the fire.
Heat, then, is movement of particles. Energy can be changed into heat, as the savage finds when he rubs the bits of wood to produce heat and fire. Friction causes heat, and chemical combination produces heat; and, if “visible energy can be turned into heat, heat can be turned back into visible energy.” For fire heats water, water expands into steam, and steam produces motion and energy in the steam-engine.
If we heat water in Wollaston’s bulb,—the opening of which is hermetically stopped by a piston,—the vapour will raise the piston. If we cool the bulb we condense the steam, and the piston falls. Here we have the principle of the steam-engine.
Steam is the vapour of water educed by heat, and we may give a few particulars concerning it. Its mechanical properties are the same as those of other gases, and pure steam is colourless and transparent—in fact, invisible. Its power when confined in boilers and subjected to pressure is enormous, for the volume of the steam is far greater than the water which gave rise to it. One cubic inch of water will produce 1,700 cubic inches of steam—in other words, a cubic inch of water produces a cubic foot of steam. When we obtain steam at 212°, we do so under the pressure of one atmosphere; but by increasing the pressure we can raise the boiling point, and thus water at the pressures of sixteen atmospheres will not steam till it reaches 398°. It is thus we obtain pressure for locomotives, and other engines, although a very small portion of the steam does work. Much the largest portion is expended in overcoming cohesion, and one way and another, taking into consideration defects in machinery, only about one-tenth of the heat is employed in doing the work. The force exercised by steam under atmospheric pressure is sufficient to raise a ton weight one foot.
To obtain very high temperatures we shall find the thermometer of no use, for mercury boils at 662°, so an instrument called a Pyrometer is used to ascertain the fusing point of metals. Mr. Wedgwood, the celebrated china manufacturer, invented an instrument made of small cylinders of clay moulded and backed, placed between two brass rods as gauges divided into inches and tenths. But this instrument has been long superseded by Professor Daniell’s Pyrometer, which consists of a small bar of platina in an earthenware tube. The difference of expansion between the platina and the tube is measured on a scale on which one degree is equal to seven degrees of Fahrenheit. Thus the melting temperatures of metals are ascertained.
The reflection and refraction of heat are ruled by the same laws as the reflection and refraction of light. A convex lens will bring the heat or light to a focus, and will act as a burning-glass if held in the sunlight. Gunpowder has been ignited by a lens of ice, and more than one house has been mysteriously set on fire at midday in summer by the sun’s rays shining through a glass globe of water containing gold fish, and falling upon some inflammable substance. Professor Tyndall performed a series of experiments of a very interesting nature, described in his book, “Heat considered as a Mode or Motion,” and showed the transmutation of invisible heat rays into visible rays, by passing a beam of electric light through an opaque solution, and concentrating it upon a lens. The dark heat rays were thus brought to a focus, all the light was cut off, and at the dark focus the heat was found to be intense enough to melt copper and explode gunpowder. This change of invisible heat into light is termed Calorescence.
It was Sir William Herschell who discovered that there were heat rays beyond the red end of the spectrum. When light is split up into its component rays, or decomposed, Sir William found that the heat increased as the thermometer passed from violet to indigo, and so on to blue, green, orange, and red, and the last were the hottest, while beyond the spectrum there was heat even greater. A Heat Spectrum was thus discovered, and by comparing, by means of the thermometer, the various degrees of heat within certain limits, Professor Tyndall found that the invisible Heat Spectrum is longer than the visible Light Spectrum.

CHAPTER IX.
LIGHT AND ITS SOURCES—WHAT IS LIGHT?—VELOCITY OF LIGHT—REFLECTION AND REFRACTION—RELATIVE VALUE OF LIGHTS.
The subject of Light and the science of Optics are so interesting to all of us that some short history of light is necessary before we can enter upon the scientific portion of the subject. The nature of the agent (as we may term light) upon which our sight depends has employed man’s mind from a very early period. The ancients were of opinion that the light proceeded from the eye to the object looked at. But they discovered some of the properties of light. Ptolemy of Alexandria, who was born A.D. 70, made some attempts to discover the law of Refraction; and we are informed that Archimedes set the Roman fleet on fire with burning-glasses at Syracuse. The Arabian treatise of Alhagen, in 1100 A.D., contains a description of the eye and its several parts; and the writer notices refraction and the effects of magnifying glasses (or spectacles). Galen, the physician, practically discovered the principle of the stereoscope, for he laid down the law that our view of a solid body is made up of two pictures seen by each eye separately.
Still the science of optics made little progress till the law determining the path of a ray of light was made known, and the laws of refraction discovered. Refraction means that a ray is deflected from its straight course by its passage from one transparent medium to another of different density. The old philosophers found out the theory of sound, and they applied themselves to light. Newton said light consisted of minute particles emanating from luminous bodies. Huyghens and Euler opposed Newton’s theory of the emission of light; and it was not till the celebrated Thomas Young, Professor at the Royal Institution, grappled with the question that the undulating or wave theory of light was found out. He based his investigations upon the theory of sound waves; and we know that heat, light, and sound are most wonderfully allied in their manner of motion by vibration. But he was ridiculed, and his work temporarily suppressed by Mr. Brougham.
Light, then, is a vibratory motion (like sound and heat), a motion of the atoms of our ether. But how is the motion transmitted? Sound has its medium, air; and in a vacuum sounds will be very indistinctly heard, if heard at all. But what is the medium of communication of light? It is decided that light is transmitted through a medium called ether, a very elastic substance surrounding us. The vibrations, Professor Tyndall and[Pg 94] other philosophers tell us, of the luminous atoms are communicated to this ether, or propagated through it in waves; these waves enter the pupil of the eye, and strike upon the retina. The motion is thus communicated by the optic nerve to the brain, and then arises the great primary faculty, Consciousness. We see light, the waves of which, or ether vibrations, are transversal; air waves or sound vibrations are longitudinal.
We have spoken of radiant heat. Light acts in the same way through the ether; and when we consider Sound we shall learn that a certain number of vibrations of a string give a certain sound, and the quicker the vibration the shriller the tone. So in light. The more quickly the waves of luminosity travel to our eye, and the faster they strike it, the greater the difference in the colour, or what we call colour. Light as we see it is composed of different colours, as visible in the rainbow. There are seven primary colours in the sunlight, which is white. These can be divided or “dispersed,” and the shortest rays of the spectrum are found to be violet, the longest red. It has been calculated that 39,000 red waves make an inch in length. Light travels at a rate of nearly 190,000 miles a second, so if we multiply the number of inches in that distance by the number of red waves, we shall have millions of millions of waves entering the eye in a single second of time. The other waves enter more rapidly still, and “the number of shocks corresponding to the impression of violet is seven hundred and eighty-nine millions of millions” per second! Or taking the velocity of light at 186,000 miles in a second, it would be six hundred and seventy-eight millions of millions (Tyndall). There may be other colours which we cannot see because the impressions come too rapidly upon the retina; but the violet impression has been thus accurately determined. See page 168.
We have seen that heat is a kind of motion of particles in a body—a vibratory motion which, instead of being apparent to the ear, is apparent to the eye in rays of light. Thus heat, sound, and light are all intimately connected in this way. We have also learnt that rays of light radiate and travel with tremendous speed to our eyes, but without any shock. There is no feeling connected with the entrance of light to the eye any more than there is any sensation of sound when entering the ear, except when the light is vividly and very suddenly revealed, or when a very piercing sound is heard. Then the nerves are excited, and a painful sensation is the result; but under ordinary circumstances we are not physically conscious of the entrance of light or sound.
Heat and light are considered to be one and the same thing in different degrees of intensity. The sources of light are various. The sun and fixed stars, heat, electricity, many animals, and some plants, as well as decaying animal matter, give out light. There are luminous and non-luminous bodies. The moon is non-luminous, as she derives her light from the sun, as does the earth, etc.
Light is distributed in rays. These rays are straight in all directions. The velocity of light is almost inconceivable. It travels at a rate of 186,500[Pg 95] miles a second. The latest computation with electric light has given a rate of 187,200 miles a second; but the blue rays in the light experimented on probably account for the difference, for blue rays travel quicker by one per cent. than red rays. Römer first found out the velocity of light, which comes to us from the sun—ninety millions of miles—in eight minutes. Fizeau calculated the velocity by means of a wheel, which was set moving with tremendous speed by making the light pass between the teeth of the wheel and back again.
When rays of light meet substances they are deflected, and the phenomena under these circumstances are somewhat similar to the phenomena of heat and sound. There are three particular conditions of rays of light: (1) they are absorbed; (2) they are reflected; (3) they are refracted.
Firstly. Let us see what we mean by light being absorbed; and this is not difficult to understand, for any “black” substance shows us at once that all the sunlight is taken in by the black object, and does not come out again. It does not take in the light and radiate it, as it might heat. The rose is red, because the rays of light pass through it, and certain of them are reflected from within. So colour may be stated to be the rays thrown out by the objects themselves—those they reject or reflect being the “colour” of the object.

Secondly. Bodies which reflect light very perfectly are known as mirrors, and they are termed plane, concave, or convex mirrors, according to form. A plane mirror reflects so that the reflected ray d i forms the same angle with the perpendicular as the incident ray r i; in other words, the angle of incidence is always equal to the angle of reflection, and these rays are perpendicular to the plane from which they are reflected. The rays diverge, so that they appear to come from a point as far behind the mirror as the luminous point is in front, and the images reflected have the same appearance, but reversed. There is another law, which is that “the angular velocity of a beam reflected from a mirror is twice that of the mirror.” The Kaleidoscope, with which we are all familiar, is based upon the fact of the multiplication of images by two mirrors inclining towards each other.

A concave mirror is seen in the accompanying diagram, and may be called the segment of a hollow sphere—V W. The point C is the geometrical centre, and O C the radius; F is the focus; the line passing through it is the optical axis; O being the optical centre. All perpendicular rays pass through C. All rays falling in a direction parallel with the optical axis are reflected and collected at F. Magnified images will be produced, and if the object be placed between the mirror and the focus, the image will appear at the back; while if the object be placed between the geo[Pg 96]metrical centre and the focus, the image will appear to be in front of the mirror.
We can understand these phenomena by the accompanying diagrams. Suppose a ray A n passes from one object, A B, at right angles, it will be reflected as n A C, the ray A C being reflected to F. These cannot meet in front of the mirror, but they will if produced meet at a, and the point A will be reflected there; similarly B will be reflected at b, and thus a magnified image will appear behind or at the back of the mirror’s surface. In the next diagram the second supposed case will produce the image in the air at a b, and if a sheet of paper be held so that the rays are intercepted, the image will be visible on the sheet. In this case the perpendicular ray, A n, is reflected in the same direction, and the ray, a c, parallel with the axis is reflected to the focus. These rays meet at a and corresponding rays at b, when the image will be reproduced; viz., in front of the mirror.


The concave mirror is used in the manufacture of telescopes, which, with other optical instruments, will be described in their proper places. We will now look at the Refraction of light.
Bodies which permit rays of light to pass through them are termed transparent. Some possess this property more than others, and so long as the light passes through the same medium the direction will remain the same. But if a ray fall upon a body of a different degree of density it cannot proceed in the same direction, and it will be broken or refracted, the angle it makes being termed the angle of refraction.

For instance, a straight stick when plunged into water appears to be broken at the point of immersion. This appearance is caused by the rays of light taking a different direction to our eyes. If in the diagram (fig. 89) our eye were at o, and the vessel were empty, we should not see m; but when water is poured into the vessel the object will appear higher up at n, and all objects under water appear higher than they really are.

One may also place a piece of money at the bottom of a basin, and then stoop down gradually, until, the edge of the basin intervening, the coin is lost to view. If an operator then fills the basin with water, the piece of money appears as though the bottom had been raised. The glass lenses used by professors may be very well replaced by a round water-bottle full of water. A candle is lighted in the darkness, and on holding the bottle between the light and a wall which acts as a screen, we see the reflected light turned upside down by means of the convergent lens we have improvised (fig. 90). A balloon of glass constitutes an excellent microscope. It must be filled with perfectly clear, limpid water, and closed by means of a cork. A piece of wire is then rolled round its neck, and one end is raised, and turned up towards the focus; viz., to support the object we wish to examine, which is magnified several diameters. If a fly, for instance, is at the end of the wire, we find it is highly magnified when seen through the glass balloon (fig. 91). By examining the insect through the water in the balloon, we can distinguish every feature of its organism, thanks to this improvised magnifier. This[Pg 98] little apparatus may also serve to increase the intensity of a luminous focus of feeble power, such as a lighted candle. It is often employed in this manner by watchmakers. If a bottle full of water is placed on a table, and exposed to the rays of the sun, the head of a lucifer match being placed in the brightest centre of light caused by the refracted rays, the match will not fail to ignite. I have succeeded in this experiment even under an October sun, and still more readily in warm weather.

In the Conservatoire des Arts in Paris a visitor will always notice a number of people looking at the mirrors in the “optical” cabinets. These mirrors deform and distort objects in a very curious manner, and people find much amusement in gazing into them till they are “moved on” by the attendants. Such experiments create great interest, and a very excellent substitute for these may be found in a coffee-pot or even in a large spoon, and all the grotesque appearance will be seen in the polished surface. The least costly apparatus will sometimes produce the most marvellous effects. Look at a soap-bubble blown from the end of a straw. When the sphere has a very small diameter the pellicule is colourless and transparent; but as the air enters by degrees, pressing upon all parts of the concave surface equally, the bubble gets bigger as the thickness decreases, and then the colours appear,—feeble at first, but stronger and stronger as the thickness[Pg 99] diminishes. The study of soap-bubbles and of the effects of the light is very interesting. Newton made the soap-bubble the object of his studies and meditations, and it will ever hold its place amongst the curious phenomena of the Science of Optics. But before going into all the phases of Lights and Optics we will proceed to explain the structure of the eye, as it is through that organ that we are enabled to appreciate light and its marvellous effects.

It is often considered an embarrassing matter to fix precisely the value of two lights. Nothing, however, can be easier in reality, as we will show. In comparing different lights, it is necessary to bear in mind the amount of waste, the colour of the light, the luminous value of the source, and the steadiness of the flame. The luminous value of a lamp-burner is generally equalled by that of a wax candle, and we will take as an example one of those at six to the pound. Very precise appliances are used for this experiment when great exactness is required; but it is easy to calculate in a simple manner the differences in ordinary lights. Supposing we desire to test the value of light given by a lamp and a wax candle, they must both be placed on the table at an equal height, B and A, (fig. 93), in front of some opaque body, A, and then a large sheet of paper must be fixed as vertically as possible to form a screen. When B and A are lighted, two shadows, E and F, are produced, to which it is easy to give exactly the same[Pg 100] intensity, by advancing or withdrawing one of the two sources of light. The intensities of the two lights will then be inversely proportional to the squares of the measured distances, AB and AC. By a similar careful calculation it has been possible to draw up a table of the relative values of various ordinary lights. We have not included here the electric light, which has recently attracted so much attention, because this system of lighting can hardly be said to have yet penetrated the domain of domestic life; but when we consider electricity, as we hope to do in a future part, we[Pg 101] intend to study this question fully, for there is no doubt that electricity is becoming more and more adapted to our daily life.

The measurement of intensity of light is called Photometry, and the instruments used are Photometers. Bunsen’s instrument consists of a screen of writing-paper, saturated in places with spermaceti to make it transparent. A sperm candle is placed on one side, and the light to be compared on the other. The lights are provided with graduated bars, and these lights are then removed farther and farther from the screen till the spots of grease are invisible. The relative intensities are as the squares of the distance from the screen.

We append a table showing the comparative cost of light given by Dr. Frankland at the Royal Institution some few years ago. The standard of comparison was 20 sperm candles burning for 10 hours at the rate of 120 grains an hour:—
| s. | d. | |
| Wax | 7 | 2½ |
| Sperm Oil | 1 | 10 |
| Paraffin | 3 | 10 |
| Spermaceti | 6 | 8 |
| Coal Gas | 0 | 4½ |
| Paraffin Oil | 0 | 6 |
| Tallow | 2 | 8 |
| Cannel Gas | 0 | 3 |
| Rock Oil | 0 | 7⅔ |
There are many other interesting experiments connected with Light,—Spectrum Analysis, etc., etc.,—all of which we will defer for a time until we have examined the Eye and some effects produced upon it by Light, illustrated by numerous diagrams in the pages next following.
CHAPTER X.
VISION AND OPTICAL ILLUSIONS—THE EYE DESCRIBED—ACCOMMODATION OF THE EYE—CHROMATIC ABERRATION—SPINNING TOPS.
The eye is an optical instrument that may be compared with those constructed by physicists themselves; the media of which it is composed have surfaces like those which enter into the construction of optical instruments. It was Kepler who at the end of the eighteenth century discovered the passage of light into the eye. Soon after the discovery of the inner chamber he found that the eye realized the conditions that Porta had combined to obtain the reflection of external objects.

We will now briefly state that the coats of this organ are constituted of a fibrous membrane, T (fig. 95), termed sclerotic, which is opaque, except in the anterior portion of the eye, where it forms the transparent cornea. The crystalline, C, enshrined behind the cornea, is the convergent lens of the inner chamber; it is covered with a transparent membrane, or capsule, and is bathed in two fluids, the aqueous humour, between the crystalline humour and the cornea, and the vitreous body, a gelatinous humour lodged between the crystalline and the back of the eye. The image of exterior objects which is produced by the passage of light through these refracting surfaces, is received by a nervous membrane, the retina, B, formed by an expansion of the optic nerve, N. We must also mention the choroid, a membrane lined with a dark pigment, which absorbs the light, and prevents interior reflections, and in front of the crystalline lens, a curtain with an opening, H, called the iris, which gives to the eyes their colour of blue, grey, or black. The opening in the centre of the iris is called the pupil.
The penetration of light through the surfaces of the eye is easily demonstrated. An object throws divergent rays on the cornea, a part penetrates into the eye and falls upon the retina, leaving a perfectly retained image of the object. Magendie has proved in the following manner the truth of this mathematical deduction. The eye of a rabbit is very similar to an[Pg 103] albino’s; that is to say, the choroid contains no black pigment, but a transparent matter, and when placed before a brilliant object, the image can be seen inverted on the retina. The experiment succeeds also with the eye of a sheep or a cow, if the sclerotic has been lessened. The optic centre of the eye is the point where the secondary axes cross; the optic axis passes through the geometrical axis of the organ, and directs itself spontaneously towards the point that attracts the eye.

We will now point out in what distinct vision consists. A screen placed behind a lens will only receive the image of a lighted object, A B, if placed in a position, R R (fig. 96). If placed nearer at R″ R″, or further off at R´ R´, the light from the object is thrown on the screen, and the image is confused. To prove the imperfection of sight which is shown by the application of these theoretic rules, MM. Boutan and d’Alméïda10 cite the following experiment:—If the head of a pin is placed from one to two inches from the eye, nothing will be perceived but a confused haziness of vague outline. The distance of distinct vision is that at which an object of small dimensions may be placed to be plainly perceived. This distance, which averages fifteen inches, varies with different individuals. It can be determined for different sights by means of an apparatus constructed by Lepot. A white thread, a, is stretched horizontally on a dark board (fig. 97). We look at it by placing our eye at one end behind a little screen pierced with an aperture, O; it then appears much reduced in length, but either nearer or farther off it seems to enlarge and swell, having the appearance of a white surface, becoming larger and larger in proportion as we move away from the point at which it is seen most distinctly. In this manner we can easily obtain a measure of the distance of distinct vision. One of the most remarkable properties of the eye consists in the faculty which this organ possesses of seeing different distances. If we consider it as a dark chamber, there is but one distance at which an object will be perfectly visible; nevertheless a metal wire, for example, can be seen as well at a distance of seven, as ten, fifteen, or twenty inches by good sights.

This faculty of accommodation in the eye is thus demonstrated: we place two pins, one in front of the other, one eye only being open; we first look at the nearest pin, which appears confused if it is near the eye, but by an effort of will the image becomes clear. If, while preserving the clearness of the image, we then carry our attention to the second pin, we find that it, too, presents a confused appearance. If we make an effort to distinguish the[Pg 104] contour of the second pin, we at last succeed, and the first once more appears ill-defined. It is only since the experiments of M. Cramer and M. Helmholtz that the explanation of this phenomenon could have been given. M. Cramer has succeeded in determining on the living eye the curved ray of the cornea, and of the two surfaces of the crystalline lens. In so doing he followed Samson’s method, and observed the images thrown by a luminous object, whose rays strike the different refracting surfaces of the eye. A candle, L (fig. 98), is placed before the eye, O, and throws as in a convex mirror a straight image of the flame, A (fig. 99). The other portion of the light, which has penetrated the pupil, falls on the crystalline lens, and produces likewise a second straight image, B. Then the light refracted by the lens reaches the posterior surface; a portion is reflected on a concave mirror, and gives the inverted image, C, very small and brilliant. M. Cramer observed it through a microscope, and studied the variations in the size of images when the eye passed from the observation of adjacent to distant objects. He stated:—


1. That the image, A, formed on the surface of the cornea, remains the same size in both cases; the form of the cornea therefore remains unaltered.
2. That the image, B, formed on the upper surface of the lens, diminishes in proportion as the eye is nearer the object; the surface therefore becoming more and more convex, as the focal distance diminishes—a result indicated by the theory that it is possible in the vision of near objects to receive the image on the retina.
3. That the third image, C, produced on the posterior surface of the lens, remains nearly invariable.
We may confirm Cramer’s statements by an easy experiment. We place ourselves in front of the eye of someone who looks in turn at two objects placed on the same black line at unequal distances from him, and are able to distinguish by the dimension of the images of the candle, which object it is that he is regarding. M. Helmholtz has carried M. Cramer’s methods to perfection, and has been able to formulate a complete theory of all the phenomena of accommodation. The laws of optics show that the rays emitted by a luminous point may unite at another point by the action of the refracting surfaces of the eye. Nevertheless, a white light being composed of rays of diverse refrangibility, particular effects, known under the name of chromatic aberration, are produced through the decomposition of light, which we will proceed to study, under M. Helmholtz’s auspices11.[Pg 105] We make a narrow opening in a screen, and fix behind this opening a violet glass, penetrable only by red and violet rays. We then place a light, the red rays of which reach the eye of the observer after having passed through the glass and the opening in the screen. If the eye is adapted to the red rays, the violet rays will form a circle of diffusion, and a red point encircled with a violet aureola is seen. The eye may also be brought to a state of refraction, so that the point of convergence of the violet rays is in front, and that of the red rays behind the retina, the diameters of the red and violet circles of diffusion being equal. It is then only that the luminous point appears monochromatic. When the eye is in this state of refraction, the simple rays, whose refrangibility is maintained between the red and the violet rays, unite on the retina.
There is another kind of aberration of luminous rays of one colour emitted through a hole, which generally only approach approximately to a mathematical focus, in consequence of the properties of refracting surfaces; it is called aberration of sphericity. The phenomena are as follows:—

1. We take for our object a very small luminous point (the hole made by a pin in some black paper, through which the light passes), and having also placed before the eye a convex glass, if we are not near-sighted, we fix it a little beyond the point of accommodation, so that it produces on the retina a little circle of diffusion. We then see, instead of the luminous point, a figure representing from four to eight irregular rays, which generally differ with both eyes, and also with different people. We have given the result of M. Helmholtz’s observations in fig. 100; a corresponds to the right eye, and b to the left. The outer edges of the luminous parts of an image, produced in this way by a white light, are bordered with blue; the edges towards the centre are of a reddish yellow. The writer adds that the figure appears to him to have greater length than breadth. If the light is feeble, only the most brilliant parts of the figure can be seen, and several images of the luminous point are visible, of which one is generally more brilliant than the others. If, on the other hand, the light is very intense,—if, for example, the direct light of the sun passes through a small opening,—the rays mingle with each other, and are surrounded by aureola of rays, composed of numberless extremely fine lines, of all colours, possessing a much larger diameter, and which we distinguish by the name of the aureola of capillary rays.

The radiating form of stars, and the distant light of street-lamps belong to the preceding phenomena. If the eye is accommodated to a greater distance than that of the luminous point,—and for this purpose, if the luminous point itself is distant, we place before the eye a slightly convex lens,—we see another radiating image appear,[Pg 106] which M. Helmholtz represents thus (fig. 101): at c as it is presented to the right eye, and at d as seen by the left.
If the pupil is covered on one side, the side opposite to the image of diffusion disappears; that is to say, that part of the retinal image situated on the same side as the covered half of the pupil. This figure, then, is formed by rays which have not yet crossed the axis of the eye. If we place the luminous point at a distance to which the eye can accommodate itself, we see, through a moderate light, a small, round, luminous spot, without any irregularities. If the light, on the contrary, is intense, the image is radiated in every position of accommodation, and we merely find that on approaching nearer, the figure which was elongated, answering to a distant accommodation, gradually diminishes, grows rounder, and gives place to the vertically elongated figure, which belongs to the accommodation of a nearer point. When we examine a slender, luminous line, we behold images developed, which are easily foreseen, if for every point of the line we suppose radiating images of diffusion, which encroach on each other. The clearest portions of these images of diffusion mingle together and form distinct lines, which show multiplied images of the luminous line. Most persons will see two of these images; some, with the eyes in certain positions, will see five or six.

To show clearly by experiment the connection existing between double images and radiated images from points, it is sufficient to make in a dark sheet of paper a small rectilinear slit, and at a little distance from one end, on a line with the slit, a small round hole, as shown at a in fig. 102. Looking at it from a distance we shall see that the double images of the line have exactly the same distance between them that the most brilliant parts of the starred figure of diffusion have from the point, and that the latter are in a line with the first, as will be seen at b (fig. 102), where in the image of diffusion of the luminous point, we only see the clearest parts of star a of the figure.
On lighted surfaces, to which the eye is not exactly accommodated, multiplied images are often remarked through the passage from light to darkness being made by two or three successive steps.
A series of facts which have been collected under the title of irradiation, and which show that brightly-lighted surfaces appear larger than they are in reality, and that the dark surfaces which surround them appear diminished to a corresponding degree, explains this by the circumstance that the luminous sensation is not proportional to the intensity of the objective light. These phenomena affect very various appearances, according to the form of respective figures; they are generally seen with the greatest ease and intensity when the eye is not exactly accommodated to the object examined, either by the eye being too near or too far off, or by using a concave or convex lens, which prevents the object being seen clearly. Irradiation is not completely wanting, even when the accommodation is exact, and we notice it clearly in very luminous objects, above all when they are small; small[Pg 107] circles of diffusion increase relatively the dimensions of small objects much more than of large ones, with regard to which, the dimensions of the small circles of diffusion which the eye furnishes, when properly accommodated, become insensible.

1. Luminous surfaces appear larger. We can never judge exactly of the dimensions of a slit or small hole through which a bright light escapes; it always appears to us larger than it really is, even with the most exact accommodation. Similarly, the fixed stars appear in the form of small luminous surfaces, even when we make use of a glass which allows of perfect accommodation. If a gridiron with narrow bars—the spaces intervening being exactly equal to the thickness of the bars—is held over a light surface, the spaces will always appear wider than the bars. With an inexact accommodation, these phenomena are still more remarkable. Fig. 103 exhibits a white square on a black foundation, and a black square on a white foundation. Although the two squares have exactly the same dimensions, the white appears larger than the black, unless with an intense light and an inexact accommodation.

2. Two adjacent luminous surfaces mingle together. If we hold a fine metallic wire between the eye and the sun, or the light of a powerful lamp, we shall cease to see it; the lighted surfaces on all sides of the wire in the visual range pass one into the other, and become mingled. In objects composed of black and white squares, like those of a draught-board (fig. 104), the angles of the white squares join by irradiation, and separate the black squares.
3. Straight lines appear interrupted. If a ruler is held between the eye and the light of a bright lamp or the sun, we perceive a very distinct hollow on the edge of the ruler in the part corresponding to the light. When one point of the retina is affected by a light which undergoes periodical and regular variations, the duration of the period being sufficiently short, there results a continuous impression, like that which would be produced if the light given during each period were distributed in an equal manner through[Pg 108]out the whole duration of the period. To verify the truth of this law, we will make use of some discs, such as that represented in fig. 105. The innermost circle is half white and half black; the middle circle has two quarters, or half its periphery, white, and the outer circle has four eighths’ white, the rest being black. If such a disc is turned round, its entire surface will appear grey; only it is necessary to turn it with sufficient force to produce a continuous effect. The white may also be distributed in other ways, and provided only that on all the circles of the disc the proportion of the angles covered with white is the same, they will always exhibit the same grey colour. Instead of black and white we may make use of different colours, and obtain the same resultant colour from all the circles, when the proportion of the angles occupied by each of the colours in the different circles is the same.

If we paint on a disc a coloured star, which is detached from a foundation of another colour (fig. 106), during the rapid rotation of the disc the centre affects the colour of the star; the outer circle assumes that of the background, and the intermediate parts of the disc present the continuous series of the resultant colours. These results are in accordance with the theory of the mixture of colours.

Rotative discs, which are so much used in experiments in optical physiology, were employed for the first time by Müsschenbroeck; the most simple is the top. M. Helmholtz ordinarily uses a brass spinning-top, which fig. 107 represents at a third the natural size. It is set in motion by the hand, and its quickness may be increased or moderated at will; but it cannot be made to spin quicker than six rounds in a second; this motion will be kept up for three or four minutes. Thus, with a feeble movement of rotation, a uniform luminous impression can only be obtained by dividing the disc into four or six sections, on each of which we repeat the same arrangement of colours, light, and shade. If the number of repetitions of the design is less, we obtain, with a bright light, a more or less shot-coloured disc.

It is easy to place designs on the disc, even when in motion, or to make any desired modification, by superposing on the first disc another disc with sectors, of which we can vary the position by slightly touching it, or even blowing on it, thus producing during the rotation of the disc very[Pg 109] varied modifications. If, for instance, we place on a disc covered with blue and red sectors of equal size, a black disc, of which the sectors are alternately filled in or empty, the disc, as it turns round, will appear blue if the black sectors of the upper disc exactly cover the [red] sectors of the lower disc; and it appears red, if, on the contrary, the blue sectors are covered with the black; while in the intermediate positions we obtain different mixtures of red and white, and during the rotation of the disc may vary the colour insensibly by a gentle touch. By dividing the different sectors with broken or curved lines, instead of straight ones, we can produce an arrangement of coloured rings of great variety and beauty. To give the top greater speed, we set it in motion by drawing a string twined round its stem. The simplest method, as shown in fig. 108, consists in the employment of a handle similar to that of the German top. It is a hollow cylinder of wood set into a handle with two circular holes; and at right angles with these is a groove for the passage of the string. The stem of the top is passed through the holes of the cylinder, one end of the string is fixed in the small hole in the stem, and is rolled round by turning the top in the hand. The part of the stem on which the string is twisted becomes sufficiently thick for the top to remain suspended to the handle; then holding it a little above the table, and giving the string a powerful pull, we set the top in motion, and as the string unrolls it falls on the table, where it will continue its rotation for some time. The top represented in fig. 109 is constructed so that the discs may be firmly pressed by the stem, which is necessary in experiments for demonstrating Newton’s theory of the mingling of colours. We make use for this purpose of a variety of discs, made of strong paper of different sizes, having an opening in the centre and a slit, as in fig. 110; each of the discs is covered uniformly with a single colour; and if two or more are superposed, with their slits placed one over the other, we obtain sectors, the size of which we may vary at will, so that we can modify in a continuous manner the proportions of the colours. The most perfect construction is that of Busold’s chromatic top (fig. 111), which should only be employed for very rapid rotations. The disc, which weighs 5 lbs., is made of an alloy of zinc and lead, about an inch and a quarter in diameter. The brass axis[Pg 110] terminates at its lower end with a blunt point of untempered steel; the cylindrical part of the axis is roughened to encourage the adherence of the string; the axis is placed between the clamps of a vice, and a plate is put underneath; we then pull the string firmly with the right hand, and when the top is in motion it is separated from the clamps. By pulling the string very powerfully it is possible to obtain a speed of sixty turns in a second, and the movement will be kept up for three quarters of an hour.



Besides tops, we may make use of different kinds of discs, with an axis rotating between two clamps; they are moved either by a kind of clock-work, or by the unrolling of a string, like the tops. Generally, however, these contrivances have this inconvenience, that the discs cannot be changed without stopping the instrument, and partly taking it to pieces. On the other hand, we have the advantage of being able to turn them on a vertical plane, so that we can conveniently carry on our experiments before a numerous auditory, which is a more difficult matter with tops. Montigny contrived to obtain the mingling of colours by means of a turning prism, which he caused to throw its shadow on a white screen. The Thaumatrope is a small rectangle of cardboard, which is made to rotate on an axis passing through the centres of the longest sides. We shall describe it at greater length when we come to consider a new apparatus known under the name of the Praxinoscope.

More complicated contrivances have also been constructed on the same principle, by which one may perceive the rotating disc through slits which turn at the same time. We will now describe the construction of some discs invented by Plateau under the name of the Phenakistoscope. These discs are made of strong cardboard, from six to ten inches in diameter (fig. 112), on which a certain number of figures (eight to twelve) are placed[Pg 111] in circles at an equal distance from each other, presenting the successive phases of a periodical movement. This disc is placed on another opaque circle of rather larger diameter, which has on its margin as many openings as the first disc has figures. The two discs are placed one on the other, and are fixed in the centre by means of a screw at the anterior extremity of a small iron axis, the other end being fitted into a handle. To make use of this contrivance we place ourselves in front of the glass, towards which we turn the disc with the figures, placing the eye so as to see the figures through one of the holes of the large disc. Directly the apparatus begins to turn round, the figures seen in the glass appear to execute the particular movements which they represent in different positions. Let us designate by means of the figures 1, 2, 3, the different openings through which the eye successively looks, and point out by the same numbers the figures in the radiuses thus numbered. If the experimenter looks in the glass through opening 1, he will see first figure 1, which appears in the glass to pass before his eyes; then the rotation of the disc displaces opening 1, and the cardboard intervenes, until opening 2 appears; then figure 2 takes the place of figure 1, until it in turn disappears, and opening 3 presents figure 3 to view. If these figures were all similar, the spectator would have but a series of visual impressions, separate but alike, which by a sufficiently rapid rotation mingle together in one durable impression like a perfectly immovable object. If, on the contrary, the figures differ slightly from each other, the luminous sensations will also mingle in a single object, which will however appear to be modified in a continuous manner, conformably with the differences of successive images. With a difference of speed, we obtain a new series of phenomena. A most simple contrivance of this kind is a top[Pg 112] of C. B. Dancer, of Manchester (fig. 113). It will be seen that the axis carries another disc, pierced with openings of different shapes, to the edge of which a thread is attached. This second disc is carried along by the friction of the axis, but its rotation is less rapid because of the great resistance offered by the air to the piece of thread which participates in the movement. If the lower disc has several differently-coloured sectors, they produce a very motley appearance, which seems to move sometimes by leaps, and sometimes by continuous motion. We must distinguish between the phenomena of successive contrast and simultaneous contrast.


Phenomena of successive contrast develop what are called accidental images. If we fix our eyes for a considerable time on a coloured object,[Pg 113] and then suddenly direct them towards a uniform white surface, we experience the sensation of the object as it is, but it appears coloured with a complementary tint; that is to say, it has the colour which, superposed on the genuine tint, we obtain from pure white. Thus a red object produces a consecutive green object. The experiment can be tried by gazing at the sun when it is setting, and then directing one’s eyes towards a white wall in the same direction.
Phenomena of simultaneous contrast arise from the influence exercised over each other by different shades and colours which we see simultaneously. That we may be certain that we have really obtained phenomena of this kind, the experiments must be arranged in such a manner that accidental images are not produced, and that the part of the retina affected by the sensation of colour does not receive, even momentarily, a passing image.

The phenomena of simultaneous contrast appear with the greatest clearness with slight differences of colour, and are therefore exactly the contrary of phenomena of successive contrast, which are favoured by strong oppositions of colour and light. We can, in general, characterise phenomena of simultaneous contrast as governed by this law, common to all perceptions of the senses: the differences clearly perceived appear greater than the differences equal to them, but perceived with greater difficulty, either because they only affect the observation in an uncertain manner, or that the memory fails to judge of them. A man of middle height appears small beside a tall man, because at the moment it is forcibly impressed on us that there are taller men than he, and we lose sight of the fact that there are smaller. The same man of medium height appears tall beside a man of small stature. We can easily make experiments on simultaneous contrast with a sheet of transparent paper. We fasten together a sheet of green and a sheet of rose-coloured paper, so as to obtain a sheet half red and half green. On the line of separation between the two colours we place a strip of grey paper, and cover the whole with a sheet of thin letter-paper of the same size. The grey strip will then appear red at the edge touching the green, and green at the edge touching the red; the centre presenting an intermediate shade. It presents a still more decided appearance if the grey strip is perpendicular with the[Pg 114] line of separation of the two colours; the piece of grey then stretching into the green will present as deep a red as the red foundation on the other side. If the line of grey colour exactly covers the line of separation between the two colours, the contrasting colour is more feeble; the edges of the grey paper then present complementary strips of colour. Similar effects may be obtained by superposing, in gradually diminishing layers, strips of thin paper, so as to form successive bands of different thicknesses. If it is then lit up from behind, the objective intensity is evidently constant through the extent of each layer; nevertheless every strip appears darker at the edge touching a more transparent layer, and lighter at the edge in contact with a thicker layer. The dull tints of China ink, superposed in layers, will produce a similar effect. The phenomena are produced by means of rotative discs of most beautiful and delicate gradations of colour. Let us give the sectors of the disc the form represented by fig. 114, and make them black and white; and when in rotation we shall see a series of concentric rings of a shade that becomes darker and darker towards the centre. The angular surface of the dark portions is constant in each of these rings. The intensity, therefore, of each ring is uniform during rapid rotation; it is only between one ring and another that the intensity varies. Each ring also appears lighter on its inner side when it borders on a darker ring, and darker on its outer side when in contact with a lighter ring. If the differences of intensity in the rings are very slight, one can scarcely judge sometimes if the inner rings are darker than the outer; the eye is only struck by the periodical alternations of light and shade presented by the edges of the rings. If, instead of white and black, we take two different colours, each ring will present two colours on its two edges, although the colour of the rest of the ring will be uniform. Each of the constituent colours presents itself with more intensity on that edge of the ring which borders on another ring containing a smaller quantity of the colour. Thus, if we mix blue and yellow, and the blue predominates in the exterior and the yellow in the[Pg 115] interior, every ring will appear yellow at its outer, and blue at its inner edge; and if the colours present together very slight differences, we may fall into the illusion which causes the differences really existing between the colours of the different rings to disappear, leaving instead, on a uniformly coloured background, the contrasting blue and yellow of the edges of the rings. It is very characteristic that in these cases we do not see the mixed colours, but seem to see the constituent colours separately, one beside the other, and one through the other.
All the experiments we have described afford great interest to the student; they can easily be performed by those of our readers who are particularly interested in these little-known subjects. Any one may construct the greater part of the appliances we have enumerated, and others can be obtained at an optician’s. The discs in particular are extensively manufactured, and with great success.

CHAPTER XI.
OPTICAL ILLUSIONS—ZOLLNER’S DESIGNS—THE THAUMATROPE—PHENOKISTOSCOPE—THE ZOOTROPE—THE PRAXINOSCOPE—THE DAZZLING TOP.
We shall now continue the subject by describing some illusions more curious still—those of ocular estimation. These illusions depend rather on the particular properties of the figures we examine, and the greater part of these phenomena may be placed in that category whose law we have just formulated: the differences clearly perceived appear greater than the differences equal to them, but perceived with greater difficulty. Thus a line —— when divided appears greater than when not divided; the direct perception of the parts makes us notice the number of the sub-divisions, the size of which is more perceptible than when the parts are not clearly marked off. Thus, in fig. 115, we imagine the length ab equals bc, although ab is in reality longer than bc. In an experiment consisting of dividing a line into two equal parts, the right eye tends to increase the half on the right, and the left eye to enlarge that on the left. To arrive at an exact estimate, we turn over the paper and find the exact centre.


Illusions of this kind become more striking when the distances to be compared run in different directions. If we look at A and B (fig. 116), which are perfect squares, A appears greater in length than width, whilst B, on the contrary, appears to have greater width than length. The case is the same with angles. On looking at fig. 117, angles 1, 2, 3, 4 are straight, and should appear so when examined. But 1 and 2 appear pointed, and 3 and 4 obtuse. The illusion is still greater if we look at the figure with the right eye. If, on the contrary, we turn it, so that 2 and 3 are at the bottom, 1 and 2 will appear greatly pointed to the left eye. The divided angles always appear relatively greater than they would appear without divisions.
The same illusion is presented in a number of examples in the course of daily life. An empty room appears smaller than a furnished room, and a wall covered with paperhangings appears larger than a bare wall. It is a well-known source of amusement to present someone in company with a hat, and request him to mark on the wall its supposed height from the ground. The height generally indicated will be a size and a half too large.
We will relate an experience described by Bravais: “When at sea,” he says, “at a certain distance from a coast which presents many inequalities, if we attempt to draw the coastline as it presents itself to the eye, we shall find on verification that the horizontal dimensions have been correctly sketched at a certain scale, while all the vertical angular objects have been represented on a scale twice as large. This illusion, which is sure to occur in estimates of this kind, can be demonstrated by numerous observations.”
M. Helmholtz has also indicated several optical illusions.



If we examine fig. 118, the continuation of the line a does not appear to be d,—which it is in reality,—but f, which is a little lower. This illusion is still more striking when we make the figure on a smaller scale (fig. 119), as at B, where the two fine lines are in continuation with each other, but do not appear to be so, and at C, where they appear so, but are not in reality. If we draw the figures as at A (fig. 118), leaving out the line d, and look at them from a gradually increasing distance, so that they appear to diminish, it will be found that the further off the figure is placed, the more it seems necessary to lower the line f to make it appear a continuation of a. These effects are produced by irradiation; they can also be produced by black lines on a white foundation. Near the point of the two acute angles, the circles of diffusion of the two black lines touch and mutually reinforce each other; consequently the retinal image of the narrow line presents its maximum of darkness nearest to the broad line, and appears to deviate on that side. In figures of this kind, however, executed on a larger scale, as in fig. 118, irradiation can scarcely be the only cause of[Pg 118] illusion. We will continue our exposition as a means of finding an explanation. In fig. 120, A and B present some examples pointed out by Hering; the straight, parallel lines, a b, and c d, appear to bend outwards at A, and inwards at B. But the most striking example is that represented by fig. 121, published by Zollner.
The vertical black strips of this figure are parallel with each other, but they appear convergent and divergent, and seem constantly turned out of a vertical position into a direction inverse to that of the oblique lines which divide them. The separate halves of the oblique lines are displaced respectively, like the narrow lines in fig. 119. If the figure is turned so that the broad vertical lines present an inclination of 45° to the horizon, the convergence appears even more remarkable, whilst we notice less the apparent deviation of the halves of the small lines, which are then horizontal and vertical. The direction of the vertical and horizontal lines is less modified than that of the oblique lines. We may look upon these latter illusions as fresh examples of the aforesaid rule, according to which acute angles clearly defined, but of small size, appear, as a rule, relatively larger when we compare with obtuse or right angles which are undivided; but if the apparent enlargement of an acute angle shows itself in such a manner that the two sides appear to diverge, the illusions given in figs. 118, 120, and 121, will be the result.

In fig. 118 the narrow lines appear to turn towards the point where they penetrate the thick line and disappear, to appear afterwards in continuation of each other. In fig. 120 the two halves of each of the two straight lines seem to deviate through the entire length in such a manner that the acute angles which they form with the oblique lines appear enlarged. The same effect is shown by the vertical lines of fig. 121.
M. Helmholtz is of opinion (figs. 120, 121) that the law of contrast is insufficient to entirely explain the phenomena, and believes that the effect is also caused by the movements of the eye. In fact, the illusions almost entirely[Pg 119] disappear, if we fix on a point of the object in order to develop an accidental image, and when we have obtained one very distinctly, which is quite possible with Zollner’s design (fig. 121), this image will present not the slightest trace of illusion. In fig. 118 the displacement of the gaze will exercise no very decided influence on the strengthening of the illusion; on the contrary, it disappears when we turn our eyes on the narrow line, ad. On the other hand, the fixing of the eyes causes the illusion to disappear with relative facility in fig. 120, and with more difficulty in fig. 121; it will, however, disappear equally in the latter design, if we fix it immovably, and instead of considering it as composed of black lines on a white background, we compel ourselves to picture it as white lines on a black foundation; then the illusion vanishes. But if we let our eyes wander over the illustration, the illusion will return in full force. We can indeed succeed in completely destroying the illusion produced by these designs by covering them with a sheet of opaque paper, on which we rest the point of a pin. Looking fixedly at the point, we suddenly draw away the paper, and can then judge if the gaze has been fixed and steady according to the clearness of the accidental image which is formed as a result of the experiment.


The light of an electric spark furnishes the surest and simplest means of counteracting the influence of movements of the eyes, as during the momentary duration of the spark the eye cannot execute any sensible movement. For this experiment the present writer has made use of a wooden box, A B C D (fig. 122), blackened on the inside. Two holes are made for the eyes on each side of the box, f and g. The observer looks through the openings, f, and in front of openings, g, the objects are placed; these are pierced through with a pin, which can be fixed by the eyes in the absence[Pg 120] of the electric spark, when the box is perfectly dark. The box is open, and rests on the table, B D, to allow of changing the object. The conducting wires of electricity are at h and i; in the centre of the box is a strip of cardboard, white on the side facing the spark, the light of which it shelters from the eye of the observer and throws back again on the object. With the electric light the illusion was completely perceptible with fig. 118, while it disappeared altogether in fig. 120; with fig. 121 it was not entirely absent, but when it showed itself, it was much more feeble and doubtful than usual, though the intensity of light was quite sufficient to allow of the form of the object being very distinctly examined. Thus two different phenomena have to be explained; first, the feeble illusion which is produced without the intervention of movements of the eye; and secondly, the strengthening of the illusion in consequence of these movements. The law of contrast sufficiently explains the first; that which one perceives most distinctly with indirect vision is the concordance of directions with dimensions of the same kind. We perceive more distinctly the difference of direction presented at their intersection by the two sides of an acute or obtuse angle, than the deviation that exists between one of the sides and the perpendicular which we imagine placed on the other side, but which is not marked. By being distributed on both sides, the apparent enlargement of the angles gives way to displacements, and changes of direction of the sides. It is difficult to correct the apparent displacement of the lines when they remain parallel to their true direction; for this reason, the illusion of the figure is relatively more inflexible. Changes of direction, on the contrary, are recognised more easily if we examine the figure attentively, when these changes have the effect of causing the concordance of the lines (which accord in reality) to disappear; it is probably because of the difference in aspect of the numerous oblique lines of figs. 120 and 121 that the concordance of these lines escapes the observer’s notice. As regards the influence exercised by the motion of[Pg 121] the eyes in the apparent direction of the lines, M. Helmholtz, after discussing the matter very thoroughly, proves the strengthening of the illusion in Zollner’s illustration to be caused by those motions. It is not now our intention to follow out the whole of this demonstration; it will be sufficient to point out to the reader a fruitful force of study, with but little known results.
The Romans were well acquainted with the influence of oblique lines. At Pompeii, fresco paintings are to be found, in which the lines are not parallel, so that they satisfy the eye influenced by adjacent lines. Engravers in copper-plate have also studied the influence of etchings on the parallelism of straight lines, and they calculate the effect that they will produce on the engraving. In some ornamentations in which these results have not been calculated, it sometimes happens that parallel lines do not appear parallel because of the influence of other oblique lines, and a disagreeable effect is produced. A similar result is to be seen at the railway station at Lyons, the roof of which is covered with inlaid work in point de Hongrie. The wide parallel lines of this ceiling appear to deviate, a result produced by a series of oblique lines formed by the planks of wood.

Having given a long account of the result of M. Helmholtz’s labours, we will pass to the consideration of another kind of experiments, or rather appliances, based on the illusions of vision, and the persistence of impressions on the retina.
The Thaumatrope, to which we have already referred, is a plaything of very ancient origin, based on the principle we have mentioned. It consists of a cardboard disc, which we put in motion by pulling two cords. On one side of the disc a cage, a, is portrayed, on the other a bird, b (fig. 123). When the little contrivance is turned round, the two designs are seen at the same time, and form but one image—that of a bird in its cage (fig. 124). It is of course hardly necessary to add that the designs may be varied.
We have already referred to M. Plateau’s rotating disc (the Phenakistoscope). Through the narrow slits we perceive in succession representations of different positions of a certain action. The persistence of the luminous impressions on the retina gives to the eye the sensation of a continuous image, which seems animated by the same movements as those portrayed in the different phases (fig. 125).


The Zootrope (fig. 126) is a perfected specimen of this apparatus. It is composed of a cylinder of cardboard, turning on a central axis. The cylinder is pierced with vertical slits at regular intervals, and through which the[Pg 122] spectator can see the designs upon a band of paper adapted to the interior of the apparatus in rotation. The designs are so executed that they represent the different times of a movement between two extremes; and in consequence of the impressions upon the retina the successive phases are mingled, so the spectator believes he sees, without transition, the entire movement. We give a few specimens of the pictures for the Zootrope (fig. 127). We have here an ape leaping over a hedge, a dancing “Punch,” a gendarme pursuing a thief, a person holding the devil by the tail, a robber coming out of a box, and a sportsman firing at a bird. The extremes of the movement are right and left; the intermediary figures make the transitions, and they are usually equal in number to the slits in the Zootrope. It is not difficult to construct such an instrument, and better drawings could be made than the specimens taken at random from a model. The earth might be represented turning in space, or a fire-engine pumping water could be given, and thus the Zootrope might be quite a vehicle of instruction as well as of amusement. This instrument is certainly one of the most curious in the range of optics, and never fails to excite interest. The ingenious contrivances which have up to the present time reproduced it, all consist in the employment of narrow slits, which besides reducing the light to a great extent, and consequently the light and clearness of the object, require the instrument to be set in rapid rotation, which greatly exaggerates the rapidity of the movements represented, and without which the intermissions of the spectacle could not unite in a continuous sensation.


We present here an apparatus based on a very different optical[Pg 123] arrangement. In the Praxinoscope12 (a name given by the inventor, Mr. Reynaud, to this new apparatus), the substitution of one object for another is accomplished without interruption in the vision, or solution of continuity, and consequently without a sensible reduction of light; in a word, the eye beholds continuously an image which, nevertheless, is incessantly changing before it. The result was obtained in this manner. Having sought unsuccessfully by mechanical means to substitute one object for another without interrupting the continuity of the spectacle, the inventor was seized with the idea of producing this substitution, not with the objects themselves, but with their virtual images. He then contrived the arrangement which we will now describe. A plane mirror, AB (fig. 129), is placed at a certain distance from an object, CD, and the virtual image will be seen at C′D′. If we then turn the plane mirror and object towards the point, O, letting BE and DF be their new positions, the image will be at C″D″. Its axis, O, will not be displaced. In the positions, AB and CD, first occupied by the plane mirror and the object, we now place another mirror and object. Let us imagine the eye placed at M. Half of the first object will be seen at OD″, and half of the second at OC′. If we continue the rotation of the instrument, we shall soon have mirror No. 2 at TT′, and object No. 2 at SS′. At the same moment the image of object No. 2 will be seen entirely at C‴D″. Mirror No. 2 and its object will soon after be at BE and DF. If we then imagine another mirror and its corresponding object at AB and CD, the same succession of phenomena will be reproduced. This experiment therefore shows that a series of objects placed on the perimeter of a polygon[Pg 124] will be seen successively at the centre, if the plane mirrors are placed on a concentric polygon, the “apothème” of which will be less by one-half, and which will be carried on by the same movement. In its practical form, M. Reynaud’s apparatus consists of a polygonal or simply circular box (fig. 128), (for the polygon may be replaced by a circle without the principle or result being changed), in the centre of which is placed a prism of exactly half a diameter less, the surface of which is covered with plane mirrors. A strip of cardboard bearing a number of designs of the same object, portrayed in different phases of action, is placed in the interior of the circular rim of the box, so that each position corresponds to a plate of the glass prism. A moderate movement of rotation given to the apparatus, which is raised on a central pivot, suffices to produce the substitution of the figures, and the animated object is reflected on the centre of the glass prism with remarkable brightness, clearness, and delicacy of movement. Constructed in this manner, the Praxinoscope forms an optical toy both interesting and amusing. In the evening, a lamp placed on a support ad hoc, in the centre of the apparatus, suffices to light it up very clearly, and a number of persons may conveniently assemble round it, and witness the effects produced.


Besides the attractions offered by the animated scenes of the Praxinoscope, the apparatus may also be made the object of useful applications in the study of optics. It permits an object, a drawing, or a colour, to be substituted instantaneously in experiments on secondary or subjective images, etc., on the contrast of colours or the persistence of impressions, etc. We can also make what is called a synthesis of movements by placing before the prism a series of diagrams of natural objects by means of photography.
M. Reynaud has already arranged an apparatus which exhibits in the[Pg 125] largest dimensions the animated reflection of the Praxinoscope, and which lends itself to the demonstration of curious effects before a numerous auditory. The ingenious inventor has recently contrived also a very curious improvement in the original apparatus. In the Praxinoscope Theatre he has succeeded in producing truly ornamental tableaux, as on a small Lilliputian stage, in the centre of which the principal object moves with startling effect. To obtain this result, M. Reynaud commences by cutting out in black paper the different figures, the whole of which will form an object animated by the[Pg 126] rotation given to the Praxinoscope. To supply the decorations, he arranges on the black foundation the image of an appropriate coloured design by means of a piece of glass. It is well known that transparent glass possesses the property of giving a reflection of the objects on the nearest side as well as on the farthest. We may recall the applications of this optical effect in theatres, and also in courses of physics, under the title of impalpable spectres. It is also by reflection on thin, transparent glass, that M. Reynaud produces the image of the ornamentations in the Praxinoscope Theatre. The decorations are really placed in the lid, which is held by a hook in a vertical position, thus forming the front side of the apparatus (fig. 130). In this side a rectangular opening is made, through which the spectator (using both eyes) perceives at the same time the animated reflection of the Praxinoscope, and the immovable image of the decorations reflected in the transparent glass. The position of the latter and its distance from the coloured decorations are arranged so that the reflection is thrown behind the moving figure, which consequently appears in strong relief against the background, the effect produced being very striking. It is evident that to change the decorations it is only necessary to place in succession on a slide the different chromos representing landscapes, buildings, the interior of a circus, etc. It is easy to choose an arrangement suitable for each of the moving figures[Pg 127] placed in the Praxinoscope. By this clever and entirely novel optical combination, the mechanism of the contrivance is entirely lost sight of, leaving only the effect produced by the animated figures, which fulfil their different movements on the little stage. The Praxinoscope Theatre can also be used as well in the evening as in the daytime. By daylight, it is sufficient to place it before a window, and in the evening the same effects may be produced, perhaps in even a more striking manner, by simply placing a lamp on the stand, with a small plated reflector, and a lamp-shade. The illusion produced by this scientific plaything is very complete and curious, and[Pg 128] M. Reynaud cannot be too much commended for so cleverly applying his knowledge of physics in the construction of an apparatus which is at the same time both an optical instrument and a charming source of amusement.


Amongst the toys founded upon the persistency of impressions upon the retina we may instance the “Dazzling Top” (fig. 131). This remarkable invention is quite worthy of a place in every cabinet, and is an ingenious specimen of a perfected Helmholtz top. It is a metallic toy put in motion by means of a cord wound round a groove. The axis is hollow, admits a metallic stem, and fits into a handle which is held in the hand. The top is placed upon a little cup in an upright position, and it is then set spinning in the usual way with the cord. The stem and handle are then withdrawn, and as the top will continue to spin for a long time, discs and various outline shapes can be fixed upon it, and various objects will be shadowed thereon. Cups, bowls, candlesticks, and jugs can be seen plainly revolving as the top carries the wire representation in outline rapidly past the eyes. Coloured cardboard can be worked into various patterns, and much amusement will be created amongst children and young people.
CHAPTER XII.
OPTICAL ILLUSIONS CONTINUED—EXPERIMENTS—THE TALKING HEAD—GHOST ILLUSIONS.
The enumeration of optical illusions is so considerable that we have no intention of describing them all, and will merely cite a few other examples. The following facts have been communicated to us by M. Nachet:—

When examining algæ under the microscope, we notice the spaces which separate the streaks ornamenting the silicious covering of these various organisms, and it is explained that they are formed by hexagons visible only when we examine the object with a powerful microscope. “For a long time,” says M. Nachet, “I occupied myself with the examination of the hexagonal appearance of the points constituting the streaks. Why should these hexagons show themselves, and how could they be other than the visible base of small pyramids piled very closely one on the other; and if this were the case, why were not the points of the little pyramids visible? Or, was the structure before me analogous to that of the eyes of insects? Then the carapace would be but a surface of perforated polygonal openings. This latter hypothesis was attractive enough, and would have explained many things; but some careful observations with very powerful object[Pg 130]-glasses, quite free from blemishes, had shown me that these hexagons had round points, contrary to the descriptions of micrographs. These observations, corroborated by the micrographic photographs of Lackerbauer, the much-regretted designer, and by Colonels Woodward and Washington, left not the slightest doubt that it was necessary to discover why the eye persistently saw hexagons where there were circles. To elucidate this point, it was necessary to find some means of reproducing artificially what nature had accomplished with so much precision on the surfaces of algæ. After many fruitless attempts, I decided on making a trial of a stereotype plate covered with dots arranged in quincunxes, very close together” (figs. 132 and 133). “The result was more successful than I had hoped; the effect produced is exactly that of the arrangement of the so-called hexagons of the most beautiful of the algæ, the Pleurosigma angulata. If these stereotypes are examined with one eye only, we shall be immediately convinced that we have to do with hexagonal polygons.” It is useless to give any long exposition of a figure so clearly explanatory; it is simply an effect of the contrast and opposition of the black and white in the sensation of the retina. This effect is particularly striking with fig. 134, a negative photograph heliographically engraved according to fig. 133. In this the white points seem to destroy the black spaces, and to approach each other tangentially, and the irradiation is so intense that the white circles appear much larger than the black of fig. 133, although of the same diameter. There are in these facts many points which may interest not only students of micrography, but also artists. As to the algæ, the origin of this investigation, it remains to be discovered if these circles which cover their silicious carapace are the projection of small hemispheres, or the section of openings made in the thick covering. Certain experiments, however, seem to prove that they are hemispheres, and the theory is also confirmed by a microscopic photograph from Lackerbauer’s collection, magnified 3,000 diameters, in which a black central point is seen in the centre of each circle, a certain reflection of the luminous source reproduced in the focus of each of the small demi-spheres which constitute the ornament of the algæ. The microscope, which has progressively shown first the streaks, then the hexagons, and then the round points, will surely clear up the point some day or other.


Mr. Silvanus P. Thompson, Professor of Physics at University College,[Pg 131] Bristol, has recently presented the French Society of Physical Science with a curious example of optical illusion, the true cause of which is not clearly known, but which we may compare with other facts made known some time ago, of which no precise explanation has been given. Let us first consider in what the effect discovered by Mr. S. P. Thompson consists, according to the description that has been given of it by M. C. M. Gariel; the illustrations here given will also allow of our verifying the truth of the statements.

Mr. Thompson’s optical illusion. Give a circular movement to these figures, and the circles will appear to turn round.
The first illustration consists of a series of concentric circles of about the width of a millimetre, separated by white intervals of the same size (fig. 135). These dimensions are not absolute; they vary with the distance, and may even be a few inches in width if it is desired to show the phenomenon to a rather numerous auditory. If we hold the design in the hand, and give it a twirl by a little movement of the wrist, the circle appears to turn round its centre, and the rotation is in the same direction, and is equally swift; that is to say, the circle appears to accomplish a complete turn, whilst the cardboard really accomplishes one in the same direction. For the second effect we draw a dark circle, in the interior of which are placed a number of indentations at regular intervals (fig. 136). Operating in the same manner as described above, this notched wheel appears to turn round its centre, but this time in a different direction from the real movement. In this, however, as in the other design, the effect is more satisfactory if we do not look directly at it; the movements also are particularly striking in combinations such as that represented in fig. 137, in which the multiplicity of circles does not allow us to fix one specially. We may add that the same effects may be obtained with eccentric wheels, or even with other curves than circles. By means of a photograph on glass, Mr. Thompson has been able to reflect these designs on a screen where they were obtained on a large scale; a circular movement was communicated to the photographic plate, so that the design moved in a circular manner on the screen, and in this case also there existed the illusion that every circle seemed[Pg 132] turning round its centre. And what is the explanation of these curious effects? Mr. Thompson does not believe (and we share his opinion) that the faculty possessed by the retina of preserving images during a certain time (persistence of impressions on the retina) can entirely explain these phenomena. Without desiring to formulate a decided theory, Mr. Thompson is of opinion that we may class these facts with others which have been known for some time, and that perhaps it is necessary to attribute to the eye some new faculty which may explain the whole at once.

Brewster and Adams have described phenomena which are equally curious, the principal of which we will describe, adding also some analogous investigations due to Mr. Thompson. The result seems to be that there exists in the eye a badly-defined purpose of nature, which in a certain way compensates (Brewster) for the real phenomenon, because it has a contrary effect, which will continue for some time after the cessation of the phenomena, and which gives by itself a sensation contrary to that which the real movement would have produced. Thus, after having fixed our eyes for two or three minutes on a rushing waterfall, if we suddenly turn our glance on the adjacent rocks, the latter appear to move from top to bottom. It is not a question here of the effect of the relative movement to be observed on regarding simultaneously the falling water and the rocks; if one can succeed in abstracting oneself to such an extent that the water appears motionless, the rocks appear to take a contrary movement. In the phenomenon we describe there is no simultaneous comparison; the eyes are turned successively first on the water, and then on the rocks. In a rapid river, such as the Rhine above the fall at Schaffhausen, the stream is not equally swift in every part, and the current is noticeably more rapid in the middle of the river than near the banks. If we look fixedly at the centre of the stream, and then[Pg 133] suddenly turn our eyes towards the banks, it will appear as though the river were flowing back towards its source. This kind of compensation does not only produce an apparent displacement, but also changes in size. When travelling at great speed in a railway train, the objects of the surrounding country as one flies by them gradually appear smaller and smaller. If, when this occurs, we suddenly remove our eyes to the interior of the railway carriage, and fix them on immovable objects, such as the sides of the compartment, or the faces of our travelling companions, the images on the retina will really preserve the same size, and yet the objects will appear larger. Such are some of the interesting facts among those discovered by Mr. Thompson; and though we do not intend to push the inquiry further, we think it may not be without interest to describe here another illusion of that organ whose properties are in every way so curious and remarkable.


Another experiment to show the existence of impressions received by the retina can be made with the figure above (138). If the gaze be fixed upon the dark spot in the centre of the white figure for about half a minute, and the eyes then directed to the ceiling, or a sheet of white paper, the white figure will be reproduced in black. This result is based upon the principle of complementary colours. A red design, for instance, will be reproduced in green.
There is a dark spot in every human eye—that is, a spot which is insensible to light. The eye is generally regarded as a perfect instrument, but it is not yet so by any means. One of our great philosophers remarked that if an instrument were sent home to him so full of errors he would feel justified in returning it to the optician. But the eye has its dark place, the punctum cæcum, and it can be discovered by covering the left eye with the hand, and holding the present page at arm’s length with the other. Then fix the gaze on the small cross in the picture, and bring the book close up. At a little distance the white ball will disappear from the page (fig. 139).

The illustration (fig. 140) shows us a very curious optical illusion, and one very easy to practise. Roll up a sheet of paper, and look through it, as through a telescope, with the right eye, keeping both eyes open. Then place the left hand open palm towards you against the roll of paper, you will then appear to be looking through a hole in your left hand. Sometimes the effect is produced without holding up the other hand to the roll, as shown in fig. 140.
Among optical illusions there are a great number that may be produced by means of mirrors. The divided telescope is an example. The apparatus, raised on a firm stand, allows of one apparently seeing an object through a stone or other opaque object, as shown in fig. 141. The illustration shows the arrangement of the apparatus. The observer, looking through it, plainly[Pg 135] perceives the object through the glass; the image is reflected four times before reaching his eye, by means of small mirrors concealed in the instrument.

Convex or concave mirrors distort images in a singular manner, and produce very interesting effects. Anamorphoses constitute particular objects belonging specially to the class of experiments relating to cylindrical mirrors. They are images made according to determined rules, but so distorted that when regarding them fixedly we can only distinguish confused strokes. When they are seen reflected in the curved mirrors, they present, on the contrary, a perfectly regular appearance. Fig. 142 exhibits an Anamorphosis made by a cylindrical mirror. It will be seen that the confused image of the horizontal paper is reflected in the cylindrical mirror, producing the figure of a juggler. It is easy to contrive similar designs one’s-self; and comical mirrors may also be employed which produce particular effects of a no less interesting kind. The next illustration is of a set of figures which in a cylindrical mirror look like the ten of hearts (fig. 143).


One of the most remarkable applications of mirrors in amusing experiments is undoubtedly that of the severed and talking head. A few years back this trick obtained considerable success in Paris and a number of other towns. The spectators beheld a small space set apart, in which was placed a table on three legs; on this table was a human head, placed in cloth on a dish. The head moved its eyes and spoke; it evidently belonged to a man whose body was completely hidden. The spectators thought they saw an empty[Pg 136] space beneath the table, but the body of the individual who was really seated there was concealed by two glasses placed at an inclination of 45° to the walls on the right and left. The whole was arranged in such a manner that the reflection of the walls coincided with the visible part of the wall at the[Pg 137] back of the room. The three walls were painted in one colour, and a subdued light increased the illusion, the effect of which was remarkable (fig. 144).

The spectres designed by Robin also attracted considerable public attention within recent times. They were images formed by the medium of transparent glass. Glass panes often produce the phenomenon of spectres. In the evening, when it is dark out of doors, it is easy to prove that the reflection of objects in a lighted room can be reproduced behind the window panes by reason of the darkness outside. If we approach the window pane,[Pg 138] we see also the real objects outside, a balcony, tree, etc. These real objects mingle with the reflected image, and combine to produce very curious effects. In this way M. Robin has contrived the effects of the theatre. He throws on the stage the reflection of a person dressed as a Zouave, and he himself, armed with a sabre, stabs the spectre through the body. A great number of other singular effects have been obtained in the same manner. Pepper’s Ghost was managed in this way.

Within recent times, images produced in a similar way have been[Pg 139] utilized to facilitate the study of drawing. A piece of glass is fixed vertically on a black board (fig. 146). A model to copy from is placed on one side of the piece of glass, and is arranged so that the visual ray passes obliquely through the glass, and we perceive the reflection of the design very clearly on the other side. It is then very easily reproduced with a pencil on a sheet of white paper by tracing the outlines.

CHAPTER XIII.
VISION—THE EYE—THE STEREOSCOPE—SPECTRUM ANALYSIS—THE SPECTROSCOPE—THE TELESCOPE AND MICROSCOPE—PHOTOGRAPHY—DISSOLVING VIEWS—LUMINOUS PAINT.
The eye and vision are such important subjects to all of us that we may be excused for saying something more concerning phenomena connected with them, and the instruments we use for assisting them. We do not propose to write a treatise upon the physiology of vision, for we know the image in the eye is produced physically in the same manner as the image in a camera obscura. In the eye the sides of the box are represented by the sclerotic (see chap. x. fig. 95); the dark inner surface has its parallel in the pigment of the choroid; the opening in the box in the pupil of the eye; the convex lens in the crystalline and the cornea; and the retina receives the image. But why we see—beyond the fact that we do see—no one can explain. Science is dumb on the subject. Thought and consciousness elude our grasp; and, as Professor Tyndall says on this subject, “we stand face to face with the incomprehensible.”
But there are many interesting facts connected with our vision which may be plainly described. Some people are obliged to carry an object (or a book) to within ten inches of the eye to see it distinctly; and a person who does not possess convergent power of the eye will have to move it farther off, or use convex glasses; while a “near-sighted” person, whose eyes are too quickly convergent, will use concave glasses to bring the object near to the eye.
There is but one small place in the retina of the eye which admits of perfect vision. This, the most sensitive portion, is called the “yellow spot,” and vision becomes more and more indistinct from this point towards the circumference. This can be proved by any one; for in reading we are obliged to carry our eyes from word to word, and backwards and forwards along the lines of print. Another very important element in our vision is the contraction and enlargement of the iris around the pupil. In cases where strong light would only dazzle us the iris expands, and the pupil is contracted to a sufficient size to accommodate our vision. At night, or in a darkened room, the pupil is enlarged. This change will account for our not being immediately able to see objects when we have passed from darkness to great light, or vice versâ. The iris must have time to accommodate itself to the light.
Now, outside the small space of perfect vision above mentioned, there is a circle of considerable extent, called the “field of vision.” In man this field,[Pg 141] when the eyes are fixed, subtends an angle of about 180°, because beyond that the rays cannot enter the pupil of the eye. But in the lower animals, the fish and birds,—notably the ostrich,—the field of vision is much more extensive, because the pupils are more prominent, or the eyes are set more towards the sides of the head. The ostrich can see behind him, and fish can see in any direction without apparent limit. Man can only see indistinctly; and though he can move his eyes rapidly, he can see distinctly but a small portion of any object at a time, yet he sees with both eyes simultaneously a single object, because the two lines of vision unite at a single point, and as the two images cover each other we perceive only one image. Beyond or within this point of meeting the vision is indistinct, but the angle of convergence is always varied according to the distance of the object. If we hold up a penholder in front of us, and in a line with any other defined object,—say an ink-bottle,—we can see the penholder distinctly, and the ink-bottle indistinctly, as two images. If we then look at the ink-bottle we shall see it single, while the penholder will appear double, but with imperfect outlines.


Again, if we look at a box both eyes will see it equally well, but the right eye will see a little more on its right side, and the left eye on the left. It is on this principle that the Stereoscope is constructed. Sir Charles Wheatstone was the inventor, and the instrument may be thus described:—Two pictures are taken by photography—one as the landscape is seen by the right eye, the other as it is viewed by the left; the points of view thus differing slightly. When both eyes are simultaneously applied to the instrument the view is seen exactly as it would appear to the beholder at the actual place it represents. The views are taken singly; one side at one time, and another after, as in the camera (fig. 148). A is the first view; B is kept dark; C is the shutter for A. There are Reflecting and Refracting Stereoscopes. In the former a mirror reflects the image into each eye; in the latter the views are pasted on a card, side by side, and looked at through prismatic lenses. The principles of Binocular Vision have been applied to the Microscope.
In foregoing chapters we have given many examples with diagrams of the temporary impressions made upon the retina of the eye. It is a fact that a wheel revolving at a great rate will appear to be standing still when suddenly[Pg 142] illuminated by a flash of lightning, because the eye has not time to take in the motion in the instant of time, for the spokes of the wheel are not moving fast enough to convey the impression of motion in that half second to the eye; yet the perfect outline of the wheel is distinctly visible.
Indeed, distinct vision can be exercised in a very small fraction of a second. It was calculated by Professor Rood, and proved by experiment, that forty billionths of a second is sufficient time for the eye to distinguish letters on a printed page. It this instance the illuminating power was an electric spark from a Leyden Jar.
We have remarked upon the distinctness with which we can see an object when we direct our gaze upon it, and this appears a self-evident proposition; but have any of our readers remarked the curious fact that when they want to see a faint and particular star in the sky it will at once disappear when they gaze at it? The best way to see such very faint orbs as this is to look away from them,—a little to one side or the other,—and then the tiny point will become visible again to the eye. There is also a degree of phosphorescence in the eye, which any one who receives a blow upon that organ will readily admit. Even a simple pressure on the closed lid will show us a circle of light and “colours like a peacock’s tail,” as the great Newton expressed it. There are many occasions in which light is perceived in the eye—generally the result of muscular action; and the Irish term to “knock fire out of my eye” is founded upon philosophical facts.
We are many of us aware of “spots” on our eyes when our digestion is out of order, and the inability of the eye to see figures distinctly in a faint light—within a proper seeing distance, too—has often given rise to the “ghost.” These shadowy forms are nothing more than affections of the eye, and, as well remarked in Brewster’s Letters on Natural Magic, “are always white because no other colour can be seen.” The light is not sufficiently strong to enable the person to see distinctly; and as the eye passes from side to side, and strives to take in the figure, it naturally seems shadowy and indistinct, and appears to move as our eyes move. “When the eye dimly descries an inanimate object whose different parts reflect different degrees of light, its brighter parts may enable the spectator to keep up a continued view of it; but the disappearance and reappearance of its fainter parts, and the change of shape which ensues, will necessarily give it the semblance of a living form; and if it occupies a position which is unapproachable, and where animate objects cannot find their way, the mind will soon transfer to it a supernatural existence. In like manner a human figure shadowed forth in a feeble twilight may undergo similar changes, and after being distinctly seen while it is in a situation favourable for receiving and reflecting light, it may suddenly disappear in a position before and within the reach of the observer’s eye; and if this evanescence takes place in a path or roadway where there is no sideway by which the figure could escape, it is not easy for an ordinary mind to efface the impression which it cannot fail to receive.” This will account for many so-called “ghosts.”
Accidental colours, or ocular spectra, are, so to speak, illusions, and differently-coloured objects will, when our gaze is turned from them, give us different “spectra” or images. For instance, a violet object will, when we turn to a sheet of white paper, give us a yellow “spectrum”; orange will be blue; black and white will change respectively; red will become a blue-green. From a very strong white light the accidental colours will vary.

The Solar Spectrum is the name given to the coloured band formed by the decomposition of a beam of light into its elementary colours, of which there are seven. This is an easy experiment. A ray of light can be admitted into a darkened room through a hole in the shutter, and thus admitted will produce a white spot on the screen opposite, as at g in the diagram (fig. 149). If we interpose a prism—a triangular piece of glass—the “drop” of a chandelier will do—we cause it to diverge from its direct line, and it will produce a longer streak of light lower down. This streak will exhibit the prismatic colours, or the “colours of the rainbow”; viz., red (at the top), orange, yellow, green, blue, indigo (blue), and violet last. These are the colours of the Solar Spectrum. The white light is thus decomposed, and it is called mixed light, because of the seven rays of which it is composed. These rays can be again collected and returned to the white light by means of a convex lens.
“White light,” said Sir Isaac Newton, “is composed of rays differently refrangible,” and as we can obtain the colours of the rainbow from white light, we can, by painting them on a circular plate and turning it rapidly round, make the plate appear white. Thus we can prove that the seven colours make “white” when intermingled. But Newton (1675) did not arrive at the great importance of his experiment. He made a round hole in the shutter, and found that the various colours overlapped each other. But, in 1802, Dr. Wollaston improved on this experiment, and by admitting the light through a tiny slit in the wood, procured an almost perfect spectrum of “simple” colours, each one perfectly distinct and divided by black lines.
But twelve years later, Professor Fraunhofer made a chart of these lines, which are still known by his name. Only, instead of the 576 he discovered, there are now thousands known to us! To Fraunhofer’s telescope Mr. Simms added a collimating lens, and so the Spectroscope was begun; and now we use a number of prisms and almost perfect instruments, dispersing the light through each. We have here an illustration of a simple Spectroscope, which is much used for chemical analysis (fig. 150).
In the spectrum we have long and short waves of light, as we have long and short (high and low) waves in music, called notes. The long or low notes are as the red rays, the high notes as the blue waves of light. (Here we have another instance of the similarity between light and sound.) But[Pg 144] suppose we shut out the daylight and substitute an artificial light. If we use a lamp burning alcohol with salt (chloride of sodium), the spectrum will only consist of two yellow bands, all the other colours being absent. With lithium we obtain only two, one orange and one red. From this we deduce the fact that different substances when burning produce different spectra; and although a solid may (and platinum will) give all seven colours in its spectrum, others, as we have seen, will only give us a few, the portion of the spectrum between the colours being black. Others are continuous, and transversed by “lines” or narrow spaces devoid of light; such is the spectrum of the sun, and by careful and attentive calculation and observation we can get an approximate idea of the matter surrounding the heavenly bodies.

We have said there are lines crossing the spectrum transversely; these are called Fraunhofer’s lines, after the philosopher who studied them; they were, however, discovered by Wollaston. These lines are caused by light from the lower portion of the sun passing through the metallic vapours surrounding the orb in a state of incandescence, such as sodium, iron, etc. One of Fraunhofer’s lines, a black double line known as D in the yellow portion of the spectrum, was known to occupy the same place as a certain luminous line produced by sodium compounds in the flame of a spirit lamp. This gave rise to much consideration, and at length Kirchkoff proved that the sodium vapour which gives out yellow light can also absorb that light; and this fact, viz., that every substance, which at a certain temperature emits light of a certain refrangibility, possesses at that temperature the power to absorb that same light. So the black lines are now considered the reversal of luminous lines due to the incandescent vapours by which the sun is surrounded. Thus the presence of an element can be found from black or luminous lines, so the existence of terrestrial elements in celestial bodies has[Pg 145] been discovered by means of preparing charts of the lines of the terrestrial elements, and comparing them with the lines of stella spectra.
We have supposed the beam of light to enter through a slit in the shutter, and fall upon a screen or sheet. The solar spectrum shown by the passage of the beam through a prism is roughly as below—

Fraunhofer substituted a telescope for the lens and the screen, and called his instrument a Spectroscope. He then observed the lines, which are always in the same position in the solar spectrum. The principal of them he designated as A, B, C, D, E, F, G, H. The first three are in the red part of the spectrum; one in the yellow, then one in the green; F comes between green and blue, G in the indigo-blue, and H in the violet. But these by no means exhaust the lines now visible. Year by year the study of Spectrum Analysis has been perfected more and more, and now we are aware of more than three thousand “lines” existing in the solar spectrum. The spectra of the moon and planets contain similar dark lines as are seen in the solar spectrum, but the fixed stars show different lines. By spectrum analysis we know the various constituents of the sun’s atmosphere, and we can fix the result of our observations made by means of the Spectroscope in the photographic camera. By the more recent discoveries great studies have been made in “solar chemistry.”
What can we do with the Spectroscope, or rather, What can we not do? By Spectroscopy we can find out, and have already far advanced upon our path of discovery, “the measure of the sun’s rotation, the speed and direction of the fierce tornados which sweep over its surface, and give rise to the ‘maelstroms’ we term ‘sunspots,’ and the mighty alps of glowing gas that shoot far beyond the visible orb, ever changing their form and size; even the temperature and pressure of the several layers and their fluctuations are in process of being defined and determined.” This is what science is doing for us, and when we have actually succeeded in ascertaining the weather at various depths in the atmosphere of the sun, we shall be able to predict our own, which depends so much upon the sun. Last year (1880) Professor Adams, in his address to the British Association, showed that magnetic disturbances, identical in kind, took place at places widely apart simultaneously. He argues that the cause of these identical disturbances must be far removed from the earth.
“If,” he says, “we imagine the masses of iron, nickel, and magnesium in the sun to retain even in a slight degree their magnetic power in a gaseous state, we have a sufficient cause for all our magnetic changes. We[Pg 146] know that masses of metal are ever boiling up from the lower and hotter levels of the sun’s atmosphere to the cooler upper regions, where they must again form clouds to throw out their light and heat, and to absorb the light and heat coming from the hotter lower regions; then they become condensed, and are drawn back again towards the body of the sun, so forming those remarkable dark spaces or sunspots by their down rush to their former levels. In these vast changes we have abundant cause for those magnetic changes which we observe at the same instant at distant points on the surface of the earth.” So we are indebted to the Spectroscope for many wonderful results—the constitution of the stars, whether they are solid or gaseous, and many other wonders.
The manner in which we have arrived at these startling conclusions is not difficult to be understood, but some little explanation will be necessary.
The existence of dark lines in the solar spectrum proves that certain rays of solar light are absent, or that there is less light. When we look through the prism we perceive the spaces or lines, and we can produce these ourselves by interposing some substance between the slit in the shutter before mentioned and the prism. The vapour of sodium will answer our purpose, and we shall find a dark line in the spectrum, the bright lines being absorbed by the vapour. We can subject a substance to any temperature we please, and into any condition—solid, liquid, or gaseous; we can also send the light the substance may give out through certain media, and we can photograph the spectrum given out under all conditions. The distance of the source of the light makes no difference. So whether it be the sun, or a far-distant star, we can tell by the light sent to us what the physical condition of the star may be. It was discovered in 1864 that the same metallic body may give different spectra; for instance, the spectrum might be a band of light,—like the rainbow,—or a few isolated colours; or again, certain detached lines in groups. The brightness of the spectrum lines will change with the depth of the light-giving source, or matter which produces it.
We have become aware by means of the Spectroscope that numerous metals known to us on earth are in combustion in the sun, and new ones have thus been discovered. In the immense ocean of gas surrounding the sun there are twenty-two elements as given by Mr. Lockyer, including iron, sodium, nickel, barium, zinc, lead, calcium, cobalt, hydrogen, potassium, cadmium, uranium, strontium, etc. Not only is the visible spectrum capable of minute examination, but, as in the case of the heat spectrum already mentioned when speaking of Calorescence, the light spectrum has been traced and photographed far beyond the dark space after the blue and violet rays, seven times longer than the visible solar spectrum—a spectrum of light invisible to our finite vision. Although a telescope has been invented for the examination of these “ultra violet” rays, no human eye can see them. But—and here science comes in—when a photographic plate is put in place of the eye, the tiniest star can be seen and defined. Even the Spectroscope at length fails, because light at such limits has been held to[Pg 147] be “too coarse-grained for our purposes”! “Light,” says a writer on this subject “we can then no longer regard as made of smooth rays; we have to take into account—and to our annoyance—the fact that its ‘long levelled rules’ are rippled, and its texture, as it were, loose woven”!
Twenty years ago Professors Kirchkoff and Bunsen applied Fraunhofer’s method to the examination of coloured flames of various substances, and since then we have been continually investigating the subject; yet much remains to be learnt of Spectrum Analysis, and Spectroscopy has still much to reveal. From Newton’s time to the present our scientists have been slowly but surely examining with the Spectroscope the composition of spectra, and the Spectroscope is now the greatest assistant we possess.
“Spectrum Analysis, then, teaches us the great fact that solids and liquids give out continuous spectra, and vapours and gases give out discontinuous spectra instead of an unbroken light” (Lockyer). We have found out that the sunlight and moonlight are identical, that the moon gives us spectrum like a reflection of the former, but has no atmosphere, and that comets are but gases or vapours. The most minute particles of a grain of any substance can be detected to the millionth fraction. The 1/1000 of a grain of blood can be very readily distinguished in a stain after years have passed. The very year of a certain vintage of wine has been told by means of “absorption,” or the action of different bodies on light in the spectrum. It is now easy, “by means of the absorption of different vapours and different substances held in solution, to determine not only what the absorbers really are, but also to detect a minute quantity.” The application of this theory is due to Dr. Gladstone, who used hollow prisms filled with certain substances, and so thickened the “absorption lines.” By these lines, or bands, with the aid of the Spectrum Microscope, most wonderful discoveries have been made, and will continue to be made. We will close this portion of the subject with a brief description of the Spectroscope in principle.
The instrument consists of two telescopes arranged with two object-glasses on a stand (fig. 150). A narrow slit is put in place of the eye-piece of one, the arrangement admitting of the slit being made smaller or larger by means of screws. The glass to which the slit is attached is called the collimating lens. The light, at the end of the slit seen from the other telescope, being separated by the prisms between the two telescopes, will produce the spectrum. The Spectroscope is enclosed, so that no exterior light shall interfere with the spectra the student wishes to observe. This merely indicates the principle, not the details, of the Spectroscope, which vary in different instruments.
We may now pass from the Spectroscope to the Telescope and the Microscope, instruments to which we are most largely indebted for our knowledge of our surroundings in earth, air, and water.
The word Telescope is derived from the Greek tele, far, and skopein, to see; and the instrument is based upon the property possessed by a convex lens[Pg 148] or concave mirror, of converging to a focus the rays of light falling on it from any object, and at that point or focus forming an image of the object. The following diagram will illustrate this. Let VW be a lens, and AB an object between the glass, and F the focus. The ray, Ac, is so refracted as to appear to come from a. The ray from b likewise appears in a similar way, and a magnified image, ab, is the result (fig. 152).
The ordinary Telescope consists of an object-glass and an eye-lens, with two intermediates to bring the object into an erect position. A lens brings it near to us, and a magnifier enlarges it for inspection. We will now give a short history of the Telescope and its improved construction.
Roger Bacon was supposed to have had some knowledge of the Telescope, for in 1551 it was written: “Great talke there is of a glass he made at Oxford, in which men see things that were don.” But a little later, Baptista Porta found out the power of the convex lens to bring objects “nearer.” It was, however, according to the old tale, quite by an accident that the Telescope was discovered about the year 1608.

In Middleburg, in Holland, lived a spectacle-maker named Zachary Jansen, and his sons, when playing with the lenses in the shop, happened to fix two of them at the proper distance, and then to look through both. To the astonishment of the boys, they perceived an inverted image of the church weathercock much nearer and much larger than usual. They at once told their father what they had seen. He fixed the glasses in a tube, and having satisfied himself that his sons were correct, thought little more about the matter. This is the story as told, but there is little doubt that for the first Telescope the world was indebted either to Hans Lippersheim or Joseph Adriansz, the former a spectacle-maker of Middleburg; and in October 1608, Lippersheim presented to the Government three instruments, with which he “could see things at a distance.” Jansen came after this. The report of the invention soon spread, and Galileo, who was then in Venice, eagerly seized upon the idea, and returning to Padua with some lenses, he managed to construct a telescope, and began to study the heavens. This was in 1609. Galileo’s Tube became celebrated, and all the first[Pg 149] telescopes were made with the concave eye-lens. Rheita, a monk, made a binocular telescope, as now used in our opera- and field-glasses approximately.
But the prismatic colours which showed themselves in the early telescopes were not got rid of, nor was it till 1729 that Hall, by studying the mechanism of the eye, managed a combination of lenses free from colour. Ten years before (in 1718) Hadley had established the Reflector Telescope; Herschel made his celebrated forty-foot “reflector” in 1789.

However, to resume. In 1747, Euler declared that it was quite possible to construct an arrangement of lenses so as to obtain a colourless image, but he was at first challenged by John Dollond. The latter, however, was afterwards induced to make experiments with prisms of crown and flint glass. He then tried lenses, and with a concave lens of flint, and a convex lens of crown, he corrected the colours. The question of proper curvature was finally settled, and the “Achromatic” Telescope became an accomplished fact.
There are two classes of Telescopes—the reflecting and refracting. Lord Rosse’s is an instance of the former. Mr. Grubb’s immense instrument in Dublin is a refractor.
The Microscope has been also attributed to Zacharias Jansen, and Drebbel, in 1619, possessed the instrument in London, but it was of little or no use. The lens invented by Hall, as already mentioned, gave an impetus to the Microscope. In the simple Microscope the objects are seen directly through the lens or lenses acting as one. The compound instrument is composed of two lenses (or a number formed to do duty as two), an eye-lens, and an object-lens. Between these is a “stop” to restrain all light, except what is necessary to view the object distinctly. The large glass near the object bends the rays on to the eyeglass, and a perfect magnified image is perceived. We annex diagrams, from which the construction will be readily understood.

We have in the previous chapter mentioned the effect of light upon the eye and its direction, and when an object is placed very near the eye we know it cannot be distinctly seen; a magnified image is thrown upon the retina, and the divergency of the rays prevents a clear image being perceived. But if a small lens of a short “focal length” be placed in front of the eye, having PQ for its focus, the rays of light will be parallel, or very nearly so, and will as such produce “distinct vision,” and the image will be magnified at pq. In the Compound Refracting Microscope, BAB is[Pg 150] the convex lens, near which an object, PQ, is placed a little beyond its focal length. An inverted image, pq, will then be formed. This image is produced in the convex lens, bab′, and when the rays are reflected out they are parallel, and are distinctly seen. So the eye of the observer at the point E will see a magnified image of the object at PQ brought up to pq (fig. 155).

Sir Isaac Newton suggested the Reflecting Microscope, and Dr. Wollaston and Sir David Brewster improved the instrument called the “Periscopic Microscope,” in which two hemispherical lenses were cemented together by the plane surfaces, and having a “stop” between them to limit the aperture. Then the “Achromatic” instrument came into use, and since then the Microscope has gradually attained perfection.

We have so frequently mentioned lenses that it may be as well to say something about them. Lenses may be spherical, double-convex, plane-convex, plane-concave, double-concave, and concave-convex. Convex lenses bring the parallel lines which strike them to a focus, as we see in the “burning-glass.” The concave or hollow lens appears as in fig. 156. The rays that follow it parallel to its axis are refracted, and as if they came from a point F in the diagram. But converging rays falling on it emerge in a parallel direction as above, or diverge as in fig. 158.

1. Focus of parallel rays. 2. Focus of divergent rays. 3. Focus of divergent rays brought forward by more convex lens.
The use of spectacles to long or short-sighted people is a necessity, and the lenses used vary. The eye has usually the capacity of suiting itself to viewing objects—its accommodation, as it is termed—near or far. But when the forepart of the eye is curved, and cannot adapt itself to distant objects, the person is said to be short-sighted. In long sight the axis of the eyeball is too short, and the focus falls beyond the retina; in short sight it is too long. In the diagrams herewith fig. 159 shows by the dotted lines the position of the retina in long sight, and fig. 160 in short sight, the clear lines showing in each case the perfectly-formed eye. For long sight and old sight the double[Pg 151]-convex glass is used, for short sight the double-concave (fig. 162). We know the burning-glass gives us a small image of the sun as it converges the rays to its focus. But lenses will do more than this, and in the Photographic Camera we find great interest and amusement.

Photography (or writing by light) depends upon the property which certain preparations possess of being blackened by exposure to light while in contact with matter. By an achromatic arrangement of lenses the camera gives us a representation of the desired object Fig. 163 shows the image on the plate, and figs. 164 and 165 the arrangement of lenses.



To Porta, the Neapolitan physician, whose name we have already mentioned more than once, is due the first idea of the Photographic Camera. He found that if light was admitted through a small aperture, objects from which rays reached the hole would be reflected on the wall like a picture. To this fact we are indebted for the Camera Obscura, which receives the picture upon a plane surface by an arrangement of lenses. In fact, Porta nearly arrived at the Daguerreotype process. He thought he could teach[Pg 152] people to draw by following the focussed picture with a crayon, but he could not conquer the aërial perspective.
So the camera languished till 1820, when Wedgwood and Sir Humphrey Davy attempted to obtain some views with nitrate of silver, but they became obliterated when exposed to the daylight.

As early as 1814, however, M. Niepce had made a series of experiments in photography, and subsequently having heard that M. Daguerre was turning his attention to the same subject, he communicated with him. In 1827 a paper was read before the Royal Society, and in 1829 a partnership deed was drawn up between Daguerre and Niepce for “copying engravings by photography.” Daguerre worked hard, and at length succeeded in obtaining a picture by a long process, to which, perhaps, some of our readers are indebted for their likenesses forty years ago. By means of iodine evaporated on a metal plate covered with “gold-yellow,” and exposing the plate then in a second box to mercurial vapour, he marked the image in the camera, and then he immersed the plate in hyposulphate of soda, and was able to expose the image obtained to daylight.

But the mode now in use is the “collodion” process. We have all seen the photographer pouring the iodized collodion on the plate, and letting the superfluous liquid drain from a corner of the glass. When it is dry the glass-plate is dipped into a solution of nitrate of silver, and then in a few minutes the glass is ready. The focus is then arranged, and the prepared plate conveyed in a special slide—to keep it from the light—to the camera. When the “patient” is ready, the covering of the lens is removed, and the light works the image into the sensitive plate. The impression is then[Pg 153] “brought up,” and when developed is washed in water, and after by a solution which dissolves all the silver from the parts not darkened by the light. Thus the negative is obtained and printed from in the usual manner.
Instantaneous photography is now practised with great success. An express train, or the movements of a horse at full speed, can thus be taken in a second or less. These results are obtained by using prepared plates, and the “emulsion process,” as it is called, succeeds admirably. The mode of preparation is given in a late work upon the subject, and the photographic plates may also be obtained ready for use. Gelatine and water, mixed with bromide of ammonium, nitrate of silver, and carbonate of ammonium, mixed with certain proportions of water, form the “emulsion.” We need not go into all the details here. Information can easily be obtained from published works, and as the plates can be purchased by amateurs, they will find that the best way.
Aside from the art interest in the new plates is quite another, that springs from the fact that it is now possible to take pictures of men, animals, and machinery in rapid motion, thus enabling us to view them in a way that would be impossible with the unaided eye. The first experiments in this direction were applied to the movements of a horse moving at full speed. The pictures, taken in series, showed that he performed muscular actions that were not before comprehended or even imagined. These pictures at the time attracted great attention, and instantaneous pictures have been since taken of dancers in a ball-room, of vessels and steam-boats in rapid movement, of all kinds of animals in motion, and of machinery in operation. As the pictures represent the movements at one instant of time, they give, as it were, a fixed view of a motion, precisely as if it were suddenly arrested in full action. In the case of animals, the motions of the nostrils are represented in the most singular manner, and the spokes of a steam-boat’s paddle-wheel are shown apparently perfectly still while the spray and waves appear in active motion, or, rather, as they would look if they could be instantly frozen. It is clear the new process and pictures will open a wide and instructive field in art and in the study of mechanical action.
While on the subject of Photography we may mention a very ingenious little apparatus called a Scenograph, the invention of Dr. Candize. It is really a pocket-camera, and is so easily manipulated that it will be found a most pleasant and useful holiday companion. Any one may obtain good results with it, and friends of ours have had occasion to put it in practice during a series of excursions, when it was found to answer in every instance.
The Scenograph is something like a common Stereoscope in outward appearance, and would, perhaps, be at first regarded as a mere toy, did not a more intimate acquaintance prove it a great acquisition, particularly to explorers and tourists. The tripod stand which supports the apparatus is, when not in actual use in that capacity, a very excellent walking-stick, in which the two other “legs” are carried. The instrument, as will be per[Pg 154]ceived from the illustration (fig. 166), is very handy. It produces pictures about the “cabinet” size, and the whole is so arranged that it can be packed and carried in the pocket with ease.

Photography, as a rule, necessitates a dark room or cabinet, and many preparations as we all know—a “messing” about with chemicals and considerable practice before we can become proficient; so it is not surprising that few amateurs take to it—they prefer to purchase the pictures. But in the new apparatus of which we are speaking, the glass plates are already prepared to receive the image. It is not at all necessary for the operator to stain his fingers and knuckles and nails with nitrate of silver, or any other “chemicals” whatever. He just inserts the plate in the Scenograph,[Pg 155] and then his apparatus being steadily set up, he removes the covering from the lens. To develop the image (in the dusk of the evening or by candle-light) it is necessary to put some drops of ammonia in a saucer, breathe upon the plate so as to soften the collodion, and hold it above the ammonia, and then, under the influence of the vapour, the picture will appear. After this simple operation the picture will be found fixed for a lengthened period—practically indefinitely. Thus on the return of the pedestrian he can reproduce, at small expense, a whole series of little pictures faithfully representing his holiday tour. The illustration shows a small apparatus by which on thin plates small photographs can be taken and fixed till it is found desirable to enlarge them.
The Photophone, one of the most recent contributions to science, is an instrument which, in combination with the telephone principle, makes it possible to convey sounds by means of a ray of light, and by means of a quivering beam “to produce articulate speech at a distance. The success of the Photophone depends upon a rare element, selenium, which has its “electrical resistance” affected by light. Professor Adams demonstrated that the resistance of selenium was reduced just in proportion as the intensity of the light which was acting upon it. Here was the key to the Photophone as thought out by Professor Bell. He fancied that he might by means of his telephone produce sound if he could vary the intensity of the beam of light upon the selenium, which he connected with his telephone and battery.
The Photophone consists of a transmitter for receiving the voice and conveying it along the beam of light, and a receiver for taking the light and converting it into sound—the receiver being the telephone. There is a small mirror (silvered mica has been used) suspended freely for vibration. A lens is used to transmit to this the beam of light, and this beam is again reflected by another lens to the receiver, which consists of a reflector which has a cell of selenium in its focus, connected, as already stated, with the telephone and battery. The speaker stands behind the mirror, and the sound of his voice against the reverse side makes it vibrate in unison with the sounds uttered. The movements cause a quivering in the reflected beam, and this in its changing intensity acts on the selenium, which changes its resistance accordingly, and through the telephone gives forth a sound!
This is the apparently complicated but really simple, and at the same time wonderful, invention of Professor Bell. By the Photophone not only sounds but movements can be converted into sound; even the burning of a candle can be heard! The Photophone is still capable of improvement, and has not as yet arrived at its full development, for it is stated it can be made quite independent of a battery or telephone.
There are many phenomena connected with the Polarization of Light. This requires some notice at our hands. We know that a ray of ordinary light is supposed to be caused by vibrations of the highly attenuated medium, æther. These vibrations occur across the direction of the ray; but when[Pg 156] they occur only in one plane the light is said to be “polarized.” Polarization means possessing poles (like a magnet); the polarized rays have “sides,” as Newton said, or, as explained by Dr. Whewell, “opposite properties in opposite directions, so exactly equal as to be capable of accurately neutralizing each other.” There are some crystals which possess the property of “double refraction,” and thus a ray of common light passing through such a crystal is divided into two polarized rays, taking different directions. One is refracted according to the usual laws of refraction; the other is not, and the planes of polarization are at right angles. It is difficult within the limits of this chapter to explain the whole theory of Polarization. In order to account for certain phenomena in optics, philosophers have assumed that rays possess polarity; and polarized light is light which has had the property of Polarization conferred upon it by reflection, refraction, or absorption. Common light has been compared to a round ruler, and polarized light to a flat ribbon. Huygens found out, when engaged upon the investigation of double refraction, that the rays of light, divided by passing through a crystal (a rhomb) of Iceland spar, possessed certain qualities. When he passed them through a second rhomb, he found that the brightness, relatively, of the rays depended upon the position of the second prism, and in some positions one ray disappeared entirely. The light had been reduced to vibrations in one plane. In 1808, Malus, happening to direct a double refracting prism to the windows then reflecting the sunset, found that as he turned the prism round, the ordinary image of the window nearly disappeared in two opposite positions; and in two other positions, at right angles, the “extraordinary” image nearly vanished. So he found that polarization was produced by reflection as well as by transmission. The differences between common and polarized light have been summed up by Mr. Goddard as follows:—
| Common Light | Polarized Light |
| “Is capable of reflection at oblique angles of incidence in every position of the reflector. | “Is capable of reflection at oblique angles only in certain positions of the reflector. |
| “Will pass through a bundle of plates of glass in any position in which they may be placed. | “Will only pass through such glasses when they are in certain positions. |
| “Will pass through a plate of tourmaline, cut parallel to the axis of the crystal, in every position of the plate.” | “Will only pass in certain positions, and in others will not pass at all.” |
The bundle of glass plates or the tourmaline plate is thus the test for polarized light, and is termed an analyzer.
The arrangement called a “Nichol’s prism,” made by cutting a prism of Iceland spar and uniting the halves with a cement, so that only one polarized ray can pass through it, is termed a Polarizer. It only permits one of the two rays produced by “double refraction” to pass, and the ray (as said above) will contain none but transverse vibrations. Polarized light will[Pg 157] produce beautiful colours. The whole subject is very interesting to the scientist, but rather a difficult one for the general reader to understand.
Amongst the uses to which light has been put is that of a milk-tester. The Lactoscope will show the quantity of butter contained in a certain quantity of milk, by diluting it till it displays a certain degree of transparency. There is another method, by the transmission of light.
The first test is obtained by means of a glass tube about nine inches long, closed at one end, and containing a small porcelain rod marked with black lines. A small quantity of milk is measured and placed in the tube. The black lines cannot at first be seen through the tube, but by adding water the milk is rendered transparent, and the black lines become visible. The surface of milk in the tube, by a graduated scale upon it, shows the percentage of butter.

The second method is not so simple. A short tube of tin, blackened on the inside, and supported upright, has an opening on one side, and opposite this, inside the tube, is a mirror placed at an angle of 45°. “By placing a lighted candle at a known distance opposite the opening, its light is reflected in the mirror and thrown upward through the tube. On top of the tube is placed a round vessel of glass or metal, closed at the bottom by a sheet of clear glass. The vessel is closed at the top by a cover having an opening in the centre, in which slides up and down a small tube closed at the bottom with glass, and having an eye-piece at the top. The milk to be tested is placed in this vessel on the top of the tin tube, so that the light of the candle reflected from the mirror passes upward through the milk. Then, by looking through the sliding tube and moving it up and down, a point may be found where the image of the candle in the mirror can be seen through the milk. This device depends, as will be seen, on observing the light transmitted through a film of milk, and the thickness of the film is the measure of the value of the milk. The movable tube contains a graduated scale, and by comparison of this with a printed table, the percentage of butter in the milk may be ascertained.”
In concluding this chapter we give a few hints for some pleasant[Pg 158] relaxation for young people, which has many a time created amusement. The experiment consists in cutting out in paper or cardboard certain portions of a face or figure, as per the illustration herewith. Fig. 167 gives the card as cut with the scissors, and the two subsequent faces are the result of the same held at a less or greater distance from a screen. The illustrations (fig. 168) will assist those who wish to amuse children by making rabbits, etc., on the wall. The shadows will be seen perfectly thrown if the hands be carefully fixed near a good light.

We are all so familiar with the “Magic Lantern,” and the apparatus[Pg 159] for dissolving views by an arrangement of lenses and manipulation of slides, that we need do no more than refer to them.

The various ghost illusions, etc., produced by indirect mirrors, have already been referred to, the ghost being merely the reflection of an individual seen through a sheet of glass between the spectators and the stage. The strong light throws a reflection from a parallel mirror lower down, and this reflected image can be made to appear amongst the real actors who are behind the plate-glass in full view of the audience, who are, however, ignorant of the existence of the glass screen.
For the winter evenings one may easily procure an apparatus for dissolving views by the oxy-hydrogen light. One, as shown in the illustration herewith (fig. 169), will answer every purpose, and by this double arrangement phantasmagoria may be produced, or a fairy tale may be illustrated. The effect of gradually-approaching night may be given to the picture by means of a special glass in the lower lanthorn. The apparatus is exhibited by means of a Drummond light, and is very simple, although a certain supply of gas is necessary for the performance. But this can be easily procured by an indiarubber tube, or in a bag supplied for the purpose. Almost any objects can be used, photographs, etc., etc., and many very comical arrangements can be made.
We have lately been reading a curious method of obtaining light from oyster-shells in a Trans-Atlantic magazine. We give an extract wherewith to close this chapter. The compound is “luminous paint.”
“It has been known that certain compounds of lime and sulphur had the property of absorbing light, and giving it out again when placed in the dark. A simple way to do this is to expose clean oyster-shells to a red heat for half an hour. When cold, the best pieces are picked out and packed with alternate layers of sulphur in a crucible, and exposed to a red heat for an hour. When cold, the mass is broken up, and the whitest pieces are placed in a clean glass bottle. On exposing the bottle to bright sunshine during the day, it is found that at night its contents will give out a pale light in the dark. Such a bottle filled more than a hundred years ago still gives out light when exposed to the sun, proving the persistency of the property of reproducing light. Very many experiments have been more recently made in this direction, and the light-giving property greatly enhanced. The chemicals, ground to a flour, may now be mixed with oils or water for paints, may be powdered on hot glass, and glass covered with a film of clear glass, or mixed with celluloid, papier-maché, or other plastic materials. As a paint, it may be applied to a diver’s dress, to cards, clock dials, sign-boards, and other surfaces exposed to sunlight during the day; the paint gives out a pale violet light at night sufficient to enable the objects to be readily seen in the dark. If the object covered with the prepared paint is not exposed to the sun, or if the light fades in the dark, a short piece of magnesium wire burned before it serves to restore the light-giving property.”

CHAPTER XIV.
SPECTRAL ILLUSIONS.
A SPECTRE VISIBLE—CURIOUS ILLUSIONS—GHOSTS.
We have already given numerous examples of the effects produced by impressions on the retina by mechanical appliances. We can now in a short chapter speak of the cause of many spectral illusions, commonly supposed to be “ghosts” or “spirits.” That there are many “well-authenticated ‘ghost stories’” no one can doubt who has read the literature of the day; and we ourselves do not in any way desire to throw any doubt upon the existence of certain so-called “ghosts.” That appearances of some kind or another are seen by people we know. We ourselves have seen such, but we cannot say we believe in the popular ghost.
In ancient times mirrors were much employed by the so-called magicians, and in our day many wonderful ghost effects have been shown at the (late) Polytechnic Institution. Some people are believers in table-turning and spiritualism, and mesmerists still attract large audiences, and appear to possess extraordinary power over some individuals. But apparitions have been seen by people eminently worthy of credit. The experience of the learned Doctor, which appeared some months ago in the Athenæum, is a case in point. This narrative is concise and clear. The spectre was there. How did it get there? Was the “appearance” objective or subjective? Let us give an extract from the Reverend Doctor’s narrative, and comment upon it afterwards. We may premise that Dr. Jessopp had gone over to Lord Orford’s (Mannington Hall), and at eleven o’clock was busy writing in the library, and was “the only person downstairs.” We will give this ghost story in the Doctor’s own words. After taking up a certain volume—time about 1 a.m.:—
“I had been engaged on it about half an hour, and was beginning to think my work was drawing to a close, when, as I was actually writing, I saw a large white hand within a foot of my elbow. Turning my head, there sat a figure of a somewhat large man with his back to the fire, bending slightly over the table, and apparently examining the pile of books that I had been at work upon.”... After describing the appearance of the nocturnal visitor, Dr. Jessopp proceeds:—
“There he sat, and I was fascinated; afraid not of his staying, but lest he should go. Stopping in my writing I lifted my left hand from the paper, stretched it out to the pile of books, and moved the top one—my arm passed[Pg 162] in front of the figure, and it vanished.”... Shortly after the figure appeared again, and “I was penning a sentence to address to him, when I discovered I did not dare to speak. I was afraid of the sound of my own voice! There he sat, and there sat I. I turned my head and finished writing. Having finished my task, I shut the book, and threw it on the table; it made a slight noise as it fell;—the figure vanished.”
Now here we have a perfectly plain narrative, clear and full. A ghost appeared; he is described distinctly. How can we account for the apparition? In the first place, someone might have played a trick, but that idea was put aside by Dr. Wilks, who attempted to explain the appearances. He went fully into the question, and as it bears upon our explanation of the reality of Spectral Illusions, we may condense his evidence. It will of course be conceded that all the usual objects seen by people are material, and the image of what we look at is formed upon the retina in the manner already explained. But all images upon the retina are not immediately observed; the impression may, to a certain extent, remain. Words are often impressed upon the brain,—words which we in our sober senses would never think of repeating,—and yet when we are delirious we give vent to these expressions, of whose very nature and meaning we are perfectly unconscious. It is, according to our reference (Dr. Wilks), “quite possible for the perceptive part of the brain to be thrown into an active condition quite independent of the normal stimulus conducted to it from the retina.” If, under these circumstances, an object be viewed independently, and, as it were, unconsciously, it is merely, we believe, a parallel to the impression of words before noted. Sound and light are governed by the same laws. In fevers we fancy we see all kinds of things which have no existence. In dreams we hear noises; and many a time people dreaming have been awakened by the report of a gun, or the ringing of a bell which had no material origin,—the nerves were excited, the “perceptive centre” of the brain was moved.
But if sight and hearing thus have their origin from the brain and not from without, there must have been some predisposing cause, some excitement to induce such a condition of things. “The impressions become abnormal and subjective,—the normal condition being objective,—the impression is received from without, and impressed upon the eye.
Now, let us consider the “ghost”! Lately there have been many instances brought forward of “spiritual” appearances, but we think nobody has ever seen a “material” ghost; yet on the other hand none of us have any knowledge of anything in the likeness of a ghost, or that has not a material basis which can bring forward an image on the retina! Therefore we are brought to the conclusion that apparitions are spectres emanating from within the brain, not from any outward manifestation, because it is within the experience of everybody that in bad health, or disordered digestive functions, images are produced in the brain and nerves of the eye.
These remarks have perhaps been made before in one form or other, but[Pg 163] as much popular interest is always awakened by the supernatural, or what is supposed to be supernatural, we may go a little farther, and inquire how it was that the ghost seen by Dr. Jessopp disappeared when he raised his arm. Would any ghost be afraid of the Doctor extending his hand? The fact no doubt occurred as related. The explanation is that the narrator had been much impressed by a certain picture, which a correspondent soon identified as a portrait of “Parsons, the Jesuit Father.” The description given is that of the priest who was described by the Doctor in one of his books. The association of ideas in the library of a Norfolk house connected with the Walpoles, with whom Parsons had been a leader, gave rise, during a period of “forty winks” at midnight, to the spectre.
In the interesting letters written upon “Natural Magic” by Sir David Brewster, the subject of Spectral Illusions is treated at some length, and with undoubted authority. Sir David thought the subject worth discussing with reference to the illusions or spectres mentioned by Dr. Hibbert. Sir David Brewster gives his own experiences which occurred while he was staying at the house of a lady in the country.
The illusions appear to have affected her ear as well as the eye. We shall see in the next chapter how intimately sound and light are connected, and how the eyes and ears are equally impressed, though in a different way, by the vibration of particles. The lady referred to was about to go upstairs to dress for dinner one afternoon, when she heard her husband’s voice calling to her by name. She opened the door, and nobody was outside; and when she returned for a moment to the fire she heard the voice again calling, “Come to me; come, come away,” in a somewhat impatient tone. She immediately went in search of her husband, but he did not come in till half an hour afterwards, and of course said he had not called, and told her where he had been at the time—some distance away. This happened on the 26th December, 1830, but a more alarming occurrence took place four days after.
About the same time in the afternoon of the 30th December, the lady came into the drawing-room, and to her great astonishment she perceived her husband standing with his back to the fireplace. She had seen him go out walking a short time previously, and was naturally surprised to find he had returned so soon. He looked at her very thoughtfully, and made no answer. She sat down close beside him at the fire, and as he still gazed upon her she said, “Why don’t you say something!” The figure immediately moved away towards the window at the farther end of the room, still gazing at her, “and it passed so close that she was struck by the circumstance of hearing no step nor sound, nor feeling her dress brushed against, nor even any agitation of the air.” Although convinced this was not her husband, the lady never fancied there was anything supernatural in the appearance of the figure. Subsequently she was convinced that it was a spectral illusion, although she could not see through the figure which appeared as substantial as the reality.
Were it advisable, we could multiply instances. In the Edinburgh Journal of Science these, and many more instances of spectral illusions were narrated by the husband of the lady. She frequently beheld deceased relatives or absent friends, and described their dress and general appearance very minutely. On one occasion she perceived a coach full of skeletons drive up to the door, and noticed spectral dogs and cats (her own pets’ likenesses) in the room. There can be no doubt upon these points; the appearances were manifest and distinct. They were seen in the presence of other people, in solitude, and in the society of her husband. The lady was in delicate health, and very sensitive. The spectres appeared in daylight as well as in the dark, or by candle-light.
Let us now, guided by what we have already written, and by Sir David Brewster’s experience, endeavour to give a rational explanation of these illusions. “The mind’s eye is really the body’s eye, and the retina is the common tablet upon which both classes of impressions are painted, and by means of which they receive their visual existence according to the same optical laws.”
“In the healthy state of mind and body the relative intensity of the two classes of impressions on the retina are nicely adjusted—the bodily and mental are balanced. The latter are feeble and transient, and in ordinary temperaments are never capable of disturbing or effacing the direct images of visible objects.... The mind cannot perform two different functions at the same instant, and the direction of its attention to one of the two classes of impressions necessarily produces the extinction of the other; but so rapid is the exercise of mental power, that the alternate appearance and disappearance of the two contending impressions is no more recognized than the successive observations of external objects during the twinkling of the eyelids.”
We have before illustrated, by means of the pen and the ink-bottle, how one object is lost sight of when the other is attentively regarded, and a material picture or scene may be equally lost sight of, and a mental picture take its place in the eye, when we recall places or people we have seen or remembered.
We have all heard numerous anecdotes of what is termed “absent-mindedness.” Some people are quite absorbed in study, and can see or hear no one in the room when deeply occupied. We may be satisfied then that “pictures of the mind and spectral illusions are equally impressions upon the retina, and only differ in the degree of vividness with which they are seen.” If we press our eyes the phosphorescence becomes apparent, and we can make a picture of the sun or a lamp visible for a long time to our closed eyes if we stare at either object for a few seconds, and shut our lids. So by increasing the sensibility of the retina we can obtain the image, and alter its colour by pressure on the eye.
It is well known that poisons will affect sight, and belladonna applied to the eyes will so affect them as to render the sight nil, by enlargement of[Pg 165] the “pupil.” If one is out of health there is practically a poisoning of the system, and when we have a “bilious headache” we see colours and stars because there is a pressure upon the blood-vessels of the eye. The effects of a disordered stomach, induced by drinking too much, are well known; objects are seen double, and most ghosts may be traced to a disordered state of health of mind or body, brought on by excitement or fatigue. We could relate a series of ghost stories,—some in our own experience, for we have seen a ghost equally with our neighbours,—but this is not the place for them. Although many apparently incontrovertible assertions are made, and many spectres have been produced to adorn a tale, we must put on record our own opinion, that every one could be traced to mental impression or bodily affection had we only the key to the life and circumstances of the ghost-seer. Many celebrated conjurers will convince us almost against our reason that our pocket-handkerchief is in the orange just cut up. They will bring live rabbits from our coat-pockets or vests, and pigeons from our opera-hats. These are equally illusions. We know what can be done with mirrors. We have seen ghosts at the Polytechnic, but we must put down all apparitions as the result of mental or bodily, even unconscious impressions upon the retina of the eye. There are numerous illusions, such as the Fata Morgana, the Spectre of the Brocken, etc., which are due to a peculiar state of the atmosphere, and to the unequal reflection and refraction of light. Those, and many other optical phenomena, will, with phenomena of heat and sound, be treated under Meteorology, when we will consider the rainbow and the aurora, with many other atmospheric effects.

CHAPTER XV
ACOUSTICS.
THE EAR, AND HEARING—PHYSIOLOGY OF HEARING AND SOUND—SOUND AS COMPARED WITH LIGHT—WHAT IS SOUND?—VELOCITY OF SOUND—CONDUCTIBILITY—THE HARMONOGRAPH.
Before entering upon the science of Acoustics, a short description of the ear, and the mode in which sound is conveyed to our brain, will be no doubt acceptable to our readers. The study of the organs of hearing is not an easy one; although we can see the exterior portion, the interior and delicate membranes are hidden from us in the very hardest bone of the body—the petrous bone, the temporal and rock-like bone of the head.

Fig. 170- 1. Temple bone. 2. Outer surface of temple. 3. Upper wall of bony part of hearing canal. 4. Ligature holding “hammer” bone to roof of drum cavity. 5. Roof to drum cavity. 6. Semicircular canals. 7. Anvil bone. 8. Hammer bone. 9. Stirrup bone. 10. Cochlea. 11. Drum-head cut across. 12. Isthmus of Eustachian tube. 13. Mouth of tube in the throat. 14. Auditory canal. 15. Lower wall of canal. 16. Lower wall of cartilaginous part of canal. 17. Wax glands. 18. Lobule. 19. Upper wall of cartilaginous portion of canal. 20. Mouth of auditory canal. 21. Anti-tragus.
The ear (external) is composed of the auricle, the visible ear, the auditory canal, and the drum-head, or membra tympani. The tympanum, or “drum,” is situated between the external and the internal portions of the ear. This part is the “middle ear,” and is an air cavity, and through it pass two[Pg 167] nerves, one to the face, and the other to the tongue. The internal ear is called the “labyrinth,” from its intricate structure. We give an illustration of the auditory apparatus of man (fig. 170).
The auricle, or exterior ear, is also represented, but we need not go into any minute description of the parts. We will just name them (fig. 171).
Sound is the motion imparted to the auditory nerve, and we shall see in a moment how sound is produced. The undulations enter the auditory canal, having been taken up by the auricle; the waves or vibrations move at the rate of 1,100 feet a second, and reach the drum-head, which has motion imparted to it. This motion or oscillation is imparted to other portions, and through the liquid in the labyrinth. The impressions of the sound wave are conveyed to the nerve, and this perception of the movement in the water of the labyrinth by the nerve threads and the brain causes what we term “hearing.”

Let us now endeavour to explain what sound is, and how it arises. There are some curious parallels between sound and light. When speaking of light we mentioned some of the analogies between sound and light, and as we proceed to consider sound, we will not lose sight of the light we have just passed by.
Sound is the influence of air in motion upon the hearing or auditory nerves. Light, as we have seen, is the ether in motion, the vibrations striking the nerves of the eye.
There are musical and unmusical sounds. The former are audible when the vibrations of the air reach our nerves at regular intervals. Unmusical sounds, or irregular vibrations, create noise. Now, musical tones bear the same relation to the ear as colours do to the eye. We must have a certain number of vibrations of ether to give us a certain colour (vide table). “About four hundred and fifty billion impulses in a second” give red light. The violet rays require nearly double. So we obtain colours by[Pg 168] the different rate of the impingement of impulses on the retina. The eyes, as we have already learned, cannot receive any more rapidly-recurring impressions than those producing violet, although as proved, the spectrum is by no means exhausted, even if they are invisible. In the consideration of Calorescence we pointed this out. These invisible rays work great chemical changes when they get beyond violet, and are shown to be heat. So the rays which do not reach the velocity of red rays are also heat, which is the effect of motion.
Thus we have Heat, Light, and Sound, all the ascertained results of vibratory motion. The stillness of the ether around us is known as “Darkness”; the stillness of the air is “Silence”; the comparative absence of heat, or molecular motion of bodies is “Cold”!
In the first part we showed how coins impart motion to each other.
| VELOCITY OF LIGHT WAVES. | ||
|---|---|---|
| According to Sir J. Herschel. | ||
| Colour of the Spectrum. |
No. of Undulations in an inch. |
No. of Undulations in a second. |
| Extreme Red | 37,640 | 458,000,000,000,000 |
| Red | 39,180 | 477,000,000,000,000 |
| Intermediate | 40,720 | 495,000,000,000,000 |
| Orange | 41,610 | 506,000,000,000,000 |
| Intermediate | 42,510 | 517,000,000,000,000 |
| Yellow | 44,000 | 535,000,000,000,000 |
| Intermediate | 45,600 | 555,000,000,000,000 |
| Green | 47,460 | 577,000,000,000,000 |
| Intermediate | 49,320 | 600,000,000,000,000 |
| Blue | 51,110 | 622,000,000,000,000 |
| Intermediate | 52,910 | 644,000,000,000,000 |
| Indigo | 54,070 | 658,000,000,000,000 |
| Intermediate | 55,240 | 672,000,000,000,000 |
| Violet | 57,490 | 699,000,000,000,000 |
| Extreme Violet | 59,750 | 727,000,000,000,000 |
When an impulse was given the motion was carried from coin to coin, and at length the last one in the row flew out. This is the case with sound. The air molecules strike one upon another, and the wave of “sound” reaches the tympanum, and thus the impression is conveyed to the brain. We say we hear—but why we hear, in what manner the movement of certain particles affects our consciousness, we cannot determine.
That the air is absolutely necessary to enable us to hear can readily be proved. The experiment has frequently been made; place a bell under the receiver of an air-pump, and we can hear it ring. But if we exhaust the air the sound will get fainter and fainter. Similarly, as many of us have experienced upon high mountains, sounds are less marked. Sound diminishes in its intensity, just as heat and light do. Sound is reflected and refracted, as are light and radiant heat. We have already shown the effect of reflectors upon heat. Sound is caught and reflected in the same way as[Pg 169] light from mirrors, or as the heat waves in the reflectors. We have what we term “sounding boards” in pulpits, and speaking tubes will carry sound for us without loss of power. Echoes are merely reflected sounds.
The velocity of sound is accepted as 1,100 feet in a second, which is far inferior to the velocity of light. Fogs will retard sound, while water will carry it. Those who have ever rowed upon a lake will remember how easily the sound of their voices reached from boat to boat, and Dr. Hutton says that at Chelsea, on the Thames, he heard a person reading from a distance of a hundred and forty feet. Some extraordinary instances could be deduced of the enormous distances sound is said to have travelled. Guns have been heard at eighty miles distant, and the noise of a battle between the English and Dutch, in 1672, was heard even in Wales, a distance of two hundred miles from the scene of action.
Sound always travels with uniform velocity in the air in the same temperature. But sound! What is the cause of it? How does it arise? These questions can now be fully answered with reference to the foregoing observations. Phenomena of vibration render themselves visible by light, heat, and sound, and to arrive at some definite ideas of sound vibrations we may compare them to waves, such as may be produced by throwing a stone into a pond.
There are, so to speak, “standing” waves and “progressive” waves. The former can be produced (for instance) by thrumming a fiddle-string, and when the equilibrium of the cord is disturbed, the position of the equilibrium is passed simultaneously by the string-waves. In water the waves or vibrating points pass the position of equilibrium in succession.
Waves consist of elevations and depressions alternately, and when we obtain two “systems” of waves by throwing two stones into water, we can observe some curious effects. It can be seen how one series of depressions will come in contact with the other series of depressions, and the elevations will likewise unite with the result of longer depressions and elevations respectively; or it may very well be that elevation will meet depression, and then the so-called “interference” of waves will produce points of repose. These points are termed nodes. The waves of the string proceed in the plane of its axis; water waves extend in circles which increase in circumference.
The progression or propagation of sound may be said to begin when some tiny globule of matter expands in the air. The air particles strike one against the other, and so the motion is communicated to the air waves, which in time reach the ear. But the velocity of the sound is not equal in all substances. Air will convey it around our earth at the rate of 765 miles an hour, or 1,090 feet in a second. That is, we may accept such rate as correct at a temperature of 32° Fahr., and at a pressure of thirty inches, and the velocity increases almost exactly one foot per second for each degree of temperature above 32°. Therefore on an average, and speaking in “round numbers,” the estimate of 1,100 feet in a second may be[Pg 170] accepted as correct. In hydrogen gas the rate is much higher. Through water again it is different, and still faster through iron, glass, and wood, as will be seen in the following table:—
| TAKING AIR AS 1. | |
|---|---|
| Whalebone | 6⅔ |
| Tin | 7½ |
| Silver | 9 |
| Walnut | 10⅔ |
| Brass | 10⅔ |
| Oak | 10⅔ |
| Earthen pipes | 11 |
| Copper | 12 |
| Pear-wood | 12½ |
| Ebony | 14⅔ |
| Cherry | 15 |
| Willow | 16 |
| Glass | 16⅔ |
| Iron or Steel | 16⅔ |
| Deal | 18 |
So there is a considerable difference in the velocities of sound through the solid substances quoted, but these figures cannot be taken as exact, as different samples may give different results. In wires and bells the bodies themselves produce the sounds we hear. In wind instruments and the voice the air is the cause of the sound.
The very deepest notes are produced by the fewest vibrations. Fourteen or fifteen vibrations will give us a very low note, if not the very lowest. The pipe of sixteen feet, closed at its upper end, will produce sound waves of thirty-two feet. High notes can be formed from vibrations up to 48,000 in a second. Beyond these limits the ear cannot accept a musical sound.

We will explain the phenomenon of the vibration of strings by means of the illustration. In the cut we find a string or wire, which can be lengthened or shortened at pleasure by a movable bridge, and stretched by weights attached to the end (fig. 172).
We can now easily perceive that the shorter and thinner the string is, and the tighter it is, the number of vibrations will be greater and greater. The density of it is also to be considered, and when these conditions are in the smallest proportion then the tone will be highest. The depth will naturally increase with the thickness, density, and length, and with a decreasing tension. But we have strings of same thickness stretched to different degrees of tension, and thus producing different notes. Some strings are covered with wire to increase their gravity, and thus to produce low notes.
When a number of separate sounds succeed each other in very rapid course they produce a sound, but to appear as one sound to the ear they must amount to fifteen or sixteen vibrations every second. The particles of matter in the air form a connected system, and till they are disturbed they remain in equilibrium; but the moment they are in any way thrown out of this state they vibrate as the pendulum vibrates. The particles thus strike[Pg 171] each other, and impart a motion to the elastic medium air, so a sound comes to us.
The intensity of sounds gets less the farther it goes from us, or the loudness of sound is less the greater its distance. The law is, that in an unvarying medium the loudness varies inversely as the square of the distance. But Poisson has shown that when air-strata, differing in density, are existing between the ear and the source of the sound, the intensity or loudness with which it is heard depends only on the density of the air at the place the sound originated. This fact has been substantiated by balloonists who heard a railway whistle quite distinctly when they were nearly 20,000 feet above the ground. It therefore follows that sound can be heard in a balloon equally well as on the earth at certain given distances. But as the density of the air diminishes the sound becomes fainter, as has been proved by the bell rung in the receiver of an air-pump. The velocity of sound, to a certain extent, depends upon its intensity, as Earnshaw sought to prove; for he instanced a fact that in the Arctic regions, where sound can be heard for an immense distance, in consequence of the still and homogeneous air, the report of a cannon two miles and a half away was heard before the loud command to “fire,” which must have preceded the discharge. Another instance showing the difference in hearing through mixed and homogeneous media may be referred to. In the war with America, when the English and their foes were on opposite sides of a stream, an American was seen to beat his drum, but no sound came across. “A coating of soft snow and a thick atmosphere absorbed the noise.” Glazed, or hard snow, would have a contrary effect. Reynault also experimentally verified his theory, that sound when passing through a space of nearly 8,000 feet lost velocity as its intensity diminished, and in that distance between its arrival at 4,000 feet and at 7,500 feet, the sound velocity diminished by 2·2 feet per second. He also tried to demonstrate that sound velocity depended upon its pitch, and that lower notes travelled with the greater speed.
The reflection and refraction of sound follows the same fundamental laws as the reflection and refraction of light. The reflection of sound is termed an Echo, which is familiar to all tourists in Switzerland and Ireland particularly. There are several very remarkable echoes in the world: at Woodstock, and at the Sicilian cathedral of Gergenti, where the confessions poured forth near the door to priestly ears were heard by a man concealed behind the high altar at the opposite end. It is curious that such a spot should have been accidentally chosen for the Confessional. The whispering gallery in St. Paul’s is another instance of the echo.
Echoes are produced by the reflection of sound waves from a plane or even surface. A wall, or even a cloud, will produce echoes. Thunder is echoed from the clouds. (The celebrated echo of “Paddy Blake,” at Killarney, which, when you say “How do you do,” is reported to reply, “Very well, thank you,” can scarcely be quoted as a scientific illustration.) And the hills of Killarney contain an echo, and the bugle sounds are beautifully[Pg 172] repeated. In the cases of ordinary echo, when the speaker waits for the answer, he must place himself opposite the rock. If he stand at the side the echo will reply to another person in a corresponding place on the farther side, for the voice then strikes the rock at an angle, and the angle of reflection is the same, as in the case of light.
But if it should happen that there are a number of reflecting surfaces the echo will be repeated over and over again, as at the Lakes of Killarney. The Woodstock Echo, already referred to, and mentioned by several writers, repeats seventeen syllables by day, and twenty by night. In Shipley there is even a greater repetition. Of course the echo is fainter, because the waves are weaker if the reflecting surface be flat. But, as in the case of the mirrors reflecting light, a circular or concave surface will increase the intensity. A watch placed in one mirror will be heard ticking in the other focus. Whispering galleries carry sound by means of the curved surface. Sir John Herschel mentions an echo in the Menai Suspension Bridge. The blow of a hammer on one of the main piers will produce the sound from each of the crossbeams supporting the roadway, and from the opposite pier 576 feet distant, as well as many other repetitions.
Refraction of sound is caused by a wave of sound meeting another medium of different density, just as a beam of light is refracted from water. One sound wave imparts its motion to the new medium, and the new wave travels in a different direction. This change is refraction. The sound waves are refracted in different directions, according to the velocity it can acquire in the medium. If a sound pass from water into air it will be bent towards the perpendicular, because sound can travel faster in water than in air. If it pass from air into water its force will cause it to assume a less perpendicular direction, there being greater velocity in water. The velocity in air is only 1,100 feet in a second in our atmosphere. In water sound travels 4,700 feet in the same time. When the wave of sound falls upon a medium parallel to the refracting surface there is, however, no refraction—only a change of velocity, not direction.
When sound waves are prevented from dispersing the voice can be carried a great distance. Speaking tubes and trumpets, as well as ear trumpets, are examples of this principle, and of the reflection of sound.
There are many very interesting experiments in connection with Acoustics, some of which we will now impart to our readers. We shall then find many ingenious inventions to examine,—the Audiphone, Telephone, Megaphone, and Phonograph, which will occupy a separate chapter. We now resume.
Amongst the experiments usually included in the course of professors and lecturers who have a complete apparatus at their command, and which at first appear very complicated and difficult, there are some which can be performed with every-day articles at hand. There is no experiment in acoustics more interesting than that of M. Lissajons, which consists, as is well known to our scientists, of projecting upon a table or other surface, with[Pg 173] the aid of oxy-hydrogen light, the vibratory curves traced by one of the prongs of a tuning-fork. We can perform without difficulty a very similar experiment with the humble assistance of the common knitting-needle.
Fix the flexible steel needle firmly in a cork, which will give it sufficient support; fasten then at the upper extremity a small ball of sealing wax, or a piece of paper about the size of a large pea. If the cork in which the needle is fixed be held firmly in one hand, and you cause the needle to vibrate by striking it, and then letting it sway of itself, or with a pretty strong blow with a piece of wood, you will perceive the little pellet of wax or paper describe an ellipse more or less elongated, or even a circle will be described if the vibrations be frequent. The effect is much enhanced if the experiment be performed beneath a lamp, so that plenty of light may fall upon the vibrating needle. In this case, the persistence of impressions upon the retina admits of one seeing the vibrating circle in successive positions, and we may almost fancy when the needle is struck with sufficient force, that an elongated conical glass, like the old form of champagne glass, is rising from the cork, as shown in the illustration annexed (fig. 173).

Acoustics may be studied in the same way as other branches of physical science. We will describe an interesting experiment, which gives a very good idea of the transmission of sounds through solid bodies. A silver spoon is fastened to a thread, the ends of which are thrust into both[Pg 174] ears, as shown in fig. 174; we then slightly swing the spoon until we make it touch the edge of the table; the transmission of sound is in consequence so intense that we are ready to believe we are listening to the double diapason of an organ. This experiment explains perfectly the transmission of spoken words by means of the string of a telephone, another contrivance which any one may make for himself without any trouble whatever. Two round pieces of cardboard are fitted to two cylinders of tin-plate, as large round as a lamp-glass, and four-and-a-half inches in length. If the two rounds of cardboard are connected by a long string of sixteen to eighteen yards, we can transmit sounds from one end to the other of this long cord; the speaker pronouncing the words into the first cylinder, and the listener placing his ear against the other. It is easy to demonstrate that sound takes a certain time to pass from one point to another. When one sees in the distance a carpenter driving in a stake, we find that the sound produced by the blow of the hammer against the wood only reaches the ear a few seconds after the contact of the two objects. We see the flash at the firing of a gun, before hearing the sound of the report—of course on the condition that we are at a fairly considerable distance, as already remarked upon.


We can show the production of the Gamut by cutting little pieces of wood of different sizes, which one throws on to a table; the sounds produced vary according to the size of the different pieces. The same effect may be[Pg 175] obtained much better by means of goblets more or less filled with water; they are struck with a short rod, and emit a sound which can be modified by pouring in a greater or less quantity of water; if the performer is gifted with a musical ear, he can obtain, by a little arrangement, a perfect Gamut by means of seven glasses which each give a note (fig. 175). A piece of music may be fairly rendered in this manner, for the musical glasses frequently produce a very pure silvery sound. We will complete the elementary principles of acoustics by describing a very curious apparatus invented by M. Tisley, the Harmonograph. This instrument, which we can easily describe, is a most interesting object of study. The Harmonograph belongs to mechanics in principle, and to the science of acoustics in application. We will first examine the apparatus itself. It is composed of two pendulums, A and B (fig. 176), fixed to suspensions. Pendulum B supports a circular plate, P, on which we may place a small sheet of paper, as shown in the illustration. This paper is fixed by means of small brass clips. Pendulum A supports a horizontal bar, at the extremity of which is a glass tube, T, terminating at its lower extremity with a capillary opening; this tube is filled with aniline ink, and just rests on the sheet of paper; the support and the tube are balanced by a counterpoise on the right. The two pendulums, A and B, are weighted with round pieces of lead, which can be moved at pleasure, so that various oscillations may be obtained. The ratio between the oscillations of the two pendulums may be exactly regulated by means of pendulum A carrying a small additional weight, the height of which may be regulated by means of a screw and a small windlass. If we give to[Pg 176] pendulum A a slight movement of oscillation, the point of tube T traces a straight line on the paper placed in P; but if we move pendulum B, the paper also is displaced, and the point of tube T will trace curves, the shape of which varies with the nature of the movement of pendulum B, the relation between the oscillations of the two pendulums, etc. If the pendulums oscillate without any friction the curve will be clear, and the point will pass indefinitely over the same track, but when the oscillations diminish, the curve also diminishes in size, still preserving its form, and tending to a point corresponding with the position of repose of the two pendulums. The result is therefore that the curves traced by the apparatus, of which we produce three specimens (figs. 177, 178, 179), are traced in a continuous stroke, commencing with the part of the greatest amplitude.

By changing the relation and phases of the oscillations we obtain curves of infinitely varied aspect. M. Tisley has a collection of more than three thousand curves, which we have had occasion to glance over, in which we failed to meet with two corresponding figures. The ratio between these curves corresponds with some special class, of which the analyst may define the general characters, but which is outside our present subject. By giving the plate P a rotatory movement, we obtain spiral curves of a very curious effect, but the apparatus is more complicated. Considered from this point of view it constitutes an interesting mechanical apparatus, showing the combination of oscillations, and resolving certain questions of pure mechanics.[Pg 177] From the point of view of acoustics it constitutes a less curious object of study. The experiments of M. Lissajons have proved that the vibrations of diapasons are oscillations similar to, though much more rapid than those of the pendulum. We can therefore with this apparatus reproduce all the experiments of M. Lissajons, with this difference, that the movements being slower are easier to study. When the ratio between the number of vibrations—we purposely use the term vibration instead of the term oscillation—is a whole number, we obtain figs. 177 and 178. If the ratio is not exact, we obtain fig. 179, which is rather irregular in appearance, corresponding to the[Pg 178] distortions noticeable in M. Lissajon’s experiments. Fig. 178 has been traced in the exact ratio 2:3; fig. 177 in the ratio 1:2; and fig. 179 corresponds to the ratio 1:2 and a small fraction, which causes the irregularity of the figure.





In considering the harmony of figs. 177 and 178,—the first of which corresponds to the octave, the second to the fifth, whilst fig. 179 corresponds to the disagreeable interval of the ninth,—one is almost tempted to put a certain faith in the fundamental law of simple ratios as the basis of harmony. At first sight this appears beyond doubt, but perhaps musicians would be hardly content with the explanation. M. Tisley’s Harmonograph, it will be seen, is a rather complicated apparatus; and I will now explain how it may be constructed by means of a few pieces of wood. I endeavoured to construct as simple an apparatus as possible, and with the commonest materials, feeling that it is the best means of showing how it is possible for everybody to reproduce these charming curves of musical intervals. Also I completely excluded the employment of metals, and I constructed my apparatus entirely with pieces of wooden rulers, and old cigar boxes. I set to work in the[Pg 179] following manner: on the two consecutive sides of a drawing board I fixed four small pieces of wood (fig. 180), side by side in twos, having at the end a small piece of tin-plate forming a groove (fig. 181). In these grooves nails are placed which support the pendulums. The piece of wood is placed on the corner of the table, so that the pendulums which oscillate in two planes at right angles, are in two planes that are sensibly parallel to the sides of the table. The pendulums are made of a thin lath, with two small pieces of wood fixed to them containing some very pointed nails, on which the pendulum oscillates. Fig. 182 gives an illustration. The pendulums have a pin fixed in vertically, which passes through a piece of wood, and by means of a hinge connects the upper ends of the two pendulums. This contrivance of the pin is very useful, and if care is taken to make the hole through the hinge in the form of a double cone, as shown in fig. 182, c, it makes a perfect joint, which allows the piece of wood to be freely moved.

To complete the apparatus, the heads of the two pendulums are united by the hinge, at the bend of which a slender glass tube is fixed, which traces the curves. The hinge is given in fig. 184, and to its two extremities are adjusted the two pins of the pendulum (fig. 183). The pendulums are encircled with round pieces of lead, which can be fixed at any height by means of a screw.

CHAPTER XVI.
ACOUSTICS (Continued).
THE TOPOPHONE—THE MEGAPHONE—THE AUTOPHONE—THE AUDIPHONE—THE TELEPHONE—THE PHONOGRAPH—THE MICROPHONE.
We propose in this chapter to give as shortly as possible a description of the various instruments lately come into use, by means of which, and electricity, sounds can be carried from place to place, and their locality identified. It is only within the last few years that these wonderful inventions have come into use, and in a measure superseded the at one time invincible electric telegraph. The Telephone is now in daily use in London and other places, and its novelty, if not all its capability, has been discounted. The Phonograph has also been frequently seen. So we will on this occasion commence with the Topophone, a rather novel instrument.
As the name indicates, the Topophone is an apparatus for discovering the position of a sound, from the Greek words signifying a “place” and “sound.” The sources of sound can be found by it, and indeed this is its actual and practical use. It is claimed for this new apparatus that it stands in the same relation to the sailor as his old and trusty friends, the compass and sextant. These in navigation inform the steersman as to his course, and tells him his position by observation. The Topophone will tell him whence a sound arises, its origin wherever it may be; and this in a fog is no mean advantage. Suppose a ship to be approaching a dangerous coast in a fog. We are all aware how deceptive sounds are when heard through such a medium. We cannot tell from what precise direction the horn, whistle, or bell is sounding. The Topophone will give us the exact spot, and we can then, from our general knowledge of the locality, work our vessel up the river, or into the harbour, in safety.
The Topophone was invented in 1880, by Professor Alfred Mayer, an American, and is based upon the well-known theory of sound waves. These, as we have already explained, exist in the air; and if the theory of sound waves has perfected the Topophone, we can fairly say that it has confirmed the supposed form of the sound waves. “Sound,” says the inventor of the apparatus, “is supposed to be a particle continually expanding in the air, composed of a wave produced by compression, and followed by rarefaction.[Pg 181] A continuous sound is a series of these particles or globules spreading and expanding as the water-rings in a pond.” This much will be at once perceived.
Now, suppose a person up to his shoulders in a pond of water, and someone throws a stone into it. If that person extend his arms and hands at right angles facing the sound, each hand would touch the edge of a ripple as it came towards him across the pond. He would then be facing the source of the ripples or waves, and look along a radius of the circle formed by the waves. But if he please, he can move his body so that both hands shall touch the same wave at the same time, or he might turn away from the source, and only one hand would touch the wave. But when both hands are actually washed by the same circular ripple he must be facing the source of it. Any position in which his fingers did not touch the ripple almost at the same instant, would not be facing the source of the wave ripples. So by turning and extending his hands, he could with his eyes shut find out whether he was or was not facing the original source of the waves.
This applied to sound waves in the air is the whole theory of the Topophone, which, however, depends for its usefulness upon the same note being sounded by all horns and whistles. One note must be better than all the others, and that note, probably C (treble), caused by about two hundred and sixty vibrations per second, has been found most applicable. If all whistles and horns can by law be compelled to adjust themselves to this note, then the Topophone will be a real and lasting benefit.
Let us now look at the apparatus itself.
It being conceded that the resonators are in the same key as the Foghorn,—and this is necessary,—they are placed upon the deck of the vessel. An ear-tube of indiarubber is carried from each of these “resonators” into the cabin. These tubes unite and again separate, ending in small pieces ready to be fitted to the ears. The apparatus is fixed on deck, and the arrangement which supports it passes into the cabin, and can be turned about in any direction. Of course in this case a dial point is necessary to indicate the direction in which the instrument is turned. If the machine be worn on the shoulders of the officer of the watch he can move as he pleases, and wants no indicator.
The Topophone when used is so constructed, that when a horn is heard, and when the listener is facing the sound, he can hear nothing! When not facing the origin of the sound he can hear the horn very well, but the moment the resonators receive the sound together as they face the source, a very low murmur is heard, or perhaps no sound at all.—Why?
A certain pitch of tone is composed of vibrations or waves of equal length. In all waves there is a hollow and a crest. One neutralizes the other. The hollow of a sound wave meeting the crest of another wave “interferes” to produce silence, stillness, a dead level. So in “light”; two rays will produce darkness. We will endeavour to explain this.
If we have two equal strings, each performing an equal number of[Pg 182] vibrations in a second, they will produce equal sound waves, and the sound produced by both together will be uninterrupted, and twice as loud as one of them. But if one string vibrate, say one hundred times, and the other one hundred and one times in a second, they will not be in unison, and one will gain upon the other string, till after it has got to fifty vibrations it will be half a vibration ahead. At that moment they will neutralize each other, and silence will ensue for an appreciable time.

In the case of light suppose a red ray strikes the eye, and another red ray to come upon it from somewhere else. If the difference between its distance and the other point from the spot in the retina on which the first ray fell, is the 258/1000 part of an inch, or exactly twice, thrice, four times as much, etc., that distance, the light will be seen twice as strong. But if the difference in the distances between the points whence the light comes be only one-half the 258/1000 part of an inch, or 1½, 2½, 3½, or 4½ times that distance, one light will extinguish the other, and darkness will be the result. Now this is precisely what happens in the case of the Topophone. To return to our simile of water waves. If two stones be cast into a pond, and two equal and similar waves produced, and if they reach a certain place at the same moment, they will make one large wave. But if[Pg 183] one followed the other a little, so that the hollow of one coincided with the crest of the other, and vice versâ, the waves would obliterate each other, and a dead level would result. One tube of the Topophone is half a wave length longer than the other, and when the resonators are in a line and receive the wave at the same time, one ear hears the elevation of the sound wave, and the other the depression,—the sound is neutralized, and comparative, if not actual, silence results. The sailor knows in what direction the land lies, and can calculate his distance, or anchor if he please.
If amongst our readers there be any who wish to make for themselves an acoustic signalling apparatus there is physically nothing to prevent them from constructing such an instrument as that shown in the annexed woodcut (fig. 185). It is founded upon the speaking-trumpet principle, which is supposed to have been originated by Samuel Markland, in 1670.
Kircher, in his “Ars magna et umbra,” and in his “Phonurgia,” mentions a kind of speaking-trumpet, or porte voix, of gigantic dimensions, and called the “Horn of Alexander.” According to Kircher, the instrument was used by Alexander the Great to summon his soldiers from a distance of ten miles. The diameter of the circumference was about eight feet, and Kircher conjectured that the instrument was mounted upon three supports.
During the last century, a German professor, named Huth, made a model of the horn, and found it answered every purpose of a speaking-trumpet with most powerful results, but we beg leave to doubt whether the instrument really carried the voice to any very great distance.
The Acoustic Cornet, which is the counterpart of the speaking-trumpet, has been made in many different forms during the last two centuries, but none of them to the present time consist of anything more intricate than a simple tube with a mouthpiece and bell-shaped orifice.
Professor Edison, however, in his researches regarding the conveyance of sounds, has made numerous and interesting experiments. On one occasion, with his Megaphone he carried on a conversation at a distance of nearly two miles, without any other assistance from instruments except a few little cornets of cardboard. These constitute the Megaphone, which may be regarded as a curiosity, considering the effects produced by such simple means. The illustration (fig. 185) represents the instrument which is (or was lately) fixed upon the balcony of Mr. Edison’s house. At a mile-and-a-half distant from the house, at a spot indicated by the two birds in the picture, another instrument was fixed, and conversation was carried on with ease.
Perhaps the present opportunity will be the most convenient to speak of the Autophone, although it is more a musical than an acoustic instrument. Until lately Barbary organs and piano organs have been the only means by which poor people have been able to hear any music, and that not of a very elevated class. Besides, there is a good deal of expense connected with the possession of an organ. But the Americans, with a view to popularize music, have invented the Autophone, which is simply a[Pg 184] mechanical accordeon, manufactured by the Autophone Company, of Ithaca, New York.
The principle of the instrument is represented in fig. 186, and is extremely simple. An upright frame carries within it on one side a bellows, and on the other a flexible air chamber, which serves as a reservoir.
The upper portion contains a set of stops like an accordeon, but the escape of the air through the small vibrating plates can only take place by the upper surface of the frame work, upon which slides a thin plate of Bristol board pierced with holes at convenient distances, and set in motion by the mechanism shown in the annexed diagram (fig. 187).

The figure represents an axle furnished with a series of “washers,” which, acting upon the plate, cause it to move round. It is the bellows movement that turns the axle by the aid of two “catches,” B and C, which work upon a toothed wheel fixed upon it.
The “catch” B moves the paper on which the tune is “perforated,” when the bellows is empty, the other catch when it is distended; but a counter catch, D, represented by the dotted lines in the illustration, is so arranged that the paper cannot pass on except the tooth of the catch D is opposite a hole pierced upon the plate above. In the contrary case there is no movement of the paper during the dilatation of the bellows. The effect of this very ingenious arrangement is to give to the “musical” band of “board” an irregular movement, but it economises it in the case of sustained notes. The whole action of the instrument depends upon the correct working of the bellows.
The effect, from an artistic point of view, certainly leaves something to be desired, but the instrument is cheap, and not cumbersome, and the[Pg 185] slips of paper upon which the music is “cut out” can be made by machinery, and consequently are not dear. So far, the Autophone is fitted for popular favour and use, and may supersede the barrel organ.

The Audiphone is an instrument to conduct sound to the ear, to supplement it when temporary or partial deafness has occurred. Very likely many of our readers have observed ladies carrying large black fans on occasions,—at church, or lecture, or theatre,—and wondered why, perhaps. Those “fans” are Audiphones. The instrument is made of vulcanized rubber, and consists of a long flexible disc supported by a handle. To the upper edge of the “fan” are attached cords, which pass through a clip on the handle. If the person who wishes to hear by means of the Audiphone will hold the fan against the upper teeth,—the convex side of the fan outward,—he or she will hear distinctly, for the vibrations of sound are collected and strike upon the teeth and bones, and act upon the auditory nerves from within, precisely as the vibrations act from without through the auricle. We need hardly add that if the ear be injured the Audiphone will be of no use. A writer says: “From personal observation with the Audiphone it appears to convey the sonorous vibrations to the ear through the teeth, just as a long wooden rod held in the teeth will convey the vibrations of the sounding-board of a piano, though the piano is in another room and out of hearing by the ear. In using the Audiphone during conversation there is no movement or vibration felt by the teeth; in listening to a piano there is a very faint sensation as if the Audiphone vibrated slightly, while with the handle of the Audiphone resting on the sounding-board of the piano the vibrations are so violent as to be painful to the teeth. By closing the ears a person with even acute hearing can observe the admirable manner in which the instrument conveys spoken words to the ear. The Audiphone will prove to be of great value to deaf mutes, as it enables them to hear their own voices, and thus to train them to express words, while, before, they could only make inarticulate sounds.”
We have a variation of this instrument which has been introduced employing a diaphragm held in a telephone mouthpiece, and free to vibrate under the influence of sounds. This is connected by a string to a bit of wood that may be held in the teeth. In use the hearer places the wood between his teeth, the string is drawn tight, and the speaker speaks through the telephone mouthpiece, the vibrations of the diaphragm being then conveyed to the teeth through the stretched string. This apparatus works very successfully, and ladies use it, but it is not so convenient for general use as the Audiphone.

The Telephone is now in daily use in London, and is by no means strange to the majority of our countrymen, still some description of it will probably be acceptable, and a glance at its history may prove interesting.

In speaking of the Telephone, we must not lose sight of the facts before mentioned, as regards our sense of hearing, and the manner in which the ear acts by the series of bones termed the hammer, the anvil, and stirrup. In the process of reproduction of tone in the magnetic instruments, the mechanism of the human ear was, to a certain extent, imitated, and a diaphragm, by vibrations, generates and controls an electric current.
Professor Wheatstone was the first person to employ the electric wire for the transmission of sounds, but Professor Philip Reiss, of Friedrichsdorf, was the first to make the experiment of producing musical sounds at a distance. His[Pg 187] first instrument was of a most primitive nature; subsequently he produced an instrument of which fig. 188 is the Telephone, fig. 189 the “receiver.”
In fig. 188, it will be seen that there is an aperture on the top and one at the side; the latter is the mouthpiece. The top aperture is covered with a membrane which is stretched very tightly. When a person speaks or sings into the mouthpiece his voice is at once concentrated upon the tight membrane, which it causes to vibrate in a manner corresponding with the vibrations of the voice. There are two binding screws, one at each side. To the centre of the tight membrane a piece of platinum is fixed, and this is connected with the binding screw on one side, in which a wire from the battery is fixed. On the membrane is a tripod, the feet of which (two) rest in metal cups, one of them being in a mercury cup connected with the binding screw at the opposite side to that already mentioned. The third “foot”—a platinum point—is on the platinum in the centre of the membrane or top, and moves with it. Every time the membrane is stretched by a vibration the platinum point is touched, and the closed circuit is broken by the return of each vibration.

a. Electro-magnet. b. Diaphragm. c. Collar. d. Collar and tube. f. Screw. g. Mouthpiece. h. Battery. i. Wire from battery to coil. k. Telegraph wire. l. Through binding screw. m. Pillar holding magnet.
The receiving instrument (fig. 189) consists of a coil enclosing an iron rod, and fixed upon a hollow sounding box. It is founded upon a fact discovered by Professor Henry, that iron bars when magnetized by an electric current become a little longer, and at the interruption of the current resume their former length. Thus in the receiver the iron will become alternately longer and shorter in accordance with the vibrations of the membrane in the box far away, and so the longitudinal vibrations of the bar of iron will be communicated to the sounding box, and become perfectly audible. This instrument, however, could only produce the “pitch” of sound, “not different degrees of intensity, or other qualities of tones.” It merely sang[Pg 188] with its own little trumpet whatever was sung into it; for all the waves were produced by an electric current of a certain and uniform strength, and therefore the sound waves were of the same size.
But in 1874, Mr. Elisha Gray, of Chicago, improved Reiss’ instrument, and discovered a method by which the intensity or loudness of tones, as well as their “pitch,” were transmitted and reproduced. In this method he employed electrical vibrations of varying strength and rapidity, and so was enabled to reproduce a tune. Subsequently he conceived the notion of controlling the vibrations by means of a diaphragm, which responded to every known sound, and by this he managed to transmit speech in an articulate manner.

In 1876, Professor Graham Bell sent a Telephone to the Centennial Exhibition at Philadelphia. Mr. Bell, according to the report, managed to produce a variation of strength of current in exact proportion to the particle of air moved by the sound. A piece of iron attached to a membrane, and moved to and fro in proximity to an electro magnet, proved successful. The battery and wire of the electro magnet are in circuit with the telegraph wire, and the wire of another electro magnet at the receiving station. This second magnet has a solid bar of iron for core, which is connected at one end, by a thick disc of iron, to an iron tube surrounding the coil and bar. The free circular end of the tube constitutes one pole of the electro magnet, and the adjacent free end of the bar core the other. A thin circular iron disc held pressed against the end of the tube by the electro-magnetic attraction, and free to vibrate through a very small space without touching the central pole, constitutes the sounder by which the electric effect is reconverted into sound. The accompanying illustrations (figs. 190, 191) show Mr. Bell’s Telephone as described.
The Telephone, subsequently simplified by Professor Bell, is shown in the two following illustrations (figs. 192, 193). The voice strikes against the[Pg 189] diaphragm, and it begins to vibrate. The sound is not conveyed by the wire; the motion is communicated, and the vibrations become sound waves again. The Telephone consists of a cylindrical magnet encircled at one end by a bobbin, on which is wound a quantity of fine insulated copper wire. The magnet and coil are contained in a wooden case, the ends of the coil being soldered to thick copper wire, which traverse the “wooden envelope,” and terminate in the binding screws. In front of the magnet is a thin circular iron plate, in which is the mouthpiece. The drawings will explain the instrument.


Fig. 193.—a. Bobbin of coil wire round magnet. b. Diaphragm. c. Mouthpiece. d. Permanent magnet. e. Wires to binding screws. f. Both wires as one for convenience. g. Adjusting screw-holding magnet.
Mr. Edison also invented a Telephone like Gray’s, and made the discovery, that when properly prepared, carbon would change its resistance with pressure, and that the ratio of these changes corresponded with the pressure. This solved the problem of the production of speech. The carbon is placed between two plates of platinum connected in the circuit and near the diaphragm, and the carbon receives the pressure from it by means of the mouthpiece.
When we come to Magnetism and Electricity we may have some[Pg 190]thing more to say respecting the mysteries of the Telephone and its later developments. At present we are only concerned with it as a sound conveyer, and it answers its purpose admirably, although somewhat liable to attract other sounds or vibrations from neighbouring wires.
The Phonograph, a mechanical invention of Mr. Edison, does not make use of electricity, although the vibratory motion of the diaphragm is utilized. It, in a simple form, consists of a diaphragm so arranged as to operate upon a small stylus, placed just opposite and below the centre, and a brass cylinder, six or eight inches long, by three or four in diameter, mounted upon a horizontal axis, extending each way beyond its ends for a distance about its own length.
“A spiral groove is cut in the circumference of the cylinder, from one end to the other, each spiral of the groove being separated from its neighbour by about one-tenth of an inch. The shaft or axis is also cut by a screw thread corresponding to the spiral groove of the cylinder, and works in screw bearings; consequently when the cylinder is caused to revolve, by means of a crank that is fitted to the axis for this purpose, it receives a forward or backward movement of about one-tenth of an inch for every turn of the same, the direction, of course, depending upon the way the crank is turned. The diaphragm is firmly supported by an upright casting capable of adjustment, and so arranged that it may be removed altogether when necessary. When in use, however, it is clamped in a fixed position above or in front of the cylinder, thus bringing the stylus always opposite the groove as the cylinder is turned. A small, flat spring attached to the casting extends underneath the diaphragm as far as its centre and carries the stylus, and between the diaphragm and spring a small piece of india-rubber is placed to modify the action, it having been found that better results are obtained by this means than when the stylus is rigidly attached to the diaphragm itself.

“The action of the apparatus will now be readily understood from what follows. The cylinder is first very smoothly covered with tin-foil, and the diaphragm securely fastened in place by clamping its support to the base of the instrument. When this has been properly done, the stylus should lightly press against that part of the foil over the groove. The crank is now turned, while, at the same time, someone speaks into the mouthpiece of the instrument, which will cause the diaphragm to vibrate, and as the vibrations of the latter correspond with the movements of the air producing them, the soft and yielding foil will become marked along the line of the groove by a series of indentations of different depths, varying with the amplitude of the vibrations of the diaphragm; or in other words, with the inflections or modulations of the speaker’s voice. These inflections may therefore be looked upon as a sort of visible speech, which, in fact, they really are. If now the diaphragm is removed, by loosening the clamp, and the cylinder then turned back to the starting point, we have only to replace the diaphragm and turn in the same direction as at first, to hear repeated all that has been spoken into the mouthpiece of the apparatus; the stylus, by this means, being caused to traverse its former path, and consequently, rising and falling with the depressions in the foil, its motion is communicated to the diaphragm, and thence through the intervening air to the ear, where the sensation of sound is produced.

a. Compound magnet. d. Diaphragm. e. Speaking tube. f. Telegraph wire. g. Line to earth. b, c. Small spaces.
“As the faithful reproduction of a sound is in reality nothing more than a reproduction of similar acoustic vibrations in a given time, it at once becomes evident that the cylinder should be made to revolve with absolute uniformity at all times, otherwise a difference more or less marked between the original sound and the reproduction will become manifest. To secure this uniformity of motion, and produce a practically working machine for automatically recording speeches, vocal and instrumental music, and per[Pg 192]fectly reproducing the same, the inventor devised an apparatus in which a plate replaces the cylinder. This plate, which is ten inches in diameter, has a volute spiral groove cut in its surface on both sides from its centre to within one inch of its outer edge; an arm guided by the spiral upon the under side of the plate carries a diaphragm and mouthpiece at its extreme end. If the arm be placed near the centre of the plate and the latter rotated, the motion will cause the arm to follow the spiral outward to the edge. A spring and train of wheel-work regulated by a friction governor serves to give uniform motion to the plate. The sheet upon which the record is made is of tin-foil. This is fastened to a paper frame, made by cutting a nine-inch disc from a square piece of paper of the same dimensions as the plate. Four pins upon the plate pass through corresponding eyelet-holes punched in the four corners of the paper, when the latter is laid upon it, and thus secure accurate registration, while a clamping-frame hinged to the plate fastens the foil and its paper frame securely to the latter. The mechanism is so arranged that the plate may be started and stopped instantly, or its motion reversed at will, thus giving the greatest convenience to both speaker and copyist.
“The articulation and quality of the Phonograph, although not yet perfect, is full as good as the Telephone was. The instrument, when perfected and moved by clock-work, will undoubtedly reproduce every condition of the human voice, including the whole world of expression in speech and song, and will be used universally.
“The sheet of tin-foil or other plastic material receiving the impressions of sound, will be stereotyped or electrotyped so as to be multiplied and made durable; or the cylinder will be made of a material plastic when used, and hardening afterward. Thin sheets of papier maché, or of various substances which soften by heat, would be of this character. Having provided thus for the durability of the Phonograph plate, it will be very easy to make it separable from the cylinder producing it, and attachable to a corresponding cylinder anywhere and at any time. There will doubtless be a standard of diameter and pitch of screw for Phonograph cylinders. Friends at a distance will then send to each other Phonograph letters, which will talk at any time in the friend’s voice when put upon the instrument.” (Scribner.)
The Microphone (an outcome of the Telephone) was discovered by Professor Hughes, of London. It is an instrument which in its main features consists of a carbon “pencil,” so suspended that one end rests upon a carbon “die.” The instrument being connected with a Telephone by the circuit wires, will reproduce faint sounds very distinctly. Once a Microphone was put into a preacher’s pulpit, and joined to a private telegraph wire which led to a gentleman’s house. The owner was thus enabled to hear the sermon. So long as it is thus connected every minute sound, even a fly’s footstep, will be faithfully reproduced.
CHAPTER XVII.
THE TUNING-FORK—THE SYREN—SOUND FIGURES—SINGING FLAMES.
We cannot close the subject of Sound without some mention of the Musical Pitch, and various instruments and experiments which have from time to time been made to discover the pitch, sound, and vibrations, and even to see Sound. To understand the vibrations or “pitch” of a musical note we may study the illustration, which shows us a tuning-fork in vibration.
You will perceive that each prong of the tuning-fork beats the air in an opposite direction at the same time, say from a to b (fig. 196). The prong strikes the air, and the wave thus created strikes again outward, and the condensation thus created travels along the back beat, rarefying the air, and both these, the rarefaction and the condensation, move with the same rapidity one behind the other.

The tuning-fork of course vibrates a very great many times in a second, every vibration generating a wave. “Pitch,” in a general sense, is the number of vibrations per second which constitute a note. For instance, the note A, the standard pitch consists of four hundred and thirty-five complete vibrations per second. Concert pitch is slightly higher, for there are a few more vibrations in the second. The lowest sound pitch is forty vibrations, the highest forty thousand. “Pitch” may be determined by an instrument termed the “Syren,” or by a tooth-wheeled apparatus.
The Syren was invented by Cagniard de Latour. It consists of a metal cylinder, a tube passes through the bottom, and through the tube air is blown into the cylinder. On the top a number of holes are drilled, while just over the cylinder top, almost in contact with it, is a metallic disc, which rotates upon a vertical axis. The disc is perforated with holes equal in number to those in the cylinder top, but the holes are not perpendicular, they slope in opposite directions. So when the air is forced through the holes in the top of the cylinder it impinges upon one side of the holes in the rotating disc, and blows it round.
The disc in one revolution will therefore open and shut as many holes as there are in the disc and cylinder, and the air blown in will escape in so many puffs—the number of puffs in a given time depending upon the rapidity of rotation. There is an arrangement to show the number of turns. By these rotations a sound is produced which rises in pitch as the revolutions are increased in number.

To determine the pitch of a certain sound we must find the number of times the plate revolves in that time, then we shall have the number of vibrations per second required to produce the note we desire. The arrangement working in a notched wheel tells us the number of rotations of the disc. Successive, and rapidly-successive puffs or beats are heard as the rotation increases, and at length the two sounds will disappear, and merge into one, which is perhaps that of the tuning-fork, whose note you require to find the “pitch” of. By maintaining this rate for a minute or less, and setting the gear to tell the revolutions, the number will be found marked on the dial of the apparatus. So by multiplying the number of revolutions of the disc by the number of the holes, and dividing the product by the number of seconds during which the disc was in connection with the recording gear, we shall have the number of vibrations per second necessary to produce the pitch corresponding to the given sound. The above is the description of one form of Syren; there are others, which, however, we need not detail.
We have seen that there are certain nodal points, or resting-places, in vibrations, and this can easily be shown upon a fiddle-string, from which paper discs will fall off except on the nodal point, showing that there is no[Pg 195] vibration there. The same experiment may be made by means of plates, which will give us what are termed Chladni’s figures. Suppose we strew a glass-plate with fine sand, and stroke the edge with a fiddle-bow. The vibrations of the plates will make certain patterns, and cast the sand upon those points of repose to form nodal lines in various directions. The plates must, of course, be held or fastened, and a variety of sound figures may be produced. (See figs. 198 and 199.)
The relation between the number of segments on the plate and the pitch of the note, can be ascertained by using a circular plate clamped in the centre. “If the finger on the plate and the fiddle-bow are one-eighth of the circumference apart, the fundamental note will be produced. If one-sixteenth apart, the higher octave will be heard.”
Sensitive flames will detect air vibrations, and flames can also be made to sing. Sensitive flames were discovered by Mr. Barrett, who noticed the effect a shrill note had upon a gas flame from a tapering jet. The flame was a very long one (fourteen inches), and when the sound was produced it shortened at once, while the upper part expanded like a fan; the same effects, in a less marked degree, were observable when the shrill sound was prolonged from a distance of forty feet. Professor Tyndall was immediately interested in this discovery, and in January 1867 he lectured upon it at the Royal Institution.
If any one wish to try the experiment, a piece of glass tubing should be obtained, and let the mouth be tapered down to a small orifice one-sixteenth of an inch in diameter. Then when the highest pressure is on for the evening, light the gas and sound a shrill whistle. The flame will sink down and spread out. The illuminating power may thus be increased, and many experiments may be made. For instance, if a person be in the room and try to read, he will probably not be able to do so at a little distance; but if his friend whistle to the gas it will so expand itself as to enable him to read, so long as the whistle lasts.
A very ingenious burglar-detector was made upon the principle of the sensitive flame, which expands at a noise and heats a welded plate of gold, silver, and platinum. The plate swerves aside, the metals being unequally affected by heat, and as it is connected with a battery, rings a bell by electricity. A small high flame has been made sensitive to the chinking of coin, or even to the ticking of a watch. We will now give some explanation, derived partly from Professor Tyndall, of the cause of sensitive flames.
A sensitive flame is one just on the point of “roaring,” and about to change its aspect. “It stands,” says Tyndall, “on the edge of a precipice. The proper sound pushes it over.... We bring it to the verge of falling, and the sonorous pulses precipitate what was already imminent.” The flame is in a state of vibration, so sounds being vibrations, practically increase the pressure; and the flame acknowledges the pressure thus invisibly applied by air waves.
Singing Flames are produced by burning hydrogen in a tube; a[Pg 196] musical note is thus produced in the same way as the air causes a note in an organ pipe. Faraday attributed the sound to rapid vibration caused by successive explosions of the burning gas. The Gas Harmonicon has been made on this principle. The air, being heated in the glass tube, ascends, and the flame is thus permitted to come up more forcibly in the tube; so violent agitation results when the air tries to get into the opening above. The size of the flame and its position in the tube will give a certain note which will be the same note as the air would emit if in a pipe, for the vibrations give the sound.
Sir Charles Wheatstone has shown by experiment how sound can be transmitted by placing a rod on a musical-box, and carrying the rod through the ceiling. When a guitar or violin was placed upon the rod, the sounds of the musical-box were distinctly heard in the upper room. A Phantom Band can be made by connecting certain instruments with others being played on under the stage. Every one will then appear to play by itself.

CHAPTER XVIII
ELECTRICITY.
DERIVATION OF ELECTRICITY—SEALING-WAX EXPERIMENT—THE ELECTROPHORUS—LEYDEN JAR—POSITIVE AND NEGATIVE—THE ELECTROSCOPE—ELECTRIC MACHINES.
We have now briefly and of course imperfectly reviewed the phenomena of Vibration, as exemplified in what we term Heat, Light, and Sound. We now come to a most mysterious servant of mankind, as mysterious as any Djinn of romance; viz., Electricity.
The term Electricity is derived from the Greek word electron, meaning “amber”; because from amber the properties of what we call “Electricity” were first discovered. Six hundred years before the Christian Era, Thales wrote concerning the attraction which amber, when rubbed, possessed for light and dry bodies. But it is to an Englishman named Gilbert that we owe the word “Electricity,” which he derived from the Greek, and in his works (about 1600 A.D.) he discusses the force of the so-called “fluid.” Otto von Guerike, of “air-pump” celebrity, and many other philosophers after him, continued the investigation of the subject. At the beginning of the last century great attention was paid to the Electric Machine. The Leyden Jar was, as its name denotes, discovered by Muschenbrock, of Leyden, (though the honour was disputed). Franklin made the first lightning conductor in 1760. Volta and Galvani, to whose invention we owe “Voltaic Electricity” and “Galvanism,” and Faraday in more modern times gave a great impetus to electrical science. The great part that electricity has been playing in the domestic history of the world since Faraday’s lamented death, is probably known to the youngest of our readers. What the future of this agent may be we can only guess, but even now we may regard electricity as only in its infancy.
There are few scientific studies more attractive to the general reader than electricity, and few admit of more popular demonstration. The success of the late electrical exhibition in Paris, and its successor in London at the present time, are proofs of the interest taken in this great and mysterious agent whose origin we are in ignorance of, and of whose nature and powers we are daily discovering more and more, and finding there is still an immense field for its application.
Some fundamental facts regarding electricity may very easily be studied with the assistance of every-day objects at hand. Amber was the[Pg 198] first substance to show attraction when rubbed, but Gilbert found out that glass and sealing-wax, etc., possessed like properties with amber.
If we rub a stick of sealing-wax with a piece of cloth, we shall see that it will attract some small fragments of paper placed near it. Nothing is easier than to construct a small pendulum to show with perfect clearness the phenomenon of electric attraction. A piece of iron is fixed on a wooden pedestal, and supports a thread of silk, to the end of which is fastened a little ball cut out of a piece of cork. The stick of sealing-wax after being rubbed with the cloth will attract the ball as shown in fig. 200.

By means of a piece of paper we can produce a spark. I take a large, strong sheet of drawing paper, heat it very thoroughly, and lay it on a wooden table. I rub it with a perfectly dry hand, or with a piece of woollen material until it adheres to the table. That done, I place a bunch of keys in the centre of the sheet of paper, which I raise, lifting it by two corners. If at this moment any one touches the bunch of keys with his finger, a bright spark will be elicited. The metal is charged with the electricity developed on the paper; if the weather is dry, and the paper thoroughly heated several times, the spark may attain nearly an inch in length.
We can easily construct other electrical apparatus. For instance, an “Electrophorus,” or instrument for obtaining electricity by means of induction, or a Leyden jar, can both be made at home. Let us proceed to construct the former, of which we give an illustration (fig. 201).
We take a lacquered tea-tray about a foot long, and cut out a sheet of thick wrapping paper, so that it will lie over all the level portion of the tray. At each side of this sheet of paper we fix two bands of paper, as in the illustration (fig. 201), so as to serve as handles. The tea-tray should be placed upon two tumblers to support it and to insulate it, glass being a “non-conductor.” (We will speak of conductors and non-conductors presently.) We have now our Electrophorus made ready for action; let us proceed to see how it will act.

First, rub the thick packing paper over a hot fire or a stove, and the friction must be continued for some time, until the paper has become thoroughly dry, and as hot as possible without charring. When this has been accomplished, place it quickly upon a wooden table, and rub it rapidly and energetically with a clothes’ brush, dry and hard as can be obtained. Place the paper upon the tray; touch the tray with the knuckle, and draw away the paper by the handles fixed to it (see fig. 201); a spark will result. Then if the paper be replaced upon the tray, and the hand again presented, the same result will follow. This experiment may be repeated five or six times, at least, with success.
We have in this tea-tray and its paper covering a real electric machine. How can we manage to provide a Leyden jar to contain our electricity? Nothing is more easy. Let us take a tumbler and partly fill it with shot;[Pg 200] insert into the glass a tea-spoon, and if all the articles are quite dry we shall possess a Leyden jar.
To charge the jar we have thus provided we must work the Electrophorus we have already described. While one person lifts off the paper as directed, another must hold the glass filled with shot close to the edge of the tray, and touch the corner with the tea-spoon; the spark will then enter the “jar” or tumbler. We can thus charge the jar as we please, and by presenting the finger as in the illustration (fig. 202), we shall obtain a discharge from it.

Mr. Louis Figuier, in his “Merveilles de la Science,” relates that Wollaston, meeting one of his friends one evening in the streets of London, drew from his pocket a copper thimble, and proceeded to turn it into a microscopic pile.13
In order to do this he removed the bottom of the thimble, flattened it with a stone, so as to bring the two internal surfaces about on a line with each other, then placed between the copper surfaces a small strip of zinc, which was not in contact with the copper, owing to the interposition of a little sealing-wax. He then placed it in a glass cup, previously filled with the contents of a small phial of water, acidulated with sulphuric acid. He[Pg 201] next wound round the strip of zinc and its copper covering a piece of platinum wire, the wire becoming red through the electricity developed in the pile. The dimensions of this platinum wire were extremely small; it was only 30/1000 of an inch in diameter, and 1/30 of an inch in length. By reason of its small dimensions it could not only be reddened, but fused by the little battery.
Thus Wollaston’s friend, who was a witness of the experiment, was able to light a tinder at the red wire. In this little battery of Wollaston’s the copper enveloped the strip of zinc in every part; that is to say, the negative element was on a higher surface than the positive metal.

After considering Electricity, it is not impossible to approach the study of Magnetism, and even to construct a mariner’s compass. We shall find the method of doing so by borrowing an interesting passage from the “Magasin Pittoresque.” Let us take a small cork and pass through it an ordinary knitting-needle (fig. 203), which we have already magnetized by placing it N.S., rubbing it gently, and always in the same direction, with one of those little iron magnets with which children amuse themselves. After the needle has been passed through the cork, we also fix into it a sewing-needle, or rather a pin, the point of which rests in one of the little holes in the upper part of the thimble. In order to balance the magnetised needle, we thrust a match into both sides of the cork, as shown in the illustration, and fasten to the ends of each a ball of wax. Thus the needle, the balls, and the pin are all balanced at once, so that the contrivance has the appearance of the illustration.
As it is very important that with such a sensitive instrument any agitation of the air should be avoided, the thimble must be placed at the bottom of a common earthen pan, B D T, which should be covered over with a piece of glass, V. To graduate the compass a circle is described on a piece of paper. On this dial we trace the divisions sufficiently close only at the north extremity of the needle, and the paper is fixed underneath, as in fig. 203. Then we fix a piece of wax at the end of the match pointing N., opposite the northern extremity of the needle inside the basin. In this way we have a very useful and inexpensive compass.
We may also magnetize a fine sewing-needle, and grease it by rubbing[Pg 202] it with a little suet. It is then capable of floating on the surface of water running in the direction of the north pole. We might go on multiplying indefinitely examples of physical experiments without apparatus, but we have probably already given a sufficient number to aid our readers in imagining others.
We have now in a simple manner shown how we can easily produce electricity. We may understand that electrical phenomena are produced—(1) friction between different bodies; (2) by placing bodies which differ in contact; (3) by the transition of bodies from one condition to another; (4) by chemical changes; (5) by animals. The two first, and the fourth, are the most usual causes.
We know that certain substances when rubbed with silk or wool acquire the property of attracting other substances. But in the case of a rod of glass or stick of wax, the attraction will only be perceived when the rubbing has been applied. But metal will behave differently. Any part of the metal rod will continue to attract. So metals are Conductors of electricity; while glass, wax, silk, amber, sulphur, etc., are bad, or Non-Conductors. Metals are the best conductors we have, but trees, plants, liquids, and the bodies of animals, including men, are all good conductors of electricity. Dry air is a bad conductor.

There are two kinds of electricity, known as positive and negative (plus or minus), vitreous or resinous. We saw in fig. 200 that we can attract a small ball of pith or cork by a piece of sealing-wax rubbed with flannel. If we then present a glass rod rubbed with silk to it, it will be equally attracted, but will be at once repelled; and after being so repelled, if we put the wax to it, it will be attracted to the sealing-wax again. So wax at first attracts then repels the ball, and so does glass, but either will attract the ball if presented alternately (fig. 204). The reason for this is as follows :—
When we have rubbed the glass with silk, we charge it with positive electricity, and when the rod touches the ball, the latter imbibes that electricity, and flies away from the glass rod. The sealing-wax imparts negative electricity in the same way.
The law is, that bodies charged with the same kind of electricity repel each other, and those containing the opposite kinds attract each other. Positive repels positive; negative repels negative. But positive attracts negative, and negative attracts positive. Opposite electricities unite, and so neutralize each other that no effect is perceived; but it must be borne in mind that all bodies possess both electricities in some quantity, greater or less. By rubbing we separate these electricities, the rubber becoming negative, the rubbee positive. The friction of glass supplies positive electricity, and sealing-wax supplies negative electricity, or we can obtain the same effect by rubbing either with certain material.
The manner in which a body is electrified depends upon its nature[Pg 203] and condition; but we may accept as a general axiom,—but by no means as a law,—that when two bodies are rubbed together, that which gets the hotter in the process takes the negative kind of electricity. In the following list the substances have been so arranged that each is negatively electrified by those preceding, and positively by those succeeding it. 1, cat’s skin; 2, glass; 3, woollen stuffs; 4, feathers; 5, wood; 6, paper; 7, silk; 8, shellac; 9, rough glass. We append a list of conducting and non-conducting bodies in their order:—
| Conductors. | ||
|---|---|---|
| Metals. | Pure water. | Hot air. |
| Lime, coal, or coke. | Vegetable tissues. | Steam. |
| Saline mixtures. | Animal tissues. | Rarefied air. |
| Non-Conductors. | ||
| Ice. | Dry gases. | Diamond. |
| India-rubber. | Paper. | Glass. |
| Marble. | Wool. | Wax. |
| Porcelain. | Silk. | Sulphur. |
| Resin. | Shell-lac. | |


It should be observed that the degree of value as a conductor or non-conductor depends somewhat upon the atmosphere. For instance, glass is an excellent insulator, or non-conductor, when dry, but when wet it changes to a conductor. So insulators are at times covered with a solution of shell-lac, or fat, to keep away moisture. We may reasonably conclude that bodies[Pg 204] which are good and bad conductors are good and bad conductors of electricity. Water is a good conductor, air is a bad one; were it otherwise, electricity would escape from the ground into the air; as it is, the air manages in some degree to retain the electricity at the surface of bodies, for it is on the surface that we find the electric “fluid.”
We have mentioned electrical induction in a former experiment with the tea-tray. We will now explain it more fully, as a consideration of it will bring us to the electric spark, or lightning, with the account of the discovery of the Conductor and the Electrical Machine.
Let us look at the illustration next below. A B is a cylinder supported on a glass rod, and at each extremity is a small pith ball, a and b. The cylinder is in a neutral condition, as is evidenced at first by the pellets being in a vertical position. But suppose we bring a ball, C, towards the cylinder. C is charged with positive electricity, which attracts the negative to itself, and so repels the positive away at the opposite side. So the pellet at one side will be attracted to C, and the other will fly in an opposite direction.

Let us take another illustration. Here we have a horizontal metal rod, cc′, insulated on a glass stand. Two balls of cork are attached at both ends of the rod by metallic wires. Hold a rod of resin, r, which has been made negatively electrical, and apply it to one pair of the cork balls. The positive electricity will be attracted at c′ and the negative repulsed, and fly away at c. If we remove the resin the equilibrium will be again established, and the balls will fall to a vertical position.

We can also by drawing off the negative electricity by the finger at c, while the resin rod is still held to the other side, c′, fill the whole of the metal rod with the positive electricity when the finger and the resin have been removed respectively first and last. The balls will then fly in opposite directions again, in consequence of the repulsion exercised by the positive poles.
The “Electrophore,” or “Electrophorus,” we have already learned to make for ourselves, as also the Leyden Jar. But we give cuts of them. The former is very simple, and can be made by mixing two parts of shell-lac and one of turpentine, and pouring the mixture upon a metal plate. If this be rubbed with a cat’s skin when dry, and a metal cover with a glass handle be placed upon it, it will be found that the positive and negative electricity are collected on the lower and upper surfaces of the plate respectively, and can be drawn away with a spark as before, and made use of.

The Leyden Jar requires a little more detailed description, as it is to it we are indebted for our Battery. It is a common glass bottle or jar, coated both inside and out with tinfoil nearly as high as the shoulder, a a. The mouth should be firmly closed with a bung of wood, g g; a hole should be bored in the bung, through which a brass rod is tightly pushed. The rod, too, is topped by a brass knob, and a brass chain is attached to the other extremity. The interior of the tinfoil receives positive electricity, and the exterior negative when the jar is charged from the “Electrophorus.” To discharge the jar and create a shock it is necessary to put one hand on the outside, and the other on the knob of the jar. A brilliant spark and a severe shock will result if the jar has been fully charged. It is as well to be cautious when trying this experiment. The effect of the shock may be felt by any number of persons joining hands, if one at one end of the row, and one at the other end, touch the knob and the outside of the jar simultaneously.

This electric discharge is lightning in miniature, and it is to Benjamin Franklin that the world is indebted for the discovery. The philosopher was greatly interested in the science of Electricity and, having retired from business, he devoted himself to the consideration of thunderstorms. He wrote a treatise to show that points drew off electricity, and that electricity and lightning were similar. He urged that metallic rods might be attached to ships and buildings, so that during thunderstorms, or at other times, the electricity might be harmlessly carried into the ground. This suggestion he made without being able to explain why points did carry off electricity without a spark. The reason is because there is no place to store it; it runs away at once, without having time to collect, as in a ball.
Franklin made one or two experiments before his renowned kite-flying arrangement, which convinced him that electricity was by no means an agent to be played with. He endeavoured to kill a turkey by electricity, but by incautious handling of the jars in which the “fluid” was stored, he discharged them, and describes the result: “The flash was very great, and the crack was as loud as a pistol; yet my senses being instantly gone, I neither saw the one nor heard the other, nor did I feel the stroke on my hand, though I afterwards found it raised a round swelling where the fire entered[Pg 206] as big as half a pistol bullet.” On a subsequent occasion he was again struck senseless while endeavouring to administer a shock to a paralytic patient.
It was not until June 1752 that Franklin made the experiment with the kite, which resulted in such great discoveries. He made his kite of a silk pocket-handkerchief, and he fixed a pointed rod upon the upright portion of the frame at the top; the string ended in a foot or so of silk, which was held by the philosopher, and to the end of the hempen portion of the string a large key was tied. For some time, notwithstanding the approach of most unmistakable thunder-clouds, his patience was tried. But at last the strands of the hempen string began to bristle up, and soon after, when Franklin applied his knuckle to the key, a spark was obtained. The great discovery was made. Franklin subsequently obtained lightning in his own house, and performed several experiments with it.

The Electroscope (fig. 211) is an instrument by which we can ascertain whether electricity is present or not, and the nature of it. If we bring an object unelectrified close to the ball or knob on the top of the glass shade, the two needles, or strips of gold-leaf, which are often used, will remain still. But if the body has been electrified it will communicate the electricity to the rod inside, and attract to itself the fluid of opposite quality; the same kind of electricity then is in action in the gold-leaf or needles, and they fly apart—repel each other. Supposing that positive electricity were first communicated, we can cause the contraction of the leaves or wires by applying a negative kind, which, meeting the positive, neutralizes it, and the wires collapse.
If the electricity with which the instrument is charged be positive, by approaching the baton to the ball, A, we shall see the wires diverge more than before, and they will finally be discharged by the knobs within. If the electricity be contrary to that in the baton, the wires will approach each other, but by gradually withdrawing the baton they will again separate, and even to a greater distance than before.
The Electric Machine is shown in the illustration (fig. 212). It consists of a large plate of glass fixed upon a glass stand, between wooden supports. The handle is of glass; two pairs of rubbers are fastened above and below; the plate is turned between them, and becomes “positively” electrified. The rubbers are covered with leather and stuffed with horsehair, DD, and press very tightly against the glass, so that the friction is constant. The rubbers are covered with an amalgam made of mercury, zinc, and tin, two parts of the first to one each of the others. A chain (of metal) connects the machine with the ground. The conductors, PP, are united by a cross[Pg 207]-piece, Q, and sustained upon glass supports. At the end of the conductors are two curved rods, CC, which are provided with points to take the electricity from the plate, but do not touch it.

The electricity is thus stored in the insulated conductors as the machine is turned. The negative portion is carried into the ground by the chain from the rubbers, while the positive electricity is retained. The longer we turn the more we shall obtain, and the quantity is measured by an electric pendulum on one of the conductors, which flies out by degrees as the charge increases, and indicates its power by means of a needle it works upon an ivory index.
It is not difficult to make an electric machine out of a glass bottle. This will furnish the glass cylinder. If a stick be run through it (for which purpose a hole must be drilled in the bottom of the bottle), a handle can be fixed, and the bottle mounted on a stand. A wash-leather cushion, stuffed, can be so arranged that it will press against the bottle as it is turned; a piece of silk should be permitted to hang from the cushion frame over the glass. A conductor may be made from a piece of wood neatly rounded and smoothed,[Pg 208] and coated with tinfoil. The ends should be rounded like “knobs.” Stick pins in to collect the electricity (and it will be readily obtained). The cushion should of course be well smeared with amalgam. From this, as well as from the glass-plate machine, the “positive” electricity can be drawn off and stored in a Leyden jar, and then discharged by the “discharging rod,” which is represented on the cut. It may have one or two handles, and one knob is placed outside the jar, the other near the ball surmounting it. The glass being a non-conductor saves the operator, and some long sparks and loud reports may be obtained.

The Electric Machine is always assumed to give off positive electricity.
Sir William Armstrong’s Electric Machine is a mode of obtaining electricity by moist steam. The design is Armstrong’s, and Professor Faraday subsequently went into all the conditions to produce the “fluid” by the friction of steam. The machine was something like a small boiler supported on glass legs. A row of nozzles was fixed upon the escape pipe so as to create a great velocity and friction in the escaping steam. Round the nozzles was a box of cold water, for that fluid was found necessary for the production of electricity as demonstrated by Professor Faraday. The steam rushed against a row of points attached to the prime conductor of an electric machine, and the electricity of the steam was thus given off to the conductor. There are many other forms of electric machines, but it will serve no purpose to detail them.

The Electric Battery (see fig. 206) is formed by a collection of Leyden jars. The inside and outside coatings are connected in a box divided into partitions lined with tinfoil. The rods of the jars are also connected, as in the illustration, by brass rods, and when this battery is charged people should be careful how they handle it, for a shock may be produced which would[Pg 209] cause serious injury, if not death. The battery can be charged from the machine by a chain fastened to the central ball, while a second chain connects the exterior of the box and all the outside of the jars, by means of the handle, to the ground.
When electricity is at rest it is termed “static electricity,” and when in motion “dynamic” electricity. The latter treats of electric currents which can be sent through wires or chains. We can keep this current moving by means of a machine, and the battery called a Voltaic battery, from Volta. We will describe it presently. Electric currents can be measured, for they may be of different strengths according to the battery, and they are measured by the Galvanometer. Electricity can therefore be transferred and carried by the conducting substances, and much heat will be engendered as the “electric fluid” passes along a wire. Lightning frequently fuses bell-wires as it passes, and when we touch upon Galvanism or Dynamical Electricity we shall hear more about it.
By the Electric Machine we can obtain some very powerful currents of electricity; we can produce many pleasing effects, and perform a number of experiments, such as making balls or figures of pith dance, and several other easy and entertaining tricks, which will be found in books more specially devoted to the entertainment of young people.

We have now given some explanation of the manner in which electrical phenomena can be produced,—viz., by the Electric Machine and by the Leyden Jar,—but we must not expect to find any electricity inside any charged body. It has been proved that all the electricity is upon the surface of bodies, even if in varying quantity, and that equal quantities of electricity are always produced when bodies are excited by friction, but the kinds are different. The rubbing body is of one kind, the body rubbed another, and consequently the forces neutralize each other. The two forces or kinds of electricity we have seen repel or attract each other, and we can imagine the farther they are apart the less will be the force, and the rate of diminution of force, according to distance, is ascertained by an ingenious apparatus called a “Torsion” Electromoter, which was constructed by Coulomb, and was frequently used by Faraday.
Perhaps some people may not be aware of the term “torsion.” It means twisting, and “the torsion of a thread suspended vertically is the force tending to twist the lower extremity when the upper end is turned through an angle.” This instrument is really an Electromoter, and is not considered suited to beginners, and it is scarcely accurate in its workings. We need not therefore describe it in detail. There are some excellent Electromoters, the Elliott being, we believe, the best for use. A full and detailed description of the Quadrant Electromoter will be found in Mr. Gordon’s treatise on Electricity.
Recapitulation of foregoing Chapter. So far, we have seen there is electricity in everything, although some bodies are termed conductors and others non-conductors; though, as in applying the terms heat and cold, we must remember that no body is entirely devoid of electricity, and no body is therefore an absolute non-conductor any more than any object is absolutely devoid of heat. Faraday, indeed, was of opinion that “conduction and insulation are only extreme degrees of one common condition”; they are identical both in principle and action, except that in conduction an effect common to both is raised to the highest degree, and in the case of insulation it occurs in an almost insensible quantity.
We have also read of positive and negative electricities, and we must not fancy there is any particular reason for this distinction. It was Du Fay, whom we have mentioned, who gave the names “vitreous” and “resinous” to the two kinds, as one was developed by rubbing glass, and the other by rubbing resin. But, as shown by our experiments, either kind of electricity can be excited in glass or sealing-wax, and both kinds are produced at once. You cannot get “positive” without negative electricity. “Positive” is the term applied to the kind produced by rubbing glass with silk or wool; “negative” is the term applied to the kind developed by rubbing sealing-wax, but the kind developed by friction depends on the rubbing substance and certain conditions.
Bodies charged with the same electricity repel; if charged with different kinds they attract each other. The more readily displaced particles when bodies are rubbed become negatively electrified as a rule.
Similar electricities repel each other with a force inversely proportional to the squares of the distance between their centres, as established by Coulomb. So if the space between any two similarly electrified bodies be reduced by say one-half, the force of the repulsion will be increased four times. The rule for attraction is similar; so when two bodies are charged with opposite electricities, and the distance between them is increased, the attractive force is diminished in proportion as the square of the distance between them. Many confirmations of this theory were made by the late friend of our boyhood, Sir W. Snow Harris, and published in the Philosophical Transactions.
The following full list of conductors and non-conductors (copied from Professor Noad’s Text-book of Electricity, and compared with De La Rive’s Treatise) may be useful:—
| Conducting Bodies in Order of Conducting Power |
Insulators in the Inverse Order of Insulating Power. |
||
|---|---|---|---|
| All the metals. | Dry metallic oxides. | ||
| Well-burnt charcoal. | Oils (heavier the better). | ||
| Plumbago. | Vegetable ashes. | ||
| Concentrated acids. | Transparent dry crystals. | ||
| Powdered charcoal. | Ice below 13° Fahr. | ||
| Dilute acids. | Phosphorus. | ||
| Saline solutions. | Lime. | ||
| Metallic ores. | Dry chalk. | ||
| Animal fluids. | Native carbonate of baryta. | ||
| Sea-water. | Lycopodium. | ||
| Spring-water. | Caoutchouc. | ||
| Rain-water. | Camphor. | ||
| Ice above 13° Fahr. | Silicious and argillaceous stones. | ||
| Snow. | Dry marble. | ||
| Living vegetables. | Porcelain. | ||
| Living animals. | Dry vegetables. | ||
| Flame smoke. | Baked wood. | ||
| Steam. | Leather. | ||
| Salts soluble in water. | Parchment. | ||
| Rarefied air. | Dry paper. | ||
| Vapour of alcohol. | Hair. | ||
| Vapour of ether. | Wool. | ||
| Moist earth and stones. | Dyed silk. | ||
| Powdered glass. | Bleached silk. | ||
| Flowers of sulphur. | Raw silk. | ||
The following may be added to the Insulators, viz.:—
| Transparent precious stones. | Sulphur. |
| Diamond. | Resins. |
| Mica. | Amber. |
| All vitrefactions. | Gutta-percha. |
| Glass. | Shell-lac (or gum-lac). |
| Jet. | Ebonite. |
| Wax. |
There are, as we know, two kinds of electricity, the static and dynamic; and when the latter state is instantaneous, it is referred to as the “electric discharge,” which occurs when opposite electricities seek each other, and the bodies return to a state of equilibrium or neutralization. “These bodies, if insulated, obtain no more electricity after the spark has passed; but if there be a constant source of negative electricity supplying one, and a constant source of negative electricity supplying the other, there will be a succession of sparks; and if they communicate by a conductor there will be, through this conductor, an uninterrupted neutralization of a continual reunion of the two electricities, and this is what is termed the continuous dynamic state or electric current” (De la Rive).

CHAPTER XIX.
VELOCITY OF ELECTRICITY—EXPERIMENTS—THE ELECTRIC EGG—FORCE OF THE ELECTRIC SPARK.
We are now acquainted with many facts concerning electricity, and have seen that electrical phenomena can be produced by the Electric Machine and the Leyden Jar. (An insulating stool—a stool with glass legs—is a very desirable adjunct for those who wish to experiment with the machine). Glass is a great insulator, or non-conductor, as a Russian philosopher found to his cost. He had an iron lightning-conductor from his house into his room, the end not connected with the earth but with a glass. One day the lightning came down the rod and reached the glass; had a communication been made with the earth by a chain, or directly, no mischief would have ensued. As it happened, however, the current was checked by the glass, and immediately darted towards him; it struck him in the head, and killed the poor man on the spot. If no insulating stool were used, the body charged would be discharged upon contact with the ground.
The velocity of electricity is very great, and experiments have frequently been made. Wheatstone undertook to ascertain the speed of the electric fluid, and the instrument he employed he called a “Chronoscope.” He caused a mirror to revolve with enormous velocity, and measured the speed by the vibrations of air, which produced a certain note by the same motive power. (We know already that certain notes are produced by a certain number of vibrations per second.) Wheatstone’s Chronoscope consisted of this mirror, in front of which was placed a circular block of wood, in which, in a row, were set six wires carrying small knobs; round these and over the wood he put an insulating varnish. A Leyden jar was connected outside with the first knob; between the second and third a quarter of a mile of copper wire was coiled, and a like length of wire between the fourth and fifth; the inside of the Leyden jar was then connected with the last knob, and the spark passed; it ran from knob to knob over the long coils of wire. If all the flashes over the wire and knobs occurred simultaneously the mirror would show them side by side; if not, as the mirror turned a trifle, the difference would be observed. The mirror did show a slight retardation in the passage of the flash, and from certain measurements and calculations Wheatstone estimated the velocity of the spark to be 288,000 miles a second.[Pg 213] This rate will carry electricity round the earth in about a twelfth of a second, a rate Puck never dreamed of when he promised to “put a girdle round the earth in forty minutes.”
But it appeared from investigations subsequently made that it was not possible to express the velocity of electricity with any certainty, and a number of experiments were made as per the following table, with very different results. Sir William Thomson and Faraday endeavoured to account for these stupendous discrepancies, and the principles of retardation of electricity were established. The differences are shown below:—
| Nature of Wire. |
Velocity per Second. |
|
|---|---|---|
| Wheatstone’s Experiment in 1834 | Copper | 288,000 |
| Gonella and Fizeau | Copper | 111,834 |
| Iron | 62,130 | |
| Mitchell | Iron | 28,331 |
| Walker | Iron | 18,639 |
| Gould | Iron | 15,830 |
| Astronomers in Greenwich | Copper | 7,600 |
| Asronomers in Brussels | Copper | 2,700 |
| Result in Atlantic Cable, 1857 | Copper | 1,430 |
| Result in Atlantic Cable, 1858 | Copper | 3,000 |
To account for the comparatively low velocities of the cables, Faraday proved that they act very much as a Leyden jar acts; that is, it takes time to fill, as it were, and to discharge them, the wire coating of the cable in air acting like the outer coating of the jar or the water in the case of an immersed cable, and the retardation observed is owing to resistance of conduction, and depends upon the way in which the electrical impulses traverse the wire. “There is a long, gradual swell, and still more gradual subsidence of the electric current, and the length of time that elapses between the initial impulse and the attainment of maximum strength, is proportional to the square of the length of the line.”
The duration of the electric spark has been calculated at the 1/24000 part of a second, but Professor Tyndall regards this as the longest or nearly the longest time it is perceptible; the shortest time is almost inconceivable. The brightest portion of a spark has been ascertained to last only forty-six millionths of a second, and certain experiments were made to ascertain the actual duration with various numbers of Leyden jars. It was discovered by Messrs. Lucas and Cuzin, by an application of the Vernier, with batteries consisting variously of two to eight jars, and obtained the following results14—
| No. of Jars. | Duration in millionths of a Second. |
|---|---|
| 2 | 26 |
| 4 | 41 |
| 6 | 45 |
| 8 | 47 |
“So,” adds the writer, “the duration (of spark) increases in proportion with the number of the jars. It increases also with the striking distance, but[Pg 214] is independent of the diameter of the balls or globes between which the spark strikes.”
Many examples might be given of the spark discharge of the electric current. This form is seen in the blue line extending between the knob of a machine and the hand, and the duration of a spark with a jar charged with an induction coil is stated by Professor Rood to vary, but the brightest portion with a jar of 114 square inches only existed for the 175th billionth of a second, and with a smaller surface was much shorter. Such a spark may be conducted to a plate of gunpowder and will not ignite it, because the time of the duration of the “fire” is not sufficiently long; the powder will be scattered, but not ignited. If, however, a partly non-conducting medium be interposed between the jar and the powder, so that the spark be retarded a little, the gunpowder will be fired.
While speaking of electric discharge we may remark upon the beautiful effect of lightning. These discharges are sometimes miles long, and by the return stroke from the cloud may kill a person a long way from the actual discharge. This phenomenon was illustrated by Viscount Mahon in 1779, in a very interesting book on the principles of electricity.
There are different ways in which the electric discharge shows itself. We have spoken about the spark discharge which, however, is found to present very different appearances in varying conditions. Professor Faraday proved that the colour of the electric sparks showed in air, when obtained with brass balls, the intense light and blue colour so familiar to all. In nitrogen they are even bluer. In oxygen again the sparks are much brighter than in air, but not so brilliant. In hydrogen they become crimson, but the sound is almost inaudible because of the physical character of the gas. In carbonic acid gas they are almost the same as in atmospheric air, only more irregular. In dry muriatic gas they are nearly white and very bright. In coal gas the colours vary—sometimes being green and sometimes red. Occasionally the same spark will be red and green at different extremities, and even black portions have been observed. The density and pressure of the atmosphere has been proved to exercise considerable influence upon the spark discharge.
The “Brush” discharge is shown in “a series of intermittent discharges which appear continuous.” This discharge assumes the shape of a fan. “It is accompanied with a low chattering sound,” which is the result of the separate and continuous discharges, and Faraday also demonstrated that its effects varied according to the medium in which it was exhibited.
The effect of the air pressure on electricity may be observed in the following way:—
If we pass a spark through rarefied air by an apparatus known as the Electric Egg, we may obtain many curious effects. The “egg” consists of a glass globe, through which enter two rods with a knob upon each inside end. The upper rod is moveable, and held in its place by a “cap” like the lower rod. There is a stop-cock in the lower cap, so that the egg may be fastened to any plate or stand. When the egg is filled with air, the[Pg 215] electric spark passed into the glass globe has the usual appearance, but as the air is gradually rarefied by an air-pump, the spark assumes beautiful forms and colours. As the exhaustion continues, however, we shall find the spark decreasing in brilliancy, and finally the spark will cease to be visible. It thus is shown that the colour of the spark depends upon the gaseous medium and on the material of the conductors, and when the electric spark is faint this medium can be observed, for nitrogen will produce a blue tinge and carbonic acid a green; hydrogen gives us a red, as already remarked. By multiplying the number of eggs and plates of glass, and placing discs of tinfoil in various shapes at certain distances, many beautiful figures may be observed when the spark is set free.
Professor Tyndall at the Royal Institution showed a very pretty experiment. He took a funnel with a very fine bore, and permitted sand to flow from it as it will in the hour-glass. When he permitted the electric current to come in contact with the sand, however, it, instead of falling vertically to the table, spread out fan-like, each grain repelling and being repelled by its neighbour with an effect very beautiful to see. Luminous effects have frequently been produced by passing an electric spark through various bodies. For instance, a lump of sugar can be made quite brilliant in the dark by passing electricity through it, and there are other substances similarly affected. Even eggs and some fruits are thus made phosphorescent. The illumination of the “diamond” covered Leyden jar is familiar to all who ever attended a lecture on Electricity.
The various effects of the electric discharge need not here be described. We have witnessed the results of lightning, but even in our laboratory many pretty little experiments can be made, such as the perforation of a card by the electric discharge. The chemical effects are various. Decomposition of water is effected by electricity, and the discharge can also be, and has been utilized for military purposes, such as employed by Professor Abel in his fuse, and in his apparatus for firing mines. Experiments at Chatham and elsewhere have been very successful in the application of electricity to modern warfare.
We will illustrate one or two of these. A thick card should be placed, as in the illustration (fig. 216), between two insulated points, and to the lower portion of the apparatus a chain be attached, held in the hand, and wound round the Leyden jar. If then the knob of the jar and the knob above the upper point be brought together, the spark will pass through the card.

In the same manner a glass may be perforated if the current be stronger. Of course the whole apparatus—and particularly the plate—must be quite dry, and it will be better to put a drop of oil under the upper needle point so as to prevent the electricity spreading over the glass.[Pg 216] The glass will be found pierced by the electric spark when the Leyden jar is brought into requisition (fig. 217).
It was at one time contended that the sudden expansion of the air by the electric spark caused heat to be generated, and a thermometer was invented by Kinnersley to show this. The illustration (fig. 218) will explain it. When the electric spark passed between the balls in the large tube the water rose in the smaller. But the immediate return of the water to its level showed that the disturbance was only mechanical, and not owing to heat.

Fig. 217.—Experiment with glass.

Fig. 218.—Kinnersley’s thermometer.
We may now pass from the “frictional” to the other kind—viz., “dynamical” electricity, and we shall begin with the consideration of Galvani’s experiments and the Voltaic Pile.

CHAPTER XX.
GALVANISM.
GALVANI’S DISCOVERY—THE FROGS ELECTRIFIED—EXPERIMENTS—VOLTA’S PILE—THE TEST—ITS USEFULNESS—FARADAY’S “RESEARCHES.”
Galvanism owes its origin to the researches of Galvani, the celebrated professor of Bologna, and we are indebted to what was a mere “accident” for our knowledge of this science.
Before Galvani’s time there had been many instances adduced of animal electricity. The Rev. F. Lunn, in his article upon Electricity,15 mentions the fact that fire streamed from the head of Servius Tullius when about seven years of age, and Virgil we know refers to flame emitted by the hair of Ascanius—
“Lambere flamma comas, et circum tempora pasci”;
and if any one will comb his or her hair with an ebonite comb in the dark, with what is sometimes called an “india-rubber comb,” the hair will give out sufficient light to enable the operator to see himself in a looking-glass. In olden days it is related that a lady when touched with a linen cloth emitted sparks, and the same phenomenon was observable when a bookseller at Pisa removed his under-garment or vest (De Castro). We are all aware of the electricity of the cat and of certain fishes (see Electricity of Animals in sequel), and “torpedos.” Galvani had of course a knowledge of this property, and had occupied himself for some time making experiments upon the electricity in animals. He was not in his laboratory that day when the great discovery was made by means of the edible frog.
Galvani’s wife was just then in a very delicate state of health, and in accordance with usage had been ordered soup made from frogs. It is related that some of these animals, ready skinned, were lying upon the laboratory table, for the Professor had been just previously investigating the question of what he opined was “animal” electricity; that is, he fancied that muscular motion depended upon that subtle force.
The electric machine was in action, and one of the attendants happening to approach or touch one of the frogs, the man as well as Madame Galvani observed that the limbs were violently agitated. Galvani was at once informed of this, and he made repeated experiments, which showed him that the convulsive movements only took place when a spark was drawn from the[Pg 218] prime conductor of the electric machine, and while the nerve was touched by a conductor. Galvani then suspended a number of frogs to a railing by metal hooks, with a view to experiment upon them with atmospherical electricity. But the frogs’ limbs were again agitated when no electricity was apparent, and Galvani after some consideration came to the conclusion that the movement was owing to the position the animals assumed with reference to the metallic bodies. Thus when muscle and nerve were in contact with metallic bodies and connected by metal, the movements of the limbs were observable, and the greater the surface contact the greater was the convulsion. The philosopher next tried various metals, and discovered that the most powerful combination was zinc and silver.
Galvani, in 1791, published his discovery and his theory that the body acted as a Leyden jar, different parts being in a different state of electricity. No sooner were his deductions published than all Europe was in a ferment, and philosophers of all nations were discussing it. Fowler, Valli, Robison, Wells, Humboldt, etc., all were deeply interested, but none of them appear to have arrived at so correct conclusions as did Volta, the physician of Pavia. “Wherever frogs were to be found,” says Du Bois Reymond, “and where two different kinds of metal could be procured, everybody was anxious to see the mangled limbs of frogs brought to life in this wonderful way. Physiologists believed that at length they should realize their visions of a vital power, and physicians thought no cure was impossible.”
But notwithstanding the popular theory, Volta, in his letters to Carallo, while giving a full and clear account of the discovery made by Galvani and his own experiments, attacked and finally defeated the Professor. Volta quite upset Galvani’s Leyden-jar theory; Volta says that it was by accident that Mr. Galvani discovered the phenomenon, and by which he was more astonished than he ought to have been. Volta’s letters will be found in the Philosophical Transactions of the Royal Society (in French), and he attributes the effect to the metals which produced a small amount of electricity. He found that the nerve was acted upon on even parts of a muscle laid upon two different metals, and if those were united, a contraction took place.
“Many experiments were made in all parts of Europe,” says Doctor Roget, and “an opinion had been very prevalent that the real source of the power developed existed in the muscle and nerve which formed part of the circuit, and that the metals which composed the other part acted merely as the conductors by which that agency was transferred from the one to the other of these animal structures. But the discoveries of Volta dispelled the error, by proving that the sources of power were derived from the galvanic properties of the metals themselves when combined with certain fluids,” and decided that this principle was electricity. From this the “general fact” was deduced—viz., “that when a certain portion of a nerve which is distributed to any muscle is made part of a galvanic circuit, convulsions, generally of a violent and convulsive kind, are produced in that muscle.”
Volta at length made the discovery that when two metals were brought[Pg 219] together electricity was developed, and by uniting a disc of copper and one of zinc, and subjecting them to the test of an Electroscope, he found positive and negative electricity developed in the zinc and copper respectively; so Volta came to the conclusion that each metal parted with electricity, and one became all “positive” and the other all “negative.” But when he came further to consider the possibility of building up a “pile” of these metal discs sufficiently strong to produce electric effects, he found that if his theory were correct he would lose from one side of the metal all he would gain from the other, and therefore he could never obtain more than the slight effect he had originally produced.
This was at first a difficulty apparently impossible to remove. It was so self-evident that the discs of metal, if placed in a pile in a series of pairs, would continually exercise like effects to the first pair of discs, that Volta was puzzled, and for some time he could not arrive at any reasonable solution. At last it struck him that if he placed between the discs some slow-conducting substance, the electricity would not pass from disc to disc, and the force developed or set in motion would be more powerful.
He made the experiment. The result was the Voltaic pile made in 1800, of which we give an illustration (fig. 219). A communication on the subject of Electricity by contact, written by M. Volta, is to be found in the Philosophical Proceedings for the year 1800.

Volta constructed the pile which bears his name, on the assumption that “every two heterogeneous bodies form a galvanic circle or arc in which electricity is generated.” The “pile” consisted of a number of discs of zinc and copper separated by discs of card soaked in water. This combination of metals separated by a bad conductor, developed considerable electricity, the “positive” going to the zinc at the top, and the “negative” turning to the opposite end. By touching the zinc and copper extremities simultaneously with wetted fingers we shall experience a shock. “I don’t need your frog,” Volta said, when he had proved his theory; “give me two metals and a moist rag, and I will produce your animal electricity. Your frog is nothing but a moist conductor, and in this respect it is inferior to my wet rag!”
After this discovery the theory of animal electricity died away for many years, till in 1825, Nobili, and afterwards Matteucci, proved the existence of galvanic currents in muscles.
After Volta had succeeded in obtaining a shock from his “pile,” he proceeded to the construction of another instrument, or rather apparatus,[Pg 220] which he denominated “Couronne des tasses” (fig. 220). It consisted of a series of small glasses containing water or a saline solution. He then procured a number of “metallic arcs,” partly composed of zinc and partly of copper; these were inserted into the glasses, so that every glass contained the zinc of one and the copper of another arc, not in contact, but one at the right hand the other at the left. The electro motion, supposed to be the primary cause of the galvanic action, was thus produced as well as from the “pile.” The principle was just the same in both apparatus, the metals being divided by the water in one case, and by a wet card or cloth in the other.
Volta, in 1800, addressed to the Royal Society his celebrated letter upon electricity excited by contact of conducting substances, and then the English philosophers proceeded to make further experiments. It was Fabroni of Florence who had just before suggested that chemical action was really the cause of the phenomena exhibited. Sir Humphrey Davy warmly advocated this theory, and made numerous experiments with the view to establish it. Nicholson, Carlisle, and Cruickshank also paid great attention to the subject. Volta, although he had laid the foundation, did not venture to build upon it. Messrs. Nicholson and Carlisle found the two kinds of electricity in the pile, the zinc being positive and the silver negative. They also found that the water was decomposed both in the circuit and in the body of the pile. Subsequently Cruickshank confirmed Nicholson’s observations, and made use of what is termed the “trough” apparatus. He found that hydrogen was emitted from the silver or upper end, and oxygen from the other.

These discoveries opened up a wide field. “The power of the pile in decomposing chemical substances was now established.” Dr. Henry employed galvanism for analysis, and Sir Humphrey Davy invented new combinations of substances. He formed a pile of charcoal and zinc, and found out that a pile could consist of only one metal, different fluids being applied to the opposite surfaces separated by water, and one fluid “capable of oxidating the metal, the other of preventing the effect of oxidation.” Soon after a pile was made of charcoal.
In 1806, Sir H. Davy gave the results of his researches to the world upon the electro-chemical action of bodies. In the course of his experiments he found out the chemical constituents of the alkalies, and a surprising number of new things were brought to light, and chemical science received a most astonishing ally. Sir W. S. Harris says: “A series of new substances[Pg 221] were speedily discovered, the existence of which had never before been imagined. Oxygen, chlorine, and acids were all dragged, as it were, to the positive pole, while metals, inflammable bodies, alkalies, and earths became determined to the negative pole of the (galvanic) battery. When wires connected with each extremity of the new battery were tipped with prepared and well-pointed charcoal, and the points brought near each other, then a most intense and pure evolution of light followed, which on separating the points extended to a gorgeous arc.” So the elements of all bodies were separated and the composition of their compounds closely investigated.
Michael Faraday threw himself con amore into the question. He set about to classify the pile phenomena, and arranged them with appropriate terms, and in a series of papers, between the years 1830 and 1840 (see his “Experimental Researches”), he explained the chemical effects of voltaic electricity and electro-magnetic induction. He showed that the electricities obtainable from the voltaic pile and the electrical machine are essentially the same in their action. He proved that the theory held respecting the necessity for the presence of water in electro-chemical composition was erroneous, and that many other fluids and compounds were equally effective. We have not space at our disposal to include a digest of his various lectures and papers. He calculated that as much electricity is employed in holding the gases oxygen and hydrogen together in a grain of water, “as is present in a discharge of lightning.” When water is decomposed by the electric current, the force which determines the oxygen and acid matter held in solution to the positive, while the hydrogen passes to the negative pole, is not in the poles, but in the body decomposed, he says. “The poles,” writes Faraday, “are merely the surfaces or doors by which the electricity enters into or passes out of the decomposing substance. They limit the extent of that substance in the course of the electric current, being its termination in that direction. Hence the elements evolved passed so far and no farther.” Faraday named the poles “electrodes”—the way (in or out) of electricity.

A very simple voltaic pile may be constructed with “gold-leaf” paper. Take two sheets of the gold paper and paste them back to back, and two of silver paper; cut them into discs about the size of a five-shilling-piece (or even of half-a-crown), and place them one on the top of the other, so as the gold and silver may be alternate; press the discs together slightly when a good many layers have been piled up, and introduce them into a glass tube; close the ends of the tubes with corks through which wires are passed from the discs top and bottom. It will be found that the ends are charged with opposite electricities. This is the Zamboni pile, or the dry pile, which was constructed of hundreds of paper discs “tinned on one side, and covered with binoxide of manganese on the other,” put into a tube, and closed with brass stoppers. The electricity will last a long time in a dry pile.
In the accompanying illustration of the Galvanic Pile a disc of copper[Pg 222] is at the bottom and a disc of zinc at the top. The latter, P, is the positive pole; the former, N, the negative. When the wires are united the current is closed, and no sign of disturbance can be detected, although the action, of course, is proceeding within the pile. The opposite kinds of electricity neutralize each other, and if a continuous supply were not kept up the electricity would disappear; but as it is, a powerful current is obtained, and if the wire be divided a spark will be observed.

There are many forms of galvanic batteries. The Trough Battery or Cruickshank has been mentioned. There is Wollaston’s Pile, Bunsen’s Battery, Grove’s Battery, and Daniell’s, called the “Constant” Battery. In this last a porous earthenware cell is placed within a cylinder of copper; in the cell a rod of zinc is inserted, the cell being filled with diluted sulphuric acid,—one part of acid to ten parts of water,—and in the outer cylinder is a solution of sulphate of copper.


The cut above illustrates Daniell’s Battery (fig. 223) with connectors.
In Bunsen’s Battery (or the Zinc-Carbon Battery), which is very like the “Daniell” arrangement, as will be seen from the plates (figs. 222, 223), the porous cell has a prism of carbon immersed in it, and is apparently a modification of the powerful “Grove” Battery (fig. 224). This consists of slips of platinum, h, placed in porous cells, g, each cell being surrounded by a glass cylinder. The outer (glass) cells are filled, or nearly filled, with diluted sulphuric acid; nitric acid is used in the porous cells, and a platinum plate inserted. The chemical action of the Grove cell is thus explained by[Pg 223] Professor Stewart: “The zinc dissolves in the dilute sulphuric acid, and during this process hydrogen gas is given off. But this hydrogen does not rise up in the shape of bubbles; it finds its way into the porous vessel which contains the strong nitric acid. It there decomposes the acid, taking some oxygen to itself, so as to become water (hydrogen and oxygen forming water), and thereby turning the nitric into nitrous acid, which shows its presence by strong orange-coloured fumes.” By this decomposition of the nitric acid the polarization of the platinum (due to hydrogen) is avoided. The porous cell, while keeping the liquids apart, does not interfere with the chemical action.
A great number of cells are used in the Grove Battery; perhaps even a hundred may be employed.
Smee’s Battery consists of a plate of platinized silver, S, with a bar of wood to prevent contact with the zinc on each side, Z. These are immersed in a glass jar, A, which contains dilute sulphuric acid. The current is obtained by metallic communication with the binding-screws on the top. This battery has much the same general arrangement as Wollaston’s—the position of the plates being, however, reversed; in the latter there are two negative plates to one positive. In Smee’s Battery there are two positive (zinc) plates to one negative plate.

Fig. 225.—Smee’s Cell.

Fig. 226.—Smee’s Battery.
It will now be understood how an electric current is produced; the electricity passing through the cells, etc., to wires, confers certain properties upon the wires, and we can ascertain the effect of the current by means of a Galvanometer, an instrument used to detect the strength and direction of electric currents. The current will evolve heat and light; it will excite muscular action, and will decompose substances into their constituent elements. The deflection of the magnetic needle by the electric current is considered the best evidence of its power; it is on this that the Galvanometer is based.
We can perform a few simple experiments with the current. Suppose, for instance, that a piece of fine wire be fixed between the pole wires of the battery; it will be heated “white hot.” Or if two carbon points be approached in a glass of water, as in the illustration (fig. 227), they will emit a brilliant light in the fluid from the voltaic arc which has given us the electric light. The current is the passage of electricity along the wire, and continues[Pg 224] until the working power or “potential” of one conductor is equal to that of the other. When they become equal of course the action ceases, as there is equilibrium. But when an apparatus like the galvanic battery is brought to bear so that the force of electricity from one conductor is made always greater than that of the other conductor, we have a continuous flow while the action of the battery goes on. One view of the principle is thus expressed by Professor Gordon:16
“If two metals be placed near together, but not in contact, in a liquid which acts chemically more upon one than upon the other, the metals become charged, so that the one least acted on is of higher potential than the one most acted on. The difference of potential produced depends only upon the nature of the metals and of the liquid, and not on the size or position of the plates. As soon as the difference of potential has reached its constant value the chemical action ceases.

“If now the metals are connected by a wire outside the liquid the difference of potential begins to diminish, and an electric current flows through the wire. As soon as the difference of potential becomes less than the maximum for the metals and liquid, chemical action recommences and brings it up to the maximum; and thus if no disturbing cause interferes the current will continue until the metal most acted on is entirely dissolved.”
The metal most acted on is considered the “generating plate,” and is “positive.” The other attacked less is “negative,” and is known as the “collecting plate,” and the zinc is the positive plate. Sir W. Thomson has shown that the electrical movement in the galvanic circuit is entirely due to the electrical difference produced at the surfaces of contact of the dissimilar metals. The electro-motive force obtained is not the same with all metals. We have mentioned that some are electro-positive and some electro-negative, and it is with reference to each other that the metals are considered to be endowed with these properties respectively. It all depends how the metals are arranged or coupled. With reference to their behaviour in this respect scientists have arranged them in a series, as follows:—
- Zinc.
- Cadmium.
- Tin.
- Lead.
- Iron.
- Nickel.
- Bismuth.
- Antimony.
- Copper.
- Silver.
- Gold.
- Platinum.
- Graphite.
Each metal in the list is arranged so that it is electro-positive to any one below, and electro-negative to any one above it.
There is another curious fact which should be mentioned. In associating these metals it has been found that when two are brought into contact the electro-motive force becomes greater the more distant they are in the series given above; in other words, the force between any two is equal to the sum of the forces between those intervening between those two. So when zinc is used with copper its force is not so great as when used with platinum.
It was Herr G. S. Ohm who laid down the law that the strength of the electric current is equal to the electro-motive force divided by the resistance, for he proved that the “resistance was inversely proportional to the strength of a current.”
There are two other laws respecting currents; viz.,—
(1.) Parallel currents in the same direction attract each other.
(2.) Parallel currents in opposite directions repel each other.

Upon these two hang all the varied phenomena of electro-dynamics. That chemical action develops electricity we can perceive with the aid of the two cuts (figs. 228 and 229). If the wires be attached to the collecting-plate of a condenser of electricity and the metal plate of a cell, as shown in the figure (fig. 228), the electricity on the plate will be negative. If the operation be reversed, and the plate be put in connection with the acid, and the metal with the earth, the instrument will be charged with positive electricity. In the other case, when two cups are used, united by a magnet so that the solutions (one acid and the other alkaline) can by capillary attraction unite upon the binding of the magnet, and we place the wires as in fig. 229, the charge on the plate will be positive if it be in connection with the acid, and negative if in communication with the alkaline solution. Every time there is chemical action between two bodies in contact electricity is produced—positive on one negative on the other, and that is the fundamental principle of the voltaic pile.
The decomposition of water can also be effected by means of the electric current. If two tubes or vessels be placed in a vase of water, and the wires from the battery be inserted in them respectively, the oxygen will go to the platinum or positive pole wire, and the hydrogen to the zinc or negative pole. This decomposition or “splitting up” of components was termed Electrolysis by Faraday, who gave a series of names to the action and the actors in these phenomena (fig. 230).
Any liquid body, such as the water we have just decomposed for instance, Faraday termed an electrolyte; the surfaces where the current enters or leaves the body were called electrodes—the “ways,” from odos, a “way”; the entry is the anode; the leaving point the katode, from ana, “up,” and kata, “down.” The electrolyte is divided into two portions, “ions” (“movers”), which move towards the electrodes, which are positive and negative. In the case of the decomposition of water the hydrogen goes to the negative electrode, the oxygen to the positive.

There are a few observations to be made respecting electrolysis. One rule is, that it “never takes place unless the electrolyte is in a liquid state.” The liquid state is essential. It is also observed that the components go to the different electrodes; such elements as go to the negative electrode are termed electro-positive, the others electro-negative; or, as Faraday termed them, “anions” or “kations:” The chemical power or electrolytic action of the current is the same at all parts of the circuit; the quantity of the substance decomposed is in exact proportion to the strength of the current. Faraday measured the strength of the electric current, and invented for the purpose an instrument called the Voltameter. We have mentioned the Galvanometer more than once, and will proceed to describe it. There are several forms of this instrument: the Tangent, the Marine, and the Reflecting Galvanometers, and the Astatic, or “Multiplier.” In the first-named the direction of the current is determined by Ampère’s rule, which is as follows:—
“Imagine an observer placed in the wire so that the current shall pass[Pg 227] through him from his feet to his head; let him turn his face to the needle: its north pole is always deflected to his left side.”
The “Tangent” Galvanometer consists of a vertical circle like an upright ring, across which is a support in the centre holding a copper wire, through which the electric current passes. On this point (where the wire is) a needle is very lightly supported, and when the instrument is to be used it is placed so that the plane of the circle is parallel to the line in which the needle points. The current passes, and the needle is deviated. By noting which side the north end of the needle goes the direction of the current is ascertained, and the length of the needle being small in comparison with the diameter of the circle through which the current passes, the strength of the current in the vertical circle is in proportion to the tangent of the angle through which the needle turns. Hence the term “Tangent” Galvanometer.
The “Reflecting” instrument is the invention of Sir William Thomson, in which a mirror is attached to the needle, and reflects a small focus of light upon a scale. The movements, however minute, are easily read. Sir W. Thomson’s Galvanometers are extremely sensitive. We need not mention any other varieties, as full descriptions can easily be obtained. We only need to indicate the mode of working.

The accompanying illustration (fig. 231) shows an Astatic Galvanometer which may be used in two ways—either to measure strength of current, or to find out a current; in the latter case it would be termed a Galvanoscope. It is a compound needle instrument, and consists of two needles placed in parallel directions with opposite poles above each other in a coil. The wire coil is wound round a bobbin, and the astatic needle is placed therein and suspended freely, as in the illustration, by a cocoon thread. The upper needle moves upon a scale, O O, and the instrument is enclosed in a glass shade. The screw, V, communicates with the upper needle, and fixes it at zero point when ready for use. The wires are fastened to the binding-screws, and the current is then sent. The needle is deflected accordingly, and the number of degrees on the scale can be read off.
The uses of the galvanic current are many. Amongst them Electroplating is perhaps the most generally useful, though Electrotyping is also a very important process in art. A visitor to Birmingham may view the process carried on there by some enterprising firms, who have succeeded wonderfully in producing electro-plate. The principle is very simple and easy to understand, but the greatest care and watchfulness are required on the part of the men employed. The principle, as we have said, is simple,[Pg 228] and consists in the fact that if a plate of metal be suspended and attached to the positive pole of a galvanic battery and immersed in a solution of the same metal, the conducting substance hung opposite at the negative pole becomes coated with the metal immersed in the solution.


Suppose we take a plate of silver, and immerse it in cyanide of silver dissolved in cyanide of potassium; a coating of silver will be deposited upon the nickel spoon or other article suspended at the other pole. But to make the coating adhere the spoons, forks, etc., are prepared for the bath by cleansing in caustic potash to remove grease, and washed in nitric acid to remove all traces of oxide, then are scoured with sand. Next, a thin coating of mercury is put on by immersion in solution of nitrate of mercury. Finally, they are hung in the bath. A metal rod is hung across the bath (fig. 232), and the plate is immersed. If the rod to which the articles are suspended be attached to the zinc or negative pole, and the plate of silver to the positive pole of the battery, decomposition begins, and the silver begins to attach itself to the suspended objects. If it be desirable to give the plated articles a thick coating, they are retained for a long time in the bath, which is of some non-conducting material. The dull appearance is easily removed by brushing and burnishing, and then the “Electro-plate” is[Pg 229] ready for the warehouse. The gilding process is performed in the same manner, a gold plate being substituted for the silver.


Electrotyping may be briefly explained as follows:—Take two vessels, A and B, and in one, A, put some dilute sulphuric acid and two plates, one of zinc, Z, the other of copper, D, but be sure they are not touching each other; each of these plates must have a piece of wire fastened, by soldering to their upper parts. In the vessel, B, put some solution of sulphate of copper and a small quantity of dilute sulphuric acid, and attach another copper plate to the wire which comes from the copper plate in the acid; this second copper plate is to be immersed in the solution of sulphate of copper, and to the wire from the zinc plate is to be fixed the object to be coated. If a medallion or other object in plaster, it should be soaked in very hot wax and then brushed over with blacklead until the surface is perfectly blackened and bright; the wire should be bound all round the margin and soldered (as it were) with melted wax to the medallion, taking care that this wax also is well coated with blacklead. If the object be now immersed in the sulphate of copper solution and kept at a short distance from the plate (it must not touch it), a coating of copper will soon cover the surface and form a perfect cast, which, when of sufficient thickness, may be removed[Pg 230] by filing the edge all round. If instead of the plaster cast a copper coin or other copper object be used, the blackleading is not required, but the surface must be first made clean and bright.
Many uses are made of the galvanic current by medical men. If the circuit of the pile is closed and we take a wire in each hand and break contact, a concussion will be felt in the joints of the arm and fingers, and a certain contraction of the muscles. The currents of electricity cause the shocks, and by a peculiar arrangement by which the circuit can be closed or broken at pleasure, a series of shocks can be sent through the body when it forms the connection between the poles of the battery. We give illustrations of a medico-galvanic machine. In fig. 235 there are two batteries, A and B, with cells, C D. Each battery consists of a central plate of platinized silver separated from the zinc plates by a piece of wood, E and F; the binding-screws are fastened to the silver plates, and G H retain the zinc plates; I is a copper band connecting the zinc plate of one battery with the silver plate of the other. At Z and opposite are wires leading to the coil machine. The quantity and intensity of the current are regulated respectively by the indicator, O, and the wires, Q. There is a point, R S, for the breaking of the contact; P N are screws retaining the wires which lead to the handles, U V, grasped by the patients.

Horse-shoe magnets.
The electric current is employed in many diseases, and is of great use in some cases, but the further consideration of it with reference to its medical applications does not fall within the scope of our present work. We will now pass on to one of the most useful applications of the electric force, the Telegraph, and in dealing with it we must make a few remarks upon magnetism. First, let us make an experiment or two, and see the reciprocal action between electricity and magnetism.
(1.) If we take a piece of iron of the form of a horse-shoe (fig. 236), and wind around it copper wire, and pass through the wire an electric current from our battery, the iron will exhibit strong magnetic properties, which it will lose when the current is interrupted. The conducting wires are insulated with silk, and the current will then travel in one direction.
(2.) If we cover the ends of a non-magnetic piece of iron with coils of wire, and rotate the magnet, A B, so as to cause the poles to approach[Pg 231] each end of the iron alternately, an electric current will be established in the wire.
(3.) Referring to the first experiment, if we bring a needle in contact with the iron horse-shoe, while the current is passing through the wire we shall find that the needle has become a magnet; i.e., that it will point due north and south when suspended.
We will now see what a Magnet is, and why it has obtained this name.

In Magnesia, in Lydia, in olden times was found a stone of peculiar attributes, which had the property of attracting small portions of iron. The Chinese were acquainted with it, and nowadays it is found in many places. In our childhood we have all read of it in the story of “Sinbad the Sailor.” Popularly it is known as the loadstone; chemists call it magnetic oxide of iron (F2O3). This stone is a natural magnet. In Sweden it exists in great quantities as “magnetic iron,” for it has a great affinity for that metal.
If we rub a piece of steel upon the loadstone we convert the former into a magnet—an artificial magnet as it is called, and the magnetic needle so useful to us in our compasses and in the working of one form of the electric telegraph is thus obtained. Let us see how this needle acts.

Fig. 240.—Simple touch.

Fig. 241.—Double touch.
Take a magnetic needle and dust upon it some iron filings. You will observe that the filings will be attracted to both ends of the magnet, but the centre will remain uncovered. The ends of a magnet are termed “poles,” the centre the equator. So one end is north and the other south, and we might perhaps imagine that the same characteristics would abide in the bar when it is cut in two. But we find that as when a worm is divided, each portion gets a new head or tail, and makes a perfect worm, so in the magnet each divided half becomes a perfect magnet with separate poles, one of which always points to the north.
The poles of the magnet display the same phenomena as regards attraction and repulsion, as do the opposite kinds of electricity. If we suspend a magnet and bring the north pole of another to the north pole of the suspended magnet, the latter will turn away; but if we apply the north pole of one to the south pole of the other they will be attracted just as opposite electricities attract each other.
Magnetization is the term applied to the making of artificial magnets, which act is accomplished by bringing the needle in contact with other magnets, or sometimes by means of the electric current. If we carefully stroke the needle with the magnet, always in the same direction, lifting the magnet and beginning afresh every time, we shall magnetize the needle, but with a different polarity from the pole it was rubbed with. A magnet rubbing its north pole against a needle will make the latter’s point south, and vice versâ.
Now that we have seen how the “magnetic needle” is arrived at, we can proceed to explain the electric telegraph. The term telegraph is derived from the Greek words tele, “far,” and graphein, “to write,” and now includes all modes of signalling. Signalling, or telegraphing, is of very ancient origin; the Roman generals spelt words by fire. The beacons fired on the hills, the “Fiery Cross,” and other ancient modes are well known. The semaphore and flags have long been and are still used as modes of signalling, while the flashing of the heliograph “telegraphs” to a distant camp.
The Semaphore was invented by Chappé, and was really the first practical system of telegraphy. It was adopted in 1794, but before this, in 1753, a letter appeared in the Scots Magazine, by Charles Marshall, suggesting that signals should be given by means of electric wires, equal in number to the letters of the alphabet. Soon afterwards Lesage, of Geneva, made an electric telegraph to be worked by frictional electricity, and many ingenious attempts were subsequently made to utilize electricity for signalling purposes, but without any permanent success; indeed, the British government were quite content with their semaphores, for they wrote that “telegraphs of any kind are now wholly unnecessary, and no other than the one now in use will be adopted”!
The Electric Telegraph has had considerable antiquity claimed for it, but it is pretty certain that the discovery made by Doctor Watson, in 1747, that electricity would pass through wires, and that the earth would complete the circuit, gave the first impetus to the Electric Telegraph. Doctor Watson was enabled to transmit shocks across the Thames, and made experiments at Shooters Hill. Franklin did likewise across the Schuykill in 1748, and De Luc performed the same experiments on the Lake of Geneva. Both Lesage and Lomond caused pith balls to diverge at distant points, and in 1794 Reizen made use of the electric spark for transmitting signals, and made strips of foil show out certain letters when the spark passed. He had a wire and a return wire for each letter of the alphabet.
These were all slow advances, and subsequently many learned men in[Pg 233] Europe sought to improve upon the ideas then promulgated. We read of telegraphs constructed at Madrid by Salvá and Betancourt in 1797 and 1798, one extending for more than twenty miles. The first-named gentleman finally proposed to substitute the Voltaic pile for the usual machine, and Ronalds and Dyar in England and New York respectively employed frictional electricity with some success. The latter sent charges of frictional electricity through a wire, and they were recorded by being made to pass through litmus paper. The distances between the discharges were intended to indicate the letters of the alphabet, but even if the experiment was fairly tried it failed, for little was heard of the result.
After the invention of Volta’s pile, which Salvá wished to adopt, Sömmering began his experiments. He used thirty-five wires, set up vertically at the bottom of a glass reservoir of water, and terminating in gold points. These wires ended in the opposite direction in brass plates attached to a bar of wood. At one end the points and at the other the plates bore the same letters respectively; hydrogen at one gold point, and oxygen at another, and two different letters were indicated when the current was sent through any two plates. This arrangement was afterwards improved upon, and only two wires retained.
It was not until electro-magnetism had been developed, however, that Œrstead found out the power of electricity to deflect the magnetised needle, and in 1820, Scheweigger added a “multiplier.” Then came Arago into the field with his discovery, that a “wire carrying a current could magnetise a steel rod.” Ampère substituted a helix for a straight wire, and Sturgeon used soft iron for steel, and developed the electro-magnet. Daniell’s battery, and Faraday’s discoveries of magneto-electricity and the induction coil were the means of putting a constant supply of electricity at the service of the telegraph and so on, till 1830 brought out a more practical method introduced by Schilling.
In that year Baron Schilling made a telegraph, and exhibited it in 1832 at Bonn. This invention, with five vertical needles, was shown to Mr. Cooke in 1836. But in 1834, Gauss and Weber had succeeded in sending signals by means of a voltaic current acting upon a magnetised needle, and this apparatus was really the first practical electric telegraph in use, and it was much improved by Professor Steinheil of Munich. They employed a magnetic-electro machine, and caused a bar to move in certain directions to indicate certain letters of the alphabet. This was really of value, but Steinheil, the pupil of Gauss, assisted by his government, employed only a single wire, and made the earth complete the circuit for him instead of having a return wire as his predecessors had. This telegraph was perfected by a series of bells, which gave different tones for different letters, and he also caused the needle to make certain tracings as it moved upon a paper slip, something like the Morse pattern, which was completed in 1837.
Professor Morse, in 1832, conceived the idea of an electric telegraph but his claim was disputed by a Doctor Jackson, who was on the same vessel[Pg 234] when the subject was discussed. We need not enter into the details of the controversy. Mr. Morse won the day, and patented his invention.
“It was once a popular fallacy in England and elsewhere that Messrs. Cooke and Wheatstone were the original inventors of the electric telegraph. The electric telegraph had, properly speaking, no inventor.... Messrs. Cooke and Wheatstone were, however, the first who established a telegraph for practical purposes comparatively on a large scale, and in which the public were more nearly concerned.... Therefore it was that the names of these enterprising and talented inventors came to the public ear, while those of Ampère and Steinheil remained comparatively unknown.17 The telegraph, as used in Great Britain, was the result of the co-operation of Professors Cooke and Wheatstone.
Mr. Cooke, in 1836, having seen the needle telegraph when in Heidelberg, made certain designs, and soon entered into partnership with Professor Wheatstone for the application of electric telegraphs to railways. Their apparatus with five needles and five wires was put up on the London and North-Western (then London and Birmingham) and Great Western lines, but proved too expensive. The instrument was subsequently modified, and is used on the English railways still.

We may now proceed to look at the Wheatstone needle telegraph and see the method of working it. We know already that when a pair of metallic plates are immersed in a fluid which acts chemically more rapidly on the one than the other, and a wire connects the upper parts of these plates, this wonderful agency is set in motion, and circulates from the one plate to the other (fig. 242). This arrangement may be best shown by using one plate of zinc and the other of copper, and a dilute solution of sulphuric acid for the liquid; this, however, produces by far too little of the agent to be used on a telegraphic line, there are therefore combinations of such pairs of plates, so arranged that the power of one pair shall be added to the next in such a way that at the end of the series (called a “battery”) there shall be a great increase of the power accumulated; this arrangement is shown in fig. 244. Now (if the power be sufficient) it does not signify what length of wire there may be between the two ends of this arrangement or “battery”; whether they be connected by a few feet or many hundred miles, the electricity passes instantaneously from one end to the other; and furthermore, it has been found in practice, that this electrical influence can be transmitted through the earth in one direction if sent by a wire in the other; for instance, if a wire from one end of the battery be carried on from London to Liverpool, instead of having another from Liverpool to London, to connect the two ends of the battery, it is found to answer the same purpose if the end of the wire at Liverpool be fastened to a plate of metal buried beneath the surface of the earth, and the other end of the battery at London furnished with a similar plate, also buried. In this arrangement,[Pg 235] the electricity will pass beneath the surface of the earth from Liverpool to London, and through the wire from London to Liverpool, thus completing the circuit. The end from which the electricity passes is called the “positive electrode,” that to which it returns, the “negative electrode.” Fig. 245 will show this arrangement.




Magnetic needles.
If a bar-magnet be suspended on a pivot so that it may turn freely, it will (as is well known) turn with one end to the north, which is owing to a current of natural electricity passing round the earth in the direction of east and west, the magnet crossing the current at a right angle; and if a coil of wire coated with silk (to keep one part of the coil from another) be placed round, above, and below the long axis of a bar of steel, as shown at fig. 246, and a current of electricity passed through the wire, the steel becomes a magnet, and will take a direction similar to the natural magnet, more or less, at right angles to this coil, as in fig. 247, according to the intensity of the current; and the instant this electrical current is stopped, it will resume its former direction. This fact has been made use of to form the principal feature of all English telegraphs; such a needle is mounted in an upright position, and instead of its tendency to turn to the north, a tendency to maintain the upright position is given to it by having one of the arms of the magnet a little heavier than the other; such a magnet having a coil of[Pg 236] wire surrounding it. When the electric current passes through the coil, it will turn out of the upright position to either one side or the other, according to the direction of the current, from its tendency to assume a position at an angle thereto (fig. 248); if the current be stopped even for an instant, then the needle, or magnet, will again assume its upright position. The pivot of this magnet is brought forward, and has on its front part another needle, which turns with it; this is visible on the outside of the apparatus, and is looked at to ascertain the movement of the one within. There is also an arrangement called a “commutator,” so contrived, that by moving a handle to the right or left, a connection shall be made with either end of the battery, and thereby cause the direction of the current and needle to be changed at pleasure; also by moving the handle into an upright position the current shall be stopped; and finally, by a third movement, a bell shall be rung. Now, as has already been explained, when the current goes in one direction, the magnetic needle is deflected in that direction; and when the current is reversed the position of the needle is also reversed, and when the current is cut off the needle will resume its perpendicular position. If two such needles and two such handles be at each station, when the handles at one station are moved, the needles at the other station will take on a similar movement; and when the handles at that station are moved, the needles at the first station will be moved to correspond. This constitutes the system of communication kept up by the electric telegraphs in England; but it remains to be shown how all the letters of the alphabet and numerals can be represented by the movements of the two handles. These handles can be placed in eight positions (besides the upright one) by a single movement of each hand, as may be seen in fig. 249; and these eight signals if repeated, or made twice in rapid succession will make eight more, and by being repeated three times will constitute a third eight, making twenty-four; finally, by a rapid motion right and left, they may be caused to signify a[Pg 237] fourth eight, or thirty-two signals, which are found to be sufficient for every purpose, and by practice may be both produced and read off with facility. Before a message is about to be delivered the commutator is so placed as to ring a bell, which is done by the same arrangement as in a common alarm-clock, but the action is set in motion by a peculiar contrivance, which depends upon the property a bar of soft iron has of becoming magnetic when a wire is wound round it and a current of electricity passed through this wire; this magnetic property exists only as long as the current passes, and stops the instant it is cut off. The catch of the alarm is disengaged by the movement of a bar of iron being drawn to the magnet while the current passes, and forced back again by a spring when it is stopped, thus setting in action the mechanism of the alarm; or in some cases there is a simple contrivance for causing a rapid flow and stoppage of the electricity, so that the bar is alternately attracted by the magnet and released by the spring, and this motion rings the bell as long as it is continued. The bell is always rung to give notice that a message is about to be sent, and at the station where it rings, the bell at the former station is rung in return, to show that they are prepared to receive the message: which is then spelt, letter after letter, by moving the handles into the proper positions, and as it is being sent, the eye is kept on the dials, certain single signs are made and recognised, which will communicate any reply from the station to which the message is being sent, such as “repeat,” or “not understood.” The wires which convey the electricity are made of galvanised iron (iron coated with zinc), and as they must be kept from all communication with the earth by some substance incapable of conducting it, they are therefore stretched between wooden poles (fig. 250), and rest upon sockets or supports of glass or glazed earthenware, which are both substances incapable of conducting the electricity[Pg 238] to the earth (fig. 251), and in order that these may be quite dry, an inverted cup of metal, glass, or earthenware is placed over it, or the whole is blown or moulded in one piece. If the support for the wires were not kept from the rain, the wet would form a conducting surface, and allow the electricity to escape into the earth.



The Telegraph Alphabet, in the two-needle instrument, now not generally used in England, is given below.
| Two-Needle Alphabet. | |||
|---|---|---|---|
| Movements of First Needle. | Of Second Needle. | Of both Needles. | |
| A | is signified by moving needle once to right |
||
| B | once to left | ||
| C | By moving needle once to right | ||
| D | once to left | ||
| E | Moving to right. | ||
| F | Moving to left. | ||
| G | twice to right | ||
| H | twice to left | ||
| I (or J) | Twice to right | ||
| K | Twice to left | ||
| L | Twice to right. | ||
| M | Twice to left. | ||
| N | One to right, one to left | ||
| O | One to left, one to right | ||
| P | One to right, one to left | ||
| O | One to left, one to right | ||
| R | One to right, one to left. | ||
| S | One to left, one to right. | ||
| T | Two to right, one to left | ||
| U | One to right, two to left | ||
| V | Two to right, one to left | ||
| W X | One to right, two to left | ||
| Y | Two to right, one to left. | ||
| Z | One to right, two to left. | ||
In the single needle instrument the letters are indicated by right and left vibrations, from A one right, to B one right and left, and so on, increasing to Z. This mode is now generally used.
The manner in which the current passes is shown by the following illustrations (figs. 252, 253).

For the sake of clearness, the diagram has been drawn with simple lines only. In the real needle-machine the construction is much more complicated; perspective drawings of it may be seen in Lardner’s “Electric Telegraph,” and numerous other works. In fig. 1, B is a single cell of a battery containing a plate of copper, C, and a plate of zinc, Z, immersed in sulphuric acid and water. H is the handle of the instrument, turning from left to right, and vice versâ, like the handle of a door, consisting of two pieces of brass insulated from each other by being inserted in an axis of ivory. To the ends of the two pieces of brass are fixed the wires, CW and ZW, leading from the copper and zinc ends of the cell respectively. Fixed[Pg 239] on each side of the handle are two plates of metal, which may be called LP, the left plate, and RP, the right plate. They are connected with the needle wire, NW, which passes before and behind the magnetized needle, N, suspended perpendicularly on its axis, with its north pole upwards. As long as the wires, CW and ZW, remain insulated from each other, no current passes from the cell; but as soon as the handle, H, is turned, so that the copper end touches the left plate (fig. 2), and the zinc end touches the right, communication is established between the plates of the cell, and the current commencing at the copper passes along CW, the top half of H, into LP, along N W, travelling up before and down behind the needle, causing it to deflect to the observer’s left, according to the rule given above. Reaching RP, it passes downwards to the cell to Z, and so on to C, continuing its travels and keeping the needle deflected as long as the handle remains in contact with the plates. If it is required to deflect the needle to the right, the handle is turned to the right, bringing its copper end in contact with the right plate, causing the current to travel in the opposite direction. By following the current from the copper to the zinc, as indicated by the arrows in fig. 3, it will be seen that it now travels up behind and down before the needle, deflecting it to the observer’s right. Thus, by causing a current of voltaic electricity to pass alternately up before and down behind, and up behind and down before, the needle is moved to the left or the right at will. The way in which the current is made to act on a distant needle is now simple. The following figure (fig. 253) shows the arrangement. The left portion of the figure represents an instrument at London, that on the right an instrument at York. The needle-wire, instead of being continued directly to the zinc plate of the battery, passes away from the needle over poles to York, where it joins an instrument similar in all respects to that at London. It passes similarly before and behind a magnetized needle, joining the right plate of the instrument. As long as the two plates are unconnected, no current can pass. The current is therefore completed by a contrivance which may be represented by the semicircular piece of metal, K. In practice[Pg 240] the two plates or springs, which, when not in use, are always pressed against the connector, K, which is a cross-piece on the top of the handle, keeping the London needle in circuit with the York battery, and vice versâ. As soon as London uses his handle, it presses the spring-plate, and puts his needle out of the York circuit, the current he sets up sending York needle to the right or left, as the case maybe. The second wire connecting the left York plate with the right London plate is, it will be seen, not carried along like the first wire. Use is made in this case of the conducting power of the earth itself, plates from the wires being buried many feet below the surface at London and York. When London wishes to speak to York, he first signifies his intention of so doing by ringing York’s alarum. This he effects by sending a current through an electro-magnet placed above York’s instrument. The armature is attracted, and frees the detent of the alarum, setting it ringing until York signals ready. London then stops the bell, and commences his message. By following the direction of the current, when the handle is turned to the left, as in fig. 4[within fig. 253], it will be readily seen how this is effected: commencing with London’s copper, LC, it passes up before and down behind London’s needle, flowing along the wire between the two cities to York’s needle, up before and down behind which it travels, sending it also to the left. It then passes to York’s right plate, through the connector to the left plate, and so on to earth at York, coming to the surface again at London, passing through London’s right plate and through the lower part of the handle to the zinc of the battery. The reverse current may be easily followed. Any number of instruments with similar needles may be interposed along the course of the wire. When the operator wishes to speak to any particular one, he rings all the bells for attention, and then signals Derby or Nottingham, as the case may be. They all then throw their instruments out of current except the one required. The mode by which the needle movements are converted into language is simple. A is signalled by causing the needle to vibrate once to the right, B once right and once left, C once right and twice left; and so on, as arranged.
The following is the alphabet (with numbers) once in use on the South-Eastern Railway for the double-needle instrument. The table is taken from Mr. Walker’s translation of De la Rive’s work on Electricity and Magnetism.
| A | is signified | by two | movements of | left needle | to left. |
| B | ” | by three | ” | ” | ” |
| C | (and fig. 1) | by two | ” | ” | right first, then left. |
| D | (and fig. 2) | by two | ” | ” | left first, then right. |
| E | (and fig. 3) | by one | ” | ” | to the right. |
| F | by two | ” | ” | ” | |
| G | by three | ” | ” | ” | |
| H | (and fig. 4) | by one | ” | right needle to the left. | |
| I | by two | ” | ” | ” | |
| J | (same as G). | ||||
| K | by three | ” | ” | ” | |
| L | (and fig. 5) | by two | ” | ” | right and left. |
| M | (and fig. 6) | by two | ” | ” | left and right. |
| N | (and fig. 7) | by one | ” | ” | to the right. |
| O | by two | ” | ” | ” | |
| P | by three | ” | ” | ” | |
| Q | (same as K). | ||||
| R | (and fig. 8) | by one parallel movement of lower points, both needles to the left. | |||
| S | by two | ” | ” | ” | |
| T | by three | ” | ” | ” | |
| U | (and fig. 9) | by two | ” | ” | first right, then left. |
| V | (and fig. 0) | by two | ” | ” | first left, then right. |
| W | by one movement of both needles (lower points) to right. | ||||
| X | by two | ” | ” | ” | |
| Y | by three | ” | ” | ” | |
| Z | (same as S) or specially. | ||||
The Morse system of telegraphy was first brought out in 1844, and was worked by means of a Voltaic battery, an electro-magnet being used at the receiving station. This magnet attracted an “armature,” and by it dots or lines are marked on a moving paper band by a point at the other end of the wire, on the register in which the paper is carried by rollers which move out by clockwork. The lever being “tapped” down in fast or slow pressures will give a corresponding series of dots or lines (according as the pressure is long or short) upon the moving strip of paper at the receiving station. Three taps will give C, one tap and a pause will make A. The dots are “taps” on the key, the lines brief “rests” on it, as will be seen from the alphabet below, which is given as a specimen.
| Morse Alphabet. | |||
|---|---|---|---|
| A .- | G —. | M — | S ... |
| B -... | H .... | N -. | T - |
| C .. . | I .. | O . . | U ..- |
| D -.. | J -.-. | P ..... | V ...- |
| E . | K -.- | Q ..-. | W .— |
| F .-. | L - | R . .. | X .-.. |
| Y .. .. | Z ... . | ||
| Numbers. | |
|---|---|
| 1 .—. | 6 ...... |
| 2 ..-.. | 7 —.. |
| 3 ...-. | 8 -.... |
| 4 ....- | 9 -..- |
| 5 —- | 0 ___ |
The various stops are also indicated in the same manner by combinations of dots and lines.
The Atlantic telegraph cables and similar enclosed wires between other countries are too well known to need detailed description. There is a great variety of telegraphic instruments. The dial, and other arrangements, are very common, and the Wheatstone Key instrument is supplied to private firms as being the most handy. It requires but a very short apprenticeship, and any person who is handy can easily learn to work it in a few minutes. The apparatus consists of a dial upon which the letters of the alphabet are printed, each letter being supplied with a key or stop. A pointer is placed in the centre, as in the wheel barometer, and there is a handle beneath. In front, upon a sloping board, is another dial plate and pointer; thus we have the receiver and transmitter before us in a very small space.

When it is necessary to work the instrument a bell is rung by turning the handle rapidly. To speak by the instrument it is necessary to keep turning the handle with the right hand while the fingers of the left are employed in pressing down in as rapid succession as practice will permit the keys corresponding to the letters on the dial while the handle is kept turning. When a word is completed the operator must stop at the + at the top, and then begin again, stopping after each word. When all is said, a couple of rapid turns of the dial will signify that you have ended.
There are many other systems of telegraph, but all are dependent upon the same principles. The accompanying illustrations (figs. 254, 255) show a dial telegraph of a simple kind, which almost explains itself.
The first figure is the receiver, on which is a pointer fixed to a dial-plate having the letters of the alphabet inscribed around it. When the manipulator is being worked the dart points to the letters in succession of the words used, and they are separately spelt. The manipulator (fig. 255), by closing and opening the circuit, works the needle.
In the manipulator we have a wheel with an index point fixed above it. In this wheel are thirteen teeth, with the openings between them filled[Pg 243] with ivory. The axis of the wheel is in contact with the wire from the positive pole, p, and a spring attached to the wire or by the binding-screw, t, presses against the circumference of the wheel, and completes the circuit. When the wheel is placed so that the arrow point is above the +, the needle of the receiver is also at +. By turning the wheel to bring the needle to A, the spring on the circumference is passed from an ivory “tooth” to a “metal” one; the circuit is closed, the point of the receiver also turns to A, and so on through the word by successive closing and breaking of the circuit.
As there are a great many other applications of electricity of which we have to treat,—the Electric Light, and Mr. Edison’s other inventions,—our space will not permit a much more detailed account of the telegraph, but there are some incidents connected with its progress which it would be as well to mention.


Alexander Bain, about 1840, attempted to produce a printing telegraph, and in 1846 he actually accomplished a registering apparatus, which was an application of the principles of Dyar and Davy. But although Bain’s system was good, Morse had the advantage of possession in the United States, where it was tried, and Bain went out of fashion. Bain’s system was, in fact, the present chemical “automatic” telegraph, which has been perfected for rapid transmission.
Bakewell’s instrument, which has been improved upon by later electricians, is termed the fac-simile telegraph. The message to be sent is written with a pen which has been dipped in varnish (for ink), and the characters are inscribed upon prepared tinfoil. The message is then put upon a cylinder covered with prepared paper, and has a pointer attached. There is a precisely similar cylinder at the receiving station. When the cylinders are simultaneously set going, the point at one will trace a spiral line as the first (transmitting) point passes round its cylinder. However, as the latter “stylus” meets the varnish letters a break occurs, and these spaces are exactly reproduced as blanks at the other end, and the form of the letters can be seen. Coselli, in his adaptation, caused dark letters to be registered on a white ground, and thus simplified matters. Since then we have had printing telegraphs, and dials, and writing machines, one of which will be described presently.
Submarine telegraphs were, it is said, first suggested by Salvá in[Pg 244] 1797, and Wheatstone, in 1840, declared that it was quite possible to connect England and France by wire. Morse and Calt experimented with submarine cables in America, and Lieutenant Siemens first applied gutta-percha to the wires as an insulator in the Prussian line of telegraph across the Rhine. The English laid a wire between Dover and Calais, which was broken, but successfully relaid. And so on, till in 1857 the great project of the Atlantic cable was broached. We give illustrations of the cables; the circumstances connected with the laying of which, and the enthusiasm over the successful accomplishment of the task, must be in the memory of all. The readings of the messages were shown by delicate galvanometers, the beam of light being reflected from a mirror. This cable was lost, and in 1862 Mr. Field came over to urge the importance of the submarine cable between this country and America. The cable was shipped on the Great Eastern in 1865, and was 2,186 miles long. It consisted of seven copper wires twisted, and covered with gutta-percha. The outside coating consists of ten iron wires surrounded by manilla yarn. But this cable broke, and a third was made and laid in 1866. The old cable was then recovered and spliced. There are some two hundred cables now in existence, the last being the Cape cable, laid when the Boer War was engaging our attention. The transmitting apparatus of Mr. Varley and Sir W. Thomson has greatly accelerated the rapidity of messages, and Thomson’s syphon recorder farther increased the speed.
The following description of a new system is from Scribner’s Magazine for 1880:—
“New Telegraphic System.
“A new system of sending and receiving electrical impulses over an insulated wire has recently been brought into successful operation, that seems to promise not only a radical change in the present methods of telegraphing, but a material gain in the speed and cost of sending messages by wire. It is founded on a union of the so-called “automatic” and “chemical” systems of telegraphy. The first of these employs a strip of paper having, by some mechanical means, a series of small holes punched in it, the design being to pass the perforated strip under a needle, or stylus, in electrical connection with the line. This stylus, on passing over the paper, opens the circuit, but in passing one of the holes, drops through and closes it,—this alternate making and breaking of the circuit transmitting the message. The chemical telegraph records any electrical impulses sent over a line by staining a strip of prepared paper passing under it. This is founded on the fact that electricity has the power of decomposing certain chemicals, and if paper is soaked in these chemicals and submitted to the action of electricity, it will be discoloured wherever the current passes. While both of these systems have been used, neither has been able to compete with the more simple Morse key and sounder, and it has remained for the new system to bring them to a position where they may come into general use. The new system[Pg 245] is a modification and combination of the automatic and chemical systems, the transmitting being performed by means of a perforated strip of paper, and the receiving of the message being recorded by the discolouration of chemically prepared paper. The process is entirely mechanical and chemical, the telegraph operator having no direct control over the message, either by sight, sound, or touch. The written message is sent to the operating-room, and given to the person using the perforating machine. This consists of a small key-board, with black and white keys, each marked with a letter or sign, and an ingenious system of levers, operated by the keys, for punching small holes in a ribbon of paper moving past the side of the machine. The machine stands upon a small table, and under it is a treadle for giving motion to the feeding apparatus for supplying the paper to the machine. The operator moves the treadle with his feet, and at the same time touches each key to spell out the message. In a very few seconds the message is imprinted on the ribbon in the form of a double row of small perforations, each group of two holes representing a dash, and each single hole a dot, as in the Morse alphabet. Each letter is separated from the next by a longer dash, and each word by a still longer dash, and each sentence by a dash of indefinite length. This spacing of the letters is performed automatically, the spacing of words and sentences is performed by the operator. The perforated slip containing the message is then sent to the transmitting machine. This consists essentially of a metallic wheel, divided into two sections by means of a thin insulation of hard rubber. One section of the wheel is connected with the positive pole of the battery, and the other section with the negative pole. A pair of fine metallic brushes, both of which are connected directly with the line, are suspended above the wheel, and are arranged so as to press lightly upon the latter, when desired. When resting on the wheel the circuit is closed, and when raised above it the circuit is broken. The perforated strip is, by a simple piece of mechanism, made to pass over the face of this wheel and under the brushes. While the paper is passing, both brushes are raised from the wheel, and slide over the paper, and the circuit is broken. On passing a hole, one of the brushes drops through and closes the circuit for an instant. On passing two or more holes, arranged in a series close together, the brush closes the circuit for a shorter or longer time, according to the number of holes, and as the perforations on the paper are arranged in two rows, alternating from one to the other, the brushes are used alternately, and the polarity of the current is continually changed with every impulse sent over the line. No special skill is required in sending a message, as the operator has only to put the perforated strip in the machine and turn a hand-crank, to cause it to pass rapidly under the brushes, and with a little practice, a young girl can send messages at the rate of one thousand words a minute, with absolute precision. The receiving apparatus consists essentially of a simple piece of mechanism for causing a strip of chemically prepared paper to pass rapidly under two small needles that are connected with the line.[Pg 246] As the paper passes the needles, the electricity sent over the line from the transmitting machine seeks the earth through the wet paper and the machine, and in passing discolours the paper, each stain representing a dot or dash, and the message is printed on the paper in a double row of marks at the same speed with which it was dispatched. In practice, a Morse key and sounder is placed at each end of the line, and on sending a message the transmitting operator calls the receiving station, and when the operator at the distant end replies, both turn the cranks in their machine swiftly, and the message is sent and received at an average speed of one thousand words a minute. The message received is given to a person using a type-writer, and at once translated into print and sent out by the messenger boy. It is found in practice that two operators, one at each end of a single wire of indefinite length, can keep fifteen operators fully employed in preparing the messages, and fifteen girls busy in translating and printing the messages for delivery. The system is of American origin.”
Of the hundred and one uses to which electric wires are now appropriated—of the alarms, fire-calls, clocks, etc.—we need not speak. We must pass on to the Writing Machine (fig. 258) before we make mention of Mr. Edison’s inventions.
The Writing Machine is as remarkable for the simplicity of its mechanism as for the facility and ease with which it can be used. It was invented by Remington, the American, whose name is so universally known in connection with a repeating rifle. He makes these writing machines in his own factory, where he associates them with rifles and sewing machines—implements for war and peace.
The appearance of the Writing Machine may be easily perceived from the illustration (fig. 258), which is drawn to scale one-fourth of the actual size. It comprises a key-board, upon which there are forty-four keys or stops, including numbers from 2 to 9, the i and o of the alphabet serving for numbers 1 and 0, and all the letters of the alphabet arranged in the manner most convenient for manipulation. There are also the various accents and stops, with note of interrogation, etc. The flat ruler at the base of the key-board is struck when it is necessary to separate one word from another.
In the interior of the apparatus every letter is attached to a small hammer, and corresponds to the pressure bestowed upon the notes, which are disposed in a circle. If A, for example, be touched upon the key-board, the hammer will bring A to the centre of the circle, and so every letter of the word will be, by such action, brought to the centre of the circle in succession. The paper upon which the letter is printed is wound upon a cylinder mounted upon a slide, as seen in the upper portion of the illustration.
When the letter is pressed down on the key-board the corresponding hammer strikes against the cylinder, between which and the hammer is a ribbon prepared with a special ink. The letter being in relief like ordinary type is impressed upon the paper. The slide upon which the paper is mounted is so arranged as to move from right to left exactly a letter-breadth[Pg 247] after each impression. Thus as every hammer strikes at the same spot a regular succession of letters are printed off, the paper moving with regularity. When the line is filled—that is, when the paper has moved across the cylinder—a bell rings, and a handle is moved by the operator who is thus warned. The lever moved brings the slide back again, and a new plain surface is ready to commence upon the cylinder moving upwards at the same time, and displaying the printed line.

In operating both hands may be employed, but between each word care should be taken to press down the flat board at the base of the key-board, which has the effect of leaving a space upon the paper. Immediately the sound of the warning bell is heard the lever at the right-hand side must be lowered. The word can be finished in the line following if it be not concluded, the hyphen button being pressed to indicate the continuation.
The paper used must not exceed the width of the cylinder, but it may[Pg 248] be of any less width, and a post-card or any small sheet of paper may be substituted. If the width be thus limited the length may be indefinite, and a very long line of paper may be used if desirable. The cylinder being made of gutta-percha offers a soft surface to the impression of the hammer, and causes the letter to assume greater distinctness.
The inked ribbon which passes underneath the paper is so arranged that no two successive letters strike it on the same place. It moves from an ink reservoir on the right to another on the opposite side, and it can be made to return beneath the paper, thus keeping up the supply. The impression being made in copying ink, the message or letter when finished can easily be reproduced in an ordinary press. The characters are all “capitals.”
At first it may be found a slow means of writing, and the manipulator may imagine he can do better without it. But if the author be certain of what he intends to say, after a little practice at the instrument, and when he becomes accustomed to the positions of the various letters, etc., the rate at which words can be printed off will far exceed that at which even rapid writers can work. A young English lady after some days’ practice was able to write as many as ninety words a minute with this machine—a rate more than double the average writing rate of penmanship. When such a rate or an approximation to it can be attained, those who are quick in their ideas will find the machine a great saving of time, and for any one afflicted with “writer’s cramp” the gain must be enormous. We need not insist upon the advantages the adaptation of the apparatus would confer upon editors and readers of MSS. too often badly written, and to compositors the invention is a great boon.
Finally, the working of the machine could be entrusted to the blind, and by teaching them the form of letters which could be raised upon the key-board, those so sadly afflicted could write with facility. Some methods for teaching the blind to manipulate and to read from the impressions of the hammers on the paper have already been tried with success.
The Electric Pen, an invention of the fertile brain of Mr. Edison, is shown in fig. 259. The “writing” consists of a series of little holes close together, made by a fine steel point like a put-crayon. This point is thrust in and out with great rapidity, and passes quickly over the paper. If the characters cannot be formed so quickly as with an ordinary pen, the writing is very distinct.
The alternative movement is given to the pen by an electric motor at once simple and ingenious, which is placed on the top of the penholder. The general appearance of the apparatus will be understood from the cut on next page.
The point is the termination of a wire which traverses the penholder, and the upper extremity of which catches on the motor by an eccentric. This eccentric has three teeth or cogs, and it makes sixty revolutions a second, thus producing one hundred and eighty beats in that time. The axle carries a plate of soft iron, which acts like the armature of an electro[Pg 249]-magnet, before which it turns with great rapidity, the current being interrupted twice in every revolution by the commutator. The current which moves this little apparatus is furnished by a pile of two elements in bichromate of potash, according to Mr. Edison’s arrangement, which is considered very successful. Carbon and zinc are employed, and when ready for action the battery assumes the appearance of the cells in the illustration. When the operator wishes to discontinue writing, he simply raises the stem which has the electrodes attached to it, and the elements are thus preserved for a future time.
Under these circumstances the battery could be made to last several days without any renewal of the liquid, and the plates will last for weeks. Thus a very simple arrangement is at our disposal. Let us see what use can be made of it.

When we use the electric pen we obtain a great number of small holes close to each other. Such hand-writing is not easy to decipher by mere inspection like ordinary writing. By holding it up to the light it is more easy to read, but in both instances reading is not easy, nor does it come by nature as Dogberry declares. But if we consider the paper as a “negative,” we may obtain a number of positive proofs or copies of the writing. To obtain these successfully we must use a press, as shown in the accompanying illustration (fig. 260).
The writing, or negative, is placed upon the cover to the left, where it is firmly fastened. Upon the body of the press a sheet of white paper is placed, and when the lid is shut down the negative comes in contact with the paper. By means of a roller, represented in the box, the writing is blackened,—the ink penetrates into all the holes which are upon the paper,—and after the manner of a stencil plate the impression will be found upon the paper when[Pg 250] the cover is removed. The writing will have a curious effect, but practice will speedily remove all deficiencies. The same negative will serve for a great many impressions, quite a thousand having been taken from one. By people accustomed to such work as many as six proofs a minute may be obtained. Of course a little practice will be necessary in this, as in every other case, before a correct or rapid result can be obtained, but there is no difficulty in the practice.
There are two or three other applications of electricity which we must refer to; such as the electric stamp, of which we give an illustration, and a curious method of stopping a horse by electricity. The electric stamp might be very advantageously employed in our post offices to obliterate the “Queen’s Head.” The description, with illustration of this apparatus, is annexed. (See fig. 261.)

At the lower end of the apparatus is a thin platinum wire, so arranged as to form either a design or an initial; by this the postage stamp can be defaced. The stamp being put in communication with the pile, the circuit is closed by the pressure of the finger, as shown in the illustration. The platinum grows heated and carbonises the paper, and thus proves itself an ineffaceable stamp.
This apparatus may easily be used, not only by the post office authorities, but by every one who is obliged to deface a certain number of stamps every day, and wishes to do so rapidly and without possibility of error.
An ingenious, if scarcely necessary arrangement for conquering restive horses, and frightening them into submission, is shown in the illustration (fig. 262). Many means have been tried to stop or conquer a restive horse, but the most efficacious has been designed by M. Defoy; and the director of[Pg 251] the Paris General Omnibus Company has experimented successfully, as we are informed, with the arrangement we are about to describe. A small magneto-electric machine is contained in a box beside the driver, within easy and convenient reach of his hand. The reins contain a wire, one end of which terminates in the horse’s bit, and the other in the electro-magnetic apparatus. When the electro-magnet is put in action an electric current is generated, which gives the horse a shock in the mouth, and so astonishes him that he suddenly stops in his course. If the operator have the humanity and good sense to unite kindness to the abrupt application of the electricity,—which in our opinion should be only used as a last resource,—no doubt some excellent results may be obtained even with vicious animals.

M. Bella, the Director of the Omnibus Company, has reported that the apparatus was tried in his presence and found very successful, and quite easy of application; and that even the most unruly animals have been subjected by it. On one occasion a most restive animal was thus treated on the way to the forge. He had a tremendous objection to be shod, and made no secret of his dislike. But a gentle application of the electric current put quite an opposite complexion upon the matter, and after a few minutes the animal permitted himself to be patted and caressed, and even allowed the smith to feel his legs and inspect his feet without making any objection whatever. His shoes were taken off, and the horse was re-shod without any of the dangerous demonstrations hitherto indulged in by the animal.
We may quote another instance of the efficacy of this method, which is reported from Paris by M. Camille.

“Many experiments have been made upon horses which had been most difficult to shoe, and in each case we have succeeded when the electric apparatus has been put in requisition. One horse, in particular, nothing could subdue. He kicked and bit and jumped about in such a manner as to render all approach impossible. We had recourse at length to M. Defoy’s apparatus, and after the first application, and without any great difficulty, we were able to raise the animal’s feet; but after a second lesson we were permitted to shoe him without his offering the slightest resistance. He was completely subdued.”
M. Defoy recently made the experiment with a very dangerous animal, which he stopped instantaneously in full gallop (see fig. 262). It may be remarked that the application of the current is not sufficiently strong to stop the horse too suddenly. It merely causes a very unpleasant sensation—he is not stupefied nor galvanized by the electricity. The narrator has felt the shock applied without inconvenience, and the conclusion arrived at is, that this method of employing electricity is far superior to the violent and inhuman treatment so often employed to break horses, which renders them subsequently sulky and vindictive.
M. Defoy has completed an electric bit and an electric stick quite as ingenious as the electric rein. The modus operandi is simple and effective, the wires being insulated by leather, and terminating at the extremities of the stick. The current is induced, as before, by a small magneto-electric machine.

CHAPTER XXI.
MAGNETISM.
THE LOADSTONE—MAGNETIC CURVES—THE MAGNETIC NEEDLE—THE MARINER’S COMPASS—MAGNETO-ELECTRICITY.
We have already mentioned some of the properties of the loadstone or magnet; but as we are now about to enter more fully into the considerations of its attributes and of the compass, etc., we will add some further interesting particulars.
Ancient writers (Pliny, Homer, and Aristotle) mentioned the existence of the magnet, and Humboldt refers to the knowledge of it possessed by the ancients. Pliny says “the magnet-stone is found in Cantabria,” and we have heard of the loadstones that are supposed to support Mahomet’s coffin at Medina. The origin of this fable was (probably) owing to the order given by Ptolemy to his architect, Dinochares. Ptolemy wished the roof of a temple at Alexandria to be roofed with the magnet-stone, so that the own image of his sister, Arsinoe, should remain suspended therein. But the death of the king and his architect prevented the project from being carried out.
The name “magnet” is said to have been derived from a shepherd named Magnes, who, when tending his flock on Mount Ida, found that his iron crook was attracted to a certain stone; and six hundred years before the Christian era Thales wrote respecting amber and the magnet; and because they attracted various substances, he supposed they possessed life and power. They were the germs of the science now so developed in their applications, and whose full powers we are scarcely yet acquainted with.
We may remark that other bodies besides iron and steel are capable of magnetization; nickel and cobalt have the like property. Magnetism, properly so called, treats of certain bodies known as Magnets, describes the properties they possess, and the influence of magnetic force upon other substances. Electricity and magnetism are always associated, but practically the force is the same, electricity being the current or motive power, so to speak; and it is to Faraday that the world is indebted for the discovery of magneto-electricity.
Epinus’ theory of magnetism was that all bodies possessed a substance he termed magnetic fluid, the particles of which repelled each other. But[Pg 255] while supposed to repel each other, they attracted particles in other bodies. Thus they attracted iron. Coulomb asserted that there were two fluids—a north and south fluid. Ampère’s theory was that magnetic bodies are made up of molecules, round which currents are always circulating in all directions when non-magnetized, but when magnetized the currents all flow in the same direction. The space through which a magnet diffuses its influence was called by Faraday the Magnetic Field. The lines of magnetic force will be understood from the accompanying illustration (fig. 263). If we cover a magnet with a paper and scatter iron filings over it, we shall see the manner in which the filings arrange themselves. They radiate in curves from the poles of the magnet, and are dependent upon its form. If it be a straight bar magnet, evenly magnetized, they will turn inward in oval curves.


The manner of magnetization has already been mentioned, but here we will give further illustrations of the method of magnetization. Four magnets are used, two being placed with their opposite poles apart, and upon them is placed the bar of which a magnet is to be made. Two other magnets separated by a piece of wood are then brought near, and subsequently drawn from the centre to the ends of the bar. This is the separated touch system; the double touch of Mitchell is completed by moving the upper two magnets from end to end backwards and forwards, and finally lifting them away from the centre.
A magnet, then, is a bar of steel endowed with certain properties, such as attracting iron, etc.; and electro-magnetism is the term applied to the production of magnetism by means of electricity, the medium being the[Pg 256] electro-magnet. To understand the science it will be necessary to mention Ampère’s theory of magnetism.
It was Œrsted who observed that when a magnet is placed within reach of an electric current and free to move, it sets itself at right angles to the direction of the current; and Ampère defined the law already referred to when treating of the electric current,—viz., “that if a person be imagined as placed in the wire so that the current shall pass through him from feet to head, if he turn his face toward the magnetic needle the north pole will always be deflected to his left-hand side.” When the current is passed above the needle from south to north poles, the deflection is to the west; when from north to south the deflection is east. When the current is below the needle the contrary is the case. Ampère decided that currents circulating in the same direction attracted each other, and when running in opposite ways they repelled each other. He supposed currents to circulate within all magnetic substances, and then—that is, when the body is magnetized—these currents flow in planes parallel to each other, and the material which offers the least resistance to the circulation of these currents becomes the most magnetic.
The earth being supposed to be an immense magnet has currents circulating through it in a direction from east to west; and having the property or power of turning a magnetized bar in a direction similar to that in which the bar would be turned by a magnet, the earth is considered a magnetic mass. This influence is due to what is called “terrestrial magnetism.” If we suspend a bar by a thread it will point in no particular direction, but may be turned towards any side we please. But when once the needle is magnetized it will point north and south; or, as we say (but not correctly), the north pole of the magnet points to the north of the globe. It is really the south pole that points to the north, and the north pole of the magnet points south, as can be proved by suspending the bar over another magnetized bar. So if the earth be considered a magnet our English terms are inconsistent with our theories. Continental writers are more correct.
The line of the magnetic needle’s direction, which differs in different places, is called the magnetic meridian, and the amount of its divergence from the astronomical meridian is termed its declination or variation. When the amount of this variation is known it is allowed for, and the needle can be considered as pointing due north and south.
But the needle does not assume a position perfectly parallel to the horizon. It dips down in different hemispheres. As we approach the north pole the dip or inclination will become greater, and the same effect is observable at the south pole. Again, there are certain places on the earth where the attraction is so evenly balanced that the needle is perfectly horizontal. The line uniting these places is the magnetic equator. This does not coincide with the earth’s equator any more than the magnetic poles coincide with the geographical poles of the earth.
The declination of the needle varies from the meridian of Greenwich at[Pg 257] different times. If we travel to the west the variation increases westerly, and is greatest in the Atlantic. It then decreases; the needle points due north in North America. Going still forward the variation becomes easterly, increases, and decreases to nothing in Eastern Russia. Thence the variations are westerly. Columbus discovered the variation of the compass needle in September 1493. In places where the needle is due north and south the lines drawn through them are termed lines of no variation.
The variation, however, is not always the same in the same place. In the year 1580, in London, for instance, the variation was 11° 11´ E. A little more than one hundred years later London was on the line of no variation, and now the tendency is westerly. On the other hand, there are places where there is no deviation, and Sir John Herschell says that West India property has been saved from litigation in consequence of the invariability of magnetic declination there, for all surveys were made by the compass. Lines of equal variation are called isogonial; those of equal dip or inclination, isoclinical; and those of equal intensity, isodynamical.
As we have said, the magnetic elements are not always the same, and the variations of the compass are daily and annually observed with certain instruments. What are termed secular variations take place at long intervals, as the following table will show:—
| In | 1576 | the angle of declination | in England was | 11° 15´ | East. |
| 1622 | ” | ” | 6° 12´ | ” | |
| 1660 | ” | ” | 0° | ” | |
| 1730 | ” | ” | 13° | West. | |
| 1760 | ” | ” | 19° 30´ | ” | |
| 1800 | ” | ” | 24° 36´ | ” | |
| 1818 | ” | ” | 24° 41´ | ” | |
| 1850 | ” | ” | 22° 29´ | ” | |
| 1870 | ” | ” | 19° 55´ | ” | |
| 1873 | ” | ” | 19° 58´ | ” | |
| 1879 | ” | ” | 19° 7´ | ” |
In the year 1818 therefore the maximum declination was reached in London. In Paris the maximum was arrived at in 1814, and was 22° 34´. The rate of decrease is about 8´ a year, but varies in different periods, as may be seen. The discovery of the fact that an annual variation took place in the angle of declination, is attributable to Cassini, and the diurnal variation was discovered by Graham in 1722. From 8 o’clock in the morning, when the needle is pointing a little to the east of its “mean position,” it turns towards the west until 1 p.m. It then returns towards the east again, and passing westerly again between midnight and three o’clock a.m., settles down till eight a.m., when it begins afresh. This variation does not apply to all places.
Magnetic inclination is besides subject to changes. There are also variations of magnetic force which occur at very irregular periods, and cannot be said to follow any laws. These disturbances are called Magnetic Storms, of which the Aurora Borealis is one result.
Professor Faraday in his memorable experiments divided a long list of different substances into para-magnetic and dia-magnetic bodies. He classed them under these two heads, according as they took up a certain position parallel or perpendicular to the axial or equatorial line. This definition of “dia-magnetic” was “a body through which the lines of magnetic force are passing, and which does not by their action assume the usual magnetic state of iron or loadstone.” He concluded that all bodies were magnetic, and by suspending a great number of various substances he found they placed themselves axially,—that is, lying between the poles of the magnet, or equatorially,—viz., at right angles to that line. If the magnets be suspended at each side the same bodies will assume a position with their longest diameters between the poles, while others will be repelled by the magnets even if the poles be reversed. So those bodies which are attracted and lie in the axial line are termed para-magnetic; those repelled into the equatorial line are termed dia-magnetic. In the “Proceedings of the Royal Society for 1846,” Faraday’s account of the various experiments can be studied in detail. We can only give a brief resumé of them here; and he showed that the motions displayed by dia-magnetic bodies in a magnetic field are all reducible to one simple law—viz., that the particles of the dia-magnetic tend to move into the positions of the weakest magnetic force.
He experimented upon a large number of bodies and gases; he tested crystals, metals, liquids, and solids, and proved in whatever state a body might be in the effect was the same; whether simple or compound, it made no difference. Of course in a compound the preponderance of the dia-magnetic or para-magnetic property would influence the result, and the medium in which the body operated on was placed, was a condition in the experiment. He proved that if a body be suspended in a medium or surrounded by a medium whose power either way is stronger than the body, that body is para-magnetic or dia-magnetic, according as it is surrounded by a medium whose power is weaker or stronger than the body itself. The arrangement of the bodies is as follows, from the para-magnetic to the dia-magnetic, bismuth being the most dia-magnetic of all:—
Para-magnetic Metals.
- Iron.
- Nickel.
- Cobalt.
- Manganese.
- Chromium.
- Cerium.
- Titanium.
- Palladium.
- Platinum.
- Osmium.
Dia-magnetic.
- Bismuth.
- Antimony.
- Zinc.
- Tin.
- Cadmium.
- Sodium.
- Mercury.
- Lead.
- Silver.
- Copper.
- Gold.
- Arsenic.
- Uranium.
- Rhodium.
- Iridium, etc.
Common air was also discovered to have a magnetic action, and hot air is more dia-magnetic than cold. Oxygen is as para-magnetic in the air as iron is on the earth, and this, it was considered, may give rise to magnetic storms, and account for the declination of the needle.
We may now proceed to consider the Mariner’s Compass. The compass, or the mariner’s compass, is so common that it is scarcely necessary[Pg 259] to give a long description of it. Its history is unknown. The Chinese seem to have been aware of its usefulness long before the western nations adopted it. It was about the time of the Crusades that it was brought into western prominence, but was not generally known till the thirteenth century. Chinese writings ascribe to the compass a great antiquity; they maintain that it was discovered two thousand five hundred years before the Christian Era, and used for travelling on land. But, according to other accounts, it was not used at sea till the year 300 A.D.
The Chinese put the south first when speaking of the points of the compass, and in the Chinese empire and Thibet west goes likewise before east. So the imperial edifices in China face the south, and the needle, in their expression, points south and north—not as we say, north and south. The antiquity of the compass may be inferred from the recorded fact in Chinese chronicles, written in the second century before the Christian Era, that nine hundred years previously to the date of the chronicle the Emperor gave magnetic cars to certain ambassadors to guide them home in safety. These cars were fitted with a magnetic needle which communicated with a figure. Its outstretched hand and finger followed the compass-direction, and pointed out the way.
The Chinese subsequently (in the twelfth century) suspended the needle by a thread, and it is said their philosophers at that time noticed the variation of the needle. But Columbus first, in 1492, and Cabot, in 1540, certainly remarked it in Europe. It is to Marco Polo that we are indebted for the direct introduction of the needle into Europe, although it probably had been in use in the Levant previously, for we have seen a quotation by an Arab writer, who, in 1242, described the needle as being used at that time on his voyage from Tripoli in Syria to Alexandria, two years previously.
Friar Bacon possessed a loadstone, and there are many instances in which it is referred to in ancient writings. The inventor of the compass we cannot trace, but no doubt exists as to its being of Chinese origin.
The ordinary compass is shown in the illustration herewith (fig. 265). It consists of a magnetized needle, suspended freely, and fixed to a circular card, which is divided and subdivided into thirty-two points, as in the cut. This compass is suspended upon gimbals to keep it in an upright position when the vessel rolls or plunges. The gimbals are concentric rings, the compass being fastened to the inner one, and keeps its position in all weathers. It is then enclosed in the binnacle, a glass receptacle. The card moves with the needle which points north. There is a dark line (lubber line) which indicates the ship’s course, and when sailing the steersman must keep that line opposite the compass direction-point which indicates the course. At night a lamp is lighted in the binnacle, and the card being transparent and the points opaque they are easily seen.
The magnetism of iron ships has a tendency to disturb the needle, and many suggestions have been made and discussed with a view to obviate this. To put the compass at the mast-head was one, to surround the compass[Pg 260] with “counter-irritants” another. But the usual way is to “swing the ship,” and so adjust the compass. Swinging the ship means turning her round point by point, and marking the deflection of the needle with reference to a certain object. The amount of deflection at each point is read and noted, and subsequently taken into consideration when sailing.
The Azimuth Compass is a mariner’s compass fitted with brass uprights slit through the centre, through which the heavenly bodies may be seen. These are the sights. The card is divided into degrees and quarters. A fine wire is fixed upon one of the sights, and in the other slit is a prism to reflect the divisions of the card to the eye. The object—the azimuth distance of which it is desirable to know—is looked at through the slit, and bisected by the wire. The divisions of the scale are at the same time reflected, and the number read gives the azimuth distance required.

The compass has led us away slightly from our consideration of the electro-magnet, but we will now examine it and its effects as briefly as possible.
An electro-magnet is formed by wrapping a copper wire round a piece of soft iron shaped like a horse-shoe; the wire should be insulated with silk. If the wire be wound round the iron in the same direction, and a current be merely sent through the coil, it will be found that the horse-shoe iron is highly magnetic, but if the current be stopped the power is lost. Such magnets will carry weights much heavier than themselves, and by careful consideration of certain laws, and with reference to the number of coils and the strength of the current, these magnets will sustain a weight some thousands of times greater than their own weight.

If we cover a non-magnetic piece of iron with a wire coil, and taking a magnet turn it rapidly beneath the wire-bound iron, so that the magnetic poles approach each other alternately, an electrical current will be generated in the wire. The electro-magnetic machine is thus made; but although strong currents may be generated as a source of motive power it is a failure.
To Faraday our knowledge of magneto-electricity is due. “He knew” (says Professor Tyndall in his interesting work, “Faraday as a Discoverer”) “that under ordinary circumstances the presence of an electrified body was sufficient to excite by induction an unelectrified body. He knew that the wire which carried an electric current was an electrified body, and still all attempts had failed to make it excite in other wires a state similar to its own.”
But while he was making his experiments on the induction of electric currents he noticed that at the time the current was passing from the battery[Pg 261] through the coils of wire that no motion was perceptible in the galvanometer. But when the circuit was opened, and when it was closed, there was a slight motion of the needle in the galvanometer, but in different directions. After consideration the philosopher came to the conclusion “that a battery current through one wire induced a similar current through the other, but for an instant only.”
Œrsted had already demonstrated that all magnetic effects were attributable to the attraction and repulsion of electric currents; and founding his views upon the theory of Ampère, Faraday came to the conclusion that electricity could be produced from magnetism, or that the electric current could be obtained from magnets. This he succeeded in doing. By inserting a steel magnet about half its length into a coil of wire, Faraday induced a current to pass through the wire in two directions. Thus he proceeded to solve all the mysteries of magneto-electricity, and stated that to produce currents it was only necessary to “cut appropriately the lines of magnetic force.”
The application of the magnet to the machines for electric lighting will be shown further on. Very powerful currents are obtained by the induction coil; but the currents would not be of practical service were it not for the apparatus called a Commutator, or key, which reverses the connection of the bobbins, and turns the current at every half revolution. Just as if a current were being sent across and back over a table, and when the current has reached the end, an instantaneous wheel round, or pivoting of the table, sends the current on, in continuation (but on the table all the time), because of the sudden change of its position. The back rush being on the table, the movement of the latter really makes the line continuous, and by quickly breaking and reversing the current in the commutator, the effect is gained in the machine.

CHAPTER XXII.
SUNDRY ELECTRICAL APPLIANCES—MR. EDISON’S INVENTIONS—THE ELECTRIC LIGHT—THE GYROSCOPE—A NEW ELECTROPHORUS—ELECTRIC TOYS.
The Electro-Motograph—although perhaps even yet scarcely developed—has already proved a very useful invention. The idea of it first occurred to Mr. Edison in 1873, when he was prosecuting some researches in chemical telegraphy. “One day,” says Mr. Fox, in his account of the invention, “as he sat pondering over his work, he happened to take in hand the metallic point through which, as it rested upon the paper, the current was wont to pass. When again he closed the circuit to let the current through the paper, he held the metallic point loosely, and unintentionally allowed it to rest upon the paper. Every time he moved the metallic strip on the paper the latter became wonderfully smooth. Edison was determined to find the reason of this, and he decided that the electricity very much lessened the friction of the metal on the paper. He made many experiments, and brought the subject before the Royal Society in 1874, but nothing came of the idea till 1876, when Edison was perfecting his musical telephone.
“The new appliance is, in fact, the same invention revived and now perfected by the original inventor, and brought to complete practical success under the title of the ‘electro-motograph.’ The action of the ‘electro-motograph’ depends on the fact, discovered during former experiments, and employed imperfectly in the musical telephone, that the friction of moving bodies varies in greater or less degree with their electrical condition. In the electro-motograph a cylinder made of prepared chalk, and saturated with a strong solution of caustic alkali, is set upon supports, so that it can be turned upon its axis. A strip of metal fastened to the mica diaphragm rests on the cylinder, and is pressed so firmly by its spring upon the cylinder that when it is turned by means of the handle the friction of the strip on the cylinder tends to pull the diaphragm out of shape, causing it to bulge inward as long as the cylinder is in motion. If now, while this motion of the cylinder is maintained, an electric current passes through the strip of metal, and then through the chalk cylinder to earth, the amount of this friction is varied or it is destroyed altogether, and the strip slides freely on the cylinder. This was the basis of the former invention. The[Pg 263] release from friction by a change in electric condition in the first instrument failed simply from ignorance of some slight matters of detail, that in the electro-motograph are corrected and made practical. In the musical telephone the releasing of the frictional resistance by electric action caused the sounding-board of a guitar to vibrate, and thus set up sonorous vibrations. In the electro-motograph the mica disc takes the place of the guitar, and, by the improved construction of the apparatus, intricate and complex vibrations, such as are produced in speaking, are reproduced in their original or even in greater volume. When the apparatus is at rest the diaphragm is motionless, and electric currents shot through the apparatus produce no effect. In the same manner the mere turning of the cylinder without electric action produces no effect, except to pull the diaphragm slightly out of shape. If while the cylinder is being turned an electric impulse arrives, the pull on the diaphragm, caused by the friction of the strip on the cylinder, is more or less released, and the diaphragm is free to vibrate or spring back into its original condition. If now, the electric impulses follow one another in regular order in correspondence with the sonorous vibrations imparted to the transmitting telephone, the alternate slipping and catching of the metal strip on the cylinder will follow in the same order, and thus the diaphragm will be made to vibrate in unison with the original vibrations, and thus reproduce the original words. As the mica disc is much larger than the disc of the transmitting instrument, the amplitude of its swing may be much greater, and consequently it will repeat the words with greater power. The electro-motograph is practically an apparatus for transforming electric action received from a distance into mechanical work. The amount of electric action has nothing to do with the amount of the mechanical work performed, because the movement of the cylinder is controlled by power independently of the electric action, the electricity merely releasing this power by destroying the friction in greater or less degree. The electric action set up by the sonorous vibrations at the transmitting end of the line may be very slight, while the mechanical action at the distant end may be powerful, and in this manner the amplitude of the vibrations may be increased to an indefinite extent, and a whisper may reappear as a loud shout.
“The electro-motograph is not only a solution of the telephone, making it capable of sounds of every quality and pitch and in greatly increased volume, but by this conversion of electrical action into mechanical work at a distance makes it possible to unite the telephone and phonograph. Telephonic messages by the electro-motograph may be impressed upon a self-acting (clock-work) phonograph, the same current starting and stopping the phonograph after the manner of the stock-reporting machines, and afterward the phonograph may be made to repeat the message impressed upon it.”
[The above extract, which explains the principle fully, has been taken from a long article on the subject which formerly appeared in Scribner’s Magazine.]
The uses to which the electro-motograph may be applied are various. It can produce mechanical motion even at a distance, and is useful to lessen friction by machinery; and in this way its service to railways and other locomotive systems may be estimated. It is a great help to telegraphy by increasing the speed of transmission, and can ascertain the beatings of the heart of the apparently dead. It amplifies sound in a much greater degree than the microphone, by which even a fly can be heard moving. In fact, the limit of the usefulness of this wonderful machine has not been reached.
Another very ingenious apparatus has been developed by Professor Bell. This is for the purpose of ascertaining the position of bullets in the body. The following is condensed from the Times:—
“Two conductors are used, and the ball completes the circuit. Professor Bell inserts a fine needle in the suspected region. It is connected by wire with one of the binding screws of a telephone, which the surgeon holds to his ear; the other binding screw being connected with a metallic mass applied to the skin. When the needle point touches the ball, an electric couple is formed, and the current generates the sound in the telephone. The surgeon may then use his knife with confidence, guided by the needle. He may make several insertions of the needle if necessary without danger, and any pain may be obviated by etherization. This simple method (which should prove useful on the field of battle) was tried with success with a lead ball introduced into a piece of beef. Contact of the needle with bone had no effect, but a very distinct sound was heard each time the ball was reached. A modification consists in inserting a vibrator in the circuit; this gives a musical note in the telephone at each contact of ball and needle. Again, if the circuit include a battery, the telephone sounds may be heard by several persons at once. A sound is heard, in this case, whenever the needle enters the skin; but, on reaching the ball, it is much intensified, owing to lessened resistance. A galvanometer may be used in place of the telephone.”
Mr. C. Vernon Boys has exhibited and described a very ingenious new integrating machine of his invention, and its application as a measurer of the electric energy in the circuit of an electric lamp or a dynamo-electric motor. Mr. Boys’ mechanical integrator belongs to the class termed tangent machines, and consists essentially of a small disc or wheel running along the surface of a drum or cylinder. When the wheel runs straight along the drum parallel to its axis there is no rotation of the latter, but when the wheel is inclined to the axis the drum rotates, and the integral is represented by the amount of rotation. Continuous action is secured in giving the drum a reciprocating motion along its axis, so that when the wheel has travelled to one end of the cylinder it can travel back again. The new integrator is especially adapted for measuring forces which are either delicate or variable. It is applied by causing the varying force to be measured to vary in a corresponding manner the inclination of the wheel to the axis of the rotating cylinder.[Pg 265] In this way it can be used to find the work done by a fluid pressure reciprocating engine, or the energy transmitted by a shaft or belt from one part of a factory to another. By making the wheel very small and light, the strength of an electric current may be continuously measured, if the disc is inclined by means of the needle of a galvanometer in circuit. Mr. Boys has constructed on the same principle an electric energy meter, which integrates the product of the strength of current and the difference of potential between two points with respect to time. In it the current is passed through a pair of concentric solenoids or coils of wire, and in the annular space between these is hung a third solenoid, the upper half of which is wound in the opposite direction to its lower half. By the use of what Mr. Boys calls “induction traps” of soft iron, the magnetic force is confined to a small portion of the suspended solenoid, and by this means the attracting force of the fixed solenoids upon it is independent of position. The middle solenoid is hung from the end of a balance beam, and its motion is retarded by a counterweight, which admits of regulating the meter to give standard measure as a clock gives standard time. The motion of the beam is caused to incline the integrating wheel, and the rotation of the cylinder gives the energy expended in foot-pounds by means of an indicator or diagram, as the case may be. The object in giving an equal number of turns in opposite directions to the suspended solenoid is to render the instrument insensible to external magnetic forces.
We have, in a former portion of this work, explained the construction of the telephone and phonograph with other inventions to make sounds audible at a distance, so we need not repeat the explanations here. A brief reference to them will, however, be found in this chapter, in which the electro-magnet and the methods of lighting by magneto-electric machines are treated of. We will proceed to give some particulars concerning the electric light before considering the means by which it is produced, as such an arrangement is more convenient.
The light is very easily produced by uniting and then separating the terminals of a strong battery. The passage of the electric current induces intense heat and a most brilliant light. But if this were continued the wires would melt, and therefore some non-fusible substance is placed at the ends of the wires, which will be at once a conductor and infusible. Now in gas-carbon (the deposited substance found in gas retorts) we have a substance suited to these conditions. The carbon is heated to an intense brightness, and particles of it are passed across the arc of flame almost in a state of fusion. Combustion does not actually take place, because it has been proved that the wires will give out light under water, and in the vacuum of an air-pump the light is even increased, so that had the oxygen of the air any part in the production of the light it would not remain unaffected under these conditions. The heat arising from this Voltaic arc is intense, and even platinum may be fused with the assistance of the gas carbon. The carbon points are of course liable to be worn away, and one side more than another. The positive pole[Pg 266] is generally more concave than the other, for it sheds its particles in a greater degree, and is the more intensely heated. The electric light first appeared in public at the opera in Paris in 1836, to illustrate a sunrise, but it was not till 1843 that it was experimented upon in the open air. We need not trace it farther at present, for a full account of its origin, rise, and progress is published in a small shilling volume by Messrs. Ward, Lock, & Co. We will proceed to the methods of bringing out the light.

Fig. 267.—The Maxim light.

Fig. 268.—Mechanism of Maxim’s lamp.
There are various lamps, many of which required a regulator in consequence of the wearing away of the carbon points, as already explained. We append two illustrations of the Maxim lamp, the invention of Hiram Maxim, of New York. In both cuts the letters refer to the same portions.
In the first illustration (fig. 267), A and B are the positive and negative carbon-holders respectively, and the carbon points are controlled[Pg 267] by an armature, which is, in its turn, adjusted by the screw, D. When it happens that the magnetic force is reduced the spring acts and permits the points to approach again, and the light is rekindled; the carbons are then locked till required to move. The second illustration (fig. 268) shows a section of the lamp with the wheel arrangements for controlling the advance of the carbon points as they waste away.


In the “Brush” light, which is in use in London, and is fitted for large spaces, the carbon points are held by a regulator side by side, and they last eight hours without renewal. The power is generated by an electro-dynamic engine. We give illustrations of the lamps of Wallace and Houston (figs. 269, 270). The current is conveyed through b and the magnet, m. The armature, a, separates the electrodes, and the weakened current is restored by b, and the light continues. The pillar, p, is hollow, with a wire running through it. The positive electrode is supported by J, the negative by C; V is a button which comes in contact with the lever, T, when the carbon points are exhausted, and cuts the lamp out of the circuit by passing it direct through mercury cups.
The Jablochkoff candle and chandelier are also represented (figs. 271, 272). The candles consist of carbons connected at the top, but otherwise insulated, and fixed in a socket. They do not last very long without renewal. The exhibition at the Crystal Palace will be essentially an Electric Light Exhibition, and all the latest forms can be studied there. The great attraction will doubtless be, as at Paris, the varied and numerous inventions[Pg 268] of Mr. Edison. The early career of that American “magician” is now tolerably well known; his tremendous energy and application are fully appreciated. With only a few months schooling all his life he has taken a foremost place in the scientific world. In ten years he has invented the phonograph, the electric pen, a system of fast telegraphy, the electro-motograph, the telephone, a tasimeter, and other useful applications of electricity, besides solving the problem of electric light for domestic purposes.
Mr. Edison’s electric light18 requires something more than a passing notice, and we will therefore endeavour to give a sketch of the general subject. Now that the electric light has been made available for domestic purposes, and the very simple lamp (consisting of an exhausted glass globe, two platinum wires, and a piece of charred paper) can be obtained, people will no doubt soon largely adopt electric lighting in their houses. The light has found a success at the theatre, in the streets, and in the train; there is no reason why it should not be adopted generally, being more economical and more healthy than gas.


If we sever an electric wire, and bring the ends, tipped with carbon, into juxtaposition, we obtain a brilliant light. This is the Voltaic arc we have already mentioned, produced by the incandescence of finely-divided matter; it was the first method of illuminating by electricity, and was discovered by Sir Humphrey Davy, who obtained a very brilliant light, but at great expense—about a guinea a minute! But the Daniell and Grove batteries and generators, and modern improvements in 1860, brought the use of the electric light into prominence. Faraday lighted a lighthouse with its assistance.
But when the Gramme Generator was invented the needed impetus was applied. The Jablochkoff candles followed, and now we have the electric light in full operation. So far we have sketched the history of illumination by the Voltaic arc, and descriptions of the various apparatus will be found at the end of this chapter. But the method of lighting with an incandescent solid was introduced in 1845 by Starr and Peabody, who took out a patent for the use of platinum. Later on Drs. Draper and Despretz made experiments with platinum and carbon. The latter gentleman sealed the carbon in an exhausted globe, and then introduced nitrogen in place of the air. But the method died out and was forgotten, and in 1873 a medal was actually given by the Academy of St. Petersburg for the “discovery” to Messrs. Sawyer and Mann.
In 1878 Paris was lighted with the electric candles of Jablochkoff.[Pg 269] This application of electricity stirred up our transatlantic cousins, and Mr. Edison was requested—backed up by many influential persons—to make the investigation whether the light could be produced for domestic purposes. The celebrated electrician undertook the commission, and certainly came unprejudiced to the encounter, for he had not at that time even seen an electric light.
He perceived at once that “permanence in the lamp and the subdivision of the light” were the two desiderata. He put the Voltaic arc aside as unsuitable, and addressed himself to the problem of obtaining the desired results from an incandescent solid. The subdivision of the light is really an important point, and a comparison between divided and undivided burners is in favour of the more diffused light in a number of burners. This subdivision Edison worked hard to secure, and, as it is said of him, “With a steadfast faith in the fulness of nature, a profound conviction that if a new substance were demanded for the carrying out of some beneficial project, that substance need only be sought for, he set to work.”
Mr. Edison found difficulties in his way. One was the apparent impossibility of illuminating by means of an incandescent solid, for even platinum will melt at a heat too low for use. But this apparent impossibility was overcome by the inventor’s genius. He, after many trials, found that if he raised the platinum to a white heat in a vacuum he would practically obtain a new metal which would sustain the required heat.

“In making an electric lamp without a regulator,” says Mr. Upton, “two things are essential,—great resistance in the wire, and a small radiating surface. Mr. Edison sought to combine these two essential conditions by using a considerable quantity of insulated platinum wire wound like thread on a spool.” This platinum, as shown in the accompanying cut (fig. 273), was suspended in a glass bulb in vacuo, the air contained in it being expelled by electricity, heating it, and suddenly cooling the platinum, and squeezing out the air by the process. But, after all, the great difficulty of the inventor was to insulate his wires so perfectly that they would not meet and become a conductor. For, to perfect his lamp, this non-conducting principle was a necessity, otherwise the current would flow across instead of going all along the wires. He had previously made many uses of carbon, which we know is infusible. He tried lampblack tar, but it contained air, and would not do.
Thread answered his purpose, but was too fragile and uneven in texture. It suddenly occurred to him that paper—charred paper—cut into a thread-like form would satisfy all his conditions.
The problem was solved—the lamp was a fact. But how can paper, so easily burned, answer? We will endeavour to explain. “A piece of charred paper, cut into horse-shoe shape, so delicate that it looked like a fine wire firmly clamped to the two ends of the conducting and discharging wires, so as to form part of the electric circuit, proved to be the long-sought combination.”
We will now explain the construction of this little lamp, which is shown in the illustration (fig. 274) one-half of its actual size. The illuminating is equal to ten or twelve ordinary gas jets.

The manner in which the paper is prepared is, like many other very important inventions, extremely simple, and, we may add, almost costless. Cardboard will furnish us with the loops, and these “horseshoes” are placed in layers in an iron box with tissue paper between each. The box is then hermetically sealed, and made red hot. The carbonized paper remains till all the air has been got rid of, and although it will burn freely to ashes in atmospheric air, in the vacuum prepared for it it is never consumed. That is the plain fact—the secret of the Edison lamp.
A vacuum can now be produced almost perfect. It is of course impossible to extract every tiny particle of air from the globes, but by the Sprengel pump, in which mercury is employed, excellent vacuums are obtained. Several very curious phenomena have been observed in these vacuums, and the Royal Society has been engaged upon their consideration. Another advantage of the vacuum, as applied by Edison, is that little or no heat is generated. The electricity is all, or very nearly all, converted into light. Thus the glass globes remain almost unheated, and are unbroken.
The electric current passes along the wire, W, and at a certain place marked B, the copper is soldered to a platinum wire, which enters at C, and so by platinum clamps into the horse-shoe, L. The return wire is similarly arranged; the carbon is enclosed in a glass bulb, GG, and all the air is extracted by the pumps; the end is then sealed up by melting it at F.
The world is now in possession of a lamp for household use, and we are surprised that it is not more extensively adopted in England. There are some Swan lamps used in parts of the British Museum, and when we have explained the application of the light, and the uses to which the motive power can be applied, we shall, we believe, convince the most conservative gas bill advocate that Edison’s lamp is cheaper, safer, and far better in illuminating power than gas, if the success of the electric lamp can be assured.
We need not dwell upon the construction of the “pumping station,” for that is virtually what the magneto-electric generator is. Several of these stations can be established in various parts of the city, and each station will supply a district with electricity. The wires are laid in a tight box along the street, beneath the footpath, or other convenient position, and we are informed that the frost rather improves their electrical condition. Here is one advantage over gas.
From the main wires smaller ones enter the houses, and are carried through a “meter” containing a safety valve. There are two wires—a distributing wire and a waste—coloured, one red and the other green, which communicate respectively with the main supply and return wires to the “pumping station” or generator. The electricity is admitted between carbon points and flows round a magnet, the armature of which is held above it by a spring. If too much force be put on and any danger incurred, the magnet will attract the armature, and the current will cease. A snap connected by a small wire will then be closed by the electricity, and melting from the heat will cut off all the current. In ordinary circumstances the electricity passes through regulators (wire wound on spools) and on to a copper plate, “through a solution of copper salt.” Thus for every unit of current a certain quantity of copper is deposited. A certain standard amount represents five cubic feet, and the bills, based on the accumulation of copper, are made out like gas bills.
When the lamp is required a small handle is turned, and is instantly lighted; the reverse motion cuts off the current. “By touching a knob in the bedroom the whole house can be simultaneously lighted up” if desirable. No matches are necessary, as the lamps light themselves.
By adding a small electro-motor to the furniture of the house, and turning a handle, the sewing-machine can be worked by electricity, or lathes turned; and any business operations, such as lifting by cranes, etc., can be easily carried on.
The Swan electric lamps, which, with Mr. Edison’s, were exhibited in Paris, and will be found at Sydenham, give about twelve candle-power light. Edison’s lamps are made in two sizes, and vary accordingly. The Swan lamps give a very soft light, and are as easily manipulated as Edison’s. The Siemens system of lighting was also well seen in Paris, and the Faure storage system enables our trains to be lighted instantaneously by simply turning a handle. A full description of the Faure battery was given in the Times by Sir William Thomson, and in his address to the British Association at York in September last. He pointed out that in the accumulators of M. Faure,—which can be seen at 446, West Strand, London,—by means of a large battery it is quite easy to draw off electricity and to apply it as Edison proposed to do, in lighting our houses and do any little service. The electricity thus stored would be always ready for use, and would be supplied and paid for. It can be applied to any purpose, and locomotion by its means will ere long become more general. In Paris Dr. Siemens exhibited[Pg 272] his electric tramway. This was an improvement upon the first Berlin tramway, for in it the horses frequently received shocks which they resented. In the later application the current comes from the generator by metal rods carried above the heads of the passengers alongside the line. Little rollers upon these are united with an electric machine in the tram-car. The current is sent along the wires, and reconverted into mechanical energy in the second machine, turns the wheels of the cars. In this way, as the car proceeds, the rollers overhead or alongside the track are kept moving by the car, and the connection is never broken.
But this is a digression. The electric light as applied to lighthouses was also exhibited, and any reader desirous to obtain full information upon the subject of lights and lighthouses will find it in a very pleasantly-written work by Mr. Thomas Stevenson, in which the various systems of lighting by electricity and otherwise are fully recounted, the conclusion being in favour of electricity, which is employed and has been used for years in France and in some English beacons. If its penetrative power can be finally established,—for some authorities maintain that the electric is more easily absorbed by fog than other light,—there is no doubt about its being universally adopted.
It is very interesting to watch the uses to which the electric light is being put. The latest experiment has been made by an Austrian, Doctor Mikerliez. Almost incredible as it may seem, the interior of the human stomach can now be illuminated by means of a wonderful little instrument called the Gastroscope, which is said to be actually in use and to have been favourably reported upon by the medical faculty of Vienna. There is at the end of a jointed flexible tube (which can be passed down the gullet) a miniature lamp, far more marvellous and mysterious than that of Aladdin, in which a strip of platinum is fixed and connected with fine wires conducting the electricity from a small battery. When contact is made, and the “light turned on,” the cavernous interior of the stomach is lit up. Still more extraordinary is the fact that the tube can be made to revolve, and the light reflected from the walls of the stomach and directed to the eye of the observer. There is necessarily a bend in the instrument, so that the light has literally to turn a corner before it reaches the surgeon’s eye; here the inventor’s skill and thorough knowledge of the laws of optics are brought into requisition. The reflected rays of light fall upon a sort of window situated a little above the lantern, and by means of prisms and a series of lenses, the light is twisted and turned about until it arrives at the eye-piece. No sensation of heat is to be feared, the little lamp being kept constantly cool by a reservoir of water.
Several contrivances have been invented within the last few years for examining the interior of the body, but they are very costly; the Gastroscope is likely to render great service to medical science.
The term “magneto-electric machine” is given to a collection of parts of mechanism intended to create or gather together induced electric[Pg 273] currents. The invention of the magneto-electric machine was by no means a sudden inspiration, but the gradual result of a series of experiments and discoveries, the first of which, dating from 1820, may be said to be Œrsted’s observation, that a magnetised needle is deflected by the approach of an electric current as well as by that of a magnet, clearly proving that magnetism and electricity have some relation to one another. In the same year Arago discovered that a coil of insulated wire wound round a core of soft iron, converts it into a powerful magnet (i.e., an electro-magnet) when a current passes through the coil. It was in 1830, however, that our countryman Faraday proved the creation of a current by the action of a magnet on a coil of wire, and his experiment proved shortly as follows:—If a coil of wire be wound on a hollow core, and a permanent bar magnet be introduced into the hollow core, whilst introducing it a current may be proved (by a galvanometer), to be induced in the coil flowing in a certain direction, A B, which ceases as soon as the magnet is at rest in the centre of coil. On the withdrawal of the magnet a second current is induced flowing in the opposite direction, B A. Therefore it is clear that if a magnet be incessantly approached to and withdrawn from a coil of wire a constant succession of currents will be produced, and if a charged coil (i.e., a coil connected with the poles of a voltaic battery) take the place of the magnet a precisely similar result will be obtained. Now it will have been noticed that two opposite currents are constantly being formed, and as the object is to obtain a continuous flow of electricity in one given direction, or, in fact, divert or reverse the current instantly on its formation to make it practically the same current, for this purpose a commutator is used, and as for most purposes a commutator is one of the essentials of a magneto-electric machine, we will here give a description thereof. (See fig. 275.) The machine is composed of a cylinder, consisting of two metallic conducting halves, separated by a non-conducting layer. Whilst it is at rest the alternating currents, from being connected with the halves by the current, will pass to the two contact springs, and thence through the circuit. Now if (as is the case) the current is constantly changing, as has been noticed, the inverse current will at the first change pass through the same channels, but in another direction; but if at the instant of the reversal of the current the cylinder be revolved, the current flowing the reverse way will be guided through other channels respectively, instead of the original channels, and the direction of the current being changed at the same moment as the current itself, the two inversions neutralize themselves, and one constant current is produced. In a magneto-electric machine the commutator revolves identically with the magnet or armature, and the point at which sparks are being constantly produced is where the contact is being continually broken and made by the passage of the friction springs from over the non-conducting layer. The first machine formed on the basis of Faraday’s experiments was Pixii’s. It was composed of two uprights and a cross bar, to which is attached, hanging poles downwards, an electro-magnet; underneath this, the[Pg 274] poles upwards, revolves a magnet. The commutator is fixed on the same axle and revolves with the permanent magnet. Saxton, and subsequently Clarke, made the obvious improvement of making the magnet less cumbrous and fixed, and causing the bobbins of the electro-magnet to revolve before or rather beside its poles; the commutator was fixed at the end of the axle on which the revolving bobbins (or armature) are fixed. Niaudat formed a compound Clarke machine, by setting two horse-shoe magnets a short distance apart. The armature revolves between them, and consists of twelve coils set between two plates; the coils are set alternately and connected,—i.e., the poles of the electro-magnets are set beside one another,—N. to S., S. to N., and so on, so that the N. pole receding produces a current; but the N. pole receding makes the S. pole approach, and produces another current, A B; in fact, a continuation of the same, for the approach of a N. pole naturally produces the same current as the recession of a S. pole; then as the S. pole in turn recedes it produces an inverse current, B A, which is in turn kept up by the approach of the next N. pole, and so on. Each coil is attached to a radiating metal bar, which conveys the current to be redirected to the commutator, which is affixed to the axle of the revolving armature as in Clarke’s machine. In 1854 Siemens completed his machine, the chief peculiarity of which was its cylindrical bobbin; the core is grooved deeply, parallel with its axis, and the wire is wound on cylindrically and covered with plates of brass; one end of the coil is fixed to the metal axis, the other to an insulated ferule at the end of the axis, where is also situate the commutator. This armature revolves between the poles by which it is closely embraced. One of the most celebrated of the magneto-electrical machines is that known as the “Alliance,” invented by Nollet, and perfected by Van Malderen. It is composed of four or six bronze discs, revolving on an axle, round the external circumference of each of which are set sixteen bobbins. This rotating compound armature revolves between four to six sets of horse-shoe magnets, which, being fixed radially to the centre, present in each set sixteen poles to the sixteen bobbins. It will be readily understood that this immense quantity of poles and bobbins produces a highly concentrated current, the ends of which proceed from the axle and an insulated ferule at its extremity.

In 1869 Mr. Holmes perfected his machine, which differs from all previous ones (except Pixii’s), in that the electro-magnets revolve in front of the coils instead of vice versâ; and besides magnetising his electro-magnets with part of the self-produced electricity, his bobbins are so disposed as to be able to keep several independent lights going at once. The Wylde machine consists, as it were, of two Siemens machines, one on the top of the other, the lower and larger of which is worked by an electro-magnet, which is magnetised by the action of the upper or smaller one, consisting in the ordinary way of a permanent magnet apparatus, which is termed “the exciting machine.” The longitudinal bobbin revolved between these permanent poles produces alternating currents, which are commutated (or redirected), and[Pg 275] pass to work the larger and lower electro-magnet, which is composed of two large sheets of iron connected by a plate (on which stands the exciter). Its poles are two masses of iron separated by a layer of copper, and in this armature revolves the larger longitudinal bobbin. This lower machine is called the generator. Both bobbins are simultaneously revolved, and an intense current of electricity is thereby generated. Almost simultaneously with this one Mr. Ladd invented his machine, which is distinguished from all hitherto described by being composed of two parallel bar electro-magnets, between the extremities of which are placed two Siemens armatures, one smaller than the other; both being revolved, the smaller excites the electro-magnets, and the larger generates the electricity required. The wire is wound round the magnets so that the N. and S. poles face each other at each end. The chief advantage of the Ladd machine is the conversion of dynamic force into electricity, there always being just sufficient magnetism in an iron bar (by induction from terrestrial magnetism and other causes) to produce a very feeble current in the Siemens bobbin, and the bobbin taking it up and returning it to the electro-magnet, and the electro-magnet at once giving it back to the bobbin, the current gradually increases till the maximum is reached. And when we take into consideration this modicum of utilisable terrestrial magnetism, we may truly say in the words of M. Hippolyte Fontaine, “The mind is lost in contemplation of the succession of discoveries completing one another, and showing that with apparatus of small dimensions an infinite source of electricity could be produced if matter could withstand infinite velocities.” The Lontin machine, which supplied the current for the electric light which used to make night bright outside the Gaiety, is also composed of two parts, one dividing, the other generating the electricity produced. The principle of the dividing machine is somewhat similar to the alliance, excepting that a number of electro-magnets arranged radially round a core, revolve close to a corresponding number of bobbins fixed inside an iron cylinder, outside which is the collecting and dividing apparatus.[Pg 276] The Maxim machine is constructed on the principle of sets of coils rotating between powerful electro-magnets. The Wallace machine was invented by the inventor of the Wallace-Farmer lamp. It consists of two horse-shoe electro-magnets placed side by side, the opposing poles facing each other. Each magnet has a rotating armature of twenty-five bobbins, on which the wire is wound quadruply, and the current generated by these coils is conducted away, passing through and exciting the electro-magnets, thus utilizing the residual and terrestrial magnetism before mentioned in connection with the Ladd machine; otherwise it partakes of the nature of the Niaudet machine.

We now come to what is perhaps the most perfect magneto-electric machine, which was first constructed by M. Gramme, a Parisian, in 1872, and differs in principle and construction from all those hitherto noticed. Its essential characteristic is a soft iron ring, round which is coiled one single continuous wire (i.e., the two ends are joined). Round the exterior surface of the wire coil a band is bared, and on this bared part two friction springs act. If the ring and coil be placed before the poles of a magnet, the ring will have two poles, S. and N., induced opposite the opposing poles N. and S. of the magnet; and if the ring revolve the poles will remain stationary, and as the coil revolves each coil of the wire will pass this induced pole, and as naturally half the coil will be inducted with one current, the other half (acted on by the other pole) will be charged with another or opposite current, which two kinds of electricity are carried away by the friction springs before mentioned. In the machine, as actually constructed, the soft iron ring is composed like the magnet or wire bundle of an induction coil, and the coils are set upon it side by side. Inside the ring are radially set insulated pieces, to each of which is attached the issuing end of one and the entering end of another bobbin; these answer the same purpose as the denudation of the external layer of wire. These pieces are bent so as to come out of the centre of the ring at right angles, and lay side by side (insulated) round a small cylinder. These, as they revolve, are touched by friction springs, which draw off the electricity induced in the coils in one continuous current. No sparks are produced at the contact of the friction springs, and there is no tendency to become heated. To obviate the inconvenience of the secondary[Pg 277] or inverted current produced by the stopping of the machine, the inventor has contrived a circuit breaker on the principle of the electro-magnet, the magnets holding the circuit breaker in contact so long as the machine is working; but the decrease of velocity lessening the attractive power of the magnet, the circuit breaker opens by its own weight (or a counter-weight), and all danger of a reverse current is obviated. Experimental machines are manufactured by Bréquet & Cie (Paris), composed of Jamin’s magnets, and turned with a handle, and produce a force of eight Bunsen cells.
A great revolution, or rather the beginning of a new era in the history of electricity, may be said to have commenced with the perfection of M. Faure’s accumulators. These are troughs containing eleven lead plates, each coated with oxide of lead and wrapped in felt, the fluid being dilute sulphuric acid. The application of them to the electric light is one of their most valuable features; at the depôt in the Strand, where they may be seen at work, there are thirty such elements, each weighing about 50 lbs. It takes a two-horse-power engine working an Edison or Gramme machine six to eight hours to charge them, and when charged they will keep almost any number of lamps of sixteen-candle-power going some eight hours. They are used on the Brighton and South Coast Railway, and seem peculiarly adapted to lighting by incandescence, by Swan, or Edison’s lamp. The elements fully charged may be carried any distance without losing their electric power. And the stored force may be used for charging the accumulators themselves afresh from the machine. These accumulators may be seen any day at 446, Strand, and are well worth a visit.
The Gyroscope, though now an instrument common and familiar to all students, is none the less the subject of a problem, the solution of which is still to seek. It has indeed been entitled the paradox of mechanics; for though it depends on gravitation, gravitation yet appears indifferent to it. In order to render the operation of the Gyroscope as continuous as possible, so as to facilitate the profound study of its working, and also to unite another influence with those of the ordinary Gyroscope, producing phenomena of which this instrument affords us the spectacle, a learned American has employed electricity as a motive power.

The Gyroscope, shown in fig. 277, has a large, heavy pedestal, with a pointed column, which supports the instrument itself. The frame, of which the electro-magnets form a part, is connected with a rod, having at one end a hollow cavity which rests on the point of the vertical column. One of the extremities of the magnetic spool is attached to this cavity, the other end communicating with the bar which unites the two magnets. Over this bar is a spring which breaks the current, supported by an insulator in hard india-rubber; it is adjusted so that it touches a small cylinder on the axis of the wheel twice during every rotation of the latter. The wheel’s plane of rotation is at right angles with the magnets, and it carries an armature of soft iron, which rotates close to the magnet without touching it. The armature is so placed in relation to the surface of contact with the cylinder that breaks the current, that twice[Pg 278] during each rotation, as the armature approaches the magnets, it is attracted; but immediately afterwards, as the armature comes directly in front of the magnets, the current is broken, and the acquired impulsion is sufficient to move the wheel until the armature comes again under the influence of the magnet. The spring which interrupts the current is connected with a thin copper wire, which stretches back as far as the point of the column, entwining it several times to render it flexible, finally bending down and plunging into some mercury enclosed in a round vulcanite cup placed on the column near the pedestal. The pedestal also bears two small stakes[Pg 279] for receiving the wires of the battery, one connected with the column, and the other communicating by a small wire with the mercury contained in the vulcanite vessel. The magnets, the wheel, and all the connected parts can move in any direction round the point of the column. When two large Bunsen cells, or four small ones, are connected with the Gyroscope, the wheel turns with great rapidity, and allowing the magnets to operate, it not only sustains itself, but also the magnets and the other objects which are between it and the point of the column in opposition to the laws of gravitation. The wheel, besides turning rapidly round its axis, also effects a slow rotation round the column in the direction of the movement experienced by the lower part of the wheel. By placing the arm and the counterpoise of the machine as shown in fig. 277, so that the wheel and the magnets balance exactly on the pointed column, the whole machine rests stationary; but if we give the preponderance to the wheel and the magnets, the apparatus begins to rotate in a direction contrary to or following that of the upper part of the wheel.
The Gyroscope exemplifies very clearly the persistence with which a body undergoing a movement of rotation maintains itself in the plane of its rotation in spite of gravitation. It shows also the result of the combined action of two forces tending to produce rotations round two axes which are separate, but situated in the same plane. The rotation of the wheel round its axis, produced, in the present instance, by the electro-magnet, and the tendency of the wheel to fall or turn in a vertical plane, parallel to its axis, produce, as a result, the rotation of the entire instrument round a new axis which coincides with the column.
Peiffer’s Electrophorus.
It will now perhaps interest our readers to describe a charming little plaything which is a great favourite with children, and which has the incontestable merit of early initiating them into all the principal phenomena of the statics of electricity, and teaching them the science of physics in an amusing form.
It is a small electrophorus invented by M. J. Peiffer, and reduced to such a point of simplicity, that it consists merely of a thin plate of ebonite, about the size of a large sheet of letter paper. The tinned wooden disc of the electrophorus which is found described in most treatises on physics, is replaced by a small sheet of tin, about the size of a playing-card, fastened on to the surface of the ebonite. The ebonite electrophorus produces electricity with remarkable facility. It must be placed flat on a wooden table, and thoroughly rubbed with the hand; if it is then lifted, and the sheet of tin lightly touched, a spark is elicited from ¼ inch to ½ inch in length. The electrophorus is completed by the addition of a number of small accessories in the shape of small dolls made of elder-wood, which exhibit in a very amusing manner the phenomena of attraction and repulsion. After the board has been charged with electricity, place the three little[Pg 280] figures on the sheet of tin, and lift up the apparatus, so as to isolate it from any support. You will then see one little doll extending its arms, another with its silky hair standing on end, and a third, lighter than the others, leaping like a clown, and displacing as he does so the two small balls of elder-wood which have been placed on each side of him. We have given an illustration of the three figures performing at once (fig. 278), but they are generally used separately. M. Peiffer has indeed collected every known accessory for an electric machine, such as Geissler’s tube, the electric carillon, etc. These different experiments are all reduced to their simplest form, and, with their appliances, are all contained in a cardboard box. They are placed beside the electrophorus, which thus takes the place of an unwieldy electric machine. M. J. Peiffer accompanies this little portable cabinet with an exhaustive pamphlet, which is a valuable guide to the young physicist in studying the first principles of electricity.

“It is easy to discover in the education of children,” says M. Peiffer in his preface, “how to turn their budding faculties to the best account. Would you utilize them in a satisfactory manner?—Then put in their hands playthings which, in an attractive form, serve to familiarize them at an early age with those sciences, a knowledge of which will be at a later period absolutely indispensable to them; and they will be much more amused than with ordinary commonplace toys.”
These are sensible words, in which we heartily concur. Yes! Science properly taught, and properly understood, can indeed be brought within the range of children; it should give a lasting interest to all amusements, and form a part of the culture of the youthful mind, as at a later period it will contribute to the perfect development of the grown man.
Magic Fish.
An ingenious physicist, M. de. Combettes, who is a civil engineer at Paris, has devoted himself to constructing a number of playthings and scientific appliances for young people, among which we will describe the very curious one represented in fig. 279. A jar is filled with water, holding in suspension some fish made of tin, similar to those which children put in water and attract with a magnet. In this case, however, the mechanism is hidden, and the operator can turn the fish first in one direction and then in the other at pleasure. The secret of this experiment is easily explained by examining the illustration (fig. 279). In the wooden stand which supports the jar there is concealed a small electro-magnet which acts on the soft iron contained in the floating fish. When the current passes the small magnet turns round and attracts the little fish swimming in the water. This gyratory movement can be changed at pleasure by means of a regulator.


We will give an illustration of a few electric toys which M. Trouvé has found for us. In the picture (fig. 281) we see three different objects,—a rabbit beating a small bell, a representation of a bird with outstretched wings, and a pin surmounted by a skull. All these are capable of having movement imparted to them by means of electricity, although made and intended for ordinary use in the form of scarf-pin or other ornament.
Let us take the “death’s head” pin first. It is in gold, and enamelled[Pg 282] with diamond eyes and articulated jaws. The rabbit is also gold, and carries two small drumsticks, with which he can play a tiny bell. This device also can be worn as a scarf-pin.

A conducting wire leads from the pin into the waistcoat pocket, where a small “pile,” about the size of a cigarette, is hidden away. If any one particularly admires the scarf-pin, all you have to do is to insinuate your fingers into your pocket, and you will, by contact, cause the electric current to act upon the pin in your scarf. The death’s head will at once begin to roll its eyes and grind its teeth, while the rabbit, under similar circumstances, will begin to play its bell with the greatest energy.
The handsome diamond bird represented in the centre of the illustration belongs to Madame de Metternich. When any lady wears it in her hair, she can, by the concealed wire, make it flap its jewelled wings, and by so doing cause much surprise amongst the spectators.
We will now endeavour to give a description of the manner in which these toys play their parts in company with the “hermetic-pile” which M. Trouvé has applied to many specialities that he has supplied to doctors, who use them largely.
This pile is formed by a “couple” of carbon and zinc hermetically enclosed in an ebonite box. The carbon and zinc only occupy one-half of the case. The liquid occupies the other. The sketch (fig. 280) on preceding page will explain the apparatus.
So long as the case is in its normal position the elements are not immersed in the solution, and consequently no electricity is developed. But as soon as the figure is placed in a horizontal or leaning position the force is generated; on readjusting the box the electric current is cut off, and all development ceases. Many curious electrical toys can be seen in Paris. Dolls are made to talk, and many other wonders for children can be easily procured.
Animal and Atmospheric Electricity.
Before concluding the subject of electricity we must devote a few pages to the consideration of the electric influence possessed by certain fishes, and to some of the phenomena of the atmosphere, especially thunderstorms. We have seen how Galvani experimented upon the limbs of frogs, and maintained that they possessed electricity; he attributed the current in the muscles to that cause. This theory Volta denied, but subsequently Nobili, in 1827, proved the existence of a current in the frog by means of a Galvanometer. This was conclusive, and the experiment was performed in the following manner:—He filled two vessels with salt and water, and into one he dipped the crucal muscles of a frog, and in the other the lumbar nerves were immersed. By putting these vessels in communication with his improved Galvanometer, which was extremely sensitive, he perceived a current passing from the feet towards the head of the animal.
It is, however, to Matteucci and Du Bois Reymond that the investigation of the phenomena of the courant propre are due. The former formed a “pile” of the thighs of frogs, and by placing the interior and exterior muscles in contact he formed a current from the inside to the outside muscles. This current is supposed to be occasioned by certain chemical changes which are continually taking place, and it continues longer in the case of a cold-blooded animal than in a warm-blooded one. There are many interesting papers on this subject included amongst the “Philosophical Transactions”; and the “Physical Phenomena of Living Beings” is fully treated in Matteucci’s lectures on that subject. In the “Transactions” for 1848 and subsequent[Pg 284] years, other experiments may be perused, but space will not permit us to dilate upon them. The fact has been established, and we are told that muscles and nerves, as well as certain glands of the body, possess certain electrical properties.
The electricity of fishes, and the power possessed by the torpedo—whose name is now chiefly known in connection with warlike appliances—and the gymnotus, have been known for a very long time. This fish, popularly known as the electric eel, inhabits the warm fresh-water lakes of Africa, Asia, and America. A specimen was exhibited at the Polytechnic some years ago. This was the fish experimented on at the Adelaide Gallery by Professor Faraday, who clearly demonstrated the fact that the electricity of the animal and the common electricity are identical. Numerous experiments were made, and the circuit shock and even sparks were obtained from the gymnotus. In fact, the gymnotus is a natural electric machine. The force of the shock given by the electric eel is very great, for Faraday has put on record that a single discharge of the eel is equal to fifteen Leyden jars charged as highly as possible. Its power does not even end there, for having shocked people to that extent, it was capable of a second and occasionally of a third shock of less violence.

The manner in which the gymnotus acts is from a regular battery in the head, the sides of which are filled with a fluid. These cells are something like a honeycomb in appearance. The shock is quite voluntary on the part of the fish. Sometimes it will kill its prey, on other occasions it is merely numbed. Professor Faraday on one occasion placed a live fish in the tub with the gymnotus, which curled itself so as to enclose the unsuspecting one. In a second the prey was struck dead, and floated on the water. The gymnotus immediately devoured it, and went in quest of more. Another, but an injured fish, was then introduced, but the electric eel took no trouble about this one. It did not trouble to give it a shock, seeing it was disabled, it merely swallowed without killing it. It is also on record that on one occasion an electric eel had stunned a fish which, before he began to eat it, gave signs of returning animation; the eel immediately gave it another shock and killed it.

There were some other curious peculiarities connected with the electric eel. It appears to be quite capable of discriminating between animate and[Pg 285] inanimate touch. For instance, when touched with a glass rod it at first gave signs of electricity, and discharged a shock at the attacking party. But on subsequent occasions, when touched with metal rods or glass, the fish declined to “shock”; nevertheless the Professor succeeded the moment he touched the animal with his hands.
The torpedo is something like the well-known skate; it is sometimes called the electric ray, and is common enough in the Bay of Biscay and in the Mediterranean Sea. It sometimes pays England a visit, or is caught by fishermen and brought in. We have seen one at Plymouth, and a very ugly-looking fish it was. Its electric power is considerable.

c, brain; m e, spinal chord; o, eye; e, electric organs; b, gills; np, nl, nerves; n, spinal nerve.
There is yet another fish known as the malapterurus; one species is called the thunder-fish. Professor Wilson has written a paper upon the electric fishes as applied to the remedy of disease, and considers them the “earliest electric machines ever known.”
Humboldt relates that the South-American Indians capture the gymnotus by driving horses into ponds which the electric eels are known to inhabit. The result is that the fish deliver shock after shock upon the unfortunate quadrupeds. Mules and horses have frequently been killed by these powerful eels, and even Faraday experienced a very great shock when he touched the head and tail of the captive gymnotus with either hand.
The malapterurus to which we have referred is an inhabitant of the African rivers, chiefly in the Nile and Senegal. Such a fish has been known with others for some hundreds of years; its electrical powers are not great. There are one or two other species of fish which possess electrical qualities, but none apparently to the same extent as the torpedo and the gymnotus.

The electricity of plants also is in some cases very marked. Flashes have been seen to come from some flowers in hot and dry weather. Currents of electricity have been detected, and Wartmann investigated the subject closely. He says the currents in flowers are feeble, but in succulent fruits and some kinds of grain they are very marked. These currents depend[Pg 286] upon the season, and are greatest in the spring, when the plant is bathed in sap. These experiences were confirmed by Bequerel in 1850, and he concludes that the rank vegetation in some parts of the world must exercise considerable influence on the electric phenomena of the atmosphere. M. Buff has more recently made experiments in this direction, and he examined plants and trees, and even mushrooms. M. de la Rive, after carefully summing up the various theories, comes to the conclusion that it is to chemical reactions that the traces of electricity are due.
The subject of atmospherical electricity properly belongs to meteorology, and under that heading we will treat of it more fully. But lightning is so identified with electricity, and being the most common form observable to all, we will say something about thunderstorms and the electric discharges accompanying them.

Before Franklin’s ever-memorable experiment with his kite established the identity of lightning and electricity, the resemblance between the two discharges had been frequently noticed. The Etruscans pretended to bring down lightning from heaven, and Tullus Hostilius, when experimenting or performing certain “ceremonies,” was killed by the electric discharge he desired to attract. But after all, we cannot attribute any knowledge of electric science to the ancients, although they were, of course, familiar with electric phenomena.
It is to Dr. Wall that testimony points as the first person who remarked the analogy between the electric spark and lightning. This was in 1708. Grey and other philosophers supported the theory, but could not establish it. To Franklin, who in June 1752 actually brought down the[Pg 287] lightning by his kite and a key, is the actual discovery due. We have already detailed the circumstances (page 206) and need not repeat the account of the experiment.
Of course the American philosopher found numerous imitators, not always with impunity. Professor Richmann was killed by the spirit he was invoking; Lemounier and Beccaria confirmed the theory that the air was full of electricity; while Du Saussure, from his investigations on the Alps, and Volta from the invention of the pile, are most famous in the history of electricity. They applied themselves with much success to the investigation of the electric condition of the atmosphere, of which the disturbances called thunderstorms are the result.
The amount of electricity varies in the atmosphere at different times in the day and night. Towards midday and midnight the development is generally greatest, and this fact will account for the prevalence of storms during our hours of rest. Again, different kinds of clouds have different degrees of electricity, and of different kinds. Under certain conditions these clouds will give forth lightning, and a storm will begin. The more clouds the more globules, and therefore in summer, while there is more production of vapour from solutions of salts, etc., we are more likely to have the storms. We are most of us familiar with the mass of the “thunder cloud” rising in the distance, light at the upper part, very dark below, and throwing out tentacles like the octopus, coming up sometimes—frequently, indeed—“against the wind,” impelled by an upper current, or following the course of a river, which is not unusual. Below, there is perhaps an army of thin dark clouds. The nature and height of clouds have also a great deal to do with the phenomena displayed. In general, storm-clouds are positively electrified.

Clouds are good conductors of electricity, and yet they may be so insulated by the dry air surrounding them that they will accumulate it; and when thus charged, if they encounter other clouds charged with opposite electricity, the opposing masses will attract each other until a discharge[Pg 288] takes place. This is what we term lightning, and under such conditions electricity, though very dazzling, is harmless. It is when the cloud comes near to the earth, and a discharge is released, that lightning is so dangerous to persons who remain in the fields. Sometimes the discharge comes from the earth to meet that from the cloud. Sheep are frequently killed by ground lightning, and once, at Malvern, we had an escape from an upward stroke. The back-stroke from a cloud is also dangerous. It may happen that the cloud has discharged itself upon the earth many miles away, but a return discharge takes place at the other end, and if that end be near the earth the consequences may be serious. As a rule, the return stroke is not so violent as the first discharge.
The colour of lightning varies very much. We have the white, the blue, the violet, and red. The colour depends upon the distance and intensity of the lightning, and the more there is of it the whiter the light. We can illustrate the varied hues of the electric “fluid” by passing a spark through the receiver of an air-pump. If the air be rarefied, or there be a vacuum, we shall perceive a blue or violet light. Therefore we may conclude that the blue and violet flashes have birth in high strata of the atmosphere.

We have all heard how dangerous it is to stand under a tree during a thunderstorm, or rather, we should say, when the storm is approaching us nearly. The tree is a conductor, and the lightning having no better one at hand will pass through the tree on its way to the earth, and if we are standing against the tree we shall be included in the course, and die from the shock to the nerves while the lightning is passing through us. The best position in a thunderstorm, if we are in the neighbourhood of trees, is to sit or lie down on the ground some little distance from the base of the nearest tree. If the tree be sixty feet high suppose, and we sit fifty feet or less from the trunk, we shall be pretty safe, because the lightning will reach the tree top before it can reach us. We are protected by it as by a conductor, bad though it be. Standing up in a boat during a storm is not wise. Lightning has an affinity for water, and besides, if no higher objects are near, our body will act[Pg 289] as a conductor. Bed is the safest place, as blankets are non-conductors. Cellars are not the safest by any means. Lightning may, and it frequently does, strike the house and descend to the basement. If the air be very full of electricity, and a flash be near, a person running away may conduct the lightning to himself by creating a vacuum into which the flash may dart.

Arago classified lightning into three kinds: zig-zag, globular, and sheet. The first we call forked lightning, and frequently this kind branches out at the end, so that although there may be only one flash, it may strike out in two or three directions at the same time. This may be accounted for by the unequal power of the air strata to conduct the electricity. The forked flashes are of very great length, extending frequently for miles, and the bifurcations also are often miles apart. The duration of the flash is less than the thousandth part of a second; so instantaneous is it that no motion can be perceived even in a most rapidly-moving wheel, as proved by Professor Wheatstone. We sometimes fancy that the flash lasts longer, but the impression received by the eye quite accounts for the apparently prolonged sight of the lightning.
Sheet lightning, the faint flashes frequently seen upon the horizon, are quite harmless. Sheet lightning is that which is seen reflected behind clouds or from far-distant storms. It is sometimes very beautiful. Ball, or globular lightning, is dangerous, and globes of fire have been seen to descend, and striking the ground, bound onwards for some distance. The descent of these forms of electric discharge has given rise to the popular notion of “thunderbolts.” The “Mariner’s Lights,” or St. Elmo’s fire, is frequently observed in ships. It is usually regarded as a fortunate occurrence. It was noticed by Columbus. One voyager describes the phenomena as follows:—“The sky was suddenly covered with thick clouds.... There were more than thirty of St. Elmo’s fires on the ship. One of them occupied the vane of the mainmast. I sent a sailor to fetch it. When he was aloft he heard a noise like that which is made when moist gunpowder is burned. I ordered him to take off the vane. He had scarcely executed this order, when the fire quitted it and placed itself at the apex of the mainmast, whence it could not possibly be removed.”

There have been occasions when the manes and tails of horses, and even the ears of human beings, have shown a phosphorescent light which emitted a hissing noise. Alpine travellers have noticed similar phenomena; and Professor Forbes, when crossing the Theodule Pass into Italy, heard[Pg 291] the hissing sound in his alpenstock. The tips of rocks and grass points were all hissing too. The party were in the midst of an electric cloud. When the Professor turned the point of his alpenstock upwards, a vivid flash was emitted, but no thunder followed. They descended as quickly as possible from such a dangerous neighbourhood.

It is observable that the properties of lightning and of the electric spark are identical—the faint crackle of the latter being magnified into the loud rolling of the thunder. The disturbance of the atmosphere is the cause of the loud reverberations, and echoes produced from clouds tend to intensify and prolong the peal. The sound rises and falls, and varies accordingly as the cloud is near or far. A smart sharp report or rattle denotes the nearness of the lightning, while the gradual swelling and subsidence, followed, mayhap, by an increasing volume of sound, which in its turn dies away, tells us that the danger is not imminent. The cause o£ this loud rolling, unless it proceeds from echoes from different clouds, has not been satisfactorily explained. Sound travels less quickly than light, and therefore we only hear the thunder some seconds after we have perceived the flash. It is therefore conceivable that we may hear the last reverberations and its echoes first, and the sound of the first disturbance with its echoes last of all. Thus there will be distinct sounds. Firstly, the actual noise we call thunder from the air strata nearest to us; secondly, the echoes of that disturbance from the clouds, of course fainter; then we hear the sound caused by the tearing asunder of the air particles farthest off, and again the echoes of that disturbance. This theory will, we think, account for the swelling peals of thunder, and the successive loud and fainter reverberations. At any rate, in the absence of any other theory, we submit it for consideration. The sound of thunder is seldom or never heard at a distance greater than fifteen miles.
Lightning conductors are such every-day objects that no description is necessary; but the reason the lightning runs along it harmlessly is because the galvanized iron rod is the best conductor in the immediate neighbourhood. Where there is not a good conductor lightning will accept the next best, and so on, any conductor being better than none. The point of the rod cannot contain any electricity, there being no room for it, and the “fluid,” as it is termed, runs down to the ground, to terminate, when possible, in water or charcoal. A great deal of electricity is no doubt carried away from the air by the numerous conductors without any spark passing. Until Sir W. Snow Harris brought forward his lightning conductors for ships, the loss was great at sea. But now we rarely hear of any vessel being disabled by lightning. We owe to Franklin the idea of the lightning conductor.
According to observations made by Mr. Crosse, the following statement shows the tendency of the atmosphere, in certain conditions, to thunderstorms. We may accept the deduction of M. Peltier that grey and slate-colour clouds are charged with negative, and white, rose-colour, and orange clouds with positive electricity. The order of arrangement in the following table places the most likely source of thunderstorms first, and the least likely source at the end, with regular rotation of intermediate probabilities intervening:—
- Regular thunder clouds.
- Driving fog with small rain.
- Fall of snow, or hailstorm.
- Smart shower on a hot day.
- Smart shower on a cold day.
- Hot weather after wet days.
- Wet weather after dry days.
- Clear frosty weather.
- Clear warm weather.
- Cloudy days.
- “Mackerel” sky.
- Sultry weather and hazy clouds.
- Cold damp night.
- Cold, dry north-east winds.
We have thus briefly touched upon some of the atmospherical phenomena directly attributable to electricity. In our articles upon Meteorology we will consider the aurora and many other interesting facts concerning the atmosphere, and the effects of sound, heat, and light upon the air.

CHAPTER XXIII.
AERONAUTICS.
PRESSURE OF AIR IN BODIES—EARLY ATTEMPTS TO FLY IN THE AIR—DISCOVERY OF HYDROGEN—THE MONTGOLFIER BALLOONS—FIRST EXPERIMENTS IN PARIS—NOTED ASCENTS.
In the first part of this volume we entered into the circumstances of air pressure, and in the Chemistry section we shall be told about the atmosphere and its constituents. We know that the air around us is composed principally of two gases, oxygen and nitrogen, with aqueous vapour and some carbonic acid. An enormous quantity of carbonic acid is produced every day, and were it not for the action of vegetation the amount produced would speedily set all animal life at rest. But our friends, the plants, decompose the carbonic acid by assimilating the carbon and setting free the oxygen which animals consume. Thus our atmosphere keeps its balance, so to speak. Nothing is lost in nature.
We have illustrated the pressure of the atmosphere by the Magdeburg hemispheres, and we know that the higher we ascend the pressure is lessened. The weight of the atmosphere is 15 lbs. to the square inch at sea level. This we have seen in the barometer. Now pressure is equal. Any body immersed in a liquid suffers pressure, and we remember Archimedes and the crown. It displaced a certain amount of water when immersed. A body in air displaces it just the same. Therefore when any body is heavier than the air, it will fall just as a stone will fall in water. If it be of equal weight, it will remain balanced in the air, if lighter it will rise, till it attains a height where the weight of the atmosphere and its own are equal; there it will remain till the conditions are altered. Now we will readily understand why balloons float in the air, and why clouds ascend and descend in the atmosphere.
In the following pages we propose to consider the question of ballooning, and the possibility of flying. We all have been anxious concerning the unfortunate balloonist who was lost in the Channel, so some details concerning the science generally, with the experiences of skilled aeronauts, will guide us in our selection of material. We will first give a history of the efforts made by the ancients to fly, and this ambition to soar above the earth has not yet died out.
From a very early period man appears to have been desirous to study the art of flying. The old myths of Dædalus and Icarus show us this, and it is not to be wondered at. When the graceful flight of birds is noticed, we feel envious almost that we cannot rise from the earth and sail away at our pleasure over land and sea. Any one who has watched the flight of the storks around and above Strasburg will feel desirous to emulate that long, swift-sailing flight without apparent motion of wing, and envy the accuracy with which the bird hits the point aimed at on the chimney, however small. It is small wonder that some heathens of old time looked upon birds as deities.
The earliest flying machine that we can trace is that invented by Archytas, of Tarentum, B.C. 400. The historian of the “Brazen Age” tells us how the geometrician, Archytas, made a wooden pigeon which was able to sustain itself in the air for a few minutes, but it came down to the ground after a short time, notwithstanding the mysterious “aura spirit” with which it was supposed to be endowed. The capability of flying has for centuries been regarded as supernatural. Putting angels aside, demons are depicted with wings like bats’ wings, while witches, etc., possessed the faculty of flying up chimneys upon broomsticks. We even read in childish lore of an old woman who “went up in a basket” (perhaps a balloon-car), and attained a most astonishing altitude-an elevation no less than “seventy times as high as the moon!”
But to descend to history. It is undoubtedly true that in the time of Nero, Simon Magus attempted to fly from one house to another by means of some mechanical contrivance, and failing, killed himself. Roger Bacon, the “admirable doctor,” to whom the invention of gunpowder is generally attributed, had distinct notions of flying by means of machines, and “hollow globes,” and “liquid fire.” But he did not succeed, nor did many successive attempts succeed any better in subsequent years. Bishop Wilkins treated of the art of flying, but most, if not all who discussed the subject appear to have been indebted to Roger Bacon for the idea.
When the nature and pressure of the atmosphere by Torricelli’s experiments became better known, Father Lana, a Jesuit priest, constructed a flying machine or balloon of curious shape. He proposed to fix four copper globes, very thin, and about twenty feet in diameter, and to these he fastened a boat or car, looking very much like a basin. His idea was to empty his great copper globes, and that their buoyancy would then bear the weight of the traveller. But he overlooked or was ignorant of the effect of the atmospheric pressure, which would have speedily crushed the thin copper globes when empty. Lana’s suggestion was made in 1670, the barometer had been discovered in 1643.
There were some fairly successful experiments made in flying in 1678 and in 1709. The former attempt was made by Besmir, a locksmith of Sable, who raised himself by means of wings up to the top of a house by leaps, and then succeeded in passing from one house to another lower down[Pg 295] by supporting himself in the air for a time. He started from an elevated position, and came down by degrees. Dante, a mathematician, also tried to fly, but without great success. He broke his thigh on one occasion. Laurence de Gusman claimed an invention for flying in 1709, and petitioned for a “patent,” which was granted by the king’s letter. The machine appears to have borne some resemblance to a bird.
It was not till 1782, however, that the true art of aerial navigation was discovered. The knowledge of hydrogen gas possessed by Cavendish in 1766 no doubt led up to it, and in the year following its discovery Professor Black, lecturing in Edinburgh, stated that it was much lighter than the atmosphere, and that any vessel filled with the gas would rise in the air. We now come to the invention of the Balloon (so called from its shape being similar to a vessel used in the laboratory) by the Brothers Montgolfier.

Stephen and James Montgolfier were paper-makers, and carried on their business at Annonay, near Lyons, but it was partly by accident that the great discovery was made. They had no knowledge of the buoyancy of hydrogen gas. They took their idea of the balloon (inflated) from noticing an ascending column of smoke. It occurred to Stephen that if a paper bag were filled with smoke it would ascend into the air. A large bag was made and some paper burnt beneath it in a room. When the smoke had filled the bag it was released, and immediately ascended to the ceiling. Here was[Pg 296] the germ of the Montgolfier or heated air balloon. The experiment was repeated in the open air with even greater success, and a trial upon a larger scale was immediately determined upon. A story is related of Mongolfier when prosecuting his researches, that a widow whose husband had belonged to the printing firm with whom Montgolfier was then connected in business, saw the smoke issuing from the room in which the little balloon was being filled. She entered, and was astonished to see the difficulty experienced by the experimenter in filling the balloon. It swerved aside, and increased the trouble he had to keep it above the chafing dish. Montgolfier was greatly troubled, and seeing his disappointment, the widow said, “Why don’t you fasten the balloon to the chafing dish?” This had not occurred to the experimenter, and the idea was a valuable one. That was the secret of success.
The Montgolfier Brothers determined to exhibit their successful experiment, and accordingly on the 5th of June, 1783, a great concourse assembled to see the wonderful sight. A large canvas or linen balloon was made and suspended over a fire of chopped straw. The heated air quickly filled the balloon, which rose high in the air, and descended more than a mile away. This balloon contained 22,000 cubic feet of heated air, which is lighter than cold air, and of course rising carried the globe with it. As soon as the air began to cool the balloon ceased to rise, and as it got colder descended.
Here was the actual discovery of the science of Aerostatics. The intelligence of the success achieved soon spread from France to other countries. Paris, however, was in advance, and the Brothers Robert applied hydrogen gas to a balloon which was sent up from the Champ de Mars in August 1783. There was some trouble experienced in filling it, but when the balloon was at length released it realized all expectations by remaining in the air nearly an hour. When at length it fell it met with a worse fate than it deserved, for the ignorant and superstitious peasantry at once destroyed it. After this Montgolfier exhibited his experiment next time at Versailles in the presence of the Court. The first aerial travellers appeared on this occasion—viz., a sheep, a cock, and a duck, which were secured in the car. They all descended in safety, and this success encouraged M. Pilatre de Rozier to make an attempt in a “fire balloon.” He went up first in a captive balloon, and at length he and a friend, the Marquis d’Arlandes, ascended from the Bois de Boulogne. The trip was a decided success, and the possibility of navigating the air was fully demonstrated.
Soon after this,—viz., in December 1783,—an Italian Count, named Zambeccari, made an ascent in London, and came down safely at Petworth. MM. Charles and Robert ascended from Paris in December, and in February a balloon crossed the English Channel. We must pass over some time and come to the ascents of Lunardi, which caused great excitement in London. His balloon was a very large one, and was inflated, or rather partially so, at the Artillery ground. Some delay occurred, and fearing a riot, M. Lunardi proposed to go up alone with the partially-filled balloon. A Mr. Biggin who[Pg 297] had intended to ascend was left behind. The Prince of Wales was present, with thousands of spectators. Lunardi cast off and ascended rapidly, causing great admiration from the whole metropolis. Judge and jury, sovereign and ministers, all turned out to gaze at the balloon; a guilty prisoner was acquitted hurriedly, so that no time was lost in discussion, and one lady died of excitement. Lunardi was regarded as a hero, and made many other ascents. He died in 1806.
In those earlier days one or two fatal accidents happened. Count Zambeccari and a companion were in a balloon which caught fire, and both occupants of the car leaped from it as they were descending. The Count was killed on the spot, and his companion was much injured. Pilatre de Rozier made an attempt to cross the channel to England in 1785; he had reached three thousand feet when the balloon caught fire, and the unfortunate traveller was precipitated to the ground. His associate only survived him a few minutes.


It is to the celebrated English aeronaut, Mr. Green, that the substitution of carburetted hydrogen or street gas for hydrogen is due, and since his ascent in 1821 no other means of inflation have been used. A great many quite successful and a few unsuccessful ascents have been made for pleasure or profit. Mr. Green, in the Nassau balloon, passed over to Nassau, a distance of five hundred miles, in eighteen hours. This exploit was the cause of the name being bestowed upon the balloon. The Giant of M. Nadar was exhibited in England, and it was an enormous one, being an hundred feet high, and nearly as wide in the widest part. But even this machine was outdone by[Pg 298] the Godard “Montgolfier” balloon, which was one hundred and seventeen feet high, and carried a stove. We give illustrations of these celebrated balloons, and will now pass on to the more scientific portion of the subject and the ascents of Mr. Glaisher and other aeronauts for the purpose of making meteorological observations, and the use of balloons for purposes of observation in war.
It appears that the first ascent for scientific investigation was made in the year 1803. The aeronauts were Messrs. Robertson and Lhoest. They ascended from Hamburg and came down at Hanover, and made meantime several experiments with reference to the electrical condition of the atmosphere, its influence upon a magnetic needle, and some experiments with regard to acoustics and heat. The report was presented to the St. Petersburg Academy, and contains the result of their interesting observations. The travellers ascertained that at the elevation to which they attained,—viz., 25,500 feet,—the temperature was on that July day fifty degrees colder, falling to 19·6°, while on the earth the thermometer had shown 68°. They ascertained that glass and wax did not become electric when rubbed, that the Voltaic battery lost much of its power, that the oscillation of a “dipping needle” increased as they mounted into the air, while sound was certainly less easily transmitted at that elevation, and struck them as less powerful in tone. The heat experiment was not a success, owing to the breaking of the thermometer. They wished to find the temperature of boiling water at that elevation, but when the experiment was about to be made Robertson accidentally plunged the instrument into the fire instead of into the water. So the question was not settled.
The effect upon the aeronauts was a sensation of sleepiness, and two birds died. The muscular powers of the voyagers also appear to have been much affected, and similar sensations may be experienced by travellers on high mountains who find their breath very short and a disinclination to exertion oppress them.
MM. Biot and Gay-Lussac made a very interesting ascent in 1804. We will detail their experiences at some length, for the coolness displayed and the value of the observations made are remarkable in the history of scientific ballooning. They started, at 10 o’clock a.m. on the 23rd of August, and when the balloon had carried them up to an altitude of 8,600 feet they commenced their experiments. They had some animals in the car with them, a bee amongst the number, and the insect was let go first. It flew away swiftly, not at all inconvenienced apparently. The sun was very hot at 56° Fahr. Their pulses were beating very fast, but no inconvenience was felt.
When 11,000 feet had been reached a linnet was permitted to go at large, but after a little time the bird returned to the balloon. It remained perched for a few minutes, and then dashed downwards at a tremendous pace. A pigeon was then liberated. It also appeared very uncertain, and wheeled around in circles for a time. At last it gained confidence, and[Pg 299] descended, and disappeared in the clouds beneath. They made other experiments, but descended without having obtained as accurate results as had been anticipated.


On the next occasion, however, every care was taken, and on the 15th of September the important ascent was made by Gay-Lussac alone. He fixed hanging ropes to the balloon with the view to check the rotating movements, and having provided himself with all necessary apparatus and two vacuum flasks to bring down some of the upper air, the young man started. The barometer marked 30·66°, the thermometer 82° (Fahr.). At an elevation of 12,680 feet Lussac perceived that the variation of the compass was the same as on land. Two hundred feet higher up he ascertained that a key held in the magnetic direction repelled with the lower, and attracted with its upper extremity the north pole of a needle. This experiment was repeated with the same result at an elevation of 20,000 feet, which shows how the earth exercises its magnetic influence. The temperature of the air was found to decrease in proportion as the ascent up to 12,000 feet, where the reading was 47·3". It then increased up to 14,000 feet by 6°, and then regularly diminished again as the balloon rose, till at the greatest elevation reached, 23,000 feet,[Pg 300] there was a difference of 67° in the temperature on the earth, for at the maximum height attained the thermometer stood at 14·9°.
But the most important fact ascertained, and one which set many theories at rest, was the composition of the atmosphere in those high altitudes. We mentioned that Gay-Lussac took up two empty flasks from which the air had been taken. The vacuum was almost perfect. When the aeronaut had reached 21,460 feet he opened one flask, and it was quickly filled; he secured it carefully; and when at his highest point,—four miles and a half above the sea-level,—he opened the other flask. The barometer stood at 12.95 inches, and the cold was very great. The voyager felt benumbed, and experienced difficulty of breathing; his throat was parched and dry. So Lussac determined to return, he could go no higher. He dropped gently near Rouen, and soon reached Paris. As soon as possible the air in the flasks was submitted to very delicate tests, and to the satisfaction of the scientists engaged it was found to be in exactly the same proportions as that collected near the earth—two hundred and fifteen parts of oxygen to every thousand of atmospheric air.
Messrs. Banal and Bixio, in 1850, also made some observations, and found the temperature very variable. At 23,000 feet they found the thermometer at minus 38·2° Fahr., which was much below the cold experienced by Gay-Lussac. We may still conclude that the various currents of the atmosphere cause considerable variation, and that it is impossible to lay down anything respecting the degrees of heat and cold likely to be found at certain elevations. We quote Arago’s observations upon this ascent:—
“This discovery” (the ice particles found in the air) “explains how these minute crystals may become the nucleus of large hailstones, for they may condense round them the aqueous vapour contained in the portion of the atmosphere where they exist. They go far to prove the truth of Mariotte’s theory, according to which these crystals of ice suspended in the air are the cause of parahelia—or mock-suns and mock-moons. Moreover, the great extent of so cold a cloud explains very satisfactorily the sudden changes of temperature which occur in our climates.”
M. Flammarion gives in his “Voyages” some very interesting and amusing particulars, as well as many valuable scientific observations. During one ascent he remarked that the shadow of the balloon was white, and at another time dark. When white the surface upon which it fell looked more luminous than any other part of the country! The phenomenon was an anthelion. The absolute silence impressed the voyager very much. He adds, “The silence was so oppressive that we cannot help asking ourselves are we still alive! We appear to appertain no longer to the world below.” M. Flammarion’s observations on the colour of what we term the sky are worth quoting—not because they are novel, but because they put so very clearly before us the appearance we call the “blue vault.” He says,—speaking of the non-existence of the “celestial vault,”—“The air[Pg 301] reflects the blue rays of the solar spectrum from every side. The white light of the sun contains every colour, and the air allows all tints to pass through it except the blue. This causes us to suppose the atmosphere is blue. But the air has no such colour, and the tint in question is merely owing to the reflection of light. Planetary space is absolutely black; the higher we rise the thinner the layer of atmosphere that separates us from it, and the darker the sky appears.”

Some beautiful effects may be witnessed at night from a balloon, and considering the few accidents there have been in proportion to the number of ascents, we do not wonder at balloon voyages being undertaken for mere pleasure. When science has to be advanced there can be no objection made, for then experience goes hand-in-hand with caution. It is only the ignorant who are rash; the student of Nature learns to respect her, and to attend to her admonitions and warnings in time. The details of the ascents of famous aeronauts give us a great deal of pleasant and profitable reading. The phenomena of the sky and clouds, and of the heavens, are all studied with great advantage from a balloon, or “aerostat,” as it is the fashion to call it. The grand phenomena of “Ulloa’s circles,” or anthelia, which represent the balloon in air, and surrounded by a kind of glory, or aureola, like those represented behind saintly heads, appear, as the name denotes, opposite to the sun.
The various experiments made to ascertain the intensity of sounds have resulted in the conclusion that they can be heard at great distances. For instance, the steam whistle is distinctly audible 10,000 feet up in the[Pg 302] air, and human voices are heard at an altitude of 5,000 feet. A man’s voice alone will penetrate more than 3,000 feet into the air; and at that elevation the croaking of frogs is quite distinguishable. This shows that sound ascends with ease, but it meets with great resistance in its downward course, for the aeronaut cannot make himself audible to a listener on the earth at a greater distance than 300 or 400 feet, though the latter can be distinctly heard at an elevation of 1,600 feet. The diminution of temperature noted by M. Flammarion is stated to be 1° Fahr. for every 345 feet on a fine day. On a cloudy day the mean decrease was 1° for every 354 feet of altitude. The temperature of clouds is higher than the air surrounding them, and the decrease is more rapid near the surface, less rapid as the balloon ascends. We may add that at high elevations the cork from a water-bottle will pop out as if from a champagne flask.
We have hitherto referred more to M. Flammarion and other French aeronauts, but we must not be considered in any way oblivious of our countrymen, Messrs. Glaisher, Green, and Coxwell, nor of the American,—one of the most experienced of aerial voyagers,—Mr. Wise. The scientific observations made by the French voyagers confirmed generally Mr. Glaisher’s experiments. This noted air-traveller made twenty-eight ascents in the cause of science, and his experiences related in “Travels in the Air,” and in the “Reports” of the British Association, are both useful and entertaining. For “Sensational ballooning” one wishes to go no farther than his account of his experience with Mr. Coxwell, when (on the 5th of September, 1862) he attained the greatest elevation ever reached, viz., seven miles, or thirty-seven thousand feet.
We condense this exciting narrative for the benefit of those who have not seen it already.
The ascent was made from Wolverhampton. At 1.39 p.m., the balloon was four miles high, the temperature was 8°, and by the time the fifth mile had been reached the mercury was below zero, and up to this time observations had been made without discomfort, though Mr. Coxwell, having exerted himself as aeronaut, found some difficulty in breathing. About 2 o’clock, the balloon still ascending, Mr. Glaisher could not see the mercury in the thermometer, and Mr. Coxwell had just then ascended into the ring above the car to release the valve line which had become twisted. Mr. Glaisher was able to note the barometer, however, and found it marked 10 inches, and was rapidly decreasing. It fell to 9¾ inches, and this indicated an elevation of 29,000 feet! But the idea was to ascend as high as possible, so the upward direction was maintained. “Shortly afterwards,” writes Mr. Glaisher, “I laid my arm upon the table possessed of its full vigour, and on being desirous of using it I found it powerless,—it must have lost power momentarily. I tried to move the other arm, and found it powerless also. I then tried to shake myself, and succeeded in shaking my body. I seemed to have no limbs. I then looked at the barometer, and whilst doing so my head fell on my left shoulder.”
Mr. Glaisher subsequently quite lost consciousness, and “black darkness” came. While powerless he heard Mr. Coxwell speaking, and then the words, “Do try, now do.” Then sight slowly returned, and rousing himself, Mr. Glaisher said, “I have been insensible.” Mr. Coxwell replied, “You have, and I, too, very nearly.” Mr. Coxwell’s hands were black, and his companion had to pour brandy upon them. Mr. Coxwell’s situation was a perilous one. He had lost the use of his hands, which were frozen, and had to hang by his arms to the ring and drop into the car. He then perceived his friend was insensible, and found insensibility coming on himself. There was only one course to pursue—to pull the valve line and let the gas escape, so as to descend. But his hands were powerless! As a last resource he gripped the line with his teeth, and bending down his head, after many attempts succeeded in opening the valve and letting the gas escape. The descent was easily made, and accomplished in safety.

Some pigeons were taken up on this occasion, and were set free at different altitudes. The first, at three miles, “dropped as a piece of paper”; the second, at four miles, “flew vigorously round and round, apparently taking a dip each time”; a third, a little later, “fell like a stone.” On descending[Pg 304] a fourth was thrown out at four miles, and after flying in a circle, “alighted on the top of the balloon.” Of the remaining pair one was dead when the ground was gained, and the other recovered.
The observations noted are too numerous to be included here. Some, we have seen, were confirmed by subsequent aeronauts, and as we have mentioned them in former pages we need not repeat them. The results differed very much under different conditions, and it is almost impossible to decide upon any law. The direction of the wind in the higher and lower regions sometimes differed, sometimes was the same, and so on. The “Reports” of the British Association (1862-1866) will furnish full particulars of all Mr. Glaisher’s experiments.
We have scarcely space left to mention the parachutes or umbrella-like balloons which have occasionally been used. Its invention is traced to very early times; but Garnerin was the first who descended in a parachute, in 1797, and continued to do so in safety on many subsequent occasions. The parachute was suspended to a balloon, and at a certain elevation the voyager let go and came down in safety. He ascended once from London, and let go when 8,000 feet up. The parachute did not expand as usual, and fell at a tremendous rate. At length it opened out, and the occupier of the car came down forcibly, it is true, but safely. The form of the parachute is not unlike an umbrella opened, with cords attaching the car to the extremities of the “ribs,” the top of the basket car being fastened to the “stick” of the umbrella.
Mr. Robert Cocking invented a novel kind of parachute, but when he attempted to descend by it from Mr. Green’s balloon it collapsed, and the unfortunate voyager was dashed to pieces. His remains were found near Lee, in Kent. Mr. Hampton did better on Garnerin’s principle, and made several descents in safety and without injury.
The problem of flying in the air has attracted the notice of the Aeronautical Society, established in 1873, but so far without leading to practical results, though many daring and ingenious suggestions have been put forth in the “Reports.”
It is not within our province to do more than refer to the uses of the balloon for scientific purposes, but we may mention the services it was employed upon during the French war, 1870-71. The investment of Paris by the German army necessitated aerial communication, for no other means were available. Balloon manufactories were established, and a great number were made, and carried millions of letters to the provinces. Carrier-pigeons were used to carry the return messages to the city, and photography was applied to bring the correspondence into the smallest legible compass. The many adventures of the aeronauts are within the recollection of all. A few of the balloons never reappeared; some were carried into Norway, and beyond the French frontier in other directions. The average capacity of these balloons was 70,000 cubic feet.
Of course it will be understood how balloons are enabled to navigate the[Pg 305] air. The envelope being partly filled with coal-gas-heated air and hydrogen, is much lighter than the surrounding atmosphere, and rises to a height according as the density of the air strata diminishes. The density is less as we ascend, and the buoyant force also is lessened in proportion. So when the weight of the balloon and its occupants is the same as the power of buoyancy, it will come to a stand, and go no higher. It can also be understood that as the pressure of the outside becomes less, the expansive force of the gas within becomes greater. We know that gas is very compressible, and yet a little gas will fill a large space. Therefore, as the balloon rises, it retains its rounded form, and appears full even at great altitudes; but if the upper part were quite filled before it left the ground, the balloon would inevitably burst at a certain elevation when the external pressure of the air would be removed, unless an escape were provided. This escape is arranged for by a valve at the top of the balloon, and the lower part above the car is also left open very often, so that the gas can escape of itself. When a rapid descent is necessary, the top valve is opened by means of a rope, and the balloon sinks by its own weight. Mr. Glaisher advises for great ascensions a balloon of a capacity of 90,000 cubic feet, and only filled one-third of that capacity with gas. Six hundred pounds of ballast should be taken.

A very small quantity of ballast thrown away will make a great difference; a handful will raise the balloon many feet, and a chicken bone cast out occasions a rise of thirty yards. The ballast is carried in small bags, and consists of dry sand, which speedily dissipates in the air as it falls. By throwing out ballast the aeronaut can ascend to a great height—in fact, as high as he can go, the limit apparently for human existence being about seven miles, when cold and rarefied air will speedily put an end to existence.
It is a curious fact, that however rapidly the balloon may be travelling through the air, the occupants are not sensible of the motion. This, in part, arises from the impossibility of comparing it with other objects. We pass nothing stationary which would indicate the pace at which we travel. But the absence of oscillation is also remarkable; even a glass of water may be filled brim-full, and to such a level that the water is above the rim of the glass, and yet not a drop will fall. This experiment was made by M. Flammarion. When the aeronaut has ascended some distance the earth loses its flat appearance, and appears as concave as the firmament above. Guide ropes are usually attached to balloons, and as they rest upon the ground they relieve the balloon of the amount of weight the length trailing would cause. They thus act as a kind of substitute for ballast as the balloon is descending. Most of the danger of aerial travelling lies in the descent; and though in fine weather the aeronaut can calculate to a nicety where he will descend, on a windy day, he must cast a grapnel, which catches with an ugly jerk, and the balloon bounds and strains at her moorings.
Although many attempts have been made to guide balloons through the air, no successful apparatus has ever been completed for use. Paddles, sails, fans, and screws have all been tried, but have failed to achieve the desired end. Whether man will ever be able to fly we cannot of course say. In the present advancing state of science it may not be impossible ere long to supply human beings with an apparatus worked by electricity, perhaps, which will enable them to mount into the air and sustain themselves. But even the bird cannot always fly without previous momentum. A rook will run before it rises, and many other birds have to “get up steam,” as it were, before they can soar in the atmosphere. Eagles and such heavy birds find it very difficult to rise from the ground. We know that vultures when gorged cannot move at all, or certainly cannot fly away; and eagles take up their positions on high rocks, so that they may launch down on their prey, and avoid the difficulty of rising from the ground. They swoop down with tremendous momentum and carry off their booty, but often lose their lives from the initial difficulty of soaring immediately. We fear man’s weight will militate against his ever becoming a flying animal. When we obtain a knowledge of the atmospheric currents we shall no doubt be able to navigate our balloons; but until then—and the information is as yet very limited, and the currents themselves very variable—we must be content to rise and fall in the air, and travel at the will of the wind in the upper regions of the atmosphere.
CHAPTER XXIV.
CHEMISTRY.
INTRODUCTION.
WHAT CHEMISTRY IS—THE ELEMENTS—METALLIC AND NON-METALLIC—ATOMIC WEIGHT—ACIDS—ALKALIS—BASES—SALTS—CHEMICAL COMBINATION AND STUDY.
Chemistry is the science of phenomena which are attended by a change of the objects which produce them. We know that when a candle burns, or when wood is burned, or even a piece of metal becomes what we term “rusty,” that certain chemical changes take place. There is a change by what is termed chemical action. Rust on iron is not iron; it is oxide of iron. The oxygen of the air causes it. So we endeavour, by Chemistry, to find out the nature of various bodies, their changes, and the results.

In nature we have simple and compound bodies. The former are called Elements. We must not confuse these elements with the so-called elements—earth, air, fire, and water. These are really compound bodies. An element is a substance or a gas which is not composed of more than one constituent; it is itself—a compound of perfectly identical particles. Every “compound” body, therefore, must be made up of some of the elements, of which there are sixty-five. These bodies are divided into non-metallic and metallic elements, and all bodies are composed of them, or are these bodies[Pg 308] themselves. The list is as follows. The non-metallic elements are “metalloids.” We have omitted fractions from the weights, on which chemists differ.
TABLE OF ELEMENTS WITH THEIR CHEMICAL SYMBOLS AND COMBINING WEIGHTS.
| Name. | Symbols. | Atomic or Combining Weights. |
Derivation of Name. | |
|---|---|---|---|---|
| Oxygen | O | 16 | Gr. Oxus, acid; gennaō, to make. | |
| Hydrogen | Gaseous | H | 1 | Gr. Udor, water; gennaō, to make. |
| Nitrogen | N | 14 | Gr. Natron, nitre; gennaō, to make. | |
| Chlorine | Cl | 35 | Gr. Chloros, green. | |
| Iodine | Solid | I | 127 | Gr. Ioeides, violet. |
| Fluorine | F | 19 | Fluor spar, the mineral. | |
| Carbon | C | 12 | Lat. Carbo, coal. | |
| Sulphur | S | 32 | Lat. Sulphurium. | |
| Phosphorus | P | 31 | Gr. Phos, light; pherein, to carry. | |
| Arsenic* | As | 75 | Gr. Arsenicon, potent. | |
| Silicon | Si | 28 | Gr. Silex, flint. | |
| Boron | B | 11 | Gr. Borax, Arab., baraga, to shine. | |
| Selenium | Se | 79 | Gr. Selene, the moon. | |
| Tellurium | Te | 129 | Lat. Tellus, the earth. | |
| Bromine | Fluid | 80 | Gr. Bromos, offensive smell. |
METALS.
| Name. | Symbols. | Atomic or Combining Weights. |
Derivation of Name. |
|---|---|---|---|
| Aluminium | Al | 27 | Lat. Alumen, alum. |
| Antimony (Stibium) | Sb | 122 | Gr. Anti, against; minos, one. |
| [Arsenic] | As | 75 | (Not known.) |
| Barium | Ba | 137 | Gr. Barsù, heavy. |
| Bismuth | Bi | 210 | Ger. Weissmuth, white matter. |
| Cadmium | Cd | 112 | Gr. Cadmeia, calamite. |
| Cæsium | Cs | 133 | Lat. Cæsius, sky-blue. |
| Calcium | Ca | 40 | Lat. Calx, lime. |
| Cerium | Ce | 141 | The planet Ceres. |
| Chromium | Cr | 52 | Gr. Chroma, colour. |
| Cobalt | Co | 58 | Ger. Kobald, a sprite. |
| Copper | Cu | 63 | Lat. Cuprum (Cyprium), Cyprus. |
| Didymium | D | 147 | Gr. Didumos, twins. |
| Erbium | E | — | Ytterby in Sweden. |
| Gallium | Ga | 70 | (Not known.) |
| Glucinum | Gl | 9 | Gr. Glukos, sweet. |
| Gold | Au | 197 | From Hebrew, to shine (doubtful). |
| Indium | In | 113 | Indigo colour. |
| Iridium | Ir | 198 | Gr. Iris, rainbow. |
| Iron | Fe | 56 | Hebrew, to meet (doubtful). |
| Lanthanum | La | 139 | Gr. Lanthanein, to lie hid. |
| Lead | Pb | 207 | (Plumbum) malubodos (galena). |
| Lithium | Li | 7 | Gr. Lithos, stone. |
| Magnesium | Mg | 24 | Magnesia, Asia Minor. |
| [Pg 309]Manganese | Mn | 55 | Mangana, E. I. (or Magnesia). |
| Mercury | Hg | 200 | Heathen deity (quick). |
| Molybdenum | Mo | 96 | Gr. Molybdena, lead ore, like lead. |
| Nickel | Ni | 58 | Ger. Kupfer nikel, false copper. |
| Niobium (Columbium) | Nb | 94 | Columbite. |
| Osmium | Os | 199 | Osme, an odour. |
| Palladium | Pl | 106 | Pallas, Minerva. |
| Platinum | Pt | 197 | Spanish, platina, little silver. |
| Potassium (Kalium) | K | 39 | Potash. |
| Rhodium | Rh | 104 | Gr. Roda, rose. |
| Rubidium | Rb | 85 | Lat. Rubidus, red. |
| Ruthenium | Ru | 104 | (Not known.) |
| Silver (Argentum) | Ag | 108 | Hebrew, money. |
| Sodium (Natrium) | Na | 23 | Salsoda plant. |
| Strontium | Sr | 87 | Strontian, N.B. |
| Tantalum | Ta | 182 | Tantalite mineral. |
| Terbium | Tr | — | (Not known.) |
| Thallium | Tl | 204 | Gr. Thallos, green twig. |
| Thorium | Th | 230 | Thor, deity. |
| Tin (Stannum) | Sn | 118 | (Not known.) |
| Titanium | Ti | 50 | Titans. |
| Tungsten (Wolfram) | W | 184 | Swedish. |
| Uranium | U | 240 | Urania. |
| Vanadium | V | 51 | Vanadis, a goddess in Sweden, etc. |
| Yttrium | Y | 93 | (Not known.) |
| Zinc | Zn | 65 | Ger. Zinken, nails. |
| Zirconium | Zr | 89 | Ger. Zircon, four-cornered (Ceylon). |
| * Arsenic is sometimes considered a non-metallic and sometimes a metallic substance. | |||
The term “combining weight” requires a little explanation. We are aware that water, for instance, is made up of oxygen and hydrogen in certain proportions. This we will prove by-and-by. The proportions are in eighteen grains or parts of water, sixteen parts (by weight) of oxygen, and two parts (by weight) of hydrogen. These are the weights or proportions in which oxygen and hydrogen combine to form water, and such weights are always the same in these proportions. Chemical combination always occurs for certain substances in certain proportions which never vary in those compounds, and if we wish to extract oxygen from an oxide we must take the aggregate amount of the combining weights of the oxide, and we shall find the proportion of oxygen; for the compound always weighs the same as the sum of the elements that compose it. To return to the illustration of water. The molecule of water is made up of one atom of oxygen and two atoms of hydrogen. One atom of the former weighs sixteen times the atom of the latter. The weights given in the foregoing table are atomic weights, and the law of their proportions is called the Atomic Theory.
An atom in chemistry is usually considered the smallest quantity of matter that exists, and is indivisible. A molecule is supposed to contain two or more atoms, and is the smallest portion of a compound body. The[Pg 310] standard atom is hydrogen, which is put down as 1, because we find that when one part by weight of hydrogen is put in combination, it must have many more parts by weight of others to form a compound. Two grains of hydrogen, combining with sixteen of oxygen, makes eighteen of water, as we have already seen.
Take an example so plainly given by Professor Roscoe, remembering that the numbers in our table represent the fixed weight or proportion by weight in which the simple body combines. The red oxide of mercury contains sixteen parts by weight of oxygen to two hundred parts by weight of mercury (we see the same numbers in the table); these combined make two hundred and sixteen parts of oxide. So to obtain 16 lbs. of oxygen we must get 216 lbs. of the powder. It is the same all through, and it will be found by experiment that if any more parts than these fixed proportions be taken to form a compound, some of that element used in excess will remain free. Lime is made up of calcium and oxygen. We find calcium combining weight is forty, oxygen sixteen. Lime is oxide of calcium in these proportions (by weight).
When we wish to express the number of atoms in a compound we write the number underneath when more than one; thus water is H2O. Sulphuric acid H2SO4. As we proceed we will give the various formulæ when considering the chief elements.
In chemistry we have acids, alkalis, and salts, with metallic oxides, termed bases, or bodies, that when combined with acids form salts. Alkalis are bases.
Acids are compounds which possess an acid taste, impart red colour to vegetable blues, but lose their qualities when combined with bases. Hydrogen is present in all acids. There are insoluble acids. Silicic acid, for instance, is not soluble in water, has no sour taste, and will not redden the test litmus paper. On the other hand, there are substances (not acids) which possess the characteristics of acids, and most acids have only one or two of these characteristics.
Thus it has come to pass that the term “acid” has in a measure dropped out from scientific nomenclature, and salt of hydrogen has been substituted by chemists. For popular exposition, however, the term is retained.
Alkalis are bases distinguished by an alkaline taste. The derivation is from Arabic, al-kali. They are characterized by certain properties, and they change vegetable blues to green, and will restore the blue to a substance which has been reddened by acid. They are soluble in water, and the solutions are caustic in their effects. Potash, soda, and ammonia are alkalis, or chemically, the oxides of potassium, sodium, ammonium, lithium, and cæsium are all alkalis. Potash is sometimes called “caustic” potash. There are alkaline earths, such as oxides of barium, strontium, etc. Bases may be defined as the converse of acids.
Acids and alkalis are then evidently opposite in character, and yet they readily combine, and in chemistry we shall find that unlike bodies are very[Pg 311] fond of combining (just as opposite electricities attract each other), and the body made by this combination differs in its properties from its constituents.
Salts are composed of acids and bases, and are considered neutral compounds, but there are other bodies not salts, which likewise come under that definition—sugar, for instance. As a rule, when acids and alkalis combine salts are found.
Chemical phenomena are divided into two groups, called inorganic and organic, comprising the simple and compound aspects of the subject, the elementary substances being in the first, and the chemistry of animals or vegetables, or organic substances, in the latter. In the inorganic section we shall become acquainted with the elements and their combinations so often seen as minerals in nature. Chemical preparations are artificially prepared. To consider these elements we must have certain appliances, and indeed a laboratory is needed. Heat, as we have already seen, plays a great part in developing substances, and by means of heat we can do a great deal in the way of chemical decomposition. It expands, and thus diminishes cohesion; it counteracts the chemical attraction. Light and electricity also decompose chemical combinations. But before proceeding it will be as well to notice a few facts showing how Nature has balanced all things.
The earth, and its surrounding envelope, the atmosphere, consist of a number of elements, which in myriad combinations give us everything we possess,—the air we breathe, the water we drink, the fire that warms us, are all made up of certain elements or gases. Water, hydrogen and oxygen; air, oxygen and nitrogen. Fire is combustion evolving light and heat. Chemical union always evolves heat, and when such union proceeds very rapidly fire is the result.
In all these combinations we shall find when we study chemistry that not a particle or atom of matter is ever lost. It may change or combine or be “given off,” but the matter in some shape or way exists still. We may burn things, and rid ourselves, as we think, of them. We do rid ourselves of the compounds, the elements remain somewhere. We only alter the condition. During combustion, as in a candle or a fire, the simple bodies assume gaseous or other forms, such as carbon, but they do not escape far. True they pass beyond our ken, but nature is so nicely balanced that there is a place for everything, and everything is in its place under certain conditions which never alter. We cannot destroy and we cannot create. We may prepare a combination, and science has even succeeded in producing a form like the diamond—a crystal of carbon which looks like that most beautiful of all crystals, but we cannot make a diamond after all. We can only separate the chemical compounds. We can turn diamonds into charcoal it is true, but we cannot create “natural” products. We can take a particle of an element and hide it, or let it pass beyond our ken, and remain incapable of detection, but the particle is there all the time, and when we retrace our steps we shall find it as it was before.
This view of chemistry carries it as a science beyond the mere holiday[Pg 312] amusement we frequently take it to be. It is a grand study, a study for a lifetime. Nature is always willing, like a kind, good mother as she is, to render us up her secrets if we inquire respectfully and lovingly. The more we inquire the more we shall find we have to learn. In these and the following pages we can only tell you a few things, but no one need be turned away because he does not find all he wants. We never do get all we want in life, and there are many first-rate men—scientists—who would give “half their kingdom” for a certain bit of knowledge concerning some natural phenomena. There are numerous excellent treatises on chemistry, and exhaustive as they are, at present they do not tell us all. Let these popular pages lead us to the study of nature, and we shall find our labour far from onerous and full of interest, daily increasing to the end, when we shall know no more of earth, or chemistry.
As a preliminary we will put our workshop aside, and show you something of Chemistry without a Laboratory.

CHAPTER XXV.
CHEMISTRY WITHOUT A LABORATORY.
We have already pointed out the possibility of going through a course of physics without any special apparatus, we shall now endeavour to show our readers the method of performing some experiments in chemistry without a laboratory, or at any rate with only a few simple and inexpensive appliances. The preparation of gases, such as hydrogen, carbonic acid, and oxygen, is very easily accomplished, but we shall here point out principally a series of experiments that are not so much known. We will commence, for example, by describing an interesting experiment which often occurs in a course of chemistry. Ammoniacal gas combined with the elements of water is analogous to a metallic oxide which includes a metallic root, ammonium. This hypothetically composed metal may be in a manner perceived, since it is possible to amalgamate it with mercury by operating in the following manner:—We take a porcelain mortar, in which we pour a quantity of mercury, and then cut some thin strips of sodium, which are thrown into the mercury. By stirring it about with the pestle a loud cracking is produced, accompanied by a flame, which bears evidence to the union of the mercury and the sodium, and the formation of an amalgam of sodium. If this amalgam of sodium is put into a slender glass tube containing a concentrated solution of hydrochlorate of ammonia in water, we see the ammonia expand in an extraordinary manner, and spout out from the end of the tube, which is now too small to contain it, in the form of a metallic substance (fig. 302). In this case, the ammonium, the radical which exists in the ammoniacal salts, becomes amalgamated with the mercury, driving out the sodium with which it had previously been combined; the ammonium thus united with the mercury becomes decomposed in ammoniacal gas and hydrogen, the mercury assuming its ordinary form. Phosphate of ammonia is very valuable from its property of rendering the lightest materials, such as gauze or muslin, incombustible. Dip a piece of muslin in a solution of phosphate of ammonia, and dry it in contact with the air; that done, you will find it is impossible to set fire to the material; it will get charred, but you cannot make it burn. It is to be wished that this useful precaution were oftener taken in the matter of ball-dresses, which have so frequently been the cause of serious accidents. There is no danger whatever with a dress that[Pg 314] has been soaked in phosphate of ammonia, which is very inexpensive, and easily procured.

For preparing cool drinks in the summer ammoniacal salts are very useful; some nitrate of ammonia mixed with its weight in water, produces a considerable lowering of the temperature, and is very useful for making ice. Volatile alkali, which is so useful an application for stings from insects, is a solution of ammoniacal gas in water, and sal-volatile, which has such a refreshing and reanimating odour, is a carbonate of ammonia. We often see in chemists’ shops large glass jars, the insides of which are covered with beautiful transparent white crystals, which are formed over a red powder placed at the bottom of the vase. These crystals are the result of a combination of cyanogen and iodine. Nothing is easier than the preparation of iodide of cyanogen, a very volatile body, which possesses a strong tendency to assume a definite crystalline form. We pound in a mortar a mixture of 50 grams of cyanide of mercury, and 100 grams of iodine; under the action of the pestle the powder, which was at first a brownish colour, assumes a shade of bright vermilion red. The cyanogen combines with the iodine, and transforms itself into fumes with great rapidity. If the powder is placed at the bottom of a stoppered glass jar, the fumes of the iodide of cyanogen immediately condense, thereby producing beautiful crystals which often attain considerable size (fig. 303). Cyanogen forms with sulphur a remarkable substance, sulpho-cyanogen, the properties of which we cannot describe without exceeding the limits of our present treatise; we shall therefore confine ourselves to pointing out one of its combinations, which is well known at the present day, owing to its singular properties. This is sulpho-cyanide of mercury, with which small combustible cones are made, generally[Pg 315] designated by the pompous title of Pharaoh’s serpents. For making these, some sulpho-cyanide of potassium is poured into a solution of nitrate acid on mercury, which forms a precipitate of sulpho-cyanide of mercury. This is a white, combustible powder, which after passing through a filter, should be transformed into a stiff pulp by means of water containing a solution of gum. The pulp is afterwards mixed with a small quantity of nitrate of potash, and fashioned into cones or cylinders of about an inch and a quarter in length, which should be thoroughly dried. The egg thus obtained can be hatched by the simple application of a lighted match, and gives rise to the phenomenon. The sulpho-cyanide slowly expands, the cylinder increases in length, and changes to a yellowish substance, which dilates and extends to a length of twenty or five-and-twenty inches. It has the appearance of a genuine serpent, which has just started into existence, and stretches out its tortuous coils, endeavouring to escape from its narrow prison (fig. 304). The residue is composed partly of cyanide of mercury and of para-cyanogen; it constitutes a very poisonous substance, which should be immediately thrown away or burned. It can be easily powdered into dust in the fingers. During the decomposition of the sulpho-cyanide of mercury, quantities of sulphurous acid are thrown off, and it is to be regretted that Pharaoh’s serpent should herald his appearance by such a disagreeable, suffocating odour.


After these few preliminary experiments, we will endeavour to show the interest afforded by the study of chemistry in relation to the commonest substances of every-day life. We will first consider the nature of a few pinches of salt. We know that kitchen salt, or sea salt, is white or greyish, according to its degree of purity; that it has a peculiar flavour, is soluble[Pg 316] in water, and makes a peculiar crackling when thrown in the fire. But though its principal physical properties may be familiar enough, many people are entirely ignorant of its chemical nature and elementary composition. Kitchen salt contains a metal, combined with a gas possessing a very suffocating odour; the metal is sodium, the gas is chlorine. The scientific name for the substance is chloride of sodium (salt).19 The metal contained in common salt in no way resembles ordinary metals; it is white like silver, but tarnishes immediately in contact with air, and unites with oxygen, thus transforming itself into oxide of sodium. To preserve this singular metal it is necessary to protect it from the action of the atmosphere, and to keep it in a bottle containing oil of naptha. Sodium is soft, and it is possible with a pair of[Pg 317] scissors to cut it like a ball of soft bread that has been kneaded in the hand. It is lighter than water, and when placed in a basin of water floats on the top like a piece of cork; only it is disturbed, and takes the form of a small brilliant sphere; great effervescence is also produced as it floats along, for it reduces the water to a common temperature by its contact. By degrees the small metallic ball disappears from view, after blazing into flame (fig. 305).

This remarkable experiment is very easy to carry out, and sodium is now easily procured at any shop where chemicals are sold. The combustion of sodium in water can be explained in a very simple manner. Water, as we know, is composed of hydrogen and oxygen. Sodium, by reason of its great affinity for the latter gas, combines with it, and forms a very soluble oxide; the hydrogen is released and thrown off, as we shall perceive by placing a lighted match in the jar, when the combustible gas ignites.
Oxide of sodium has a great affinity for water; it combines with it, and absorbs it in great quantities. It is a solid, white substance, which burns and cauterizes the skin; it is also alkaline, and brings back the blue colour to litmus paper that has been reddened by acids.
Sodium combines easily also with chlorine. If plunged into a jar containing this gas it is transformed into a substance, which is sea salt. If the chlorine is in excess a part of the gas remains free, for simple substances do not mingle in undetermined ratios; they combine, on the contrary, in very definite proportions, and 35·5 gr. of dry chlorine always unites with the same quantity of soda equal to 23 grams. A gram of kitchen salt is formed, therefore, of 0·606 gr. of chlorine, and 0·394 gr. of sodium. Besides sea salt, there are a number of different salts which may be made the object of curious experiments. We know that caustic soda, or oxide of sodium, is an alkaline product possessing very powerful properties; it burns the skin, and destroys organic substances.
Sulphuric acid is endowed with no less powerful properties; if a little is dropped on the hand it produces great pain and a sense of burning; a piece of wood plunged into this acid is almost immediately carbonized. If we mix forty-nine grams of sulphuric acid and thirty-one grams of caustic soda a very intense reaction is produced, accompanied by a considerable elevation of temperature; after it has cooled we have a substance which can be handled with impunity; the acid and alkali have combined, and their properties have been reciprocally destroyed. They have now originated a salt which is sulphate of soda. This substance exercises no influence on litmus paper, and resembles in no way the substances from which it originated.
There are an infinite number of salts which result in like manner from the combination of an acid with an alkali or base. Some, such as sulphate[Pg 318] of copper, or chromate of potash, are coloured; others, like sulphate of soda, are colourless. The last-mentioned salt, with a number of others, will take a crystalline form; if dissolved in boiling water, and the solution left to stand, we shall perceive a deposit of transparent prisms of very remarkable appearance. This was discovered by Glauber, and was formerly called Glauber’s salts.

Sulphate of soda is very soluble in water, and at a temperature of thirty-three (Centigr.) water can dissolve it in the greatest degree. If we pour a layer of oil on a solution saturated with Glauber’s salts, and let it stand, it will not produce crystals; but if we thrust a glass rod through the oil into contact with the solution, crystallization will be instantaneous. This singular phenomenon becomes even more striking when we put the warm concentrated solution into a slender glass tube, A B, which we close after having driven out the air by the bubbling of the liquid (fig. 306). When the tube has been closed, the crystals of sulphate of soda will not form, even with the temperature at zero; nevertheless the salts, being less soluble cold than hot, are found in the fluid in a proportion ten times larger than they would contain under ordinary conditions. If the end of the tube be broken the salt will crystallize immediately. We will describe another experiment, but little known and very remarkable, which exhibits in a striking manner the process of instantaneous crystallizations. Let one hundred and fifty parts of hyposulphite of soda be dissolved in fifteen parts of water, and the solution slowly poured into a test-glass, previously warmed by means of boiling water, until the vessel is about half-full. One hundred parts of acetate of soda is then dissolved in fifteen parts of water, and poured slowly into the first solution, so that they form two layers perfectly distinct from each other. The two solutions are then covered with a little boiling water, which, however is not represented in our illustration. After it has been left to stand[Pg 319] and cool slowly, we have two solutions of hyposulphite of soda and acetate of soda superposed on each other. A thread, at the end of which is fixed a small crystal of hyposulphite of soda, is then lowered into the test-glass; the crystal passes through the solution of acetate without disturbing it, but it has scarcely reached the lower solution of hyposulphite than the salt crystallizes instantaneously. (See the test-glass on the left of fig. 307.) We then lower into the upper solution a crystal of acetate of soda, suspended from another thread. This salt then crystallizes also. (See experiment glass on the right of fig. 307.) This very successful experiment is one of the most remarkable belonging to the subject of instantaneous crystals. The successive appearance of crystals of hyposulphite of soda, which take the form of large, rhomboidal prisms, terminating at the two extremities with an oblique surface, and the crystals of acetate of soda, which have the appearance of rhomboidal, oblique prisms, cannot fail to strike the attention and excite the interest of those who are not initiated into these kinds of experiments.

Another remarkable instantaneous crystallization is that of alum. If we leave standing a solution of this salt it gradually cools, at the same time becoming limpid and clear. When it is perfectly cold, if we plunge into it a small octahedral crystal of alum suspended from a thread, we perceive that crystallization instantly commences on the surface of the small crystal; it rapidly and perceptibly increases in size, until it nearly fills the whole jar.
Common Metals and Precious Metals.
How many invalids have swallowed magnesia without suspecting that this powder contains a metal nearly as white as silver, and is malleable, and capable of burning with so intense a light that it rivals even the electric light in brilliancy! If any of our readers desire to prepare magnesium themselves it can be done in the following manner:—Some white magnesia must be obtained from the chemist, and after having been calcined, must be submitted to the influence of hydrochloric acid and hydrochlorate of ammonia. A clear solution will thus be obtained, which by means of evaporation under the influence of heat, furnishes a double chloride, hydrated and crystallised. This chloride, if heated to redness in an earthenware crucible, leaves as a residue a nacreous product, composed of micaceous, white scales, chloride of anhydrous magnesium.

If six hundred grams of this chloride of magnesium are mixed with one hundred grams of chloride of sodium, or kitchen salt, and the same quantity of fluoride of calcium and metallic sodium in small fragments, and the mixture is put into an earthenware crucible made red-hot, and heated for a quarter of an hour under a closed lid, we shall find on pouring out the fluid on to a handful of earth, that we have obtained instead of scoria, forty-five grams of metallic magnesium. The metal thus obtained is impure, and to remove all foreign substances it must be heated in a charcoal tube, through which passes a current of hydrogen.
Magnesium is now produced in great abundance, and is very inexpensive. It is a metal endowed with a great affinity for oxygen, and it is only necessary to thrust it into the flame of a candle to produce combustion; it burns with a brightness that the eye can scarcely tolerate, and is transformed[Pg 321] into a white powder—oxide of magnesium, or magnesia. Combustion is still more active in oxygen, and powder of magnesium placed in a jar filled with this gas produces a perfect shower of fire of very beautiful effect. To give an idea of the lighting power of magnesium, we may add that a wire of this metal, which is 29/100 of a millimetre in diameter, produces by combustion a light equal to that of seventy-four candles.

The humble earth of the fields—the clay which is used in our potteries, also contains aluminium, that brilliant metal which is as malleable as silver, and unspoilable as gold. When clay is submitted to the influence of sulphuric acid and chloride of potassium, we obtain alum, which is a sulphate of alumina and potash. Alum is a colourless salt, which crystallizes on the surface of water in beautiful octahedrons of striking regularity. Fig. 308 represents a group of alum crystals. This salt is much used in the colouring of fabrics; it is also used for the sizing of papers, and the clarification of tallow. Doctors also use it as an astringent and caustic substance. When alum is submitted to the action of heat in an earthenware crucible, it loses the water of crystallization which it contains, and expands in a singular manner, overflowing from the jar in which it is calcined (fig. 309).

Iron, the most important of common metals, rapidly unites with oxygen, and, as we know, when a piece of this metal is exposed to the influence of damp air, it becomes covered with a reddish substance. In the well-known experiment of the formation of rust, the iron gradually oxidises without its temperature rising, but this combination of iron with oxygen is effected much more rapidly under the influence of heat. If, for example, we redden at the fire a nail attached to a wire, and give it a movement of rotation as of a sling, we see flashing out from the metal a thousand bright sparks due to the combination of iron with oxygen, and the formation of an oxide. Particles of iron burn spontaneously in contact with air, and this property for many[Pg 322] centuries has been utilized in striking a tinder-box; that is to say, in separating, by striking a flint, small particles of iron, which ignite under the influence of the heat produced by the friction. We can prepare iron in such atoms that it ignites at an ordinary temperature by simple contact with the air. To bring it to this state of extreme tenuity, we reduce its oxalate by hydrogen. We prepare an apparatus for hydrogen as shown in fig. 310, and the gas produced at A is passed through a desiccative tube, B, and finally reaches a glass receptacle, C, in which some oxalate of iron is placed. The latter salt, under the combined influence of hydrogen and heat, is reduced to metallic iron, which assumes the appearance of a fine black powder. When the experiment is completed the glass vessel is closed, and the iron, thus protected from contact with the air, can be preserved indefinitely; but if it is exposed to the air by breaking off the end of the receptacle (fig. 311), it ignites immediately, producing a shower of fire of very beautiful effect. Iron thus prepared is known under the name of pyrophoric iron. Iron is acted upon in a very powerful manner by most acids. If some nitric acid is poured on iron nails, a stream of red, nitrous vapour is let loose, and the oxidised iron is dissolved in the liquid to the condition of nitrate of iron. This experiment is very easy to perform, and it gives an idea of the energy of certain chemical actions. We have endeavoured to represent its appearance in fig. 312. Fuming nitric acid does not act on iron, and prevents it being attacked by ordinary nitric acid. This property has given rise to a very remarkable experiment on passive iron. It consists in placing some nails in a glass, into which some fuming nitric acid is poured, which produces no result; the fuming acid is then taken out, and is replaced by ordinary nitric acid, which no longer acts on the iron rendered passive by the smoking acid. After[Pg 323] this, if the nails are touched by a piece of iron, which has not undergone the action of nitric acid, they are immediately acted upon, and a giving off of nitrous vapour is manifested with great energy. Lead is a very soft metal, and can even be scratched by the nails. It is also extremely pliable, and so entirely devoid of elasticity that when bent it has no tendency whatever to return to its primitive form. Lead is heavy, and has a density represented by 11·4; that is to say, the weight of a quart of water being one kilogram, that of the same volume of lead is 11·400 k.

Fig. 313 represents cylindrical bars of the best known metals, all weighing the same, showing their comparative density.

Lead, like tin, is capable of taking a beautiful crystalline form when placed in solution by a metal that is less oxydisable. The crystallization of lead, represented in fig. 314, is designated by the name of the Tree of Saturn. This is how the experiment is produced: Thirty grams of acetate of lead are dissolved in a quart of water, and the solution is poured into a vase of a spherical shape. A stopper for this vase is made out of a piece of zinc, to which five or six separate brass wires are attached; these are plunged into the fluid, and we see the wires become immediately covered with brilliant crystallized spangles of lead, which continue increasing in size.
The alchemists, who were familiar with this experiment, believed that it consisted in a transformation of copper into lead, while in reality it only[Pg 324] consists in the substitution of one metal for another. The copper is dissolved in the liquid, and is replaced by the lead, but no metamorphosis is brought about. We may vary at will the form of the vase or the arrangement of the wire; thus it is easy to form letters, numbers, or figures, by the crystallization of brilliant spangles.

Copper, when it is pure, has a characteristic red colour, which prevents it being confounded with any other metal; it dissolves easily in nitric acid, and with considerable effervescence, giving off vapour very abundantly. This property has been put to good use in engraving with aqua fortis. A copper plate is covered with a layer of varnish, and when it is dry some strokes are made on it by means of a graver; if nitric acid is poured on the plate when thus prepared, the copper is only acted on in the parts that have been exposed by the point of steel. By afterwards removing the varnish, we have an engraved plate, which will serve for printing purposes.

Among experiments that may be attempted with common metals, we may mention that in which salts of tin are employed. Tin has a great tendency to assume a crystalline form, and it will be easy to show this property by an interesting experiment. A concentrated solution of proto-chloride of tin, prepared by dissolving some metallic tin in hydrochloric acid, is placed in a test glass; then a rod of tin is introduced, as shown in fig. 315. Some water is next slowly poured on the rod, so that it gradually trickles down, and prevents the mingling of the proto-chloride of tin. The vessel is then left to stand, and we soon see brilliant crystals starting out from the rod. This crystallization is not effected in the water; it is explained by an electric influence, into the details of which we cannot enter without overstepping our limits; it is known as “Jupiter’s Tree.” It is well known that alchemists, with their strange system of nomenclature, believed there was a certain mysterious relation between the seven metals then known and the seven planets; each metal was dedicated to a planet; tin was called Jupiter; silver,[Pg 325] Luna; gold, Sol; lead, Saturn; iron, Mars; quicksilver, Mercury; and copper, Venus. The crystallization of tin may be recognised also by rubbing a piece of this metal with hydrochloric acid; the fragments thus rubbed off exhibit specimens of branching crystals similar to the hoar-frost which we see in severe winter weather. If we bend a rod of tin in our hands the crystals break, with a peculiar rustling sound.
When speaking of precious metals, we may call to mind that the alchemists considered gold as the king of metals, and the other valuable ones as noble metals. This definition is erroneous, if we look upon the useful as the most precious; for, in that case, iron and copper would be placed in the first rank. If gold were found abundantly on the surface of the soil, and iron was extremely rare, we should seek most eagerly for this useful metal, and should despise the former, with which we can neither make a ploughshare nor any other implement of industry. Nevertheless, the scarcity of gold, its beautiful yellow colour, and its unalterability when in contact with air, combine to place it in the first rank in the list of precious metals. Gold is very heavy; its density is represented by the figure 19·5. It is the most malleable and the most ductile of metals, and can be reduced by beating to such thin sheets that ten thousand can be laid, one over the other, to obtain the thickness of a millimetre. With a grain of gold a thread may be manufactured extending a league in length, and so fine that it resembles a spider’s web. When gold is beaten into thin sheets it is no longer opaque; if it is fastened, by means of a solution of gum, on to a sheet of glass, the light passes right through it, and presents a very perceptible green shade. Gold is sometimes found scattered in sand, in a condition of impalpable dust, and, in certain localities, in irregular lumps of varying size, called nuggets. Gold is the least alterable of the metals, and can be exposed, indefinitely, to the contact of humid atmosphere without oxidizing. It is not acted on by the most powerful acids, and only dissolves in a mixture of nitric acid and hydrochloric acid. We can prove that gold resists the influence of acids by the following operation:—
Some gold-leaf is placed in two small phials, the first containing hydrochloric acid, and the second nitric acid. The two vessels are warmed on the stove, and whatever the duration of the ebullition of the acids, the gold-leaf remains intact, and completely resists their action. If we then empty the contents of one phial into the other, the hydrochloric and nitric acids are mixed, and we see the gold-leaf immediately disappear, easily dissolved by the action of the liquid (aqua regia). Gold also changes when in contact with mercury; this is proved by suspending some gold-leaf above the surface of this liquid (fig. 316); it quickly changes, and unites with the fumes of the mercury, becoming of a greyish colour.
Silver is more easily affected than gold, and though so white when fused, tarnishes rapidly in contact with air. It does not oxidize, but sulphurizes under the influence of hydro-sulphuric emanations. Silver does not combine directly with the oxygen of the atmosphere; but under[Pg 326] certain conditions it can dissolve great quantities of this gas. If it is fused in a small bone cupel, in contact with the air, and left to cool quickly, it expands in a remarkable manner, and gives off oxygen.

Nitric acid dissolves silver very easily, by causing the formation of abundant fumes. When the solution evaporates, we perceive white crystals forming, which are nitrate of silver. This fused nitrate of silver takes the name of lunar caustic, and is employed in medicine. Nitrate of silver is very poisonous; it possesses the singular property of turning black under the action of the sun’s rays, and is used in many curious operations in photography. It is also employed in the manufacture of dyes for the hair; it is applied to white hair with gall-nut, and under the influence of the light it turns black, and gives the hair a very dark shade. Salts of silver in solution with water have the property of forming a precipitate under the influence of chlorides, such as sea salt. If a few grains of common salt are thrown into a solution of nitrate of silver, it forms an abundant precipitate of chloride of silver, which blackens in the light. This precipitate, insoluble in nitric acid, dissolves very easily in ammonia.
Platinum, which is the last of the precious metals that we have to consider, is a greyish-white colour, and like gold is only affected by a mixture of nitric acid and hydrochloric acid. It is the heaviest of all the[Pg 327] ordinary metals; its density is 21·50. It is very malleable and ductile, and can be beaten into very thin sheets, and into wires as slender as wires of gold. Platinum wires have even been made so fine that the eye can scarcely perceive them; these are known as Wollaston’s invisible wires. Platinum resists the action of the most intense fire, and we can only fuse it by means of a blow-pipe and hydro-oxide gas. Its inalterability and the resistance it opposes to fire render it very valuable for use in the laboratory. Small crucibles are made of it, which are used by chemists to calcine their precipitates in analytical operations, or to bring about reactions under the influence of a high temperature. Platinum may be reduced to very small particles; it then takes the form of a black powder. In this pulverulent condition it absorbs gases with great rapidity, to such an extent that a cubic centimetre can condense seven hundred and fifty times its own volume of hydrogen gas. It also condenses oxygen, and in a number of cases acts as a powerful agent. Platinum is also obtained in porous masses (“spongy platinum”), which produce phenomena of oxidation.

A very ingenious little lamp may be constructed which lights of itself without the help of a flame. It contains a bell of glass, which is filled with hydrogen gas, produced by the action exercised by a foundation of zinc on acidulated water. If the knob on the upper part of the apparatus is pressed, the hydrogen escapes, and comes in contact with a piece of spongy platinum, which, acting by oxidation, becomes ignited. The flame produced sets fire to a small oil lamp, which is opposite the jet of gas. This very ingenious lamp is known under the name of Gay-Lussac’s lamp. Platinum can also produce, by mere contact, a great number of chemical reactions. Place in a test glass an explosive mixture formed of two volumes of hydrogen and one volume of oxygen; in this gas plunge a small piece of spongy platinum,[Pg 328] and the combination of the two bodies will be instantly brought about, making a violent explosion. Make a small spiral of platinum red-hot in the flame of a lamp, having suspended it to a card; then plunge it quickly into a glass containing ether, and you will see the metallic spiral remain red for some time, while in the air it would cool immediately. This phenomenon is due to the action of oxidation which the platinum exercises over the fumes of ether. This curious experiment is known under the name of the lamp without a flame. This remarkable oxidizing power of platinum, which has not yet been explained, was formerly designated by the title of catalytic action. But a phrase is not a theory, and it is always preferable to avow one’s ignorance than to simulate an apparent knowledge. Science is powerful enough to be able to express her doubts and uncertainties boldly. In observing nature we find an experience of this, and often meet with facts which may be put to profit, and become useful in application; nevertheless it is often the case that the why and the wherefore will for a long time escape the most penetrating eye and lucid intelligence. It is true the admirable applications of science strike us with the importance of their results, and the wonderful inventions they originate; but if they turn to account the observed facts of nature, what do they teach us as to the first cause of all things, the wherefore of nature?—Almost nothing. We must humbly confess our powerlessness, and say with d’Alembert: “The encyclopædia is very abundant, but what of that if it discourses of what we do not understand?”

Artificial Colouring of Flowers.
In a course of chemistry, the action exercised by sulphurous acid on coloured vegetable matter is proved by exposing violets to the influence of this gas, which whitens them instantaneously. Sulphurous acid, by its dis-oxidating properties, destroys the colour of many flowers, such as roses, periwinkles, etc. The experiment succeeds very readily by means of the little apparatus which we give in fig. 317. We dissolve in a small vessel some sulphur, which ignites in contact with air, and gives rise, by its combination with oxygen, to sulphurous acid; the capsule is covered with a conical chimney, made out of a thin sheet of copper, and at the opening at the top the flowers that are to be discoloured are placed. The action is very rapid, and a few seconds only are necessary to render roses, periwinkles, and violets absolutely white.

M. Filpol, a distinguished savant, has exhibited to the members of the Scientific Association, Paris, the results which he obtained by subjecting flowers to the influence of a mixture of sulphuric ether and some drops of ammonia; he has shown that, under the influence of this liquid, a great number of violets or roses turn a deep green. We have recently made on this subject a series of experiments which we will here describe, and which may be easily attempted by those of our readers who are interested in the[Pg 330] question. Some common ether is poured into a glass, and to it is added a small quantity of liquid ammonia (about one-tenth of the volume). The flowers with which it is desired to experiment are then plunged into the fluid (fig. 318). A number of flowers, whose natural colour is red or violet, take instantaneously a bright green tint; these are red geranium, violet, periwinkle, lilac, red and pink roses, wall-flower, thyme, small blue campanula, fumeter, myosotis, and heliotrope. Other flowers, whose colours are not of the same shade, take different tints when in contact with ammoniacal ether. The upper petal of the violet sweet-pea becomes dark blue, whilst the lower petal turns a bright green colour. The streaked carnation becomes brown and bright green. White flowers generally turn yellow, such as the white poppy, the variegated snow-dragon, which becomes yellow and dark violet, the white rose, which takes a straw colour, white columbine, camomile, syringa, white daisy, potatoe blossom, white julian, honeysuckle, and white foxglove, which in contact with ammoniacal ether assume more or less deep shades of yellow. White snap-dragon becomes yellow and dark orange. Red geranium turns blue in a very remarkable fashion; with the monkey-flower the ammoniacal ether only affects the red spots, which turn a brownish green; red snap-dragon turns a beautiful brown; valerian takes a shade of grey; and the red corn-poppy assumes a dark violet. Yellow flowers are not changed by ammoniacal ether; buttercups, marigolds, and yellow snap-dragon preserve their natural colour. Leaves of a red colour are instantly turned green when placed in contact with ammoniacal ether. The action of this liquid is so rapid that it is easy to procure green spots by pouring here and there a drop of the solution. In like manner violet flowers, such as periwinkles, can be spotted with white, even without gathering them. We will complete our remarks on this subject with a description of experiments performed by M. Gabba in Italy by means of ammonia acting on flowers. M. Gabba simply used a plate, in which he poured a certain quantity of solution of ammonia. He placed on the plate a funnel turned upside down, in the tube of which he arranged the flowers on which he wished to experiment. He then found that under the influence of the ammonia the blue, violet, and purple flowers became a beautiful green, red flowers black, and white yellow, etc.
The most singular changes of colour are shown by flowers which are composed of different tints, their red streaks turning green, the white yellow, etc. Another curious example is that of red and white fuchsias, which, through the action of ammonia, turn yellow, blue, and green. When flowers have been subjected to these changes of colour, and afterwards plunged into pure water, they preserve their new tint for several hours, after which they gradually return to their natural colour. Another interesting observation, due to M. Gabba, is that asters, which are naturally inodorous, acquire an agreeable aromatic odour under the influence of ammonia. Asters of a violet colour become red when wetted with nitric acid mixed with water. On the other hand, if these same flowers are enclosed in a wooden box, where they[Pg 331] are exposed to the fumes of hydrochloric acid, they become, in six hours’ time, a beautiful red colour, which they preserve when placed in a dry, shady place, after having been properly dried. Hydrochloric acid has the effect of making flowers red that have been rendered green by the action of ammonia, and also alters their appearance very sensibly. We may also mention, in conclusion, that ammonia, combined with ether, acts much more promptly than when employed alone.
Phosphorescence.
Artificial flowers are frequently to be seen prepared in a particular manner, which have the property of becoming phosphorescent in darkness, when they have been exposed to the action of a ray of light, solar or electric. These curious chemical objects are connected with some very interesting phenomena and remarkable experiments but little known at the present time, to which we will now draw the reader’s attention.
The faculty possessed by certain bodies of emitting light when placed in certain conditions, is much more general than is usually supposed.
M. Edmond Becquerel, to whom we owe a remarkable work on this subject, divides the phenomena of phosphorescence into five distinct classes:
1. Phosphorescence through elevation of temperature. Among the substances which exhibit this phenomenon in a high degree we may mention certain diamonds, coloured varieties of fluoride of calcium, some minerals; and sulphur, known under the name of artificial phosphorus, when it has previously been exposed to the action of the light.
2. Phosphorescence through mechanical action. This is to be observed when we rub certain bodies together, or against a hard substance. If we rub together two quartz crystals in the dark, we perceive red sparks; and when pounding chalk or sugar, there is also an emission of sparks.
3. Phosphorescence through electricity. This is manifested by the light accompanying disengagement of electricity, and when gases and rarefied vapours transmit electric discharges.
4. Spontaneous Phosphorescence is observed, as every one knows, in connection with several kinds of living creatures,—glow-worms, noctilucids, etc., and similar phosphorescent effects are produced also with organic substances, animal or vegetable, before putrefaction sets in. It is manifested also at the flowering time of certain plants, etc.
5. Phosphorescence through insolation and the action of light. “It consists,” says M. Edmond Becquerel, “in exposing for some instants to the action of the sun, or to that of rays emanating from a powerful luminous source, certain mineral or organic substances, which immediately become luminous, and shine in the dark with a light, the colour and brilliancy of which depend on their nature and physical character; the light gradually diminishes in intensity during a period varying from some seconds to several hours. When these substances are exposed anew to the action of light, the same effect is[Pg 332] reproduced. The intensity of the light emitted after insolation is always much less than that of the incidental light.” These phenomena appear to have been first observed with precious stones; then, in 1604, in calcined Bologna stone, and later, in a diamond by Boyle, in 1663; in 1675 it was noticed in Baudoin phosphorus (residuum of the calcination of nitrate of lime), and more recently still in connection with other substances which we will mention. The substances most powerfully influenced by the action of light are sulphates of calcium and barium, sulphate of strontium, certain kinds of diamonds, and that variety of fluoride of calcium, which has received the name of chlorophane.

Phosphorescent sulphate of calcium is prepared by calcining in an earthenware crucible a mixture of flowers of sulphur and carbonate of lime. But the preparation only succeeds with carbonate of lime of a particular character. That obtained from the calcination of oyster shells produces very good results. Three parts of this substance is mixed with one part of flowers of sulphur, and is made red-hot in a crucible covered in from contact with the air. The substance thus obtained gives, after its insolation, a yellow light in the dark. The shells of oysters, however, are not always[Pg 333] pure, and the result is sometimes not very satisfactory; it is therefore better to make use of some substance whose composition is more to be relied on.
“When we desire to prepare a phosphorescent sulphate with lime, or carbonate of lime,” says M. E. Becquerel, “the most suitable proportions are those which in a hundred parts of the substance are composed of eighty to a hundred of flowers of sulphur in the first case, and forty-eight to a hundred in the second, that is, when we employ the quantity of sulphur which will be necessary for burning with carbonate of lime to produce a monosulphate.20 It is necessary to have regard to the elevation of the temperature in the preparation. By using lime procured from arragonite, and reducing the temperature below five hundred degrees for a sufficient time for the reaction between the sulphur and lime to take place, the excess of sulphur is eliminated, and we have a feebly luminous mass, of a bluish tint; if this mass is raised to a temperature of eight hundred or nine hundred degrees, it will exhibit a very bright light.”
Sulphate of calcium possesses different phosphorescent properties according to the nature of the salt which has served to produce the carbonate of lime employed. If we transform marble into nitrate of lime, by dissolving it in water and nitric acid, and form a precipitate with carbonate of ammonium, and use the carbonate of lime thus obtained in the preparation of sulphate of calcium, we have a product which gives a phosphorescence of a violet-red colour. If the carbonate of lime used is obtained from chloride of calcium precipitated by carbonate of ammonia, the phosphorescence is yellow. If we submit carbonate of lime, prepared with lime water and carbonic acid, to the influence of sulphur, we obtain a sulphur giving a phosphorescent light of very pure violet. Carbonate of lime obtained by forming a precipitate of crystallized chloride of calcium with different alkaline carbonates also gives satisfactory results.
Luminous sulphates of strontium may be obtained, like those of calcium, by the action of sulphur on strontia or the carbonate of this base, by the reduction of sulphates of strontia with charcoal. Blue and green shades are the most common. Sulphates of barium also present very remarkable phenomena of phosphorescence; but to obtain very luminous intensity a higher temperature is needed than with the other substances mentioned, and we have the same result when we reduce native sulphate of baryta with charcoal; that is to say, when the reaction takes place which produces the phosphorus formerly known as phosphorus of Bologna. Preparations obtained from baryta have a phosphorescence varying from orange-red to green.
The preparation of such substances as we have just enumerated afford an easy explanation of the method of manufacturing the luminous flowers which we described at the commencement of this chapter. We obtain some artificial flowers, cover them with some liquid gum, sprinkle with phosphorescent sulphur, and let them dry. The pulverulent matter then adheres to them securely, and it is only necessary to expose the flowers[Pg 334] thus prepared to the light of the sun, or the rays emanating from magnesium wire in a state of combustion (fig. 319), to produce immediate phosphorescent effects. If taken into a dark room (fig. 320) they shine with great brilliancy, and give off very exquisite coloured rays. Phosphorescent sulphates are used also in tracing names or designs on a paper surface, etc., and it can easily be conceived that such experiments may be infinitely varied according to the pleasure of the experimenter.

But let us ask ourselves if these substances are not capable of being put to more serious uses, and of being classed among useful products. To this we can reply very decidedly in the affirmative. With phosphorescent matter we can obtain luminous faces for clocks placed in dark, obscure spots, and it is not impossible to use it for making sign-boards for shops, or numbers of houses, which can be lit up at night. Professor Norton even goes so far as to propose in the “Journal of the Franklin Institute,” not only coating the walls of rooms with these phosphorescent substances, but also the fronts of houses, when he considers it would be possible to do away entirely with street lights, the house-fronts absorbing sufficient light during the day to remain luminous the whole of the night.
Chemistry Applied to Sleight of Hand.
While physics has provided the species of entertainment called “sleight of hand” with a number of interesting effects, chemistry has only offered it very feeble contributions. Robert Houdin formerly made use of electricity to move the hands of his magic clock, and the electric magnet in making an iron box so heavy instantaneously that no one could lift it. Robin has made use of optics to produce the curious spectacle of the decapitated man, spectres, etc. Those persons who are fond of this kind of amusement may, however, borrow from chemistry some original experiments, which can be easily undertaken, and I will conclude this chapter by describing a juggling feat which I have seen recently executed before a numerous audience by a very clever conjuror.

The operator took a glass that was perfectly transparent, and placed it on a table, announcing that he should cover the glass with a saucer, and then, retiring to some distance, would fill it with the smoke from a cigarette. And this he carried out exactly, standing smoking his cigarette in the background, while the glass, as though by enchantment, slowly filled with the fumes of the smoke. This trick is easily accomplished. It is only necessary to pour previously into the glass two or three drops of hydrochloric acid, and to moisten the bottom of the saucer with a few drops of ammonia. These two liquids are unperceived by the spectators, but as soon as the saucer is placed over the glass, they unite in forming white fumes of hydrochlorate of ammonia, which bear a complete resemblance to the smoke of tobacco.
This experiment excited the greatest astonishment among the spectators present on the occasion, but understanding something of chemistry myself, I easily guessed at the solution of the mystery. The same result is obtained in a course of chemistry in a more simple manner, and without any attempt at trickery, by placing the opening of a bottle of ammonia against the opening of another bottle containing hydrochloric acid.

CHAPTER XXVI.
CHEMISTRY AND ALCHEMY—CHEMICAL COMBINATIONS—THE ATMOSPHERIC AIR.
We have in the foregoing pages given some experiments, and considered several of the metals, but there are numerous very interesting subjects still remaining; indeed, the number is so great that we can only pick and choose. All people are desirous to hear something of the atmosphere, of water, and the earth; and as we proceed to speak of crystals and minerals, and so on to geology, we shall learn a good deal respecting our globe—its conformation and constituents. But the atmospheric air must be treated of first. This will lead us to speak of oxygen and nitrogen. Water will serve to introduce hydrogen with a few experiments, and thus we shall have covered a good deal of ground on our way towards various other elements in daily use and appreciation. Now let us begin with a few words concerning Chemistry itself.
At the very outset we are obliged to grope in the dark after the origin of this fascinating science. Shem, or “Chem,” the son of Noah, has been credited with its introduction, and, at any rate, magicians were in Egypt in the time of Moses, and the lawgiver is stated by ancient writers to have gained his knowledge from the Egyptians. But we need not pursue that line of argument. In more modern times the search for the Philosopher’s Stone and the Elixir of Life, which respectively turned everything to gold, and bestowed long life upon the fortunate finder, occupied many people, who in their researches no doubt discovered the germs of the popular science of Chemistry in Alchemy, while the pursuit took a firm hold of the popular imagination for centuries; and even now chemistry is the most favoured science, because of its adaptability to all minds, for it holds plain and simple truths for our every-day experience to confirm, while it leads us step by step into the infinite, pleasing us with experiments as we proceed.
Alchemy was practised by numerous quacks in ancient times and the Middle Ages, but all its professors were not quacks. Astrology and alchemy were associated by the Arabians. Geber was a philosopher who devoted[Pg 337] himself entirely to alchemy, and who lived in the year 730 A.D. He fancied gold would cure all disease, and he did actually discover corrosive sublimate, nitric acid, and nitrate of silver. To give even a list of the noted alchemists and magicians would fill too much space. Raymond Sully, Paracelsus, Friar Bacon, Albertus Magnus, Thomas Aquinas, Flamel, Bernard of Treves, Doctor Dee, with his assistant Kelly, and in later times Jean Delisle, and Joseph Balsamo (Cagliostro), who was one of the most notorious persons in Europe about one hundred years ago (1765-1789), are names taken at random; and with the older philosophers chemistry was an all-absorbing occupation—not for gold, but knowledge.
The revelation was slow. On the temperature of bodies the old arts of healing were based—for chemistry and medicine were allies. The elements, we read, existed on the supposition “that bodies were hot or cold, dry or moist”; and on this distinction for a long time “was based the practice of medicine.” The doctrine of the “three principles” of existence superseded this,—the principles being salt, mercury, and sulphur. Metals had been regarded as living bodies, gases as souls or spirits. The idea remained that the form of the substance gave it its character. Acid was pointed; sweet things were round.
Chemistry, then, has had a great deal to contend against. From the time of the Egyptians and Chinese, who were evidently acquainted with various processes,—dyeing, etc.,—the science filtered through the alchemists to Beecher and Stahl, and then the principle of affinity—a disposition to combine—was promulgated, supplemented in 1674 by Mayow, by the theory of divorce or analysis. He concluded that where union could be effected, separation was equally possible. In 1718 the first “Table of Affinities” was produced. Affinity had been shown to be elective, for Mayow pointed out that fixed salts chose one acid rather than another. Richter and Dalton made great advances. Before them Hales, Black, Priestley, Scheele, Lavoisier, and numerous others penetrated the mysteries of the science whose history has been pleasantly written by more than one author who we have not been able to consult, and have no space to do more than indicate. In later days Faraday, De la Rive, Roscoe, and many others have rendered chemistry much more popular, while they have added to its treasures. The story of the progress of chemistry would fill a large volume, and we have regretfully to put aside the introduction and pass on.
Before proceeding to investigate the elements, a few words concerning the general terms used in chemistry will be beneficial to the reader. If we look at the list of the elements, pp. 308-9, we shall see various terminations. Some are apparently named from places, some from their characteristics. Metals lately discovered by the spectroscope (and recently) end in ium; some end in “ine,” some in “on.” As far as possible in late years a certain system of nomenclature has been adhered to, but the old popular names have not been interfered with.
When elements combine together in certain proportions of each they[Pg 338] receive certain names. The following table will explain the terms used ; for instance, we find that—
| Compounds of | Oxygen | are termed | Oxides, as oxide of copper. |
| ” | Hydrogen | ” | Hydrides, as hydride of potassium. |
| ” | Chlorine | ” | Chlorides, as chloride of sodium. |
| ” | Nitrogen | ” | Nitrides, as nitride of boron. |
| ” | Bromine | ” | Bromides, as bromide of potassium. |
| ” | Iodine | ” | Iodides, as iodide of potassium. |
| ” | Sulphur | ” | Sulphides, or Sulphurets, as sulphuret of lead. |
| ” | Selenium | ” | Selenides, as selenide of mercury. |
| ” | Carbon | ” | Carbides, or Carburets, as carbide of nitrogen, and so on. |
The above examples refer to the union in single proportion of each, and are called Binary Compounds. When more than one atom of each element exists in different proportions we have different terms to express such union. If one atom of oxygen be in the compound it is called a “monoxide” or “protoxide”; two atoms of oxygen in combination is termed “dioxide” or “binoxide”; three, “trioxide,” or “tritoxide”; four is the “tetroxide” or “per-oxide,” etc. When more than one atom, but not two atoms is involved, we speak of the sesqui-oxide (one-and-a-half),—“oxide” being interchangeable for “sulphide” or “chloride,” according to the element.
There are other distinctions adopted when metals form two series of combinations, such as ous and ic, which apply, as will be seen, to acids. Sulphuric and sulphurous acids, nitric and nitrous acid are familiar examples. In these cases we shall find that in the acids ending in “ous” oxygen is present in less quantity than in the acids ending in ic. The symbolic form will prove this directly, the number of atoms of oxygen being written below,
Sulphurous Acid = H2 SO3
Nitrous Acid = HNO2.
Sulphuric Acid = H2SO4.
Nitric Acid = HNO3.
Whenever a stronger compound of oxygen is discovered than that denominated by ic, chemists adopt the plan of dubbing it the per (ὑπέρ over), as per-chloric acid, which possesses four atoms of oxygen (HClO4), chloric acid being HClO3. The opposite Greek term, ὑπὸ (hupo, below), is used for an acid with less than two atoms of oxygen, and in books is written “hypo”-chlorous (for instance). Care has been taken to distinguish between the higher and lower; for “hyper” is used in English to denote excess, as hyper-critical; and hypo might to a reader unacquainted with the derivation convey just the opposite meaning to what is intended.
While speaking of these terminations we may show how these distinctive endings are carried out. We shall find, if we pursue the subject, that when wehave a salt of any acid ending in ic the salt terminates in “ate.” Similarly the salts of acids ending in ous, end in “ite.” To continue the same example we have—
Sulphurous Acid, which forms salts called Sulphites.
Sulphuric Acid, which forms salts called Sulphates.
Besides these are sulphides, which are results of the unions or com[Pg 339]pounds of elementary bodies. Sulphites are more complicated unions of the compounds. Sulphates are the salts formed by the union of sulphuric acid with bases. Sulphides or sulphurets are compounds in which sulphur forms the electro-negative element, and sulphites are salts formed by the union of sulphurous acids with bases, or by their action upon them.

The symbolical nomenclature of the chemist is worse than Greek to the uninitiated. We frequently see in so-called popular chemical books a number of hieroglyphics and combinations of letters with figures very difficult to decipher, much less to interpret. These symbols take the place of the names of the chemical compounds. Thus water is made up of oxygen and hydrogen in certain proportions; that is, two of hydrogen to one of oxygen. The symbolic reading is simple, H2O, = the oxide of hydrogen. Potassium again mingles with oxygen. Potassium is K in our list; KO is oxide of potassium (potash). Let us look into this a little closer.
The union of one particle of a simple body with a particle of another simple body can be easily understood; but, as we have seen, it is possible to have substances consisting of four or five different particles, though the greater number of chemical combinations consist of two or three dissimilar ones. In the diagram (fig. 322) we have some possible combinations.
In these combinations we may have one particle of a in combination with one, two, three, four, or five of b, and many particles of a can unite with various molecules of b. Suppose we have oxygen and sulphur compounds as follows:—
Thus there are three different compounds of these two elements—SO, SO2, SO3 (without water).

A compound body may combine with another compound body, and this makes a complicated compound. Suppose we have a mixture of sulphuric acid and potash. We have a sulphate of potassium (K2SO4) and combinations of these combinations may likewise be formed. We must read these symbols by the light of the combining weights given in the table, and then we shall find the weight of oxygen or other elements in combination. Thus when we see a certain symbol (Hg.S for instance), we understand that they form a compound including so many parts of mercury and so many of sulphur, which is known as vermilion. Hg.O is oxide of mercury, and by reference to the table of Atomic Weights, we find mercury is Hg., and its combining weight is[Pg 340] 200; while oxygen is O, and its weight is 16. Thus we see at once how much of each element is contained in oxide of mercury, and this proportion never varies; there must be 200 of one and 16 of the other, by weight, to produce the oxide. So if the oxygen has to be separated from it, the sum of 216 parts must be taken to procure the 16 parts of oxygen. When we see, as above, O2 or O3, we know that the weight must be calculated twice or three times, O being 16; O2 is therefore 32 parts by weight. So when we have found what the compounds consist of, we can write them symbolically with ease.
Composition of the Atmospheric Air.
We have already communicated a variety of facts concerning the air. We have seen that it possesses pressure and weight. We call the gaseous envelope of the earth the atmosphere, and we are justified in concluding that other planets possess an atmosphere also, though of a different nature to ours. We have seen how easy it is to weigh the air, but we may repeat the experiment. (See illustration, fig. 45, page 50.) We shall find that a perfectly empty glass globe will balance the weights in the scale-pan; admit the air, and the glass globe will sink. So air possesses weight. We have mentioned the Magdeburg hemispheres, the barometer, the air-pump, and the height and the pressure of the atmosphere have been indicated. The density of the atmosphere decreases as we ascend; for the first seven miles the density diminishes one-fourth that of the air at the sea-level, and so on for every succeeding seven.
In consequence of the equal, if enormous, pressure exercised in every direction, we do not perceive the inconvenience, but if the air were removed from inside of a drum, the parchment would quickly collapse. We feel the air when we move rapidly. We breathe the air, and that statement brings us to consider the composition of the atmosphere, which, chemically speaking, may vary a little (as compared with the whole mass) in consequence of changes which are continually taking place, but to all intents and purposes the air is composed as follows, in 100 parts:
| Nitrogen | 79 parts. |
| Oxygen | 20 parts. |
| Carbonic Acid | 04 parts. |
with minute quantities of other ingredients, such as ammonia, iodine, carbonetted hydrogen, hydrochloric acid, sulphuretted hydrogen, nitric acid, carbonic oxide, and dust particles, as visible in the sunbeams, added.
The true composition of the atmosphere was not known till Lavoisier demonstrated that it consisted of two gases, one of which was the vital fluid, or oxygen, discovered by Priestley. To the other gas Lavoisier gave the name of Azote,—an enemy of life,—because it caused death if inhaled alone. The carbonic acid in the air varies very much, and in close, heated, and crowded rooms increases to a large quantity, which causes lassitude and headache.
We can easily prove the existence of carbonic acid gas as exhaled from the lungs. Suppose we take a glass and fill it partly with clear lime-water; breathe through a glass tube into the water in the glass, and very quickly you will perceive that the lime-water is becoming cloudy and turbid. This cloudiness is due to the presence of chalk, which has been produced by the action of the carbonic acid gas in the lime-water. This is a well known and always interesting experiment, because it leads up to the vital question of our existence, and the functions of breathing and living.
A popular writer once wrote a book entitled, “Is Life Worth Living?” and a witty commentator replied to the implied question by saying, “It depends upon the liver.” This was felt to be true by many people who suffer, but the scientific man will go farther, and tell you it depends upon the air you breathe, and on the carbonic acid you can raise to create heat,—animal heat,—which is so essential to our well-being. We are always burning; a furnace is within us, never ceasing to burn without visible combustion. We are generating heat by means of the blood. We know that we inhale air into the lungs, and probably are aware that the air so received parts with the oxygen to renew the blood. The nitrogen dilutes the oxygen, for if we inhaled a less-mixed air we should either be burnt up or become lunatics, as light-headed as when inhaling “laughing-gas.” This beautifully graduated mixture is taken into our bodies, the oxygen renews the blood and gives it its bright red colour; the carbon which exists in all our bodies is cold and dead when not so vivified by oxygen. The carbonic acid given off produces heat, and our bodies are warm. But when the action ceases we become cold, we die away, and cease to live. Man’s life exemplifies a taper burning; the carbon waste is consumed as the wax is, and when the candle burns away—it dies! It is a beautiful study, full of suggestiveness to all who care to study the great facts of Nature, which works by the same means in all matter. We will refer to plants presently, after having proved by experiment the existence of nitrogen in the air.
Rutherford experimented very cruelly upon a bird, which he placed beneath a glass shade, and there let it remain in the carbonic acid exhaled from its lungs, till the oxygen being at length all consumed by the bird, it died. When the atmosphere had been chemically purified by a solution of caustic potash, another bird was introduced, but though it lived for some time, it did not exist so long as the first. Again the air was deprived of the carbonic acid, and a third bird was introduced. The experiment was thus repeated, till at length a bird was placed beneath the receiver, and it perished at once. This is at once a cruel and clumsy method of making an experiment, which can be more pleasantly and satisfactorily practised by burning some substance in the air beneath the glass. Phosphorus, having a great affinity for oxygen, is usually chosen. The experiment can be performed as follows with a taper, but the phosphorus is a better exponent.
Let us take a shallow basin with some water in it, a cork or small plate floating upon the water, and in the plate a piece of phosphorus.[Pg 342] We must be careful how we handle phosphorus, for it has a habit, well known, but sometimes forgotten by amateur chemists, of suddenly taking fire. Light this piece of phosphorus,—a small piece will do if the jar be of average “shade” size,—and place the glass over it, as in the illustration (fig. 325). The smoke will quickly spread in the jar, and the entry of air being prevented, because the jar is resting under water, phosphoric acid will be formed, and the oxygen thereby consumed. The water, meanwhile, will rise in the jar, the pressure of the air being removed. The burning phosphorus will soon go out, and when the glass is cool, you will be able to ascertain what is inside the jar. Put a lighted taper underneath, and it will go out. The taper would not go out before the phosphorus was burnt in the glass, and so now we perceive we have azote in the receptacle—that is, nitrogen. The other, the constituent of our atmosphere, carbonic acid, as we have seen, is very injurious to the life of animals, and as every animal breathes it out into the air, what becomes of it? Where does all this enormous volume of carbonic acid, the quantities of this poison which are daily and nightly exhaled, where do they all go to? We may be sure nature has provided for the safe disposal of it all. Not only because we live and move about still,—and of course that is a proof,—but because nature always has a compensating law. Remember nothing is wasted; not even the refuse, poisonous air we get rid of from our lungs. Where does it go?

It goes to nourish the plants and trees and vegetables that we delight to look upon and to eat the fruit of. Thus the vegetable world forms a link between the animals and the minerals. Vegetables obtain food, so to[Pg 343] speak, and nourishment from water, ammonia, and carbonic acid, all compound bodies, but inorganic.
Water consists of oxygen and hydrogen, carbonic acid of carbon and oxygen, and ammonia of hydrogen and nitrogen. Water and ammonia are present in the air; so are oxygen and nitrogen. Water falls in the form of rain, dew, etc. So in the atmosphere around us we find nearly every necessary for plant-life; and in the ground, which supplies some metallic oxides for their use, we find the remainder. From the air, then, the plant derives its life.

The vegetable kingdom in turn gives all animals their food. This you will see at a glance is true. Certainly animals live on animals. Man and wilder animals live on the beasts of the field in a measure, but those beasts derive their nourishment from vegetables—the vegetable kingdom. So we live on the vegetable kingdom, and it separates the carbonic acid from the air, and absorbs it. What we do not want it takes. What we want it gives. Vegetables give out oxygen, and we consume it gladly. We throw away carbonic acid, and the plants take it greedily; and thus the atmosphere is retained pure for our use. We can, if desirable, prove that plants absorb carbonic acid and give out oxygen by placing leaves of a plant in water, holding the acid in solution, and let the sun shine upon them. Before long we shall find that the carbonic acid has disappeared, and that oxygen has come into the water.
Carbonic acid is sufficiently heavy to be poured from one vessel to another; and if we have obtained some in a glass, we can extinguish a taper by pouring the invisible gas on to the lighted taper, when it will be immediately extinguished.
From the foregoing observations it will be perceived how very desirable it is that ventilation should be attended to. People close up windows and doors and fireplaces, and go to bed and sleep. In the morning they complain of headache and lassitude; they wonder what is the matter, and why the children are not well. Simply because they have been rebreathing the carbonic acid. Go into a closed railway carriage which is nearly filled (and it is astonishing to us how people can be so foolish as to close every outlet), and you will recoil in disgust. These travellers shut the ventilators and windows “because of the cold.” A very small aperture will ventilate a railway carriage; but a close carriage is sickening and enervating, as these kind of travellers find out by the time they reach their journey’s end. Air was given us to breathe at night as well as by day; and though from man’s acts or omissions there may be circumstances in which “night” air may affect the health, we maintain that air is no more injurious naturally than “day” air. Colder it may be, but any air at night is “night” air, in or out of doors at night; and we are certain that night air in itself never hurt any healthy person. It is not nature’s plan to destroy, but to save. If a person delicate in constitution gets hot, and comes out into a colder atmosphere, and defy nature in that way, he (or she) must take the consequences. But air and ventilation (not draught) are necessaries of health, and to say they injure is to accuse nature falsely. There are many impurities in the air in cities, and in country places sometimes, but such impurities are owing to man’s acts and omissions. With average sanitary arrangements and appliances in a neighbourhood no one need be afraid to breathe fresh air night or day; and while many invalids have, we believe, been retarded in recovery from being kept in a close room, hundreds will be benefited by plenty of fresh air. We should not so insist upon these plain and simple truths were there not so many individuals who think it beneficial to close up every avenue by which air can enter, and who then feel ill and out of spirits, blaming everything but their own short-sightedness for the effect of their own acts. An inch or two of a window may be open at night in a room, as the chimney register should be always fully up in bedrooms. When there are fires the draught supplies fresh air to the room with sufficient rapidity. But many seaside journeys might be avoided if fresh air were insisted on at home.
There is another and an important constituent of the atmosphere called Ozone, which is very superior oxygen, or oxygen in what is termed the “Allotropic” state, and is distantly related to electricity, inasmuch as it can be produced by an electrical discharge. This partly accounts for the freshness in the air after a thunderstorm, for we are all conscious that the storm has “cleared the air.” The fresh, crisp ozone in the atmosphere is evident. Ozone differs from oxygen in possessing taste and smell, and it is heavier by one-half than the oxygen gas. There is a good deal of ozone in the sea breeze, and we can, though not infallibly, detect its presence by test-paper prepared with iodide of potassium, which, when ozone is present, will turn[Pg 345] blue. We have still something to learn about ozone, which may be considered as “condensed oxygen.”

We have frequently mentioned “combustion,” and as under ordinary circumstances such effects cannot take place without atmospheric air, we will consider it. Combustion is chemical action accompanied by light and heat. Chemical union is always attended by the development of heat, not always by light, because the union varies in intensity and quickness. But when a candle is burning we can study all the interesting phenomena of combustion. We have already spoken of Heat and Light, so we need only refer the readers to those subjects in the former parts of this volume. Heat is referable to chemical action, and varies according to the energy of union. Heat is always present, remember, in a greater or less degree; and when visible combustion takes place we see light. Invisible combustion goes on in our bodies, and we feel heat; when we get cold we feed the fire by eating, or blow it by exercise and air in our lungs.

We shall speak, however, of combustion now as it affects us in daily life; our fires, our candles, gas, etc., and under these ordinary circumstances hydrogen and carbon are present. (We shall hear more about carbon presently.) These unite with the oxygen to form water and carbonic acid; the water being visible as we first put the cold shade upon the lighted lamp, and the carbonic acid renders the air impure.
In the case of a common candle, or lamp, combustion takes place in the same way. The wick is the intermediary. The oil mounts in the lamp wick, where it is converted into a gas by heat; it then “takes fire,” and gives us light and heat. The candle-flame is just the same with one exception: the burning material is solid, not liquid, though the difference is only apparent, for the wax is melted and goes up as gas. The burning part of the wick has a centre where there is no combustion, and contains carbon. We can prove this by placing a bent tube, as in the illustration (fig. 326), one end in the unburning part of the flame. We shall soon see a dark vapour come over into the receiver. This is combustible, for if we raise the tube without the glass we can light the gas (fig. 327). If we insert the end of the tube into the brilliant portion of the flame we shall perceive a black vapour, which will extinguish the combustion, for it is a mixture of carbonic acid gas and aqueous vapour, in which (fig. 328) particles of carbon are floating.

Fig. 329.—Davy’s safety lamp.

Fig. 330.—Davy lamp (section).
When we proceed to light our lamps to read or to write by, we find some difficulty in making the wick burn at first. We present to it a lighted taper, and it has no immediate effect. Here we have oil and cotton, two[Pg 347] things which would speedily set a warehouse in flames from top to bottom, but we cannot even ignite them, try all we can. Why?—Because we must first obtain a gas, oil will not burn liquid; it must be heated to a gaseous point before it will burn, as all combustion depends upon that,—so flames mount high in air. Now in a candle-flame, as will be seen in the diagram (fig. 331.), there are three portions,—the inner dark core, which consists of unburnt gas; the outer flame, which gives light; and the outside rim of perfect combustion non-luminous. In the centre, A, there is no heat. If we place a piece of gauze wire over the flame at a little distance the flame will not penetrate it. It will remain underneath, because the wire, being of metal, quickly absorbs the heat, and consequently there is no flame. This idea led to the invention of the “safety” lamp by Sir Humphrey Davy, which, although it is not infallible, is the only lamp in general use in mines (figs. 329, 330).

Mines must have light, but there is a gas in mines, a “marsh” gas, which becomes very explosive when it mixes with oxygen. Of course the gas will be harmless till it meets oxygen, but, in its efforts to meet, it explodes the moment the union takes place; instead of burning slowly like a candle it goes off all at once. This gas, called “fire damp,” is carburetted hydrogen, and when it explodes it develops into carbonic acid gas, which suffocates the miners.

CHAPTER XXVII.
NON-METALLIC ELEMENTS.
OXYGEN—SYMBOL O; ATOMIC WEIGHT 16.
Oxygen is certainly the most abundant element in nature. It exists all around us, and the animal and vegetable worlds are dependent upon it. It constitutes in combination about one-half of the crust of the earth, and composes eight-ninths of its weight of water. It is a gas without taste or colour. Oxygen was discovered by Priestley and Scheele, in 1774, independently of each other.

Oxygen can be procured from the oxides of the metals, particularly from gold, silver, and platinum. The noble metals are reducible from their oxides by heat, and this fact assists us at once. If we heat chlorate of potash, mixed with binoxide of manganese, in a retort in a furnace, the gas will be given off. There are many other ways of obtaining oxygen, and we illustrate two (figs. 333, 335).
The red oxide of mercury will very readily evolve oxygen, and if we heat a small quantity of the compound in a retort as per illustration (fig. 333) we shall get the gas. In a basin of water we place a tube test-glass, and the gas from the retort will pass over and collect in the test tube, driving out the water.

The other method mentioned above,—viz., by heating chlorate of potash, etc., in a furnace, is shown in the following illustration. Oxygen, as we have said, is a colourless and inodorous gas, and for a long time it could not be obtained in any other form; but lately both oxygen and hydrogen have[Pg 349] been liquified under tremendous pressure at a very low temperature. Oxygen causes any red-hot substance plunged into it to burn brightly; a match will readily inflame if a spark be remaining, while phosphorus is exceedingly brilliant, and these appearances, with many others equally striking, are caused by the affinity for those substances possessed by the gas. Combustion is merely oxidation, just as the process of rusting is, only in the latter case the action is so slow that no sensible heat is produced. But when an aggregate of slowly oxidising masses are heaped together, heat is generated, and at length bursts into flame. This phenomenon is called “spontaneous combustion.” Cases have been known in which the gases developed in the human body by the abuse of alcoholic drinks have ended fatally; in like manner the body being completely charred. (Combustion must not be confounded with ignition, as in the electric light.) Oxygen then, we see, is a great supporter of combustion, though not a combustible itself as coal is. When the chemical union of oxygen with another substance is very rapid an explosion takes place.

Oxidation occurs in various ways. Besides those already mentioned, all verdigris produced on copper, all decays of whatever kind, disintegration, and respiration, are the effects of oxygen. The following experiment for the extraction of oxygen directly from the air was made by M. Boussingault, who passed the gas upon a substance at a certain temperature, and released it at a higher. The illustration on page 351 will show the way in which the experiment was performed.
Boussingault permitted a thin stream of water to flow into a large empty flask, and by this water the air was gradually driven out into a flask containing chloride of calcium and sulphuric acid, which effectually dried it. This dry air then passed into a large tube inside the reverberatory furnace, in which tube were pieces of caustic baryta. Heated to a dull redness this absorbs oxygen, and when the heat is increased to a bright red the superabundant gas is given off. Thus the oxygen was permitted to pass from the furnace-tube into the receiving glass, and so pure oxygen was obtained from the air which had been in the glass bottle at first (fig. 338).

HYDROGEN—SYMBOL H; ATOMIC WEIGHT 1.
Hydrogen is abundant in nature, but never free. United with oxygen it forms water, hence its name, “water-former.” It is to Parcelcus that its discovery is due, for he found that oil of vitriol in contact with iron disengaged a gas which was a constituent of water. This gas was subsequently found to be inflammable, but it is to Cavendish that the real explanation of hydrogen is owing. He explained his views in 1766.
Hydrogen is obtained in the manner illustrated in the cut, by means of a furnace, as in fig. 339, or by the bottle method, as per fig. 340. The first method is less convenient than the second. A gun-barrel or fire-proof tube is passed through the furnace, and filled with iron nails or filings; a delivery tube is at the farther end, and a flask of water boiling at the other. The oxygen combines with the iron in the tube, and the hydrogen passes over. The second method is easily arranged. A flask, as in the cut, is provided, and in it some zinc shavings are put. Diluted sulphuric acid is then poured upon the metal. Sulphate of zinc is formed in the flask, and the hydrogen passes off.
Hydrogen being the lightest of all known bodies, its weight is put as 1, and thus we are relatively with it enabled to write down the weights of all the other elements. Hydrogen is fourteen-and-a-half times lighter than atmospheric air, and would do admirably for the inflation of balloons were it not so expensive to procure in such large quantities as would be necessary. Ordinary coal gas, however, contains a great deal of hydrogen, and answers the same purpose.

A very pretty experiment may be made with a bladder full of hydrogen gas. If a tube be fitted to the bladder already provided with a stop-cock, and a basin of ordinary soap-suds be at hand, by dipping the end of the tube in the solution and gently expressing the gas, bubbles will be formed which are of exceeding lightness (fig. 341). They can also be fired with a taper.
Another experiment may be made with hydrogen as follows:—If we permit the gas to escape from the flask, and light it, as in the illustration, and put a glass over it, we shall obtain a musical note, higher or lower, according to the length, breadth, and thickness of the open glass-tube (fig. 342). If a number of different tubes be employed, we can obtain a musical instrument—a gas harmonium.

Hydrogen burns with a blue flame, and is very inflammable. Even water sprinkled upon a fire will increase its fierceness, because the hydrogen burns with great heat, and the oxygen is liberated. Being very light, H can be transferred from one vessel to another if both be held upside down. Some mixtures of H and O are very explosive. The oxyhydrogen blow-pipe is used with a mixture of O and H, which is forcibly blown through a tube and then ignited. The flame thus produced has a most intense heating-power.
A very easy method of producing hydrogen is to put a piece of sodium[Pg 352] into an inverted cylinder full of water, standing in a basin of water. The sodium liberates the hydrogen by removing the oxygen from the liquid.
WATER—SYMBOL H2O; ATOMIC WEIGHT 18.
At page 59 of this volume we said something about water, and remarked (as we have since perceived by experiment) that “water is composed of oxygen and hydrogen in proportions, by weight, of eight of the former to one of the latter gas; in volume, hydrogen is two to one”; and we saw that “volume and weight were very different things.” This we will do well to bear in mind, and that, to quote Professor Roscoe, “Water is always made up of sixteen parts of oxygen to two parts of hydrogen by weight”; sixteen and two being eighteen, the combining weight of water is eighteen.


We can prove by the Eudiometer that hydrogen when burnt with[Pg 353] oxygen forms water; and here we must remark that water is not a mere mechanical mixture of gases, as air is. Water is the product of chemical combination, and as we have before said, is really an oxide of hydrogen, and therefore combustion, or electricity, must be called to our assistance before we can form water, which is the result of an explosion, the mixture meeting with an ignited body—the aqueous vapour being expanded by heat.
The ancients supposed water to be a simple body, but Lavoisier and Cavendish demonstrated its true character. Pure water, at ordinary temperatures, is devoid of taste and smell, and is a transparent, nearly colourless, liquid. When viewed in masses it is blue, as visible in a marked degree in the Rhone and Rhine, at Geneva, and Bâle respectively. Its specific gravity is 1, and it is taken as the standard for Sp. Gravity, as hydrogen is taken as the standard for Atomic Weight. The uses of water and the very important part it plays in the arrangements of nature as a mechanical agent, geology can attest, and meteorology confirm. It composes the greater portions of animals and plants; without water the world would be a desert—a dead planet.

We sometimes speak of “pure” spring water, but such a fluid absolutely pure can scarcely be obtained; and though we can filter water there will always remain some foreign substance or substances in solution. It is well known that the action of water wears away and rounds off hard rocks, and this power of disintegration is supplemented by its strength as a solvent, which is very great. Rain-water is purest in the country as it falls from the clouds. In smoky towns it becomes sooty and dirty. It is owing to the solvent properties of water, therefore, that we have such difficulty in obtaining a pure supply. There is hard water and soft water. The former[Pg 354] is derived from the calcareous formations, and contains lime, like the Kent water. This can be ascertained by noticing the incrustations of the vessels wherein the water is boiled. But water rising from hard rocks, such as granite, can do little to disintegrate them at the moment, and therefore the water rises purer. Springs from a great depth are warm, and are known as “thermal springs”; and when they come in contact with carbonic acid and some salts in their passage to the surface, they are known as “mineral waters.” These waters hold in solution salts of lime and magnesia, or carbonates of soda with those of lime and magnesia; salts of iron, and compounds of iodine and bromine are found in the natural mineral waters also, as well as sulphurous impregnations, instances of which will occur to every reader.


We mentioned the Eudiometer just now, and we give an illustration of it. This instrument is used to ascertain the proportions in which the elements of water are composed by synthesis, or a putting together of the constituents of a body to make it up. This is distinguished from analysis, which means separating the compound body into its elements, as we do when we pass the electric current through water.
The Eudiometer consists of a stout glass tube sealed hermetically at one end; two platinum wires are pushed in through the glass just before the end is sealed. The tube is now filled with mercury, and inverted in a bowl of the same metal. Hydrogen, and then oxygen, are admitted through the mercury in the recognised proportions of two to one. By the time the mercury is somewhat more than half displaced, the tube should be held[Pg 355] upon a sheet of india-rubber at the bottom of the vessel to keep the metal in the tube, for when the necessary explosion takes place the mercury might also be driven out. A spark from the electrophorus or from a Leyden jar may now be passed through the gases in the tube. The explosion occurs, and water is formed inside. If the mercury be again admitted it will rise nearly to the very top of the tube, driving the bubble up. Thus we find we have formed water from the two gases.
The decomposition of water is easily affected by electricity, and if a little sulphuric acid be added to the water, the experiment will be thereby facilitated. Two wires from a battery should be inserted through a glass filled with the water, and into two test tubes also filled. The wires terminate in platinum strips, and are fastened at the other end to the positive and negative poles of the galvanic battery. The gases will collect in the test tubes, and will be found in proper proportions when the current passes.


So much for water in its liquid state. The solid condition of water (ice) is equally interesting. When we apply heat to water, we get a vapour called “steam”; when we cool water to 32° Fahr., we get a solid mass which weighs just the same as the liquid we have congealed, or the steam we have raised from an equal amount of water. But water expands while in the process of solidification, just as it does when it becomes gaseous, and as we have remarked before, our water-pipes bear full testimony to this scientific fact. When ice forms it has a tendency to crystallize, and some of these ice crystals are, as we see, very beautiful. Snow is only water in a nearly solid form, and the crystals are extremely elegant, appearing more like flowers than congealed water, in tiny six-pointed ice crystals. Many philosophers of late years have written concerning these tiny crystals, which, in common with all crystals, have their own certain form, from which they[Pg 356] never depart. Snowflakes are regular six-sided prisms grouped around a centre forming angles of 60° and 120°. There are a number of forms, as will be seen from the accompanying illustrations, and at least ninety-six varieties have been observed. One snowflake, apparently so like all other flakes that fall, can thus be viewed with much interest, and yet, while so very various, snowflakes never get away from their proper hexagonal structure. It has been remarked that snowflakes falling at the same time have generally the same form.
Of the latent heat of ice, etc., we have already spoken in our article upon Heat, and therefore it will be sufficient to state that the latent heat of water is 79 thermal units, because when passing from the liquid to the solid state a certain amount of water absorbs sufficient heat to raise an equal quantity of the liquid 79°. This can be proved by taking a measured quantity (say a pint) of water at 79° and adding ice of the same weight to the water. The mixture will be found to be at zero. Therefore the ice has absorbed or rendered latent 79° of heat which the water possessed. If we melt ice until only a trace of it is left, we shall still find the water as cold as the ice was; all the latent heat is employed in melting the ice. So it will take as much heat to bring a pound of ice at zero to a pound of water at zero, as it would to raise 79 pounds of water 1°. The same law applies to steam.

Water can be distilled in small quantities by an apparatus, as figured in the illustration, and by these means we get rid of all impurities which are[Pg 357] inseparable from the liquid otherwise. When it is desirable to distil large quantities of water a larger apparatus is used, called an “Alembic.” The principle is simply to convert the liquid by heat into vapour, then cool it, by condensation, in another vessel.

The evaporation of water, with its effects upon our globe, belong more to the study of Meteorology.

Rain-water is the purest, as we have said, because it goes through the process of distillation by nature. The sun takes it up, by evaporation, into the air, where it is condensed, and falls as rain-water. Water containing carbonate of lime will petrify or harden, as in stalactite caverns. The carbonic acid escapes from the dripping water, the carbonate in solution is deposited as a stalactite, and finally forms pillars in the cave. Sea-water[Pg 358] contains many salts; its composition is as follows, according to Dr. Schwertzer, of Brighton:—
| Water | 964·74372 grains. |
| Chloride of sodium (salt) | 28·05948 ” |
| Chloride of potassium | 0·76552 ” |
| Chloride of magnesium | 3·66658 ” |
| Bromide of magnesium | 0·02929 ” |
| Sulphate of magnesia | 2·29578 ” |
| Sulphate of lime | 0·40662 ” |
| Carbonate of lime | 0·03301 ” |
| (With traces of iodine and ammonia). | |
| 1000·00000 grains. |

There is much more oxygen in water than in air, as can be ascertained by analysis of these compounds. This great proportion in favour of water enables fish to breathe by passing the water through the gills. Marine animals (not fishes), like the whale,—which is a warm-blooded creature, and therefore not suited to exist without air,—are obliged to come to the surface to breathe. The density of salt water is much greater than that of fresh water, and therefore swimming and flotation is easier in the sea than in a river. We shall have more to say of water by-and-by.
NITROGEN—SYMBOL N; ATOMIC WEIGHT 14.
We have already made some reference to this gas when speaking of the atmosphere and its constituents, of which nitrogen is the principal. From its life-destroying properties it is called “azote” by French chemists, and when we wish to obtain a supply of nitrogen all we have to do is to take away the oxygen from the air by burning phosphorus on water under a glass. Nitrogen is not found frequently in solid portions of the globe. It is abundant in animals. It is without colour or smell, and can be breathed in air without danger. It is heavy and sluggish; but if we put a taper into a jar of nitrogen it will go out, and animals die in the gas for want of oxygen, as nitrogen alone cannot support life.

The affinity of nitrogen for other substances is not great, but it gives rise to five compounds, which are as below, in the order they are combined with oxygen:—
| Nitrous oxide (“laughing gas”) | (Monoxide) | N2O. |
| Nitric oxide | Dioxide | N2O2. |
| Nitrous acid | Trioxide | N2O3. |
| Nitric peroxide | Tetroxide | N2O4. |
| Nitric acid | Pentoxide | N2O5. |
These compounds are usually taken as representative examples of combining weight, and as explanatory of the symbolic nomenclature of chemistry, as they advance in such regular proportions of oxygen with nitrogen. The combining weight of nitrogen is 14, and when two parts combine with five of oxygen it makes nitric acid, and we put it down as N2O5; on adding water, HNO3, as we can see by eliminating the constituents and putting in the proportions. Actually it is H2N2O6, or, by division, HNO3.
Nitrogen plays a very important part in nature, particularly in the vegetable kingdom. Nitric acid has been known for centuries. Geber, the alchemist, was acquainted with a substance called “nitric,” which he found would yield a dissolvent under certain circumstances. He called it “dissolving fluid.” At the end of the twelfth century Albert Magnus investigated the properties of this acid, and in 1235 Raymond Lully prepared nitre with clay, and gave the liquid the name of “aqua-fortis.” But till 1849 nitric acid was only known as a hydrate,—that is, in combination with water,—but now we have the anhydrous acid.

Oxygen and nitrogen combine under the influence of electricity, as shown by Cavendish, who passed a current through an atmospheric mixture of oxygen and nitrogen, in a tube terminating in a solution of potash, lime, and soda. Every time the spark passed, the volume of gas diminished, and nitric acid was formed, as it is in thunderstorms, when it does not remain free, but unites with ammonia, and forms a highly useful salt, which promotes vegetable growth. Here is another instance of the usefulness of thunderstorms, and of the grand provisions of nature for our benefit. Nitric acid is obtained by distilling nitre with sulphuric acid. The liquid is, when pure, colourless, and is a powerful oxidizer. It dissolves most metals, and destroys vegetable and animal substances. By an addition of a little sulphuric acid the water is taken from the nitric acid, and a very powerful form of it is the result. The acid is of great use in medicine, and as an application to bites of rabid animals or serpents. It converts cotton waste into “gun-cotton” by a very simple process of steeping, washing, and pressing. From the hydraulic press it comes in discs like “quoits,” which will burn harmlessly and smoulder away, but if detonated they explode with great violence. As a rule, when damp, it is not dangerous, but it can be fired even when wet. It will explode at a less temperature than gunpowder, and, moreover,[Pg 361] yields no smoke, nor does it foul a gun. Gun-cotton, when dissolved in ether, gives us collodion for photographic purposes.

In speaking farther of the compounds of nitrogen with oxygen, we will limit ourselves to the monoxide, or laughing gas. This is now used as an anæsthetic in dentistry, etc., and is quite successful, as a rule. People afflicted with heart disease should not use it without advice, however. When inhaled into the lungs it makes the subject very hilarious, and the effect is rather noisy. It is obtained from the nitrate of ammonia, which, on the application of heat, decomposes into nitrous oxide and vapour. Warm water should be used for the trough. The gas is a powerful supporter of combustion.

Binoxide of nitrogen is of importance in the manufacture of sulphuric acid.

Nitrogen combines with hydrogen, forming various compounds. These are the “amines,” also ammonia, and ammonium. Ammonia possesses the properties of a base. Its name is derived from Jupiter Ammon, near whose temple it was prepared, from camels’ dung. But bodies containing nitrogen give off ammonia in course of distilling, and hartshorn is the term applied to horn-cuttings, which yield ammonia, which is a colourless gas of strong odour and taste now obtained from gas-works.



To obtain ammonia heat equal parts of chloride of ammonia (sal ammoniac) and quick-lime powdered (see fig. 357). The gas must be collected over mercury, because it is very soluble in water. Ammonia is useful to restore tipsy people and fainting ladies. A solution of ammonia is used for cauteries. Ammoniacal gas is remarkable for its solubility in water. To prepare the solution the gas is forced through a series of flasks. The tubes carrying the gas should be continued to the bottoms of the flasks, else the solution, being lighter than water, the upper portion alone would be saturated. The tubes carrying away the solution are raised[Pg 363] a little, so that the renewal is continually proceeding. The gas liquifies under a pressure of six atmospheres, at a temperature of 10° Cent. This experiment can be artificially performed by heating chloride of silver saturated with ammonia, and the silver will part with the gas at a temperature of 40° C. The gas will then condense in a liquid form in the tube. The experiment may be facilitated by placing the other extremity of the tube in snow and salt, and by the liquid we can obtain intense cold. This experiment has been made use of by M. Carré in his refrigerator (which was described in the Physics’ section), by which he freezes water. We may, however, just refer to the process. Whenever the condition of a body is changed from that of liquid to a gas, the temperature is greatly lowered, because the heat becomes “latent.” The latest freezing machine consists of an apparatus as shown in the illustrations herewith (figs. 359 and 360). The machine is of wrought iron, and contains, when ready for action, a saturated[Pg 364] solution of ammonia at zero. This is in communication with another and an air-tight vessel, of which the centre is hollow. The first process is to heat the solution, and the gas escapes into the second “vase,” which is surrounded by cold water, and quite unable to escape. A tremendous pressure is soon obtained, and this, added to the cold water, before long liquifies the ammonia, and when the temperature indicates 130° the hot vessel is suddenly cooled by being put into the water. The gas is thus suddenly converted into a liquid, the water in the second hollow vase is taken out, and the[Pg 365] bottle to be frozen is put into the cavity. The cold is so great, in consequence of the transformation of the liquid ammonia into a gas, that it freezes the water in any vessel put into the receiver. The ammonia can be reconverted into liquid and back again, so no loss is occasioned by the process, which is rapid and simple. This is how great blocks of ice are produced in water-bottles.

The one important point upon which care is necessary is the raising of the temperature. If it be elevated beyond 130° C., the pressure will be too great, and an explosion will occur.

The abundant formation of ammonia from decaying animal matter is evident to everyone, and depends upon the presence of moisture to a great extent. Chloride of ammonia is called sal-ammoniac, and the carbonate of ammonia crystallizes from the alkaline liquid produced by the distillation of certain animal matter. The compounds of ammonia are easily recognized by a certain sharp taste. They are highly valuable remedial agents, acting particularly upon the cutaneous system, and when taken internally, produce the effect of powerful sudorifics. Their volatility, and the facility with which they are expelled from other substances, render them of great importance in chemistry, and peculiarly fit them for the purposes of many chemical analyses. The ammonia compounds display a remarkable analogy to the corresponding combinations of potash and soda. The compounds of ammonia are highly important in their relation to the vegetable kingdom. It may be assumed that all the nitrogen of plants is derived from the ammonia which they absorb from the soil, and from the surrounding atmosphere.

The similarity of ammonia to the metallic oxides has led to the conjecture that all its combinations contain a compound metallic body, which has received the name ammonium (NH4); but no one has yet succeeded in its preparation, although by peculiar processes it may be obtained in the form of an amalgam.
Ammonias, in which one or more atoms of hydrogen are replaced by basic radicals, are termed Amides, or Amines.
CHAPTER XXVIII.
NON-METALLIC ELEMENTS (continued).
CHLORINE—BROMINE—IODINE—FLUORINE—CARBON—SULPHUR—PHOSPHORUS—SILICON—BORON—TELLURIUM—ARSENIC.
Chlorine (Cl.) is usually found with sodium in the mineral kingdom, and this chloride of sodium is our common salt. Chlorine can be obtained by heating hydrochloric acid with binoxide of manganese. (Atomic weight 35·5.)

Chlorine possesses a greenish-yellow colour, hence its name “Chloros,” green. It should be handled carefully, for it is highly injurious and suffocating. It possesses a great affinity for other substances, and attacks the metals. For hydrogen it has a great affection, and when hydrogen is combined with any other substances chlorine immediately attacks them, and in time destroys them. But even this destructive and apparently objectionable quality makes chlorine very valuable; for if we carry the idea to its conclu[Pg 367]sion, we shall find that it also destroys offensive and putrid matter, and purifies the atmosphere very much. Most colouring matters include hydrogen, and therefore they are destroyed by chlorine, which is a great “bleacher” as well as a purifier. If we dip any vegetable dyes into a jar of chlorine, they will become white if the dyed substances are damp.
Hydrochloric acid is known as muriatic acid and spirits of salt. It is obtained when salt is treated with sulphuric acid and the gas comes off into water. Equal parts of the acid and the salt are put into a flask as in the cut (fig. 362), and diluted with water. The mixture is then heated. The gas is condensed in the bottles half-full of water. The result gives sulphate of soda and hydrochloric acid. This acid is procured in soda manufactories, and with nitric acid is called “aqua regia,” a solvent for gold. When chlorine and hydrogen are mixed in equal proportions they explode in sunlight. In the dark or by candle-light they are harmless. Dry chlorine gas can be obtained by interposing a glass filled with some chloride of calcium. The gas being heavier than air (about 2½ times), displaces it in the flask, and when it is filled another can be placed in position. This mode causes a little waste of gas, which should not be breathed.

Chlorine possesses a great affinity for certain bodies. If the gas be thrown upon phosphorus, the latter will burn brilliantly. Arsenic, tin, and antimony when powdered and poured from a shoot into a vase of chlorine will burst into brilliant sparks, and other metals will glow when introduced to this gas. Chlorine forms many unstable combinations with oxygen. Its combination with hydrogen has already been referred to.
Bromine is a rare element. (Symbol Br. Atomic weight 80.)
It is deep brownish red, very volatile, and of a peculiar odour. Bromine unites with the elementary bodies, and forms some oxygen compounds. It resembles chlorine in its properties, and is used in medicine and in photography. It is found in saline springs and in salt water, combined with soda and magnesium. The presence of bromine may easily be[Pg 368] detected in the strong smell of seaweed. Its combinations with metals are termed bromides. It is a powerful poison.
Iodine is another relative of chlorine. It is found in seaweed, which by burning is reduced to kelp. When iodine is heated a beautiful violet vapour comes off, and this characteristic has given it its name (“iodes,” violet). Iodine was discovered by Courtois, of Paris, and in 1813, Gay Lussac made it a special study. It is solid at ordinary temperatures, and assumes crystallized forms in plates of metallic lustre. It is an excellent remedy in “goitre” and such affections. (Symbol I. Atomic weight 127.)
Fluorine is very difficult to prepare. Fluor spar is a compound of fluorine and calcium. This element is gaseous, and combines so rapidly that it is very difficult to obtain in a free state. Etching on glass is accomplished by means of hydrofluoric acid, for fluorine has a great affinity for silicic acid, which is contained in glass. The glass is covered with wax, and the design is traced with a needle. The acid attacks the glass and leaves the wax, so the design is eaten in. (Symbol F. Atomic weight 19.)

Chlorine, fluorine, bromine, and iodine are termed “Halogens” (producers of salts). They appear, as we have seen, in a gaseous, liquid, and solid form respectively.
Carbon is the most, or one of the most, largely diffused elements in nature, and claims more than a passing notice at our hands, though even that must be brief. We may put down carbon next to oxygen as the most important element in the world. The forms assumed by carbon are very variable, and pervade nature in all its phases. We have carbon in crystals,[Pg 369] in the animal and vegetable kingdoms, and amongst the chief minerals a solid, odourless, tasteless, infusible, and almost insoluble body. In various combinations carbon meets us at every turn; united with oxygen it forms carbonic acid, which we exhale for the plants to imbibe. We have it in coal, with hydrogen and oxygen. We have it building up animal tissues, and it is never absent in two out of the three great divisions of nature—the plants and the animals (Symbol C; Atomic W. 12).


We have carbon in three different and well-known conditions; as the diamond, as graphite, or black-lead, and as charcoal. The properties of the diamond are well known, and we shall, when we get to Crystallography, learn the forms of diamond or crystals of carbon. At present we give an illustration or two, reserving all explanation for the present. Diamond cutting is a matter of some difficulty, and it requires skill to cut in the proper direction. Diamonds are found in India, Brazil, and at the Cape of Good Hope, in alluvial soil. The identity of diamond and charcoal was discovered accidentally. An experiment to fuse a few small diamonds[Pg 370] resulted in their disappearance, and when the residue was examined it was found that the diamonds had been burned, that they had combined with oxygen and formed carbonic acid, just as when coal burns. The diamond is the hardest of all substances, the most valuable of gems, and the purest condition in which carbon appears.
Graphite (Plumbago) is termed “black-lead,” and is the next purest form of carbon. It crystallizes and belongs to the primitive formations. In Cumberland it is dug up and used to make pencils; the operations can be seen at Keswick. It has other uses of a domestic character.
Charcoal is the third form of carbon, and as it possesses no definite form, is said to be amorphous. Charcoal is prepared in air-tight ovens, so that no oxygen can enter and burn the wood thus treated. Coke is the result of the same process applied to coal. The gas manufactories are the chief depôts for this article, and it is used in locomotive engines. The various smokeless coals and prepared fuels, however, are frequently substituted.

Coke ovens were formerly much resorted to by the railway companies, who found the ordinary coal too smoky for locomotive purposes, and apt to give rise to complaints by passengers and residents near the line.
The origin of wood charcoal we have seen. All vegetable substances contain carbon. When we burn wood, in the absence of air as far as possible, oxygen and hydrogen are expelled. The wood is piled in layers as in the illustration (fig. 368), covered over with turf and mould, with occasional apertures for air. This mass is ignited, the oxygen and hydrogen are driven[Pg 371] off, and carbon remains. (Animal charcoal is obtained from calcining bones). Wood charcoal attracts vapours, and water, if impure, can be purified by charcoal, and any impure or tainted animal matter can be rendered inoffensive by reason of charcoal absorbing the gases, while the process of decay goes on just the same. Housekeepers should therefore not always decide that meat is good because it is not offensive to the olfactory nerves. Charcoal will remove the aroma, but the meat may be nevertheless bad. The use of charcoal in filters is acknowledged universally, and as a constituent of gunpowder it is important.

Carbon is not easily affected by the atmospheric air, or in the earth; so in many instances wood is charred before being driven into the ground; and casks for water are prepared so. Soot is carbon in a pulverised condition, and Indian ink is manufactured with its assistance.

The preparation of wood charcoal gives occupation to men who are frequently wild and untutored, but the results of their labour are very beneficial. Care should be taken not to sleep in a room with a charcoal stove burning, unless there is ample vent for the carbonic acid gas, for it will cause suffocation. Lampblack is obtained by holding a plate over the flame of some resinous substance, which deposits the black upon it. There is a special apparatus for this purpose.

Carbon combines with oxygen to make carbonic acid gas, as we have already mentioned, and in other proportions to form a more deadly compound [Pg 372]than the other. The former is the dioxide (CO2), the latter the monoxide, or carbonic oxide (CO). The dioxide is the more important, being held in the atmosphere, and combined with lime in chalk. All sparkling beverages contain carbonic acid, to which their effervescence is due. The soda and other mineral waters owe their sparkle to this gas. Soda-water consists of a weak solution of carbonate of soda and the acid. There is a vessel holding chalk and water, and another containing some sulphuric acid. When the sulphuric acid is permitted to unite with the chalk and water, carbonic acid is liberated. A boy turning a wheel forces the gas into the water in the bottles, or the water and carbonate of soda is drawn off thus impregnated into bottles and corked down, in the manner so familiar to all. The bottles are made of the shape depicted, so that the[Pg 373] bubble of air shall be at the top when the bottle lies down. If it be not kept so, the air will eventually escape, no matter how tightly the cork be put in. The ordinary “soda-water” contains scarcely any soda. It is merely water, chalk, and carbonic acid. The “Gazogene” is made useful for small quantities of soda-water, and is arranged in the following manner. The appearance of it is familiar to all. It consists of a double vessel, into the upper part of which a solution of any kind—wine and water, or even plain water—is put, to be saturated with carbonic acid, or “aerated,” and into the lower one some carbonate of soda and tartaric acid. A tube leads from this lower to the top of the upper vessel, which screws on and off. By shaking the apparatus when thus charged and screwed together, some of the liquid descends through the tube into the lower vessel and moistens the soda and acid, which therefore act on each other, and cause carbonic acid to be disengaged; this, rising up through the tube (which is perforated with small holes at the upper part), disperses itself through the liquid in small bubbles, and causes sufficient pressure to enable the liquid to absorb it, which therefore effervesces when drawn off by the tap.

Carbonic acid can be liquified, and then it is colourless. In a solid form it resembles snow, and if pressed with the fingers it will blister them. Being very heavy the gas can be poured into a vase, and if there be a light in the receptacle the flame will be immediately extinguished.

That even the gas introduced into seltzer-water is capable of destroying life, the following experiment will prove. Let us place a bird within a[Pg 374] glass case as in the illustration (fig. 373), and connect the glass with a bottle of seltzer-water or a siphon. As soon as the liquid enters, the carbonic acid will ascend, and this, if continued for a long time, would suffocate the bird, which soon begins to develop an appearance of restlessness.

We have already remarked upon the important part taken by this gas in nature, so we need only mention its existence in pits and caves. There are many places in which the vapour is so strong as to render the localities uninhabitable. In the Middle Ages the vapours were attributed to the presence of evil spirits, who were supposed to extinguish miners’ lamps, and suffocate people who ventured into the caves. In the Grotto Del Cane there is still an example, and certain caves of Montrouge are often filled with the gas. A lighted taper held in the hand will, by its extinction, give the necessary warning. Oxygen and carbon are condensed in carbonic acid, for the gas contains a volume of oxygen equal to its own. If we fill a glass globe, as per illustration (fig. 374), with pure oxygen, and in the globe insert two carbon points, through which we pass a current of electricity, we shall find, after the experiment, that if the stop-cock be opened, there is no escape of gas, and yet the mercury does not rise in the tube, so the oxygen absorbed has been replaced by an equal volume of carbonic acid.

The other combination of carbon with oxygen is the carbonic oxide (CO), and when a small quantity of oxygen is burnt with it it gives a blue flame, as on the top of the fire in our ordinary grates. This gas is present[Pg 375] in lime kilns, and is a very deadly one. We must now pass rapidly through the compounds of carbon with hydrogen, merely referring to coal for a moment as we go on.
Coal, of which we shall learn more in Mineralogy and Geology, is a combination, mechanical or otherwise, and is the result of the decomposition of vegetable matter in remote ages,—the so-called “forests,” which were more like the jungles than the woods of the present day. Moss and fern played prominent parts in this great transformation, as we can see in the Irish peat-bogs, where the first steps to the coal measures are taken.

The compounds of carbon with hydrogen are important. There is the “light” carburetted hydrogen (CH4), which is usually known as fire-damp in coal mines. It is highly inflammable and dangerous. The safety-lamp invented by Davy is a great protection against it, for as the gas enters it is cooled by the wire, and burns within harmlessly. The explosion warns the miner. “Heavy” carburetted hydrogen possesses double the quantity of carbon (C2H4). It is also explosive when mixed with oxygen.

The most useful compound is coal-gas, and though its principal function appears to be in some manner superseded by electricity, “gas” is still too important to be put aside. It can easily be obtained by putting small fragments of coal in the bowl of a tobacco-pipe, closing the bowl with clay, and putting it in[Pg 376] the fire. Before long the gas will issue from the stem of the pipe, and may either be lighted or collected in a bladder. For the use of the “million,” however, gas is prepared upon a very large scale, and is divided into three processes—its “formation,” “purification,” and its “collection” for distribution to consumers. The first process is carried on by means of retorts shown in the illustration (fig. 376). The first portion of the next figure is a section of a furnace, the other part shows two furnaces from the front. The following is the mode employed. The coal is put into retorts fitted to the furnace, so that they are surrounded by the flames, and terminating in a horizontal tube called the hydraulic main, E, which is in its turn connected with a pit or opening for the reception of the tar and ammoniacal liquor, etc., which condenses from the gas. It then passes up and down a series of tubes in water, called a “condenser,” and in this are reservoirs or receptacles for any tar and ammonia that remain. But sulphur is still present, so the gas is carried to the purifying apparatus (D in fig. 378), which consists of a large cylindrical vessel air-tight, with an inverted funnel, nearly filled with a mixture of lime and water. The gas bubbles in, and the sulphur unites with the lime, while the gas rises to the top (trays of lime are used when the gas enters from the bottom). The Gasometer, a large vessel closed at the top and open below, dips into a large trough of circular shape. The gasometer is balanced by weights and chains,[Pg 377] and may be raised (See fig. 379). When quite empty the top rests upon the ground, and when the gas enters it is raised to the top of the frame which supports it. We have now our Gasometer full. When the time comes to fill the pipes for lighting purposes, some of the weights are removed, the Gasometer falls down slowly, and forces the gas through the tubes into the main supply to be distributed. About four cubic feet of gas is obtained from every pound of coal. When gas and air become mixed, the mixture is very explosive. In a house where an escape of gas is detected let the windows be opened at the top, and no light introduced for several minutes.


Fig. 377.—Section. Front view.

Fig. 378.—Condenser. Purifier. Gasometer.

It has been calculated that one ton of good coal produces the following:—
| 1 | Chaldron of coke | weighing | 1,494 lbs. |
| 12 | Gallons of tar | “ | 135 lbs. |
| 12 | Gallons of ammoniacal liquor | “ | 100 lbs. |
| 5,900 | Cubic feet of gas | “ | 291 lbs. |
| Loss (water) | “ | 220 lbs. | |
| Total | 2,240 lbs. |

We can thus estimate the profits of our gas companies at leisure. The analysis of gas made by Professor Bunsen is as under, in 100 parts.
| Hydrogen | 45·58 |
| Marsh gas | 34·90 |
| Carbonic oxide | 6·64 |
| Olefiant gas | 4·08 |
| Butyline | 2·38 |
| Sulphide of hydrogen | 0·29 |
| Nitrogen | 2·46 |
| Carbonic acid | 3·67 |
| 100·00 |
Gas, therefore, is very injurious, for it rapidly vitiates the atmosphere[Pg 378] it burns in, and is very trying to the eyes, as well as destructive to gilt ornaments.
Tar is familiar to all readers, and though unpleasant to handle or to smell, it produces the beautiful aniline dyes. Tar pills are very efficacious for some blood disorders, and will remove pimples, etc., from the face, and cure “boils” effectually. If a dose of five be taken first, in a day or two four, and so on, no second remedy need be applied. We have known cases finally cured, and no recurrence of boils ever ensued after this simple remedy.

Tar is one of the results left in the distillation both of wood and coal: in places where wood is plentiful and tar in request, it is produced by burning the wood for that purpose; and in some of the pits in which charcoal is produced, an arrangement is made to collect the tar also. Coal-tar and wood-tar are different in some respects, and are both distilled to procure the napthas which bear their respective names. From wood-tar creosote is also extracted, and it is this substance which gives the peculiar tarry flavours to provisions, such as ham, bacon, or herrings, cured or preserved by being smoked over wood fires. Tar is used as a sort of paint for covering wood-work and cordage when much exposed to wet, which it resists better than anything else at the same price; but the tar chiefly used for these purposes is that produced by burning fir or deal wood and condensing the tar in a pit below the stack of wood; it is called Stockholm tar, as it comes chiefly from that place.
Carbon only combines with nitrogen under peculiar circumstances. This indirect combination is termed cyanogen (CN). It was discovered by Gay-Lussac, and is used for the production of Prussian blue. Hydrocyanide of potassium (Prussic acid) is prepared by heating cyanide of[Pg 379] potassium with sulphuric acid. It is a deadly poison, and found in peach-stones. Free cyanogen is a gas. The bisulphide of carbon is a colourless, transparent liquid. It will easily dissolve sulphur and phosphorus and several resins. When phosphorus is dissolved in it, it makes a very dangerous “fire,” and one difficult to extinguish. We must now leave carbon and its combinations, and come to sulphur.

Sulphur is found in a native state in Sicily and many other localities which are volcanic. It is a yellow, solid body, and as it is never perfectly free from earthy matter, it must be purified before it can be used. It possesses neither taste nor smell, and is insoluble in water. Sulphur is purified in a retort, C D, which communicates with a brick chamber, A. The retort is placed over a furnace, K, and the vapour passes into the chimney through the tube, D, where it condenses into fine powder called “flowers of sulphur” (brimstone). A valve permits the heated air to pass off, while no exterior air can pass in, for explosions would take place were the heated vapour to meet the atmospheric air. The danger is avoided by putting an air reservoir outside the chimney which is heated by the furnace. The sulphur is drawn out through the aperture, r, when deposited on the floor of the chamber. The sulphur is cast into cylinders and sold. Sulphur is soluble in bisulphide of carbon, and is used as a medical agent.
The compounds of sulphurs with oxygen form an interesting series. There are two anhydrous oxides (anhydrides),—viz., sulphurous and sulphuric [Pg 380]anhydride (SO2 and SO3). There are two notable acids formed by the combination with water, sulphurous and sulphuric, and some others, which, as in the case of nitrogen, form a series of multiple proportions, the oxygen being present in an increasing regularity of progression, as follows:—
| Name of Acid. | Chemical Formula. |
|---|---|
| Hypo-sulphurous acid | H2SO2 |
| Sulphurous acid | H2SO3 |
| Sulphuric acid | H2SO4 |
| Thio-sulphuric, or hypo-sulphuric acid | H2S2O3 |
| Dithionic acid | H2S2O6 |
| Trithionic acid | H2S3O6 |
| Tetrathionic acid | H2S4O6 |
| Pentathionic acid | H2S5O6 |
The last four are termed “polythionic,” because the proportions of sulphur vary with constant proportions of the other constituents.

The sulphurous anhydride mentioned above is produced when we burn sulphur in the air, or in oxygen; it may be obtained in other ways. It is a colourless gas, and when subjected to pressure may be liquified, and crystallized at very low temperature. It was formerly called sulphuric acid. It is a powerful “reducing agent,” and a good antiseptic. It dissolves in water, and forms the H2SO3, now known as sulphurous acid.

Sulphuric acid is a most dangerous agent in wicked or inexperienced hands, and amateurs should be very careful when dealing with it. It takes the water from the moist air, and from vegetable and animal substances. It carbonizes and destroys all animal tissues. Its discovery is due to Basil Valentine, in 1440. He distilled sulphate of iron, or green vitriol, and the result was “oil of vitriol.” It is still manufactured in this way in the Hartz district, and the acid passes by retorts into receivers. The earthen retorts, A, are arranged[Pg 381] in the furnace as in the illustration, and the receivers, B, containing a little sulphuric acid, are firmly fixed to them. The oily brown product fumes in the air, and is called “fuming sulphuric acid,” or Nordhausen acid. Sulphuric acid is very much used in chemical manufactures, and the prices of many necessaries, such as soap, soda, calico, stearin, paper, etc., are in close relationship with the cost and production of sulphur, which also plays an important part in the making of gunpowder. The manufacture of the acid is carried on in platinum stills.

Sulphuretted hydrogen, or the hydric sulphide (H2S), is a colourless and horribly-smelling gas, and arises from putrefying vegetable and animal matter which contains sulphur. The odour of rotten eggs is due to this gas, which is very dangerous when breathed in a pure state in drains, etc. It can be made by treating a sulphide with sulphuric acid. It is capable of precipitating the metals when in solution, and so by its aid we can discover the metallic ingredient if it be present. The gas is soluble in water, and makes its presence known in certain sulphur springs. The colour imparted to egg-spoons and fish-knives and forks sometimes is due to the presence of metallic sulphides. The solution is called hydro-sulphuric acid.
Phosphorus occurs in very small quantities, though in the form of phosphates we are acquainted with it pretty generally, and as such it is absorbed by plants, and is useful in agricultural operations. In our organization—in the brain, the nerves, flesh, and particularly in bones—phosphorus is present, and likewise in all animals. Nevertheless it is highly poisonous. It is usually obtained from the calcined bones of mammalia by obtaining phosphoric acid by means of acting upon the bone-ash with sulphuric acid.[Pg 382] Phosphorus when pure is colourless, nearly transparent, soft, and easily cut. It has a strong affinity for oxygen. It evolves white vapour in atmospheric air, and is luminous; to this element is attributable the luminosity of bones of decaying animal matter. It should be kept in water, and handled—or indeed not handled—but grasped with a proper instrument.
Phosphorus is much used in the manufacture of lucifer matches, and we are all aware of the ghastly appearance and ghostly presentment it gives when rubbed upon the face and hands in the dark. In the ripples of the waves and under the counter of ships at sea, the phosphorescence of the ocean is very marked. In Calais harbour we have frequently noticed it of a very brilliant appearance as the mail steamer slowly came to her moorings. This appearance is due to the presence of phosphorus in the tiny animalculæ of the sea. It is also observable in the female glow-worm, and the “fire-fly.” Phosphorus was discovered by Brandt in 1669.

It forms two compounds with oxygen-phosphorous acid, H2PO4, and phosphoric acid, H3PO4. The compound with hydrogen is well marked as phosphuretted hydrogen, and is a product of animal and vegetable decomposition. It may frequently be observed in stagnant pools, for when emitted it becomes luminous by contact with atmospheric air. There is a very pretty but not altogether safe experiment to be performed when phosphuretted hydrogen has been prepared in the following manner. Heat small pieces of phosphorus with milk of lime or a solution of caustic potash; or make a paste of quick-lime and phosphorus, and put into the flask with some quick-lime powdered. Fix a tube to the neck, and let the other end be inserted in a basin of water. (See illustration, fig. 388.) Apply heat; the phosphuretted hydrogen will be given off, and will emerge from the water in the basin in luminous rings of a very beautiful appearance. The greatest care should be taken in the performance of this very simple experi[Pg 383]ment. No water must on any account come in contact with the mixture in the flask. If even a drop or two find its way in through the bent tube a tremendous explosion will result, and then the fire generated will surely prove disastrous. The experiment can be performed in a cheaper and less dangerous fashion by dropping phosphate of lime into the basin. We strongly recommend the latter course to the student unless he has had some practice in the handling of these inflammable substances, and learnt caution by experience. The effect when the experiment is properly performed is very good, the smoke rising in a succession of coloured rings.

Silicon is not found in a free state in nature, but, combined with oxygen, as Silica it constitutes the major portion of our earth, and even occurs in wheat stalks and bones of animals. As flint or quartz (see Mineralogy) it is very plentiful, and in its purest form is known as rock crystal, and approaches the form of carbon known as diamond. When separated from oxygen, silicon is a powder of greyish-brown appearance, and when heated in an atmosphere of oxygen forms silicic “acid” again, which, however, is not acid to the taste, and is also termed “silica,” or “silex.” It is fused with great difficulty, but enters into the manufacture of glass in the form of sand. The chemical composition of glass is mixed silicate of potassium or sodium, with silicates of calcium, lead, etc. Ordinary window-glass is a mixture of silicates of sodium and calcium; crown glass contains calcium and silicate of potassium. Crystal glass is a mixture of the same silicate and lead. Flint glass is of a heavier composition. Glass can be coloured by copper to a gold tinge, blue by cobalt, green by chromium, etc.[Pg 384] Glass made on a large scale is composed of the following materials, according to the kind of glass that is required.
Flint glass (“crystal”) is very heavy and moderately soft, very white and bright. It is essentially a table-glass, and was used in the construction of the Crystal Palace. Its composition is—pure white sea-sand, 52 parts, potash 14 parts, oxide of lead, 34 parts = 100.
| Plate Glass. | Crown Glass. | Green (Bottle) Glass. | |||
|---|---|---|---|---|---|
| Pure white sand | 55 parts. | Fine sand | 63 parts. | Sea sand | 80 parts. |
| Soda | 35 ” | Chalk | 7 ” | Salt | 10 ” |
| Nitre | 8 ” | Soda | 30 ” | Lime | 10 ” |
| Lime | 2 ” | ||||
| 100 ” | 100 ” | 100 ” | |||
The ingredients to be made into glass (of whatever kind it may be) are thoroughly mixed together and thrown from time to time into large crucibles placed in a circle, A A (fig. 389), in a furnace resting on buttresses, B B, and heated to whiteness by means of a fire in the centre, C, blown by a blowing machine, the tube of which is seen at D. This furnace is shown in prospective in fig. 390. The ingredients melt and sink down into a clear fluid, throwing up a scum, which is removed. This clear glass in the fused state is kept at a white heat till all air-bubbles have disappeared; the heat is then lowered to a bright redness, when the glass assumes a consistence and ductility suitable to the purposes of the “blower.”

Glass blowing requires great care and dexterity, and is done by twirling a hollow rod of iron on one end of which is a globe of melted glass, the workman blowing into the other end all the time. By reheating and twirling a sheet of glass is produced. Plate glass is formed by pouring the molten glass upon a table with raised edges. When cold it is ground with emery powder, and then polished by machinery.

Many glass articles are cast, or “struck-up,” by compression in moulds, and are made to resemble cut-glass, but they are much inferior in appearance.[Pg 385] The best are first blown, and afterwards cut and polished. Of whatever kind of glass the article may be, it is so brittle that the slightest blow would break it, a bad quality which is got rid of by a process called “annealing,” that is, placing it while quite hot on the floor of an oven, which is allowed to cool very gradually. This slow cooling takes off the brittleness, consequently articles of glass well annealed are very much tougher than others, and will scarcely break in boiling water.

The kind generally used for ornamental cutting is flint-glass. Decanters and wine-glasses are therefore made of it; it is very bright, white, and easily cut. The cutting is performed by means of wheels of different sizes and materials, turned by a treadle, as in a common lathe, or by steam power; some wheels are made of fine sandstone, some of iron, others of tin or copper; the edges of some are square, or round, or sharp. They are used with sand and water, or emery and water, stone wheels with water only.


In a soluble form silicic acid is found in springs, and thus enters into the composition of most plants and grasses, while the shells and scales of “infusoria” consist of silica. As silicate of alumina,—i.e., clay,—it plays a very important rôle in our porcelain and pottery works.
Boron is found in volcanic districts, in lakes as boracic acid, in combination with oxygen. It is a brownish-green, insoluble powder, in a free state, but as boracic acid it is white. It is used to colour fireworks with the beautiful green tints we see. Soda and boracic acid combine to make[Pg 386] borax (or biborate of soda). Another and inferior quality of this combination is tinkal, found in Thibet. Borax is much used in art and manufactures, and in glazing porcelain. (Symbol B, Atomic Weight 11).
Selenium is a very rare element. It was found by Berzilius in a sulphuric-acid factory. It is not found in a free state in nature. It closely resembles sulphur in its properties. Its union with hydrogen produces a gas, seleniuretted hydrogen, which is even more offensive than sulphuretted hydrogen. (Symbol Se, Atomic Weight 79).
Tellurium is also a rare substance generally found in combination with gold and silver. It is like bismuth, and is lustrous in appearance. Telluretted hydrogen is horrible as a gas. Tellurium, like selenium, sulphur, and oxygen, combines with two atoms of hydrogen. (Symbol Te, Atomic Weight 129).

Arsenic, like tellurium, possesses many attributes of a metal, and on the other hand has some resemblance to phosphorus. Arsenic is sometimes found free, but usually combined with metals, and is reduced from the ores by roasting; and uniting with oxygen in the air, is known as “white arsenic.” The brilliant greens on papers, etc., contain arsenic, and are poisonous on that account. Arsenic and hydrogen unite (as do sulphur and hydrogen, etc.), and produce a foetid gas of a most deadly quality. This element also unites with sulphur. If poured into a glass containing chlorine it will sparkle and scintillate as in the illustration (fig. 395). (Symbol As, Atomic Weight 75).
Before closing this division, and passing on to a brief review of the Metals, we would call attention to a few facts connected with the metalloids we have been considering. Some, we have seen, unite with hydrogen[Pg 387] only, as chlorine; some with two atoms of hydrogen, as oxygen, sulphur, etc., and some with three, as nitrogen and phosphorus; some again with four, as carbon and silicon. It has been impossible in the pages we have been able to devote to the Metalloids to do more than mention each briefly and incompletely, but the student will find sufficient, we trust, to interest him, and to induce him to search farther, while the general reader will have gathered some few facts to add to his store of interesting knowledge. We now pass on to the Metals.


CHAPTER XXIX.
THE METALS.
WHAT METALS ARE—CHARACTERISTICS AND GENERAL PROPERTIES OF METALS—CLASSIFICATION—SPECIFIC GRAVITY—DESCRIPTIONS.
We have learnt that the elements are divided into metalloids and metals, but the line of demarcation is very faint. It is very difficult to define what a metal is, though we can say what it is not. It is indeed impossible to give any absolute definition of a metal, except as “an element which does not unite with hydrogen, or with another metal to form a chemical compound.” This definition has been lately given by Mr. Spencer, and we may accept it as the nearest affirmative definition of a metal, though obviously not quite accurate.

A metal is usually supposed to be solid, heavy, opaque, ductile, malleable, and tenacious; to possess good conducting powers for heat and electricity, and to exhibit a certain shiny appearance known as “metallic lustre.” These are all the conditions, but they are by no means necessary, for very few metals possess them all, and many non-metallic elements possess several. The “alkali” metals are lighter than water; mercury is a fluid. The opacity of a mass is only in relation to its thickness, for Faraday beat out metals into plates so thin that they became transparent. All metals are not malleable, nor are they ductile. Tin and lead, for example, have very little ductility or tenacity, while bismuth and antimony have none at all. Carbon is a much better conductor of electricity than many metals in which such power is extremely varied. Lustre, again, though possessed by metals, is a characteristic of some non-metals. So we see that while we can easily say what is not a metal, we can scarcely define an actual metal, nor depend upon unvarying properties to guide us in our determination.
The affinity of metals for oxygen is in an inverse ratio to their specific gravity, as can be ascertained by experiment, when the heaviest metal will be the least ready to oxidise. Metals differ in other respects, and thus classification and division become easier. The fusibility of metals is of a very wide range, rising from a temperature below zero to the highest heat obtainable in the blow-pipe, and even then in the case of osmium there is a difficulty. While there can be no question that certain elements, iron, copper, gold, silver, etc., are metals proper, there are many which border upon the line of demarcation very closely, and as in the case of arsenic even occupy the debatable land.
Specific Gravity is the relation which the weight of substance bears to the weight of an equal volume of water, as already pointed out in Physics. The specific gravities of the metals vary very much, as will be seen from the table following—water being, as usual, taken as 1:—
| Aluminium | 2·56 | Lead | 11·3 | Rubidium | 1·5 |
| Antimony | 6·7 | Lithium | ·593 | Ruthenium | 11·4 |
| Arsenic | 6· | Magnesium | 1·74 | Silver | 105 |
| Bismuth | 9·7 | Manganese | 8· | Sodium | ·972 |
| Cadmium | 8·6 | Mercury | 13·5 | Strontium | 2·5 |
| Calcium | 1·5 | Molybdenum | 8·6 | Thallium | 11·8 |
| Chromium | 6·8 | Nickel | 8·8 | Tin | 7·2 |
| Cobalt | 8·9 | Osmium | 21·4 | Titanium | 5·3 |
| Copper | 8·9 | Palladium | 11·8 | Tungsten | 17·6 |
| Gold | 19·3 | Platinum | 21·5 | Uranium | 18·4 |
| Indium | 7·3 | Potassium | ·865 | Zinc | 7·1 |
| Iridium | 21·1 | Rhodium | 12·1 | Zircon | 4·3 |
Some metals are therefore lighter and some heavier than water.
The table underneath gives the approximate fusing points of some of the metals (Centigrade Scale)—
| (Ice melts at 0°.) | |||||
| Platinum21 | about 1500° | Zinc | ” | 400° | |
| Gold | ” 1200° | Lead | ” | 330° | |
| Silver | ” 1000° | Bismuth | ” | 265° | |
| Cast iron | 1000-1200° | Tin | ” | 235° | |
| Wrought iron | ” 1500° | Sodium | ” | 97° | |
| Copper | ” 1100° | Potassium | ” | 60° | |
| Antimony | ” 432° | Mercury | ” | 40° | |
There are some metals which, instead of fusing,—that is, passing from the solid to the liquid state,—go away in vapour. These are volatile metals. Mercury, potassium, and sodium, can be thus distilled. Some do not expand with heat, but contract (like ice), antimony and bismuth, for instance, while air pressure has a considerable effect upon the fusing point. Some vaporise at once without liquefying; others, such as iron, become soft before melting.
Alloys are combinations of metals which are used for many purposes, and become harder in union. Amalgams are alloys in which mercury is one constituent. Some of the most useful alloys are under-stated:—
| Name of Alloy. | Composition. |
|---|---|
| Aluminium bronze | Copper and aluminium. |
| Bell metal | Copper and tin. |
| Bronze | ” |
| Gun metal | ” |
| Brass | Copper and zinc. |
| Dutch metal | ” |
| Mosaic gold | ” |
| Ormulu | ” |
| Tombac | ” |
| German silver | Copper, nickel, and zinc. |
| Britannia metal | Antimony and tin. |
| Solder | ” |
| Pewter | Tin and lead. |
| Type metal | Lead and antimony (also copper at times). |
| Shot | Lead and arsenic. |
| Gold currency | Gold and copper. |
| Silver currency | Silver and copper. |
| Stereotype metal | Lead, antimony, and bismuth. |
Metals combine with chlorine, and produce chlorides,
Metals combine with sulphu, and produce sulphides,
Metals combine with oxygen, and produce oxides, and so on.
The metals may be classed as follows in divisions:—
| Metals of the alkalies | as Potassium, Sodium, Lithium, Ammonium. |
| Metals of the alkaline earths | as Barium, Calcium, Magnesium, Strontium. |
| Metals of the earths | as Aluminium, Cerium, Didymium, Erbium, Glucinium, Lanthanum, Terbium, Thorium, Yttrium, Zirconium. |
| Metals proper— | |
| Common Metals | as {Iron, Manganese, Cobalt, Nickel, Copper, Bismuth, Lead, Tin, Zinc, Chromium, Antimony. |
| Noble Metals | as {Mercury, Silver, Gold, Platinum, Palladium, Rhodium, Ruthenium, Osmium, Iridium. |
We cannot attempt an elaborate description of all the metals, but we will endeavour to give a few particulars concerning the important ones, leaving many parts for Mineralogy to supplement and enlarge upon. We shall therefore mention only the most useful of the metals in this place. We will commence with Potassium.
Metals of the Alkalies.
Potassium has a bright, almost silvery, appearance, and is so greatly attracted by oxygen that it cannot be kept anywhere if that element be present—not even in water, for combustion will immediately ensue on water; and in air it is rapidly tarnished. It burns with a beautiful violet colour, and[Pg 391] a very pretty experiment may easily be performed by throwing a piece upon a basin of water. The fragment combines with the oxygen of the water, the hydrogen is evolved, and burns, and the potassium vapour gives the gas its purple or violet colour. The metal can be procured by pulverizing carbonate of potassium and charcoal, and heating them in an iron retort. The vapour condenses into globules in the receiver, which is surrounded by ice in a wire basket. It must be collected and kept in naphtha, or it would be oxidised. Potassium was first obtained by Sir Humphrey Davy in 1807. Potash is the oxide of potassium, and comes from the “ashes” of wood.

The compounds of potassium are numerous, and exist in nature, and by burning plants we can obtain potash (“pearlash”). Nitrate of potassium, or nitre (saltpetre), (KNO3), is a very important salt. It is found in the East Indies. It is a constituent of gunpowder, which consists of seventy-five parts of nitre, fifteen of charcoal, and ten of sulphur. The hydrated oxide of potassium, or “caustic potash” (obtained from the carbonate), is much used in soap manufactories. It is called “caustic” from its property of cauterizing the tissues. Iodide, bromide, and cyanide of potassium, are used in medicine and photography.

Soap is made by combining soda (for hard soap), or potash (for soft soap), with oil or tallow. Yellow soap has turpentine, and occasionally palm oil, added. Oils and fats combine with metallic oxides, and oxide of lead with olive oil and resin forms the adhesive plaister with which we are all familiar when the mixture is spread upon linen. Fats boiled with potash or soda make soaps; the glycerine is sometimes set free and purified as we have it. Sometimes it is retained for glycerine soap. Fancy soap is only common soap coloured. White and brown Windsor are the same soap—in the latter case browned to imitate age! Soap is quite soluble in[Pg 392] spirits, but in ordinary water it is not so greatly soluble, and produces a lather, owing to the lime in the water being present in more or less quantity, to make the water more or less “hard.”

Sodium is not unlike potassium, not only in appearance, but in its attributes; it can be obtained from the carbonate, as potassium is obtained from its carbonate. Soda is the oxide of sodium, but the most common and useful compound of sodium is the chloride, or common salt, which is found in mines in England, Poland, and elsewhere. Salt may also be obtained by the evaporation of sea water. Rock salt is got at Salzburg, and the German salt mines and works produce a large quantity. The Carbonate of Soda is manufactured from the chloride of sodium, although it can be procured from the salsoda plants by burning. The chloride of sodium is converted into sulphate, and then ignited with carbonate of lime and charcoal. The soluble carbonate is extracted in warm water, and sold in crystals as soda, or (anhydrous) “soda ash.” The large quantity of hydrochloric acid produced in the first part of the process is used in the process of making chloride of lime. A few years back, soda was got from Hungary and various other countries where it exists as a natural efflorescence on the shores of some lakes, also by burning sea-weeds, especially the common bladder wrack (Fucus vesiculosus), the ashes of which were melted into masses, and came to market in various states of purity. The bi-carbonate of soda is obtained by passing carbonic acid gas over the carbonate crystals. Soda does not attract moisture from the air. It is used in washing, in glass manufactories, in dyeing, soap-making, etc.
Sulphate of Soda is “Glauber’s Salt”; it is also employed in glass-making. Mixed with sulphuric acid and water, it forms a freezing mixture. Glass, as we have seen, is made with silicic acid (sand), soda, potassa, oxide of lead, and lime, and is an artificial silicate of soda.

Lithium is the lightest of metals, and forms the link between alkaline and the alkaline earth metals. The salts are found in many places in solution. The chloride when decomposed by electricity yields the metal.
Cæsium and Rubidium require no detailed notice from us. They were first found in the solar spectrum, and resemble potassium.
Ammonium is only a conjectural metal. Ammonia, of which we have already treated, is so like a metallic oxide that chemists have come to the conclusion that its compounds contain a metallic body, which they have named hypothetically Ammonium. It is usually classed amongst the alkaline metals. The salts of ammonia are important, and have already been mentioned. Muriate (chloride) of ammonia, or sal-ammoniac, is analogous to chloride of sodium and chloride of potassium. It is decomposed by heating it with slaked lime, and then gaseous ammonia is given off.
The Metals of the Alkaline Earths.

Barium is the first of the four metals we have to notice in this group, and will not detain us long, for it is little known in a free condition. Its most important compound is heavy spar (sulphate of baryta), which, when powdered, is employed as a white paint. The oxide of barium, BaO, is termed baryta.
Nitrate of Baryta is used for “green fire,” which is made as follows:—Sulphur, twenty parts; chlorate of potassium, thirty-three parts; and nitrate of baryta, eighty parts (by weight).
Calcium forms a considerable quantity of our earth’s crust. It is the metal of lime, which is the oxide of calcium. In a metallic state it possesses no great interest, but its combinations are very important to us. Lime is, of course, familiar to all. It is obtained by evolving the carbonic acid from carbonate of lime (CaO).
The properties of this lime are its white appearance, and it develops[Pg 394] a considerable amount of heat when mixed with water, combining to make hydrate of lime, or “slaked lime.” This soon crumbles into powder, and as a mortar attracts the carbonic acid from the air, by which means it assumes the carbonate and very solid form, which renders it valuable for cement and mortar, which, when mixed with sand, hardens. Caustic lime is used in whitewashing, etc.
Carbonate of Lime (CaCO3) occurs in nature in various forms, as limestone, chalk, marble, etc. Calc-spar (arragonite) is colourless, and occurs as crystals. Marble is white (sometimes coloured by metallic oxides), hard, and granular. Chalk is soft and pulverizing. It occurs in mountainous masses, and in the tiniest shells, for carbonate of lime is the main component of the shells of the crustacea, of corals, and of the shell of the egg; it enters likewise into the composition of bones, and hence we must regard it as one of the necessary constituents of the food of animals. It is an almost invariable constituent of the waters we meet with in Nature, containing, as they always do, a portion of carbonic acid, which has the power of dissolving carbonate of lime. But when gently warmed, the volatile gas is expelled, and the carbonate of lime deposited in the form of white incrustations upon the bottom of the vessel, which are particularly observed on the bottoms of tea-kettles, and if the water contains a large quantity of calcareous matter, even our water-bottles and drinking-glasses become covered with a thin film of carbonate of lime. These depositions may readily be removed by pouring into the vessels a little dilute hydrochloric acid, or some strong vinegar, which in a short time dissolves the carbonate of lime.
Sulphate of Lime (CaSO4) is found in considerable masses, and is commonly known under the name of Gypsum. It occurs either crystallized or granulated, and is of dazzling whiteness; in the latter form it is termed Alabaster, which is so soft as to admit of being cut with a chisel, and is admirably adapted for various kinds of works of art. Gypsum contains water of crystallization, which is expelled at a gentle heat. But when ignited, ground, and mixed into a paste with water, it acquires the property of entering into chemical combination with it, and forming the original hydrate, which in a short time becomes perfectly solid. Thus it offers to the artist a highly valuable material for preparing the well-known plaster of Paris figures, and by its use the noblest statues of ancient and modern art have now been placed within the reach of all. Gypsum, moreover, has received a valuable application as manure. In water it is slightly soluble, and imparts to it a disagreeable and somewhat bitterish, earthy taste. It is called “selenite” when transparent.
Phosphate of Lime constitutes the principal mass of the bones of animals, and is extensively employed in the preparation of phosphorus; in the form of ground bones it is likewise used as a manure. It appears to belong to those mineral constituents which are essential to the nutrition of animals. It is found in corn and cereals, and used in making bread; so we derive the phosphorus which is so useful to our system.
Chloride of Lime is a white powder smelling of chlorine, and is produced by passing the gas over the hydrate of lime spread on trays for the purpose. It is the well-known “bleaching powder.” It is also used as a disinfectant. The Fluoride of Calcium is Derbyshire spar, or “Blue John.” Fluor spar is generally of a purple hue. We may add that hard water can be softened by adding a little powdered lime to it.
Magnesium sometimes finds a place with the other metals, for it bears a resemblance to zinc. Magnesium may be prepared by heating its chloride with sodium. Salt is formed, and the metal is procured. It burns very brightly, and forms an oxide of magnesia (MgO). Magnesium appears in the formation of mountains occasionally. It is ductile and malleable, and may be easily melted.
Carbonate of Magnesia, combining with carbonate of lime, form the Dolomite Hills. When pure, the carbonate is a light powder, and when the carbonic acid is taken from it by burning it is called Calcined Magnesia.
The Sulphate of Magnesia occurs in sea-water, and in saline springs such as Epsom. It is called “Epsom Salts.” Magnesium wire burns brightly, and may be used as an illuminating agent for final scenes in private theatricals. Magnesite will be mentioned among Minerals.
Strontium is a rare metal, and is particularly useful in the composition of “red-fire.” There are the carbonate and sulphate of strontium; the latter is known as Celestine. The red fire above referred to can be made as follows, in a dry mixture. Ten parts nitrate of strontia, 1½ parts chlorate of potassium, 3½ parts of sulphur, 1 part sulphide of antimony, and ½ part charcoal. Mix well without moisture, enclose in touch paper, and burn. A gorgeous crimson fire will result.
Metals of the Earths.
Aluminium (Aluminum) is like gold in appearance when in alloy with copper, and can be procured from its chloride by decomposition with electricity. It occurs largely in nature in composition with clays and slates. Its oxide, alumina (Al2O3), composes a number of minerals, and accordingly forms a great mass of the earth. Alumina is present in various forms (see Minerals) in the earth, all of which will be mentioned under Crystallography and Mineralogy. The other nine metals in this class do not call for special notice.
Heavy Metals
Iron, which is the most valuable of all our metals, may fitly head our list. So many useful articles are made of it, that without consideration any one can name twenty. The arts of peace and the glories of war are all produced with the assistance of iron, and its occurrence with coal has[Pg 396] rendered us the greatest service, and placed us at the head of nations. It occurs native in meteoric stones.
Iron is obtained from certain ores in England and Sweden, and these contain oxygen and iron (see Mineralogy). We have thus to drive away the former to obtain the latter. This is done by putting the ores in small pieces into a blast furnace (fig. 402) mixed with limestone and coal. The process of severing the metal from its ores is termed smelting, the air supplied to the furnace being warmed, and termed the “hot blast.” The “cold blast” is sometimes used. The ores when dug from the mine are generally stamped into powder, then “roasted,”—that is, made hot, and kept so for some time to drive off water, sulphur, or arsenic, which would prevent the “fluxes” acting properly. The fluxes are substances which will mix with, melt, and separate the matters to be got rid of, the chief being charcoal, coke, and limestone. The ore is then mixed with the flux, and the whole raised to a great heat; as the metal is separated it melts, runs to the bottom of the “smelting furnace,” and is drawn off into moulds made of sand; it is thus cast into short thick bars called “pigs,” so we hear of pig-iron, and pig-lead. Iron is smelted from “ironstone,” which is mixed with coke and limestone. The heat required to smelt iron is so very great, that a steam-engine is now generally employed to blow the furnace. (Before the invention of the steam-engine, water-mills were used for the same purpose.) The smelting is conducted in what is called a blast furnace. When the metal has all been “reduced,” or melted, and run down to the bottom of the furnace, a hole is made, out of which it runs into the moulds; this is called “tapping the furnace.”

Smelting is often confounded with melting, as the names are somewhat alike, but the processes are entirely different; in melting, the metal is simply liquefied, in smelting, the metal has to be produced from ores which often have no appearance of containing any, as in the case of ironstone, which looks like brown clay.
The cone of the furnace, A, is lined with fire-bricks, i i, which is encased by a lining, l l; outside are more fire-bricks, and then masonry, m n;[Pg 397] C is the throat of the furnace; D the chimney. The lower part, B, is called the boshes. As soon as the ore in the furnace has become ignited the carbon and oxygen unite and form carbonic acid, which escapes, and the metal fuses at last and runs away. The coal and ore are continually added year after year. The glassy scum called “slag “ protects the molten iron from oxidation.

The metal drawn from the blast furnace is “pig iron,” or “cast” iron, and contains carbon. This kind of iron is used for casting operations, and runs into sand-moulds. It contracts very little when cooling. It is hard and brittle.


Bar Iron is the almost pure metal. It is remarkably tenacious, and may be drawn into very fine wire or rolled. But it is not hard enough for tools. It is difficult to fuse, and must be welded by hammering at a red heat. Wire-drawing is performed by taking the metal as a bar, and passing it between rollers (fig. 404), which flattens it, and then between a new set, which form cutting edges on the rolled plate (fig. 405), the projections of one set fitting into the hollows of the other closely as in the illustration. The strips of metal come out at the aperture seen at A in the next illustration. These rods are drawn through a series of diminishing holes in a steel plate, occasionally being heated to keep it soft and ductile. When the wire has got to a certain fineness it is attached to a cylinder and drawn away, at the same[Pg 398] time being wound round the cylinder over a small fire. Some metals can be drawn much finer than others. Gold wire can be obtained of a “thickness” (or thinness) of only the 5,000th part of an inch, 550 feet weighing one grain! But platinum has exceeded this marvellous thinness, and wire the 30,000th part of an inch has been produced. Ductility and malleability are not always found in the same metal in proportion. The sizes of wires are gauged by the instrument shown in the margin. The farther the wire will go into the groove the smaller its “size.”


Steel contains a certain amount of carbon, generally about 1 to 2 per cent. Cast steel is prepared from cast iron. Steel from bar-iron has carbon added, and is termed bar-steel. The process is called “cementation,” and is carried on by packing the bars of iron in brick-work boxes, with a mixture of salt and soot, or with charcoal, which is termed “cement.” Steel is really a carbide of iron, and Mr. Bessemer founded his process of making steel by blowing out the excess of carbon from the iron, so that the proper amount—1·5 per cent.—should remain.

A brief summary of the Bessemer process may be interesting. If a bar of steel as soft as iron be made red-hot and plunged into cold water, it will become very hard. If it be then gently heated it will become less hard, and is then fitted for surgical instruments. The various shades of steel are[Pg 399] carefully watched,—the change of colour being due to the varying thickness of the oxide; for we know that when light falls upon very thin films of a substance,—soap-bubbles, for instance,—the light reflected from the under and upper surfaces interfere, and cause colour, which varies with the thickness of the film. These colours in steel correspond to different temperatures, and the “temper” of the steel depends upon the temperature it has reached. The following table extracted from Haydn’s “Dictionary of Science” gives the “temper,” the colour, and the uses of the various kinds of steel.

| Temperature Cent. Fahr. |
Colour. | Uses of Steel. |
|---|---|---|
| 220° = 430° | Faint yellow | Lancets. |
| 232° = 450° | Pale straw | Best razors and surgical instruments. |
| 243° = 470° | Yellow | Ordinary razors, pen-knives, etc. |
| 254° = 490° | Brown | Small shears, scissors, cold chisels, etc. |
| 265° = 510° | Brown and purple spots | Axes, pocket-knives, plane-irons, etc. |
| 277° = 530° | Purple | Table-knives, etc. |
| 288° = 550° | Light blue | Swords, watch-springs, etc. |
| 293° = 560° | Full blue | Fine saws, daggers, etc. |
| 316° = 600° | Dark blue | Hand and pit saws. |
The Bessemer process transfers the metal into a vessel in which there are tubes, through which air is forced, which produces a much greater heat than a bellows does. Thus in the process the carbon of the iron acts as fuel to maintain the fusion, and at the same time by the bubbling of the carbonic acid mixes the molten iron thoroughly.
During the bubbling up of the whole mass of iron, and the extreme elevation of temperature caused by the union of the carbon of the impure iron with the oxygen of the air, the oxide of iron is formed, and as fast as it forms fuses into a sort of glass; this unites with the earthy matters of the “impure” iron, and floats on the upper part as a flux, thus ridding the “cast iron” of all its impurities, with no other fuel than that contained in the[Pg 400] metal itself, and in the air used. When the flame issuing from the “converter” contracts and changes its colour, then the time is known to have arrived when the iron is “ de-carbonized.” The amount of carbon necessary is artificially added, ebullition takes place, a flame of carbonic oxide comes out, and the metal is then run into ingots.
The compounds of iron which are soluble in water have a peculiar taste called chalybeate (like ink). Many mineral springs are so flavoured, and taste, as the immortal Samuel Weller put it, “like warm flat-irons.” Iron is frequently used as a medicine to renew the blood globules.
Protoxide of Iron is known only in combination.
Sesqui-Oxide of Iron is “red ironstone.” Powdered it is called English rouge, a pigment not altogether foreign to our use. In a pure state it is a remedy for arsenical poisoning, and is really the “rust” upon iron.

Bisulphide of Iron is iron pyrites, and is crystalline.
Chloride of Iron is dissolved from iron with hydrochloric acid. It is used in medicine.
Cyanide of Iron makes, with cyanide of potassium, the well-known prussiate of potash (ferro-cyanide of potassium), which, when heated, precipitates Prussian blue (cyanogen and iron).
The Sulphate of the Protoxide is known as copperas, or green vitriol, and is applied to the preparation of Prussian blue.
Manganese is found extensively, but not in any large quantities, in one place; iron ore contains it. It is very hard to fuse, and is easily oxidised. The binoxide is used to obtain oxygen, and when treated with[Pg 401] potassium and diluted, it becomes the permanganate of potassium, and is used as “Condy’s fluid.” It readily oxides organic matters, and is thus a disinfectant. It crystallizes in long, deep, red needles, which are dissolved in water. It is a standard laboratory test. There are other compounds, but in these pages we need not detail them.
Cobalt and Nickel occur together. They are hard, brittle, and fusible. The salts of cobalt produce beautiful colours, and the chloride yields an “invisible” or sympathetic ink. The oxide of cobalt forms a blue pigment for staining glass which is called “smalt.” Nickel is chiefly used in the preparation of German silver and electro-plating. The salts of nickel are green. Nickel is difficult to melt, and always is one of the constituents of meteoric iron, which falls from the sky in aërolites. It is magnetic like cobalt, and is extracted from the ore called kupfer-nickel. A small United-States coin is termed a “nickel.”

Copper is the next metal we have to notice. It has been known for centuries. It is encountered native in many places. The Cornish copper ore is the copper pyrites. The fumes of the smelting works are very injurious, containing, as they do, arsenic and sulphur. The ground near the mines is usually bare of vegetation in consequence of the “smoke.” Sheet copper is worked into many domestic utensils, and the alloy with zinc, termed Brass, is both useful and ornamental. Red brass is beaten into thin leaves, and is by some supposed to be “gold leaf”; it is used in decorative work. Bronze is also an alloy of copper, as are gun-metal, bell-metal, etc.
Next to silver, copper is the best conductor of electricity we have. It is very hard and tough, yet elastic, and possesses malleability and ductility in a high degree. It forms two oxides, and there are several sulphides; the principal of the latter are found native, and worked as ores. The sulphate of copper is termed blue vitriol, and is used in calico-printing, and from it all the (copper) pigments are derived. It is also used in solution by agriculturists to protect wheat from insects. When copper or its alloys are exposed to air and water, a carbonate of copper forms, which is termed verdigris. All copper salts are poisonous; white of eggs is an excellent remedy in such cases of poisoning.
Lead is obtained from galena, a sulphide of lead. It is a soft and easily-worked metal. When freshly cut it has quite a bright appearance,[Pg 402] which is quickly tarnished. Silver is often present in lead ore, and is extracted by Pattison’s process, which consists in the adaptation of the knowledge that lead containing silver becomes solid, after melting, at a lower temperature than lead does when pure. Pure lead therefore solidifies sooner.
One great use of lead is for our domestic water-pipes, which remind us in winter of their presence so disagreeably. Shot is made from lead, and bullets are cast from the same metal. Shot-making is very simple, and before the days of breech-loading guns and cartridges, no doubt many readers have cast bullets in the kitchen and run them into the mould over a basin of water or a box of sand. For sporting purposes lead is mixed with arsenic, and when it is melted it is poured through a sort of sieve (as in the cut) at the top of a high tower. (See figs. 413 and 414). The latter illustration gives the section of the shot tower; A is the furnace, B is the tank for melting the lead, and the metal is permitted by the workman at C to run through the sieve in fine streams. As the lead falls it congeals into drops, which are received in water below to cool them. They are, of course, not all round, and must be sorted. This operation is performed by placing them on a board tilted up, and under which are two boxes. The round shot rush over the first holes and drop into the second box, but the uneven ones are caught lagging, and drop into box No. 1. They are accordingly sent to the furnace again.

The next process is to sort the good shot for size. This is done by sieves—one having holes a little larger than the size of shot required. This sieve passes through it all of the right size and smaller, and keeps the bigger ones. Those that have passed this examination are then put into another sieve, which has holes in it a little smaller than the size of shot wanted. This sieve retains the right shot, and lets the smaller sizes pass, and so on. The shot are sized and numbered, glazed by rolling them in a barrel with graphite, and then they are ready for use. Bullets are made by machinery by the thousand, and made up into cartridges with great speed.

The compounds of lead are also poisonous, and produce “colic,” to[Pg 403] which painters are subject. Red lead, or minium, is a compound of the protoxide and the binoxide, and may be found native. The former oxide is litharge; white lead, or the carbonate of lead, is a paint, and is easily obtained by passing a stream of carbonic acid into a solution of acetate of lead. It is used as a basis of many paints.

Tin is another well-known metal. It is mentioned by Moses. It possesses a silver-like lustre, and is not liable to be oxidised. The only really important ore is called Tinstone, from which the oxygen is separated, and the metal remains. Cornwall has extensive tin mines. Tin is malleable and ductile, and can be beaten into foil or “silver leaf,” or drawn into wire. It prevents oxidation of iron if the latter be covered with it, and for tinning copper vessels for culinary purposes. The Romans found tin in Cornwall, and the term “Stanneries” was applied to the courts of justice among the tin miners in Edward the First’s time. We have already mentioned the alloys of tin. The oxides of tin, “Stannous” and “Stannic,” are useful to dyers. The latter is the tinstone (SnO2). Sulphide of tin is called “Mosaic gold,” and is much used for decorative purposes.

Zinc is procured from calamine, or carbonate of zinc, and blende, or sulphide of zinc. It has for some years been used for many purposes for which lead was once employed, as it is cheap and light. Zinc is a hard metal of a greyish colour, not easily bent, and rather brittle; but when made nearly red-hot, it can be rolled out into sheets or beaten into form by the hammer. Zinc is about six-and-three-quarter times heavier than water. Like many other metals, it is volatile (when heated to a certain extent it passes off into vapour), and the probable reason that it was not known or used of old is that it was lost in the attempt to smelt its ores. Zinc is now obtained by a sort of distil[Pg 404]lation; the ores are mixed with the flux in a large earthen crucible or pot.
We have already noticed the alloy of zinc with copper (brass), and the use of zinc to galvanize iron by covering the latter with a coating of zinc in a bath is somewhat analogous to electro-plating. The metal is largely used as the positive element in galvanic batteries, and for the production of hydrogen in the laboratory. Zinc forms one oxide (ZnO), used for zinc-white. The sulphate of zinc is white vitriol, and the chloride of zinc is an “antiseptic.” Certain preparations of the metal are used in medicine as “ointments” or “washes,” and are of use in inflammation of the eyelids.
Chromium. This “metallic element” is almost unknown in the metallic state. But although little known, the beautiful colours of its compounds make it a very interesting study. The very name leads one to expect something different to the other metals—chroma, colour. The metal is procured from what is known as chrome-ironstone, a combination of protoxide of iron and sesqui-oxide of chromium (FeOCr2O3). By ignition with potassium we get chromic acid and chromate of potassium, a yellow salt which is used to make the other compounds of chromium. The metal is by no means easy to fuse.
Sesqui-Oxide of Chromium is a fine green powder employed in painting porcelain.
Chromate of Lead is termed “chrome yellow,” and in its varieties is employed as a paint.
Chromate of Mercury is a beautiful vermilion. There are numerous other combinations which need not be mentioned here.

Antimony was discovered by Basil Valentine. The Latin term is Stibium, hence its symbol, Sb. It is very crystalline, and of a peculiar bluish-white tint. It will take fire at a certain high temperature, and can be used for the manufacture of “Bengal Lights,” with nitre and sulphur in the proportions of antimony “one,” the others two and three respectively.
The compounds of antimony are used in medicine, and are dangerous when taken without advice. They act as emetics if taken in large quantities. Our “tartar emetic” is well known.
Antimony, in alloy with lead and a little tin, form the type metal to[Pg 405] which we are indebted for our printing. Type-casting is done by hand, and requires much dexterity. A ladle is dipped into the molten metal, and the mould jerked in to fill it properly, and then the type is removed and the mould shut ready for another type; and a skilful workman can perform these operations five hundred times in an hour,—rather more than eight times a minute,—producing a type each time; this has afterwards to be finished off by others. The metal of which type is made consists of lead and antimony; the antimony hardens it and makes it take a sharper impression. The letters are first cut in steel, and from these “dies” the moulds are made in brass, by stamping, and in these the types are cast.
Stereotype consists of plates of metal taken, by casting, from a forme of type set up for the purpose: an impression was formerly carried on by plaster-of-Paris moulds, but lately what is termed the papier-maché process is adopted. The paper used is now made in England, and the prepared sheet is placed upon the type and beaten upon it. Paste is then filled in where there are blanks, and another and thicker sheet of the prepared paper is placed over all, dried, and pressed. When this is properly done the paper is hardened, and preserves an impression of the type set up. The paper mould is then put into an iron box, and molten metal run in. In a very short time a “stereotype” plate is prepared from the paper, which can be used again if necessary. The metal plate is put on the machine.
There are several compounds of antimony, which, though valuable to chemists, would not be very interesting to the majority of readers. We will therefore at once pass to the Noble Metals.
The Noble Metals.
There are nine metals which rank under the above denomination:—Mercury, Silver, Gold, Platinum, Palladium, Rhodium, Ruthenium, Osmium, Iridium. We will confine ourselves chiefly to the first four on the list.
Mercury, or Quicksilver, is the first of the metals which remain unaltered by exposure to atmospheric air, and thus are supposed to earn their title of nobility. Mercury is familiar to us in our barometers, etc., and is fluid in ordinary temperatures, though one of the heaviest metals we possess. It is principally obtained from native cinnabar, or sulphide of mercury (vermilion), and the process of extraction is very easy. Mercury was known to the ancients, and is sometimes found native. In the mines the evil effects of the contact with mercury are apparent.
This metal forms two oxides,—the black (mercurous) oxide, or suboxide (Hg2O), and the red (mercuric) oxide, or red precipitate. The chlorides are two,—the subchloride, or calomel, and the perchloride, or corrosive sublimate. The sulphides correspond with the oxides; the mercuric sulphide has been mentioned. Its crimson colour is apparent in nature, but the Chinese prepare it in a particularly beautiful form. Many[Pg 406] amalgams are made with mercury, which is useful in various ways that will at once occur to the reader.
Silver is the whitest and most beautiful of metals, and its use for our plate and ornaments is general. It is malleable and ductile, and the best conductor of electricity and heat that we have. It is not unfrequently met with in its native state, but more generally it is found in combination with gold and mercury, or in lead, copper, and antimony ores. The mines of Peru and Mexico, with other Western States of America, are celebrated—Nevada, Colorado, and Utah in particular. The story of the silver mine would be as interesting as any narrative ever printed. The slavery and the death-roll would equal in horror and in its length the terrible records of war or pestilence. We have no opportunity here to follow it, or its kindred metals with which it unites, on the sentimental side; but were the story of silver production written in full, it would be most instructive.

Silver is found with lead (galena), which is then smelted. The lead is volatilized, and the silver remains. It is also extracted by the following process, wherein the silver and golden ore is crushed and washed, and quicksilver, salt, and sulphate of copper added, while heat is applied to the mass. From tank to tank the slime flows, and deposits the metals, which are put into retorts and heated. The mercury flies off; the silver and gold remain in bars.
In some countries, as in Saxony and South America, recourse is had to another process, that of amalgamation, which depends on the easy solubility of silver and other metals in mercury. The ore, after being reduced to a fine powder, is mixed with common salt, and roasted at a low red heat, whereby any sulphide of silver the ore may contain is converted into chloride. The mixture is then placed, with some water and iron filings, in a barrel which revolves round its axis, and the whole agitated for some time, during which process the chloride of silver becomes reduced to the metallic state. A portion of mercury is then introduced, and the agitation continued. The mercury combines with the silver, and the amalgam is then separated by washing. It is afterwards pressed in woollen bags to free it from the greater part of the mercury, and then heated, when the last trace of mercury volatilizes and leaves the silver behind.
Nitrate of Silver is obtained when metallic silver is dissolved in nitric acid. It is known popularly as lunar caustic, and forms the base of “marking inks.” Chloride of silver is altered by light, but the iodide of silver is even more rapidly acted on, and is employed in photography. Fulminating silver is oxide of silver digested in ammonia. It is very dan[Pg 407]gerous in inexperienced hands. It is also prepared by dissolving silver in nitric acid, and adding alcohol. It cools in crystals. Fulminating mercury is prepared in the same way.
Gold is the most valuable of all metals,—the “king of metals,” as it was termed by the ancients. It is always found “native,” frequently with silver and copper. Quartz is the rock wherein it occurs. From the disintegration of these rocks the gold sands of rivers are formed, and separated from the sands by “washing.” In Australia and California “nuggets” are picked up of considerable size.
It is a rather soft metal, and, being likewise costly, is never used in an absolutely pure state. Coins and jewellery are all alloyed with copper and silver to give them the requisite hardness and durability. Gold is extremely ductile, and very malleable. One grain of gold may be drawn into a wire five hundred feet in length, and the metal may be beaten into almost transparent leaves 1/200000 of an inch in thickness!

Aqua-regia, a mixture of hydrochloric and nitric acids, is used to dissolve gold, which is solved only by selenic acid, though the free chlorine will dissolve it. Faraday made many experiments as to the relation of gold to light. (See “Phil. Trans.,” 1857, p. 145.) The various uses of gold are so well known that we need not occupy time and space in recording them. Gilding can be accomplished by immersing the articles in a hot solution of chloride of gold and bicarbonate of potash mixed; but the electro process is that now in use, by which the gold precipitates on the article to be plated.
We have already described the process of electro-plating in the case of silvered articles, and we need only mention that electro-gilding is performed very much in the same way. But gilding is also performed in other ways; one of which, the so-called water gilding, is managed as follows. Gilding with the gold-leaf is merely a mechanical operation, but water-gilding is effected by chemistry.
Water-gilding is a process (in which, however, no water is used) for covering the surface of metal with a thin coating of gold; the best metal for water-gilding is either brass, or a mixture of brass and copper. A mixture of gold and mercury, in the proportion of one part of gold to eight of mercury, is made hot over a fire till they have united; it is then put into a bag of chamois-leather, and the superfluous mercury pressed out. What remains is called an “amalgam”; it is soft, and of a greasy nature, so that it can be smeared over any surface with the fingers. The articles to be gilt[Pg 408] are made perfectly clean on the surface, and a liquid, made by dissolving mercury in nitric acid (aqua-fortis), is passed over them with a brush made of fine brass wire, called a “scratch-brush.” The mercury immediately adheres to the surface of the metal, making it look like silver; when this is done, a little of the amalgam is rubbed on, and the article evenly covered with it. It is then heated in a charcoal fire till all the mercury evaporates, and the brass is left with a coating of gold, which is very dull, but may be burnished with a steel burnisher and made bright if necessary. In former times articles were inlaid with thin plates of gold, which were placed in hollows made with a graver, and melted in, a little borax being applied between.
When a solution of “chloride of gold” is mixed with ether, the ether takes the gold away from the solution, and may be poured off the top charged with it. This solution, if applied to polished steel by means of a camel-hair pencil, rapidly evaporates, leaving a film of gold adhering to the steel, which, when burnished with any hard substance, has a very elegant appearance. In this way any ornamental design in gold may be produced, but it is not very durable. The gilt ornaments, scrolls, and mottoes on sword-blades, are sometimes done in this way.
Platinum is the heaviest of all metals, gold being next. Platinum is practically infusible, and quite indifferent to reagents. It is therefore very useful in certain manufactories, and in the laboratory. It can be dissolved by aqua-regia. The stills for sulphuric acid are made of platinum, and the metal is used for Russian coinage, but must be very difficult to work on account of its infusible property.

In the finely-divided state it forms a gray and very porous mass, which is known as spongy platinum, and possesses the remarkable property of condensing gases within its pores. Hence, when a jet of hydrogen is directed upon a piece of spongy platinum, the heat caused by its condensation suffices to inflame the gas. This singular power has been applied to the construction of a very beautiful apparatus, known as Döbereiner’s lamp, which consists of a glass jar, a, covered by a brass lid, e, which is furnished with a suitable stop-cock, c, and in connection with a small bell jar, f, in which is suspended, by means of a wire, a cylinder of metallic zinc, z. When required for use, the outer jar is two-thirds filled with a mixture of one part sulphuric acid and four parts water, and the stop-cock opened to allow the escape of atmospheric air, the spongy platinum contained in the small brass cylinder, d, being covered by a piece of paper. The stop-cock is then closed, and the bell jar, f, allowed to fill with hydrogen, and after it has been filled and emptied several times, the paper is removed from the platinum and the cock is again opened, when the gas, which escapes first, makes the metal red-hot and finally inflames. This property of platinum is also used in the “Davy” lamp.
The remaining metals do not call for detailed notice.
In conclusion, we may refer to the following statement, which in general terms gives the properties of the metals, their oxides and sulphides for ordinary readers.
General Classification of the Metals.
The metals admit of being really distinguished by the following table, in which they are presented in several groups, according to their peculiar properties, and each distinguished by a particular name:—
| Metals. | Properties of the | |
|---|---|---|
| Oxides. | Sulphides. | |
| (A.) Light Metals. Specific gravity from 0·8 to 1; never occur in the uncombined state. |
Powerful bases; possessing a strong affinity for water, and form with it hydrates. They yield their oxygen to carbon only at a white heat. | Powerful bases, which oxidize in the air, and form sulphates; when treated with acids evolve hydrosulphuric acid. |
| (a.) Alkaline Metals. 1. Potassium. 2. Sodium. (Ammonium.) |
Highly caustic; powerful bases, separate all other oxides from their combinations with acids; are very soluble in water, and do not lose their water of hydration at the highest temperatures; attract carbonic acid rapidly from the air. |
Caustic; strong bases; very soluble in water, and dissolve a large quantity of sulphur, which is separated on addition of an acid as a white powder, termed milk of sulphur; they were formerly termed liver of sulphur. |
| (b.) Metals of the Alkaline Earths. 3. Calcium. 4. Barium. 5. Strontium. |
Caustic; strong bases; slightly soluble in water; lose their water of hydration at a moderate heat, and powerfully absorb carbonic acid. | Caustic; strong bases; dissolve sulphur, and are partly soluble in water, and partly insoluble. |
| (c.) Metals of the Earths proper. 6. Magnesium. 7. Aluminium. |
Weak bases, Feebly caustic, or not caustic. insoluble in water. |
Insoluble in water. |
| (B.) Heavy Metals. Specific gravity from 5 to 21; are found chiefly in combination with oxygen, and frequently with sulphur and arsenic; some are native. |
Feebler bases than the foregoing, some are acids; insoluble in water, and lose their water of hydration at a moderate heat. | Neutral compounds; insoluble in water; antimony and several of the rarer metals produce compounds with sulphur, which deport themselves as acids. |
| (a.) Common Metals. Become oxidized in the air. 8. Iron. 9. Manganese. 10. Cobalt. 11. Nickel. 12. Copper. 13. Bismuth. 14. Lead. 15. Tin. 16. Zinc. 17. Chromium. 18. Antimony. |
With few exceptions, are soluble in acids, and, when ignited with carbon at a red heat, yield their oxygen; are, for the most part, fusible and non-volatile. | Those occurring in nature are somewhat brass-like in appearance, and are termed pyrites and blendes. Those which are artificially prepared have peculiarcolours; by heat they are converted into sulphates. |
| (b.) Noble Metals. Unchangeable in the air. 19. Mercury. 20. Silver. 21. Gold. 22. Platinum. |
Have more the properties of acids than of bases; are decomposed by ignition into oxygen and metal. | With the exception of sulphide of mercury, they leave the pure metal when ignited. |
CHAPTER XXX.
ORGANIC CHEMISTRY.
RADICALS—ACIDS—BASES—NEUTRALS.
In the introduction to these brief chapters upon Chemistry, we said that the science was divided into two sections, the first section consisting of the simple combinations, and the other of compound combinations. The latter being met with chiefly in animal and vegetable matter, as distinguished from dead or inert matter, was termed Organic. This distinction will be seen below.
| COMBINATIONS OF SIMPLE GROUPS. | COMBINATIONS OF COMPOUND GROUPS. |
|---|---|
| Inorganic. | Organic. |
| I. Elements and their Combinations. (1) Non-Metallic. (2) Metallic. |
I. Compound Radicals and their Combinations. |
| II. Peculiar Decompositions of the above. (1) By Electricity. (2) By Light. |
II. Peculiar Decompositions of the above. (1) Spontaneous. (2) Dry Distillation. |
We have already placed before our readers the elements and their simple combinations, and have incidentally mentioned the decomposition by electricity and by light. In the section upon Electricity the positive and negative poles are explained. Oxygen appears always at the positive pole, potassium at the negative. The other simple bodies vary. Chlorine, in combination with oxygen, is evolved at the negative pole, but when with hydrogen at the positive pole. In the series below each element behaves electro-negatively to those following it, and electro-positively to those above it; and the farther they are apart the stronger their opposite affinities are.
Electrical Relation of the Elements.
- Oxygen.
- Sulphur.
- Nitrogen.
- Chlorine.
- Bromine.
- Iodine.
- Fluorine.
- Phosphorus.
- Arsenic.
- Carbon.
- Chromium.
- Boron.
- Antimony.
- Silicium.
- Gold.
- Platinum.
- Mercury.
- Silver.
- Copper.
- Bismuth.
- Lead.
- Cobalt.
- Nickel.
- Iron.
- Zinc.
- Hydrogen.
- Manganese.
- Aluminium.
- Magnesium.
- Calcium.
- Strontium.
- Barium.
- Sodium.
- Potassium.
The importance of these facts to science is unmistakable, and, indeed, many attempts have been made to explain, from the electrical condition of the elements, the nature of chemical affinity, and of chemical phenomena in general.
Electrotyping is another instance of decomposition by means of electricity, and respecting decomposition by light we know how powerful the action of the sun’s rays are upon plants, and for the evolution of oxygen. The daguerreotype and photographic processes are also instances which we have commented upon. So we can pass directly to the consideration of the compound groups.
In nearly every complex organic compound we have a relatively simple one of great stability, which is termed the radical, which forms, with other bodies, a compound radical.22 In these complex groups we find certain elements generally,—viz., carbon, hydrogen, nitrogen, sulphur, and phosphorus. Some compounds may consist of two of these, but the majority contain three (hydrogen, oxygen, and carbon). Many have four (carbon, oxygen, hydrogen, and nitrogen), and some more than four, including phosphorus and sulphur. Others, again, may contain chlorine and its relatives, arsenic, etc., in addition. Now we will all admit that in any case in which carbon is present in composition with other simple bodies forming an organic body, and if that body be ignited in the air, it burns and leaves (generally) a black mass. This is a sure test of the presence of carbon, and forms an organic compound. Similarly in decomposition nitrogen and sulphur in combination inform us they are present by the odour they give off. We need not go farther into this question of radicals and compound radicals than to state that a compound radical plays the part of an element in combination. We find in alcohol and ether a certain combination termed Ethyl. This “compound radical” occurs in same proportions in ether, chloride of ethyl, iodide of ethyl, etc., as C2H5; so it really acts as a simple body or element, though it is a compound of carbon and hydrogen. A simple radical is easily understood; it is an element, like potassium, for instance. We may now pass to the organic combinations classified into Acids, Bases, and Indifferent, or Neutral, Bodies.
I. Acids.
There are several well-known organic acids, which we find in fruits and in plants. They are volatile and non-volatile; acids are sometimes known as “Salts of Hydrogen.” We have a number of acids whose names are familiar to us,—viz., acetic, tartaric, citric, malic, oxalic, tannic, formic, lactic, etc.
Acetic acid (HC2H4O2) is a very important one, and is easily found when vegetable juices, which ferment, are exposed to the air, or when wood and other vegetable matter is subjected to the process of “dry distillation.[Pg 412]” Vinegar contains acetic acid, which is distilled from wood, as we shall see presently. Vinegar is made abroad by merely permitting wine to get sour; hence the term Vin-aigre. In England vinegar is made from “wort,” of malt which is fermented for a few days, and then put into casks, the bung-holes of which are left open for several weeks, until the contents have become quite sour. The liquid is then cleared by isinglass. The vinegar of commerce contains about 6 per cent. of pure acetic acid, and some spirit, some colouring matter, and, of course, water. Wood vinegar (pyroligneous acid) is used for pickles. The ordinary vinegar when distilled is called white vinegar, and it may also be obtained from fruits, such as gooseberries or raspberries.


Acetic acid, or “wood vinegar,” is prepared as follows:—There are some large iron cylinders set in brickwork over furnaces, and these cylinders have each a tube leading to a main pipe in which the liquid is received for condensation. The cylinders, which contain about seven or eight hundredweight, are filled with logs of wood, either oak, beech, birch, or ash, the door is closely fastened, and the joints smeared with clay; the fires are now lighted and kept up all day, till the cylinders are red-hot; at night they are allowed to cool. In the morning, the charcoal, into which the wood is now converted, is withdrawn, and a fresh charge supplied; it is then found that about thirty or forty gallons of liquid has condensed in the main tube from each cylinder, the remainder being charcoal and gases which pass off; the liquid is acid, brown, and very offensive, and contains acetic acid,[Pg 413] tar, and several other ingredients, among which may be named creosote; it is from this source all the creosote, for the cure of toothache, is obtained. To purify this liquid it is first distilled, and this separates much of the tar; it is then mixed with lime, evaporated to dryness, and heated to expel the remaining tar and other impurities; it is next mixed with sulphate of soda and water, and the whole stirred together; the soda, now in union with the acetic acid, is washed out from the lime and strained quite clear; it is afterwards evaporated till it crystallises, and vitriol (sulphuric acid) then added; finally the acetic acid is distilled over, and the sulphuric acid left in union with the soda, forming sulphate of soda, to be used in a similar process for the next batch of acid. The acetic acid is now quite colourless, transparent, and very sour, possessing a fragrant smell. This is not pure acetic acid, but contains a considerable quantity of water. The acetic acid of commerce, mixed with seven times its bulk of water, forms an acid of about the strength of malt vinegar, perfectly wholesome, and agreeable as a condiment.

Pure acetic acid may be made by mixing dry acetate of potash with oil of vitriol in a retort, and distilling the acetic acid into a very cold receiver; this, when flavoured with various volatile oils, forms the aromatic vinegar sold by druggists. It is a very strong acid, and if applied to the skin will quickly blister it.

Acetate of lead, or sugar of lead, is obtained by dissolving oxide of[Pg 414] lead in vinegar. A solution of this salt makes the goulard water so familiar to all. Acetate of lead is highly poisonous.
Acetate of copper is verdigris, and poisonous. Other acetates are used in medicine.
We may pass quickly over some other acids. They are as follows:—
Tartaric Acid (C4H6O6) is contained in grape juice, and crystallizes in tabular form. The purified powdered salt is cream of Tartar.
Citric Acid (C6H8O7) is found native in citrons and lemons, as well as in currants and other fruits. It is an excellent anti-scorbutic.
Malic Acid (C4H6O5) is found chiefly in apples, as its name denotes (malum, an apple). It is prepared from mountain-ash berries.
Oxalic Acid (C2H2O4). If we heat sugar with nitric acid we shall procure this acid. It is found in sorrel plants.
Tannic Acid (C27H22O17). It is assumed that all vegetables with an astringent taste contain this acid. Tannin is known for its astringent qualities. The name given to this acid is derived from the fact that it possesses a property of forming an insoluble compound with water, known as leather. Tanning is the term employed. Tannin is found in many vegetable substances, but oak bark is usually employed, being the cheapest. The “pelts,” hides, or skins, have first to be freed from all fat or hair by scraping, and afterwards soaking them in lime and water. Then they are placed in the tan-pit between layers of the bark, water is pumped in, and the hides remain for weeks, occasionally being moved from pit to pit, or relaid, so as to give all an equal proportion of pressure, etc. The longer the leather is tanned—it may be a year—the better it wears.
Skins for gloves and binding are tanned with “sumach,” or alum and salt. Sometimes the leather is split by machinery for fine working. Parchment is prepared from the skins of asses, sheep, goats, and calves, which are cleaned, and rubbed smooth with pumice stone.
Tannic acid, with oxide of iron, produces Ink, for the gall-nut contains a quantity of the acid. All the black inks in use generally are composed of green vitriol (sulphate of iron) in union with some astringent vegetable matter; the best is the gall-nut, although, for cheapness, logwood and oak bark have each been used. An excellent black ink may be made by putting into a gallon stone bottle twelve ounces of bruised galls, six ounces of green vitriol, and six of common gum, and filling up the bottle with rain water; this should be kept three or four weeks before using, shaking the bottle from time to time.
Blue ink has lately been much used; it is made by dissolving newly-formed Prussian blue in a solution of oxalic acid. To make it, dissolve[Pg 415] some yellow prussiate of potash in water in one vessel, and some sulphate of iron in another, adding a few drops of nitric acid to the sulphate of iron; now mix the two liquids, and a magnificent blue colour will appear, in the form of a light sediment; this is to be put upon a paper filter, and well washed by pouring over it warm water, and allowing it to run through; a warm solution of oxalic acid should now be mixed with it, and the Prussian blue will dissolve into a bright blue ink.

Red ink is made by boiling chips or raspings of Brazil wood in vinegar, and adding a little alum and gum; it keeps well, and is of a good colour. A red ink of more beautiful appearance, but not so durable, may be made by dissolving a few grains of carmine in two or three teaspoonfuls of spirit of hartshorn.
Marking ink is made by dissolving nitrate of silver in water, and then adding some solution of ammonia, a little gum water, and some Indian ink to colour it. Printers’ ink is made by grinding drying oil with lamp-black.
The powdered gall-nut is an excellent test for iron in water. It will turn violet if any iron be present.

Formic Acid (CH2O2) is the caustic means of defence employed by ants, hence the term formic. It can be artificially prepared by distilling a mixture of sugar, binoxide of manganese, and sulphuric acid. On the skin it will raise blisters.
Lactic Acid (C3H6O3) is present in vegetable and animal substances. Sour whey contains it, and the presence of the acid in the whey accounts for its power of removing from table-linen stains. When what is called “lactic fermentation” occurs, milk is said to be “turned.”
II.
Bases.
The definition of a base is not easy. We have described bases as substances which, combining with acids, form salts, but the definition of a base is as unsatisfactory as that of acid or salt. All vegetable bases contain nitrogen, are usually very bitter, possess no smell or colour, and are insoluble in water. They are usually strong poisons, but very useful in medicine.
The most important are the following bases:—
Quinine is contained in the cinchona (yellow) bark. One hundred parts of the bark have been calculated to yield three of quinine.
Morphine is the poisonous base of opium, which is the juice of the poppy, and is prepared chiefly in India and China.
Nicotine is the active principle of tobacco, and varies in quantity in different tobaccos. Havannah tobacco possesses the least. It is a powerful poison, very oily, volatile, and inflammable.
Conia is prepared from the hemlock. It is fluid and volatile. It is also a deadly poison, and paralyses the spine directly.

Strychnine is found in poisonous trees, particularly in the nux-vomica seeds of Coromandel. It produces lock-jaw and paralysis. There is no antidote for strychnine; emetics are the only remedy.
The above are chiefly remarkable for their uses in medicine, and in consequence of their highly poisonous character are best left alone by unpractised hands.
A German chemist, named Serturner, was the first to extract the active principle from Opium. The question of opium importation has lately been attracting much attention, and the opinions concerning its use are divided. Probably in moderation, and when used by ordinary people (not demoralized creatures), it does little harm.

Opium is the juice of the “common” poppy, and derives its name from the Greek opos, juice. The plant is cultivated in India, Persia, and Turkey. After the poppy has flowered the natives go round, and with a sharp instrument wound, or puncture, every poppy head. This is done very early in the morning, and under the influence of the sun during the day the juice oozes out. Next morning the drops are scraped off. The juice is then placed in pots, dried, and sent for export. The “construction” of opium is very complicated, for it contains a number of ingredients, the most important being morphia, narcotine, meconic acid, and codeia. It is to the first named constituent that the somnolent effect of opium is due.
III.
Indifferent Substances.
There are a great number of so-called “indifferent” substances to which we cannot be indifferent. Such bodies as these have neither acid nor basic properties, and stand no comparison with salts. They are of great importance, forming, as they do, the principal nutriment of animals. Some contain nitrogen, some do not; they may therefore be divided into nitrogenous and non-nitrogenous substances; the former for solid portions of the body, the latter for warmth.
We will take the latter first, and speak of some of them—such as starch, gum, sugar, etc.
Starch is found in the roots of grain, in the potato, dahlia, artichoke, etc., and by crushing the parts of the plant, and washing them, the starch can be collected as a sediment. In cold water and in spirits of wine starch is insoluble. The various kinds of starch usually take their names from the plants whence they come. Arrowroot is obtained from the West Indian plant Maranta Arundinacea. Cassava and tapioca are from the manioc; sago, from the sago palm; wheat starch, and potato starch are other examples.

If starch be baked in an oven at a temperature of about 300° it becomes, to a great extent, soluble in cold water, forming what is called “British gum”; this is largely used for calico printing and other purposes; if boiled in water under great pressure, so that the temperature can be raised to the same degree, it is also changed into an adhesive sort of gum, “mucilage”; this is the substance made use of by the government officials to spread over the backs of postage and receipt stamps to make them adhere. The starch of grain, during germination, or growth, contains diastase, which converts the starch into gum and sugar; the same effect can be produced by heating starch with diluted sulphuric acid.
Gum found in plants is chiefly procured from the Mimosa trees, from which it flows in drops, and is called Gum Arabic. There are other so-called “gums,” but this is the one generally referred to.
Sugar exists in fruits, roots, and in the stalks of plants, in the juice of the cane, maple, and beet-root particularly. The canes are crushed, the juice is clarified with lime to prevent fermentation, and the liquid is evaporated. It is then granulated and cleared from the molasses. Sugar, when heated, becomes dark, and is called “caramel.” It is used for colouring brandy, and gives much difficulty to the sugar refiners.



Sugar refining is conducted as follows. The raw (brown) sugar is mixed into a paste with water, and allowed to drain. The sugar thus becomes white. It is then dissolved in water, with animal charcoal and bullocks’ blood. The liquid is boiled, and put into a dark cistern with holes at the bottom, and cotton fibres being fastened in the holes, are hung into another dark cistern, into which the liquid runs pure and white. It is then pumped into a copper vessel,—vacuum pan,—and condensed to the proper consistence. Subsequently it is poured into conical moulds, and pure syrup poured upon the crystal shapes. The caramel is then removed through a hole at the end. The moulds or loaves are then dried, and if not even or elegant they are turned in a lathe. Finally they are packed up as “loaf sugar.” Sugar undergoes no decomposition, and is the cause of non-decomposition in other substances. For this reason it is employed in “preserving” fruit, etc. Sugar is obtained from beet by crushing and rasping the roots, as the cane is treated.
Spirit of Wine, or Alcohol, is not a natural product. It is found by the decomposition of grape-sugar by fermentation. There is a series of alcohols which exhibit a regular gradation, founded, so to speak, upon one, two, or three molecules of water. They are called respectively alcohols, glycols, and glycerins. Thus we have—
- Alcohols.
- Methylic alcohol.
- Ethylic “
- Prophylic “
- Amylic “
- Glycols.
- Enthelein glycol.
- Prophylene “
- Butylene “
- Amylene “
- Glycerins.
- (Ordinary Glycerine is the only one known.)
The cetyl and melissylic alcohols are contained in spermaceti and bees-wax respectively. The usual alcohol is the Vinic, a transparent, colourless liquid, which is the spirituous principle of wine, spirits, and beer, and when sugar is fermented the alcohol and carbonic acid remain.
Spirits of wine has a very powerful affinity for water, and thus the use of stimulants in great quantity is to be deprecated, for alcohol absorbs the water from the mucous membranes of the stomach and the mouth, making them dry and hard. The state of “intoxication,” unfortunately so familiar, is the effect produced by alcohol upon the nerves. We append a list of the beverages which are most in use, and the percentage of alcohol in each according to Professor Hart:—
| Port | 15 | per cent. |
| Madeira | 14·5 | ” |
| Sherry | 14 | ” |
| Claret | 8 | ” |
| Ale | 6 | ” |
| Porter | 5 | ” |

Spirit of wine is contained in many mixtures, and for the purpose of ascertaining how much alcohol may be in wine, or any other liquid, a hydrometer is used (fig. 432). This instrument consists of a glass tube with a bulb at the end. It is put into water, and the place the water “cuts” is marked by a line on the stem, and called zero 0°. Spirit of wine has less specific gravity than water, so in absolute alcohol the instrument will sink lower than in water, and will descend to a point which is marked 100. In any mixture of alcohol and water, of course the hydrometer will rise or sink between the extreme points accordingly as the mixture may contain less alcohol or more. So a scale can be furnished. The instrument, as described, was invented by MM. Gay-Lussac and Tralles, and called the “percentage” hydrometer. There are many other instruments marked in a more or less arbitrary manner. We append a comparative table of a few hydrometers. (See page 420.)
Ether, or sulphuric ether, is a mixture of spirits of wine with sulphuric acid, and distilled. It loses water, and the product is ether, which is volatile, and transparent, with a peculiarly penetrating odour. It will not mix with water, and if inhaled will produce a similar effect to chloroform.
Comparative Table of Hydrometers.
| Specific Gravity. | Percentage Volume (Tralles). | Percentage Weight, at 60° F. | Degree, according to Cartier. | Degree, according to Beck. | Degree, according to Baumé. |
|---|---|---|---|---|---|
| 1·000 | 0 | 0 | 10 | 0 | 10 |
| 0·991 | 5 | 4·0 | ... | ... | ... |
| 0·985 | 10 | 8·0 | 12 | ... | ... |
| 0·980 | 15 | 12·1 | ... | 3 | 13 |
| 0·975 | 20 | 16·2 | ... | ... | ... |
| 0·970 | 25 | 20·4 | 14 | 5 | ... |
| 0·964 | 30 | 24·6 | 15 | 6 | 15 |
| 0·958 | 35 | 28·9 | ... | ... | 16 |
| 0·951 | 40 | 33·4 | ... | 9 | 17 |
| 0·942 | 45 | 37·9 | 18 | ... | ... |
| 0·933 | 50 | 42·5 | ... | 12 | 20 |
| 0·923 | 55 | 47·2 | 21 | 14 | ... |
| 0·912 | 60 | 52·2 | ... | 16 | 24 |
| 0·901 | 65 | 57·2 | 24 | 19 | ... |
| 0·889 | 70 | 62·5 | 27 | ... | 28 |
| 0·876 | 75 | 67·9 | ... | 24 | ... |
| 0·863 | 80 | 73·5 | 30 | 27 | 32 |
| 0·848 | 85 | 79·5 | 35 | 30 | 35 |
| 0·833 | 90 | 85·7 | ... | 34 | 38 |
| 0·815 | 95 | 92·4 | 40 | 38 | 42 |
| 0·793 | 100 | 100·0 | 44 | 44 | 48 |
Chloroform is transparent, and will sink in water. Diluted alcohol with hypo-chloride of lime, will produce it. When inhaled, chloroform produces a pleasing insensibility to pain, and is useful in surgery.
A certain compound of alcohol with mercury dissolved in nitric acid will cause decomposition, and white crystals will eventuate. These compound crystals are termed fulminating mercury.
We must now pass rapidly over the few remaining subjects we have to notice, such as fats and soaps, wax, oils, etc.
Fats are of the greatest use to man, particularly in cold climates, for upon them depends the heat of the body. Fatty acid, if liquid, is known as oleic acid; if solid, stearic acid. Soaps are compounds of fatty acids. Many “fats” are consumed as food, others as fuel or for lighting purposes, in the shape of oils. Such oils are not primarily useful for burning. Petroleum and other mineral oils are found in enormous quantities in America.
There are what we term fixed oils, and essential or volatile oils. A list is annexed as given by “Hadyn’s Dictionary of Science”:—
Fixed Oils.
- Drying.
- Linseed oil.
- Poppy oil.
- Sunflower oil.
- Walnut oil.
- Tobacco-seed oil.
- Cress-seed oil.
- Non-Drying.
- Almond oil.
- Castor oil.
- Colza oil.
- Oil of mustard.
- Rape-seed oil.
- Olive oil, etc.
Essential Oils.
- Oil of anise.
- Oil of bergamot.
- Oil of carraway.
- Oil of cassia.
- Oil of cedar.
- Oil of cloves.
- Oil of lavender.
- Oil of lemon.
- Oil of mint.
- Oil of myrrh.
- Oil of nutmeg.
- Oil of peppermint.
- Oil of rose.
- Oil of turpentine.
Vegetable oils are obtained by crushing seeds; animal oils come from the whale and seal tribe. Paraffin oil comes from coal. Linseed is a very drying oil, and on it depends the drying power of paint. We know olive oil will not dry on exposure to the air. Oiled silk is made with linseed oil. When oil is drying in the air considerable heat is evolved, and if oiled substances be left near others likely to catch fire, spontaneous combustion may ensue. Oil of turpentine is found in the pine and fir trees, and many of the oils above mentioned are used by perfumers, etc., the rose oil, or attar of roses, being an Eastern compound.

Allied to the volatile oils are the RESINS, which are non-conductors of electricity. They are vegetable products. They are soluble in alcohol, in the volatile oils, or in ether, and these solutions are called varnishes; the solvent evaporates and leaves the coating. Turpentine, copal, mastic, shellac, caoutchouc, and gutta-percha are all resinous bodies. Amber is a mineral resin, which was by the ancients supposed to be the “tears of birds” dropped upon the seashore. Moore refers to this in his poetic “Farewell to Araby’s Daughter”—
Amber is not soluble either in water or alcohol; it is, however, soluble in sulphuric acid. It takes a good polish, and when rubbed is very electrical. It is composed of water, an acid, some oil, and an inflammable gas, which goes off when the amber is distilled.
The well-known camphor is got from a tree called the “Laurus Camphora”; it is a white, waxy substance, and can be obtained by oxidizing certain volatile oils. It is generally produced from the Laurus Camphora in a “still.” The behaviour of a piece of camphor in pure water is curious, but its motions can be at once arrested by touching the water or dropping oil on the surface. This phenomenon is due to the surface tension of the liquid, which diminishes when it is in contact with the vapour of the substance.
Nitrogenous Substances.
There are certain albuminous compounds which we must mention here. These are albumen, fibrine, and caseine. Albumen is the white of egg; fibrine is, when solid, our flesh and muscular fibre, while caseine is the substance of cheese. These are very important compounds, and the albuminous bodies are of the very highest importance as food, for the solid portion of blood, brain, and flesh consist, in a great measure, of them. Albumen, fibrine, and caseine contain carbon, hydrogen, nitrogen, and oxygen, with sulphur and phosphorus.
Albumen. The most familiar and the almost pure form of albumen is in the white of eggs, which is albuminate of sodium. It also exists in the serum of the blood, and therefore it is largely found in the animal kingdom. It can also be extracted from seed or other vegetable substances, but it is essentially the same. Albumen is very useful as an antidote to metallic poisons. It forms about 7 per cent. of human blood. It is soluble up to about 140° Fah.; it then solidifies, and is precipitated in a white mass. Albumen is used in the purification of sugar, etc.
Fibrine is found in a liquid condition in blood. The vegetable fibrine (gluten) is prepared by kneading wheat flour in a bag till the washings are no longer whitened. Like albumen it is found both in a solid and liquid state.
Caseine is seen in the skin which forms upon milk when heated, and forms about 3 per cent. of milk, where it exists in a soluble state, owing to the presence of alkali; but caseine, like albumen, is only soluble in alkaline solutions. As we have said, it is the principal constituent of cheeses. Caseine is precipitated by the lactic acid of milk, which is produced by keeping the milk too warm. Caseine, or curds, as they are called, are thus precipitated. The milk is said to be “sour,” or turned.
Milk, the food of the young of all mammalia, is composed chiefly of water, a peculiar kind of sugar, butter, and caseine. It is this sugar in milk which causes the lactic acid mentioned above. The actual constituents of milk are as follows:—
| Water | 873·00 |
| Butter | 30·00 |
| Sugar | 43·90 |
| Caseine | 48·20 |
| Calcium (phosphate) | 2·31 |
| Magnesia | 0·42 |
| Iron | 0·07 |
| Potassium (chloride) | 1·44 |
| Sodium | 0·24 |
| Soda (with caseine) | 0·42 |
| 1000·00 |
The sugar of milk is non-fermenting, and can be procured from whey by evaporation.
Decomposition.
We have seen that animals and plants are composed of many different substances, and so it will be at once understood that these substances can be separated from each other, and then the decomposition of the body will be completed. When the sap sinks or dries up in plants they are dead. When our heart ceases to beat and our blood to flow we die, and then, gradually but surely, decay sets in. There is no fuel left to keep the body warm; cold results, and the action of oxygen of the air and light or water decays the body, according to the great and unalterable laws of Nature. “Dust thou art, and unto dust shalt thou return,” is an awful truth. The constituents of our bodies must be resolved again, and the unfailing law of chemical attraction is carried out, whereby the beautiful organism, deprived of the animating principle, seeks to render itself into less complicated groups and their primary elements.
This resolution of the organic bodies is decomposition, or “spontaneous decomposition,” and is called decay, fermentation, or putrefaction, according to circumstances. The Egyptians, by first drying the bodies of the dead (and then embalming them), removed one great source of decay—viz., water, and afterwards, by the addition of spices, managed to arrest putrefaction.
Fermentation is familiar in its results, which may be distilled for spirituous liquors, or merely remain fermented, as beer and wine. Fusel oil is prepared from potatoes, rum from cane sugar, arrack from rice. The power of fermentation exists in nature everywhere, and putrefaction is considered to be owing to the presence of minute germs in the atmosphere, upon which Professors Tyndall and Huxley have discoursed eloquently.
Plants are subjected to a process of decomposition, which has been termed “slow carbonization,” under certain circumstances which exclude the air. The gases are given off, and the carbon remains and increases. Thus we have a kind of moss becoming peat, brown coal, and coal. The immense period during which some beds of coal must have lain in the ground can only be approximately ascertained, but the remains found in the coal-measures have guided geologists in their calculations.
Having already mentioned some products of distillation, we may now close this portion of the subject and pass on to a brief consideration of minerals and crystals. We have left many things unnoticed, which in the limited space at our disposal we could not conveniently include in our sketch of chemistry and chemical phenomena.
CHAPTER XXXI.
MINERALOGY AND CRYSTALLOGRAPHY.
THE MINERALS—CHARACTERISTICS—CRYSTALS AND THEIR FORMS—DESCRIPTIONS OF MINERALS.
Minerals are constituent parts of the earth. All parts of minerals are alike. There are simple minerals and mixed. The former are the true minerals, and are generally considered under the heading Mineralogy. The others constitute a branch of Geology, as they form aggregate masses, and as such compose a large portion of the earth. We must learn to distinguish minerals and crystals as inorganic forms of nature. In the animal and vegetable kingdoms we have forms which are possessed of organs of sight, smell, taste, and certain structures indispensable to their existence and development. But in minerals we have no such attributes. They are INORGANIC, and have a similar structure; a fragment will tell us the story as well as a block of the same mineral. These inorganic substances are possessed of certain attributes or characteristics. We find they have FORM. They have chemical properties, and they behave differently when exposed to light and electricity. They are generally solid. All the elements are found in the mineral kingdom, and a mineral may be an element itself, or a chemical combination of elements. These compounds are classed according as the combination is more or less simple. An alliance of two elements is termed a binary compound, of three a ternary compound, forming a base and an acid.
We have learnt from our chemistry paper that there are between sixty and seventy elementary bodies in nature. When we speak of “elements,” we do not mean to apply the popular and erroneous definition of the word. Earth, air, fire, and water are not elements; they are compounds, as we have seen. The list of elements has been given; we will now give the names of the more important minerals. We have no space for a detailed description, but in the British Museum the cases contain some hundreds, and the student will find them classified and described with the greatest care, and according to the arrangement of Berzelius.
Principal Minerals as arranged by Professor Ansted.
| I. | |||
| Diamond. | Lignite. | Quartz. | Flint. |
| Graphite. | Bitumen. | Amethyst. | Jasper. |
| Anthracite. | Amber. | Agate. | Opal. |
| Coal. | Sulphur. | Chalcedony.[Pg 425] | |
| II. | |||
| Sal-ammoniac. | Nitre. | Rock-salt. | Borax. |
| Witherite. | Calc-spar. | Gypsum. | Sapphire. |
| Spar. | Marble. | Apatite. | Emery. |
| Strontianite. | Dolomite. | Magnesite. | Turquoise. |
| Celestine. | Fluor-spar. | Corundum. | Alum-stone. |
| IV. | |||
| Cyanite. | Jade. | Talc. | Diallage. |
| Christolite. | Emerald. | Serpentine. | Topaz. |
| Clay. | Beryl. | Zircon. | Tourmaline. |
| Fullers-earth. | Felspar. | Hornblende. | Lapis-lazuli. |
| Garnet. | Obsidian. | Asbestos. | Chrysoberyl. |
| Iolite. | Pumice. | Augite. | |
| V. | |||
| Wolfram. | Orpiment. | Iron-pyrites. | Copper pyrites. |
| Molybdenite. | Antimony (grey). | Mispickel. | Azurite. |
| Chromite. | Bismuth. | Magnetic iron ore. | Malachite. |
| Pitch-blende. | Blende. | Micaceous iron. | Mercury. |
| Uranite. | Calamine. | Hematite. | Cinnabar. |
| Pyrolusite. | Spartalite. | Spathic iron. | Silver. |
| Wad. | Tinstone. | Cobalt. | Gold. |
| Manganese-spar. | Galena. | Copper. | Platinum. |
| Arsenic. | Pyromorphite. | Oxides of copper. | Palladium. |
| Realgar. | |||
The above is the arrangement best suited for beginners.
Professor Nichol prefers the following arrangement:—
| Order I.—The Oxidised Stones. | |||
|---|---|---|---|
| Quartz. | Serpentine. | ||
| Felspar. | Hornblende. | ||
| Scapolite. | Clays. | ||
| Haloid stones. | Garnet. | ||
| Leucite. | Cyanite. | ||
| Zeolite. | Gems. | ||
| Mica. | Metallic stones. | ||
| Order II.—Saline Stones. | |||
| Calc-spar. | Gypsum. | ||
| Fluor-spar. | Rock-salt. | ||
| Heavy-spar. | |||
| Order III.—Saline Ores. | |||
| Sparry iron ores. | Copper salts. | ||
| Iron salts. | Lead salts. | ||
| Order IV.—Oxidized Ores. | |||
| Iron ores. | Red copper ores. | ||
| Tinstone. | White antimony ores. | ||
| Manganese ores.[Pg 426] | |||
| Order V.—The Native Metals. | |||
| Order VI.—Sulphuretted Metals. | |||
| Iron pyrites. | Grey copper ore | ||
| Galena. | Blende. | ||
| Grey antimony ore. | Ruby-blende. | ||
| Inflammables. | |||
| Sulphur. | Mineral resins. | ||
| Diamond. | Combustible salts. | ||
| Coal. | |||
These are only a portion of the minerals, but it would be scarcely interesting to give the list at greater length. In the foregoing we recognize the metals and various combustible and non-combustible substances familiar to us, existing, as people say sometimes, in “lumps.” But if any one will take the trouble to examine a “lump,” he will find the shape is definite and even. These regular forms of the minerals are called CRYSTALS, from the Greek word krustallos, ice. The term was originally applied to quartz, for in olden times it was thought that quartz was really congealed water. We can define a crystal as “an inorganic solid bounded by plane surfaces arranged round imaginary lines known as axes.” It must not be imagined that crystals are small bodies; they may be of any size. There are crystals of many hundredweight; and although the usual crystal is comparatively small, it may be any size.
Crystallization has occurred by cooling, or by other natural means; and we can form crystals by evaporation from certain salts deposited in water. So we may conclude also that the evaporation of water in the early periods deposited many forms of crystals. We have crystals in the air, such as snowflakes, which are vapours crystallized. Carbon, when crystallized, is the diamond. Boron is very like it. Oxygen cannot be crystallized. Alumina makes sapphires and ruby with silica. Alumina and earth give us spars, tourmaline, and garnets. Limestone also has beautiful forms, as in Iceland spar. Crystals, therefore, are certain forms of nature, corresponding in the inorganic kingdom to the animals and plants of the organic.
Let us look a little more at these. Here we have a group of crystals of different forms. Earths are metals combined with oxygen, and the principal earths are alumina, lime, and silica. To these three we are chiefly indebted for the ground we live on, and from which we dig so many useful metals and other minerals. Earths are coloured by the substances mixed with them. We can thus find copper, silver, gold, lead, etc., by noting the appearance of the soil. True earths are white. Strontia and baryta are also earths, and the latter is used in firework manufactories. Our chief assistants are Alumina, which furnishes us with bricks and slate; Lime, which gives us marble or stones for building in a carbonate form. Quicklime, by which is meant lime freed from the carbonic acid, is well known; and plaster of Paris is only lime and sulphuric acid in combination. The[Pg 427] Silicates, such as sand and flint, are in daily demand. Agate, cornelian, Scotch pebbles, rock-crystal, etc., belong to the same family. Even our gems are crystallized earths, and, as already stated, diamonds are merely carbon.
Stone, as we know, is quarried; that is, it is dug out of the earth. But perhaps many readers do not know why a stone-mine is called a “quarry.” Most kinds of stone (granite and marble are the exceptions) are found in layers, or strata, rendering them easy of removal. The blocks of stone are cut with reference to these layers in a more or less square manner, and “squared up” before they are carried away. Thus the term “quarry,” from an old French word, quarré, or carré, as now written, signifying a square. In granite quarries the stone being very hard is bored, and loosened by means of gunpowder or dynamite blasting. Slate, on the contrary, is easily divided into slabs. We will now resume the subject of Crystals.

1.—Emerald. 3.—Garnet. 5.—Diamond.
2.—Agate. 4.—Ruby. 6.—Rock crystal.
We have said that crystals vary in size, and this variety may be traced, in the cases of crystallization from fluids, to the slowness or the rapidity of the cooling process. If the work be done slowly, then the crystals obtain a size commensurate with the time of cooling, as they are deposited one upon the other. The form of minerals is the first important point, and to ascertain their forms and structure we must study Crystallography. We shall find faces, or planes,—the lines of contact of any two planes,—called edges, and the angles formed where these planes meet. We may add that crystals have, at least, four planes, making six edges and four angles. Nearly all crystals have more than this, for the forms are, if not infinite, very numerous, and are divided into six (by some writers into seven) different systems or fundamental forms from which the varieties are derived. The axis of a crystal is an imaginary line drawn from an angle to the opposite one.
The first form, the monometric, or cubic system, with three equal axes[Pg 428] at right angles, is represented by fig. 436. This crystal is limited by eight equilateral triangles. It has twelve edges and six angles. If we describe a line from any one angle to an opposite one, that line is called an axis, and in the case before us there are three such axes, which intersect each other at right angles.23 Such crystals are regular octohedra. There are irregular forms also, whose axes do not come at right angles, or they may be of unequal length. The substances which we find crystallized in this form or system are the diamond, nearly all metals, chloride of sodium (salt), fluor-spar, alum, etc.

When we say in this form we do not mean that all the minerals are shaped like the illustration (fig. 436). We shall at once see that the system admits of other shapes. For instance, a regular crystal may have been cut or rubbed (and the experiment can be made with a raw turnip). Suppose we cut off the angles in fig. 436; we then shall have a totally different appearance, and yet the crystal is the same, and by cutting that down we can obtain a cube (fig. 437). Take off its angles again we obtain a regular octohedron once more, as shown in the diagram opposite.

We will exhibit the gradations. Suppose we cut fig. 437; we will obtain (fig. 438) the cube. The next is merely the cube with angles and edges cut off; and if we proceed regularly we shall arrive at fig. 442, the rhombic dodecahedron, or twelve-sided figure, whose equal planes are rhombs.
We can, by taking away alternate angles or edges situated opposite, arrive at other secondary crystals. From the original octohedron we can[Pg 429] thus obtain figs. 443 and 444. These are known as tetrahedron. The pentagonal dodecahedron is another secondary form (fig. 445).


The cube, or hexahedron, the octohedron, and the rhombohedron are all simple forms, being each bounded by equal and similar faces, or surfaces. We can thus understand how certain primary or original natural forms of crystals can be changed in appearance by connection. Of the various substances crystallizing in this system we find salt, iron pyrites, gold, silver, copper, and platinum, and the sulphide of lead called galena, in the cube or hexahedron form. The diamond and fluor-spar, alum, etc., appear in the first form (I), fig. 436 (octohedron). The cube, we see, has six equal faces, eight equal angles, and twelve equal edges. Galena, as will be observed from the illustration herewith, shows this peculiarity in a very marked manner (fig. 446).





The second crystalline form is the Hexagonal, and in this system three of the four axes are equal and in the same plane, inclined at an angle of 60°, with a principal axis at right angles to the others. In crystals of this system are found quartz and calc-spar.
The third system is termed the Quadratic or the diametric. This form has three axes, all at right angles, two being equal and the other longer[Pg 430] or shorter than the former two. In this system crystallize sulphate of nickel, zircon, oxide of tin, etc.


The fourth, or Rhombic system, or the trimetric. Here we have three rectangular axes, all unequal and intersecting at right angles. The sulphate and nitrate of potassium crystallize in this system.



The fifth is the oblique, or Monoclinic system, which displays three unequal axes, two of which are at right angles; the third, or principal axis, is at right angles to one and oblique to the other of the preceding. Ferrous sulphate, tartaric acid, and gypsum crystallize in this system.


Fig. 453.—Crystals of the fifth system.
The sixth, or Triclinic system, or the doubly oblique. In this system[Pg 431] we have three axes differing in length, and all forms which can be arranged about these unequal and oblique axes. Sulphate of copper will be found in this group. The system has been called anorthic, or triclinic, because the axes are unequal and inclined, as in the oblique prism based upon an obliqued angled parallelogram. Axinite crystal, as annexed, will show one form in this system.

As may be gathered from the foregoing, it is not easy to determine a crystalline form with certainty,—a great part of the crystal may be invisible. A crystalline mass is a mineral, which consists of an arrangement of crystals heaped together. If it does not possess these the mineral is amorphous, or shapeless. We will now endeavour to describe some of the physical characteristics of minerals.

The Goniometer (see fig. 455) is the instrument used for measuring the angles of crystals. Wollaston’s reflecting instrument is most generally used. It consists of a divided circle, graduated to degrees, and subdivided with the vernier. The manner of working is easy, though apparently complicated. The vernier is brought to zero, when an object is reflected in one face of the crystal. The crystal is turned till the same object is viewed from another face. The angle of reflection is then measured, and can be read off on the circle.
We have already referred to the physical characteristics of the minerals, and one of these attributes is cohesion. When we find a substance is difficult to break, we say it is “hard.” This means that the cohesion of the different particles is very great. Minerals vary in hardness; some are extremely difficult to act upon by force, and a file appears useless. At the other side we find some which can be pricked or scratched with a pin; and these[Pg 432] degrees of hardness being put as extremes, we can in a manner relatively estimate the hardness of all other minerals. We can test this by scratching one against another; whichever scratches the other is the harder of the two, and thus by taking up and discarding alternately, we can at length arrive at a comparative estimate of the hardness of all. Such a scale was arrived at by Mohs, and arranged in the following order. The softest mineral comes first:—
- Talc.
- Gypsum (rock-salt).
- Calcareous spar.
- Fluor-spar.
- Apatite-spar.
- Felspar.
- Quartz.
- Topaz.
- Corundum.
- Diamond.
Talc, we see, is the softest, and diamond the hardest. Thus “diamond cut diamond” has passed into a proverb expressive of the difficulties one “sharp” person has to circumvent or “cut out” another. Diamond is used by glass-cutters. When geologists wish to express the degree of hardness of any substance, they mention it with reference to the foregoing list; and if the substance be harder than fluor-spar, but not so hard as felspar, they determine its hardness five, or perhaps between five and six, or between four and five, according as it is harder or less hard than apatite. Thus hardness, or power of cohesion, resistance to exterior force and pressure, is a prime characteristic of the mineral kingdom. The file is the best test.
We now come to another phase of the physical character of our minerals—cleavage. This is the term employed to express the facility of cutting in a certain direction which in the mineral is its direction of cleavage. Take mica, for instance. There is no difficulty in separating mica into thin layers; we can do so with our fingers. The layers, or flakes, or laminæ are so arranged that they exhibit less cohesion in one direction than when tried in other ways. We cut with the grain, as it were in the direction of the fibre when wood is concerned. Here we have another popular saying expressive of this,—“against the grain,”—which signifies an act performed unwillingly and unpleasantly. Cleavability, therefore, means cutting with the grain, as it were, and various minerals are possessed of different degrees of cleavage. It sometimes happens that electric excitement is observed when cleavage takes place. One place will become positive, and the other negative. Mica, arragonite, and calcareous spar will exhibit this action after cleavage or pressure. When a crystal of tourmaline is heated, it will develop positive electricity at one end of its principal axis, and negative at the other. Even if it be broken, the extremities of the fragments will exhibit similar phenomena, and so far like a magnet, which, as we have seen, possesses this attribute of “polarity.” But a curious fact in connection with this is that, if the heating cease the polarity ceases for a second or two, and yet as cooling goes on the polarity is restored, with the difference that the positive end has become negative, and the end previously negative has come over to the opposite pole. Electricity, therefore, must be hidden away[Pg 433] in every portion of our globe, and will some day be proved to be the mainspring of all life.
Fracture in minerals is also to be noticed. Those substances which we cannot laminate we are obliged to break, and we may require to break a mineral in a direction different from or opposed to its direction of cleavage. Under such circumstances we must break it, disintegrate it, and observe the fracture. Sometimes we shall find the surfaces very even, or uneven, or what is termed conchoidal. This is observable in the breaking of flint. There are various ways in which minerals display fracture, and the particular manner and appearance denotes the class to which the mineral belongs.
We may pass over the question of the specific gravity of minerals, as we have in a former part explained this. It is important, however, to ascertain the specific gravity. As a general rule, minerals containing heavy metals are of high specific gravity.
But the relation of minerals (crystals) with regard to light is of great interest and importance. When we were writing of polarization, we mentioned the faculty a crystal has for double refraction, by which it divides a ray of light into two prolonged rays taking different directions, the plane of vibration of one being at right angles to that of the other. This property is not possessed by all crystals. Some act as ordinary transparent media. Some crystals transmit only one polarized ray, and tourmaline is called a polarizer; and if light be passed through it to another polarizer, it will be transmitted if the latter be similarly held; but if the second be held at right angles to it the ray will be stopped. We can easily understand this if we suppose a grating through which a strip of tin is passed; but the strip will be stopped by bars at right angles to it. The coloured rings in crystals can be observed when a slice of a double refracting crystal is examined. The rings are seen surrounding a black cross in some instances, and a white cross in another. The effect when examined in the polariscope is very beautiful. Selenite is probably the best crystal for exhibiting colours.
Minerals sometimes reflect, sometimes refract light; they are said to possess lustre and phosphorescence. All these properties may be considered as belonging to the crystals which are transparent, semi-transparent, translucent, or opaque, according to the degrees in which they permit light to pass through them. All minerals are electric or non-electric, and the variety can be ascertained by rubbing and placing the mineral near the electrometer. But all do not exhibit magnetic properties. Taste and smell are strongly marked in some minerals—salts, for instance, and sulphur; some are soapy to the touch, some appear cold to the fingers. Chemistry is very useful to us in determining the nature of the mineral, and the amount of it enclosed in the substance under examination. These delicate operations are termed qualitative and quantitative analysis. The application of heat is increased by means of the blowpipe, which is in effect a small bellows. We can thus, and particularly by means of the oxy-hydrogen blowpipe, obtain a very intense heat with little[Pg 434] trouble. When the fragments of a mineral are held in the flame by platinum “tweezers,” or tongs, then the fusibility of the substance, and the colour of the blow-pipe flame will be of great assistance in determining the nature of the mineral. It is also curious to observe the different forms into which the various substances expand or contract under the influence of the blowpipe. We may have a rugged slag, an enamel, or a glass, or a bead, or “drop” of metal. The varied substances produce various colours—yellow, green, orange, or red, according to circumstances. Strontia is a vivid red, copper is green, lime orange, and so on.

It is very little use to attempt a study of mineralogy without some acquaintance with chemistry. In dealing with minerals, and in studying geology, we must try to keep our knowledge of chemical science in our minds, and thus fortified we can more easily understand the steps leading to the classification of minerals. It is impossible to teach mineralogy or geology from books. Nature must be studied, the specimens must be seen, the earth must be examined. The advance in mineralogy may be—probably will be—slow, but crystals will teach something; and when we can pass a viva voce examination in chemistry and crystallography, expressing, by the symbols, the various substances under discussion, we shall have made a considerable advance in the science. We shall have an idea of the component parts of various substances, and be able to class the various minerals according to their chemical constitution. Beginning with the metalloids, we shall pass to the metals and various compounds, salts, resinous substances, etc., such as amber.
It is impossible in the space at our command to describe all the minerals, and yet it is necessary to enumerate the most important. We may, therefore, take them in the following order. It should be added that[Pg 435] most of the simple minerals occur in comparatively small quantities, but sometimes we find them in aggregate masses (rocks). We append a table.
SYNOPTICAL TABLE OF THE MINERALS.
- First Class.—Metalloids.
- Sulphur.
- Boron.
- Carbon.
- Silicium (Silicon).
- Second Class.—Light Metals.
- Potassium.
- Sodium.
- Ammonium.
- Calcium.
- Barium.
- Strontium.
- Magnesium.
- Aluminum.
- Heavy Metals.
- Iron.
- Manganese.
- Cobalt.
- Copper.
- Bismuth.
- Lead.
- Tin.
- Zinc.
- Chromium.
- Antimony.
- Arsenic.
- Mercury.
- Silver.
- Gold.
- Platinum.
- Third Class.
- Salts.
- Earthy resins.
Sulphur is found in Sicily and Italy and other parts of Europe, in a native state, but as such has to be purified. The crystals take the form as shown in the margin. Cleavage imperfect; it is brittle. Sulphuric acid is a very important combination, and a very dangerous one in inexperienced hands. Sulphur combines with a number of elements, which combinations are “Sulphides.” (See Chemistry section.)

Selenium is a metalloid resembling sulphur, but less common. It is inodorous.
Boron is usually found near volcanic springs, and in combination with oxygen. It is soluble. Taste, acid bitter, and white in colour; friable. It is known as Sassoline, or boracic acid. (See Biborate of Soda for one of the borates.)
Carbon is one of the most important of our minerals. In the form of coal we have it in daily use, and in the form of diamond it is our most valuable gem. In the latter form it is the hardest of all minerals, a powerful refractor of light, lustrous, and transparent. It is found in the East Indies and Brazil; more lately Cape diamonds have been brought to Europe, but they do not equal the Eastern gem. Almost fabulous prices have been[Pg 436] given for diamonds, which, after all, are only carbon in a pure state. Another form of carbon is graphite (plumbago, or blacklead). It is much used for pencils and in households. It is found in Cumberland, and in many other localities in Europe and Canada.
Carbon appears in one or other of the above forms in regular octahedrons or their allied shapes. Anthracite, another form of carbon, is used as fuel for strong furnaces. It leaves little “ash,” and is smokeless when burned. Coal, in all its forms, is evidently derived from wood. Thousands of years ago vegetable matter must have been embedded in the ground and subjected to carbonization. There are different kinds of coal, all of which come under one or other of the following heads: cubical coal, slate coal, cannel coal, glance-lignite,—the last being, as its name implies, an imperfect development of wood; it is a brown coal. We are not here concerned with coal as a fuel. Charcoal is also a form of carbon prepared from wood and finds a counterpart in coke, which is prepared from coal. Carbon, as we have already seen, plays an important part in electric lighting and in the Voltaic Battery. Peat, or as it is called in Ireland, “turf,” is one of the most recent of the carboniferous formations. It is much used as fuel. It is cut from moors (“bogs,” as they are sometimes called), and the various deposits can be traced. Bog-oak is no doubt the first step towards peat, as peat is the step towards coal. The brown turf is newer than the black, and both kinds may be seen stacked in small square “bricks” along the Irish canals and in the yards of retailers of fuel.

Silicon. Silica occurs generally in combination with alumina, and never in a free state. In combination with oxygen it is called silicic acid. Silica, when crystallized, is usually called quartz.
Quartz has several varieties. We need only enumerate them, they will all be immediately recognized. We give illustrations of the crystals of quartz (fig. 459):—
1. Rock crystal appears in beautiful six-sided prisms.
2. Amethyst is coloured by protoxide of manganese, supposed by the ancients to be a charm against drunkenness.
3. Common quartz, or quartz rock, forms granite in combination, and is also known as “cat’s-eye,” “rose” quartz, etc.
4. Chalcedony, sometimes termed cornelian: used for seals, etc.
5. Flint: much used in potteries. “Flint and steel” have been superseded by phosphorus.
6. Hornstone: something like flint, resembling horn.
7. Jasper: of various colours; opaque and dull in appearance.
8. Silicious slate: a combination; used as a whetstone.
9. Agate: a mixture of quartz, amethyst, jasper, and cornelian; very ornamental.
10. Opal: a peculiar variety, containing water. It is not found in the form of crystal, but in vitreous masses. Its changeableness of hue is proverbial. The “noble” opal is much prized.
11. Smoky quartz, or cairngorm.
12. Onyx and Sardonyx.

We now arrive at some minerals which contain metals.
Potassium. This metal is so frequently combined in minerals with alumina that we may refer to it with the latter in sequel. There are two natural potassa salts—nitre, and sulphate of potassa. Nitre is known as saltpetre, and is of great use in medicine. It is the chief ingredient in the composition of gunpowder.
Sodium. We have a number of minerals in this group—viz., nitrate of soda (nitratine), which occurs in large quantities in Peru; rock salt, chloride of sodium, known as salt. It crystallizes in the cubic system. Colour usually white, but it occurs in secondary rocks in company with gypsum, etc. It is sometimes of a reddish colour, or even green and yellow. Biborate of soda is borax, and is found in and on the borders of a Thibetian lake. There are several other combinations with soda: the sulphates of soda—viz., thenardite and glauberite, anhydrous and hydrated respectively, carbonate of soda, and so on.
Ammonia combinations occur in lava fissures, and are not often met with in consequence of their volatile nature.

Calcium. This forms an important group of the minerals, which are very white in colour, and not very hard in substance. Calcium is the metallic basis of lime. Fluoride of calcium, known as fluor-spar, most frequently crystallizes in cubes in the first system. Anhydrite[Pg 438] is the anhydrous sulphate of calcium. The hydrated sulphate is called gypsum. One variety of the hydrated sulphate is selenite, another is known as alabaster. Apatite, or asparagus stone, and pharmacolite are in this group.






Fig. 461.—Crystals of Carbonate of Lime.
Carbonate of lime, not content with one system of crystals, makes its appearance in two. It is therefore divided into two minerals—namely, calcareous spar and arragonite. In the former it possesses various forms, as will be observed in the accompanying diagrams. It is a very important mineral, as will be readily acknowledged; it enters largely into the composition of all shells and bones. The minute shells, deposited by millions at the bottom of the sea, have combined to raise our chalk cliffs. Carbonate of lime is a constituent of water, as the deposits at the bottoms of kettles, upon the sides and bottoms of water-bottles, and the stalactites all testify. A little good vinegar will quickly dissolve this deposit. Calc-spar is crystallized, and the Iceland spar is celebrated. Marble, which is another form of carbonate of lime, is white, hard, and granular. It is sometimes varied, but the pure white is the most valuable. Chalk, we know well, is soft, and is useful for writing. We have also aphrite, schiefer spar,—compact limestone in various forms,—and finally, arragonite, called from the place of its nativity, Arragon,—a colourless and somewhat transparent vitreous crystal.
Barytes. The sulphate of baryta is known as heavy spar; the crystals are of tabular forms, but numerous modifications exist. One of the forms is represented in the margin.

Strontium is the metallic basis of strontia.[Pg 439] Sulphate of strontium is celestine, the mineral which colours the blow-pipe flame a fine crimson. There are certain varieties. Strontia salts are chemical preparations. A beautiful pyrotechnic “red fire” is produced by mixing nitrate of strontia with sulphur, antimony, charcoal, and chlorate of potassia.24 There is a carbonate of strontia in the same crystalline system.
Magnesium. With this metal we have a large group of minerals. Magnesite is carbonate of magnesia, and occurs as talc-spar. The magnesium limestone crystallizes as bitter spar. This dolomite is like marble or common limestone, according to colour. Talc is a combination of magnesia with silicic acid. The hydrated carbonate is termed “white magnesia.” The sulphate of magnesia is found in Siberia, and we have boracite, and native magnesia called periclase. The sulphate is generally present in mineral waters, such as the Seidlitz and Epsom Springs. Large masses have been found in the extensive caverns of Kentucky and Tennessee, etc.

Meerschaum is a hydrated silicate of magnesia. It is found in Anatolia and Negropont, also in France and Australasia. Serpentine is another similar composition. It is found in Cornwall, where it is carved into various ornaments. It is sometimes called snakestone. There are many other hydrated silicates of magnesia—viz., gymnite, picrosmine, pycrophyll, etc.

There is another family allied to magnesia, called Augites. These minerals are black or dark-green, and are contained in lava and basalt: Augite and Hornblende are the chief representatives of this family. The former crystallizes in the fourth system (see fig. 463), and there are several varieties—diallage, bronzite, diopside, etc. Hornblende belongs to the same system, and is a large factor in the composition of gneiss, syenite, and porphyry. Tremolite is a hornblende, and asbestos (amianthos), and mountain-cork are also varieties. The attribute of asbestos for sustaining heat is well known, and may be usefully employed for fire-proof purposes. The well-known jade-stone of China and calamite are other varieties.
Aluminum, or Aluminium, gives us a large class of minerals. It is the metallic basis of alumina, which, com[Pg 440]bined with silica, is the chief component of our clay. Silicic acid and this base combine to form many minerals, and contains nearly all the precious stones. Corundums consist of pure alumina, and crystallize in the hexagonal system. The following stones are varieties of this mineral:—Sapphire, a beautiful blue; ruby, a red oriental; topaz, yellow oriental; amethyst, violet; all being sapphires more or less. The finest crystals are found in the East Indies in the sands of rivers and diluvial soils. The common corundum is very hard, and is used for polishing. Emery is well known, and is found in mica-slate. It is of a bluish-grey colour, and is also a polisher.
Alum forms another family, of which we may first mention aluminite, a “basic sulphate” of alumina and found in small quantities. Alum-stone is found in Italy. Alum occurs in large crystallized masses. (See illustration, fig. 464.) There are different minerals with a composition very similar to alum, in which the potassa base of alum is supplied by others. Thus we have the potassa alum, soda alum, manganese alum, ammonia alum—all being very nearly of the same constituents, and having similar crystals in the regular system, and are thus termed isomorphous, or similarly-formed. The potassa, or potash alum, is the commonest form, and is found abundantly in England, on the Continent of Europe, and the United States. Soda alum is called salfatarite, and magnesia alum pickeringite; manganese alum is apjohnite; phosphate of alumina is wavellite.
There are compounds of alumina and magnesia called Spinels. They are hard minerals, and the same isomorphous changes take place with them as are observable with the bases of alum. There are therefore varieties such as the spinel ruby found in the East Indies, very red in colour; the balas ruby not so red, and the orange-red, termed rubicelle. Ceylon is remarkable for some fine specimens of spinels. Chromite is like the spinel, but is known as chrome iron.
Zeolites are principally compositions of silica and alumina. They contain water, and are white, vitreous, and transparent. There are several varieties of them—natrolite, stilbite, etc. We will now pass on to the Clays, which are a very important family of the aluminum group.
There are a number of hard minerals which, when disintegrated, form certain earthy masses. These we term clay, or clays, which possess various colours and receive certain names, according to the proportion of metallic oxides they contain. All clays have an affinity for water, and retain it to a very great extent. The earth has also a peculiar smell. Clay is used in various ways; pottery, for instance, we read in the Bible as having been an employment from very ancient times. One attribute of clays, the retention of water, is of the greatest use to the world in providing moisture for plants and seeds. We may mention other characteristics of clay. It absorbs oil very quickly, and therefore is useful for removing grease-spots. It cannot be burned, so we have fire-bricks and fire-clay in our stoves and furnaces.[Pg 441] There are various clays—pipe-clay, for instance, which is white; potters’ clay is coarser. There is porcelain clay as well as porcelain earth, of which more below. Yellow ochre and sienna are clays used by artists. Bole is a reddish clay; and tripoli is employed for polishing. There are, besides, andalusite, or chiastolite and disthene, crystalline forms of clay.
Porcelain has been known to the Chinese for centuries. In 1701 it was discovered in Germany by Böttcher, a chemist, who while endeavouring to make gold by Royal command, found the porcelain, and was thereby enriched. Porcelain earth is frequently found; is known in many places as kaolin, and usually comes from the decomposition of felspar. But in Cornwall we find it as decomposed granite, and the filtering process can be viewed from the railway, while both gneiss and granulite have been known to yield kaolin. It is also found in China, Saxony, and France. It is free from iron, and when ground and mixed with silicic acid, it is handed to the potter or moulder. After the vessels have been dried in the air they are put into the kiln, and then become white and hard. After that they are glazed in a mixture of porcelain earth and gypsum, or ground flints and oxide of lead, made fluid with water in the glazing of earthenware. The vessel is then put into the furnace again, or “fired,” as the process is called, and then comes out white, hard, and partly transparent.



Earthenware utensils are made of a coarser material,—clay and[Pg 442] powdered flints,—from which all the gross matter has been eliminated. Flint is not difficult to break, if made hot and thrown into cold water. A stamper is then used to break the flints. They are first ground in a mill and purified like the clay, then they are mixed and beaten, while moist, into “putty,” and turned, or forced, into moulds. The handles are fixed on afterwards. The ware is baked for two days and glazed. The various colours are obtained by mixing different clays and oxides—iron or manganese. Biscuit porcelain is made by pouring a creamy mixture of porcelain earth into plaster-of-Paris moulds, and when a thin case has formed within, the liquid is poured out again. It is then dried in the mould and shrinks. The mould is taken to pieces, and the thin biscuit porcelain is left.

Felspars are very like the zeolites, except that the former contain no water. Felspar crystallizes in a number of different forms. We annex illustrations of specimens. This spar is found in rocks, granite, gneiss, etc. One variety is the moonstone, of a peculiar lustre. Felsite is amorphous felspar. Albite contains soda instead of potash. Labradorite is nearly a pure lime felspar, and is remarkable for its colours, like a pigeon’s breast. Spodumene is like albite, and leucite, soda-lite, etc., belong to this family.

Lapis-Lazuli is a felspar distinguished by its blue tint. It was used for ultramarine colouring at one time, which colour can also be made chemically. Lapis-lazuli is found in Siberia and China. It is a mixture of mineral species. Hauyne is something like it. Obsidian is a sort of black glass, and occurs in various colours in vitreous masses. It is derived from the fusion of rocks, and is employed in the manufacture of boxes, etc. Pumice stone bears a resemblance in composition to the foregoing, but is porous, and so called spongy. It contains both potash and soda in some quantities. Pearlstone and pitchstone also attach themselves to this family group.
The Garnets possess many curious forms of crystals, which are coloured and used as gems. Tourmaline is a very particularly useful crystal, and is used in the investigations concerning the polarization of[Pg 443] light. It is found of nearly all colours. The garnet and staurolite crystals are shown (figs. 470, 471).
The former is silicate of alumina with the silicate of some other oxide, which is not always the same. This change, of course, gives us a series, as in the case of alum above mentioned.

The red varieties, called almandine, or precious garnets, are distinguished from the duller, “common” species by their clear colour. Bohemia is the most productive soil for the garnets.
Mica includes, as we have already noticed, a group of minerals which have a peculiarly laminated structure. These layers are by no means all alike, but they present a smoothness to the fingers which is highly characteristic. The chief constituents are alumina and silica, occasionally with magnesia. Mica slate is very common, and is often used instead of glass in window-frames. Muscovite, lepidolite, and phlogopite are all micas of the “potash,” “lithia,” and “magnesia” varieties.
In the list of minerals associated with the lighter metals, we need only now mention the Gems, so well known. These stones are very hard in many instances, infusible, and exhibiting beautiful colours. Amongst them are diamonds, sapphires, and rubies, of which we have spoken; the topaz, noticed under corundum. The chrysoberyl (of a pale green, or occasionally reddish hue), of which the alexandrite of Siberia is a variety, is a compound of glucina with alumina; the beryl, a silicate of the same, and the emerald of beautiful green. Zircon is another gem, and “hyacinth” is its most valued form. The latter is found in basaltic rocks. The emerald crystallizes in the hexagonal system.

We may now consider the minerals formed by the heavier metals, such as Iron, Copper, Nickel, etc.
Iron. This well-known metal fills a very important place in our mineral arrangements, for the substances formed with iron ores occur in great variety of structure, and occasionally in very large masses. They are highly magnetic, and very hard. Were we here treating of iron as a metal, we could give some information respecting its extraction and manifold uses. All we need mention here is the fact that iron occurs in nature in various ores which are essentially composed of iron and oxygen. The iron is extracted in the blast furnace, in which the process is continued for years. The “slag,” or glassy scum, protects the molten iron from the air; its[Pg 444] presence is necessary in all blast furnaces. The most important of the iron group of minerals are Magnetic Iron (magnetite), or loadstone. This mineral occurs in Sweden and North America, and is found in primary rocks, and in Scandinavia forms mountains. It crystallizes in the regular (octahedron) system, and often in the form in illustration in the margin. It is highly magnetic, as its name implies.

Native iron very rarely occurs, and then only in thin layers. The most extraordinary specimens are those termed meteoric iron, which fall from the atmosphere in great masses; and the meteoric stones, which contain ninety per cent of iron, together with other constituents in small quantities—viz., nickel, cobalt, copper, manganese, carbon, sulphur, arsenic, etc.
Red hematite crystallizes in the hexagonal system. It possesses much the same (chemical) constitution as corundum (q. v.). It is brightly metallic, and shows a red streak. It occurs in various forms, as iron glance or specular iron, which is found in Sweden and Russia; micaceous iron, bloodstone, clay, ironstone, etc.
Brown hematite has not been found in crystals, but brown ironstone (fibrous) is crystalline. The earthy brown, containing clay, gives us yellow ochre and umber. Pea-iron ore and “morass” or “bog” ore also belong to this class. Limonite is the name given to these more recent formations, of which yellow ochre is a pure specimen.

The combinations of iron with sulphur (pyrites) are also important. Iron pyrites and magnetic iron pyrites are two which may be mentioned. The latter first.
Magnetic iron pyrites (or pyrrhotin) crystallizes in six-sided prisms, and is attracted by the magnet. The composition of this mineral has not been exactly ascertained, and no chemical formula has been found for it.
Iron Pyrites (bisulphide of iron) is known as cubic pyrites, yellow pyrites, and mundic. It is generally found in the regular system of crystals, either as a cube or as a pentagonal dodecahedron. (See first system of crystals, ante.) Its colour is yellowish. It is known also as green vitriol when oxidised, and forms beautiful green crystals (copperas). This salt is used in the preparation of Prussian blue and violet dyes. With gallic acid it makes ink.
There are many other “ferruginous” minerals, such as vivianite, green ironstone, white iron pyrites, arsenical pyrites, or mispickel, etc.
A carbonate of iron, called chalybite, or spathic ironstone, is very abundant in nature, and forms obtuse rhombohedrons. It is very useful for the production of steel, as it forms the clay iron ore found in coal districts in combination. In a fibrous form it is known as sphærosiderite. It is a most useful mineral.
Chrome iron (chromite) is useful for the preparation of chromium compounds. It crystallizes in the cubic system. It is magnetic, especially when treated. Chromic acid forms scarlet “needle” crystals, and by its assistance chromate of lead, or chrome yellow, is prepared. (Chromate of lead is found in a native state as crocoisite). See Chromium.
Manganese is contained in several minerals. It usually occurs as an oxide. It colours minerals variously. In a pure state manganese is white and brittle. The chief minerals are—
Pyrolusite (the binoxide of manganese of commerce) occurs in crystals. It is black. It is used in the preparation of chlorine and oxygen. The other minerals are known as manganite, which is also found associated with pyrolusite, as are hausmannite and braunite, the other oxides.
Nickel and Cobalt are generally found together, both being similar, and the minerals are compounds of arsenic or sulphur, and occur under similar circumstances. The principal are of Nickel and of Cobalt—
- Sulphide of nickel (ullmanite).
- Arsenical nickel (nickeline).
- Nickel glance (gersdorffite).
- Nickel pyrites (siegenite).
- Arsenical cobalt (smaltine).
- Cobalt glance (cobaltine).
- Cobalt bloom (erythrine).
- Cobalt pyrites (linnæite).
Nickel ores are used for extraction of the metal, which is used as a substitute for silver. The name is derived from the German, kupfernickel, or false copper. It was discovered in 1751.
Copper, again, forms a number of minerals, and the chief is the red oxide of the metal, called cuprite. It crystallizes in the cubic system. Its colour is red, and tinges a flame green. Cuprite yields excellent copper, and is found in Cornwall, and in many places on the continent. The black oxide is rarely found. It is known as melaconite.
Malachite (carbonate of copper) is remarkable for its beautiful green colour. In Australia it is worked for copper. It is chiefly ornamental. Siberia yields the finest specimens, but the mineral is found in Cornwall and Cumberland, as well as on the continent. Chessylite (from Chessy, in France) is frequently found with malachite. It has been called blue malachite, or the azure copper ore. It is used as a paint.
Besides the above, copper unites with sulphur to form minerals, such as the needle ore (bismuthic sulphide of copper), antimonial sulphide, bournonite; purple copper, and copper pyrites, which is very abundant, and[Pg 446] furnishes us with most of our copper. There is also the “grey” copper ore, which contains various metals; even silver is obtained from it at times.
Bismuth gives us only a few minerals, of secondary importance. Native bismuth resembles antimony, but is reddish in hue. Bismuth ochre, bismuth blende, and bismuthine are the chief combinations.
Lead is more important, and is obtained from galena, the sulphide of lead, which is very abundant, and the principal lead ore. It can be at once distinguished by its high specific gravity and metallic lustre; the “cubic cleavage” also is very easy. It frequently is found containing silver, and even gold, antimony, iron, etc. There are several suphantimonites of lead, such as zinkenite, geocronite, etc., and the salts, such as sulphate of lead and white lead ore, or carbonate of lead (cerasite). The chromate of lead is found in the Ural Mountains.
Tin is not found in a native state, but as tinstone, or binoxide of tin, named cassiterite. It is found largely in Cornwall, and the mines there have yielded great quantities for generations. Tin pyrites, a union of sulphides of tin, iron, and copper, is also found in Cornwall.
Zinc is produced from the ore called (zinc) blende, or sulphide of zinc (black Jack). Its colour is very variable, sometimes red, but when pure is greenish-yellow. It is also found black and brown. The red oxide of zinc (or spartalite) is also worked for zinc. The carbonate, or zinc spar, is common, and used to make brass, as is calamine, which is possessed of a remarkable lustre, and is even luminous when rubbed. It is a silicious oxide of zinc, and is found in the sedimentary rocks. When heated, it displays strong electric properties.
Chromium occurs in very few mineral combinations; chromate of lead, chrome iron, and chrome ochre, or sesqui-oxide of chromium are the only important ones.
Antimony minerals are very hard; the tersulphide is the most common, and from this the metallic antimony is produced. Red antimony, the oxide, is a rarer ore.
Arsenic resembles antimony, and occurs in combination with many metals. White arsenic, or arsenious acid, is found in Bohemia, Alsace, Transylvania, etc. Orpiment and realgar are sulphides of arsenic, and are employed as colouring matters in paint and fireworks. Arsenic is very poisonous.
Mercury is occasionally found native, but more generally as cinnabar. Chloride of mercury (or calomel) is found associated with the cinnabar, or[Pg 447] hepatic ore. Cinnabar is easily volatilized, and possesses high specific gravity. The Californian mines are very rich. Spain also produces a large quantity. It is opaque, and carmine in colour.
Silver occurs native, or in ores. The latter are as follows:—The sulphide, or the vitreous silver (argentite); antimonial silver; and the combined sulphides, of antimony and silver. There are many silver minerals, such as the chloride (horn silver, or kerargyrite), bromide, and carbonate of silver, bismuthic silver, etc. The bromide and iodide are bromargyrite and iodargyrite. Silver occurs most frequently associated with gold; natural alloys of these two metals are found, containing from 0·16 to 38·7 per cent. of silver, which causes considerable variations both of colour and density. In addition to this alloy, we may mention sylvanite (graphic tellurium), which contains, besides gold and silver, one of the rarer metals—viz., tellurium.
Gold is our most precious mineral, and is generally found native. It exists in sand and in certain rocks. It crystallizes in various forms, and in Mexico it is found in companionship with silver and copper sulphides. Australia and California render the most valuable supplies of the metal.
Platinum is also found native, and rarely is crystals. It is often alloyed with other metals, chiefly with iron or gold; also with diamonds. We have already considered it as a metal. Little remains to be said about salts and resins, for with the exception of those we have referred to under Chemistry, they are of little value. The bitumens, rock oil, etc., which exude from the earth, are very useful, and as asphalt and petroleum play an important part in the civilized world, but scarcely come under the strict rule of minerals as we consider them, and with this reference we close our sketch of Mineralogy.

CHAPTER XXXII.
NEW LOCOMOTIVE APPLIANCES.
THE KITE—THE AEROPHANE—ICE YACHTS—SAILING TRUCKS—WATER VELOCIPEDES.
The kite, known from the earliest times, and constructed by a number of people, is a very familiar object, which we shall not describe; for we will now speak of some similar appliances of a more interesting and uncommon description.

M. Penaud has invented some appliances in which twisted india-rubber is the principal agent. Fig. 475 represents a sort of kite, which rises in the air if one twists and then looses the india-rubber round the central bow. Fig. 476 represents another kind of invention; it is an “aerophane,” with a screw at the back, so fixed that it receives no shock from striking against any obstacle. After having twisted the india-rubber, and loosened our hold of the apparatus in a horizontal position, it will first descend for an instant, then, acquiring increased speed, it rises seven or eight feet from the ground, and describes a regular movement in the air for a distance of about fifty yards; the motion lasts for several seconds.
Some models have also been constructed capable of traversing a distance of over seventy yards, remaining for thirteen seconds in the air, as lightly poised as a bird, and without any connection with the ground. During the[Pg 449] whole time the rudder restrains with perfect exactitude the ascending and descending movements as they occur; and we can plainly observe the various oscillations like those of sparrows, or more especially woodpeckers. At last, when the movements are coming to an end, the apparatus falls gently to the ground in a slanting line.

M. Penaud has also succeeded in constructing a mechanical bird, that we have seen set in motion, which will continue flying for several seconds; we give an illustration of it in fig. 477.
Another scientist, M. Tatin, has also produced some remarkable results. His efforts have been unceasingly directed towards the reproduction of the flight of a bird by means of more or less complicated arrangements. He has endeavoured to discover in the small appliances made with india[Pg 450]rubber, and used by MM. Penaud and Hureau de Villeneuve, what were the best shapes in which to reproduce the wings, in order to adapt them to a large apparatus acting by compressed air. After several attempts, he decided on the employment of long, narrow wings. Wenham had previously proved that a wing may be equally effectual whether it be narrow or wide, and M. Marcy has also declared that birds with a quick, narrow wing-stroke have always very long wings. By means of these long, narrow wings (fig. 478) M. Tatin has reduced the time during which the wing reaches a suitable position for acting on the air when it first descends. Granted the fact, so long established, that a bird flies more easily if it rests its wing against a great volume of air, it will be understood that the maximum speed of movement will also be the most advantageous as regards the reduction of expended force. The inventor, finding that he could not prevent his mechanical birds from losing force in proportion as they attained considerable speed, remedied this defect by placing the centre of gravity in front. In consequence of this, the bird in full flight preserves the same equilibrium as the bird hovering in the air, and its speed is, to a certain extent, passive, the mass of air pressing of its own accord against the wings, all expenditure of force therefore being utilized for suspension. Thus has M. Tatin been enabled to increase the weight of his appliances, without increasing the motive power, and yet obtains a double course.

The movement made by the wing round a longitudinal axis, by means of which it always exposes its lower surface in front on rising, is obtained by the mechanism illustrated in fig. 478 a.
M. Tatin’s Bird.
This apparatus, looked at sideways or from behind, is composed of a light wooden frame, on which are two small supports crossed by an axletree so as to form two cranks. This axle receives a circular movement from an india-rubber spring. The crank on the foremost plane causes the rising and falling of the wings, which move round a common axis, and pass the dead points as the cranks of a locomotive do—so the action is maintained.



But the wing does not only move as a whole; every part of it, particularly as it rises, shows a tendency to inclination, which is most marked towards the extremity; the part near the body alone preserves an invariable obliquity. M. Tatin was of opinion that it is with the screw that it is necessary to direct the twisting movement; and to obtain[Pg 452] it with all its transitions, he has substituted for silk wings, which fold up, some wings composed entirely of strong feathers, arranged in such a manner that they slipped one over the other when in motion. The arrangement was perfect, but still not suitable for adaptation to the large bird. The inventor therefore again returned to the use of the silk wings, which he appears to have definitely adopted. By means of certain modifications which he has recently introduced in his larger apparatus—viz., a change in the shape of the wings, variation of the amplitude in the flapping, etc., M. Tatin has been enabled to make great progress. The bird, acting by means of compressed air, at first could only raise three-quarters of its own weight, but finally lifted itself entirely. And we must take into consideration that the apparatus has to struggle against the weight of the steering apparatus, which nullifying the vertical and horizontal reactions of the bird during flight, constantly fulfils the office of regulator.
We will now pass to the consideration of two ingenious appliances of a very clever inventor, M. Salleron.
Small Atmospheric Boat.
The little boat shown in fig. 480, which is about the size of an ordinary plaything, is a very ingenious, if not a practical, application of the specific lightness of air acting as a propelling force. In this instance steam plays but a secondary part, which consists in carrying off the air that causes the moving of the boat.

The apparatus, as represented in fig. 481, is of extreme simplicity, as will be seen at a glance. A small cylindrical boiler, B, connected with a capillary tube, is placed on two supports over a spirit-lamp, in such a manner that the opening from which the steam issues is directly opposite the mouth of the tube, T. This tube, after forming a sudden inclination, terminates at the back of the boat in an inclined drain, R. The steam driven through the tube, T, carries along with it a certain quantity of air, which, forced under the water, propels the boat along. The little vessel soon reaches considerable speed, leaving a long track behind it. It will be seen that this is not a mechanical apparatus, capable of absorbing force or diminishing the action of steam by causing its condensation.

Let us now calculate the force engendered by this apparatus. We know that a litre of water at boiling point gives 1,700 times its volume. The steam, as it quickly issues from the opening of the boiler, carries along at least ten times its volume, or 17,000 litres of air, which, driven under the water, assumes an ascending force equal to the difference of the densities of water and air, or about the weight of the displaced water. Therefore in a litre of water transformed into 1,700 litres of the steam, which carries off into the water 1,700 × 10 = 17,000 litres of air, a force is developed represented by 34,000 kilograms. In fact, by reason of the inclined position of the drain on which the pressure of air acts, and its restricted dimensions, the quantity of force employed in the propulsion of the boat is but a fraction of the total force produced. Moreover, the resistance of traction increases with the size of the boat, and as the dimensions of the inclined pipe cannot be indefinitely enlarged, the result is that the propulsive action is soon insufficient, so that the invention is not, in its present condition, applicable to navigation on a large scale. Its superiority to the steam-engine cannot, therefore, be demonstrated; and we are only now discussing the contrivance in order to show that it is possible, with only moderately powerful generators and extremely simple mechanical appliances, to obtain considerable dynamic effects, susceptible of more serviceable application than is commonly believed.
Circulating Fountain.

The apparatus given in fig. 482 is the subject of a very charming experiment, showing the influence of capillarity on the movements of liquids.[Pg 454] Two glass balls, B B´, are connected by two tubes; one straight and of rather large diameter, the other extremely slender, and winding in and out in a more or less complicated manner. The large tube passes into ball B´, and forms a slender point, J, at the orifice of the narrow tube. At the lower end of the ball is a bulb, which is closed with a cork, and contains a coloured liquid. The apparatus is fixed to a board with a ring at each end, by which it can be hung on the wall. When commencing the experiment, it should be hung so that the ball B´ is uppermost. The liquid then flows through into the ball B, without presenting any particular phenomenon. The apparatus is then turned, and the liquid descends again with great speed, shoots through the opening, J, and rises into the twisted tube. The air displaced from ball B´ also rises, however, and mingles with the liquid, and it can be seen circulating through the winding tube in a number of air-bubbles, mingled with drops of liquid, gradually transmitting the pressure of the column contained in the upper ball and straight tube; so that by means of a similar phenomenon to that of the fountain of Nero, the liquid rises higher than the level of the reservoir, a part falling into ball B, which causes the experiment to be a little prolonged. This circulation of air-bubbles and coloured drops through the twisted tube of the apparatus has a very pretty effect.
The Pneumatic Pencil.
This ingenious invention is productive of results similar to Edison’s electric pen. It is the invention of an American gentleman, Mr. J. W. Brickenridge, of Lafayette, Indiana. The illustration (fig. 483) explains the mechanism of the pneumatic pencil. The whole apparatus is figured on the left side of the picture, while the longitudinal section of the pencil is shown on the right, the small cut at the top being a vertical section of a portion of the motive power. Compressed air furnishes the power of pressure, which is accomplished by means of a perforating needle.
If the treadle is put in motion, a backward and forward movement is imparted to a flexible diaphragm, as in the upper section in the centre of the illustration. By this movement the air is permitted to enter, and is compressed by the diaphragm into the flexible tube with which the diaphragm is connected. The air is thus brought into contact with another diaphragm at the end of the tube and presses on it. The pencil is fixed to the latter. When it is desired to use the pencil the apparatus is set in motion, and by a series of sharp, quick perforations, any writing can be traced, as by the electric pen. This indentation can be copied over and over again in a press,[Pg 455] the writing acting as the negative; and if ink be first run over it, as in a stencil plate, by a proper “roller,” the latter will come out as plainly as possible.

Tube Wells.
The principle upon which the tube well depends is very simple. It is well known that in certain localities water lies a short distance beneath the surface of the ground, and a very little trouble would satisfy us upon the point, and render us quite independent of the water companies’ supply. On the supposition that the water exists underneath our garden at, say, twenty-five feet beneath the surface of the ground, we have only to drive into the soil a tube for that distance, and by the assistance of a common pump we shall obtain a pure supply of water.
We will now proceed to describe the manner in which these wells are sunk. The first step is to fix a platform firmly upon the ground and bore a hole, by which the tube is to enter the ground. This tube should be very[Pg 456] thick, with an aperture of two inches or rather less, and three or four yards in length. The lower portion should be pierced with holes, as in the illustration, and terminating in a point of extremely fine-tempered steel. This tube can be driven into the ground by mallets, or by the suspended hammer, worked as shown in the illustration (fig. 484). This work will be easily accomplished, and when the first length of tube has been driven in, another can be fixed to it and hammered down in the same way.

When the tubes have been driven to the depth indicated it will be as well to let down a sounding line, a simple cord sustaining a pebble. If the stone be pulled up dry, another length of tube can be added, or the tubes can be pulled up, and another trial made. If, on the contrary, the pebble come up wet, the object is accomplished, and a small pump can be fixed to the upper end of the tube, as in fig. 485. At first the water will be found a little thick and muddy, in consequence of the disturbance of the soil and the particles adhering to the end of the first tube; but after an hour or so it will be found that the water has become quite clear. It need scarcely be said that if the water possesses sufficient ascensional force to rise to the level of the ground a pump need not be employed. An Artesian Well will, in that case, be the result.

The operation described on page 456 can usually be performed without any difficulty. Sometimes, however, the tube may come in contact with a large stone, and in that case the experiment must be tried elsewhere; but, as a rule, the pointed tube, in consequence of its small size and penetrative power, pushes any moderately-sized obstacle aside, readily turns aside itself, or passes between pieces of stone to the desired depth. Nine times out of ten the operation will be successful, and the experiment will not occupy more than an hour, under ordinary circumstances, and the tubing (and pump) may be obtained at a moderate price, which can even be diminished by arrangement. Ordinary wells are relatively very difficult to sink, and the soil thrown out from the pit is in the way, while a parapet is necessary to protect the opening. Besides, should water not be found after much work, the expense and trouble of digging will be uselessly incurred. Thanks to the tube system, we can search or probe for water anywhere with ease, and if we do not find it in one spot we can easily move on to another without incurring any serious trouble or expense.
We believe the idea of these “instantaneous wells” originated in the United States during the War of Secession, when some soldiers of the Northern army sunk rifle barrels into the ground, and obtained water in a barren land. To Mr. Norton the development of the idea is due, and in the Abyssinian Expedition the utility of the notion was fully demonstrated. Since that time M. Donnet of Lyons has modified and improved the tube-well, and arranged all the materials, including wider tubing and the hammers upon a carriage, thus giving[Pg 458] greater facilities to the workmen and to those desirous of sinking such wells.
The general arrangement of M. Donnet, and the carriage with its equipments utilized, is depicted in fig. 484; the actual sinking of the well is carried out just as originally performed by Mr. Norton.
A New Swimming Apparatus.

We have to mention a novel means of swimming, which may prove[Pg 459] useful to those who distrust the natural buoyancy of water and their own powers of keeping afloat or swimming. The simple apparatus, shown in fig. 486, is the invention of an American named Richardson, a citizen of Mobile, U.S.

The machine consists, essentially, of a shaft, upon which a float is fixed, and at the end of the shaft is a small screw propeller. The shaft is put in motion by a wheel arrangement worked by the hands, and by a crank moved by the feet. The swimmer rests upon the float, with his head well above water. The float sustains him, while the propeller forces him through the water, without his feeling fatigued, at the rate of about five miles an hour. A[Pg 460] certain amount of practice is necessary to obtain complete command of the machine, but when mastered the swimmer can proceed, without much exertion, at a rapid rate. The apparatus itself is not difficult to make, and persons who have tried it speak highly of its convenience and of the facilities it may afford. Captain Boyton’s swimming-dress is another useful invention, but the means of mechanical propulsion are wanting, while in this new apparatus the swimmer can drive himself through the sea with ease and expedition, and even a non-swimmer may thereby save life without danger to himself, or the person he wishes to rescue.

The Nautical Velocipede, which also deserves some notice at our hands, is the invention of M. Croce-Spinelli, who tried it upon the great lake of Vincennes and also on the Seine, when it was the object of much curiosity; but when the Franco-German war broke out the experiments were discontinued, and the inventor did not live to perfect the apparatus. He fell a victim to his love for ballooning. But M. Joberts, a practical machinist, has lately taken up the idea broached by Croce-Spinelli, and has brought out a new water velocipede of very ingenious construction, with satisfactory results. The machine is described as follows. There are two hollow tin “floats” of cylindrical form, and tapered at the ends. These floats are joined together by a platform made of very light wood, on which the seat of the worker is raised, and underneath is the machinery for propelling the velocipede. The motive power is very simple, and corresponds to that employed to propel the bicycle on land, by the feet of the rider, the wheel being furnished with paddles in the water velocipede.

A rudder, which can easily be worked by cords, gives the velocipedist complete control of the machine, the steering being performed by a handle similar to that which the bicyclist uses to turn the machine he rides. In[Pg 462] fact, the “water” velocipede is an adaptation of the “terrestrial” machine so familiar to all readers. This velocipede is equally adapted for sea or lake progression, the waves of the former being, under ordinary circumstances, no obstruction, for very little motion is imparted to the sitter. For those desirous to bathe in deep water the machine offers many facilities; and in the case of attack of cramp or faintness, rescue would not be difficult, as the swimmer could support himself upon the pointed cylinders of the water velocipede till assistance arrived. On the other hand, it is very necessary to know how to swim before attempting to work the machine.

Before describing the ice-yachts which are used in Canada when winter’s cold grasp lies on water and land, we will mention a very curious experiment in water locomotion made a year or two ago. The illustration explains itself. It is not an imaginary sketch, it is the record of fact.
This sagacious seal was exhibited in London, and was in the habit of performing certain tricks, one item of his performance being to draw the light canoe (as represented), and another accomplishment consisted in “striking the light guitar,” to the astonishment of the spectators, amongst whom was the writer. The instrument was placed between his fins, or “flappers,” and the seal twanged it more or less melodiously. He was very tame, and obedient to his master and trainer.
We all have heard of, even if we have not seen, the twin steamer Castalia, which, pending the opening of the tunnel beneath the Channel, was supposed to reduce sea-sickness to a minimum. The Castalia did not answer,[Pg 463] however, but an American has planned certain double yachts, of which we give an illustration. The sailing-boats, as represented, have had much success upon the lake of Cayuga, and are quite seaworthy,—in fact, it is impossible to overturn them.
The weight of one of these yachts is about fifteen hundred pounds, and the draught six inches. Having two keels they answer the helm very readily. The boat, in the centre of the illustration, belongs to Mr. Prentiss, and is called the Pera Ladronia. It is a very fast “ship.”
From navigation in water, we now come to navigation on water. The ice-boats are much used in Canada, and their simple but effective construction will be readily perceived from the accompanying illustration. The Americans state that these ice-yachts can run before a good breeze as fast as an ordinary train. There are, or were, models of some such (Finland) yachts in the South Kensington Museum with two sails. The American yacht, as a rule, has only one sail, and the owners say—but we will not vouch for the truth of the allegation—that they frequently run far ahead of the wind that primarily propelled them!
Sailing on Land.

It is quite possible to sail upon land, although this statement may appear contradictory in terms. “The force of the wind upon sails,” says Bishop Wilkins in his work, “Mathematical Magic,” printed in London in 1648, “can be applied to vehicles on land as well as to ships at sea. Such conveyances,” he adds, “have long been in use in China and in Spain, as well as in flat countries, such as Holland, where they have been employed with great success. In the last-named country they are propelled with greater speed than are ships before a fair wind; so that in a few hours a boat containing several persons actually travelled nearly two hundred miles, with no trouble to any one on board except the steersman, who had little difficulty in guiding the boat.”
The astonishment expressed by the good bishop was quite justified, for, as a matter of fact, a carriage or boat on wheels, with sails, as shown in the illustration, achieved a distance of nearly thirty-eight miles in an hour. This pace was quite unknown at that time; such a rate of travelling had never entered the minds of people then. “Men running in front of the machine[Pg 464] after a while appeared to be going backwards, so quickly were they overtaken and passed.” “Objects at a distance were approached in the twinkling of an eye, and were left far in the rear.” So it is evident that, had locomotion by steam not been adopted, the mode of sailing on land would have eventually become the most rapid mode of transit, and it is rather remarkable that it was never adopted as a mode of travel.

But Bishop Wilkins had not to reproach himself on this account, for he adapted the principle of the windmill to carriages, “so that the sails would turn and move his car, no matter in what direction the wind was blowing.” He proposed to make these sails act upon the wheels of a carriage, and trusted to “make it move in any direction, either with the wind or against it!” This suggestion has been lately adopted in the United States, and it is curious that after two hundred and fifty years no better mode for utilizing wind-power on land has ever been found. Perhaps the ice-boats already mentioned may be the forerunners of some new system of “land transport,” for which enormous kites have been made available.
It is somewhat remarkable that if the introduction of railroads quite “took the wind out of the sails” of any other mode of locomotion on terra firma, it is that very iron track which has led to the reintroduction of sails[Pg 465] as a mode of progression upon the rails. In the United States at the present time there are many vehicles propelled by sails across the immense prairies at a pace, with a strong wind, which equals that of the trains. We are indebted to Mr. Wood, of Hayes City, Kansas, for the photograph from which the picture of the sailing-waggon, invented by Mr. Bascom, of the Kansas Pacific Railway, is copied. This carriage travels usually at thirty miles an hour, and a speed of forty miles an hour has been obtained when the wind has been high and blowing directly “aft.” The distance of eighty-four miles has been accomplished in four hours when the wind was “on the beam,” or a little forward of it, and on some curves with an almost contrary breeze.
The newest machine has four wheels, each thirty inches in diameter; it is six feet in length, and weighs six hundred pounds. The sails are carried upon two masts, and they contain about eighty-one square feet of canvas. The main, or principal mast, is eleven feet high, four inches in diameter at the base, and two inches at the top. As in the case of the ice-boats, it is claimed for the sailing carriage that it frequently outstrips the wind that propels it along the track. On the other hand, there is a difference between the best sailing points of the two kinds of vehicle. The ice-boat goes quickest with the wind “dead aft,” the carriage makes best time with the wind “on the beam”—i.e., sideways. The greater friction and larger surface exposed to the influence of a side-wind no doubt will account for the difference between the speed of the railway sailing-carriage and the ice-boat.
Mr. Bascom informs us that the carriage we have described is in frequent use upon the Kansas Pacific Railway, where it is employed to transport materials for the necessary repairs of the line, telegraph, etc., etc. It is a very cheap contrivance, and a great economizer of labour. We all have noticed the cumbrous method of “trolly-kicking” by “navvies” along the line. A trolly fitted with a sail would, in many cases, and on many English lines, save a great deal of trouble, time, and exertion to the plate-layers.

CHAPTER XXXIII.
ASTRONOMY.
INTRODUCTORY—HISTORY OF ASTRONOMY—NOMENCLATURE.

Astronomy is the science which treats of the heavenly bodies and the laws which govern them. The term is derived from two Greek words, astron, a star, and nomos, a law. It may be included in the study of Physics, for the motion of the planetary bodies and equilibrium, gravity, etc., all have something to say to the arrangements and positions of the stars. The space in which they are set is infinite, and known as the “Firmament,” or “Heaven.” The number of the heavenly bodies must therefore be infinite also. We can see a few stars, comparatively speaking, and there must be numbers whose light has never yet reached the earth. When we calmly reason upon the immeasurable distances and the awful rapidity of motion, with the masses of matter thus in movement, we are constrained to acknowledge that[Pg 467] all our boasted knowledge is as nothing in the wondrous dispensations of Him “who telleth the number of the stars, and calleth them all by their names.”
Astronomy, no more than any other of the physical sciences, cannot stand by itself. We have seen how heat, light, electricity, etc., are all, in a manner, inter-dependent. So astronomy is dependent upon mathematics, particularly geometry and trigonometry, for the wondrous problems to be solved. But in the following sketch we do not propose to plunge the reader in the slough of calculations. We only desire to put plainly before him the great phenomena of nature with regard to the heavens, and the glorious orbs which so thickly stud the space above us. We need not detail the laborious calculations by which philosophers have arrived at certain discoveries. We may refer to the results and explain general principles, thereby indicating the road by which the student may arrive at the more difficult bypaths in the fields of scientific discovery.
The history of astronomy is nearly as old as the world itself, or rather as old as the human race. From the earliest ages we can picture men gazing upon the “spangled heavens,” and the wandering tribes of the desert were always very careful observers of the paths of the stars. To the nomads of the East the planetary system served as compass and clock, calendar and barometer.
We shall find, therefore, that many observations of the heavenly bodies were made by the ancients, and have descended to more advanced generations, and this leads us to remark that the science of astronomy can be studied without any very special or costly apparatus. In other branches of science numerous instruments are indispensable before we can reveal to ourselves the desired results. In astronomy, a telescope—even a good field glass, such as possessed by any household, will reveal many interesting facts. We will, by means of more expensive instruments, and by the aid of large telescopes particularly, enjoy the sight of the moon and planets. But even with the naked eye a great variety of phenomena may be observed. With a celestial globe in our hands upon a fine starry night, we can easily find out the position of the constellations, and trace their forms in the firmament.
It is to the Chaldeans, Indians, Chinese, and Egyptians, that our knowledge of astronomy is primarily due. They did much to facilitate the observation of the stars; they named the planets, grouped the stars, and marked the sun’s track in the sky. Astrology was cultivated in very remote ages. The Jews practised it; and the astrologers of subsequent periods played very important parts in divining the future of individuals, and casting their horoscopes. Many of these so-called predictions came true, “because,” as was remarked by Pascal, “as misfortunes are common they” (the astrologers) “are often right,” as they foretold misfortune oftener than good fortune. Still the fact remains that occasionally a very startling prediction was made, and proved true; such, for instance, as the laying waste of Germany by Gustavus Adolphus, which was foretold by Tycho Brahé after his consideration of a[Pg 468] certain comet, and the date of the king’s death was also correctly prophesied. Astrology, therefore, held a very considerable influence over the human race during the Middle Ages.
We can only give a very brief historical summary of the science. We know that the destinies of individuals and nations were at a very early period attributed to the influence of the stars. We read that “the stars in their courses fought against Sisera,” and many expressions surviving to the present time serve to remind us that the stars were at one time paramount in men’s minds. Thus we have the phrases—“unlucky star,” “born under a lucky star,” “mark my stars,” “moonstruck,” etc. Even the common term “consider”—to take counsel of the stars—is thus accounted for, and many men have a habit of looking up to the ceiling of a room or to the sky when thinking deeply—considering with the stars. “Contemplate” is another term signifying the same thing; for templum, a temple, was formerly a space marked upon the sky in imaginary lines, and traced on the ground in accordance with the supposed diagram. Thus temple became a place for heavenly “contemplation,” and by an easy transition to a place of worship. In our old poets’ writings we have many allusions to the influences of the stars.
Although from Thales, who lived B.C. 610, the real science of astronomy may be allowed to date, there can be no doubt that the ancients were acquainted with many phenomena. The Chaldeans were, doubtless, the first to place on record the rising and setting of the celestial bodies and eclipses, and used the water-clock (clepsydra). A list of eclipses from 2234 B.C. is stated to have been found at Babylon by Alexander the Great. The Chaldeans also divided the ecliptic into twelve equal parts, and the day and night into twenty-four hours. The Chinese, again, have recorded astronomical phenomena as far back as 2857 B.C.; and the Egyptians also were well versed in the science, although no records of much importance remain to us, unless the zodiac signs were their invention.
Thales predicted the eclipse of the sun B.C. 610. Aristarchus and Eratosthenes also made important observations. Hipparchus (160-125 B.C.) discovered the precession of the equinoxes, calculated eclipses, determined the length of the year, etc., etc.
Ptolemy, of Alexandria, A.D. 130-150, was the founder of a theory called the Ptolemaic System, which recognized the earth as the centre of all—the sun, moon, stars, etc., all revolving in very complicated courses around it, as figured in the diagram herewith. Even though his theory turned out to be untenable, he paved the way for his successors in other ways, and[Pg 469] left a valuable collection of observations on record. In this volume, called the “Almagest,” he reviewed the state of the science, and gave a catalogue of stars, as well as a description of the heavens. He discovered the lunar evection.

After his time astronomy, though it was not neglected, appeared to droop, and it is at a comparatively late period that we again open the records—viz., in 1543, the year in which Copernicus died. This philosopher, who was born in 1473, promulgated the true theory of the solar system. He placed the sun in the centre of the planets, and by this he explained their motion around the sun, though they appeared to be carried round the earth. The book in which he explained his theory, “De Revolutionibus Orbium Celestium,” was not finished till a day or two before he died.
The justly celebrated Tycho Brahé was the most important of the successors of Copernicus, but he opposed the Copernican theory, while other able philosophers agreed with it. Brahé was a Dane; he died in 1601. He adopted the theory that the sun and moon revolved around the earth, while the (other) planets moved around the sun. This theory did not gain much credence, but he, again, though he could not defeat Copernicus, and though he was wrong in his assumption, made many important investigations. After him came Kepler, whose observations upon the planet Mars cleared away many complications, and he laid down three laws, which are as follows:—
1. Every planet describes an elliptic orbit about the sun, which occupies one focus of each such ellipse.

2. If a line be drawn from the sun, continually, to any planet, this line will sweep over equal areas in equal times.
3. The squares of the periodic times of the planets are proportional to the cubes of their mean distances from the sun.
Kepler also remarked that gravity was a power existing between all bodies, and reasoned upon the tides being caused by the attraction of the moon for the waters.


It was about this time—viz., the beginning of the seventeenth century—that the telescope was invented, and logarithms[Pg 470] came into use. The actual discoverer of this now almost perfected instrument is uncertain. Borelli, who wrote in the seventeenth century, ascribes the discovery to Zachariah Jansen and Hans Lippersheim, spectacle makers of Middleburg. Baptista Porta, also a spectacle maker, has had the credit of discovering the magnifying power of the lens, and, so far, the originator of the telescope.

But whoever invented it, the telescope did not penetrate into southern Europe till 1608-9. Galileo then made inquiries concerning the new instrument, and Kepler made some propositions for their construction. But Harriot had used the instrument so far back as 1611 or 1612, and had observed spots upon the sun’s disc. Galileo, in 1610, had also made observations with the telescope, and discovered the satellites of Jupiter. He thereby confirmed the Copernican theory;25 and when Newton promulgated his immortal discovery of gravitation, after Picard’s researches, the relations of the sun and planets became more evident. His researches were published in the Principia, and then one-half the scientific world began to question the principle of gravitation, which was supported by Newton and his adherents. Subsequently the researches of Lagrange and Laplace, Adams and Leverrier, Sir J. Herschel, etc., brought astronomy into prominence more and more; and the innumerable stars have been indicated as new planets have been discovered. The spectroscope, which gives us the analyses of the sun and other heavenly bodies, has, in the able hands of living astronomers, revealed to us elements existing in the vapours and composition of the sun, etc. Stars are now known to be suns, some bearing a great resemblance to our sun, others differing materially. The nebulæ have been analysed, and found to be stars, or gas, burning in space—hydrogen and nitrogen being the chief constituents of this glowing matter. Instruments for astronomical observation have now been brought to a pitch of perfection scarcely ever dreamed of, and month by month discoveries are made and recorded, while calculations as to certain combinations can be made with almost miraculous accuracy. The transit of Venus, the approaches of comets, eclipses, and the movements of stars, are[Pg 471] now known accurately, and commented upon long before the event can take place.
We will close this chapter by giving a brief explanation of the various definitions most usually employed in astronomy.
1. The Axis of the earth is an imaginary line passing through the centre (north and south); the poles are the extremities of this line.
2. The Equator is an imaginary circle passing round the globe, dividing it into northern and southern hemispheres. The equinoctial is the plane of the former circle extended to the heavens, and when the sun appears in that line the days and nights are of equal duration—twelve hours each.
3. The Ecliptic is the sun’s path through the heavens—though, of course, the sun does not actually move, and therefore the track, or supposed circle, is really the earth’s motion observable from the sun. When the moon is near this circle eclipses happen. The ecliptic cuts the equinoctial at an angle of about 23°. One half is to the north and the other to the south of the equinoctial.
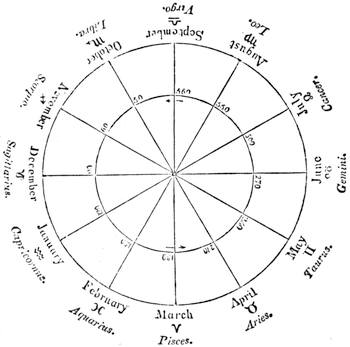
4. The Zodiac is a girdle extending 8° on each side of the ecliptic, in which space of 16° the planets move. The zodiac is divided into twelve parts of 30° each, called the “Signs.” These names are as under written:—
| Northern Signs. | |
|---|---|
| Spring. | Summer. |
| Aries, the Ram, March. Taurus, the Bull, April. Gemini, the Twins, May. |
Cancer, the Crab, June. Leo, the Lion, July. Virgo, the Virgin, August. |
| Southern Signs. | |
| Autumn. | Winter. |
| Libra, the Balance, September. Scorpio, the Scorpion, October. Sagittarius, the Archer, November. |
Capricornus, the Goat, December. Aquarius, the Waterbearer, January. Pisces, the Fishes, February. |
5. Colures are two circles dividing the ecliptic into four equal parts, and making the seasons.
6. The Horizon is the boundary line of our vision, and is called the[Pg 472] sensible (apparent) horizon. The true horizon is the circle—as on a globe—dividing the heavens into two hemispheres. The sensible horizon is enlarged according as the eye is elevated above the ground. A man six feet high can see a distance of three miles when standing on a plain. We can always find the distance visible when we know the height at which we stand, or, inversely, we can tell the height of an object if we know the distance. We have only to increase the height one half in feet, and extract the square root for the distance in miles. On giving the distance in miles reverse the operation.

For instance, for the man six feet high, as supposed, add three feet, being half his height; that makes nine feet. The square root (or number multiplied by itself to give nine) is three, which is the number of miles the man can see on a plain. Or, again, suppose we can see a tower on the level, and we know we are twelve miles away from it. The square of twelve is one hundred and forty-four feet, one-third of that is forty-eight feet, which represents the half of the original height added to the whole tower in feet; so the whole tower is ninety-six feet high. Reversing, as in the former case, we can prove this by taking the tower at ninety-six feet high and trying to find the distance we can see from its summit = 96 + 48 = 144; the square root of 144 = 12, the distance required.
7. The Nadir and the Zenith are the poles of the horizon. The zenith is exactly overhead, the nadir exactly under foot. Circles drawn through these points are azimuth circles.
8. Meridians are circles passing through the poles at right angles to the equinoctial. Every place is supposed to have a meridian, but only twenty-four are upon the globe, and they represent the sun’s, or the planets’, “movements” every hour—15° being one hour, 360° being twenty-four hours (see fig. 500). One quarter of a degree equals one minute of time. Parallels of latitude are familiar circles parallel to the equator. Latitude in astronomy is the distance from the ecliptic at a right angle north or south. This will be explained as we proceed.

9. Declination is the distance of the heavenly bodies from the equinoctial measured as a meridian.
The Tropics indicate the limits of the sun’s declination.
10. Disc is the term applied to the apparently flat surface of a planet, such as the moon, for instance.
11. The Orbit is the path described by a planet revolving round the sun. The plane of the orbit is an imaginary surface cutting through the centre of the sun and the planet, and extending to the stars. The diagram shows the plane of the earth’s orbit. The circle, A B C D (fig. 501), is the ecliptic. The inclination of an orbit is the plane of the orbit with reference to the plane of the earth; and, supposing the shaded part of the illustration to be water, a hoop held inclined towards the earth, with one half in and the other half out of the water, will describe the planetary orbit.

12. Nodes are the opposite points of a planet where its orbit cuts the ecliptic or the earth’s orbit.
13. Apogee is the point of a planet’s orbit farthest from the earth. Perigee is the nearest point.
14. The terms Culmination, Conjunction, and Opposition require no special explanation. But planets are in conjunction with each other when in the same sign and degree. A planet with the sun between it and the earth is in conjunction with the sun. With the earth between it and the sun it is in opposition.
15. Latitude and longitude upon a celestial globe are known respectively as “Declination” and “Right Ascension.”
16. The Radius Vector is a line drawn from a planet to the sun, wherever the planet may be (see fig. 497).
CHAPTER XXXIV.
ANGLES AND MEASUREMENT OF ANGLES.
THE QUADRANT—TRANSIT INSTRUMENT—CLOCKS—STELLAR TIME—SOLAR TIME—“MEAN” TIME.
We must say a few words respecting the various instruments and aids to astronomical observation before proceeding, for astronomy requires very accurate calculations; and though we do not propose to be very scientific in our descriptions, some little idea of the manner in which observations may be made is necessary. The first thing to see about is the Angle.
Suppose we draw four lines on a piece of paper, ab and cd. These intersect at a point, m. We have then four spaces marked out, and called angles. The four angles are in the diagram all the same size, and are termed right angles, and the lines containing them are perpendicular to each other.

But by altering the position of the lines (see fig. 504), we have two pairs of angles quite different from right angles; one angle, a´ m´ c´, is smaller, while a´ m´ d´ is much larger than the right angle. The former kind are called acute, the latter obtuse angles. We can therefore obtain a great number of acute angles, but only three obtuse, and four right angles around a given point, m.

The length of the sides of an angle have no effect on its magnitude, which is determined by the inclination of the lines towards each other. We now may consider the magnitude of angles, and the way to determine them. For this purpose we must describe a circle, which is figured in the diagram. But what is a circle?—A circle is a curved line which always is at the same distance from a certain fixed point, and the ends of this line meet at the point from which the line started.

If we fasten a nail or hold a pencil on the table, and tie a thread to it, and to the other end of the thread another pencil, we can describe a line around the first pencil by keeping the thread tightly stretched. This line is at all points at equal distance from the centre point.[Pg 475] Any line from the centre to the circumference is called a radius, and a line through the centre to each side of the circumference is the diameter, or double the radius. The circumference is three (3·14) times the diameter. Any portion, say k i l, is an arc, and the line, k l, is the chord of that arc. A line like m n is a secant, and o p is a tangent, or a line touching at one point only.

We may now resume our consideration of the angles by means of the circle. Let us recur to our previous figure of the right angles, around which we will describe a circle. We see that the portion of the circumference contained between the sides of the right angle is exactly one-fourth of the whole. This is termed a quadrant, and is divided into 90°—the fourth of 360 equal parts or degrees into which the whole circumference is divided. The angle of 45° so often quoted as an angle of inclination is half a right angle. To measure angles an instrument called a Protractor is used.

The Protractor, as will be seen from the accompanying illustration (fig. 507), is a semi-circle containing 180°. The lower portion is a diagonal scale, the use of which will be explained presently. The Protractor measures any actual angle with accuracy. If we put the vertical point of the angle and the centre point of the circle together, we can arrive at the dimensions of the angle by producing the lines containing it to the circumference. An angle instrument, figured herewith, may be assumed as the basis of most[Pg 476] apparatus for measuring angles. An index hand, R R, moves round a dial like the hand of a clock, and the instrument is used by gazing first at one of the two objects, between which the angle we wish to determine is made—like the church steeples (fig. 508) for instance. The centre of the instrument is placed upon the spot where lines, if drawn from the eye to each of the objects, would intersect. The index hand is then put at 0°, and in a line between the observer and the object, A. Then the index is moved into a similar position towards B, and when in line with it the numbers of degrees passed over (in this imaginary case 20), shows the magnitude of the angle.


The simple quadrant is shown in the cut (fig. 510). This was so arranged that when any object in the horizon was being looked at through the telescope attached, a plummet line is at 0°. But if the telescope be raised to C S, the quadrant will move, and the line will mark a certain number of degrees of the angle which a line if drawn from the star makes with the line of the horizon. The “Astronomical Quadrants” are as shown in fig. 516, and consist of a quadrant of wood strengthened and fitted with a telescope. The circle is graduated on the outer edge, and a “vernier” is attached. The time is determined by the observation of the altitude of a star, and then by calculation finding out at what time the star would have the observed altitude. The quadrant is now superseded by circular instruments.

An ellipse is a flattened circle, or oval, and will be understood from the diagrams. Let us fix two pegs upon a sheet of paper, and take a thread longer than the distance between the pegs; draw with the pencil controlled by the thread a figure, keeping the thread tight. We shall thus describe an oval, or ellipse. The orbit of nearly all the heavenly bodies is an ellipse. The parabola is another curved line, but its ends never meet; they become more and more distant as they[Pg 477] are continued. The comets move in parabolic curves, and consequently do not again come within our vision unless their direction be altered.


This figure has a long axis, ab (fig. 512); and perpendicular to this a short axis, de, passing through the centre, c. The two points, S S′, are called the foci of the ellipse; also, as is evident from the construction of the figure, any two lines drawn from the two foci, to any point of the circumference, for instance, S and S′m, or Sm′ and S′m′, etc., which represent the thread when the pencil is at m or m′, are together equal to the larger axis of the ellipse. These lines, and we may imagine an infinite number of such, are called radii vectores. The distance of the foci, S or S′, from the centre, c, is called the eccentricity of the ellipse. It is evident that the smaller the eccentricity is, the nearer the figure approaches to that of the circle. The superficies of the ellipse is found by multiplying the two half axes, ac and dc, by each other, and this product by the number 3·14.
The Diagonal Scale is shown in the margin. It is used to make diagrams so as to bring the relative distances before the eye. The larger divisions represent, it may be, miles, or any given distance; the figures on the left side tenths, and the upper range hundredths of a mile. So a measurement from Z to Z´ will represent two miles, we may say, with so many tenths and hundredths.

The Transit instrument is due to Roemer, a Danish astronomer. It consists of a telescope so constructed as always to point to the meridian, and rotates upon a hollow axis, directed east and west. At one end is a graduated circle. The optical axis of the telescope must be at exactly right angles to the axis of the instrument; it will then move on the meridian. There is an eye-piece filled with two horizontal and five vertical wires, very fine, the latter at equal distances apart. The star appears, and the time it takes to cross is noted as it passes between each wire, and the mean of all the transits will be the transit on the meridian. For if we add the times of[Pg 478] all the transits across the wires, and divide by five the number of them we shall get at a true result.

A good clock is also a necessary adjunct for astronomical observations, and the astronomical clocks and chronometers now in use record the time with almost perfect accuracy. The improvement in telescopes, the use of micrometers, etc., have greatly facilitated observations. In the transit clock we have a most useful timekeeper, for the ordinary clocks are not sufficiently accurate for very close observations. The sidereal time differs from solar time, and the twenty-four hours’ period is calculated from the moment a star passes the meridian until it passes it again. The sidereal day is nearly four minutes shorter than the solar day, and the sidereal clock marks twenty-four hours instead of twelve, like the old dial at Hampton Court Palace over the inner gate. The Chronograph has also been useful to astronomers, for by “pricking off” the seconds on a roller by itself, the observer can mark on the same cylinder the actual moment of transit across each wire of the instrument, and on inspection the exact moment of transit may be noted.
The Equitorial is another useful instrument, and by its means the whole progress of a star can be traced. The Equitorial consists of a telescope fixed so that when it has been pointed at a certain star a clock-work movement can be set in motion, which exactly corresponds with the motion of the star across the heavens, and so while the star moves from its rising to setting it is under observation. Thus continuous observations maybe made of that particular star or comet without any jerking or irregular movement.
We can thus see the uniform motion of the stars which go on in greater or lesser circles as they are nearer to or farther from the pole; and with the exception of the polar star, which, so far as we are concerned, may be considered stationary, every star moves round from east to west—that is, from the east of the polar star to the west of it, in an oblique direction. Therefore, as Professor Airy remarks, “Either the heavens are solid, and go all of a piece, or the heavens may be assumed to be fixed or immovable, and that we and the earth are turning instead of them.”

The Mural Circle is another very useful instrument, and is used by calling to aid the powers of reflection of quicksilver, in which a bright star will appear below the horizon at the same angle as the real star above the horizon, and thus the angular distance from the pole or the horizon of any star can be calculated when we know the inclination of the telescope. The[Pg 479] Transit Circle is also used for this purpose, and is a combination of the transit instrument with the circle. In all calculations allowance must be made for refraction, for which a “Table of Refractions” has been compiled. From the zenith to the horizon refraction increases. The effect of refraction can be imagined, for when we see the sun apparently touching the horizon the orb is really below it, for the refraction of the rays by the air apparently raises the disc.
The clock and chronometer are both very useful as well as very common objects, but a brief description of the pendulum and the clock may fitly close our remarks upon astronomical apparatus and instruments. The telescope has been already described in a previous portion of this work, so no more than a passing reference to it has been considered necessary. We therefore pass on to a consideration of the measurement of time, so important to all astronomers and to the public generally.
Time was measured by the ancients by dividing the day and night into twelve hours each, then by sun-dials and water-clocks, or clepsydra, and sand-clocks. The stars were the timekeepers for night before any mechanical means of measurement were invented.
Sun-dials were in use in Elijah’s time, and the reference to the miracle of the sun’s shadow going back on the dial as a guarantee to Hezekiah, will be recalled at once by our readers. These dials were universal, and till sunset answered the purpose. But the hours must have been very varying, and on cloudy days the sun-dials were practically useless.
The water-clocks measured time by the dripping or flow of water, and they were used to determine the duration of speeches, for orators were each allotted a certain time if a number of debaters were present. This method might perhaps be adapted to the House of Commons, and speaking by the clock might supersede clôture. We find allusions to these practices in the orations of Demosthenes. Even this system was open to objection, for the vases were frequently tampered with, and an illiberal or objectionable person was mulcted of a portion of the water, while a generous or popular adversary had his clepsydra brimming full. Some of these water-clocks were of elegant design, and a Cupid marked the time with arrows on the column of the clock of Ctesibius, while another weeping kept up the supply of water. The motive power was the water, which filled a wheel-trough in a certain time, and when full this trough turned over, and another was filled. The wheel revolved once in six days; and by a series of pinions and wheels the movements were communicated more slowly to the pillar on which the time was marked for 360 days, or with other arrangements for twenty-four hours.
The repeating of psalms by monks also marked the time, for by practice a monk could tell pretty accurately how many paternosters or other[Pg 480] prayer he could repeat in sixty seconds. At the appointed hour he then awoke the monastery to matins.
Nature also marks time for us—as, for example, the age of trees by means of rings—one for each year; and horses’ teeth will guide the initiated to a guess at the ages of the animals, while the horns of deer or cattle serve a like purpose. But man required accuracy and minute divisions of time. He had recourse therefore, to machinery and toothed wheels. Till the mechanical measurement of time was adopted, the sunrise and sunset only marked the day, and the Italians as well as Jews counted twenty-four hours from sunset to sunset. This was a manifestly irregular method. To this day we have marked differences of time in various places, and at Geneva we have Swiss and French clocks keeping different hours according to Paris or Berne “time.” This, of course, is easily accounted for, and will be referred to subsequently.

We have read that the first clock in England was put up in Old Palace yard in 1288, and the first application of the toothed-wheel clock to astronomical purposes was in 1484, by Waltherus, of Nuremberg. Tycho Brahé had a clock which marked the minutes and seconds. If we had had any force independent of gravitation which would act with perfect uniformity, so that it would measure an equal distance in equal spaces of time, all the various appliances for chronometers would have been rendered useless. In the supposed case the simple mechanism, as shown in the margin (fig. 517), would have sufficed. The same effect would be produced by the spring, were it possible that the spring by itself would always uncoil with the same force. But it will not do so: we therefore have to check the unwinding of the cord and weight, for left to itself it would rapidly increase in velocity; and if we likewise make an arrangement of wheels whereby the spring shall uncoil with even pressure all the time, we shall have the principle of the watch.
It is to Huygens that the employment of the pendulum in clocks is due, and the escapement action subsequently rendered the pendulum available in simple clocks, while the manner of making pendulums self-regulating by using different metals, has rendered timepieces very exact. Of course the length of a pendulum determines the movement, fast or slow; a long pendulum will cause the hands of the clock to go slower, for the swing will be a fraction longer. A common pendulum with the escapement is shown (fig. 518). Each movement liberates a tooth of the escapement. The[Pg 481] arrangement of wheels sets the clock going. The forms of pendulum are now very varied.

But in watches the pendulum cannot be used. The watch was invented by Peter Hele, and his watches were called “Nuremburg eggs” from their shape. The weight cannot be introduced into a watch, and so the spring and fusee are used. The latter is so arranged that immediately the watch is wound and the spring at its greatest tension, the chain is upon the smallest diameter of the fusee, and the most difficult to move. But as the spring is relaxed the lever arm becomes longer, and the necessary compensating power is retained. Watches without a “fusee” have a toothed arrangement beneath the spring.

The Pendulum. A “simple” pendulum is impossible to make, for we cannot put the connecting line between the “bob” and the clock-work out of consideration, so “simple pendulums” are looked upon as “mathematical abstractions.” The most modern clocks have what is called a “deadbeat” escapement, and a compensating pendulum. Clocks are liable to alter by reason of the state of the air and varying temperature, and until all our clocks are placed in vacuo we must be content to have them lose or gain a little. There is a magnet arrangement by which the Greenwich Observatory clocks keep time by compensation, corresponding with the fall or rise of the syphon barometer attached to it. The description need not be added. We may here state that detailed descriptions of all the instruments used in the Observatory, together with full information as to their use, will be found in a very interesting work by Mr. Lockyer, entitled “Stargazing,” to which we are indebted for some corrections in our summary.

We have spoken of solar time and sidereal time, and no doubt someone will inquire what is meant by mean time—an expression so constantly applied to the Greenwich clock time. Stellar time, we have[Pg 482] seen, corresponds to the daily revolution of a star or stars. Solar time is regulated by the sun, and this is the astronomical time generally observed, except for sidereal investigations. But the sun is not always regular; the orbit of the earth causes this irregularity partly. The earth moves faster in winter than in summer, so the sun is sometimes a little fast and sometimes a little slow. Astronomers therefore strike an average, and calculate upon a Mean Sun, or uniform timekeeper. Mean time and true (apparent) time are at some periods the same—viz., on the 15th of April, on the 14th of June, on the 31st of August, and on the 24th of December. Twice it is after, and twice before it. The time occupied by this “mean” sun passing from the meridian and its return to it, is a mean solar day, and clocks and chronometers are adjusted by it.

Twenty-four hours represents a complete revolution of the heavenly bodies. The mean solar time is 23h 56´ 4·091″, while twenty-four hours of mean time are equal to 24h 3´ 56·55″ of sidereal time. The difference between the times is given by Dr. Newcomb as follows, and is called the Equation of Time:—
| Differences between Mean and Apparent Time. | ||
|---|---|---|
| February 10th | True Sun | 15 minutes slow. |
| April 15th | ” | Correct. |
| May 14th | ” | 4 minutes fast. |
| June 14th | ” | Correct. |
| July 25th | ” | 6 minutes slow. |
| August 31st | ” | Correct. |
| November 2nd | ” | 16 minutes fast. |
| December 24th | ” | Correct. |
Measurement of Distances.
Before passing to consider the planetary system we must say a few words respecting the manner of ascertaining the distances of inaccessible objects, and by so doing, we shall arrive at an idea how the immense distances between the sun (and the planets) and the earth have been so accurately arrived at. To do this we must speak of parallax, a very unmeaning word to the general reader.

Parallax is simply the difference between the directions of an object when seen from two different positions. Now we can illustrate this by a very simple method, which we have often tried as a “trick,” but which has been very happily used by Professor Airy to illustrate the doctrine of parallax. We give the extract in his own words:—
“If you place your head in a corner of a room, or on a high-backed chair, and if you close one eye and allow another person to put a lighted candle upon a table, and if you then try to snuff the candle with one eye shut, you will find you cannot do it.... You will hold the snuffers too near or too distant—you cannot form any idea of the distance. But if you open the other eye, or if you move your head sensibly you are enabled to judge of the distance.” The difference of direction between the eyes, which is so well known to all, is ready a parallax. It can also be illustrated by the diagram herewith.

If two persons, A and C (fig. 523), from different stations, observe the same point, M, the visual lines naturally meet in the point, M, and form an angle, which is called the angle of parallax. If the eye were at M, this angle would be the angle of vision, or the angle under which the base line, A C, of the two observers appears to the eye. The angle at M also expresses the apparent magnitude of A C when viewed from M, and this apparent magnitude is called the parallax of M.
Let M represent the moon, C the centre of the earth represented by the circle, then A C is the parallax of the moon; that is, the apparent magnitude the semi-diameter of the earth would have if seen from the moon. If the moon be observed at the same time from A, being then on the horizon, and from the point B, being then in the zenith, and the visual line of which when extended passes through the centre of the earth, we obtain, by uniting the points, A C M, by lines, the triangle, A C M.
Therefore, as A M, the tangent of the circle stands at right angles to the radius, A C, the angle at A is a right angle, and the magnitude of the angle at C is found by means of the arc, A B, the distance of the two observers from each other. As soon, however, as we are acquainted with the magnitude of two angles of a triangle, we arrive at that of the third, because we know that all the angles of a triangle together equal two right angles (180°). The angle at M, generally called the moon’s parallax, is thus found to be fifty-six minutes and fifty-eight seconds. We know that in the right-angled triangle M C A, the measure of the angle, M = 56´ 58″, and also that A C, the semi-diameter of the earth = 3,964 miles. This is sufficient, in order by trigonometry, to obtain the length of the side, M C; that is, to find the moon’s distance from the earth. A C is the sine of the angle, M, and by the table the sine of an angle of 56´ 58″ is equal to 1652/100000; or, in other words, if we divide the constant, M C, the distance of the moon, into 100,000 equal parts, the sine, A C, the earth’s semi-diameter = 1,652 of these parts. And this last quantity being contained 60 times in 100,000, the distance of the moon from the earth is equal to 60 semi-diameters of the earth, or 60 × 3964 = 237,840 miles.

In a similar way the parallax of the sun has been found = 8″·6, and the distance of the sun from the earth to be 91,000,000 miles.
Let us first see how we can obtain the distance of any inaccessible or distant object. We have already mentioned an experiment, but this method is by a calculation of angles. The three angles of a triangle, we know, are equal to two right angles; that is an axiom which cannot be explained away. We first establish a base line; that is, we plant a pole at one point,[Pg 485] A, and take up our position at another point, B, at some distance in a straight line, and measure that distance very carefully. By means of the theodolite we can calculate the angles which our eye, or a supposed line drawn from our eye to the top of the object (C) we wish to find the distance of, makes with that object. We now have an imaginary triangle with the length of one side, A B, known, and all the angles known; for if all three angles are equal to 180°, and we have calculated the angles at the base, we can easily find the other. We can then complete our triangle on paper to scale, and find out the length of the side of the triangle by measurement; that is the distance between our first position, A, and the object, C. It is of course necessary that all measurements should be exact, and the line we adopt for a base should bear some relative proportion to the distance at which we may guess the object to be.
In celestial measurements two observers go to different points of the earth, and their distance in a straight line is known, and the difference of the latitudes. By calling the line between the observers a base line, a figure may be constructed and angles measured; then by some abstruse calculation the distance between the centre of the earth and the centre of the moon may be ascertained. The mean distance is sixty times the radius of the earth. The measurement of the sun’s distance is calculated by the observations of the transit of Venus across his disc, a phenomenon which will again occur on 6th December, 1882, and on 8th June, 2004, the next transit will take place; there will be no others for a long time after 2004.
All astronomical observations are referred to the centre of the earth, but of course can only be viewed from the surface, and correction is made. In the cut above, let E be the earth and B a point on the surface. From B the stars, a b c d, will be seen in the direction of the dotted lines, and be projected to e i k l respectively. But from the centre of the earth they would appear at e f g h correctly. The angles formed by the lines at b c d are the parallactic angles, f i g h and h l show the parallax. An object on the zenith thus has no parallax. (See fig. 524.)

CHAPTER XXXV.
THE SOLAR SYSTEM.
GRAVITATION—THE PLANETS—SIZE AND MEASUREMENT OF THE PLANETS—SATELLITES—FALLING STARS—COMETS—AEROLITES.

Gravitation is the force which keeps the planets in their orbits, and this theory, perfected by Newton, was partially known to Kepler. Newton brought this idea into practical shape, and applied it mathematically. We know that every object in the world tends to attract every other object in proportion to the quantity of matter of which each consists. So the sun attracts the planets, and they influence him in a minor degree. Likewise the moon and our earth reciprocally attract each other. But as the sun’s mass is far greater than the masses of the planets he influences them more, and could absorb them all without inconvenience or disturbance from his centre of gravity. We have, in a former portion of this work, spoken of the law of universal gravitation, which is the mutual attraction of any two bodies to each[Pg 487] other, is directly proportioned to their masses (not size), and inversely to the square of their distances apart.
This law operates amongst the heavenly bodies, and it is to the never-changing action of gravitation that the planets are kept in their places. Let us see how this is effected. We have read of force, and motion, and rest. Every body will remain at rest unless force compels it to change its position, and it will then go on for ever in a straight path unless something stops it. But if this body be acted on simultaneously by two forces in different directions, it will go in the direction of the greater force. Two equal forces will tend to give it an intermediate direction, and an equal opposing force will stop it. The last axiom but one—viz., the two equal forces in different, not opposing directions, gives us the key to the curving line of the planetary motions. Were it not for the attraction of the sun the planets would fly off at a tangent; while, on the other hand, were not the impelling force as great as it is, they would fall into the sun. Thus they take an intermediate line, and circle round the centre of the solar system—the Sun.
The solar system consists of the sun and the planets which revolve in space around him. These stars are called planets because they move in the heavens. We shall see that they have certain motions—going from east to west, from west to east, and sometimes they appear to be quite motionless. This change of place, appearing now at one side of the sun and now at another, has given them their title of “wanderers” (planets). Besides the planets there are comets and meteors, asteroids and satellites, all circling round the sun in more or less regular orbits. And there must be families of comets, and whole systems of meteors that have not yet appeared to us, and which make up the comets, as has been lately suggested.
Five planets were known to the ancients, and were named after gods and a goddess: Mercury, Venus, Mars, Jupiter, Saturn. In later years a great number were discovered. We must, however, confine ourselves to the consideration of the principal ones, eight in number, including our own Earth, Uranus and Neptune completing the list. Of these Venus and Mercury are the inferior, or interior planets moving between us and the sun. Mars, Jupiter, Saturn, Uranus, and Neptune are superior, or exterior, and pass quite round the heavens. All the planets are spheroids, and vary greatly in their magnitude, as will be seen by the illustration (fig. 528), the largest body being the sun. Mercury, Mars, and Venus, are not so large as the Earth. The other principal planets are considerably larger than our globe.

Mercury is the smallest of the planets, Venus being nearly as large as[Pg 488] the earth. Then comes Mars, which, though smaller than Venus, is larger than Mercury. Jupiter is the largest of all—the giant amongst planets, as Jove was the ruler of the gods of mythology. Saturn comes next, though much smaller than Jupiter, but bigger than all the rest together. Next Uranus, then Neptune, larger than Uranus, but farther away from us. We shall speak more in detail about these in their order separately.


Taking the earth as 1, the comparative VOLUMES of the planets are as follows:—
Mercury 1/25, Venus 4/5, Mars 1/5, Jupiter 1300, Saturn 900, Uranus 80, Neptune 230. Sir John Herschel gives the following illustration of magnitudes and distances:—

“Choose any well-levelled field or bowling green; on it place a globe two feet in diameter; this will represent the sun. Mercury will be represented by a grain of mustard seed on the circumference of a circle 164 feet in diameter for its orbit; Venus a pea, on a circle 284 feet in diameter; the Earth also a pea on a circle 430 feet; Mars a rather large pin’s head on a circle of 654 feet; Juno, Ceres, Vesta, and Pallas grains of sand in orbits of 1,000 to 1,200 feet; Jupiter a moderate-sized orange on a circle nearly half a mile across; Saturn a small orange on a circle four-fifths of a mile; and Uranus a full-sized cherry, or small plum, upon the circumference of a circle more than a mile and a half in diameter”

From an inspection of the following table the relative distances of the principal planets from the sun, their diameters, and other information respecting them may[Pg 489] approximately be obtained. The dates of the discovery of the more modern pair are added:—
| Names. | Diameters in English miles (about). | Distance from the sun (about). | Sidereal period of revolution. | Time of rotation on their axis. | Date of discovery. |
|---|---|---|---|---|---|
| d. h. m. | d. h. m. | ||||
| Mercury | 3,000 | 35,000,000 | 87 23 16 | 24 5 — | Antiquity |
| Venus | 7,500 | 66,000,000 | 224 16 50 | 23 21 21 | do. |
| Earth | 8,000 | 91,000,000 | 365 6 9 | 23 56 4 | do. |
| Mars | 4,500 | 139,000,000 | 686 23 31 | 24 37 20 | do. |
| Jupiter | 85,000 | 476,000,000 | 4,332 14 2 | 9 55 21 | do. |
| Saturn | 70,000 | 872,000,000 | 10,759 5 16 | 10 16 — | do. |
| Uranus | 33,000 | 1,753,000,000 | 30,686 17 21 | 9 30 — | Herschel, 1781. |
| Neptune | 37,000 | 2,746,000,000 | 60,126 17 5 | . . . | Leverrier and Galle, 1846. |
| The Sun | 850,000 | . . . . | . . . . | 25 7 48 |
Altogether there are a great number of planets and asteroids, which latter are minor planets circulating outside the orbit of Mars. They have nearly all classical names, such as Juno, Ceres, Vesta, Flora, Ariadne, Pallas, Pomona, Thalia, etc., and are all at distances from the sun ranging between 200,000,000 and 300,000,000 of miles, the periods of sidereal revolution ranging from 1,100 to 3,000 days, so their years must be from four times to nine times as long as ours. Altogether about two hundred of the minor planets have been discovered, and they are all very much smaller than the earth; some, indeed, being very tiny—only a few miles in diameter, but very massive. They do not appear to possess any satellites—at least, none have been discovered, for such very small bodies as they must be, supposing they exist, would be quite invisible even with our perfected instruments.



Satellites, however, or “planetary moons,” as they are sometimes designated, are plainly perceived attending upon the great planets. There are twenty of these at present under observation. One we are all familiar with, and the moon, par excellence, lends a beauty to our nights which no other[Pg 490] light that we can enjoy or command can ever do. It is remarkable that only this moon is specially mentioned in the Bible in connection with the sun. The stars are usually grouped, although, of course, the sun and moon are equally “stars” in the firmament. Mars possesses two moons and Jupiter four; Uranus also rejoices in the latter number; Neptune, like the Earth, has only one. It is reserved for Saturn to outstrip all the rest in his attendants, for no less than eight satellites wait upon that enormous planet. No doubt there are many more of these moons to be found, and every year will doubtless bring us further knowledge respecting them. Mars’ moons were only discovered very lately (in 1877), although they were known to exist; but being very small, unlike the others, they were missed. So we may conclude that the remaining satellites will remain for some time undiscovered, even if they actually are in existence. Jupiter’s moons are supposed to be as large as our own moon; Neptune and Uranus can boast of equally-sized attendants. But it is impossible to estimate the riches of astronomical lore which are beyond our ken. Millions of tiny planets are believed to exist, but their immense distance from us precludes all investigation. We are but mites in the scale.

Meteors, to which we have already referred, are small erratic bodies rushing through the planetary system, and getting hot in the process, appear in the atmosphere surrounding our earth as “shooting stars.” Some of these falling bodies have reached the earth, and several can be seen in the British Museum. Numbers, of course, are burnt up before they reach us, and who can tell what destruction such a catastrophe may represent, or whether it be or be not an inhabited world which has thus plunged to destruction by fire? They are of a metallic or stony nature. On certain nights in August and November it has been calculated that these meteors will appear. They fall from certain constellations[Pg 491] apparently on these occasions, and are called after their names—as Leonides, from Leo, in the November displays.

The star-showers at times attain the dimensions of a very beautiful display of rockets. Millions of them rush round the sun; and when, as occasionally happens, our earth comes near them, we have (as in 1866) a grand display of celestial “fireworks.” But the individuals composing the mass of falling stars are very small. These meteors are very much like the comets we last year had an example of, and it has been lately suggested that there is a great degree of affinity between the comets and the meteors;—in fact, that a comet is merely an aggregation of meteors. They have been supposed to be bodies of burning gas. Their mass is very great, and their brilliant tails are many millions of miles in extent.
Comets are thus distinguished by their tails, and differ very much in their orbits from the planets. The latter are direct in their wanderings, but comets are most irregular and eccentric. The name bestowed upon comets is from the Greek Kome, hair; for when the comet recedes from the sun the “tail” may be said to come out of the head, and appear as a hair in front, so to speak. But though all comets have tails, there are many luminous bodies (classed with comets) which have no tails.

The comet which created the most excitement was Halley’s in 1456, of which we append an illustration (fig. 537). A comet had been observed in 1607, and Halley made a calculation that it would reappear in 1757.[Pg 492] The calculation for its actual appearance was made by Claivant, and the expected visitor passed the perihelion in March 1759. This comet, on its appearance at Constantinople, is said to have caused much consternation, and Christians regarded it as a “sign,” for the Turks had just then captured Constantinople, and were threatening Europe. Pious people included it in their supplications for deliverance from their most dreaded enemies, and “Lord, save us from the Turks, the devil, and the comet,” was a common prayer.

There have been several very beautiful comets. Encke’s, Coggia’s, etc., and the comet of 1858 (Donatis) must be in the recollection of middle-aged readers. Others came in 1861 and 1874. In 1881 two comets appeared. Some comets of antiquity were very remarkable, and are reputed to have equalled the sun in magnitude. One tail is usually supposed to be the distinguishing mark of a comet, but in 1774 one appeared with six tails, arranged something like a fan. Sometimes the tail is separated from the head. Of the actual consistency of comets we cannot give any lengthened details. They apparently consist of elements similar to the meteors—namely, of solid masses, and have been supposed to be aggregations of meteors. Some appear at regular intervals, and their approach can be determined with accuracy. Of course we only see those which are attracted by the sun, or those which revolve in the solar system. There must be thousands of other comets which we never see at all.
The diagram (fig. 540 in the next page) represents a portion of the path of the comet of 1680. This visitor pursued its course for two months at a velocity of 800,000 miles an hour. The tail was estimated to extend 123,000,000 of miles, and a length of 60,000,000 of miles was emitted in two days. When this great comet was approaching the sun, or its perihelion, as such approach is termed, three minutes more would have seen it rush into the orb had its enormous pace been slackened, but as it was pro[Pg 493]ceeding so rapidly, and being just then 144,000 miles away, it escaped. We can scarcely estimate the results of such a collision. This comet appeared B.C. 34, and again at intervals of about 575 years. It may be expected in 2255. It is to Halley that the discovery of the elliptical orbits of comets is due.
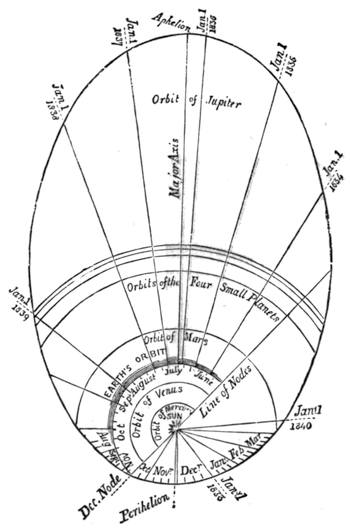
M. Biela’s comet was the cause of much anxiety in 1832, for a collision with the earth was apprehended. Fortunately a month intervened between the period at which the comet was expected at a certain place in the system and the earth’s arrival at that spot, so, as it happened, about 60,000,000 of miles intervened. We cannot say what the exact effect of such a collision would be, but some wonderful atmospheric phenomena and increased temperature would certainly result from the contact. Now the comet is supposed to have an effect upon the vintage, as “comet” wines are regarded with much favour. If comets, as is believed, do consist partly of solid particles, a collision might be unpleasant; but the weight is, as a rule, a mere nothing compared to their vapoury volume, which is enormous. That the tails must be of a very attenuated medium is evident, as we can see the stars through them, and we know that a very thin cloud will obscure a star. The “menacing” comet, mentioned in the Spectator February 1881, will not do much damage, so the scare was needless, as Mr. Proctor has explained.

Aerolites, or “Meteorites,” are falling bodies (meteors), which reach the earth in solid form. The greater mass of falling stars are burnt up ere they reach us, or are dissipated in space. But many instances of aerolites descending might be adduced. They usually consist of metals, such as iron and nickel mixed with sulphur, magnesia,[Pg 494] and silica. The theory concerning falling stars has been already mentioned.

We have thus far taken a brief general view of the solar system, with a few of the phenomena of the heavens. Our next step will be to consider the sun, the planets, and the asteroids, according to the order of magnitude. The asteroids we cannot consider separately, but the sun, moon, earth, and the principal planets will yield us much interesting information as we examine them more closely. We shall then, as far as possible, look into the domain of the fixed stars, constellations, and the nebulæ, commenting, as we proceed, upon the varied celestial and terrestrial phenomena connected with the movements of the heavenly bodies. As is due to the great centre of our system, we will commence with the Sun. But before proceeding to do so, we must say a few words about the motion of the heavenly bodies—that is, the apparent motion of the rising and setting of the sun and stars.
The attentive observation of the starry heavens, even during a single night, will convince us that all the visible stars describe circles which are the smaller, the nearer the stars are to a certain point of the heavens, P (fig. 542). In close proximity to this point there is a tolerably bright star, called the Pole Star, which has scarcely any motion, but appears to the eye as always occupying the same position. Hence a line, PP´, drawn from this star, through the centre of the earth, c, represents the axis around which all the heavenly bodies perform their apparent motions. The part of the celestial axis, PP´, passing through the earth, is the earth’s axis; the north pole, of which p is on the same side as the pole star, and the south pole, p´, is on the opposite side.

We have, therefore, by the aid of the stars, determined the position of[Pg 495] the earth’s axis, and by this latter we can assign to the equator its proper place. For if pp´ be the earth’s axis, aq´ is the greatest circle drawn round the earth, equally distant from both poles, and the plane of which cuts the earth’s axis at right angles.
Furthermore, let us suppose the plane of the equator to be extended till it reach the celestial concave; we thus find the place of the celestial equator, A Q, or equinoctial, as it is generally termed in opposition to the equator, which always means the terrestrial equator. The equinoctial divides the heavens into the northern and southern hemispheres. We cannot actually describe the equinoctial and make it visible, but we can imagine its line of direction by observing those stars through which it passes.
We are now in a condition to assign to an observer different stations in relation to the earth’s axis on the earth’s surface, which will essentially modify the aspects under which celestial phenomena are represented. One of these stations may be supposed to be at one of the two poles, for example, at p, or at any one point of the equator, as at a, or, finally, on any portion of the surface of the earth which lies between the pole and the equator, as, for example, o.

CHAPTER XXXVI
THE SUN.
MOTION OF THE SUN—THE SEASONS—CHARACTER OF THE SUN—SUNSPOTS—ZODIACAL LIGHT.
Suppose that we rise early in the morning we shall, as the reader will say see the sun rise—that is, he appears to us to rise as the earth rotates. By the accompanying diagram (fig. 544) we can understand how Sol makes his appearance, and how he comes up again; not, it will be observed, after the manner stated by the Irishman, who declared that the sun “went down, and ran round during the night when nobody was looking.” The earth rotates from west to east, and so the sun appears to move from east to west. If we look at the diagram we shall see that after rising at O, the sun advances towards the meridian in an oblique arc to A, the highest or culminating point—midday. He then returns, descending to W; this path is the diurnal arc. At Q similarly, during his passage in the nocturnal arc, he reaches the lowest or inferior culmination. HH´ is the meridian.
On the 21st of March, this path brings the sun on the “ equinoctial” line mentioned at the close of the last chapter. Day and night are then of equal duration as the arcs are equal. So this is the Vernal (or spring) Equinox. Some weeks after the sun is at midday higher up at S´, so the diurnal arc being longer, the day is longer, (Z is the zenith, Z´ is the nadir, P P´ is the celestial axis). From that time he descends again towards the equinoctial to the autumnal equinox, and so on, the diurnal arc becoming smaller and smaller until the winter solstice is reached (S).

From what has been previously said, it is evident that the sun has a twofold apparent motion—viz., a circular motion obliquely ascending from the horizon, which is explained by the rotation of the earth, and by our position, o, to the earth’s axis, p p´, and also by a rising and setting motion between the solstitial points, S and S´, which causes the inequality of the days and nights. Independently of the daily motion of the sun, we observe that at the summer solstice, on the 21st of June, at midday, the sun is at S´, and one half year later—viz., on the[Pg 497] 21st of December, at midnight, the sun is at s, from which he arrives again in the space of half a year at S´; so we are able to represent this annual motion of the sun by a circle, the diameter of which is the line, S´ s. This circle is called the Ecliptic.
The plane of the ecliptic, S´ s, cuts the plane of the equinoctial, A Q, at an angle of 23½°, and the axis of the ecliptic, S″´ s″, makes the same angle with the axis of the heavens, P P. The two parallel circles, S´ s´ and S s, include a zone extending to both sides of the equinoctial, and beyond which the sun never passes. These circles are called the Tropics, from τρέπω, I turn, because the sun turns back at these points, and again approaches the equinoctial. The parallel circles, S″ s″, and S″´ s″´, described by the poles of the ecliptic, S″´ s″, about the celestial poles, P P, are called the arctic and antarctic circles.
Whenever the sun crosses the equinoctial, there is the equinox; but the points of intersection are not invariably the same every year. There is a gradual westerly movement, so it is a little behind its former crossing place every year. (See diagram, fig. 547.)

[This is the “Precession of the Equinoxes,” because the time of the equinoxes is hastened, but it is really a retrograde movement. Hipparchus discovered this motion, which amounts to about fifty seconds in a year. So the whole revolution will be completed in about 28,000 years.]

It is obvious, then, that the sun is the most important star in the universe; and when we come to speak about the earth we shall consider the seasons, etc., more fully. Now we must endeavour to explain what the sun is like, and this can only be done with specially darkened glasses, for a look at the sun through an ordinary telescope may result in great, if not permanent, injury to the eye.
The sun is not solid so far as we can tell. It is a mass of “white-hot” vapour, and is enabled to shine by reason of its own light, which the planets and stars cannot do; they shine only by the sun[Pg 498]’s reflected light. So we may conclude the sun to be entirely gaseous, but, thanks to the recent researches in spectrum analysis (already explained), by which the light of the sun has been examined by means of the spectroscope, and split up into its component colours, Mr. Lockyer and other scientists have discovered that a number of elements (metals) exist in the sun in a fused, or rather vapourous state, in consequence of the intense heat. Hydrogen exists in the sun, with other gases unknown to us here, and many metals, discovered by their spectra, which are the same under similar circumstances.
The sun is supposed to be spherical in shape,—not like the earth, flattened at the poles,—and to be composed of materials similar to what the earth is composed of, and what it would be if it were as hot as the sun is. Thus we can argue by analogy from the spectra of earthly elements, that, as the sun and star light gives us similar spectra, the heavenly bodies are composed of the same elements as our globe. We can thus form our opinion of the sun’s constitution. Mr. Neisen says:—
“With the aid, therefore, of the additional information given us by the spectroscope, it is not very difficult to form a true idea of the probable condition of the surface of the sun, which is all that we can see. It is the upper-lying strata of a very dense atmosphere of very high temperature—an atmosphere agitated by storms, whirlwinds, and cyclones of all kinds, traversed by innumerable currents, and now and then broken by violent explosions. Above the brilliant surface which we see is a less dense and somewhat cooler upper stratum, which, though hot enough to shine quite brightly, is quite invisible in the presence of the brighter strata beneath it.”

Sun Spots, as they are generally called, are hollows in the sun’s vapoury substance, and are of enormous extent; and there are brilliant places near those spots, which are termed faculæ. These spots have been observed to be changing continuously, and passing from east to west across the sun, and then to come again at the east to go over the same space again. Now this fact has proved that the sun turns round upon his axis, and although he does not move as we imagine, from east to west, round the earth, the orb does move—in fact, the sun has three motions: one on his axis; secondly, a motion about the centre of gravity of the solar system, and a progressive movement towards the planet Hercules.
If we examine the surface of the sun through a proper telescope, we[Pg 499] shall find that the even surface we can plainly distinguish at sunset is marked, and the brightness is greater towards the centre of the orb. We can perceive various irregularities; we shall find spots, faculæ (little torches), etc. These spots were discovered by Galileo and other astronomers, and were, as we have stated, found to be surface markings, and not a series of bodies passing between the earth and the sun. The rotation of the sun was measured, and it was found that the orb revolved in about 25-1/3 days, and in such a manner as to be slightly inclined to the plane of the ecliptic.
Herschel observed a spot at least 50,000 miles in diameter, which is more than six times the diameter of the earth. The sun spots are observed to be constantly changing, and are naturally observed differently as the revolution proceeds. The dark pole, or “nucleus” (umbra), as it is called, is surrounded by a less dark surface called the penumbra, but the umbra is not really dark; it is extremely bright when viewed alone, as has been proved by Professor Langley, while the heat is even greater in proportion. But the umbra of a sun spot must be below the level of the penumbra, for the shape changed as the sun revolved on its axis. The penumbra was wider on the side nearest the edge of the solar disc, and the umbra may be due to the uprushing or downpouring of gas or vapour like “whirlpools in the solar atmosphere.”
Near the sun spots the long streaks, or faculæ, are often observed by the borders of the disc, and a transition of the luminous part of the photosphere26 into darkness has been observed, and bright bridges crossing the spots, and then gradually getting dark, were seen by M. Chacomac. The sun spots vary in direction, but the same general course is continued. Sometimes they describe curves, sometimes lines.

During solar eclipses the sun exhibits what are termed “red prominences,” which are the luminous vapours existing around the sun. When the orb is eclipsed, we can see the bright-coloured vapours shooting out from underneath the dark shadow, and this light is termed the “coronal atmosphere”; the vapours are called the sun’s chromosphere. In the coronal atmosphere are certain curious shapes of vapour thrown up, and frequently changing,—projecting, in fact, from the gaseous envelope. These red prominences were first observed in 1842, and in 1851 it was proved that they appertained to the sun, for the moon hid them as the eclipse began. Before the prominences were discovered, the red light surrounding the solar disc was known, and called the “sierra” (now chromosphere), or chromatosphere. “The luminosity of these prominences is intense,” says Secchi, “and they rise often to a height of 80,000 miles, and occasionally to more than[Pg 500] twice that; then bending back, they fall again upon the sun like the jets of our fountains. Then they spread into figures resembling gigantic trees, more or less rich in branches.” We give some illustrations of the appearances of these prominences.

The zodiacal light is often observed. It is a glow, and frequently of a rosy tint. It may be seen in England in March or April before sunset, or in the autumn before sunrise; and it is doubtful whether it be a terrestrial or an extra-terrestrial light—a lens-shaped object surrounding the sun. Some philosophers maintain that the light is caused by multitudes of minute[Pg 501] bodies travelling round the sun; but Herr Gronemann has lately fully discussed the observations, and the drift of his contention is under stated:—

There are valid observations against two items in the support of the old theory—viz., the affirmed connection of the evening and morning cones seen on the same night (if the corresponding sides be prolonged), and the participation of the cones in the daily motion of the heavens. The zodiacal light is sometimes seen when daylight has not yet disappeared; and, on the other hand, it sometimes fails to appear, though there is complete darkness. There would seem to be a real lengthening and shortening. It has been[Pg 502] observed by Schiaparelli, that the light is much more difficult to make out when it passes through the meridian, than when it is only 30° above the horizon, and is less easily seen when the air is clearest than when a sort of mist is present. Indeed, the bright parts of the Milky Way may be seen to be weakened by mist, while the zodiacal light at the same height is unaffected. The zodiacal light has temporary variations of light intensity, and it shows from time to time remarkable changes of form and position, so sudden and short as to be hard to explain on the planetary hypothesis. The elongations of the cones show a half-yearly period, which is independent of the transparency of the air. The cone follows the observer northwards or southwards, so that there is no parallactic action; and this peculiarity (so adverse to the extra-terrestrial hypothesis) cannot be explained by reflection or absorption of light. As to spectroscopic observations, the author finds (1) that the zodiacal light consists partly of proper light; (2) that its connection with polar light is but secondary, temporary, and accidental; (3) that the cause of the second phenomenon is such that it may strengthen the zodiacal light and modify its spectrum; and (4) that the results of spectrum analysis rank with other arguments tending to find the source of the zodiacal light in the neighbourhood of the earth (like the polar light). Herr Gronemann, then, thinks the zodiacal light a terrestrial phenomenon, though he will not say that it cannot be influenced by cosmic action. He throws out the suggestion that the cone may be a kind of optical illusion, arising from some fine matter—gas or dust—being more accumulated near the observer in one direction than another. The apparent length of the cone might be conditioned by the conical shadow of the earth, and the changes of length be due to cosmic and electric influences. In any case, there is need of a more scientific theory than the old one.

We may conclude our brief notice of the great luminary to which we are indebted for everything, by a resumé of his distance from us, his diameter, and a few other plain facts and figures. In the first place the actual distance of the sun from the earth has never accurately been determined,[Pg 503] but perhaps the next transit of Venus will assist the observers to a nearer estimate. It is quite sufficient for our purpose, however, to state that the sun’s distance from the earth is 92,000,000 of miles. The distance varies in winter and summer. In the former period the sun is nearer than in summer, and yet as the rays strike over us, and pass us, as it were, we feel less heat. When, as in summer, we are more in the focus of the rays, we feel the greater heat.
We have already spoken of parallax, and it is by finding the solar parallax that the distance of the sun from us is found. This parallax has not been exactly ascertained, or rather authorities differ, and as difference of 0·01″ in the solar parallax means something over 100,000 miles of distance, it is evident that exactness is almost impossible. If 8″·80 be settled as the solar parallax, 92,880,000 miles is the distance of the sun from the earth. If 8″·88 be taken we have nearly 92,000,000 exactly.
The volume of the sun is 1,253,000 times that of the earth, and yet the density of the former is only about one-fourth of the latter, so the attraction of gravitation at the sun must be more than that of the earth’s surface twenty-seven times. A body dropped near the surface of the sun would fall 436 feet in the first second, and have attained a velocity of ten miles a minute at the end of the first second. The diameter of the sun depends in our calculations upon its distance from the earth. If we suppose that to be 92,880,000 miles, the diameter is 866,000 miles. If we take 91,000,000 of miles as the distance from the earth the diameter is 850,467 miles. The sun makes (apparently) the circuit of the heavens in 365 days, 6 hours, 9 minutes, and 9·6 seconds; the transit from one vernal equinox to the next being only 365 days, 5 hours, 48 minutes, 48·6 seconds, owing to the precession of the equinoxes already mentioned.
When we consider the power and grandeur of the sun we may well feel lost in the contemplation. The sun balances the planets and keeps them in their orbits. He gives us the light and heat we enjoy, and coal-gas is merely “bottled-up sunlight.” In darkness nothing will come to maturity. We obtain rain and dew owing to the sun’s evaporative power; and no action could go on upon earth without the sun; and yet we receive only about 1/2070650000 part of its heat and light.
As to the colour of the sun, Professor Langley states that it is really blue, and not the white disc we see. The whiteness is due to the effect of absorption exerted by the vapourous metallic atmosphere surrounding our luminary; and if that atmosphere were removed, his colour would change.

CHAPTER XXXVII.
THE EARTH.
FORM OF THE EARTH—MOTION OF THE GLOBE—RATE AND MANNER OF PROGRESSION—LATITUDE AND LONGITUDE—THE SEASONS.
We have learnt from our books on Geography that the earth is shaped like an orange,—that is, our globe is round and flattened slightly at the “poles,” and we can easily see that the earth curves away, if we only try the experiment mentioned in a foregoing chapter—viz., how far a person standing (or lying) on the ground can see on a level. Our power of eyesight is not limited to three or four miles, but a man of ordinary height standing on the plain cannot see more than three miles, because the earth is curving away from him.
We know that at the seaside we can see ships gradually appear and disappear. When approaching us the masts and top-sails appear first, then the main-sails, and then the ship itself. A sailor climbing up the mast can see farther than the captain on deck, because he can see over the curve, as it were. When the vessel is at a considerable distance we see her “hull down” as it is termed,—that is, only her sails are visible to us, and at last they disappear also. If we want any other proof that the earth is round we can see when an eclipse takes place that the shadow on the moon is circular. So we may be certain of one fact; the earth is round, it is a globe. So much for the rotundity of the earth.
But the earth appears to us, except in very mountainous districts, as being almost a plane. This is because of its extent; and even from very high mountains we can only see a very small portion of the earth, and so, on a globe sixteen inches in diameter, the highest hills would be only about 1/100 of an inch, like a grain of sand.
The motion of the earth is known to most people, though as everything upon the globe passes with it, and a relative fixity is apparent, this is, of course, not real rest. The earth is moving from west to east at a tremendous rate,—viz., nearly nineteen miles a second! We think a train at sixty miles an hour a fast train; but what should we think of an express going more than 68,000 miles an hour! Yet this is about the rate at which our globe whirls around the sun. Her fastest pace is really 18·5 miles a second; the least about one mile per second less.
That is one motion of the earth; the other is its motion on its axis.[Pg 505] If we send a skittle ball rolling we perceive it turns round as it proceeds. So the earth rotates on its axis, N S, in the accompanying diagram; the extremities of the axis are called the poles. The line in the middle is the equator, which is divided into 360 equal parts, each being 69-1/10 miles in length; so there are 180 lines, or rings, drawn upon the globe from N to S, and these are meridians. In England the degrees are calculated from the Greenwich meridian. We can thus obtain the distance of localities east or west, as we may briefly show (fig. 554).


The distance of any meridian from the first meridian is termed the longitude, and it is employed in describing the situation of a place on the earth’s surface. Suppose L (fig. 554) a city, its longitude will be 30°, since it lies on a meridian which is 30° from the first. So, for example, the longitude of Oporto is 8° 37´ west, Paris 2° 22´ east, Vienna 16° 16´ east, Bagdad 44° 45´ east, reckoned from the meridian of Greenwich, and so on. At the 180th degree we have proceeded half round the globe, and reached the farthest distance from the first meridian, and are now on the opposite side of the earth, and proceeding in a similar manner in the opposite direction we get west longitude.
It will readily be perceived that a knowledge of the longitude alone is not sufficient to determine the situation of a place on the earth’s surface.[Pg 506] When we say, for example, that the longitude of a place is 30°, it may lie on any point whatever of the line, N L S, on the whole hemisphere (fig. 554). This point must therefore be determined more accurately, and hence the first meridian is divided into 90 equal parts north and south of the equator towards the poles. These are called degrees of latitude, and the lines drawn through these round the globe, parallel to the equator, are called circles or parallels of latitude, and diminish as they approach the poles.
Hence, by the latitude of a place we mean its distance from the equator towards the poles, and we speak of north and south latitude according as the place is situated in the northern or southern hemisphere.
So, for example, the point L (fig. 554), which has 30° longitude and 60° N. latitude is in Sweden.
The latitude is also observable by ascertaining the altitude of the polar star above the horizon when in the northern hemisphere. The longitude is found by the chronometer; for if we know the time at Greenwich we can calculate how far we are east or west of it by seeing whether the local time be an hour (say) earlier or later, and that difference shows we are 15° to the east or the west as the case may be.
The earth’s rotation, according to sidereal time, is less than solar time, as we have seen, so we have 365 solar days and 366 sidereal days; so a person going round the world gains or loses a day as he travels east or west according to his reckoning, as compared with the reckoning of his friends at home. We can easily ascertain the earth’s motion by watching the stars rise and set. Now the path in which the earth moves is called an ellipse,—very nearly a circle,—but it does not always move at the same rate exactly. We will now look at the relations of the sun and the earth.
Let us take an example. Suppose we have a rod, at each end of which we fix a ball (see diagram), and let one ball be three times as large as the other, the common centre of gravity will be at c, at one quarter of the distance between the centres, and there the bodies will be in equilibrium. If these masses be set spinning into space they will revolve at that distance from each other, the attraction of gravitation and the force in opposition to it equalizing each other.

The earth, as we know, proceeds with a tremendous force around the sun, not in a circle, remember, but in an ellipse or oval track, from which it never moves year by year in any appreciable degree. Now what prevents this earth of ours from rushing off by itself into space? Why should not the earth fly away in a direct line? The reason is because the sun holds it back. The force of the sun’s gravitation is just sufficient, or we may say so enormously great, that it suffices to retain our globe and all the other planets in their various orbits at the very same distance, and to counteract the force which launches them through space. Therefore, as we have[Pg 507] already noticed when considering the sun, it is to that ruler of the day that we are indebted for everything.
What would happen, then, if the earth were suddenly to increase her velocity, or the sun to contract his mass?—We should be flung into infinite space, and in a short time would be frozen up completely. Our present diurnal course would probably proceed, but all life and existence would cease as we whirled with distant planets through infinity.
Suppose, on the contrary, we were to stop suddenly. We have some of us read in a foregoing part of this volume that heat is the motion of molecules in ether, and that when a body strikes another heat is developed by contact and friction. If the earth were to be stopped suddenly, “an amount of heat would be developed sufficient to raise the temperature of a globe of lead of the same size as the earth 384,000° of the Centigrade thermometer. The greater part, if not the whole of our planet, would be reduced to vapour”, as Professor Tyndall says.

In the diagram (fig. 546, on page 497) we shall at once find the explanation of the constantly-recurring seasons, and the amount of our globe which is illuminated by the sun at various times. It will be easily understood that the poles have six months day and six months night. When the earth is at an equinox, one half of the surface is illuminated and the other half in shade, therefore the days and nights are equal. But when the north pole turns more and more towards the sun, the south pole is turning away from it in the same ratio,—the days and nights respectively are getting longer and[Pg 508] longer, and at the north and south poles day and night are continuous, for the small spaces round the poles are, during a certain period, wholly in sunshine and shade respectively.
In March (in the diagram, fig. 546) we see that exactly one half of the earth is illuminated, and the other is darkened. So in September, when we have the opposite view. In June the earth is more inclined apparently to the sun, and more of the surface is exposed to it, so the days are longer in some parts. The opposite effect is visible in December.
The summer heat and winter cold are accounted for by the more or less direct force of the sun’s rays, for the more the angle of incidence is inclined the fewer rays reach the object; and if the rays fall at an angle of 60°, the heat is only half what it would be if they came vertically. When the days are shortest the sun is lowest, and therefore gives less heat to the earth at certain periods.
The wonderful precision which has adapted the position of the earth on its axis, will be apparent from the illustration (fig. 557). Here we have a table and some bottles, a candle to represent the sun, and a ball of worsted and a knitting-needle to represent the earth and its axis. Suppose we place the ball in the position at a, with its axis perpendicular to the plane of the orbit. As the earth would turn and go round the sun in this supposed case, we should find the days and nights equal, and the sun would quickly scorch up the tropics, and the other portions would have a never-changing spring or winter all the year for ever. This would not be so pleasant, for variety is the charm of nature, and the salt of life. So we may put a aside, as the earth would be scarcely habitable under the supposed conditions, and try b. Here we find the poles directed to the sun. The whole northern hemisphere would thus be illuminated one half year, and the southern similarly; such rapid changes from heat to cold and back again would not suit us. So we fall back upon c, the actual appearance of the position of the earth, and here we find all the most favourable circumstances existing for us. This inclination gives rise to all the varied phenomena of the pleasant gradations of heat and cold, summer and winter, the charming changes of season, and the wonderful results of the ever-recurring days and nights, months and years, as the earth spins round. So we see that the sun does not really rise and set upon the earth; the globe rotates, and brings us into view of the sun, and as we turn we lose his light.

In the foregoing brief description we have learnt some few facts concerning our earth. We have ascertained that the planet we inhabit is round; we have also seen that the earth moves around the sun and around its own axis, and also that it moves at a tremendous rate; we know that that[Pg 509] rate is just counterbalanced by the attraction of gravitation, and the course round the sun gives us varying seasons, day and night. There are many subjects relating to the earth which will be more properly included under Physical Geography. We may here just add the diameter of the earth, and proceed to inquire concerning the moon. The polar diameter of our globe is 7,899 miles; the equatorial diameter 7,925 miles. It is distant from the moon 238,500 miles. We will close this chapter with the letters and characters of the Greek alphabet used in astronomical works to designate the stars.
- Α α = Alpha
- Β β = Beta
- Γ γ = Gamma
- Δ δ = Delta
- Ε ε = Eps[=ilon
- Ζ ζ = Zeta
- Ê ê = Eta
- Θ θ = Theta
- Ι ι = Iota
- Κ κ = Kappa
- Λ λ = Lambda
- Μ μ = Mu
- Ν ν = Nu
- Ξ ξ = Xi
- Ο ο = Omicron
- Π π = Pi
- Ρ ρ = Rho
- Σ ς = Sigma
- Τ τ = Tau
- Υ υ = Upsīlon
- Φ φ = Phi
- Χ χ = Chi
- Ψ ψ = Psi
- Ω ω = Omega

CHAPTER XXXVIII.
THE MOON.
WHAT IS IT LIKE?—MOON SUPERSTITIONS—DESCRIPTION OF THE MOON—PHASES—TIDES—ECLIPSES.
From the early days of childhood every man and woman has been familiar with the moon. This satellite of earth has been domesticated, so to speak, amongst us; and while the sun and other stars have been glorified in poetic and prose effusions, the moon has been always more tenderly addressed. The soft (reflected) light of our attendant moon is much more attractive than the brilliancy of the greater light “that rules the day.” The moon is regarded as our particular property, and has awakened an interest in our minds since the time that we could, as we fancied, see the “Man in the Moon.”

In ancient times the moon was supposed to possess some light of her[Pg 511] own, and to be inhabited by immense creatures; and various theories continued to be promulgated respecting her, until the telescope came into use, and then astronomers began to find out many new things concerning Luna. Now, what has the telescope told us regarding our moon?—It shows us that there are mountains and craters, and numerous traces of volcanic action. At one time it was supposed that the dark masses apparent in the surface of the moon, and which can easily be distinguished by the naked eye, were seas, and maps of the moon were made, marking continents and craters.
If it were possible to reach the moon, as M. Jules Verne’s travellers did, we should find a very irregular and corrugated surface—plains and mountains without water. We should be able to see the stars in the daytime, because there is no atmosphere around the moon, and there is a silence that “might be felt.” The appearance of our earth from the moon, and the beauty of the stars in the unclouded and waterless space around the satellite, must be very grand, and has been, in a measure, depicted in the illustration (fig. 559) on the opposite page.

In this illustration (fig. 560) we have some idea what the moon is like. We see the rugged and cratered appearance of the disc; it is a desert waste, so far as we can ascertain, without inhabitants, and, in all probability, without vegetation. For there being no moisture amongst the plains and craters and mountains of our satellite, we must conclude that the moon is dead. It is a very interesting,—nay, a fascinating study. When we take up our telescope and look from the window at the heavens the most beautiful object within our small telescopic vision is the moon shining like a silver plate, and we wonder what is up there. With a small telescope even we can discern many interesting features in the moon at the full, which will assist us in verifying the diagrams in books and their explanations.
As the moon is only a few miles away, comparatively speaking, and as the large telescopes now in use bring us within a measurable distance of the surface, we are enabled to speak more positively about our changeable satellite than of any of the planets. When we look steadily at the full moon[Pg 512] we perceive upon its surface dark and light tracts called “seas,” though they are dried up now. Thus we hear of the “Sea of Serenity,” the “Sea of Storms,” and the “Sea of Tranquillity”; and in the map upon a subsequent page you may see the names of the seas, mountains, and the general formations of the surface of the moon. Maps of the moon are now to be procured, though no personal visits can be made to the satellite. It is very interesting to observe or to read about the structure of the moon, for we may thus learn how similar the earth and her attendant are in formation; but one important agency—that of water—has made a considerable difference in the appearance of the formations. In the moon we have mountains, plains, and rugged craters; the surface is not level, because the sunlight is visible sooner at some points than others. The chief mountain chain is the Apennines, and has a great elevation; many traces of volcanic agency are discoverable amid the great desolation, and awful silence reigns throughout.

As is well known, water has a great erosive power, and its action disintegrates the surface of the earth with rapid persistency. So the physical appearance of the globe has become much changed in the course of ages: ravines exist where plains used to extend, and rivers cut their way through deep gorges to the sea. The sands and other deposits are overlaid, and thus the whole outward appearance has been altered. Not so the moon. With a very attenuated atmosphere without clouds or rain, there is no moisture, no lake, no water in the moon now. What may have been we can only conjecture. If there ever have been lakes or seas they have all been absorbed.

The heat upon one side of the moon must be very great at one period, and the cold on the opposite side intense, as one would think—yet upon this fact authorities differ somewhat. If the moon possess no atmosphere of any kind it would be fearfully cold and extremely hot at intervals, but a surrounding medium, even of very little density, would modify the extremes; and while we must accept the fact that the temperature varies very much we need not place it above 100° of heat, nor below 20° of cold. So from close observation and comparison we are enabled to form a very fair opinion of the[Pg 513] “past” of the moon, and to ascertain that the same forces of nature which have moulded the planet we inhabit, have been at work in the moon also. When we study “Selenography,” therefore, we shall find a record of a history which may some day bear a parallel to the history of our physical world.

The moon, as all are aware, moves round the earth attendant upon us, but entirely under the control of the sun; our satellite, moreover, has been the subject of many superstitions. A great many rites and even domestic actions—such as the killing of fowls—were regulated by the moon; and in Scotland, Scandinavia, and other portions of Europe, she has always been regarded as effecting destiny. There are many interesting myths connected with the moon, and indeed with astronomy generally, and from a volume entitled “Notes on Unnatural History,” some very amusing extracts might be made. It will not be out of place to mention a few of these myths.

The Chinese have an idea that a rabbit exists in the moon, and is the cause of the shadows we see. The Buddhists think a holy hare is up there. In the Pacific Islands there is a belief of a woman in the moon; she was sent there because she wished her child to have a bit of it to eat; and Mr. Buchanan has versified the old Scandinavian myth about the two children kidnapped by the moon as they returned from a well with a bucket of water slung upon a pole. The Jews placed Jacob in the moon, and the Italians say that Cain inhabits the luminary with a dog and a thorn bush. In the Inferno of Dante this is referred to, and we know that in A Midsummer Night’s Dream we have the moon coming out to shine upon the loves of[Pg 514] Pyramus and Thisbe with the dog and the thorn-bush; and in the Tempest the same idea is mentioned by Caliban. Readers of Longfellow will recall the lines how “the good Nokomis answered” Hiawatha, who asked about the moon—
But modern scientific research has exploded all these charming old myths, and laid bare the facts for us. We must now resume.

The moon moves around us in 27d 7h 43m 11·461s. Its diameter is about 2,160 miles, and it is much less dense than our earth, and so the force of gravity is less there than here. Its mean distance from us is 238,833 miles. The moon goes through certain changes or phases every twenty-nine days or so; and while rotating on its own axis our satellite goes round the earth, so that we only see one side of the moon, inasmuch as the two[Pg 515] motions occupy almost exactly the same space of time. So we generally see the same space of the moon, though there is a slight variation at times. This movement or swaying of the central point is called the moon’s “libration,” and is an optical effect, due to the inequalities in the motion of the moon in its orbit, and to the inclination of its equator and orbit to the ecliptic.
We append a map of the moon, on which the mountains, seas, and craters can be perceived, according to the list. The hill ranges extend for hundreds of miles, and the elevation reaches 30,000 feet, and even more in places. The so-called craters do not resemble volcanoes when viewed closely, but take the form of basins or valleys surrounded by lofty hills. One great plain called Copernicus is more than fifty miles across. Respecting the appearance of the moon let us quote Mr. Lockyer.

“Fancy a world without water, and therefore without ice, cloud, rain, snow; without rivers or streams, and therefore without vegetation to support animal life;—a world without twilight or any gradations between the fiercest sunshine and the blackest night; a world also without sound, for as sound is carried by the air, the highest mountain on the airless moon might be riven by an earthquake inaudibly.”
Phases of the Moon.
We have said that the moon revolves around the earth in the same[Pg 516] time as she turns upon her own axis, and always presents one side to us when she appears. Any one can ascertain this by putting a candle upon a round table, and walk round it facing the candle. The experimentalist will find that he will turn upon his own axis as well as turn around the table. Thus we shall see how the moon changes, for to be as changeable as the moon is proverbial. These different aspects or phases we shall now proceed to explain.

The time intervening between one “new” moon and another is 29d, 12h, 44m, 2s, and is termed a synodic revolution. This is longer than the sidereal revolution, because the earth is also moving in the same direction and the moon has to make up the time the earth has got on in front, as it were. So the moon travels nearly thirteen times round the earth while the latter is going round the sun.
The revolutions of the moon have been a measurement of time for ages, and her varying appearances during lunation are always observed with interest. The illustration (fig. 567) will assist us materially. The sun’s rays fall in a parallel direction upon the earth and moon, and let us suppose that S is the sun in the diagram and T the earth; C at the various points is the moon, the capital letters, A, B, C, etc., indicating the planet as she appears from the sun, and the small letters show how she appears to us from the earth.
Let us suppose that the sun, earth, and moon are in conjunction—or in[Pg 517] a direct line. The phases, C and G, are the moon’s “quadratures.” At A we see the sun shining on the moon, but we only have the dark side. It is then “new” moon; but by degrees, as she goes round in her orbit, we perceive a small crescent-shaped portion, lighted up by the sun at B and b. At c´ we have the first quarter or half-moon. When she is in opposition she is at full moon, and so on to the last quarter and conjunction again.

The moon’s phases may be easily shown by means of a medium-sized lamp to represent the earth, a smaller one to serve as moon, and a light to act as sun all at the same height. Colour the “lunar” globe white, and if we move it about the “earth” globe, we shall see the various phases of the moon in the sharp shadows.
The Tides.
The ebb and flow of our tidal waters depend upon the moon to a great extent. The phenomenon is so common, that we need only refer to it, but the cause of the tides may be stated. Twice every day we have the tides twelve hours apart, and the flow and ebb are merely examples of the attraction of gravitation, which is exercised upon all bodies, either liquid or solid. The tides are highest at the equator and lowest at the poles, because the tropics are more exposed to the influence of the lunar attraction.

By the small diagram (fig. 569) we shall be able to see in a moment how the moon acts. The moon being nearer to the earth at b, the water will be naturally attracted to the ball, m, and cause high water (a); and a similar effect will be produced opposite, because the earth is attracted, so the waves are higher than the ground which has been attracted away from the water, and the waters will flow in and cause a high tide at d, but not so high a tide as at the opposite point, a. It can then be understood that there will be low water at the other two sides, e and f, because the water has been taken away, so to speak, for the high tides at a and d. We shall learn more of this under Physical Geography.

The moon revolves round the earth in a changeable elliptical orbit, intersecting the ecliptic at certain points called Nodes. When the moon is nearest to the Earth she is said to be in perigee[Pg 518] when farthest from us she is in apogee (the line uniting these points is the line of apsides), the difference in distance being about 4,000 miles. She passes the sun periodically, and so if the moon moved in the plane of the ecliptic there would be eclipses of the sun and moon twice a month; but as the orbit is inclined a little, she escapes by moving north or south. We will now endeavour to explain this theory.
Eclipses.
We have briefly considered the Sun and Earth and the Moon separately. We are now about to regard the effects produced by them when they come in each other’s way and cause Eclipses, which are observed with so much interest. There are eclipses of the sun and of the moon. The former occur at the time of new moon, and the latter at full moon; and this will be at once understood when we remember that the sun is eclipsed by the moon passing between us and the sun; and the moon is eclipsed because the shadow of the earth falls upon her when she is opposite the sun, and therefore “full.”

Readers of the voyages of Columbus will remember that he managed to obtain supplies from negatively hostile Jamaica savages by pretending to cause an eclipse of the moon, which he knew was about to take place, and to the ancients eclipses were of dire portent. Even in enlightened Rome, to ascribe an eclipse to the causes of nature was a crime. The Chinese have an idea that great dragons are devouring the moon when she is eclipsed.
There are total, partial, and annular eclipses. The former terms speak for themselves; the latter name is derived from “annulus,” a ring; for a ring of light is left around the dark portion eclipsed, and is only seen in solar eclipses. In one sense the eclipse of the sun is really an eclipse of the earth, because it is caused by the shadow of the moon falling upon the earth.

If a bright body, A, be larger than the dark body, B, there will be two kinds of shadows—viz., the umbra and the penumbra. For instance, the umbra is the central dark part in the cut (fig. 572), and the penumbra is the lighter portion. As soon as the eye is placed on the umbra, it can perceive no part of the source of light, A, which appears to be eclipsed. On the other hand, the penumbra originates in that locality where only a portion of the light proceeding from a luminous object can fall; hence an eye in the penumbra would see a part, but not the whole of the illuminating body. This shadow also forms a cone, the apex[Pg 519] of which, if extended, will fall before the opaque body. If we receive the shadows so projected at m n, for example, on a white sheet, we have in the centre a dark circle, which is the umbra, surrounded by the penumbra, which gradually decreases in intensity towards the exterior (see fig. 573). The farther we hold the sheet from the body producing the shadow, the umbra decreases, and the penumbra is enlarged. For where (in solar eclipses) the umbra falls there is totality; within the penumbra partial eclipse only.

Lunar Eclipse.—Let A (fig. 573) be the sun, and B the earth, the length of the umbra of the latter will exceed 108 diameters of the earth. Since the moon is only about thirty terrestrial diameters distant from the earth, and as the diameter of the earth’s shadow, at this distance, is nearly three times as large as the apparent diameter of the moon, it follows that when the latter enters this shadow, she must be totally eclipsed, for at those places where the moon’s shadow falls there is total eclipse. If the moon’s orbit were coincident with the ecliptic, or if both moon and earth moved round the sun in the same plane, there would be an eclipse at every conjunction, and at every opposition,—i.e., a solar eclipse would happen at every new moon, and a lunar eclipse at every full moon. But we have seen that the lunar orbit cuts the ecliptic only in two points; consequently an eclipse of the moon is possible only when, at the time of opposition, the moon is in one of her nodes, or in close proximity to it, which can only occur twenty-nine times in the space of eighteen years.
A lunar eclipse begins on the eastern margin of the moon, and is either total, when her whole disc enters the umbra, or partial, when only part of her disc is in the shadow. A total eclipse may last for two hours.
We shall understand this better, perhaps, with the diagrams.

Solar Eclipses.—When the moon and the sun are in conjunction, the moon’s place may be represented by M (fig. 574) between the earth, T, and the sun, S. If this conjunction occur when the moon is in one of her nodes, or within 16° of it, the shadow of the moon will fall upon the earth, and the sun will be eclipsed. At other places the sun will not be entirely covered; and if the moon be moved farther off, so that its shadow will not reach the earth, and so not cover the sun up completely, we shall have an annular eclipse, because a rim of the sun will be visible.
The lunar umbra extends from the moon by a space about equal to her distance from the earth, and hence only a small portion, d, of the earth’s surface enters the lunar umbra. To the inhabitants of this part of the earth the sun will be totally eclipsed, and the eclipse will be annular if only the margin of the sun’s disc remain uneclipsed by the lunar shadow. This is only possible when the moon is in her apogee, or greatest distance from the earth, where her apparent diameter is less than that of the sun, which it cannot in general exceed more than 1´ 38″. Hence the duration of a total eclipse of the sun cannot be more than 3¼ minutes.
On the contrary, the penumbra of the moon is diffused over a much larger portion, n m, of the surface of the earth, since its section is five-ninths of the earth’s diameter. The inhabitants of this portion of the earth do not receive light from all parts of the sun, consequently a part of this luminary is invisible to them, and the eclipse is said to be partial.
Solar eclipses commence on the western margin of the sun, and advance to the eastern. On account of the proximity of the moon to us, an eclipse of the sun is, in all places above the horizon of which the sun appears, visible neither at the same time, nor is it of equal duration, nor of equal extent: in some parts it may not be visible at all. In favourable situations, the diameter of the umbra, where it reaches the earth, amounts to about 167 miles, and on this small strip of the earth’s surface only can the sun appear totally eclipsed.

CHAPTER XXXIX.
THE PLANETS AND ASTEROIDS.
Mercury.
Including our own globe there are eight principal planets—viz., Mercury, Venus, Mars, Jupiter, Saturn, Uranus, and Neptune. The two first-named being between us and the sun, are termed interior planets; the others are exterior. Mercury, Venus, and Mars are smaller than Earth. The other four are much larger.

We have already described the planets as bodies wandering through the zodiac, and reflecting the sun’s light. Their orbits are very different from the moon’s; for instance, planets take a retrograde motion as well as a direct one. The sun and the planets revolving around him constitute the solar system.
We will commence our brief consideration of them with Mercury, the planet nearest to the sun.
The distance of Mercury from the sun is 35,000,000 of miles, less than half the distance our earth is from him, and so receives much more heat and light than we do. The sun to the Mercurians, if there be any inhabitants[Pg 522] upon the planet, must appear about seven times larger than he does to us. Mercury’s year is about eighty-five days in length, so the seasons must be shorter if they follow the same rotation as ours. It passes through space with an exceedingly rapid motion, and so probably the ancients called the swift planet Mercury after the winged messenger of Jove.
Mercury is not an easy planet to observe, owing to its proximity to the sun, yet the ancients managed to descry it. But it can be seen just before sunrise and sunset in autumn, and in spring if the weather be clear. It possesses phases similar to our moon. Some authorities have stated that Mercury has an atmosphere, but this circumstance, as well as its formation, is still shrouded in mystery. Mercury’s day is a few minutes longer than ours.

A transit of Mercury is represented in the accompanying illustration (fig. 577). This phenomenon took place in 1845, but there have been many others noticed. The first recorded took place in November 1631, and these transits always occur in May or November.
Venus.
Venus is the planet next in order, and revolves about 66,000,000 of miles from the sun. It is the nearest planet to the earth, and is somewhat smaller than the latter. This planet is both a morning and evening star, and is very brilliant—so much so, that any close observation with the telescope is not possible; and when at her nearest point she is invisible as she passes between us and the sun, and of course when fully illuminated she is directly beyond the sun, and enclosed in his rays. But under other circumstances she is distinctly visible as a crescent in the evening, and nearly full as a morning star. Venus goes round the sun in 224 days, and her day is rather less than ours.

Venus has long been celebrated as the morning and evening star, as “Lucifer” and “Hesperus.” “Lucifer, son of the morning,” is mentioned by Isaiah. That Venus possesses an atmosphere denser than our own can scarcely be doubted. The observations made during the successive transits, particularly the last (1874), seem to have established the fact that aqueous[Pg 523] vapour exists around, and water in, Venus. No satellite can be found, though the ancients reported such an attendant upon this planet.
The apparent diameter of Venus varies considerably in consequence of her varying distances at the inferior and superior conjunction. When nearest the earth, if she presented her fully illuminated disc to our gaze, we should see a miniature moon, and even under the circumstances Venus throws a shadow, so brilliant is her light.

The transits of Venus have been referred to, and, like those of Mercury, are simply a passing, or “transit,” of the planet across the illuminated disc of the sun. The transits afford means to ascertain the volume and distance, etc., of the sun, and this year (1882) the next transit is expected. There will not be another for more than one hundred years.

Whether Venus has a constitution similar to our globe is of course doubtful. The matter is less dense than the earth, and there is an atmosphere half as dense again as ours. Spots have been noticed crossing the planet, which may have been vapours or clouds, and the rotation of Venus on its axis was calculated from these spots as being 23h 21m 22s. The seasons in Venus must be very different from ours, as her inclination is greater than our earth, and as the sun is so much nearer to her than to us her tropical and polar regions are close, and a vertical sun is scarcely enjoyed by two places for three successive days, and she may have two winters and summers, two springs and autumns!
Mars.
Having already considered the earth, we pass on from Venus to Mars. The orbit of the latter planet is exterior to the earth’s, as is proved by his never appearing “horned,” nor ever passing across the sun’s disc. Therefore no “transits” of Mars can take place as transits of Venus and Mercury.
Yet Mars is most favourably situated for astronomical observation by us, because it turns its full disc to us. Venus is nearer to us than Mars—but, as we have explained, when she comes nearest to us she is quite invisible. Astronomers have been enabled to ascertain a good deal concerning the planet of war—“the red planet Mars.”
Mars has been considered very like the earth. We perceive seas and continents, and the shape of Mars is like the earth. But our globe is larger than Mars, which is much less dense, so the force of gravitation is less also.[Pg 524] Mars moves upon his axis in about twenty-four hours and a half, and takes rather more than 686 days to revolve round the sun. (See page 489.) Thus its days are a little longer than, and its years twice as long as our days and years. When in “opposition,” or on the opposite side of us from the sun, Mars is at his brightest. This happened in September 1877. He will come close again to us in 1892.

All planets are wanderers, but of all the wanderers Mars has the most eccentric orbit. He curls about, so to speak, in loops and curves in a very irregular manner, and therefore his distance from the earth varies very considerably; and this eccentric behaviour of the warlike planet must have, as we believe it did, puzzled the ancients very much. But—and here reason came to human aid—this very fact, this great eccentricity of the planetary motions, caused Copernicus to investigate the subject with great attention, and he at length explained the true reason of these irregular orbits from the hypothesis that it was around the sun, and not around the earth that the planets moved in regular orbits.
It is quite ascertained that Mars is very like our earth in miniature. We annex a diagram of the planet, and when it is examined with a good telescope the seas and continents can be quite distinctly perceived. At the poles there appears to be a white or snowy region at varying periods, which would lead us to the conclusion that the atmospheric changes and the seasons are similar to our own; and as the inclination of the planet is nearly the same as the earth, this supposition may be accepted as a fact.
Thus we see that Mars is the most like earth of all the planets, and its inhabitants—if, indeed, it is now inhabited—must have a beautiful view of us when the weather is fine, for we are so much larger. Mars is also attended by two satellites, or moons, as Professor Hall reported from Washington in 1877. These moons have been named Deimos and Phobos, and are both very small, their diameter being only about six miles; but late astronomers have reasoned that they must be three times this diameter.

There have been numerous theories concerning Mars being inhabited, and of course these suggestions made respecting life on one planet may, with varying circumstances, be applied to another. Each planet may have had,[Pg 525] or may yet have, to pass through what has been termed a “life-bearing stage.” We on earth are at present in the enjoyment of that stage. So far as we can tell, therefore, Mars may be inhabited now, as he bears much the same appearance as our planet. Certain changes are going on in Mars, and all planets, just as they go on here in our earth, and as they did long, long ages before the earth was populated, and which will continue to go on after life on the earth has ceased to exist.
Mars is, as we know, much further away from the sun than earth is, and must receive less direct heat. When he was created, or formed, we can only conjecture, but in all probability he cooled before the earth did, as he is smaller. Here another theory concerning the state of Mars arises, and in support of it we may quote an American authority upon the planet.
“His mass is not much more than one-ninth of the earth’s, while his surface is about one-third of hers. Then, if originally formed of the same temperature, he had only one-ninth her amount of heat to distribute. If he had radiated it away at one-ninth of her rate, his supply would have lasted as long, but radiation takes place from the surface in proportion to the surface, hence he parted with it three times as fast as he should have done to cool at the same rate as the earth, and must have attained a condition which she will not attain until three times as long an interval has elapsed from the era of her first existence than has already elapsed. Geologists agree that the last-named period must be measured by many millions of years; hence it follows that twice as many millions of years must elapse before our earth will be in the same condition as Mars, and Mars must be three times as far on the way toward planetary decrepitude and death as our earth. Then assigning two hundred thousand years as the extreme duration of the period during which men capable of studying the problems of the universe have existed, and will exist on this earth, the theory holds that Mars would have entered on that stage of his existence many millions of years ago, and that the appearance of the planet itself implies a much later stage of planetary existence.”
Mars is a very interesting study, and the reddish hue which is so distinctive is perceived in certain spots when examined by the telescope’s aid. These red places were discovered by Cassini. Mr. Dawes made drawings of Mars, and Mr. Proctor has by their aid constructed a regular map of Mars, and a chart of the surface of the planet. There is much more land than water on Mars, as the bright surfaces which indicate land are much more extensive than the darker portions which betoken the existence of water. But these “markings” are not always visible, in consequence of something coming between us and the land on Mars, and this has been attributed to the production of vegetation, which a French savant declared was ruddy-coloured, and that this autumnal tint departed in the winter.
The seasons of Mars are not equal, in consequence of his wandering propensities, and winter is warmer up there than our winter, while summer is cooler than our summer. That there are clouds and an aqueous atmo[Pg 526]sphere surrounding Mars we learn from spectroscopic observation and analysis, and in fine we may look upon Mars as similar to our earth. Respecting the question of its habitation we take the liberty to quote Mr. Richard Proctor:—
“I fear my own conclusion about Mars is that his present condition is very desolate. I look on the ruddiness of tint to which I have referred as one of the signs that the planet of war has long since passed its prime. There are lands and seas in Mars, the vapour of water is present in his air, clouds form, rains and snows fall upon his surface, and doubtless brooks and rivers irrigate his soil, and carry down the moisture collected on his wide continents to the seas whence the clouds had originally been formed. But I do not think there is much vegetation on Mars, or that many living creatures of the higher types of Martian life as it once existed still remain. All that is known about the planet tends to show that the time when it attained that stage of planetary existence through which our earth is now passing must be set millions of years, perhaps hundreds of millions of years ago. He has not yet, indeed, reached that airless and waterless condition, that extremity of internal cold, or in fact that utter unfitness to support any kind of life, which would seem to prevail in the moon. The planet of war in some respects resembles a desolate battle-field, and I fancy that there is not a single region of the earth now inhabited by man which is not infinitely more comfortable as an abode of life than the most favoured regions of Mars at the present time would be for creatures like ourselves.”

A Peer Continent. B Herschel Continent. C Fontana Land. D Secchi Continent, East. E Secchi Continent, Central. F Secchi Continent, West. G Mädler Continent. H Leverrier Land. 1 Herschel Strait. 2 Dawes Ocean. 3 Maraldi Sea. 4 Oudemans Sea. 5 Trouvelot Bay. 6 Funchal Bay. 7 Campani Sea. 8 De la Rue Ocean.
The Moons of Mars.
We must devote a few lines to the satellites of Mars, which during the last four years have proved a very interesting study for the astronomers, and some very interesting facts have been ascertained concerning the ruddy planet, which is now proved not to be “moonless Mars,” as the poet declared.
There are two satellites, which, in consequence of their distance from[Pg 527] him, being so different, vary in apparent size. The outer one is twelve thousand, the inner one about three thousand five hundred miles from the planet, so the former would revolve in about thirty hours in a direction from west to east, and the inner moon goes round in the same way in about seven hours and a half. Mars revolves in twenty-four and a half hours from west to east. So the outer moon rises for him in the east, and the inner one in the west. This is accounted for by the fact that one travelling slower than Mars rises in the east, the other outruns him, and comes up in the west.
But if we suppose ourselves upon Mars we shall find that, after all, we have only one moon properly so called. The outer satellite is very small and very far away, so it is useless to give light—at most, it is no bigger than Mars appears to us on earth. So the Martians do not see two moons passing each other in the sky—that is, unless their eyes are of greater range and power than ours. Thus they have one moon rising in the west, appearing in all its phases every night, while our moon takes twenty-eight days to pass through her phases; for we must remember that Mars’ moon takes only seven hours and forty minutes to pass through its orbit, and therefore each quarter will not occupy quite two hours.
The Minor Planets, or Asteroids.
Passing onward from Mars towards Jupiter we arrive at a number of smaller planets, which will not concern us very much, as they are very small and scarcely visible without a good telescope. But a very interesting chapter in the history of astronomy was commenced when the discovery of these bodies was begun. In old times astronomers noticed a very considerable gap between Mars and Jupiter, which was remarkable when the regular progression of the distances between the planets was remembered. So Kepler was of opinion that some planet would be discovered having its orbit in that space between Mars and Jupiter. It is, however, to Piazzi, the Italian, that the discovery of the zone of asteroids is due.
Dec. 8th. Dec. 9th.

Piazzi was surveying the constellation Taurus, where he fancied he had discovered a change of place in a star which he had observed on the 1st of[Pg 528] January in that year (1801). He was quite sure of this change next day (the 3rd of January), and he expressed his opinion to Bode and Oriani. But letters took a long time to pass in those days, and when the other astronomers had received the advices the new star had been lost in the sun’s glory. But after a year, on the 31st December, 1801, the planet was again seen and the discovery was proved. The new planet was named Ceres.
The discovery of Ceres led to other discoveries. For, while searching for her, Olbers found other minor planets, and so on to the present day. Now we have nearly two hundred asteroids, and more are probably to be found in the zone beyond Mars.
It would answer no purpose to give a list of the asteroids. We need only remark that the first four were discovered in quick succession, and then a lapse of thirty-eight years occurred before the fifth was found, thus—
| Ceres, | discovered by | Piazzi at Palermo, January 1st, 1801. |
| Pallas, | ” | Olbers at Bremen, March 28th, 1802. |
| Juno, | ” | Harding at Lillienthal, September 2nd, 1804. |
| Vesta, | ” | Olbers at Bremen, March 20th, 1807. |
| Astræa, | ” | Hencke at Driessen, December 8th, 1845. |
Since 1848 there have been numerous minor planets discovered every year.
The hypothesis that all these asteroids are fragments of one large planet which has been destroyed was started by Olbers; and in confirmation of this view it has been determined that the asteroids have essentially the same character. The orbits of these minor planets are different from the larger “wanderers,” and cross each other, as will be seen from the accompanying diagram, so that a collision may one day ensue.

Planetoids and extra zodiacal planets are titles which have been bestowed upon these bodies, of which Vesta is the first in order in the system, and revolves in 1,325 days, at a mean distance of 225,000,000 of miles from the sun. Juno and Ceres take each about four of our years to revolve in their orbits, at greater distances still, averaging 260,000,000 of miles. Pallas and Ceres are most alike in their periods and distance from the sun; the principal asteroids are only about 300 miles in diameter, while the smaller are very tiny indeed, and one certainly has quite disappeared.
Jupiter, the Giant.
Jupiter has been well named the Giant planet, since his diameter is eleven times greater, and he is thirteen hundred times larger than our[Pg 529] planet. His inclination is very small, and you now know that under such circumstances he enjoys very small changes of seasons. Jupiter has four moons, or satellites, and an illustration of the “Jovian System” is herewith given.

Jupiter himself was well known to the ancients, but Galileo was the discoverer of the “moons.” His telescope was, of course, a very imperfect instrument, and while he was gazing at the planet he noticed three stars close by the bright disc, two on one side, but next day Galileo perceived them all at the same side. Next time he looked there were only two, and after many anxious observations he found out, not only that Jupiter had three attendant stars, but four!
These moons were found to revolve round Jupiter in times varying from nearly two days to nearly sixteen days, according as they were at a less or greater distance from him. They were found to have their times of eclipses and transits, etc., also. These moons act with respect to Jupiter very much as the inner planets act with respect to the sun, for observation showed[Pg 530] Galileo that the satellites sometimes appeared on one side of the planet, and at other times on the opposite side.

From the diagram of the Jovian System we shall understand the orbits of the moons, which are all of nearly equal size,—two thousand miles in diameter,—and cause eclipses of the sun to Jupiter. If the earth be in the same direction as the sun the moons are lost to view. The satellites disappear into the shadow, and are eclipsed at 1′″, 2′″, 3′″, 4′″, respectively, but they do not always come into view again immediately they have passed through the planet’s shadow, because the earth is a little at one side of the sun. So when the satellite gets behind the edge of Jupiter, his shadow being on the opposite side to the satellite’s, it is said that the “moon” is in “occultation”; when it disappears in the shadow it is “eclipsed.” Cassini discovered the “transit” of Jupiter’s moons. The annexed diagram illustrates the eclipses, etc., very clearly. At the four points, A B C D, we have the earth; J is Jupiter with his moons; 1 2 3 4 is their orbits. At a moon No. 1 enters his shadow, and emerges at b. From the earth at D a will be visible, but not b, because Jupiter is in the way. So at B, the coming out, or emersion, will be visible, but not the entrance into the shadow, or immersion. At A the satellite is in transit d, on the disc of the planet, J.

From the observation of the eclipses of Jupiter’s moons the rate of the transmission of light was discovered by Roëmer in 1675, and its progressive motion was calculated. The eclipses were noticed to take place later than the calculated time, when the planet was approaching conjunction. Roëmer suggested that the delay was owing to the greater distance the light had to travel—a distance equal to the diameter of the earth’s orbit, or about 190,000,000 of miles. The time was about sixteen minutes. Light was found to travel at the rate of nearly 12,000,000 of miles a minute.
Let us now endeavour to picture Jupiter himself. Here we have an[Pg 531] illustration of the planet. He is the biggest, and the brightest, except Venus, of all the planets. He revolves at a distance of 476,000,000 of miles from the sun, and his year is equal to nearly twelve of ours, while his day is scarcely ten hours long, showing a rapidity more than twenty times the rate of our earth. Jupiter, therefore, must have a very much greater diameter than the earth.

There is much less sunlight and heat found on Jupiter than upon Earth, because he is so much farther from the sun than we are, but at the same time the heat comes at less intervals than with us. And here the theory already noticed respecting the gradual cooling of the planets will be remembered. Jupiter, we can easily imagine, would take much longer to get cool than Mars or the earth, and, though his rapid rotation would assist him, he must be still in the midst of a glowing atmosphere without form and void—perhaps a furnace for cloud and vapour generation.
Now when Jupiter is examined with the telescope it will be seen that he is crossed by belts of vapour (see also page 489); and when we consider the results of the spectrum analysis of the planet, we may fairly assume that Jupiter is in a very heated state, and that we cannot really perceive the actual body of the planet at all yet. There is an immense quantity of water thus surrounding Jupiter, and he is still in the condition in which our earth was before geology grasps its state, and long ere vegetation or life appeared. The waters have yet to be “gathered together into one place,” and the dry land has yet to appear upon Jupiter, who is a very juvenile, if a very enormous planet. Under these conditions we can safely assume that there are no inhabitants of Jupiter.
The belts, or zones, of Jupiter vary in hue, and the continual changes which are taking place in this cloud region tend to show that disturbances of great magnitude and importance are occurring.
It is useless to speculate upon what will happen in Jupiter when the disc is eventually cooled. The planet, we know, has not nearly reached maturity; the earth is in the full prime of its life, and the moon is dead and deserted. What the millions of years which must elapse before Jupiter has cooled may bring forth we need not try to find out. The earth will then, in all probability, be as dreary as the moon is now, and we shall have returned to dust.
Saturn.

We now come to the most curious of all the planets—Saturn, which is an immense globe surrounded by a beautiful bright ring, or rather series of rings, and attended by eight moons. He appears to possess much the same constitution as Jupiter, but enveloped in an even denser atmosphere than the latter. Saturn’s diameter is about nine times greater than the earth; he revolves on an inclined axis in about ten hours, and has seasonal alternations of unequal length. His year is about thirty of ours (10,759 days). The most striking phenomena in connection with Saturn are his rings.
Saturn’s rings are supposed to be a close agglomeration of stars, or satellites, revolving around the planet and encircling him in a belt. The rings are apparently broad and flat and thin, resembling roughly the horizon of a globe.
The globe of the planet is not exactly in the centre of the rings, which have been measured, and are approximately as below:—

| Diameter of exterior ring | 169,000 | miles. |
| Diameter of interior ring | 124,000 | ” |
| Diameter of innermost ring | 100,000 | ” |
| Interval between innermost ring and Saturn | 19,000 | ” |
| Intervals between the rings | 18,000 | ” |
| Thickness of the rings | 130 | ” |
| Breadth of the rings | 37,000 | ” |
The rings were first recognised as such by Huyghens in 1659, but Galileo had remarked the curious appearance the planet presented. Cassini confirmed Huyghens’ discovery, and found that the ring was duplicated, and Mr. Ball made the same discovery. The two outermost rings are very bright, the inner ring being darker and partially transparent, for the ball of Saturn can be perceived through it.


But the rings are not always so plainly seen as in the foregoing diagram. Sometimes they appear as a mere line of light on each side of the planet, as shown in the margin. This occurs at the time of the equinox (fig. 591). By degrees, however,[Pg 533] as they become inclined, they appear broader (fig. 592). The inner ring may be formed of vapour, but the outer ones are of something more solid, as the shadows they cast upon the planet, and it casts upon them, at certain times (figs. 593 and 594).
Saturn possesses eight moons, seven of them revolving in orbits on the plane of the rings, but one is more inclined. These eight satellites have been named as follows:—
| Name. | Distance from Saturn in radii of Saturn. Miles. |
Time of Revolution. |
Discoverer. |
|---|---|---|---|
| d. h. min. | |||
| 1 Mimas | 3·36 (about) 120,000 | 22 37 | Herschel. |
| 2 Enceladus | 4·30 (about) 150,000 | 1 8 53 | Herschel. |
| 3 Tethys | 5·34 (about) 190,000 | 1 21 18 | Cassini. |
| 4 Dione | 6·84 (about) 240,000 | 2 17 41 | Cassini. |
| 5 Rhea | 9·55 (about) 340,000 | 4 12 25 | Cassini. |
| 6 Titan | 22·15 (about) 790,000 | 15 22 41 | Huyghens. |
| 7 Hyperion | 26·78 (about) 945,000 | 21 7 7 | Lassel and Bond. |
| 8 Iapetus | 64·36 (about) 2,250,000 | 79 0 8 | Cassini. |

But these eight moons are not so interesting as those belonging to Jupiter, because the great distance they are away precludes much examination of them. They vary much in size, Titan being the largest, and perhaps equal to Mars, Iapetus being next in magnitude. The light of these satellites and the rings is no doubt very great in the aggregate, and must have a magnificent appearance in the heavens (compare page 493). Very likely there are other attendants upon Saturn, but owing to the brilliancy of the rings it is impossible to distinguish them.
Uranus.
Uranus was discovered by Herschel in 1781, and has been called after its discoverer, and sometimes the “Georgium Sidus.” It revolves at an enormous distance from the sun—viz., 1,753,000,000 of miles. It takes about eighty-four of our years (30,686 days) to go round the sun, and possesses four moons. It is very much larger than the earth—about four times the diameter, and forty times its volume. We can only speculate[Pg 534] concerning its physical constitution, which is assumed to be similar to that of Jupiter, while the changes of temperature and seasons must vary immensely. The names of the moons are Ariel, Umbriel, Titania, and Oberon. The outer pair can be seen without much difficulty.
Neptune.
The existence of this planet was determined by calculation before it had been seen at all. Uranus was observed to be disturbed in his orbit, moving sometimes faster than at others; and even before Uranus had been discovered Saturn and Jupiter had been seen to be affected by some body in the system. M. Leverrier determined to ascertain the cause of this, and came to the conclusion that some other planet was influencing Uranus. The Newtonian theory here received a most convincing proof. While Leverrier was calculating, Mr Adams of Cambridge leaped to the same conclusion, and wrote the result of his calculations to Professor Airy, and the planet was seen, but not reported upon. Meantime Leverrier published his calculations, and the observers at Berlin detected the new planet in September 1846.

Very little can be said concerning Neptune, as its distance is too great for observation. It is at 2,746,000,000 of miles from the sun, and takes 164 years to go round it (60,126 days). It is about the same size as Uranus. It has one moon, which moves round the planet in 5d 21h, and is of great size.

CHAPTER XL.
THE FIXED STARS.
FIXED STARS—MAGNITUDE OF THE STARS—CONSTELLATIONS—DESCRIPTIONS OF THE ZODIACAL CONSTELLATIONS—NORTHERN AND SOUTHERN STAR GROUPS—DISTANCE OF STARS.
We have been considering the planets so far as they are known to astronomers, but no doubt we shall find out others some day beyond Neptune in space, for it must be assumed that there are other planets wandering about in the infinite firmament. At present, however, we cannot spare time for such speculation; we have got to peep at the stars and their groupings.
“What little bits of things the stars are,” a child said once in our hearing; and there were others present who were inclined to believe that the tiny light spots we could see looked small—not because they were distant, but because they were of no great magnitude; and when those children were told that the tiny stars were “suns” like our sun, giving heat and light millions and millions of miles away,—and, so far as we can tell, some are much bigger and hotter than our own sun,—they were very much surprised indeed, and one little girl aptly quoted Dr. Watts:—
Now let us endeavour to learn something about these apparently tiny specks, and why they “twinkle.”
At a very early period in the history of astronomy the observers of the heavens grouped stars together in fancied resemblances to men or animals; and these “constellations,” as they are termed, are combinations of fixed stars—that is, of stars which do not wander about as the planets do. But these so-called fixed stars have motions; they are only relatively fixed with reference to their positions to each other as they appear to revolve daily round the earth. But stars have a movement of their own, which is termed their “proper motion.”
It is to Halley that the discovery of these real star motions is due. He saw three very bright stars (Sirius, Aldebaran, and Arcturus) were not in the places they had been assigned. The sun also has been found to possess a “proper motion,” and, with the planets, is travelling as determined by Sir J.[Pg 536] Herschel, to a particular place in the constellation called Hercules. There are now star catalogues and star maps, for the heavens have been as closely surveyed as the earth, and by accurate observations it has now become possible to find the position of every star usually visible. Some of the stars are used as “clock” stars, by which sidereal time can be calculated accurately, and the clocks thereby corrected. The stars, though termed “fixed,” are in perpetual movement—Arcturus at the rate of fifty miles a second, and others less. Only the rates of a few are known.
The number of the stars is beyond our calculation, and even the number of stars only visible in the telescope amount to millions, and these are called telescopic stars. The visible stars amount to about six thousand, and of course these are the brightest up to the sixth magnitude. There are more visible in the southern than in the northern hemisphere. The magnitudes of the stars range in classes according to the brightness of the stars observed, for this is really the test from the first magnitude to the sixth; after that the telescopic stars are seen up to the fifteenth or sixteenth. We can only see about three thousand stars at any one time from any place, although, as remarked above, many millions may be observed with a good telescope, and as many more, probably twenty millions, are invisible.
We will now proceed to detail the constellations, which are familiar by name to everybody. We have already given the names of the zodiacal groups, which consist of many stars, each designated by a letter of the Greek alphabet so far as possible, then the Roman letters and numerals are employed. Thus α (Alpha) is the most brilliant star; β (Beta) the next bright γ (Gamma) the next, and so on; so the relative brilliancy of the stars in the constellation is indicated, but not the very biggest star of the first magnitude is intended by α, for the star δ in one constellation may equal α in another. John Bayer originated this method in 1603.
The arrangement of the constellations is plunged in the obscurity of ages, but B.C. 370 there were forty-five thus grouped. There are northern and southern constellations which are visible above our old friends Aries, Taurus, Cancer, etc. We will, as in duty bound, consider our old acquaintances first, and then give a list of the northern and southern groups of stars; but we shall find that the forms are in the greater part due to the imagination of the ancients, and do not bear out our ideas of the animals they are supposed to represent, while at the same time they cross and recross with other constellations in the skies in a very puzzling way.

The first constellation is Aries, the Ram, which is celebrated in mythology as the proud possessor of the Golden Fleece, which we may remember was[Pg 537] seized and carried away by Jason and the Argonauts. The Hellespont is so called from Helle, who fell from the Ram’s back when being carried upon it over the Black Sea. The Ram is here represented with the equinoctial ring.
We perceive in Aries two very bright stars near the head. These are (α) Arietis and (γ) Sheretan. The signs and constellations do not now correspond as they used to do, because of the change in the position of the stars, which gives rise to the Precession of the Equinoxes (vide ante., p. 497), so that the stars which two thousand years ago were in conjunction with the sun, are much more to the eastward. In olden time (when astronomy was young), the sun entered Aries on the 21st March, and now a change has taken place. But in about another twenty thousand years, they will all come right again. This will be perceived by reference to the celestial globe. The Ram has sixty-six stars in his constitution.

Taurus, the Bull, is the next constellation. He received his name from the celebrated animal into which Jupiter transformed himself when he wished to carry away Europa. The star Aldebaran (α) is the end of a kind of V in the Bull’s face. The Pleiades are on the shoulder to the right. This cluster of twinkling stars is well known, and will guide the observer towards the imaginary Bull, which we must nowadays describe as rather a fanciful delineation. Europe is called after Europa, because Jupiter, as a Bull, carried her to this continent. There are 141 stars in Taurus, according to the number found in the list of Aratus, and probably more.

Gemini, the Twins, which are supposed to be Castor and Pollux, though it is believed that two goats were the original sign—which statement, taken in connection with the ram and the bull, that were also turned out in the spring-time, may have something to recommend it. But now Castor and Pollux are generally recognized as the constellation. During the expedition for the Golden Fleece, the electric appearance, now known as St. Elmo’s Fire, became visible upon them, and their effigies were placed in the forepart of ships as a good omen. This led to the adoption of the “figure-head.” They were made into stars when Pollux was immortalized by Jupiter, for he divided the boon with his brother. The planet Uranus was discovered near this constellation, which contains eighty-five stars.

Cancer, the Crab, is the next in order, and the only derivation we can find for this is that Juno sent a crab to attack Hercules when he was busily engaged with the many-headed Hydra. The crab was directed to pinch the hero’s foot, but it appears rather a lame device for the Queen to adopt. The crab, however, was killed by Hercules, and placed amongst the stars by Juno as a reward; so he gained immortality cheaply. He, Cancer, contains more than eighty stars, but none of them of any particular note. Some writers explain the sign as reminding the ancients of “the retrograde movement of the sun to the north”; but as a crab does not move “backwards,” we will still adhere to mythology as equally satisfactory at any rate. Cancer, however, was termed the “northern gate of the sun.”

The next is Leo, the Lion, which came round in summer and at the period of much heat, so this fierce animal may have been chosen to represent that season. But mythology will have us credit the Nemæan Lion sent against Hercules by Juno as the origin of this constellation. The lion was, like the crab, placed amongst the stars when he was killed. He is a very brilliant constellation, and a very bright star called Regulus is to be seen in his chest—“Cor Leonis.” Another very fine star of the second magnitude is observable in the tail. The Lion consists of ninety-five stars, the principal ones being of the first and second magnitudes.

Virgo is supposed to be outlined by a very rich cluster of stars, and one of the first magnitude. The Virgin is by some supposed to be Astræa, the goddess, but is more likely referable to a girl gleaning, or holding an ear of corn in semblance of the harvest. This constellation contains more than one hundred stars. One of them in the wheat-ear is a particularly brilliant one, and noted for its “solitary splendour,” as no star of large magnitude is near it. The Arabs used to call it the Solitary Simak; Spica Virginis is the modern name.

Libra, which follows, may either indicate the balance, or scales of justice, of Astræa, or the equal day and night at the autumnal equinox. Virgil mentions Astræa’s balance, and thus we have a classical authority for the very mythological view of the two foregoing constellations. Libra is not very distinct; it contains fifty-one stars, four of which are very bright.

Scorpio, the Scorpion, according to classical writers, encountered Orion, who is also met with in the stellar universe. The scorpion stung Orion because he declared there was no living creature he could not overcome by force. On the other hand, this sign may have some reference to the unhealthy time of year, and the prevalence of disease about the time that Scorpio appeared. A beautiful star of reddish hue and of the first magnitude is prominent amongst the brilliant assembly of the Scorpion’s forty-four stars.

Sagittarius, the Archer, is, as one can see, a Centaur, and said to be Chiron, who was wounded by Hercules, and cured by being taken up to Heaven by Jupiter. This Chiron is represented as a great patron of the arts, and thus the fable may be said to exemplify the proverb, “Art is long, time is fleeting”; for readers of mythology will find much more in the legends than is apparent on the surface. But we can now only regard the Centaur from an astronomical, and not a philosophical standpoint. Sagittarius has no very brilliant stars. He is close to the Milky Way, and contains sixty-nine stars, five forming a sort of V in the bow, sometimes compared to a ladle or “dipper.”

Capricornus, the Goat, is supposed to be Pan—“the great god Pan,” who turned himself into a goat. The sun was in Capricornus at mid-winter, so the “southern gate of the sun” was a title be[Pg 540]stowed upon him. But now the constellation is later. It does not include any very striking stars, of which there are fifty-one in the “Goat.”

Aquarius, or the Waterbearer, may have referred to wet weather, or as others declare, to Ganymede, the Cupbearer. There are four stars in the waterpot like a Y; and more than one hundred stars of small brilliancy are included in this constellation. But here again fancy must come to our assistance, for without a diagram the ordinary observer could not distinguish the Waterbearer.

Pisces, the Fishes, are not plainly defined. It is supposed that Venus and Cupid turned themselves into fish when the Titans assailed Heaven. This Constellation occupies a triangle in the sky.
The foregoing are the zodiacal constellations, and may be more easily remembered by repeating an old rhyme, which runs as follows:—
The arrangement of the various Constellations at which we have so rapidly glanced, as well as of those that follow, has been the work of many different periods. Aratus and Ptolemy are the oldest enumerators, but modern research has added immensely to the store of knowledge. Many of the most prominent stars were named by Grecian and Arabian observers, and many of the names are still retained—such as Arcturus, Rigel, Capella, and others.
The Northern Constellations.
There are, altogether, thirty-five of these, as per list on next page. It is of course impossible to describe them all, but we will make a few remarks respecting those which will be distinguished most readily, and the manner of finding out particular stars. There are star maps published, and with a little attention and reading, a great many very pleasant evening excursions may be made across the sky, with or without a telescope. The following is the list of the northern constellations. We have put them in various types to indicate the most important.
| Name of Constellation. | “Author.” | No. of Stars. | |
|---|---|---|---|
| Ursa Major | The Great Bear | Aratus | 87 |
| Ursa Minor | The Lesser Bear | “ | 24 |
| Perseus | Perseus | “ | 59 |
| Auriga | The Waggoner | “ | 66 |
| Boötes | The Herdsman (Boötes) | “ | 54 |
| Draco | The Dragon | “ | 80 |
| Cepheus | Cepheus | “ | 35 |
| Canes Venatici | {The Greyhounds} | Hevelius | 25 |
| {Hunting Dogs | |||
| Cor Caroli | Heart of Charles | Halley | 3 |
| Triangulum | The Triangle | Aratus | 16 |
| Triangulum Minor | The Little Triangle | Hevelius | 10 |
| Musca | The Fly | Bode | 6 |
| Lynx | The Lynx | Hevelius | 44 |
| Leo Minor | The Lesser Lion | “ | 53 |
| Coma Berenices | Berenice’s Hair | Tycho Brahé | 43 |
| Camelopardalis | The Giraffe | Hevelius | 58 |
| Mons Menelaus | Mount Menalaus | “ | 11 |
| Corona Borealis | The Northern Crown | Aratus | 21 |
| Serpens | The Serpent | “ | 64 |
| Scutum Sobieski | Sobieski’s Shield. | Hevelius | 8 |
| Hercules | Hercules | Aratus | 113 |
| Serpentarius | The Serpent-bearer | “ | 74 |
| Taurus Poniatowski | Poniatowski’s Bull | Poczobat | 7 |
| Lyra | The Harp, or Lyre | Aratus | 22 |
| Vulpecula et Anser | Fox and Goose | Hevelius | 37 |
| Sagitta | The Arrow | Aratus | 18 |
| Aquila | The Eagle | “ | 71 |
| Delphinus | The Dolphin | “ | 18 |
| Cygnus | The Swan | “ | 81 |
| Cassiopeia | The Lady’s Chair | “ | 55 |
| Equuleus | The Little Horse | Ptolemy | 10 |
| Lacerta | The Lizard | Hevelius | 16 |
| Pegasus | Pegasus (Flying Horse) | Aratus | 89 |
| Andromeda | Andromeda | “ | 66 |
| Tarandus | The Reindeer | Lemounier | 12 |
| (There are a few others marked in continental maps.) | |||
The Great Bear, or “Charles’s Wain,” or the “Plough,” as Ursa Major is variously called, is of great value in indicating the pole star, which, when once known, can never be mistaken. This constellation has also been termed the “Dipper,” and is very conspicuous in the northern hemisphere. The three stars form the bear’s tail, or the handle of the “plough”; the others form the body, Charles’s Wain, or “Karl-Wagen,” the German term for peasant’s cart, is represented by the quadrangle forming the cart, and the other three stars are the horses.
The “Pointers” are the two end stars, and if a line be followed northwards from them it will lead close to Polaris, the principal star in the lesser bear. This pole star is of a very great brightness, and peeps out, almost isolated, with a pure lustre. The names of the pointers are Dubhe and Menak. The star at the tail-tip is Benetnasch, then Mizar and Alioth. Megrez and Phad are the remaining pair. We append a rough outline of the bear, for the information of those who have not yet noticed it.
The Lesser Bear is not so important as his elder brother as regards size, but he is very useful to astronomers. He resembles the Great Bear in appearance, but is smaller, and the positions of the stars are inverted. In the cut on page 555 (fig. 629) you see the little bear swinging round the polar star, which is at the tip of the Lesser Bear’s tail, so any one will be enabled to find him if they look for the polar star, and then count the three stars away from it, and the four in the body. The Great Bear’s tail points in the other direction. This movement of the earth’s axis by displacing the equinoctial points, alters the “declination” and “right ascension” of the stars (compare page 473). So Polaris is gradually approaching the actual polar point. In about 200 years he will have got as close as he can, and will then begin to recede from it, and in about 12,500 years after he will reach his most distant point.

Polaris, the Pole Star, was called “Cynosure” by the ancients, and thus we can understand the quotation, “Cynosure of neighbouring eyes,” when a person or object is very attractive. The pole star was the point to which all looked. There are some other very important stars in these constellations. For instance, in—
These stars are also designated by the Greek letters—α, lyræ, or the[Pg 543] first in the Lyre—that is, Vega; and so on for all, according to rank, as already explained.
Southern Constellations.
We must pass on to the southern constellations, of which there are forty-six; the principal ones are in capital letters:—
| Name of Constellation. | “Author.” | No. of Stars. | |
|---|---|---|---|
| * Phœnix | The Phœnix | Bayer | 13 |
| Apparatus Sculptoris | The Sculptor’s Tools | Lacaille | 12 |
| Eridanus Fluvius | The River Po | Aratus | 84 |
| * Hydrus | The Water-snake | Bayer | 10 |
| Cetus | The Whale | Aratus | 97 |
| Fornax Chemica | The Furnace | Lacaille | 14 |
| * Horologium | The Clock | ” | 12 |
| * Rheticulus Rhomboidialus | The Rhomboidal Net | ” | 10 |
| * Xiphias Dorado | The Sword-fish | Bayer | 7 |
| * Celapraxitels | The Engraver’s Tools | Lacaille | 16 |
| Lepus | The Hare | Aratus | 19 |
| Columba Noachi | Noah’s Dove | Halley | 10 |
| Orion | Orion | Aratus | 78 |
| Argo Navis | The ship Argo | ” | 64 |
| Canis Major | The Great Dog | ” | 31 |
| Equuleus Pictoris | The Easel | Lacaille | 8 |
| Monoceros | The Unicorn | Hevelius | 31 |
| Canis Minor | The Lesser Dog | Ptolemy | 14 |
| * Chameleon | The Chameleon | Bayer | 10 |
| Pyxis Nautica | The Mariner’s Compass | Lacaille | 4 |
| * Piscis Volans | The Flying Fish | Bayer | 8 |
| Hydra | The Snake | Aratus | 60 |
| Sextans | The Sextant | Hevelius | 41 |
| * Rober Carolinum | Charlie’s Oak | Halley | 12 |
| Antlia Pneumatica | The Air Pump | Lacaille | 3 |
| Crater | The Cup | Aratus | 31 |
| Corvus | The Crow | ” | 9 |
| *Crux Australis | The Southern Cross | Royer | 6 |
| Apis Musca | The South Fly | Bayer | 4 |
| * Avis Indica | The Bird of Paradise | ” | 11 |
| * Circinus | The Compass | Lacaille | 4 |
| Centaurus | The Centaur | Aratus | 35 |
| Lupus | The Wolf | ” | 24 |
| Norma | The Square | Lacaille | 12 |
| * Triangulum Australis | The Southern Triangle | Bayer | 5 |
| *Ara | The Altar | Aratus | 9 |
| * Telescopium | The Telescope | Lacaille | 9 |
| Corona Australis | The Southern Crown | Ptolemy | 12 |
| * Pavo | The Peacock | Bayer | 14 |
| * Indus | The Indian | ” | 12 |
| Microscopium | The Microscope | Lacaille | 10 |
| * Octans Hadliensis | Hadley’s Octant | ” | 43 |
| * Grus | The Crane | Bayer | 14 |
| Toucan | The Toucan | ” | 9 |
| Pisces Australis | The Southern Fish | Aratus | 24 |
| * Mons Mensa | Table Mountain | Lacaille | 30 |
We need only describe Orion and Canis Major, the principal groups. The former certainly constitutes the most glorious group, and it is visible to all the world, because the equinoctial passes through it.
Orion, as we have said, can be viewed from either hemisphere, and so can some others; but those marked with an asterisk in the foregoing list are not visible in the latitude of London.

Orion is a very brilliant constellation, and contains two fine stars of the first magnitude, and some of the second. The former are Betelgeux and Rigel. Bellatrix is the third in order. The “belt” is formed of three bright stars, and the sword is visible as five stars just below. Canis Major possesses Sirius, a very fine star (the dog star). Canis Minor has two of the first and second magnitude, and Hydra has one of the first. The Southern Cross is a beautiful constellation, invisible in our latitude, but familiar to sailors in the Southern Seas.
The Stars’ Distance and Magnitude.

When we gaze up into the sky at night, we see the stars twinkling far away, and we may remark here that this twinkling of the stars is due to the atmosphere and the changes in its power of refraction, and of course the star’s light changes its direction. But if we ascend in a balloon into very high and rarefied strata of the air, we will find the twinkling less. We have given the number of the stars according to Flamstead, but the larger the telescope the greater will be the number of stars we shall see, numbers again being too far even for our perfected instruments.
But we can gain some idea of the magnitude of the stars when we consider the distance to arrive at, which is a most difficult task, for figures seem scarcely long enough to count the millions of miles, and no instrument can detect the parallax. Even supposing the parallax to be a very small fraction of a degree we should get a result equalling trillions of miles. No. 61 in Cygni was at one time continually observed by Professor Bessel, and he found that its distance—and it is the nearest star—is sixty-two and a half trillions of miles.

Let us consider what this means. Light comes to us from the sun (91,000,000 of miles) in about eight minutes, and travels at the rate of something like 186,000 miles in a second. But even at that astounding rate[Pg 545] the light from the star called 61 Cygni took ten years to reach the earth; and there are stars whose light has never yet reached the earth, although the gleam may have been travelling at 186,000 miles a second for thousands of years. And we may presume that though we still see the light of stars, some of them may be dead, but the light left is still progressing to us through space.
So we must conclude that some stars which look large, as do Vega and Sirius for instance, must be enormous “suns,” a great deal larger than our sun, and the stars are each the centre of invisible systems just as our sun is the centre of the “solar” system. Vega is a tremendous star, and shines with her own light as do all other visible stars; for reflected light, so very visible in the moon, which is close to us, would be quite invisible at such tremendous distances. So we must call these stars “suns,” and may add an apparently astonishing fact, that our own sun is merely one of the stars in the Galaxy, or “Milky Way”!

CHAPTER XLI.
THE STARS—(continued).
DOUBLE AND MULTIPLE STARS—COLOURED AND VARIABLE STARS—CLUSTERS, GROUPS, AND NEBULÆ—THE GALAXY, OR MILKY WAY—HOW TO FIND OUT THE PRINCIPAL STARS.
Although not very clearly visible to the naked eye, there are in the sky some pairs of stars very close together apparently; but when these double stars are examined with a good telescope we find that though we fancy they are two stars very close, in reality an immense distance separates them. By Vega, which we have already mentioned, there is apparently a star, which on examination will be found really to be two stars. It is also in the constellations of the Lyre, but of much lower magnitude than Vega. But in some instances there are three or four stars thus placed together, and the frequency of the occurrence of this fact establishes the farther fact that these combinations are not accidental—that the stars are interdependent and physically connected.

There are now at least six thousand double stars known,27 and this is a very small proportion of the forty millions or so of suns which are believed to exist in space. But of these six thousand a larger proportion have been ascertained to be physically connected. More than six hundred of these pairs are double suns, while again there are other combinations of three and perhaps more. When two are thus connected we have what are termed binary systems, and when more are associated they are called triple and multiple stars. An example of the last-mentioned class is the small star above mentioned near Vega. It is ε Lyræ, and is a double of a double. In ordinary telescopes this will not be perceived, but with a high power the combination will be noticed. The same phenomenon is observable in one of the stars of Hercules and in Andromeda.
The revolution of these double suns, or binary systems, has been closely observed, and Professor Newcomb has given us a list of the binary systems of short period which are well determined. These are as follows:—
| 42 Coronæ | 26 years. |
| ζ Herculis | 35 years. |
| Struve 3,121 | 40 years. |
| η Coronæ | 40 years. |
| Sirius | 50 years. |
| ξ Cancri | 58 years. |
| ξ Ursæ Majoris | 63 years. |
| η Coronæ Borealis | 67 years. |
| α Centauri | 77 years. |
| μ Ophiuchi | 92 years. |
| λ Ophiuchi | 96 years. |
| ξ Scorpii | 98 years. |

It must be borne in mind that although these double stars appear close together from our standpoint, they may be far apart—one behind the other in a straight line. When such “pairs” exist they are known as optical pairs, or optically double stars, as distinguished from the actually physical “pairs” which revolve round the centre of a system. In Orion there has been discovered a regular system, and the θ in Orion, which appears in a common telescope a moderate star, and to the unaided eye only a speck of light, is really composed of seven stars—four are set in the form of a trapezium, as figured in the diagram in the margin by dots and asterisks. Two of these have been ascertained to possess attendants indicated by dots, and a seventh star was discovered by Lassell, and Humboldt remarks that in all probability this apparently tiny star in the constellation Orion constitutes a real system, for the five smaller stars have the same proper motion as the principal one.

Thus our imagination almost fails to grasp the infinity of the systems with our single sun, and with the distant double and even triple suns round which planets revolve perfectly independent of the other systems, as we are independent of them possessing heat and light from their own sun or suns as we receive it from ours, day and night seasons succeeding each other, and the wondrous varieties of the light produced by the appearance or withdrawal of a sun or two in the firmament of those most distant planets. These suns being double or triple would affect each other; the composition of the light given forth would produce—as we may assume—varying effects. We know something about the light of the stars by the spectroscope, and the colours of stars are due to the vapour which takes away a certain part of the light emitted, leaving the remainder to descend through the atmosphere to us.
Binary stars are most numerous of the doubles; for instance Castor, η Coronæ, Rigel, Polaris, Mivac, γ Leonis, γ Virginis, ξ Ursæ Majoris, α Hercules, 36 Andromedæ, λ Ophiuchi, and π Aquilæ. The illustration in the margin is Castor (or α Geminorum), the most northerly of the Twins. The η Coronæ is also figured, as are Polaris (see fig. 610 ante.), Boötes, Rigel, and γ Leonis.
The cuts herewith illustrate the relative positions at the periods named of the “doubles,” and of the revolution of suns around other suns as[Pg 548] mentioned. As a consequence of their proper motion the binary stars appear to vary in their distances from each other, as in the topmost of the three cuts on the (opposite) page representing γ Virginis. The stars have gradually approached each other, and so are the stars in Castor approximating, and when they have closed, and have appeared almost as a single star, as they will do, they will take open order again.

The shortest time occupied by a double star in its revolution is thirty-five years, and we have already given some of those which have been ascertained. We will close this section with a few other examples. For instance, γ Virginis revolves in one hundred and fifty years, Castor in two hundred and forty years, 4 Aquarii in three hundred years, 37 Pegasi in five hundred years. There are numerous other instances up to a period of three thousand years, and about eight hundred of these binary systems are known. We have mentioned that there are two or more suns in the multiple systems. These suns are the cause of the different colours of the stars.
Colours of the Stars.
The question of star-colour follows naturally the consideration of the multiple stars; for although single stars have been observed of a ruddy colour, there are no instances of a blue or green one unattended by a companion. This colouring has been attributed to the contrast between multiple stars, for the colours are frequently complementary; but investigation has shown that this cannot be the case. For instances have been known in which, when two are thus associated, and one is concealed from us, the other is just as bright, and retains its former colour.
Of course in cases in which colour is apparent to the unaided vision, only the brightest stars betray colour. Antares, Betelgeuse and Aldebaran are red (orange) colour. Sirius and Canopus are white. Arcturus and Capella are yellowish, so is Pollux. Vega is bluish-white. These appearances are, of course, much more marked when the stars are examined through the telescope, and telescopic stars—which are stars unobservable without a glass—are very much coloured, and the multiple stars give us blue, green, violet, and other tints, besides those already mentioned.
Again, these coloured stars do not always remain the same colour. Sirius was once red; Mars was at times white. Spectrum analysis shows that[Pg 549] the colours of many are due to absorption by the vapours of some of the rays; and the existence of certain vapours may cut off some, and at other times other vapours may exist and cut off other rays, and so the colours may be changed. Struve gives the following list of binary complements of “multiple” stars:—
| Pairs consisting of a blue and white principal star | 53 |
| Pairs consisting of a blue and a light yellow principal star | 52 |
| Pairs consisting of a blue and yellow or red principal star | 52 |
| Pairs consisting of a blue and green principal star | 16 |



We need scarcely pursue this question farther, though many ideas concerning the coloured stars will arise in every thoughtful reader’s mind. Supposing that every system has its sun or suns, can we fancy the effects of a green or blue or violet sunlight—a light unmixed? To employ the words of Sir John Herschel—“It may be more easily suggested in words than conceived in imagination what variety of illumination two suns, a red and a green, or a yellow and blue one, must afford to a planet circulating round either—or what charming contrasts and graceful vicissitudes a red[Pg 550] and a green day, for instance, alternating with a white one and with darkness, might arise from the presence or absence of one or other or both above the horizon.”
Lost and New Stars.
We may have perhaps read the “Lost Pleiad,” and wondered what has become of the star supposed to have dropped out of the cluster so well known in the constellation Taurus—the Pleiades. There are seven stars, of which six are visible to the average eye, and the ancients used to declare that one of the seven sisters (the daughters of Atlas and Pleione) hid herself because she had married a mortal, while all her sisters wedded gods. It is not improbable that one of the seven, formerly distinguishable with the unassisted eye, may have disappeared or been lost; but it is certain that strong eyesight can see more than seven now, and in the telescope there are about one hundred.
And it is a fact that some stars whose places have been carefully marked in the catalogue have subsequently disappeared. Many errors may have been made, and stars put down where no star existed, so a succeeding observer has not been able to find the star indicated. But, on the other hand, we may admit that stars have been lost to sight, and to compensate us for any such disappearances new stars are frequently observed, and these are very remarkable phenomena. About 121 B.C. Hipparchus perceived a new star, which was visible even in the daytime, and on subsequent occasions others came into existence—viz., in the years 945, 1264, and 1572. In the last-mentioned year Tycho Brahé suddenly perceived the new star, which was at first very brilliant. It grew fainter and fainter, after first gaining in intensity, and disappeared entirely in 1574; and at other times stars have been seen which remained only for a short time, and then disappeared.
The star discovered by Tycho Brahé was seen by him when walking across the fields one night, and he encountered peasants who were gazing at the new luminary. It was so bright that it threw a shadow from Brahé’s stick. The new arrival appeared in “Cassiopeia,” under the lady’s chair, forming, as pictured in the diagram, an irregular square. The strange star is the largest.

Some stars exhibit extraordinary fluctuations, and one discovered by Mr. Birmingham in 1866, decreased rapidly and sank away to about the tenth magnitude, and then got brighter, and again diminished in splendour. The “Eta” Argûs has also been subjected to many fluctuations likewise, and such alterations have gained for these luminaries the name of “Variable Stars.”

In the accompanying little chart there will be perceived two particular stars, named Algol, “the demon,” and Mira “the wonderful.” The latter is[Pg 551] the most celebrated for its variable qualities, and its cycle of change occupies nearly one of our years. For a few days it appears very bright, and then fades away for about three months, to disappear for five months, and then it reappears again, increasing in brilliancy up to the second magnitude for another three months or so. Some people account for these phenomena by stating that the sides of the star being less luminous present the dark and light portions in rotation; but we can give no satisfactory explanation of the reason, unless it be caused by an aggregation of spots upon its surface, like sun-spots on our sun, or perhaps by eclipse.
Star-Clusters and Nebulæ.

Nebulæ and Star-clusters are numerous in the heavens. The most important are the Great Nebulæ in Orion and in Andromeda. But there are other very beautiful “patches” of luminous matter or cloud appearances composed of minute stars invisible to the naked eye. We annex specimens of the Nebulæ, one or two having been already inserted. There must be thousands of these star-clouds, and they have been classified by Sir John Herschel from Sir William’s discoveries as follows:—
(1) Clusters of stars, in which the stars are clearly distinguishable, divided again into regular and irregular clusters.
(2) Resolvable Nebulæ, which may be separated into distinct stars under powerful telescopes.
(3) Nebulæ, in which there is no appearance whatever of stars, divided into classes according to brightness, etc.
(4) Planetary Nebulæ.
(5) Stellar Nebulæ.
(6) Nebulous Stars.

We learn also from the foregoing authority that Nebulæ affect a certain district; that is, they have, as it were, a preference for it, and are not distributed in a random manner over the heavens, and are found in Leo, Leo Minor, Ursa Major, Canes Venatici, Coma, Böotes, and Virgo, and more sparingly in Aries, Taurus, Orion, Perseus, Draco, Hercules, Lyra, etc. Nebulæ are found associated with stars, as is the case with η Argus; these are called nebulous stars, and in the case of this particular star many very interesting investigations have been made. The Nebulæ are as equally variable as the stars they surround.

What is termed the Nebular Hypothesis was put forward by La Place, and by it he endeavoured to account for the regular development of the stellar system, which is supposed to have originated from an immense nebular cloud. This immense mass would rotate and contract, and the outer portions would separate and develop in rings like Saturn’s rings. Then the rings break into separate portions, and each portion condenses into a planet, or the small “bits” travel round the sun like asteroids, and in this manner various systems were formed. This theory was considered to be quite exploded when stars were discerned in nebulæ by the more recent telescopes; but then the spectroscope came to our aid, and it was discovered that there were some nebulæ which are simply masses of glowing gas or aggregations of stones which are dashing against each other in so forcible a manner as to produce heat and luminosity. Mr. Lockyer appears to favour the latter theory as to nebulæ.

Mr. Proctor, however, has put forward a hypothesis that the star or meteor showers are the original cause of the sidereal system, and this rain of meteors has fallen for all time, gradually consolidating into orbs. The fact that the constituents of sun, earth and planets, comets and meteors being fundamentally the same lends probability to this hypothesis, which is fully explained by the author.
The Milky Way.
The Galaxy is familiar to all readers, and although visible all the year round, is perceived more plainly in August, September, and October, or at the beginning and ending of that period. This zone of stars was of course well known to the ancients, but it is to Galileo that we owe the first important information about the Galaxy; he decided that it was formed of stars. Sir John Herschel investigated the subject very closely, and to him much of the information concerning the Milky Way is due.
It is not very distinct in the north, but as it advances from Cepheus southwards by the Unicorn, it gets clearer, and opens out in Argo, and descends still south, becoming brighter near the Southern Cross. It then passes northward again, dividing into two branches, one of which dies out, and then over Sagittarius, and so on to Cygnus, then to Casseopeia and the starting-point. The number of stars in the Galaxy is about 18,000,000.

In this wonderful zone of stars the centre of our system, the sun, is placed. It was supposed to be divided as in the diagram above; the inner portion being the stars seen in their thickness, and the outer ring representing the stars viewed in the direction of the length and breadth. But afterwards, Herschel modified his opinions respecting the Milky Way, and since his death many astronomers—and Mr. Proctor more particularly—have devoted considerable time to an examination of this wonderful zone of stars; which, it must be remembered, is not a continuous stream; it is a series of luminous patches. On this point Professor Nichol says:—
“It is only to the most careless glance that the Milky Way appears a[Pg 554] continuous zone. Let the naked eye rest thoughtfully on any part of it, and if circumstances are favourable, it will stand out rather as an accumulation of patches and streams of light in every conceivable variety of form and brightness; now side by side, now heaped on each other, again spanning across dark spaces ... and at other times darting off into the neighbouring skies in branches of capricious length and shape, which gradually thin away and disappear.”
The Milky Way has its greatest breadth in the “Swan,” and in the “Eagle” constellation it divides itself. In the “Southern Triangle” the zone is brightest, and in the “Southern Cross” the hole or space, termed by sailors the “Coal Sack,” is very distinct. It then contracts and expands, and there is in Argo another gap. Then it is lost for a space, then it branches out, and soon crosses the Equator, dilates, contracts, opens out again, and so returns to the “Swan” again.
Philosophers have frequently discoursed upon this phenomenon, but all statements must remain more or less speculative. From Kepler’s to the present time astronomers have been considering the Milky Way, and when the Nebular theory was given up, when the Galaxy was found to be composed of stars, there was, as we have noticed, the idea of the ring and the cloven disc. Mr. R. Proctor has likened the Galaxy to a coiled serpent, and considers the openings in the Milky Way as evidence that the stratum of stars is limited, and that here we can see beyond it. In fact, it would appear that it is a very complicated question; and as the zone itself is complicated “with outlying branches beyond the range of our most powerful telescopes,” so an actual knowledge of the Milky Way is beyond us at present. It is composed of most extraordinary aggregations of stars, which appear not only impossible to count, but each one to be independent of the other. Thus we must conclude our rapid survey of the Milky Way, and close with Mr. Proctor’s remark in his “Universe of Stars.” “The sidereal system,” he says, “is altogether more complicated, altogether more varied in structure than has hitherto been supposed. Within one and the same region co-exist stars of many orders of real magnitude, the greatest being thousands of times larger than the least. All the Nebulæ hitherto discovered, whether gaseous or stellar, irregular, planetary, ring-formed, or elliptic, exist within the limits of the sidereal system. They all form part and parcel of that wonderful system, whose nearer and brighter parts constitute the glories of our nocturnal heavens.”
And a little reflection will show how true this is. Not very long ago in the world’s life the solar system was supposed to consist of one sun with a few planets wandering around him. Then some more were found, and they were called “satellites.” For a long time man fancied he had reached the “ultima thule” of astronomy in these depths; but the whole idea was changed when it was discovered that beyond Mars there lie the asteroids and the host of bodies in this solar system which we cannot do more than allude to. Then when we consider that this “sun” of ours, which we think[Pg 555] so enormous, and which keeps in subjection so many heavenly bodies, and illuminates them; when we reflect that there are in space, and visible, stars many times larger than our ruling star, each a sun, and that our sun would, if put where the great Sirius glows, be but a speck in the firmament, and his system invisible to our eyes, we may well wonder at the magnitude of the subject, and the Infinite Wisdom and Power “that telleth the number of the stars, and calleth them all by their names.”
How to read the Sky.

A few particulars, to enable a reader to identify the most prominent stars, may be given as starting-points from which some few excursions into the spangled heavens may be attempted. But the suggestions must be considered with reference to the ever-varying directions of the supposed lines in consequence of the daily revolution of the sphere. We have illustrated this in the cut in the margin, wherein the Lesser Bear is shown as swinging round the Polar Star in different positions. Sometimes the lines of direction will be vertical, sometimes inclined, but all retaining their relative positions.
We have already learnt that the “pointers” of the Great Bear indicate the Polar Star in the Lesser Bear, and we can (roughly) estimate the distance between the pointers as 5°. This will give us the distance between the pointers and the Polar Star as 29°. By following an imaginary line through the two northern stars of the “Waggon” (the Bear) away from the “horses,” we shall find Capella about 50° away.

If we pass from the first star next the waggon of “Charles’s Wain” to the Pole Star, and past it, we shall arrive at an irregular W. This is[Pg 556] Cassiopeia, about as far beyond Polaris as the Bear is below it. When the latter is low, the former is at the zenith, and so on.
A line drawn from the Pole Star through the end star of the Great Bear leads to Arcturus. A line taken from Arcturus for about an equal distance will, with the Pole Star, make a triangle with Vega. The Polar Star may be called the Apex.
Regulus may be found southwards by drawing a line through the two first stars of the square in the Bear (opposite the pointers). From Vega, almost opposite the Pole Star, and through it about twice as far away on the other side, is Sirius, a brilliant “sun.” Procyon will be found to the westward of Regulus about 30°. From Procyon to the Pole Star a line will pass through Pollux and Castor.
Another line from the pole star through the middle of the three “horses” in the “Wain” will reach Spica Virginis about 70° beyond. So we can describe a large triangle with Spica, Regulus, and Arcturus, at the angles. Regulus is the apex, Spica and Arcturus a short base line.

From the pole star through Capella, passing between Betelgeux and Bellatrix, we shall describe a line leading to the three stars of Orion’s belt. Between it and the Pleiades is Aldebaran.
There are many other stars which could be indicated; but on a fine evening, if the observer will mark them upon a piece of paper, placing the pole star in the centre, he will be able to add to his star map very rapidly.
In the foregoing chapters of Astronomy we have seen how the earth and other planets move around the sun; we have glanced at the “fixed” stars and their groups, termed the constellations, and have noted the planets and their characteristics, with many other interesting facts. There is yet a great deal to be learnt, and much study will be required with daily (nightly) observations before the young reader will obtain success as a student of astronomy; but there is no study so interesting. We have seen what a very small portion of the universe is occupied by our solar system, and what a speck our earth is on the plain of creation. We find ourselves on the border-land of the incomprehensible, and we are lost in speculations upon the unseen.

CHAPTER XLII.
NEW ASTRONOMICAL APPLIANCES.
A CELESTIAL INDICATOR—ASTRONOMICAL OR COSMOGRAPHICAL CLOCK—A SIMPLE GLOBE—A SOLAR CHRONOMETER.
Having said something concerning astronomy, we will give a few instructions respecting the instruments not already described, and make some observations, supplementing our directions in the previous chapter, for many people will be glad to learn how to read the evening skies.
Here we have an apparatus which will prove useful to amateurs; it is a sort of celestial indicator by Mauperin, and will facilitate the finding of every star or constellation, when the apparatus has been made ready by pointing the rod, T, in the direction of the object it is desired to view. This rod is mounted upon a rod, S, and is movable upwards or downwards or sideways, and in the last-named movement it will carry with it an indicator, I, which slides over the chart or diagram of the heavens. The two arms of this indicator are always parallel to the plane of the rod, T, no matter in what position they may be on the chart or the inclination of the rod. The extremities of this rod are terminated by an eye-slit, and by a crescent respectively.
When the apparatus is set, all one has to do is to look through the eye aperture, O, and view the star which we have chosen in the centre of the crescent, C. This star will be found named in the space between the arms of the sliding indicator, I.
It is easy to perform the operation inversely—that is to say, to find in the sky, by means of the sighting-rod, T, the stars we have chosen on the chart between the prongs of the indicator. The chart represents exactly the heavens as we see them, and this new mode is opposed to the manner generally adopted with celestial charts, and is very important, for it obviates the necessity of holding the map above one’s head, its face downwards.
As we have already showed, it is not difficult to find the Polar Star and the Great Bear. The latter is readily recognised by its seven stars, and the Lesser Bear glides around the pole as shown in the diagram on the preceding page (fig. 629). Now let us see how the celestial indicator will work.
Let us take the apparatus into the open air, and place it upon its[Pg 558] tripod stand. The upper portion will be found movable by loosening the screw, V. By another simple arrangement the table can be slanted, and by turning a screw we can entirely slope the side of the chart where midnight (minuit) is written. Being placed opposite the polar star we take the upper part of the chart by the button, G, and bring it before us by a horizontal rotative movement.

We now place the sliding indicator upon midday (midi), and keep it in that position while working the apparatus—that is, until we have caught sight of the polar star in the centre of the crescent, C, by means of the eye aperture, O. We have now obtained the meridian, and care should be taken to tighten the screw, V. Then the table is raised to its fixed place[Pg 559] upon the support; it is regulated according to the latitude of the place, and the apparatus is then “oriented.”
The upper disc is an elliptical opening, or aperture, which contains for every moment the stars visible upon the horizon, and the circumference is furnished with a graduated scale of hours divided into five-minute divisions, and this is fixed upon the apparatus. The dotted line between the midday and midnight points gives the meridian.
The disc placed underneath is the celestial chart, on the circumference of which we shall find the days of the months. It can be moved around the rod, S, which represents the axis of the earth around which the heavens are supposed to revolve. When the stars have to be observed, the day of the month has to be brought to the time at which the observation is about to be made. We can easily read off the chart by looking through the eye-piece as already explained. Every five minutes it is necessary to move the chart one division, which indicates that five minutes have passed; (other stars are, of course, arriving). The apparatus can be packed away when done with, or the bearings taken, and then the trouble of getting it into position again need not be repeated.
A small lamp, L, throws its light upon the chart in such a way that the eyes of the observer are not incommoded, while the table is fully illuminated. It can be placed at L´ if necessary. The inclination varies according to the latitude of the place when the observations are made. There is an arrangement underneath which admits of this inclination according to longitude.
The apparatus can also be made available to ascertain what the aspect of the heavens will be upon any particular evening of the month. We have only to place the chart at the day and hour, and we shall then see upon it all the stars visible above the horizon. We can thus find out at what time the stars rise and set, and those which do not set—to find the hour at which they pass the meridian (the line drawn between midday and midnight upon the chart), and the time of their appearance on the horizon. When the sliding indicator, I, does not show a star that is discoverable in the sky, the observer may conclude that he is viewing a planet. This apparatus is well adapted for beginners in astronomy, as no deep preparatory study is necessary, and the tyro can read the sky as easily as he could read a book.
A Cosmographical Clock.
We have, in the foregoing chapters upon Astronomy, endeavoured to give the reader some idea respecting the inclination of the earth and its rotation, and writers have often endeavoured to devise an apparatus which shall show the position of the globe in space, its diurnal motion—even its inclination and the succession of seasons in its revolution round the sun. But such reproductions of simultaneous movements have hitherto been obtained only on a very large scale, which find their place well enough in the museum or lecture-room, but which it is quite impossible to utilize[Pg 560] in our sitting-rooms, on our tables, or chimney-pieces. Besides, the usual apparatus employed is a very costly one, and only serves for occasional representation; it will not keep the facts constantly before the observer in the manner of a clock showing the time.
But for all who are interested in Astronomy, or in Cosmography, or even for a young person who desires merely to understand the reality of the earth’s motion and how our earth is placed in the universe—for any one who deems it of use that he or she should be able to see the signs and the seasons, and the days and years, and how the earth revolves, may obtain an astronomical or cosmographical clock, which will tell him or her how the “world wags”; a useful as well as an ornamental timepiece.

Now this is precisely the result which the talented inventor of the astronomical clock has arrived at. M. Mouret devoted a great portion of his life and all his available means to the realization of his great idea, and, sad to say, he died miserably in an attic the very day before his great and deserving effort brought him the reward for which he had so painfully striven and devoted himself to by a life of self-denial and labour.
M. Mouret communicated to his globe the astronomical movement, which our earth possesses, by the aid of clock-work, which conveys to it, second by second, at each stroke of the pendulum, the double movement of rotation and progression. The globe turns upon its axis in twenty-four hours, and thus one can perceive, without any mental effort, the rotation of our planet, and the portions of the globe which come under the influence of the sun in rotation, just as they do actually on the earth. Not the least interesting attribute of this ingenious arrangement is the fact that during breakfast or dinner one can see the displacement and revolution of the earth with reference to the sun to all people in the world. Here, on the meridian, all are at midday. There, on the left, near the circle which defines the limit between day and night, the sun is rising and day is beginning; opposite, on the right, the sun is setting and day is closing. Yonder is the Pacific Ocean in full daylight, while almost every continent is in darkness and the inhabitants wrapped in slumber. Now the Chinese are opening their eyes, and the Asiatic and European continents will soon be illuminated and awake. This is the movement of the world as it has ever been since time came into its calculations.
The ingenious inventor, who wished to make a clock of his apparatus, and not being able to change its place on the earth from day to day as the time changed, very cleverly reproduced the sun’s movement of declination by making it describe a double cone at the axis of the globe. At the equinoxes the poles are in a plane, and equal day and night are shown. At the winter solstice the north pole is inclined backwards at an angle 23° 28´, and our hemisphere is in the winter season. We have then only eight hours’ daylight and sixteen of darkness; six months later the pole is inclined towards the sun, and the southern pole is plunged in darkness. We have the long days and the southerners the long nights. An upright dial shows the time of the country in which the globe may happen to be, and one can ascertain at any moment what time it is anywhere else. A horizontal dial indicates the day of the month, and changes every day in a manner corresponding with the movement of the earth around the sun, reproduced by means of the arrangement with the double cone. The spectator is supposed to be turning his back to the sun.
We may add that these movements are all self-acting, and there is no need to interfere with the clock, which is wound up like ordinary timepieces. By an ingenious forethought the inventor provided that the sphere should be independent of the other movements, and it can be used for demonstration in the hands of the lecturer, and be explained with all its motions without in any way disarranging the clock-work. The globe must, of course, when replaced, be put exactly at the correct day and hour.
A Simple Terrestrial Globe.
A terrestrial globe without any mechanism, so long as its axis is parallel to that of the earth, exposed to the direct rays of the sun, represents our planet with its recurrence of day and night.
The figure (634) shows us a globe without any support. The axis is north and south, and makes, with the horizon, an angle equal to the latitude of Paris, if the support, A B, be horizontal. To make the axis of the globe parallel to the axis of our earth, the line, N S, must correspond to the meridian of the place; this can be done with the compass, for instance.
The solar rays always illuminate one-half of a sphere, no matter what its dimensions. If we look at the illustration we shall see that the line of separation between the light and dark portions of the globe corresponds with that in our earth. This globe, then, tells us the passage of light and darkness for the day, and even for the moment of the day, when it is turned as the earth moves. The place examined should be placed in the meridian of that place (Paris, for instance), and occupy the most elevated spot on the globe. The earth is then in just the same position, and daylight and darkness are shown exactly as they exist on the earth at the time.
If this globe be then observed for a few minutes, the sun will be seen[Pg 562] rising and setting, as it were, in various places (we must remember we have concentrated the sun’s rays, not a lamp, upon the globe). The places on the right, if the observer be placed facing the sun, will come out of the shade, and those on the left will enter it. The former are then really enjoying the sunrise, and the others are actually witnessing his setting.
The globe represented, making the double revolution of our planet in the year, will reproduce all the actual phenomena of day and night as taking place on the earth itself if we stand at a little distance so as to observe it all at once.

Of course, the employment of this simple apparatus should not exclude more complicated ones, for the former can only be used on a fine bright day. But the advantage claimed for it is that in it we can imitate nature exactly. Illuminated, as it is, by the real sun, the portions of light and shade are indicated by the rays and not by a metallic circle.
In order that the line of demarcation may be exactly defined, it will be necessary that the sun’s rays be concentrated upon the globe, and that no lateral or vertical light be admitted. The curtains should therefore be so arranged, and the blinds pulled down to a certain point, and if the stand or support be painted black it will be found an advantage. If the globe be[Pg 563] a small one, it will be sufficient to place the stand upon an ordinary table, without verifying the horizontal plane. With a large globe the arrangement must be very exact.
A Solar Chronometer.
M. Flechet’s chronometer, of which we give an illustration, is a kind of equitorial reduced to its most simple form. It is possible to ascertain the exact time by it very easily. It consists of a disc, AB, divided into twenty-four hours and fractions of hours. This disc turns upon itself around an arc, CD, which has a direction parallel to the axis of the world, and can be moved on a joint, E, according to the latitude of the place; F is a lens which can be moved and presented to the sun at any time, forming the centre of a concave and exactly spherical plate represented at GH.

When the instrument is fixed so that the axis, CD, is parallel to the axis of the globe, the disc, AB, is turned so that the centre of the image of the sun, produced by the lens, shall fall at m. The real time is found by an examination of the position of the index, A, upon the hour graduations of the disc. A French writer, Ch. Delounay, has mentioned this instrument, and considers it easy of arrangement, exact in time, and very useful.
CHAPTER XLIII.
PHYSICAL GEOGRAPHY.—I. GEOLOGY.
GEOGRAPHY AND GEOLOGY—THE EARTH’S CRUST—ORIGIN OF THE EARTH—DENUDATION AND EXCAVATION BY WATER—ROCKS, GRAVEL, AND SAND—CLASSES OF ROCKS.

When we were at school, and learnt the various countries of Europe, we had maps showing us the several divisions of one realm from another; the mountains, lakes, and other prominent features of the continent were learned and repeated, but we, maybe, seldom, perhaps never, bestowed a thought upon the formations of the mountains, and the manner in which rivers ran down into and through lakes to the ocean. There were the mountains, there were the lakes and rivers, and capes, and headlands, and there they are still, to all intents and purposes, the same to see, to climb up, to sail down, as the case may be. But the map of Europe has undergone a visible change. Territory has changed hands. Germany has gripped France, England has got Cyprus, Turkey has been dismembered, and Austria is annexing territory. This study is called Geography,—Political Geography,—for it marks the political boundaries. The knowledge of the formation of hills, headlands, lakes, rivers, seas, their causes, constitution, and effects, how they rose,[Pg 565] how they exist and wax or wane during the course of centuries is Physical Geography, which we propose to consider.
This tree of knowledge includes some very important branches, almost parent stems. As a magnificent oak spreads forth its brawny arms, with smaller branches and twigs, each of these great branches being as large as an ordinary tree, so Physical Geography includes other arms such as Geology, Meteorology, Botany, and Physiology—even Astronomy in its comprehensive embrace. We find it is a difficult task to separate these kindred sciences from the great tree. We may have therefore to refer to earth, air, and water, and their various forms in hills and mountains, wind, vapour, rain, glaciers, and sea. We must learn how this earth has been gradually cooled, and what the various stages of its growth have done. We must consider plant and animal life upon our planet, and how the atmosphere affects them. All this is Physical Geography, and its satellite sciences of Geology, Meteorology, “Climatology,” Botany, and Physiology.

“Everything must have a beginning,” and the earth must have had a beginning, although the actual manner of the physical creation of the planet is a disputed fact. We are not about to discuss the religious side of the question, although we should undoubtedly find that Biblical and Geologic teaching run side by side towards the same end, and the testimony of the earth and sky bears witness to the Divine hand that created the universe, which we can trace back to the dim and distant ages when “the earth was without form and void, and darkness was upon the face of the deep.”
With this brief preface, let us consider some of these aspects, and pick up interesting facts from the ground.
Geology.
In the chemical and mineral sections of this volume we have heard something concerning the formation of the globe and its composition, its clays, rocks, etc. With these internal arrangements Chemistry and Mineralogy have dealt. Geology tells us about the external surface of the earth, its stones and rocks, and how they were formed, and generally something about the conformation of the crust of the earth, and its history.
When we speak of “crust” of the earth, we do not simply mean the exterior layer of gravel, clay, or stone. The crust is a thick one, and our crust extends just so far as we can cut into it. The surface of the sea can scarcely be termed a crust, but we must penetrate that ever-moving liquid boundary, and touch upon (and examine) what lies down below far beyond the “full fathom five” of the lead line. In this study we must not forget our Book of Nature, which is always open and inviting us to read. We shall see how things are produced, and how our physical surroundings will continue to be produced until the age of miracles returns, and Providence sees fit to interfere with the otherwise immutable laws which He in His wisdom has laid down for the universe.
It will be of no use to go back into space and imagine the world a red-hot fragment of matter, whirling through the heaven around the sun which, as a larger aggregation of burning atoms, kept it, as it now keeps it, in its place. The earth was a globe of liquid fire, or in gaseous state, and the atoms gradually cooled on the surface; the fire is still under our feet. The outer part would by degrees lose all its heat, while the interior remained hot; the planet must then have been surrounded by a steamy atmosphere, and enveloped in vapours condensed from the air through which no light of the sun could by any appreciable degree penetrate.
We can give an example of this, and it will be seen how the surface of the earth gradually became formed from the vaporous condition. If any one will take the pains to evaporate any saline solution in a capsule till it is about to crystallise, and observe attentively the pellicle of salt as it forms on the surface; first a partial film will show itself in a few places, floating about and joining with others, then when nearly the whole surface is coated, it will break up in some places and sink into the liquid beneath, another pellicle will form and join with the remains of the first, and as this thickens it will push up ridges and inequalities of the surface from openings and fissures in which little jets of steam and fluid will escape; these little ridges are chains of mountains, the little jets of steam those volcanic eruptions which were at that period so frequent, the surface of the capsule is the surface of the earth, and the five minutes which the observer has contemplated it, a million years.
The next effect of the cooling of the earth would be the gradual condensation of the vapour of water with which it was surrounded; this falling upon the earth formed seas and oceans, leaving only the higher portions exposed above its level. The clearing up of the dense dark clouds for the first time let in upon the earth’s surface the glorious and vivifying rays of the sun, and this great effect possibly accords with the earliest record in the Bible of the acts of creation: “And God said, let there be light, and there was light.”
This clearing up of the vapours and the subsequent rain no doubt gave rise to terribly grand electrical phenomena—thunderings and lightnings. By degrees the waters got their own way, and then many changes took place,[Pg 567] land and water fighting, as it were, for the mastery, as they are fighting to this day.
But perhaps some reader may not think that the land and water of our earth are thus engaged. A very few minutes’ reflection will suffice to confirm our assertion. Look at the lofty crags in the Alps, for instance; what has shattered those peaks, and sent the masses toppling down in stone avalanches to the lower slopes, and then into the valleys?—Water. Water has been in the crevices, and was frozen there; in freezing it expanded and loosened the crags, which, forced asunder, gave an opening to more snow and ice, and so this powerful leverage, aided by the wind and storm, is disintegrating our mountains.

It is the same by the seashore; the cliffs are wearing away, and the sea approaches; at other places the sea recedes from the land, as coral formation and embryo chalk cliffs are rising under the surface of the ocean. Lakes dry up, and the meadow or farm arises on the site, while other old spots are submerged. No rest, no change of idea, but ever changing in physical appearance, Nature goes on her wondrous way, working now as steadily, as harmoniously, and as surely as she did before time was, and as she will continue to do when time shall be no more!
In our investigations into Geology we cannot enter into many technical details. Our object in these pages is recreation; but we shall, even under these circumstances, find plenty to interest, and sufficient to lead any one[Pg 568] who wishes to pursue the study for himself. We will endeavour so to put the features of the stones and rocks before him that they will be recognized by the passer by. We will try to show how the earth has been built up, and how the great and terrible changes through which our little globe has passed have been effected. In our own islands, Great Britain and Ireland, we shall find traces of all the materials likely to be useful to us in our quest, As has been well said, “Geology is the Physical Geography of the past.”
Constitution of the Earth.

The descent from rocks to stones, from stones to gravel, from gravel to sand, is evident to everyone, so we need not insist upon the fact that sand is powdered rock, and that an aggregation of sand particles makes stones. We have heard in the Mineralogy section that there are certain “earths”—silica, alumina, lime, etc. Of these “earths,” the two former constitute the greater portion of the ROCKS. Lime, also, is very evident, and in limestones fossils or organic remains are abundant. Now we must entirely put away from our minds the old idea that the earth we live on was created at once, or as it appeared to the first human beings. Our planet was prepared for man by degrees during millions of years. We conclude that the earth was originally composed of certain elements, and we find the same elements in the sun. Therefore, supposing (as is supposed) that the earth came from the sun, we have all the material of the globe in a fused state. As the earth cooled, rocks were formed by pressure, and then water came, and now we can read “books in the running brooks, and sermons in stones” at our leisure.

Perhaps as someone reads this he may be walking by the seashore kicking the pebbles or seated upon the sands, the grains of which are so very tiny. He will probably find sand, shingle, and gravel within reach, and perhaps the curious-looking “pudding stone.” Now what can we learn from these stones[Pg 569] or sand grains or that curious bit of conglomerate? Perhaps the reader may be at Ramsgate or Margate or another place where the “white cliffs of Albion” glisten in the sun. Take up a piece of chalk and examine it. It is soft and soils your hands, and you will throw it away, perhaps—but don’t. Take it home and put it under the microscope or a good magnifying glass. What do you see?


You will find the remains of animals—that is, shells and tiny bits of coral packed close together. Under the microscope they will become more separated, and the grains will be distinct fragments of shells, etc. If this little bit of chalk be composed of marine animals’ shells, of course the whole cliff is composed of the same kind of material. But how did the shells get into the chalk? Shells are chalk—carbonate of lime; lime was deposited at the bottom of the sea, and the infinite millions of minute animals formed themselves shells, and left them to be piled up by Nature’s forces into cliffs during countless ages.
Yes, but how did the lime get into the water to make the shells? We will endeavour to explain. Rain, when falling, takes some carbonic acid from the air, which we know contains it. This acts upon the lime in the rocks (lime is oxide of calcium, and calcium is an element in the earth), so we get a bi-carbonate of lime (soluble in water), which rises from the rocks in springs. These springs and their streams deposit lime, as we can see in caverns where we find stalactites and stalagmites. The lime is transmitted[Pg 570] to the ocean, and absorbed by the crinoideans and molluscs which produced shells. These shells hardened and crystallized became limestone, and whole mountains are formed of this “organic” rock, which is used for so many purposes.

We have spoken of Organic Rocks, but there are others, and we ought, perhaps, to have spoken of that kind before the chalk put them aside. Let us go back to our sandy shore again and look at the Sedimentary Rocks, which are the very first formation. We have all seen sandstone, and visitors to the South Devon Coast will remember the red cliffs near Dawlish and Teignmouth. These are red sandstone—not the very “old red” so pleasantly written of by Hugh Miller, but at any rate sandstone, and composed of grains of sand. When we were at Dawlish last year a piece of the sandstone had fallen on to the beach, and when the waves came up that stone was no doubt gradually washed away into sand, and then fell to the earth as sediment.
We said something a few pages back about the wear and tear which is always going on: the mountain is worn away—a mass falls, it is broken into smaller pieces; these are carried by a river; the mud is deposited, and the finer particles are ground and rounded into gravel, and finally sand. Beneath the current of the river, and at the bottom of a lake or sea, these sediments (mud, etc.) accumulate one on the top of the other in regular series called strata, and then the weight and pressure acting with the soluble mineral deposits always washing down, consolidate and bind the loose sand-grains into stone, which, in the course of ages, hardens. The stones thus formed from sediments such as gravel, mud, and sand, are termed Sedimentary Rocks; they have become rocks by enormous and continuous pressure. Thus:—
Sands have become “Sandstones”;
Gravel has become “Pudding-stone” (Conglomerate);
Mud and clay have become “Shale”;
Calcareous deposits have become “Limestone”;
Vegetable deposits have become “Coal.”
So we have sandy, clayey, limy, flinty, and corally rocks under long names respectively—Arenarious, Argillaceous, Calcareous, Silicious; and we may add Bitumenous and Ferruginous—Irony Rocks—to the list.
Speaking of sediments, it is curious to note the different colours of the Arve and the Rhone which meet near Geneva. The white sedimentary Arve can be traced for a long distance beside, not mixing with, the blue[Pg 571] Rhone. The same effect can be traced where the latter river enters the Lake of Geneva. So the land is being perpetually carried away and deposited; and where water gains on land there is somewhere else always a corresponding elevation to compensate it. Thus places disappear, and the sea washes over the site, as on the Kentish Coast, where Earl Godwin’s land was inundated, and new land is reclaimed or is elevated from the sea to make up the balance.
We have spoken of sedimentary and organic rocks. There is yet another kind called igneous, or fiery rocks—those upraised by volcanic action. Of the igneous rocks the crystalline have been evidently in a fused condition. Granite is an example; lava or basalt is the usual term for volcanic rock, and the basaltic caves of Staffa and the Giants’ Causeway bear testimony to the igneous or volcanic origin of the surroundings. The pillars and fantastic rocks of Ireland and Scotland which are so remarkable, are simply lava, which was erupted in a molten state, now cooled and contracted into blocks of curious regularity of form.

Granite, already referred to, is another igneous rock, and must have been forced upwards; for as an igneous rock granite has cooled beneath the crust of the earth, throwing out arms, while melting, into other formations, and frequently being found in mountains. There is another kind of igneous rocks formed by the continuous accumulation of the ashes, etc., vomited forth from volcanoes. Masses of mountain are thus produced in the course of years, and the material thus formed is called tufa, or tuff, when consolidated; and this (now solidified) is what caused the destruction of Pompeii and Herculaneum.

So we have two classes of Igneous Rocks, the Crystalline and[Pg 572] Fragmental (or the “Plutonic” and “Volcanic”), including basalts, pitchstones, pumice, trachytes, granite, syenite, etc.; and, on the other hand, tuff and “volcanic” breccia, with felstones, porphyries, etc., which have been classed as intermediary.
Of these three classes of rocks, the sedimentary and the organic compose the greater portion of the earth. We will now glance at the crust of the earth and its various formations.

CHAPTER XLIV.
CRUST OF THE EARTH—GEOLOGICAL SYSTEMS—EOZOIC, PRIMARY, SECONDARY, TERTIARY, PREHISTORIC FORMATIONS.

The crust of Great Britain has been carefully examined, and from the results of investigations at various periods, the earth has been divided into a series of strata which follow the same order of succession. Sometimes certain strata may not be present, and they may be replaced by others, but the same order of succession will be found. The order is as follows, commencing at the lowest. The illustration is taken in the opposite direction:—
| “Eozoic.” | ⌈Laurentian ⌊Cambrian |
Until recently believed to be without traces of living creatures; hence “Eozoic.” |
| Palæzoic, or Primary. | ⌈Silurian ⌊Cambrian ⎢Carboniferous ⌊Permian |
Shell-fish, seaweed, ferns, fish, low reptiles. |
| Mesozoic, or Secondary. | ⌈Triassic (Upper Red Sandstone) ⎢Oolitic ⌊Cretaceous |
Birds, marsupials, reptiles. |
| Kainzoic, or Tertiary. | ⌈Eocene ⎢Miocene ⎢Pliocene ⌊Post-tertiary |
Superior life. Mammals, with great vegetable life, on to plants and animals now existing. Man. |
| Quaternary. | Recent—Prehistoric |
The Palæzoic Systems.
Laurentian System. It will be perceived from the above list that the Laurentian Rocks are the oldest. The name is derived from the St. Lawrence formations, and was given to the strata by Sir William Logan. They are metamorphosed rocks older than the Cambrian. These rocks are sedimentary, of very old deposition, and of a crystalline nature, consisting of quartz, gneiss, etc. The granite was probably formed by the fusion of its component constituents, quartz,[Pg 574] mica, and felspar, which become crystallized by the excessive heat. For a long time no traces of organisms could be detected in this or the Cambrian systems, but modern research has been rewarded with a little success. The original deposits of micaceous gneiss, etc., have been altered, and many true igneous rocks, such as syenite and granite, are found in them. These very old rocks must have been originally deposited in strata converted by heat and pressure into crystalline rocks. These rocks have been divided into two series, under the names of lower and upper Laurentian. They are metamorphic, and consist “mainly of gneiss interstratified with mica-schist, with great beds of quartz, and massive beds of crystalline limestone, of which one varies from 700 to 1,500 feet in thickness. Conglomerates also occur, and there are vast deposits of magnetic and specular iron. Graphite, or blacklead, is disseminated in strings, veins, and beds through hundreds of feet of the lower Laurentian, and its amount is calculated by Dr. Dawson to be equal in quantity to the coal seams of an equal area of the carboniferous rocks” (Nicholson).



Hitherto, no distinctly recognisable fossil has been discovered, with the important exception of the Eozoön Canadense, which has been pronounced to have been a gigantic foraminifer, growing layer upon layer, and thus forming reefs of limestone; the subject, however, is still a matter of dispute. The eozoön was discovered by Mr. J. M’Mullen in 1858 in Canada.

Granite was at one time considered to be the true primitive rock. Gneiss is a word of Saxon origin, and consists of the same materials as granite in different proportions. Mica-schist is made up of two of the same constituents as the granite and gneiss. They are without fossil traces.
The Cambrian system of aqueous origin may be said to contain evidence of the dawn of organic life. It is part of the clay-slate system, and the term “Cambrian” is taken from the ancient name of Wales, where slate is plentiful. Mica-slate is also very important. These Cambrian rocks are of the next oldest formation to the Laurentian, and all the various deposits may be examined in Wales, where also traces of volcanic and ice action may readily be perceived. In the pass of Llanberis one immense ice-borne block is very prominent; no agency but ice could have put it there as it rests. It is estimated that the Cambrian and “Lower” Silurian rocks are from 20,000 to 30,000 feet in thickness, and must embrace a very lengthened period. The fossils of these formations show that zoophytes and certain primitive crustacea lived in the remote ages when these rocks were formed by sedimentary deposition. We have scarce a trace of plant-life. The organic remains include annular worms, the first arrangement of the articulated animals according to Cuvier. The flora and fauna are, of course, very low in the scale of creation, when land and sea were so differently arranged.

A, Fossiliferous grits (Bala series); B, Greenstone (intrusive); C, Porphyry; D, Volcanic ashes, sometimes calcareous and fossiliferous Bala limestone.

The Silurian system was so named by Sir. R. Murchison, after the territory formerly occupied by the Silures, but the system is, of course, universal. We have here sandstones, limestones, and shales, deposits lying upon the Welsh slate. The Upper and Lower Ludlow beds, and the “May Hill” sandstone, then the Lower Silurian, with Caradoc beds, and the Tremadoc slate, etc. In this system volcanic action is observable, and all the organic remains are those of marine animals, such as corals, shell-fish,[Pg 576] marine worms, encrinites, molluscs, and other zoophytes in great variety. We find also a number of graptolites, trilobites, echinus (sea-urchin), terebratula, and many other forms.


The Trilobites were amongst the first creatures inhabiting our globe, and it is a curious fact to contemplate, that their eyes (fig. 655) should have been preserved perfect; they present one of those wonderful objects which carry one’s thoughts backwards to the early ages of the world, probably many millions of years, and yet it is found by the peculiar structure of the eyes of these Trilobites that they were placed at the bottom of the sea with perfect power to look upwards at the light of the sun through the transparent waters. The same hand and the same power had then Divine care and solicitude for the well-being of His creatures, as great as He has for those of later ages, and these animals are mentioned in Genesis—“Let the waters bring forth abundantly the moving creature that hath life.”

Thus we see that ages of comparative quiet succeeded the first great contraction of the earth’s crust, probably millions of years, during which time the tides and currents of the ocean had to wash and wear down all the thousands of projecting rocks or inequalities, and dissolve (as before described) all the lime, depositing the sand and clay in those immense strata which form the old-named “transition series”; this appears to have taken place over nearly the whole world at that time, and ages upon ages must have elapsed to form such deposits as the sandstone, claystone, and limestone, in alternation, forming the “Llandilo,” “Caradoc,” and “Wenlock” strata, more than a mile in thickness; these are by some geologists reckoned among the primary series (by some called the “transition rocks”), and in England form the “Cambrian” and “Silurian” systems which are so rich in minerals and metallic veins.

The Old Red Sandstone, or Devonian System, is the next of the series of layers which built up our earth, but a great gap of years separates it from the Silurian. We find the “Old Red” in the Mendips and in[Pg 577] Scotland. The rocks in the West of England are apparently of later deposition and of marine origin, while the “Old Red” is apparently a fresh-water deposit. It is very “arenaceous,” and owes its tint chiefly to iron, although there are circumstances in which it appears neither as a sandstone nor with a red colour; but red sandstone describes the true formation very accurately.

In this water-deposited system, whether in lakes or by the sea, we find a considerable advance upon the Silurian. We have flora in more variety—seaweeds and ferns. The remains are all aquatic. We have nothing higher in the scale of creation than the fish, the first vertebrates; and judging by varieties a very considerable time must have elapsed during which the Old Red Sandstone was deposited. The dipterus—or double-winged—is herewith shown as an example of the fossil fish of the Old Red Sandstone period.

It is curious that no remains of any land-inhabiting animals have been discovered in this system—whether in the Old Red or the Devonian formations (the Lower and Upper Red Sandstones). We can only distinguish the remains of aquatic animals or plants. We may picture the great cuttle-fish, the nautilus, and the dipterus, with various orders of[Pg 578] mollusca, and the gradual approach to the crustacea, but no terrestrial animals have been discovered. We may take it for granted then that the Old Red Sandstone and Devonian systems are different—the former being found in Scotland and parts of England, and formed of deposits in fresh or brackish water, while in the Devonian system the marine deposits are corals, and all the indications of ocean life, separated from the great inland lakes by a range of hills. Neither of the terms (Old Red Sandstone or Devonian) limit geographically or descriptively the formations of this system. All the rocks are clearly distributed between the Silurian and the Carboniferous. The invertebrates in this last system have not developed very much, but corals are very abundant, and fish of some armoured species are plentiful and curious, while the crustacea were enormous.

We now arrive at the most important of all the rock formations, the one to which we owe our national prosperity—we mean the Coal System.
The Carboniferous Formation.
While the foregoing depositions were being made the earth was still undergoing changes. The sandstones were deposited, and the corals making use of the lime carried into the waters began to build and form masses of limestone under the sea, pushing back the water and changing the forms and positions of land and water. All this went on apparently very quietly—volcanic action was not very frequent—the water was warm. But sometimes earthquakes would heave up the submarine formations into mountains, and therefore we find the fossils of the tiny sea-animals on the hills. Extensive swamps were formed by partially retreating sea-water, and their vegetation[Pg 579] became luxuriant. Tree ferns and all the floral appearance of the tropics grew up and formed dense forests, far thicker than any we know of at the present time. It will readily be understood that the condition of the atmosphere must have been particularly favourable to the growth of plants, and therefore not suitable for air-breathing animals. Heat and carbonic acid must have been greatly developed.

We can now perceive how the gradual filling up of the earth for man’s reception was taking place. The rain was taking carbonic acid from the air, for the dead plants gave it out in enormous volumes. The carbonate of lime dissolved in the water-springs, etc., was carried to the sea for polypi to build shells from. The trees were absorbing carbonic acid, too, and while purifying the air, were retaining the carbon in their stems and leaves and branches, which (when they decayed) remained untouched, and accumulated in thick layers to sink down, and by pressure be turned into coal. This great effect was carried out several times; and it is a remarkable fact that we find coal, limestone, and ironstone so near together, all useful to us and to each other in the course of the working of the minerals—so we come to the Carboniferous system.

Coal we have already treated of in Mineralogy, and coal looks at times very different from our preconceived ideas of a sedimentary rock, which we know is regularly deposited in layers. But when we split or break the coal we find its cleavage in a certain direction. Coal is wood squeezed and petrified by ages between enormous layers of sedimentary rocks, and the coal-seam rests upon the soil in which the plants once grew—perhaps more than six hundred thousand years ago!
Of course coal, as we burn it, was not all made at once. We can trace it from the swamp as Peat, on to “Lignite,” or woody coal, through the Tertiary and New Red Sandstone to the coal measures themselves. Even lower down[Pg 580] we find the remains in more or less pure carbon forms—the anthracite and the graphite of the primary formations.
Coal appears not to have been formed equally in all places during the period in which it originated. The remains of plants found in these strata lead us to infer, that, during that period there existed an exceedingly vigorous and crowded vegetation, consisting principally of tree ferns and equisetaceæ, of which the Sphenopteris Hœninghausii (fig. 662), Pecopteris aquilina (fig. 663), and Neuropteris Loshii (fig. 664), are amongst the most beautiful that have been found, and the flora and fauna of this period were of a more or less primitive kind or low order, but very luxurious. The former display a decided advance, and reptiles of aquatic forms appear with large and predaceous fishes. Mountain limestone, which is usually found in the coal formations, includes metallic deposits, and organic remains are very abundant in it. The following are specimens of the fossils—


The Carboniferous system is a very important one, as may be seen. In these beds we have coal, limestone, sandstone, and shale. The Coal Measures consist of grit and sandstone and shale, with coal seams. The Carboniferous Limestone, or “Mountain” Limestone, has no coal in it. The[Pg 581] sandstone has been termed “Millstone Grit,” because millstones are made from it. We then have limestone shales, and the sandstone beds. Each coal seam indicates a subsidence of the land and a regular series of underclay or soil in which the plants grew,—the plants themselves,—iron, coal, and then the shale, and so on again, indicating frequent changes and a long lapse of ages.

These “Coal Measures” occupy an area of five hundred square miles in Great Britain alone; and as we have already said, the period which elapsed while these deposits were being laid down represents hundreds of thousands of years. The deposit would increase at the rate of about three feet in a thousand years. And this is only one period of the many changes to which our world has been subjected since it first began its revolution in space around the sun.

1. Carboniferous Limestone. 2. Yoredale Shales. 3. Millstone Grit.
4. Coral Measures. 5. Permian Limestone. 6. New Red Sandstone.
Coal is usually found in “basins” or depressions—a sort of trough owing to the upheaval of surrounding strata which became in time denuded (or washed away) with any coal that was there. So it is in places where it is concealed by overlying beds that protect it, that we now find the coal saved from disturbance. When we search and come upon red sandstone and grey-wacke, we may be almost certain that we are near coal, particularly if the surrounding rocks form a “basin.”

We have now briefly sketched the Carboniferous system, for in our[Pg 582] recreations we can do little more. We shall find in many places in England tree trunks in the sandy shore, and ample evidence that a forest has been at one time submerged in that spot. So inland the land sank down again and again in successive periods—water, mud, soil, vegetable growth succeeded, to be again submerged and form a new coal seam for the use of man, who was destined to appear after the lapse of ages.
The Permian Period.

At length the land remained undisturbed. It sank no more, and the trees waved luxuriously over the buried forests of past ages, and another cycle set in called the Permian, from the ancient kingdom of Permia, where all the features of that period are exhibited on a very grand scale, and which extended for several hundred miles between the Ural mountains and the Volga. In the Permian period we have the progression of animal life more distinctly developed than in the Carboniferous system, which immediately preceded it. It is true there are indications in the latter that curious animals, called the Cheirotherium and the Labyrinthodon, were alive then, and the remains of numerous insects, such as beetles and crickets, have been found; but the Permian developed them, and reptiles, saurians, and lizards have been traced; but as Sir R. Murchison states, throughout the whole extent the animals are of a single type. We have the hand-like impressions of the feet of the Cheirotherium, so called from the Greek “cheir,” a hand. The soil appears to have been very soft, and peculiarly adapted to receive impressions, and which having been in many places covered over with a stratum of fine sand, and then abandoned by the sea, the whole has hardened into stone, and being now separated, the one contains their footprints, and the other perfect casts of them! Nor are these footmarks all that these sandstones have to tell us of their day; for the ripples of the waves, and[Pg 583] even the little pits made by drops of rain as they fell, are in this most marvellous manner preserved, forming objects of wonder and admiration.
The organic remains during this period are not very abundant, and many of the fauna of the previous systems appear to have died out, while others appeared to meet with fuller development in succeeding ages. The Permian is also known as the New Red Sandstone, or Magnesian Limestone group. “Dias” has also been suggested with reference to the “Trias” group, “the Upper New Red Sandstone,” which comes next. The Permian rocks are very varied, and contain minerals, such as copper and sulphur.
As the strata below the new sandstone formation was called the “Carboniferous” system, from its containing much carbon in the form both of coal and carbonic acid, so this has been called the “Saliferous” system, from the occurrence in many places of strata of “rock-salt,” or crystallised chloride of sodium, and (where the rain finds its way down and dissolves it) of brine springs; these (in England) exist chiefly in Cheshire and Warwickshire, but in Poland and Hungary they exist on a much larger scale, the rock-salt being nearly a thousand feet thick. It has been said that these strata of salt were formed by the evaporation of salt lakes, but it is much more probable that salt is one of the natural materials of the earth, and that both salt lakes and oceans have become salt from dissolving out these strata wherever they have come into contact.
It is supposed that during the Permian period the greater portion of the continent of Europe was raised above the ocean, and the deposits were formed in salt lakes, for the appearance of the organic remains tends to establish the fact that the creatures of that period were not far from dry land even in their watery existence, and the reptiles found confirm this view. We have now to examine the Mesozoic, or Secondary System.

CHAPTER XLV.
THE MESOZOIC SYSTEM—THE TRIASSIC, OOLITIC, AND CRETACEOUS FORMATIONS—THE EOCENE, MIOCENE, AND PLIOCENE—THE GLACIAL PERIOD—PRE-HISTORIC MAN.
We trust that the general reader has gleaned from the foregoing chapter some few ideas concerning the growth of plant and animal life in the early periods of the world’s existence. From the Laurentian System we have briefly traced the conformation of the globe at the dawn of organic life through the Silurian Old Red Sandstone and Carboniferous formations, indicating as we proceeded the chief points in the world’s history, and the gradual development of life through many ages. There is no real or bold line of demarcation drawn between these systems. As seam unites to seam, and layer to layer, stratum upon stratum, so the systems almost insensibly unite, and forms of life appear, mature, and die away as the babe grows into the man, and dies away again to old age and final extinction. So one system merges into another, each and all a factor in the great work which was intended to prepare the earth for the greatest and latest development of Nature—Man!

1. Ammonites nodosus. 3. Possidonia minuta.
2. Avicula socialis. 4. Encrinites moniliformis.
But all this while the earth had been, as it still is, undergoing continual change. Sometimes gradually, in the wearing away, or elevation of beach or headland; sometimes suddenly, as when mighty hills were upheaved and[Pg 585] the deeply-laid granite or limestone was lifted to the summits of the mountains from the depths of the sea. Land and water came and went, and the ever-changing earth still brought forth abundantly “the herb yielding seed after its kind,” and the “moving things upon the ground after their kind,” ever improving and developing till they culminated in the splendid vegetation and immense animals of the Tertiary period, and lay silent afterwards in the cold grasp of the great ice age for the thousands of years of the glacial epoch.

We now enter upon the Trias, or New (Upper) Red Sandstone, which is divided into Upper and Lower Trias, “Keuper” and “Bunter.” We have three principal headings in the Secondary System—the Triassic (the oldest), the Oolitic, and the Cretaceous. In the first we find red sandstones and shelly limestone; in the second, clays and shale; in the last, chalk, or white limestone. In some districts there are traces of volcanic action.

On the top of the “Upper Trias,” or “Keuper” formation, we have the Lias, which succeeds the Rhætic beds, and in this we find many rich traces of reptiles and birds which come now before us in the rising scale of creation. In the seas of this period we have numerous crustacea, the nautilus and the cuttle-fish. The Saurians now come before our retrospective vision. It is the “Reptile Age” in all its development, and the huge labyrinthodon, the iguanodon, pterodactyle, and ichthyosaurus testify to the magnitude of the fauna of the period. The first mammal specimen, a marsupial, has been traced back to this time; and the tropical temperature was favourable for luxuriant vegetation, pines, and palms.
In the swamps or shallow waters the great reptiles disported themselves, and seized their prey, the water-fowl, which now appeared in numbers, and[Pg 586] of enormous size. Nor were insects absent. Numbers of remains have been discovered; beetles, dragon-flies, grasshoppers, etc., in multitudes yield us information, while the marine fossils, star-fish, mollusca, and various fishes, are of frequent occurrence. Animal and vegetable life during this period must have been very rich and varied—literally leaving “footprints in the sands of time.”

The “Blue Lias” is a term familiar to every reader. It is a kind of limestone mixed with clay, of a blue colour, and upon this we find the Oolitic, or Oolite System—so called because it somewhat resembles the roe of a fish. The Lias clays are used for bricks, and Whitby “jet” is also obtained from the Upper Lias. Jet is really a lignite, or wood in the process of transmutation. In this Lias formation, besides the numerous fossil remains already mentioned, we find the “snakestones” (ammonites), the stone-lily, and belemnites, with many nautili and shells.

The Oolite, or Jurassic, underlies the chalk, and overlies the Trias formation. The term “Jurassic” originates from the Jura range, which is almost entirely composed of Oolitic strata. These strata are greatly distorted by pressure, and when we reach Switzerland and the familiar Alps, we find gneiss, crystalline, limestones, and schists, into which the Oolite has[Pg 587] been metamorphosed. The Oolite is divided into Upper, Middle, and Lower, consisting of the following:—
| Upper Oolite | ⌈Pembroke Beds. ⎢Portland Beds. ⌊Kimmeridge Clay. |
| Middle Oolite | ⌈Calcareous Grit. ⎢Coral Rag. ⌊Oxford Clay. |
| Lower Oolite | ⌈“Cornbrash”—Forest Marble. ⎢Stansfield Slate. ⎢Bath Oolite. ⎢Fuller’s Earth. ⌊Inferior Oolite. |

The Oolite formation (see Map) occupies a stretch of country in England extending from Yorkshire into Dorset. The Great Oolite holds the Fuller’s earth, and the Bath stone is also well known. The Stonesfield slate holds many remains of reptiles. It is a kind of shelly limestone, and is used for roofing purposes. The Forest Marble (so called from[Pg 588] Wychwood Forest) is a sandy limestone holding marine fossils. It is used for ornaments. The Coral Rag and Oxford clay are rich in fossils, and the former, as its name implies, is composed of ancient coral reef. The Portland beds produce the well-known building stone. The Purbecks, of which there are three divisions, appear to have been deposited in fresh water, and occur in Dorsetshire.
All the Oolite strata supply organic remains. We have plants and ferns, reptiles, and a number of new genera of conchifera and cephalopods, star-fish, urchins, and the enormous bats, and the terrible megalosaurus, and the cetiosaurus, steneosaurus, and pliosaurus, of enormous size. One very remarkable bird has been found in the Bavarian limestone of this period; it is called the Archæopteryx, which is described as having a leg-bone and foot like the familiar birds, but the tail is lizard-like, with feathers springing from each joint. Sponges, corals, and fish, and many other forms of animal life are found in the Oolites. The reptiles must have had it all their own way in this period, for there were both carnivorous and vegetable feeders, and teeth of the pliosaurus have been found which measure fifteen inches, the jaws being six feet long. We have seen that corals must have built up their reefs in the waters, which then overlaid the land we call the United Kingdom.
There must have been great changes during this period, and the strata are chiefly marine. The Wealden formations are the exceptions, and in the fresh-water deposits insect forms abound. The appearance and variety of animal and vegetable life must have been curious and interesting.
The Weald or “Wold” of Kent is often spoken of, and it extends with the Surrey and Sussex Wealden formations for some distance. The strata are of fresh-water deposition, differing in this from the chalk, although the Wealden beds are included in the Cretaceous Group, which is composed as follows:—
| Lower | ⌈Wealden. ⎢Greensand. ⌊“Gault.” |
| Upper | ⌈Upper Greensand. ⎢Chalk Marl. ⎢Chalk (without Flint). ⎢Chalk (with Flint). ⌊Maestricht. |
The “Wealden” formation is divided into Hastings sand and Weald clay. The former consists of clay and sandy beds, and is observable at Hastings, and in the neighbourhood of Tunbridge. The Weald clay consists of blue and brown clays, with sandstone, and the limestone known as “Sussex Marble,” which is formed by the paludina of the rivers. There is another division often seen in Dorsetshire, and called the Punfield beds, which partake both of marine and fresh-water remains, which are distinct in the true Wealden and cretaceous formations, the former being of fresh, and the latter of salt-water origin.

The remains of enormous reptiles are numerous in the Wealden formations; crocodiles, lizards, turtles of gigantic size have been discovered, and most curious fossils have been disinterred in the Hastings district. The “Greensands” are separated by what is termed gault, a stiff blue clay found in Norfolk, Essex, and Kent. The Lower Greensand includes the well-known Kentish rag, or limestone, of which so many churches are built. The Upper Greensand is supposed to be a seashore deposit on the sides of an extensive ocean or sea, at the bottom of which the chalk was formed. After the Wealden beds were formed, they were covered by these greensand estuary-beds, or littoral strata. In these series new forms of life appeared, and the waters became the receptacle of myriads of mollusca, etc., which in time formed the great chalk cliffs and downs so often referred to. The chalk is interstratified with sand, which as “gault” and “greensand” was probably the sand of the ocean bed before the chalk was formed upon it, and the seas must have supported many marine reptiles, for stony “nodules,” or coprolites, which are the fossil excreta of the animals, are found, and now used for manure, after being buried for thousands of years. Examination of these remains has resulted in the discovery of the teeth and bones of fish which had been devoured by the gigantic reptiles. An illustration of a shell thus discovered is annexed.


We have in a former chapter spoken of the chalk and its formation. We know that it is composed of the minute foraminifera. The fossil remains are very numerous in chalk and all of a marine kind, such as the ammonites, belemnites, and such cephalopods, and the echinus, bivalve mollusca, crustacea, etc. We have occasionally flints appearing in the chalk, and this circumstance has given rise to some speculation as to how the flints got there, for they consist of nearly pure silica; and the theory of the petrifaction of sponges, madrepores, etc., has been started to account for their presence. Dr. Carpenter says: “It may be stated, as a fact beyond all question, that nodular flint and other analogous concretions (such as agates) may generally be considered as fossilised sponges or alcyonian zoophytes, since not only are their external forms and their superficial markings often[Pg 590] highly characteristic of those organisms, but when sections of them are made sufficiently thin to be transparent, a spongy texture may be most distinctly recognised in their interior.”
It is now generally admitted that the decaying animal matter acts upon the silicious spiculæ of sponges, etc., and the silica is thus deposited.
We may then surmise that at some very distant period the whole extent of the British Isles was submerged, as well as portions of the continent, and after the strata had been deposited the sea and land were disturbed by volcanic action. While the secondary strata were being deposited, very little relative alteration took place, as the deposits are seen to lie “conformably.” But when the great convulsion which upheaved the Apennines occurred, the chalk was raised as we find it in the cliffs and downs, which were the beds of seas. This is the last of the great convulsions which the earth has undergone, for the tertiary strata, which afterwards began to be deposited, rest in the hollows or basins (chiefly in the chalk) then left; the alterations in and since these deposits appear to consist chiefly of the upheaval of certain localities, the depression of others, the evaporation of inland lakes, and the wear and tear of the land from these causes, which are still in continuous action (as from the washing down of cliffs by the sea, and the formation of mud deposits at the mouths of rivers), or the volcanic agencies which in some places (as in Ireland) have cast up basalt over the chalk.

There is a sort of transition formation which is classed with the Cretaceous System, and termed “Maestricht,” after the town in Belgium. It appears that this is an upper chalk layer, an intermediary between the Secondary and Tertiary, and here on the banks of the Meuse we find the Mosasaurus, the “lizard of the Meuse,” of whose remains we give specimens in the illustration. This transition chalk—as we may call it to distinguish it—must have been laid down at a later period than the flinty chalk, and we find it in many places. It serves therefore as a fitting introduction to the Tertiary Period of Geological time.
The Tertiary Period.
We now enter upon a period when the animal creation attained its greatest development, the “Age of Mammals”; for they were then the kings of creation. The Tertiary Period is divided into three stages, viz.—
The Eocene, or the Dawning of the now existing creation.
The Miocene, or the Middle, or “minority” of existing creation.
The Pliocene, or the Recent, or still more developed period.
We will glance at them in that order, which Sir C. Lyell introduced.

The Eocene formation is shown in what is termed the “London Basin,” here illustrated by a section in which we find soft sands without fossils (Thanet Beds), and a kindred kind in Surrey, in which fossils (marine) are found. After these we get the “Reading and Woolwich” beds as we ascend. These are of clay and pebbles, etc., with river fossils. The Oldhaven beds are included on the map; they occur towards Blackheath and Herne Bay. The London clay is very stiff, and in some places blue. It is full of fossils of birds, beasts, fruits, and vegetables, trees, reptiles, and fish, and the variety of the organic remains appears to indicate the fact that at one time the Thames flowed through swampy ground to the sea, in which dwelt, in a warm climate, immense mammalia, such as the megatherium, glyptodon, tapir, etc., and some turtles of enormous size.
It is also on record from late observations that these immense animals[Pg 592] were even mixed up, and almost fabulous creatures inhabited the land where England now is. We read of antelope-horses, lion-like bears, and camel-stags. The vegetation was then of a tropical kind, and in the deep forests and jungles these enormous animals—the mammoth dinotherium, and such species—roamed and plunged in the swamps at the mouth of the Thames. At length these types died away, and gave place to the elephant and the hippopotamus, and the climate by degrees became less warm, and still slowly decreased in temperature.
A glance at Sir C. Lyell’s “Principles of Geology” will show us how, as we examine the more modern strata, we find a great increase in the European lands, which may have been compensated by the submersion of the Pacific islands. During the period of the vegetation of the Secondary epochs, our climate (between the lias and the chalk) was favourable to a tropical growth. Enormous rivers flowed through our islands, and gigantic crocodiles, etc., with flying reptiles, were masters of the land. There were numerous fishes, but the reptiles did not appear in such very great numbers.

a Lower Bagshot sand (of Hampstead). b London Clay. c Reading and Woolwich beds (including the Oldhaven beds, which occur in the south only). d Thanet sand (crops out on the south only). e Chalk with flints. f Chalk without flints. g Upper Greensand (crops out on the south only). h Gault. i Lower Greensand. k Wealden beds (on the south only). l Oolitic clays (shown only on the north, but proved to occur on the south beyond the range of the section, by the sub-Wealden boring, near Battle, in Sussex). x Old rocks, shown by borings at Kentish Town and at Meux’s Brewery, to pass under the London basin.
These large and elephantine animals must have existed while the climate of Northern Europe underwent some very considerable changes. We read of the woolly rhinoceros, and the hairy elephant, or mastodon, which has been found in Siberia. Reindeer appeared in England, and we know now that these animals inhabit cold countries. The mountains were considerably elevated during the latter Tertiary period; snow fell and ice formed upon the summits of the mountains, while glaciers crept down the sides. The warm, almost tropical climate of the prior ages was gradually but surely giving way to the Ice Age; the earth was slowly dipping, and the sun’s rays had less power.
Professor Ramsay says the “assemblage of fossils found in the London clay point to the fact that the whole of these strata were deposited in the estuary of a great continental river comparable to the Amazon and the Ganges. The palm-nuts and the host of other plants help to prove it, and the remains of river tortoises, crocodiles, snakes, marsupials, and several tapir-like mammals, all point in the same direction. The estuarine conditions begun during the deposit of the Woolwich and Reading beds were still going on when the London clay was thrown down; with this difference,[Pg 593] that by sinking of the area the estuary had become longer, wider, and deeper, but still remained connected with a vast continent, through which the Eocene river flowed.”

The Miocene deposits are not so generally important in the United Kingdom, but in America very valuable fossils have been discovered in these strata. The Pliocene strata extend along the east of Great Britain, where they are denominated “Crag,” as Norfolk Crag, Red Crag, Coralline Crag. Underneath these mammalian remains have been discovered. After the Pliocene we come to the Post-Pliocene, which really closes the long Tertiary period. During these ages the gradual development of created beings apparently reached its height. It was towards the end of the Middle Eocene that the great mountain chain of Europe came into existence, which is connected, as any casual observer may see, with the Himalaya. In fact, the whole chain, from the Thibetian range through India, the Caucasus, Alps, and Pyrenees, is continuous, and formed of the same material (“nummulitic limestone”). There is no doubt that the whole northern hemisphere enjoyed at the commencement of the Tertiary period a warm, not to say tropical, climate, which got colder and colder.
We find the increase of animals and plants more fitted to the requirements of man and our present climate. There are many signs of the successive increase of land in Europe generally, while the contrast the Tertiary period bears to the Secondary is very marked. In the former we have extensive deposits in the waters of wide, open seas; in the latter the depositions were evidently made where dry land, with its accompanying bays and lakes, were extensive and numerous. The former is marine, the latter lacustrine and marine. The seas of the Tertiary period have lately been defined.

Sir Charles Lyell, in his “Principles of Geology,” shows us this, and defines the European features at the commencement of the Tertiary epoch. At that time, the British islands, with the exception of the basins of London, the Isle of Wight, and Norfolk, had wholly emerged from the deep. But a third[Pg 594] part of France was still under water. Italy consisted only of a long and narrow ridgy peninsula, branching off from the Alps near Savona. Turkey and Greece, south of the Danube, were laid dry; and a tract of land extended from the Vosges, through central Germany, Bohemia, and the north of Hungary, perhaps to the Balkan. But the whole of the north of Europe and Asia, from Holland eastward to central Tartary, and from Saxony and the Carpathians northward to Sweden, Lapland, and the Ural chain, lay beneath the ocean. The same subterranean movements, which have subsequently raised the wide plains of our northern continents above the sea-level, have given great additional elevation to the then existing land. Thus the Alps have certainly acquired an increased height of from two thousand to four thousand feet since the commencement of the Tertiary period. The Pyrenees, whose highest ridge consists of marine calcareous beds, of the age of our chalk and greensand series, while the Tertiary strata at their foot are horizontal, and reach only the height of a few hundred feet above the sea, seem to have been entirely upheaved in the comparatively brief interval between the deposition of the chalk and these Tertiary strata. The Jura, also, owe a great part of their present elevation to convulsions which happened after the deposition of the Tertiary groups. On the other hand, it is possible that some mountain-chains may have been lowered by subsidence, as well as by meteoric degradation, during the same series of ages in this quarter of the globe; and on some points shallows may have been depressed into deep abysses. But, on the whole, everything tends to show that the great predominance of land which now distinguishes the northern hemisphere has been brought about only at a recent period, and Sir Charles holds that the shifting of the continents is sufficient to account for the variations of climate. We have every reason to believe that before the Glacial epoch England and the Continent were united, and during the Glacial period England and North America were joined, viâ Greenland and Ireland. Mr. Dawkins says that England at that time was six hundred feet above its present level. If so—and we cannot question his conclusions—the Channel was then dry.
The “Great Ice Age” then came upon the world. For the information of readers who wish to peruse the whole history of this epoch and its causes, we may add that in Professor Geikie’s most interesting work, they will find full details. We can only refer to it.
The gradual decrease of temperature upon the earth, which was the cause of the Glacial period extending over the north of Europe, has been attributed to the eccentricity of the earth’s orbit; and here astronomy steps in to our assistance. We have read in the chapters on Astronomy, how the movement of the earth, like a top near the end of its “spin,” causes the “precession of the equinoxes,” and in connection with this phenomenon the earth’s orbit becomes more and more circular at certain periods of thousands of years, and goes away from the sun. We therefore receive the light and heat at a greater angle. Consequently, less heat is received, and ice is formed, as at the North and South Poles at present.

Doctor Croll has pointed out that the great eccentricity of the earth’s orbit existed about 210,000 years ago, when there was a difference between the nearest and farthest position of the earth and the sun of 12,000,000 of miles at least.28 This is a very considerable distance even in the enormous spaces which intervene between us and the other planets of the solar system, and about that time the Glacial period arrived. Perhaps we may make this clearer by going back to the precession of the equinoxes.
The earth moves in an orbit called an ellipse, and the sun is not in the centre of this nearly circular path. We can now understand that the earth comes nearer to the sun sometimes and recedes at others. These points of[Pg 596] nearest approach and greatest distance are termed perihelion and aphelion. In the latter case we are about 9,000,000 of miles farther from the sun than when in perihelion—that is, when the greatest “eccentricity” is reached. In addition to this the axis of the earth is continually changing in direction by reason of solar attraction at the equator. This shifting, as explained in the astronomical section, is very slight every year, and in the course of 24,000 years the conditions of the seasons will have completely changed round and back again,—for the northern and southern conditions will be reversed in our hemisphere. Day and night come twenty minutes earlier every year. We are now nearer the sun in winter as shown in diagram (page 497); when we change we shall be nearest the sun in summer and farthest in winter.

Doctor Croll, who has done much in his most interesting paper on changes of climate29, tells us how this eccentricity of the earth’s orbit produced indirectly the Glacial epoch. He shows how, if in a period of the greatest “eccentricity” our winter came in aphelion, we should receive one-fifth less heat than now, but a correspondingly greater heat in summer. But if our winter under such circumstances fall (as now) in perihelion, the difference between winter and summer would be practically nil, because the sun during a period of the earth’s great eccentricity “could not warm the hemisphere whose summer happened to arrive in perihelion.” No doubt the sun’s rays would be very powerful, but the earth being covered with ice and snow could not be warmed; fogs would accrue and hide the sun, as at present in Antarctic summers, when the cold is very great. The warm ocean currents[Pg 597] would be stopped, and the northern portion of our hemisphere would be, as it undoubtedly was, frozen over and covered with snow.

When we consider the millions of years since the earth is supposed to have been launched into space, we can imagine that the Glacial periods would occur frequently, and considering the very slow “precession” movement there, and the alternating tropical climate with graduations of temperature for thousands of years they would last long. The great Glacial period is computed to have begun 240,000 years ago and lasted 160,000 years with alternations of comparative summer; and so the years went on, season succeeding season, altering the appearance of the earth, and causing successive changes in the distribution of animal and vegetable life. Then the great mammalia, the mammoth and hippopotamus, with the hyæna, lion, and other felidæ came, and went when Arctic animals usurped their places. At the later Glacial epoch man must have arrived in Britain, and “this being so,” says Professor Geikie, “it is startling to recall in imagination those grand geological revolutions of which he must have been a witness.... He entered Britain at a time when our country was joined to Europe across the bed of the German Ocean; at a time when the winters were still severe enough to freeze over the rivers in the south of England; at a time when glaciers nestled in our upland and mountain valleys, and the Arctic mammalia occupied the land. He lived here long enough to witness a complete change of climate, to see the Arctic mammalia vanish from England, and the hippopotamus and its congeners take their places. At a later date, and while a mild and genial climate still continued, he beheld the sea slowly gain upon the land, until, little by little, step by step, a large portion of our country was submerged—a submergence which, as we know, reached in Wales to the extent of 1,300 feet or thereabouts.”
We find that the land underwent many subsequent changes; it rose[Pg 598] from the sea, was again covered with ice, and many parts of Europe were devastated by immense glaciers—that of the Rhone extending for more than two hundred miles. Then came vegetation as the ice gave way, and luxuriance of the tropics reigned; more cold after that, then more heat, till the ice was finally driven to its mountain fastnesses, and “Britain for the last time became continental. Neolithic man came upon the scene; his palæolithic predecessor had, as far as Britain and northern Europe are concerned, vanished for ever.” The inquiry respecting the arrival and presence of man in Britain would lead us too far in pursuit. The fact has been established that man was living in the Thames valley while tropical animals were in the country, and he has been classed by Professor Boyd-Dawkins amongst the mid-pleistocene mammalia, and at that distant period, man as man, and not as an intermediate form connecting the human race with the lower animals, was present in Europe.
The stone implements which have been found in river beds and in caverns, associated with the bones of various animals, such as the elephant, rhinoceros, hyæna, bear, and others prove this. These very ancient and rudely-fashioned implements have been divided into two classes, the Palæolithic and the Neolithic, by Sir John Lubbock. First the stone implements were used, and stone was superseded by bronze and iron. Then we come to the historic period. In the neolithic period we find stone implements in the lake dwellings of Switzerland and Constance (as well as the Lake of Neuchatel), all of which have lately developed many treasures. Bronze tools have also been found, and so the gradual progress of man as a fashioner of weapons can be traced from age to age.
From the “river-drift” man we descend to the cave-man, who is supposed to have been identical with the Esquimaux. When Britain became an island the cave-man seems to have disappeared from our country, and in the prehistoric age the earliest of the present inhabitants came here, and brought with them domestic animals; then the Celts of the bronze age, and then the iron. The wild beasts gradually disappeared, and domestic ones occupied their places under civilized conditions.30
So we come from the “Glacial period” to the open door of history through the antechamber of the prehistoric time.
The prehistoric is the arbitrary division between the post-pliocene or pleistocene and the known “historic” periods of the world’s history, and we must dismiss it with a few general remarks, for the changes which we have attempted to follow are still taking place in the earth; volcanoes and earthquakes are unsettling the strata, and adding to the physical and geographical record which will some day have to be written by posterity and future geologists. We can see in those prehistoric times traces of men (hunters and fishers) existing with difficulty, mayhap, in the midst of enormous quadrupeds, and fighting for existence with the bears and many[Pg 599] other formidable foes. We have noticed the stone ages, the rough and the smooth as they may be called, and we can picture the primitive agriculture and work of the neolithic man. But it is by no means to be believed that neolithic man in Britain was a race all over the world. We may assume that in eastern climes the human race were in a more civilized condition as improvements made their way slowly westward. Our island history commences in the time of Julius Cæsar. Eastern chronicles go back many thousands of years farther.

It is so short a time, geologically speaking, since man appeared within the limits of history, that the earth’s changes, except from direct volcanic action or water erosion, are very trifling. The change is, as we said, continually proceeding; ceaselessly the earth is wearing away, and depositing her riches where she is undisturbed by civilization and man’s excavations and intrusions. The rock is worn by water; the grit is carried down and deposited to form sedimentary rocks as of old; the lime will continue to assist the coral to be built up; and the chalk cliffs will be born under the sea, and our organic remains shall be found to tell remote ages that we were an enlightened people. For all we can tell, and it is by no means unlikely another recurring cycle of Arctic and Tropical periods will in time pass over our earth; the bear and reindeer, the hippopotamus and the rhinoceros, may again inhabit our islands. If our generation be destroyed, the purely animal creation with the vegetable world will reign over the land, and new forests will deposit new coal measures for the support and[Pg 600] comfort of a new generation of highly organized beings, when our remains shall have passed away to the borders of a “prehistoric” age.
We have seen in the foregoing brief sketch how the world has arrived at its present beautiful condition,—how it has been step by step prepared for us, how nature’s forces have been and are still working according to the immutable laws of the Universe. And, after all, how little we know! What scraps of intelligence only are we able to gather up from the boundless quantity of material which must have been laid down, yet what wondrous results scientists have been able to adduce from even these comparatively scanty specimens! The sea and land are ever telling us the same old story. Man’s research and Bible teaching are found hand in hand in cordial and reverent agreement. Nothing is altered since the day that the Divine command, “Let there be light,” went forth into space, and till the earth be destroyed the same forces will continue in operation, guided by the Hand that made it—“ever faithful, ever sure.”

CHAPTER XLVI.
PHYSICAL GEOGRAPHY.
IGNEOUS ROCKS—LAND AND WATER—SPRINGS, WELLS, AND GEYSERS—SNOW AND ICE—THEIR EFFECTS.
In the foregoing pages we have chiefly considered the stratified rocks, but we are now approaching another branch of our subject—viz., “Physiography,” which, as distinguished from the usual so-called Physical Geography, will deal with the phenomena of the earth, air, and water, thus leading us to Meteorology as a conclusion.
We have arrived at a certain knowledge concerning the Earth as a planet, her place in the universe, and the composition of the “Crust,” as it is termed. We have examined the stratified rocks, which include sand and gravel, stones, and boulders equally. To a geologist they are all “rocks.” We must now examine the igneous rocks, which bear an important part in the structure of the Earth, whose surface we have now more minutely to examine. It has already been stated (p. 571) that igneous rocks have been upheaved while in a state of fusion—that is, while in a melted condition. These igneous, or fire-produced rocks, are divided into classes, just as the unstratified rocks are, and the divisions are called the Volcanic and Plutonic, including “Basic” and “Acidic,” according as they are possessed of less silica or more.
Sometimes the igneous rocks are classed as volcanic, trappean (from trappa, a stair, such as in the Giant’s Causeway), and granitic. The volcanic in such case being the modern or upper rocks, such as lava, scoria, etc., which, having been cast up by volcanoes, are of comparatively recent formation.
The Volcanic rocks, then, are of recent date, comparatively speaking; they form the constituent portions of the volcanoes of the present day, and are found as basaltic formations. They are traced as far back as the Tertiary period of the globe. Amongst the volcanic rocks we find basalt, augite, porphyry, serpentine, pumice, pitchstone, felspar, etc. But no doubt volcanic action has been going on ever since the beginning of the world as it is now, and will continue to do. It is somewhat curious that the very old igneous rocks should not be more evident.
The Plutonic rocks do not differ essentially from the foregoing. There is less quartz and more hornblende; and if the ages during which these formations have been existent in the earth-depths after they became[Pg 602] solidified be considered, the differences will be fully accounted for. The greenstones and syenites are prominent amongst the plutonic series.
These plutonic and volcanic rocks are separated into basic and acidic, as already remarked, but the line cannot be drawn very distinctly. Granite is the chief plutonic (acidic) rock, and we frequently find it forced upwards into other strata, its essentially eruptive character being thus decided. That granite must have taken an immense time to solidify and crystallize is evident, for no new granites are ever found. We find granite in all the old mountain chains—such as the Grampians in Scotland, and the Wicklow mountains. Our chief European (active) volcanoes are, so to speak, modern, as may be supposed when their constituents are known. It may be said that granite was first deposited as sediment heated by subterranean fire, and forced up by thermal action of water to the mountains, where it is uncovered by a slow process of denudation and surface washings of the earth.
Now without at present going any farther into the causes of volcanoes we can see at a glance that the eruption of the igneous rocks must have created a marked and essential difference in the physical geography of the globe. It is to these eruptions that the dislocation and disturbance of the stratified formations are due. The igneous rocks present ridges in the mountains; sometimes they are rounded at the summits, while the aqueous and metamorphic rocks are disposed in layers.

These two classes in their varieties form the land and the crust of the earth, which is ever being acted upon by air and water. The ice, again, polishes and scratches the valleys in which it moves. The loosened boulders that tumble from the mountains are carried down by the ice, and deposited in the glacier moraine, whence flows a stream. By degrees the stone is ground up, and carried away in the water to form sediment in a “delta” at the[Pg 603] embouchure, or to lie beneath the surface and form rock once more. The igneous rocks, composed of lavas and ashes, are volcanic rocks, deposited deep down, and then after the lapse of ages disclosed by the action of air and water.
The consideration of the land and water upon the globe shows us that they are distributed over the earth very unequally. There is nearly three times as much water in our planet as there is land, and these proportions could not be altered without giving rise to phenomena, the results of which cannot be properly estimated. Our earth has an area of 197,000,000 of square miles; about 52,000,000 of this is land, and about 145,000,000 of it water; so about three-quarters of the globe is made up of water. The first portion of our subject therefore should be directed to the examination and consideration of water, and the phenomena which arise from its presence upon the earth.

We need not go into details which every geography indicates. We will try to trace the sources, not the plain effects, which all can afterwards study from special books. In a preceding portion of this volume we have explained the chemical composition of water, and we showed by experiment that it is a fluid composed of oxygen and hydrogen gases, in the proportions of one to two volumes respectively. No matter in what form water may appear,—as water, as ice, or as steam,—these proportions never vary in pure water (see p. 352). But water on the earth is seldom, or never, pure. We know the difficulty we have to procure good drinking water, and though it may be filtered, there will remain natural salts, which are found in different degrees in all water upon the globe. We know the rain, which is perfectly[Pg 604] pure when condensed from the clouds, absorbs carbonic acid, etc., from the atmosphere. We have shown how this water as soon as it comes upon the earth attacks the rocks, and as it progresses carries away lime. After descending deep down, it rises again in the form of Springs.
Now what are these springs? They are the result of percolation of rain-water through certain strata. When water falls it is absorbed into the ground, unless it happens to rest upon an impermeable rock, in which case it becomes a rivulet. But it can penetrate between the atoms of many rocks, and thus falls through sand and harder rocks, till it reaches a stratum which will not receive it—like clay. We then find that it will flow away in a spring, or if tapped will be an Artesian well. These water-wells are of very ancient date, but the name is more modern.31 The springs flow out, and develop, with the assistance of tributaries, into rivers. These again receive more tributaries, which swell the volume of their waters, and widen out, carrying millions of gallons hourly to the sea with sediment and gravel and stone.

Water has enormous power of disintegration. We have only to cast our eyes upon the illustrations in any volume of continental travel in Europe or America to perceive the gorges and cañons worn out by the resistless and frequently gently-flowing river to estimate the part which water plays in Physical Geography and Meteorology.
But springs occur not only in the case mentioned; there are mineral springs, hot springs, and oil springs, all following the same rules of nature. The Artesian well has been mentioned. The Geysers of Iceland have often[Pg 605] been portrayed, and are amongst the most wonderful phenomena of nature. These will serve as a type of the other thermal springs, of which the districts of the Yellowstone in North America afford perhaps the most extraordinary instances. These are intermittent springs, and the water rises to a great height, at intervals of about an hour and a half; and after many successive attempts, or trials, as it were, the geyser shoots up to a great height enveloped in steam.
The cause of these well-known phenomena have been explained by Bunsen, and it has already been referred to. We know that at a certain air-pressure water boils at 212° (Fahr.), but on mountains at less pressure it will boil before that degree, because the air is rarefied. So conversely, under the ground, it may reach 212° without boiling. So the surface (warm) water falls, and reaches a high temperature before it is converted into steam. When it is so converted, the vapour is formed very rapidly, and the expansive force is tremendous, shooting up the water and all the contents of the tube with terrific violence, and with a beautiful effect. Pressure therefore alters the boiling point of water.

The mineral springs of Bath and many continental towns owe their properties to the solvent power of water, which assimilates the mineral atoms and gases. They arise just in the same way as the ordinary spring, the taste and smell depending upon the soil and strata. Perhaps the oil wells are the most curious phenomena of this kind. They are excavated upon[Pg 606] the Artesian principle. The petroleum is bored for, as we bore for water, and the oil rushes up with great force, and in enormous quantities. Gas wells are also to be found in Pennsylvania, and have supplied towns with gas for years. Both these Artesian wells are caused by the decay of vegetation. The gas is in the coal formation, and the oil has been pressed out from vegetable deposit, and as anthracite is a stony coal, petroleum is a kind of coal-tar, of natural formation.

We have alluded to the river, which emerges from the spring, which has fallen as rain. But there is another, and, to many minds, a much more interesting form of the universal fluid we call water. This is ice. Familiar as ice is, either to the stay-at-home invalid, the skater, and the traveller, there is a great deal to be said about it. It is a subject we would dwell upon had we space, for the remembrance of many a pleasant hour passed upon snow and glacier call upon us to go back again, even though only in imagination. No one who has not climbed the glacier—even the Mer de Glace to the Jardin, now such a common excursion—can fail to be struck with the beauty and grandeur of the scene presented to him, and to carry away a fond recollection of the icy regions he penetrated.
For the ordinary hard-working man there is no change, no rest so truly beneficial as a trip amongst the mountains and snowfields of Europe. He need not be a climber; that is, a climber like Tyndall or Whymper, those giants of the Alpine Club. But a stroll up to the Bel Alp, the Æggishhorn, the Riffel, the Montanvert, or the Grimsel, will give the average pedestrian some of the finest glacier scenery in Europe, and which may, we believe, compare with any in the world for beauty. These glaciers—ice-rivers—we will now consider briefly. We may take the Mer de Glace as an example[Pg 607] (see the illustration, p. 596). That gives us a very fair idea of the ice-river, but the cut below is a good specimen of a glacier.
Suppose we start up from Chamouni, or come across from Argentières, we shall reach the Montanvert by ascending through the wood, or by the “Chapeau,” across the ice-sea. As we take the former course, we walk alongside a white-flowing and rapid river, the Arve, which unites with the Rhone below Geneva. This river divides, and if we keep alongside one (the right or south branch), we shall reach the moraine and the icy grotto, from which the water issues. It is in this way many large rivers are born. The Rhine, the Rhone, the Aar, the Ticino, have all of them their sources in the ice. The Visp and the Sass waters are other almost equally well-known examples.

There used to be a grotto or cavern, into which the tourist could enter at the source of the Arveiron, and here the beautiful blue of the ice could be studied. From this place the Chapeau is reached, up a stony path amid the trees, and from the top outside the hut[Pg 608] we can see the Mer de Glace all broken and contorted. The frequently occurring roar of a falling rock which heat has deprived of its icy support, or the cracking and tumbling of ice-blocks, may be seen and heard in the forenoon. But the grandeur and majesty of the ice and snow-clad mountains is best enjoyed by moonlight.

On the ice we shall see huge stones and gravel and grit, which have been carried down by the ever-moving glacier, which is denuded in its course, and worn down upon the surface as it slides, scraping and grinding the valley through which it flows. By passing along a path now made easy by irons, but formerly without supports or guards, the surface of the glacier will be reached, and a man with a hatchet will cut steps for the timid traveller. We are now upon the deep ice-river, which has its springs in the snowy regions of the Col de Géant, in the snow which is continually falling upon the heights, and draining away to water again to form a river.
Thus the circle of events is completed,—snow, névé, ice (glacier), water, which last is again absorbed into the atmosphere, and again descends as rain or snow. And this is always going on by the action of the sun. It may here fairly be asked how snow becomes ice. Why does not the snow turn into ice at once, and form a glacier at the top of the mountain as well as at the bottom? We will endeavour to make this clear. Snow is composed of crystals, which assume certain definite forms, and when first the flakes fall they are soft and powdery. By degrees they melt a little, and when unconsolidated form what is termed névé, the border line between ice and snow. This semi-icy snow descends under pressure, and, as it increases, the glacier is formed by huge blocks and masses being pressed together on the steep slopes of the mountains. Thus the glacier descends, rounding off rocks, and scouring as it goes, moving at a certain estimated rate daily,—about twenty inches on the average,—carrying stones and débris which form the moraine, and finally when the high temperature in the valley melts the ice, it issues forth as a river into the plain, or bounds down the mountain side in a cascade. An excursion—and one by no means dangerous if a guide be taken—to the Jardin, near Chamouni, will reveal many interesting features of glacier formation, and of the glaciers themselves.
Physical Geography is therefore very much indebted to the action of water as a fluid or as a solid. In the former condition it erodes the rocks, carries down the stones and gravel and sand, forms deltas at the mouths of rivers, and elevates plains by overflowing its banks and depositing sediment. Water gives beautiful scenery, and the ever-changing features of the[Pg 609] landscape are due to it. From the time the spring emerges to the time when it has developed into a river, bearing fine ships upon its restless waters, the universal fluid is always at its work of destruction and benefit combined. From the limpid stream we pass to the salt ocean, the reservoir of all the waters of the globe.

We have in this chapter briefly considered two very important forces which have much to do with the varying conformation of the earth—viz., fire and water in their results of volcanic action and erosion. The sea will tell us something more.
CHAPTER XLVII.
THE SEA AND THE SKY.
THE SEA—SALT WATER—WAVES AND THEIR EFFECTS—UNDER WATER—THE FLOOR OF THE OCEAN.
From our childhood the sea has been the companion and playmate of thousands, the seashore their playground. Men have selected it for their professional training and livelihood. Authors write of it, poets apostrophize, scientists lecture upon it, and fathom it, bringing up from its depths many a new fact and illustration for those who cannot study it for themselves. There is nothing like it, nothing more majestic, more beautiful, more life-giving than the ocean—nothing so changeable nor so true.
From the days when we could toddle along the beach, picking up the shells, we have wondered at the ocean—What was beyond it? What did it conceal?
Let us endeavour to find out.
The first thing that strikes us is the saltness of the sea. Sea water is salt. Why? One reason is because salts are carried into it by rivers, and besides, it is more beneficial as salt water. But let us look at the facts. We know that the earth contains many “salts,” as we can see by the saline springs. We have already given the chemical constitution of sea water, but it will be useful to repeat the proportions.
| Water | 964·74372 | grains. |
| Salt (Chloride of Sodium) | 28·05948 | ” |
| Chloride of Potassium | 0·76552 | ” |
| Chloride of Magnesium | 3·66658 | ” |
| Bromide of Magnesium | 0·02929 | ” |
| Sulphate of Magnesia | 2·29578 | ” |
| Sulphate of Lime | 0·40662 | ” |
| Carbonate of Lime (with traces of Iodine and Ammonia) | 0·03301 | ” |
| 1000·00000 | ” |
Some portions of the sea are not so salt as others, or, in other words, not so dense, and the saltness of the water prevents it being frozen so quickly[Pg 611] as fresh water, which freezes at 32°. Salt water requires to be reduced to 28° before it freezes. Besides the various constituents mentioned above, sea water has been found to contain boron, bromine, strontia, etc., and even silver, for the copper of ships has been found to be impregnated with that metal.

If there is so much salt in the sea, it may be asked, why does it not continually become greatly saltier by additions. The reason is because tons of fresh water are continually pouring in, and though we can scarcely doubt that the sea is becoming gradually more salt as years pass away, the increase is very slight. On the other hand, evaporation is carrying water into the air and leaving the salt behind it. In seas like the Red Sea, where there is a great deal of evaporation and very little addition of fresh water in comparison, the water is extremely salt and bitter. The Baltic has little salt relatively to some parts of the Mediterranean.
Supposing that, as some allege, there are rocks of salt at the bottom of the sea, we must remember that springs of fresh water frequently bubble up to the surface of the ocean. This is a very curious phenomenon, and has been attested by Humboldt. He states that near Cuba these springs arise with considerable force, and the vessels trading on that coast get supplies of fresh water from these ocean springs. There is, or was, a similar uprising in the Gulf of Spezzia, and fresh water crustacea inhabit these localities. These occurrences prevent the sea from becoming too salt by evaporation. When salt water becomes tainted it is very offensive—much more so than fresh water. If, therefore, the ocean were not continually in movement, it would be very injurious.
So much for the water of the sea; let us now see what it does. We will glance at the surface ere we plunge into the depths.
In childhood, and even in after years, we most of us delight in watching the waves of the sea. What finer sight than that we can obtain on the bold Cornish coast with a westerly wind, when the great Atlantic waves come rolling in and dashing up to the tops of the Tintagel cliffs, wearing and grinding them away; hissing up the sands at New Quay, or thundering on the shores of “Bude and Boss”! Then the wind abates, the sea goes down, the billows become waves, the waves to wavelets grow, less and less, until there is a mere ripple on the surface which is never still. The mighty heaving of the ocean breast is the peculiarity of the sea.

Yet, again, as we stand to watch the waves, or run from them as they sweep in foam upon the sloping sand, we shall find that they increase or decrease in force, and the level of the water rises or sinks by degrees. The tide is flowing or ebbing as the case may be. So we know the surface has another—a current motion—besides the undulation of the water. The currents of the ocean are very valuable attributes, the Gulf Stream in particular bringing us warmth and, indeed, rain. There are three movements of the ocean—waves, currents, and tides.
The waves, perhaps, interest us most, as they come rolling in with irregular force, but all mightily impelled by the wind. We have all noticed the ripples on a puddle; the same action of the wind produces the grandeur of the waves of the ocean. The wave comes rolling in before the wind to break against the rocks or beach, and another forms to break in its place; the higher the waves the more quickly they appear to move. But when the[Pg 613] wind has subsided the rolling, or “swell,” remains,—a long, lazy, undulating motion—a rocking to sleep of the billows of the sea. Without a ripple on the surface these huge rollers will glide towards the shore and break upon the shingle with a roaring sound which can be heard for miles, dragging the pebbles after them as they recede with a rattling like bones and marbles. The pebble ridge at Westward Ho! will illustrate this vividly at times, the sound being heard far inland like continuous thunder, and on a calm night, when there is no wind stirring, the roar of the ground swell is weird and mysterious in the gloom.

The height of waves is very varied. Observers say that forty-four feet is about the highest-known wave from hollow to crest. Waves of thirty-five feet have been often met with, and off the Irish coast and in the Atlantic sailors tell of waves “as big as houses.” But houses differ in size as do waves.
The rate which waves are estimated to travel varies with the wind-propelling force. The average hurricane wave travels at about forty-five miles an hour. But earthquake waves—those set in motion by subaqueous disturbance—have been known to travel at the rate of six hundred feet in a second for thousands of miles across the ocean. Such a one occurred after the earthquake which destroyed the town of Arica in August 1868, and the wave crossed the Pacific to Chetham Islands, 5,520 miles, in fifteen hours and twenty minutes. We have many of us seen the great tidal waves, or “bores,” which at certain seasons rush up our rivers—the Severn, for instance—with great violence, and at times forty feet high.
These tidal waves are also experienced in the Ganges, the Amazon, and at Bordeaux, as well as in China and elsewhere.

It may well be imagined that the tides also affect the land, and the theory of these ocean movements is a very interesting study. We have already referred to it under Astronomy, for the Sun’s and Moon’s attraction is the main cause of the phenomenon, which is so familiar and yet so strange. But the consideration of the tides must be again entered upon here ere we proceed to view the effects of the sea upon the land, and how the physical geographical features alter.
Isaac Newton rightly attributed the cause of the tides to the attraction of the moon and sun. Spring tides occur when both luminaries are above the meridian, and the neap, or low tides, happen when the sun and moon are farthest apart. The highest tides are perceived after a new or full moon; the lowest, after she has passed the first or third quarter. In January the spring tide is highest of all, because the earth is nearest to the sun then, and his force of attraction, added to that of the moon, causes a very high tide. With the assistance of the accompanying diagrams we shall be able to make the tidal phenomena clear.

Suppose the moon to be at M, the point J (the sea) will be nearest to the moon and will be attracted, while the earth will exercise a retarding power to a certain extent. This attraction of the water from its usual level causes a kind of vacuum, into which the surrounding water flows and causes a high tide at H. At the opposite side the earth, not the water, is most attracted, and then the water rushes in to a certain extent to fill the vacancy left by the earth’s movement towards the moon. Another high tide is therefore caused at L, but not so high as the tide upon the opposite side, as the Moon is so much nearer the latter. The tide, then, is only the natural movement of the sea water to fill up the space the earth and other portions of the watery mass have vacated in obedience to lunar and solar attraction, which is, to a certain extent, counterbalanced by the attraction and resistance of the earth.
The neap tides are caused by the opposing forces of attraction of the sun and moon. The sun, as it were, pulls one way, the moon the other. The latter (being nearer) having twice the power of the former, causes a tide indeed, but it is a low one. The spring tide occurs when sun and moon together attract the water.
The effects of the rise of the tide are sometimes very disastrous,[Pg 615] and when the wind assists the sea, and heaps up the water, the sight is grand in the extreme. On the coast of Schleswig, at Hallingen, the sea has washed away a whole cluster of islands, and now the waves cause tremendous inundations. About every six years, on the average, a great flood happens for such trifles as a high tide are of no account. In 1362 and in 1834 terrible destruction was wrought; the coffins and bodies were washed out of the graves. Piles of débris are then washed up, and sand and gravel accumulates for a time till again carried away.
Travellers to France will notice the “dunes,” or sandhills of Calais, as the train winds its way to Boulogne. We find that whenever the shore is flat the shingle and sand are blown inwards and form “dunes,” and the sand is distributed far inland, checking all vegetation, and altering the features of the country. The wearing away of rocks by the water, the continual undermining of them by the waves, and sometimes the disengagement of great blocks weighing many tons—all these effects of the sea tend to alter the appearance of the land. We may observe the denudation in many places along the coast—the caves, holes, and tunnels eaten out by the water. In Norway the “Fiords” are very remarkable. They were formed by the upheaval of the land, and tell us of the glaciers which once filled them up. Thus by ice and water the solid land is ground down and eaten away hourly, daily, and for countless centuries, changing the place of the hard rock into a standing water, and the flintstone into a springing well.

We must now plunge beneath the waves, never fearing the rough surface; we shall find all smooth and quiet at the bottom of the sea.
The Bottom of the Sea.
What can we tell about the bottom of the sea to which no man has[Pg 616] ever reached living, and from which we have no information? We can lay our telegraph or telephone lines beneath the waves, and far from the restless waves in those quiet depths where no billows can reach. What treasures must lie hidden at the bottom of the sea! The treasures, the gold and silver, the merchandize, the wealth of centuries. The sailor lies sleeping there
What can we hope to find at the bottom of the sea we cannot reach? Yes, but we can reach it. By sounding with Brooke’s lead (a cannon ball, as shown in the illustration), we can arrive at a certain knowledge of the composition of the ocean bed. The right-hand figure of the two is the lead when being lowered, and while it is sinking the cord remains tight. So soon as it touches the bottom the weight of the cannon ball divides the line, and the tube is easily drawn up again. It has been well greased, and so in the cavity of the rod some shells and sand are found adhering. These fragments tell us the composition of the bottom of the sea.

Here we find tiny shells, just as we find them in chalk, the same formation as that which piled up the cliffs which have risen from, or been discovered, by the sea. By other ingenious contrivances water can be fetched up from the bottom of the ocean, and the temperature can be gauged all along the sounding line. The expedition of the Challenger brought many interesting facts to light. Far down in these solitudes are marine animals,—crustacea, star-fish, seaweeds, and shells,—all of which are carried up by the dredge worked by a steam engine; for the resistance is very great, and the weight supported at the depth of two miles must be considerable, and is equal to four atmospheres. A thermometer has come up crushed even in its iron case, and so the creatures which inhabit and find means to live at the bottom of the sea must be specially fitted by Nature for the locality.
The configuration of the ocean bed has given rise to many different opinions. It has been maintained that there are mountains and valleys, hills and dales underneath the water, all clothed with marine vegetation, equal in height and depth to the terrestrial hills and vales. Again it has been declared that the ocean bed is level; but we find raised portions, which we call islands, which may be the tops of mountains, or portions of the[Pg 617] mainland separated from their parent continent by an inroad of the sea, as are our islands of Great Britain.
The sea-bed, however, is very irregular. We find deep and steep valleys, and high hills, but the picturesque peaks caused by the action of air, frost, and water on earth are not, of course, represented under water. Between the Irish coast and Newfoundland we are told the bed is level for nearly four hundred miles. There is a deep declivity before we reach this plain. The centre of the Atlantic is a plain, and on it the most volcanic islands rise, such as Ascension and the Azores. Between England and Greenland there was at one time a land communication, as we have remarked under Geology, and there are submarine terraces now. [An immense river once ran through Western Europe somewhere about where our islands are.]

Under the Atlantic we have remains of foraminifera and other tiny animals, with red clay and volcanic remains which must have been of submarine origin. The Pacific shows us tops of mountains as islands (Hawaii Isles), and an enormous range must be hidden beneath the waters. What a change in the physical geography of the earth a slight sinking of the water of the ocean would make; England and the Continent would be united, and many sea-mountains (islands) discovered. The greatest ocean depth is four miles and a half, but in many places a few hundred feet less depth than at present would reveal many changes in the land.
Every year since the world has gained its present form the streams and rivers have been pouring water, and carrying mud, stones, and gravel ceaselessly into the ocean. In addition to this, the surface water washes the stones away, animals (corals) build up islands from the depths, and take up space in the ocean. We know that if we put our hand in a basin full of water we displace a quantity of the fluid; so we might imagine that, the sea being already full, every island formed would tend to an overflow[Pg 618] of the sea, and the land would be thereby buried. That the sea does encroach upon the earth we know, but it also recedes. Here is the balance of Nature.
Rivers pour in water and material. The sun absorbs the water and prevents overflow; tiny animals make shells from the material. All the causes we have mentioned tend to permit the encroachment of the waters, but volcanic action and even earthquakes act also to neutralize this tendency by upheaving hills and mountains, which prevent the invasion of the sea by its elevation or by land depression. We have seen in our chapters upon Geology how the ocean beds have been upheaved, and remains of marine animals are daily found upon our highest hills. Thus the forces which sometimes cause such destruction in the earth are the means whereby the waters are kept in their places. But for volcanic action the land might all disappear by denudation and continual wear and tear, and be deposited at the bottom of the sea!
If it were not for currents, of which many defined ones exist in the ocean, and the never-ceasing flow and ebb of the tides, the sea would soon lose its purity and clearness. Though the water is salt and becoming salter, animalculæ and all kinds of plant-animals would still increase and multiply; so the decay of animal and vegetable matter would quickly render the ocean a source of pestilence and death to mankind, and be most injurious to animal life generally. But the movement is so ceaseless, and the various fish and mammalia (whales, for instance), by preying upon each other, as other animals on earth do, keep up the balance of production, and the organic matter deposited in the sea is also cleared away.
That the constant currents of the sea prevent the formation and growth of seaweed is clearly shown by the great “Sargasso Sea,” or tract of weed (Fucus natans), called the Gulf-weed. This great tract embraces thousands of square miles, and is situated in the very middle of the Atlantic Ocean, where there are but few currents; but surrounding it is the Gulf-Stream, an enormous current of water running at a regular rate of four or five miles an hour. This Gulf-Stream is supposed to be caused by the same laws and influences which determine the trade-winds—namely, a constant rarefaction of the water at the tropical parts of the earth, and a corresponding condensation at the Arctic portions, for warm water is much lighter than cold, and when the waters of the tropical regions become lighter, the heavier waters of the cold regions pressing down more forcibly tend to raise them above their proper level; they therefore flow towards those very parts which have sunk down by their contraction, and a constant current takes place; this current is the Gulf-Stream. It runs from the Gulf of Mexico northwards towards Newfoundland, turning by Iceland towards the British Isles, by France and Spain, onwards to the coasts of Africa and South America, the West Indies, and again to the Gulf of Mexico, although the return current does not go by the name of Gulf-Stream. This great stream of water, warmed by the tropical sun, serves the same two purposes fulfilled by the[Pg 619] trade-winds—namely, a circulation and distribution of the superfluous heat of the equatorial regions, warming the northern countries; and cooling, by the return of under-currents, those in the tropics. The fogs of Newfoundland are caused by the great current of warm water entering the cold region and carrying with them surface-currents of moist air, which the cold condenses into fog, just as the breath is visible in a cold atmosphere. England owes its moist and mild climate to the same cause. The depth of the Gulf-Stream itself is very little. It is a mere layer of warm water. (See Sir George Nares’ reports of the Challenger expedition.)

In the foregoing pages you have now seen, and, we hope, gained, some information concerning the sea sufficient, at any rate, to induce you to enter more deeply into the subject than we can at present do. We have learnt how the sea water is composed, and what goes on on the surface. We have discussed waves, and referred to tides and currents, the wearing away and the renewal of land by the sea; we have dived beneath the surface, and found something to interest us at the bottom of the ocean. As we come up again we are surprised to find islands or reefs where none existed when we went down. What has caused this sudden appearance? They may have been slowly raised to the surface by coral insects, or suddenly by volcanic action. Let us consider the coral, which plays a very important part in our Physical Geography, before we proceed to the volcanic island.32
The low-lying islands are those formed by the skeletons of the coral insects, and the Coralline Islands are some of the most wonderful productions of nature. They are only found in warm climates, between the twenty-eighth degrees of north and south latitude, and limestone pure and simple is the chief component of the coral reef, as it is of the mountains erupted from the depths of the sea. “The detritus of corals, echinodermata shells, reticularia, and other living creatures,” says a writer on this subject, “deposit not only[Pg 620] the salts of lime extracted from the ocean, but their own dead bodies to form the hard substance of the rock.”


The coral insect is a zoophyte (Anthozoa), which, as may be seen from the illustrations, assumes curious and elegant forms, and the coral it produces is a limy or calcareous deposit, which is fixed upon a rocky base. As years go on these accretions become greater and greater, and at length rise above the water. When a little distance below it, the reefs form dangerous and frequently unsuspected barriers, upon which ships are wrecked. The red coral is dredged up from the Mediterranean, where there are extensive coral fisheries. This coral is found deep in the water, and never rises to the surface. Formerly there were coral reefs in the European seas, but the changes of temperature stopped their production. The “atolls,” or circular coral reefs with an opening at one side, have been described by Professor Darwin. “Who,” says the great naturalist, “would not be struck with wonder and admiration on catching sight for the first time of this vast ring of coral rock, often many miles in diameter? Sometimes a low green island is seen beyond it, with a shore of dazzling whiteness; outside is the foaming surf of the ocean, and within it a broad expanse of tranquil water, of pale green colour and exquisite purity.” These “atolls” mark the situation of sunken islands, and the extension of them and the barrier reefs would seem to indicate a slow but decided sinking of the bottom of the Indian and other oceans; but the “reefs” tell us that the land to which they are attached has not become depressed, and may have become elevated. We may then conclude that a continual rising and depression of the land is taking place in various oceans, indicating a sinking of the ocean bed in one locality and the result of volcanic activity in another, for no active volcanoes are found in the regions of depression.

We must now leave the sea and come to land again, to consider volcanoes and volcanic action there.
Volcanoes and Earthquakes.
The various phenomena of volcanoes form a subject very difficult to be[Pg 621] explained, as it is impossible to ascertain positively the cause of volcanic action. Whether the earth is interiorly a mass of molten rock and fire, or whether the heat is created by the intense contractile force and movement of rocks, and their motion thus developed into heat aided by chemical combination, we cannot absolutely determine. The theory restricting volcanic phenomena to the upper crust of the earth, by supposing the local accumulations of hot liquid masses of rock, which are forcibly emptied by the expansion of vapours, may perhaps be found the true one.
The majority of the volcanoes are found near, or at no very great distance from, the sea. We may therefore expect to find that water has something to do with the eruptions as it has in the case of the Geysers. But this hypothesis will scarcely hold good in every case, though volcanoes of later ages are limited to regions very different from those in which volcanic action used to be. For instance, in America we have only volcanoes on the Pacific side, and the Andes furnish several. Mexico, Central America, and California possess many volcanoes, and as far north as Alaska we find Mount Elias. There are plenty of extinct volcanoes in Europe, but the Mediterranean produces the active vents; and about the Red Sea and the Caspian, and even in the central chain of Asia, there are volcanoes far from water. The Hawaii isles, on the other hand, are all volcanic, and Australasia furnishes us with remarkable specimens; so altogether the testimony tends to prove that where volcanic remains are apparent the sea had at one time been, or now is, near at hand.
Burning mountains have been familiar to us from our childhood in pictures, and by stirring narrative of destruction wrought by them. The volcano is generally a mountain rising to a cone, but Vesuvius presented quite the appearance of a hollow basin at the top, before it suddenly broke forth and buried Herculaneum in ashes. Von Buck visited it in 1799, and declares it had at one time risen, like an island, from the sea. There are about two hundred and seventy volcanoes at present in activity; four in Europe; eleven in Iceland and Jan Meyen’s land; in Asia, ninety-three; in Africa, twenty-six; forty-six in North America and the Aleutian Isles; twenty-seven in Central America and the Antilles; in South America, thirty-one; and twenty-four islands with volcanic tendencies largely developed. There may be many more “resting.”
Volcanoes, then, are openings or vents which communicate with the melted rock within the earth, and the conical form of volcanoes is owing to the deposits of volcanic matter as it falls from the opening called the crater. If we let a small spade full of mould run through our hands, or from the spade, it will form a small cone, the heavier particles sliding to the base at a certain slope. Thus the volcano builds its own hill, and inside the crater we find cones from which smoke and steam issue. These cones within the cone are the points of issue of vapour and smoke, miniature volcanoes making up a whole.

The signs of eruptions are much the same, and usually occur a couple[Pg 622] of days before the actual outbreak takes place. First smoke is perceived, perhaps, and the escape of various noxious gases accompanied by earthquakes occur. Now the eruption may commence and blow away the summit of[Pg 623] the mountain, as in the case of the commencement of the catastrophe of A.D. 79, when the whole side of Vesuvius was torn away, and continuous showers of ashes fell for days and nights, burying everything, while the hot lava poured down the sides. Stones and ashes with vapours are hurled into the air. Clouds of steam are formed, and vivid electrical discharges take place in these clouds, while water dashes down, carrying stones (“volcanic bombs”), and reflected lurid flames from within are cast on the steaming clouds, which look like fiery columns. Then the lava issues in a white, hot, steady, irresistible stream, covering everything, and burning up all vegetation.

New volcanoes are continually in process of formation, and at Santorin for hundreds of years volcanic action has been busy in forming islands. These violent efforts of Nature frequently give rise to earthquakes, which are the most destructive of natural convulsions. The records of late occurrences are fresh in the minds of all readers, and need not be specified. The slow subsidence and gradual upheaval of the land is still going on, but we are frequently startled by the account of a rupture of the ground or the destruction of a portion of a city.
The motion of the earthquake is generally in a direct line, and undulating. Sometimes what are termed vertical shocks arise and destroy solidly-built edifices. Mountains have been overturned by earthquake shocks, and trees have been twisted round. Sometimes the ground yawns into enormous fissures. The sea is tossed into great waves and encroaches upon the land, and when the sea recedes the recession of the water is followed by a more terrible invading wave sweeping all before it. Earth tremblings often occur far away from volcanoes, and without any visible connection with volcanic action. There are many aspects of land and water which the student of[Pg 624] geography will remember, but which need not be separately treated of. We must, however, refer to plains, plateaus, and lakes. The mountains also play a most important part in Physical Geography and in “Climatology,” as they collect the vapours for rain, and make the valleys fertile, and thick with vegetation. We have spoken of the mountains under Geology, and the various formations and strata will be found enumerated there, but now we have to do with the mountain chains in their physical aspect as regards their shape and appearance on the globe.

Any elevation rising from a base more than 1,000 feet may fairly be termed a mountain, and solitary mountains are usually volcanic, because eruptive rock does not produce chains of mountains. The origin of mountains is probably due to the contraction and compression of the crust of the earth—not merely the surface, but the whole thickness between us and the supposed molten interior. Mountains did not exist from everlasting, for the very good reason that they are (in most cases) composed of stratified rocks. Stratified rocks are sedimentary rocks, and must have been deposited below water, and hardened long before they were thrust up by pressure. Moreover, we find (as has already been explained) shells and remains of marine animals on the higher summits, which prove to demonstration that these mountains are composed of rocks which were laid down under the sea.
Professor Dana was one of the first geologists to advance the theory that contraction and lateral displacement are the causes of the elevation of mountains. A very good illustration of this theory was made by Chamontier, who covered an india-rubber balloon with a thick layer of wax, and when it had hardened sufficiently he pricked a hole in the bladder, which immediately contracted, and the wax at once rose up into tiny similitudes of mountains, showing in a sufficiently clear manner that such protuberances may be[Pg 625] produced by the pressure of the earth’s contraction, and in such a mass as our earth the elevations would naturally be very great.
Professor Geikie has shown how, by a very simple experiment, the contortion of mountain strata is effected by pressure. A number of cloths or towels placed flat on a table represent the sedimentary rocks. Place a board with a weight on the top, and the towels will remain flattened. But by holding two boards at the sides and pressing them together (the weighted board still remaining), we shall find the towels crumpled and upheaved like the Jurassic strata shown in the illustration (fig. 712). Professor Heim calls the central masses wrinkles of the earth’s crust. So the Alps were pressed up or heaved into the air, the weather—rain, frost, snow, and sunshine—imparting the infinite variety of “Horn,” “Needle,” and “Peak,” so expressively applied in Alpine nomenclature;—the Matterhorn, Wetterhorn, Weisshorn; the Pic du Midi, Aiguille de Dru, Aiguille Verte, and many other mountains in well-trodden Switzerland will occur to the reader at once.

The slopes of mountains—though to the casual observer they may appear very much the same—are very different. We sometimes find a long, easy ascent, —more usually a steepish inclination, perhaps 20°;—in other places, such as on the Matterhorn, an almost perpendicular face. Forty-five degrees rise is very steep, and 53° is the limit of any great mountain’s slope. Cliffs and precipices there are, of course; witness the terrible fall from the Matterhorn to the glacier below—thousands of feet with one tremendous leap from the rock to the ice underneath; but mountain slopes are not precipices. As a rule, we find that one side of a mountain chain is steeper than the opposite one. It is harder to climb up from Italy to Switzerland than to ascend in the opposite direction. The Pyrenees are also steeper on the south side. The Scandinavian mountains likewise are steeper in the west. The Himalaya are steepest towards the sea, so are the Ghauts. We here find a difference between the slopes of the New and Old Worlds. In the former we have the less precipitous mountain slopes towards the east; in the old world they are towards the north, and an inspection of a physical map of the world leads us to the conclusion that the Atlantic and Pacific Oceans are the boundaries of entirely different degrees of slopes. The Pacific and Indian Oceans would appear to border the more precipitous mountain sides; the Atlantic and its connections those less steep.
As a rule, we have the most elevated portions of the earth, mountains, and high tablelands, in equatorial regions; and within the torrid zone every terrestrial climate is to be found, owing to the snows of the high mountains[Pg 626] and the heat of the valleys, which are naturally closely connected with the upheaval of mountain ranges. We have already spoken of the never-ceasing influences of the air and water upon the rocks, and we need say little about valleys. There are valleys of dislocation, denudation, and undulation. The great valley of Western Asia, wherein lie the Caspian and Aral seas, seems to have been caused by the upheaval of the Caucasus and the Persian plateau.
Plains are very varied. We have European Heaths and Landes; American Savannahs, Prairies, and Pampas; Asian Steppes, and African Deserts. All of these possess certain features in common, more or less vegetation, and sometimes absolute sterility.
Plateaus, or Tablelands, are elevated plains frequently undulating in character. The Plateau of Bolivia is 13,000 feet high, and extends along by the Andes. The tableland of Quito is nearly 10,000 feet high, and borders on the giants Cotopaxi and Chimbarazo.

Rivers and lakes add not only to the wealth of nations by their usefulness, but, by the additional picturesqueness of their appearance, to the beauty of the landscape. The velocity of rivers would be very much increased if it were not for the strong resistance offered by the banks and the stones to the current, and by friction. The Rhine and the Rhone, if thus unimpeded, would flow at a rate considerably over one hundred miles an hour; and our own little stream (the Thames), instead of eddying peacefully and twirling gracefully by Medmenham or Cookham, would rush along at the speed of the train which so often crosses it on its way to the sea.
The slopes of river-beds, like the slopes of mountains, vary very considerably, and the inclination of a river varies at different places; in a distance of seven hundred miles the Amazon only falls twelve feet, and the current flows chiefly by impetus already acquired. A slope of one foot in two hundred precludes all navigation, and at still greater inclines rapids and cataracts are formed—the great falls wearing away the river-bed by degrees; so it is calculated that hundreds of years ago Niagara Fall was much farther down the river, and the cataract is slowly moving up stream. In time, as the rock wears away, the height will disappear as the celebrated “Falls,” and will become a rapid within a few miles of the lake.
Lakes are derived from river-drainage and springs. Some are very salt, owing to evaporation carrying away so much water, and leaving the accumulated mineral salts. These very salt lakes are likely to dry up, as the supply of water is not equal to the demands of evaporation. Floating islands appear and disappear on many lakes. Derwentwater is one instance. On the uses of lakes and rivers it would be superfluous to dwell. We are more concerned to examine their influence on climate, and in this sense we must also consider mountains. But we will now group all the phenomena of the air and water, and their effect upon climate, under “Meteorology” in the chapters next following.

CHAPTER XLVIII.
PHYSICAL GEOGRAPHY. METEOROLOGY.
THE ATMOSPHERE—WINDS AND AIR CURRENTS—WIND PRESSURE—STORMS—RAIN-CLOUDS—WATER-SPOUTS—ATMOSPHERICAL PHENOMENA.
Under this heading we shall find the atmosphere playing a very important part. The air is composed of oxygen and nitrogen with some carbonic acid gas and aqueous vapour. We have, under the Chemistry section, discussed these constituents which unite to make up the air or atmosphere in the following proportions:—
| Oxygen | 210·0 |
| Nitrogen | 775·0 |
| Aqueous Vapour | 14·2 |
| Carbonic Acid | 0·8 |
| 1000·0 |
It is a fact that all over the world the same chemical result is found. Whether we bottle up the air in the valley, or, as Gay-Lussac did, go up to an elevation of 21,000 feet in a balloon, we shall find the air of the same chemical composition. In Europe, Asia, Africa, and America, it is all the same. The pressure is less as we ascend, and we cannot manage to breathe in very high altitudes so well as upon the ground for which we were fitted, but the air is the same.
The atmosphere, then, is not always equal in density, nor is it quite transparent. The light from sun and stars is, to a certain extent, lost, and it has been calculated that the sun’s rays lose one-fifth part of their brightness passing through the atmosphere. We all know what the air is. We breathe it, we feel it blowing, we witness its effects. Were it not composed as it is we should die or go mad; plants would not live, and the earth would become a desert. Air is everywhere—invisible; a so-called empty vessel is full of air because an animal will live in it till the atmosphere has become vitiated by the carbonic acid from the lungs. Yet air, or rather its watery portion, is visible when condensed.
Vapour is not perceptible. But how does it become so? We cannot see the air, how can we see a portion of it? We can answer this question by illustration. The steam from an engine is not visible on a very hot day. But when the day is damp and dull the vapour is condensed, and becomes visible; then air appears and is resolved into vapour again. This[Pg 629] change was effected by heating water and then cooling it, when it came back to water again. This watery vapour is always present in the atmosphere. Heat, also, is present in the atmosphere, and the sun is the origin of that heat.

Heat, we know, is the effects of the rapid motion of small particles of matter, and is radiated from our bodies—so we feel cold; it reaches our bodies, and we feel warm. So air is heated or cooled by the sun, not in its absence, except when the earth and air have been so warmed during the day that the heat is given out by them long after sunset. We have read of the pressure of the atmosphere in the Physics section, and that warm air is lighter than cold air, as shown in the ascension of the Montgolfier balloon. It is this variation of temperature of the atmosphere that gives birth to one great meteorological agent—viz., the Wind, which we will now consider.
Winds and Air Currents.
We can easily illustrate the cause of winds. Suppose we have a hot room and a cold one, and we suddenly open the door of communication between them, the heated air which has risen to the ceiling of one room will rush out through the upper part of the opening of the door, and the cooler current will flow in just above the floor. If we place a lighted candle in the upper and lower part of the opening we shall see the flame tending outwards from the heated room, and in an opposite direction from the cold room. In the centre of the open door there will be but slight disturbance.[Pg 630] So it is in nature. The warm air ascends, cooler air rushes in to fill the space, and a storm or a breeze is created. The balance must be restored. The upper current probably moves one way, and the lower the other way. Thus clouds are said to be “coming up against the wind” when they are moving in an upper current, or in a different direction to that the wind is blowing just above the earth’s surface.
The wind moves, with varying velocity. We have a gentle breeze when the motion of the air is about five or six miles an hour, a good breeze at twenty-five miles an hour, a high wind at thirty-five, and a gale at fifty. Hurricanes travel at sixty and seventy miles an hour, and do enormous damage. Near the Equator we do not find much wind, and this fact has caused the name of the Region of Calms, or “The Doldrums” of sailors, to be bestowed upon that portion of the globe, but this belt of calm has no fixed position. It follows the sun’s course, and is the region of greatest heat, and, as it were, the centre of a concentric circle of currents. The hot air rises and goes away; air rushes in north and south, and causes what are called the North-East and South-East Trades, or Trade Winds, owing to their being so useful in commerce for ships, or to the old meaning of the word trade, a “regular course.” The calms of the Tropic of Cancer are called the “Horse Latitudes.”
Readers of the life of Columbus will remember how his crew were affrighted at the persistency of the wind which bore him across, for no sail requires shifting, nor is a sheet altered while the vessel is making way with the “Trades.” Were the earth covered with water, we should find the trade-winds blowing equally over the surface, but the varying temperature of the land diverts them. The rarefaction of the air in the Sahara causes a westerly wind to prevail, which blows towards the land, instead of the trade wind we might expect to find.
The Monsoons, again, are caused in like manner, for the ordinary “trade” from the south-east is changed by the elevation of the heated air in Central Asia into a south-west wind, and so in the south, in consequence of the heated air from Australia, the north-west trade appears as a north-east monsoon, but is altered to a north-west wind. Nearly all the year round, therefore, we find the two winds, which are modifications of the “trades,” blowing in different directions and from different quarters. From November to March there is a north-east wind north of the Equator, and a north-west wind blows south of the Equator. From April to September a south-west wind blows at the north, and a south-east wind at the south of the line. The term monsoon signifies a “season,” and the changes of these winds give rise to tremendous storms causing great havoc.
Sea and Land breezes are really little monsoons; they are caused by the heat of the sun in just the same way, but with miniature results. We all know the sea-breeze which comes in as the land gets hot during the day, for the land warms more quickly than the sea under equally existing circumstances. So again, in the evening, the land loses its heat more quickly, and[Pg 631] then the cool air flows out again to take the place of the warmer sea air which is continuing to ascend. The intensity and regularity varies when the degrees of heat are most different between land and sea and in tropical regions; and the varied coast formation will of course affect the wind, but as a rule the fact may be accepted as plainly explained, sea-breeze in the morning, land-breeze at night, and amateur sailors in boats at our watering-places will do well to bear this in mind.
There are a great number of local winds deriving their names from their direction or influence. We may mention them briefly. The special terms for winds are—
- The North Wind, or Tramontana.
- The North-East Wind, or Greco.
- The East Wind, or Levanter.
- The South-East Wind, or Sirocco.
- The South Wind, or Ostro.
- The South-West Wind, or Libeccio.
- The West Wind, or Ponente.
- The North-West Wind, or Maestro-Mistral.

The Mistral, or Maestrale, is well known at Nice as the north wind, while at Toulon it is a north-east wind. The other winds, such as the Sirocco, which in some places is a warm, damp wind, in Madeira is a hot wind, and likewise in Sicily, where it is equally warm and damp like steam. It has different names in various countries, such as Samiel in Turkey, and sometimes as Föhn in Switzerland, where it may, however, be a north wind—which, as all travellers know, is a dry and a hazy-weather breeze, yet sometimes moist. The Simoon is a very hot wind raising sand-storms in the[Pg 632] deserts, and experience has shown it to be very prejudicial to life in consequence of the fine sand and the tremendous heat it carries with it. Egypt is subject to another hot wind, called the Khamsin, and the west coast of Africa is subject to the Harmattan, a dry, easterly wind. The cold, dry wind of the Himalaya is known as the Tereno. In South America there is the same wind, the Pampero blowing east and south-east. The Euroclydon, mentioned by St. Paul, is the modern bora over the Adriatic. Malta rejoices (or laments) in the Gregale, a north-east wind. There are several other terms, such as the Puna of Peru, a very drying wind; the Purgas in Labrador, the Tourmente in France, and Guxen in Switzerland. Then we have the Hurricane, from “Ouracan” of the Caribs; the Typhone, or Tae-fun of China, so called from the dreaded god Typhon of Egypt; and the Tornado—all very violent winds, and circling round, causing, so to speak, whirlwinds, by which trees are uprooted, and houses destroyed.
The measure of the velocity of wind is performed by anemometers, which record the velocity in feet per second, and the amount of pressure. The anemometer is a well-known apparatus, with its four arms terminating in “cups” and a “tablet” anemometer, which is more or less disturbed or deflected from the vertical line by each gust of wind, and thus the score of degrees is marked by an indicator, which is moved as the tablet is deflected. We annex a table of wind pressure and velocity—
Pressure of the Wind.
| Velocity. | Pressure per sq. foot. Rouse and Smeaton. |
Description of wind. | |
|---|---|---|---|
| Miles per hour. | Feet per second. | ||
| 1 | 1·47 | 0·005 | Very gentle. |
| 2 | 2·93 | 0·020 | |
| 3 | 4·40 | 0·044 | Light airs. |
| 4 | 5·87 | 0·079 | |
| 5 | 7·33 | 0·123 | Light breeze |
| 10 | 14·67 | 0·492 | |
| 15 | 22·00 | 1·107 | Brisk breeze |
| 20 | 29·34 | 1·968 | |
| 25 | 39·67 | 3·075 | Strong breez |
| 30 | 44·01 | 4·429 | |
| 35 | 51·34 | 6·027 | High wind. |
| 40 | 58·68 | 7·873 | |
| 45 | 66·01 | 9·963 | Gale. |
| 50 | 73·35 | 12·300 | |
| 60 | 88·02 | 17·715 | Heavy Gale. |
| 80 | 117·36 | 31·490 | Hurricane. |
| 100 | 146·70 | 49·200 | Tornado. |
The south-west wind is more constant than any other, and the west wind in our islands is more frequent than the east; tables have been compiled showing the average number of days upon which the winds blow from different quarters, but need not be quoted. Storms can generally be antici[Pg 633]pated by the barometer, which falls very quickly for “wind.” The quarter whence the breeze may be expected is often indicated by the streamers of clouds, or “mare’s tails,” across the sky; though we must admit the opposite direction to that anticipated by casual observers may often prove the right one.
Hurricanes and tornadoes are really whirlwinds in motion. The rotatory movement of the air is from right to left in the northern hemisphere, and from left to right in the southern—that is, in the opposite and same directions respectively as the hands of a watch move. The whirlwinds are caused by two currents of air meeting at a certain angle, just as a whirlpool is the result of opposing currents of water.

The use of the wind in nature cannot be over-estimated. It is frequently destructive and terrible in its effects, but these comparatively trifling damages are as nothing when weighed against the advantages conferred upon mankind by the wind and the currents of the atmosphere. The north cold is tempered by the warm south wind. The pollen and the seeds of plants are borne on the wings of the wind, and the clouds are carried over the land to “drop fatness” upon our fields. The want of free circulation of air is very injurious. Witness the terrible affliction of goitre, so prevalent in the closely shut-in valleys such as the Rhone Valley, where cretinism or congenital idiotcy is distressingly prevalent.
Vapour and Clouds.
Vapour, as we have heard, is invisible, and is produced by heat. As the visible steam (which is invisible as it issues from the safety valve at the actual aperture, and nearly invisible altogether on a hot day) is produced by combustion, so vapour is produced by the heat of the sun’s rays. But there are some observations to be made respecting these rays, which are the cause of vapour, and therefore of cloud, rain, dew, frost, ice, snow, and water all over the earth; and we must look at the circumstances closely.
Those who have followed us through this volume will remember that at the end of Chapter VIII. we remarked upon the spectrum, and made a few observations respecting the heat spectrum, and the velocity of light rays, which became too rapid to be observed, and then they developed heat—invisible heat—produced by non-luminous waves, which proceed from the sun as surely as visible rays or light. Professor Tyndall has written very pleasantly upon this subject, and, with his clear leading, any reader can study for himself.
We have now arrived at the conclusion that there are visible and invisible rays giving us respectively light and heat. These latter are the means whereby the ice is melted, and by which water is evaporated to vapour, and formed into Clouds when it is chilled or condensed. Here is another link in the beautiful chain constructed by Nature. We cannot penetrate far into any portion of the system of the universe without being struck with the wondrous harmony that exists between every portion of it. Thus heat and light, vapour, cloud, rain, dew, and ice are all intimately connected.
A cloud, then, is a visible body of vapour in the atmosphere, which is supported by an invisible body of vapour. It will remain thus invisible so long as the atmosphere is not saturated with moisture. The air can contain a great quantity of moisture without its being rendered visible, and so when the day is hot we see no steam from the locomotive. It is absorbed into the dry atmosphere. But when the day is “damp” we find that the air has nearly as much moisture as it can carry, and the steam is condensed, a portion falling in tiny drops like rain. This is proved every day in cold weather when ice is found in the windows—the cold air has condensed and frozen the water breathed out from our lungs, and snow has been known to fall in a ball-room when a cold current of air was admitted.
People are sometimes apt to think that if the sun were very hot, glaciers, and such icy masses, would diminish; but we think after what has been said respecting the power of the sun’s rays to evaporate water, all will see that the contrary is the fact. Without sun-heat we should have no cloud, and as clouds give us rain and snow and ice and glacier, we must come quickly to the conclusion that glaciers and snow are the direct results of the heat of the sun. The “light” rays of the sun do not penetrate snow, and that is why our eyes are so affected in snowy regions. The poor Jeannette[Pg 635] sufferers a short time since were blinded by reflected light, and dark spectacles are worn on all Alpine expeditions. The invisible rays, as we have said, dissolve the ice into rivers.
The atmosphere produces clouds by expansion of vapour, which chills or cools it, and it descends as rain. To prove that expansion cools air is easy by experiment, but if we have no apparatus we must make use of our mouths. In the body the breath is warm, as we can assure ourselves by opening our mouths wide and breathing upon our hands. But close the mouth and blow the same breath outwards through a very small aperture. It is in a slight degree compressed as it issues from the lips, and expanding again in the atmosphere feels colder. Air compressed into a machine and permitted to escape will form ice.

Water is present in clouds which assume very fantastic and beautiful forms. We know nothing more enjoyable than to sit watching the masses of cumuli on a fine afternoon. The grand masses built up like the Alps appear to be actual mountains, and yet we know they are but vapour floating in the air, and presently to meet with clouds of an opposite disposition, and produce a thunderstorm with torrents of rain. Those who will devote a few minutes every day to the steady examination of clouds, will not be disappointed. They give us all the grandeur of terrestrial scenery. Mountains, plains, white “fleecy seas,” upon which tiny cloudlets float, and low upon the imaginary yet apparent horizon, rise other clouds and mimic mountains far and farther away in never-ending distance.
A pretty, light, feathery cloud, with curling tips and fibres, is known as cirrus, and exists at a very great elevation. Gay-Lussac went up in a balloon 23,000 feet, and even at that height the cirri was far above him in space. We can readily understand that at such an extreme elevation they must be very cold, and they are supposed to consist of tiny particles of ice. Such clouds as these are very frequently observed at night, as cirro-cumulus around the moon, and a yellowish halo, apparent to all observers, is thought to be coloured by the icy particles of the lofty cirrus. The beautiful and[Pg 636] varied phenomena of perihelia, etc., are due also to the snowy or icy flakes of the cirri and cirri-cumuli, caused by the refraction of light from the frozen particles. These cirri clouds are indicative of changeable weather as “Mares’ tail” skies, and long wisps of cloud, foretelling storm.
The cirro-cumulus is the true “mackerel” sky, and is formed by the cirri falling a little and breaking off into small pieces of cumulus, which is a summer (day) cloud generally, and appears in the beautifully massive and rounded forms so familiar. The stratus is, as its name implies, a cloudy layer formed like strata of rock. It is generally observable at night and in the winter. It often appears suddenly in the sky consequent upon diminished pressure or a rapid fall of temperature. It is low-lying cloud sometimes, and at night forms fogs.

The cirro-stratus is perceived in long parallel lines, and indicates rain; when made-up rows of little curved clouds it is a certain prophet of storm, and when viewed as haze is also indicative of rain or snow. “Mock-suns” and halos are often observed in the cirro-stratus.
The nimbus is the rain-cloud, or condition of a cloud in which rain falls from it. It is upon this rain-cloud we can perceive the rainbow, and on no other cloud, but otherwise only in the sky.
We have now seen the varieties of cloud and their common origin with fogs and mists, which differ from them only in the elevation at which they come into existence, according to the condition of the atmosphere.
The uses of clouds are many and varied. Their first and most apparent use seems to be the collection and distribution of rain upon the earth. But besides this, they shelter us from the too great heat of the sun, and check the evaporation at night. Supposing we had no clouds we should have no rain. If we had no rain the earth would dry up, and the globe would appear as the side of the moon appears—a waterless desert. The invisible vapour in the atmosphere will produce cloud, but the moon can have no atmosphere in that sense. Vapour will also absorb heat, and intercept the sun’s heat rays, acting much as clouds do in preventing radiation and great changes of temperature.33
All animals and plants depend upon moisture in the atmosphere as much as upon the varying degrees of warmth. A dry east wind effects us all prejudicially; warm, soft airs influence us again in other ways. Air will be found drier as a rule in continents than in islands or maritime districts, and this will account for the clearness of the sky in continental regions. Fogs and mists arise when the air is what is termed saturated with moisture, and colder than the earth or waters upon it. So the celebrated and dangerous fogbanks of Newfoundland arise from the warm water of the Gulf Stream, which is higher in temperature than the air already saturated. And the same effect is produced when a warm wind blows against a cold mountain; the air is cooled, and condenses in cloud.
The cooling of the breath by the exterior air is exemplified in winter when we can perceive the vapour issuing from our mouths as we speak.

Rain, Snow, and Dew.
Rain is produced by the condensation of vapour. “Vesicular vapours, or minute globules of water filled with air,” compose the clouds, and at last these vesicles form drops, and get heavy enough to come to the ground. Perhaps they are not sufficiently heavy to do so, and then they are absorbed or resolved into vapour again before they can get so far, because the lower strata of air are not yet saturated, and can therefore contain more moisture.
On the other hand, we may experience rain from a cloudless sky. This is no very uncommon case, and occurs in consequence of the disturbance of the upper strata when warm and cold currents come into collision and condense the vapours.
Rain is very unequally distributed. We shall find that the region of calms, which we mentioned in a former page, is also the zone of the greatest amount of rain. The heated air rises and falls back again, there being little or no wind to carry it away. The rainy season, therefore, sets in when a place enters the zone of calms. Equatorial districts have two rainy seasons, as they enter twice a year into the region of calms, but most places have[Pg 638] only a wet and dry season, while north and south of the calm region we find rainless districts, or zones tempered by the trade winds, which are dry winds.
But if we suppose—as indeed is the case in South America—that these dry winds happen to come in contact with a cool mountain, the moisture of the air is precipitated in rain. In Australia, on the contrary, we have portions of land actually burnt up for want of rain, because the mountain chain breaks the clouds, so to speak, on a limited corner of the island, while the interior is parched. The winds also coming over India from the Bay of Bengal discharge clouds and rain in the Himalayan slopes. So we perceive that the situation of mountain chains have much to do with the rain-fall, and of necessity, therefore, with the vegetation and fertility of the land. This is another noticeable link in the great chain of Nature.

Perhaps it may now be understood why westerly and south-westerly winds bring rain upon our islands, and why the counties such as Westmoreland and Cumberland and those in Wales receive more rain than any other part of the United Kingdom. Seathwaite, so well known to tourists in the lake district, has the proud position of the wettest place in these islands. We find that when the westerly wind sets in it has come across the warm Atlantic water and become laden with moisture, which, when chilled by the mountains, is precipitated as rain.
The amount of rain that falls in the United Kingdom is carefully measured by rain-gauges, some of which are extremely simple. The water is caught in a funnel-mouthed tube, and measured in a measuring glass every four-and-twenty hours. Thereby we can tell the annual rainfall in any given district, whether it be twenty inches or a hundred. One inch of rain actually means one hundred tons of water falling upon one acre of land. Therefore, if the annual report of rainfall (including all moisture) be twenty inches, we have an aggregate of 2,000 tons of water upon every acre of surface within[Pg 639] the district. Twenty inches is a very low estimate. Some places have an annual rainfall of forty or fifty inches. In Cumberland we find 165 inches has been recorded! If we then multiply these last figures we get the enormous quantity of 16,500 tons of water upon every acre of land in the district in one year. It is reported from India that in the Khasia Hills the average is 610 inches, which must be the maximum rainfall in the world. At other places, in the north-west provinces, the fall is only seven inches. Sometimes in tropical rains we find fifteen inches of rain in a day, and that has been exceeded.
We can now judge of the enormous amount of moisture carried up by the sun and dispersed over the earth in rain, which swells our brooks and rivers, cleanses the air of its impurities, supplies our springs, carries with it into the sea lime from the rocks for the shells of marine animals, and then leaving its salts, is again evaporated to form clouds, which discharge the fresh water continually upon the earth in a never-ceasing rotation.
Snow.
“We all know what Snow is,” you will say, perhaps. Well, then, will any ordinary young reader tell me what he knows about snow? “It falls from the sky in white flakes,” says one. “It’s frozen rain,” remarks another. “Why, snow is snow,” says a third. “There’s nothing like it; it’s white rain-water frozen.”

The last answer we received is the nearest of all. Snow is not snow, paradoxical as that sounds. Snow is Ice! Flakes of snow are ice-crystals—white, because reflecting light. In the section of Mineralogy we mentioned crystals, which are certain definite shapes assumed by all substances, and we gave many examples of them. Just as alum crystallizes and rock crystal assumes varied and beautiful forms, so ice crystallizes into six-rayed stars.
It is to Professor Tyndall that the world is chiefly indebted for the descriptions of snow crystals and ice flowers. In his work upon “Heat as a Mode of Motion,” this charming writer shows us the structure of ice flowers. He describes a snow shower as a “shower of frozen flowers.” “When snow[Pg 640] is produced in calm air,” he says, “the icy particles build themselves into stellar shapes, each star possessing six rays.” We annex some drawings of snow crystals, which are, indeed, wonderfully made. Hear Professor Tyndall once again:—
“Let us imagine the eye gifted with a microscopic power sufficient to enable us to see the molecules which compose those starry crystals: to observe the solid nucleus formed and floating in the air; to see it drawing towards it its allied atoms, and these arranging themselves as if they moved to music, and ended by rendering that music concrete.” This “six-rayed star” is typical of lake ice also.

Snow sometimes reaches us in a partly melted condition; under these circumstances it is called sleet, and snow being much lighter than rain (ice is lighter than water), it descends less directly, and represents about one-tenth the depth of the rain-fall. The use of snow in warming the earth is universally acknowledged, and as it is such a bad conductor, a man in a snow hut will soon become unpleasantly warm.

Ice is only water in another form, and snow is ice; and it is the air in the snow that gives it warming properties. These are all simple facts, which any one by observation and careful reading and study may soon[Pg 641] ascertain for himself. We have another frozen fall of water from the clouds—viz., hail, which may possibly be the development of sleet.
Hail is formed by the falling rain being frozen in its descent, or when different currents meet in the atmosphere. A hail-storm is accompanied with a rushing sound, as if the hail-stones were striking against each other. They are very destructive, and actual hail showers occur in summer more frequently than in winter, and a peculiarity noticeable with regard to hail is its infrequent occurrence during the night.
Records of destructive hail storms are plentiful. The hail assumes a great size, weighing sometimes as much as two ounces, and measuring several inches round. Thunder and lightning are very frequent accompaniments of hail showers.
Dew is moisture of the atmosphere deposited on a cool surface—another form of condensation, in fact. Cold water in a tumbler will produce a “dew” upon the outside of the glass when carried into a warm atmosphere. Such is the dew upon the grass. It is produced by the air depositing moisture as it becomes colder after a warm day when much vapour was absorbed. Warm air can hold more water than cold air, and, the saturation point being reached, the excess falls as dew at the dew (or saturation) point. We have previously remarked that one use of clouds was to prevent rapid radiation of heat which they keep below. Under these circumstances—viz., when a night is cloudy—we shall find much less dew upon the grass than when a night has been quite clear, because the heat has left the atmosphere for the higher regions, and has then been kept down by the clouds; but on a clear night the air has become cooled rapidly by radiation, and having arrived at saturation point, condensation takes place.
Dew does not fall, it is deposited; and may be more or less according to circumstances, for shelter impedes the radiation, and some objects radiate less heat than others. Hence some objects will be covered with dew and others scarcely wetted.
When the temperature of the air is very low,—down to freezing point,—the particles of moisture become frozen, and appear as hoar-frost upon the ground. Thus dew and hoar-frost are the same thing under different atmospheric conditions, as are water and ice and vapour.
We have now come round again almost to whence we started. We have seen the land and water, and the parts that water, in its various forms, plays upon the land, and its effects in the air as rain, etc. We have noticed the winds and air currents as well as the ocean and its currents. We know what becomes of rain and how it is produced, and how the sea works upon the shore, and how clouds benefit us. There are besides some less common phenomena which we will now proceed to examine.

CHAPTER XLIX.
PHYSICAL GEOGRAPHY. METEOROLOGY (continued).
ATMOSPHERIC PHENOMENA—THUNDER AND LIGHTNING—AURORA BOREALIS—THE RAINBOW—MOCK SUNS AND MOCK-MOONS—HALOS—FATA MORGANA—REFLECTION AND REFRACTION—MIRAGE—SPECTRE OF THE BROCKEN.
There are a great number of interesting, and to inhabitants of these islands uncommon,—perhaps we might say fortunately uncommon,—phenomena, which overtake the traveller in other countries. We have referred to whirlwinds and tornados, and will now mention two phenomena connected with these storms. There is the water-spout, for instance, and sand-pillars in the desert, which are whirled up by these winds in spiral columns of water and sand respectively. The tiny whirlwind at cross-roads, which picks up straws and leaves, is the common appearance of whirling or crossing currents of air.

Waterspouts, when they are permitted to come near a ship at sea, or when they break upon land, which is seldom, are very destructive. The waterspout is begun generally by the agitation of the sea, and the cloud above drops to meet the water, which at last unites with it, and then the column of whirling liquid, tremendously disturbed at the base, advances with the prevailing wind. Its course is frequently changed, and ships within its influence would be speedily wrecked. The only way to save the vessel is to fire a cannon ball through the column and break it.

A waterspout once devastated a district in the Hartz mountains of Saxony. “A long tube of vapour descended to the earth, and several times was drawn upward again; but at last it reached the ground, and travelled along at the rate of four-and-a-half miles in eight minutes, destroying everything in its way.”
On another occasion at Carcassonne in 1826, “a reddish column was seen descending to the ground, and a young man was caught up by it and dashed against a rock.” His death was instantaneous.
The cause of these whirling winds is supposed to be in the action of vertical currents of air which ascend heated, and return rapidly as cold air. The “waterspouts,” etc., are quickly formed. The tornado is a monster whirlwind like a waterspout in form, and advances at a tremendous rate—eastward as a rule. It moves in leaps and bounds, passing over some portions[Pg 644] of the ground and descending again. The current of air is directed to the centre; the cyclone, as mentioned, has a spiral or rotatory movement.
Thunder and lightning have been, to some extent, described under the head of Electricity, but some observations may also be introduced here, as storms of that nature appertain to meteorology distinctly.
Electricity is always present in the atmosphere, and arises from evaporation and condensation as well as from plants. As the air becomes moist, the intensity of the so-called “fluid” increases, and more in winter than in summer. Clear skies are positively electric, and when large, heavy clouds are perceived in process of formation in a sky up to that time clear, a storm is almost certain to follow. These “thunder clouds,” in which a quantity of electricity exists, attract or repel each other respectively. The cloud attracts the opposite kind of electricity to that within it; and when at last a tremendous amount has been stored up in the cloud and in the air, or in another cloud, the different kinds seek each other, and lightning is the result, accompanied by a reverberation and commotion of the air strata, called thunder.
Lightning most frequently darts from cloud to cloud, but often strikes the ground, whereon and in which are good conductors, such as wet trees, metals, running water, etc. The “electric fluid” assumes different forms—“forked,” “sheet,” and “globular.” The second is perhaps the most familiar to us, and the third kind is the least known of all. There are many well-authenticated instances on record in which lightning with the form and appearance of fireballs has entered or struck houses and ships.
“Fulgarites” are vitreous tubes formed in sandy soils by the lightning in search of subterranean water-courses, for running water is a great conductor of electricity.34 The fire-ball form of lightning has been known to enter a school-house where a number of children were, and to singe the garments of some, killing others. The ball passed out through a pane of glass, in which it bored a hole, breaking every other pane, however, in its transit. Another instance occurred in which the lightning ran about the floor of a room, and descending the stairs, exploded without doing any injury.
Lightning, like the electric current of the laboratory, will not always set fire even to inflammable objects. An electric spark can be passed through gunpowder without setting fire to it, and lightning will often shatter the object without firing it. Death by lightning is instantaneous, and in all probability quite painless; for we may argue from analogy, that as those who have been rendered insensible by lightning have had no remembrance of seeing the flash which strikes so instantaneously, nor of hearing thunder after it, it is instantaneous in its effects. Besides, the natural attitude is preserved, and the face is usually peaceful and limbs uncontorted after death by lightning.
There are some curious electrical phenomena, such as St. Elmo’s Fire, already noticed under Electricity; and in some parts of America, in very hot weather, such a light is perceived to issue from trees as the fire glides[Pg 645] through the forest. Many instances are on record concerning the luminosity of pointed sticks, and even of the tails and manes of horses in certain conditions of the atmosphere, and of the universal power of electricity and its pervading influence in nature. The benefits conferred by thunderstorms in purifying the air, and in the production of ozone and nitric acid, are very great, and apart from the magnificent phenomena exhibited, are well worth our attention, though beyond our reach.

Terrestrial magnetism, however, is still more puzzling in its action than is electricity, and the study of the needle, its destination, inclination, and intensity, which are marked upon charts, just as are the weather reports of the Times, is an interesting one. These magnetic maps are termed the charts of Isoclinic and Isodynamic lines. The declination of the magnetic needle from the true north is its deviation from that point, and the “inclination” is its dip towards the horizon. The line of its direction being known as the magnetic meridian, its divergence from this line constitutes its declination. There are[Pg 646] places where it does not deviate, and these, in direction north and south, are called lines of “no variation.” There are also places in the equatorial regions where the needle does not “dip.” The line connecting such places is termed the Magnetic Equator, and north or south of this the needle dips respectively to north or south in degrees coinciding with the distance from the equator.
The earth, then, acts as a magnet, and attracts the needle, but the magnetic poles are not identical with the terrestrial poles. The north magnetic pole was reached in 1831 by Sir James Ross, when the dip was only one minute less than 90°, and the south magnetic pole was very nearly reached also by him in 1840. The magnetic equator passes between these two points.

It is to magnetic atmospherical disturbance that the aurora is due. These northern (or southern) phenomena are extremely brilliant and diversified. In temperate regions the aurora does not present such grand forms as in the extreme north. There the spectacle is astonishingly beautiful. The sky at first clouds over, and mist is developed. Humboldt has eloquently described the aurora borealis, and the beautiful changes of light, the constant movement, flashes, etc., denoting a “magnetic” storm, as electrical discharges indicate an electric storm, although the area affected by the former is far more extensive than that of the latter, and there is no thunder accompanying the magnetic storm, with the production of which the electricity of the earth is unassociated. To the continuous flow of this electricity the aurora is due, and the flashes are only the electric current descending[Pg 647] towards the earth. But the true reason of the phenomena may have to be yet discovered, for nothing absolutely certain is known as to the origin of the aurora.
Amongst the numerous effects of refraction and reflection of light the Rainbow is most common and the most beautiful. If we hold a chandelier “drop” in the sunlight, we shall see a brilliant representation of the rainbow on the wall or on the carpet. The three colours—red, yellow, and blue—mingle or shade away into seven—red, orange, green, blue, yellow, indigo, and violet. These colours are all found in the rainbow.

The colour of the atmosphere—the usual blue tint of the sky—arises from the blue rays of the spectrum being reflected more than the rest by the aerial particles, and the less vapour the bluer the sky, because the vapour gives it a whitish or misty tint. At sunset and sunrise the sky is red or yellow, like gold, or of crimson hue. This is because the sun’s rays have so much farther to come to us at sunrise or sunset, as you will readily perceive if you draw a line from the sun to the sides and then to the top of the arc of the heavens. The blue rays are thus lost in space, while red and yellow, which travel so much faster than blue, are transmitted to the eye, not giving the air time to absorb them.
If you go under water and look at the sun it will appear very fiery indeed, and we may likewise imagine that fiery crimson rays, which betoken atmospherical disturbance, very often are due to the moisture through which they are transmitted. Wet and storm frequently succeed a crimson sunset, which betokens much moisture in the air. The sun is similarly seen through the steam issuing from an engine, and the colours vary according to the density of the steam in its stages of condensation.

Vapour, we know, is invisible and transparent, but when it has been condensed into rain-drops, and the sun is shining, if we stand with our backs to the sun we see what we call the rainbow, because a ray of light entering the drop is reflected, and as all rays are not of equal refrangibility, the light, which is composed of three simple rays, is divided and reflected into those and the complementary colours. When the sun is at the horizon, the rainbow, to an observer on the earth (but not on a mountain), will appear to be a semi-circle. The higher the sun rises the lower is the centre of the rainbow. So we can never see rainbows at noon in summer because the sun is too high. A second rainbow is not uncommon, the second reflection producing the colours in a different order. The colours in the “original” range from violet to red; in the “copy” they extend from red to violet. “Rainbows” are often visible in the spray of waterfalls and fountains.
Halos are frequently observed surrounding the moon, and then we are apt to prognosticate rain.
is an old couplet referring to the appearance of the moon, and is supposed to foreshadow the weather by the size of the halo, which is caused, as we know, by the existence of vesicular vapour in the atmosphere.
Mock Suns, or parhelia, and mock-moons, or paraselenæ, are continually[Pg 649] observed in cold climates, where the tiny ice particles are so abundant in the air. These phenomena were recognized by the ancients, and halos round the sun can be observed by means of darkened glasses. We annex an illustration of a mock sun and moon seen on the continent of Europe. Readers of Mr. Whymper’s “Scrambles in the Alps” will remember the gorgeous, and to the guides mysterious, fog-bow or sun-bow seen as the survivors of the first and most fatal ascent of the Matterhorn in 1865 were tremblingly pursuing their descent over the upper rocks of that mountain.
The Mirage, or Fata Morgana, is a very curious but sufficiently common phenomena, and in the Asiatic and African plains it is frequently observed. When the weather is calm and the ground hot, the Egyptian landscape appears like a lake, and the houses look like islands in the midst of a widely-spreading expanse of water. This causes the mirage, which is the result of evaporation, while the different temperatures of the air strata cause an unequal reflection and refraction of light, which give rise to the mirage. Travellers are frequently deceived, but the camels will not quicken their usual pace until they scent water.
The Fata Morgana and the inverted images of ships seen at sea are not uncommon on European coasts. Between Sicily and Italy this effect is seen in the Sea of Reggio with fine effect. Palaces, towers, fertile plains, with cattle grazing on them, are seen, with many other terrestrial objects, upon the sea—the palaces of the Fairy Morgana. The inverted images of ships are frequently perceived as shown in the illustration (fig. 729), and many most extraordinary but perfectly authentic tales have been related concerning the reflection and refraction of persons and objects in the sky and on land, when no human beings nor any of the actual objects were within the range of vision.
It will be well to explain this phenomenon, and the diagrams will materially assist us in so doing, for the appearances are certainly startling when realized for the first time. The Spectre of the Brocken we see mimics our movements, and we can understand it. But when apparently solid buildings appear where no buildings have been erected,—when we see—as has been perceived—soldiers riding across a mountain by a path, or ledge, perfectly inaccessible to human beings even on foot, we hesitate, and think there is something uncanny in the sight. Let us now endeavour to explain the mirage.
Suppose that in the annexed diagram the space enclosed between the letters A, B, C, D, be a glass vessel full of water. The ship is below the horizon, the eye being situated at E—the glass vessel of course representing the atmosphere charged with moisture. The eye at E will perceive the top of the mast of the ship, S, and we may imagine a line drawn from E to S. Then put a (short focus) convex lens at a just above this (imaginary) line, and a concave one, b, just over it. Through the former an inverted ship will be seen, and an erect one through the latter at S′ and S″ respectively. We now have the effect in the air just as reproduced in nature by the dif[Pg 650]ference in temperature in air strata, which cause it to act like a concave lens when the density of the water diminishes towards the centre, and like a convex lens when it is increased.

This can be proved by heating the air (by hot irons) above the glass vessel filled with oil, and the effects will be just the same as through the lenses. Dr. Wollaston obtained the mirage by using a clear syrup,—about one-third of the vessel full,—and filling it with water. The gradual mingling of these fluids will produce the phenomenon. The illustration in the margin (fig. 731) shows us the rays proceeding from the ship’s hull, and refracted into the line reaching the eye, above the line proceeding from the mast, so the ship appears hull uppermost; the rays cross at x. But if they did not cross before they reach the eye, the image would appear as at s´ p´ in an erect position.

The Spectre of the Brocken arises from a different cause. Such appearances are only shadows,—projected on thin clouds or dense vapours at sunrise, or when the sun’s rays are directed horizontally,—for of course vertical rays will throw the shadow on the ground on to the zenith. Balloons are also reflected thus, and much interest has been caused by the appearance of a twin balloon, until the aerial voyagers have discovered the cheat by seeing the shadowy aeronaut imitating their actions, and the second balloon has been discovered to be an airy nothing.

CHAPTER L.
PHYSICAL GEOGRAPHY. CLIMATOLOGY.
WEATHER, CLIMATE, AND TEMPERATURE—ISOTHERMAL LINES—ISOBARS, WEATHER FORECASTS, AND SIGNS OF THE SKY.
It is usually considered a sign of a paucity of ideas when one begins a conversation about the “weather,” but there can be no doubt that there is no more interesting question in social life at certain times as to whether it will or will not rain. Our outdoor amusements are all dependent upon weather, and a little cloud may throw a deep shadow over all our pleasure if we neglect to bring out an umbrella, or to carry a waterproof. We are never independent of what we term the “capricious” climate, but in reality the laws of “the Weather,” though so imperfectly understood, are fixed and invariable, and if we could read the signs in the sky and learn the condition of the atmosphere, we might leave the “prayers for rain” and “for fine weather” out of the Church service, for then we should understand that unless miracles are performed for us the laws of Nature can in no wise be altered.
Of late years weather forecasts (not prophecies) have come before us in our newspapers after the manner instituted by the late Admiral Fitzroy, whose name has become a household word in England. But at the commencement of the Christian era and before that time the signs of the heavens and the behaviour of animals and birds were noted with reference to changes of weather. If we read Virgil we shall find numerous references to these portents, and the translation usually quoted will furnish us with information which must be as true nowadays as it was in Virgil’s time, for wild animals do not change their habits. Speaking of wet weather in the Georgics the poet wrote:—
We might quote further selections respecting the signs in the heaven and earth mentioned, but the foregoing verses will be sufficient to illustrate our position, and to show us that weather forecasting is, at any rate, as old as the Christian era.
The moon is generally supposed to influence the weather—a “Saturday’s Moon” being particularly objectionable, or when she appears anew at some hours after midnight thus—

Weather permitting, we can go out and study the clouds as described in the foregoing chapters, or consult the barometer, and see which way the wind blows. The child will tell us that a high “glass” means fine weather, and a low barometer indicates rain, but this is only relatively true. A high glass may be falling, a low glass may be rising. A sudden fall or a sudden rise are indicative of bad, windy weather, or a short-lived fine period. The glass may rise with a northerly wind, and rain will supervene, so careful observation is necessary before one can obtain even a superficial knowledge of the weather. (See subsequent observations on “Weather.”)
The Americans telegraph the results of their observations of coming storms across the Continent, corrected by the signs noticed and recorded by vessels arriving in New York. Thus they are frequently very accurate; steady application and observation at Sandy Hook must give them a great deal of useful information for the “forecasts.”
The word Climate is derived from the Greek klima, a slope; and thus at a glance we perceive how the aspect it presents to the rays of the sun in the earth’s revolutions, must affect the “climate” of a country. Of course the[Pg 653] position of any portion, the elevation and locality of the mountains, have also a share with the soil, winds, rains, and sea-board, in determining the climate of any region. Many points have already been touched upon in former chapters. Temperature, moisture, and vegetation are the chief natural features which determine climate, and we must find out the position of the land with reference to the sun first, to ascertain the climate.
The more vertical the sun is the hotter the atmosphere, for the rays strike directly upon the earth, which radiates the warmth received. These heat rays are, as we know, invisible. The hottest portion of the earth must be at the equator for the sun is overhead, and the rays beat down directly upon the earth. The sun is also nearer than when at the horizon, and less rays are absorbed by the atmosphere. The longer the day the greater the heat.

Temperature is registered by observation of the thermometer, and the distribution of heat is represented upon a chart across which lines are drawn at places of equal temperature. These lines are called “isothermal.” There are also terms to denote equal winter temperature and the average summer heat—isochimines and isotheres respectively.
Temperature decreases as we ascend from, and increases as we descend into, the earth. This fact proves that the air is not warmed by the sun’s heat, but by radiation from the ground. As we ascend we reach the line of perpetual snow, which varies in different parts of the globe. In the tropics it extends from 15,000 to 18,000 feet; but it varies even in places of the same latitude, according as the towns are inland or on the coast, as in the Pyrenees and Caucasus, where there is a difference of three thousand feet in the snow limit.
The line of the snow limit, as a rule, gets lower as we journey from the equator to the poles. Exception will be found in the Himâlaya, where the snow line is higher on the northern side, in consequence of the existence of the Thibetan tableland, which causes a higher temperature than that existing upon the abrupt southern slope. Countries, therefore, though in the same latitude, may have different climates according to the elevation of the land.
The proximity to the sea is another reason for climatic difference. Water takes some time to become warm, but when it has once become so it will not readily part with its heat. The Gulf Stream, with its warm current beating along our shores, gives us a high temperature and a moist climate—a very different condition to Newfoundland or Nova Scotia, which are in much the same latitude as England and Ireland. By the sea the climate is more uniform, and the extremes of heat and cold are not so distant. We send invalids to the seaside to save them the effects of such violent changes. Winters are milder and summers cooler by the sea.
We can readily understand how such circumstances affect the vegetation, and places which in winter may enjoy a mild and genial climate (comparatively speaking), may have a cold summer. Ferns may flourish in winter out of doors, but wheat will not ripen in the autumn owing to the want of heat.
The winds also, and the soil and aspect of a region, all have a share in determining its climate. Trees bring rain by evaporation, and a wooded country is a blessing to its inhabitants, defending their habitations from wind and avalanches in mountainous districts. But the climatic conditions are altering. The ground is being more and more cleared; the soil is more cultivated, and moisture is being more eliminated from it. Therefore the air becomes warmer by the radiation of the ground, and clouds are formed which keep the warm layers down nearer the earth. Mountains, as we have seen, affect the rain-fall in districts; and in Scandinavia—in Norway chiefly—the average rain-fall is very high. The sheltering effects of mountains from east or northerly winds also alter the climate, while clay or gravel soils are cold or warm inasmuch as they absorb, or evaporate, moisture. Some surfaces being different from others give out more heat.
In some mountainous districts we shall find every variety of climate from the sea-level tropical heat to the rigours of the pole. The greatest average temperature is north of the equator in Africa; the lowest in the north, to the west of Greenland. Masses of land act in a different manner to the oceans, and the former become heated and cooled with equal rapidity, while the sea, as already mentioned, is slow to lose its heat. Our land enjoys a mild and equable climate as a rule, because it is surrounded by water, and the Gulf Stream warms it. The European climate, taken altogether, may be considered the best on the globe.
We will now pass on to a few observations concerning the weather, and the means of determining it beforehand.
It is always a dangerous thing to act the part of a prophet, and the uncertainty attending an uninspired foreteller’s predictions must in time disparage him in the estimation of his hearers and disciples. But there are signs in the sky which we can discern and render valuable by the aid of instruments. We must have a reliable barometer and thermometer, and keep a record of the average conditions of the weather, if we wish to wear the mantle of the weather-prophet—a term now, in America, applied (jokingly, no doubt) to people who are not particular in their statements of facts.
But without entering upon any scientific discussion, we may state a few plain rules which can be observed, besides the indications of a rising or falling barometer. Having frequently studied the aspects of the clouds, with the assistance of the hints from the wind-currents, we can fairly prognosticate or suggest probable changes of weather.

We have already remarked upon the colours of the sunset, which are attributable to the vapours in the atmosphere, and we say a red sky foretells fine weather; a yellow sky changing into green means rain, or rain and wind; on the other hand, when the red rays appear we may anticipate fine weather, as the atmosphere is becoming less and less moist.
A “low” dawn is known as a good sign; so when the first rays appear at, or near the horizon, we may anticipate a fine day, as we may when the morning is grey.
“Evening red and morning grey”
are almost unfailing tokens of fine weather.
Very often a yellow sunset means wind; a wild, crimson sky means a gale. On the afternoon (Saturday) before the Eurydice foundered off the Isle of Wight, we particularly noted the sunset at Gravesend; and it was evident (in our estimation) that a sudden storm was imminent, and we remarked it to our companions. The sudden fall of the barometer, and the appearance of the rising clouds early on that sad Sunday afternoon, approaching in dark masses from the west and north-west, spoke of rain and (possibly) snow. How true the forecast was the event proved.
When clouds are soft and thin we expect fine weather; when they are dark and hard, rain and wind. A ragged-edged and heavy cloud indicates thunder and lightning, with squalls when we see dark clouds flying rapidly across the mass of cumuli. A “mackerel” sky and “mares’ tails” generally foretell wind, the direction and the upper currents being noted. The longer the warning given by the heavens, the longer the bad (or fine) weather will last; and the converse is also true.
The cirrus is a wispy cloud, and is often observed extending across the sky on a fine afternoon. This may or may not indicate rain; it generally points to wind. If its direction be northerly and west to southerly and east, it is a good sign, but from west to east it is a bad sign. The habits of birds and animals, and their anxiety for shelter, “pigs running with pieces of straw in their mouths,” and the low-flying swallow, are all signs of approaching rain and bad weather, and the scintillation of stars betokens moisture in the atmosphere. These are well-known appearances, but there are others regarding the winds and currents of air which require the assistance of Admiral Fitzroy’s book.
For instance, a falling barometer with rising temperature means southerly winds and rain; in winter, with low temperature, snow.
But a rising barometer with northerly wind often means rain.
A rising glass after a low fall may, and often does, indicate more wind from the north, and after that fine weather, if lower temperature also supervene. If warm weather continue under the circumstances, the wind may back and blow from the southward.
“The most dangerous shifts of wind happen soon after the barometer rises from a very low point, or if the wind veers gradually shortly after with a rising barometer.”
If the barometer rises with a southerly wind fine weather may be expected, and if it falls with a northerly wind rain, hail, and snow are imminent, for the rule is a fall for southerly, and a rise for northerly winds.
A sudden fall with west wind indicates storm from northerly quarters (N.E. to N.W.). An east gale veering southwards with falling glass indicates a change of storm-direction to a point from N.W. or N.E., suddenly and violently, though a change might have been expected from the appearance of the glass. A calm frequently occurs between these disturbances.
A backing wind—that is, a wind going in a direction opposed to the sun’s course (and with the earth)—is a bad sign after unsettled weather. The wind is said to “veer” when it goes with the sun.
The south-east wind, with clear sky, warm weather, and low clouds on the horizon, is a sign of wet. A dry east wind means fine weather. Heavy clouds in the north-west generally bring a thunderstorm. When really distant objects look very near rain must be expected.
There are many exceptions to weather rules, and none can be laid down as invariable. The ever-changing currents of air, and varying moisture of the atmosphere, give rise to barometric changes, which should be carefully noted. A little experience and close observation for one year, with notes of signs, and indications of temperature, will assist any one to tell the probable change that is approaching.
There are a great number of signs of weather which are observable in the animal and even in the vegetable kingdom, as well as in the moon and stars. Many flowers close their petals before rain comes on, and the behaviour of domestic animals often foretells storm. Sheep huddling together in a corner tell us the direction from which the tempest is approaching; sea birds fly to shore, and land birds become restless.
The naturalist will observe the domestic animals which become uncomfortable and sniff the air; the cat lies with her head down, the brain lowest; and frequently washes her face, or scampers about aimlessly. Spiders disappear, and worms come up to seek the expected water. When fine weather is coming all nature appears glad, but leeches sink into the water as far as they can.
The above are some of the domestic and common signs of coming rain, and conversely for fine weather. A wailing wind, a cloudy mountain, a greenish rainbow or too red a one, a pale moon with indistinct points, or a halo round it, are all signs of rain and possibly wind. So the most superficial observer may with these few suggestions inform himself of the chances of fine or wet weather.

CHAPTER LI.
BIOLOGY. PART I. BOTANY.
PLANTS AND ANIMALS—STRUCTURE OF PLANTS—FLOWERING PLANTS—THE STEM—THE LEAVES—FORMS OF LEAVES.
Biology is derived from the Greek word Bios, “life,” and logein, “to speak,” and constitutes the science of Organic Life. This science is divided into two branches: Botany, relating to the life of plants; Zoology, to the animals.
Plants, then, are living things, and as we proceed we shall find them born, or “germinating,” growing up as young plants, maturing as adults, and finally dying, and their particles resolving into their elements. There is more than one application of the text, “Man is but as a flower of the field.”
In the Geological section we noticed the progressive stages of the vegetable creation, and if we turn back to those pages wherein the various epochs of the earth’s formation are enumerated, we shall see how plant-life developed. Thus we find in the Cambrian the first traces of vegetable life in the weeds of primeval seas. The Silurian strata and the Devonian furnish us with many fossils of marine algæ, and if we examine the succeeding periods we shall find a progressive increase and development; pines and tree-ferns in the sandstone, and most of the plants (by which term we include all varieties) were different from those at present existing in the earth.

We spoke of climate lately, and referred to the vegetation having an influence upon it. The same is true of the effect of climate upon vegetation. The conditions of plant-life depend upon climate, as it partly depends[Pg 659] upon plant-life. But of all the necessary conditions the first created thing is the most necessary—light. Without light the plant is nothing.

Plants have many points of similarity with animals. They live, they possess organs, their compositions contain similar substances, such as carbon and albumen, and close chemical analyses have found the existence of the elements oxygen, nitrogen, hydrogen, and carbon in animals and plants. Therefore water must play a conspicuous part in all. Professor Huxley puts this question in his usual clear fashion. He says:—
“It is a very remarkable fact that not only are such substances as albumen, gluten, fibrin, and syntonin known exclusively as products of animal and vegetable bodies, but that every animal and every plant at all periods of its existence contains one or other of them, though in other respects the composition of living bodies may vary indefinitely. Thus some plants contain neither starch nor cellulose, though these substances are found in some animals; while many animals contain no horny matter and no gelatine-yielding substance. So that the matter which appears to be the essential foundation of both the animal and the plant, is the proteid united with water, though it is probable that in all animals and plants these are associated with more or less fatty and amyloid (starchy and saccharine) substances, and with very small quantities of certain mineral bodies, of which the most important appear to be phosphorus, iron, lime, and potash. Thus there is a substance composed of water, plus proteids, plus fat, plus amyloids, plus mineral matters, which are found in all animals and plants. When these are alive this substance is termed Protoplasm.”

We have taken the liberty to extract the above paragraph, as it expresses in a few words, and very clearly, the common origin of plants and animals. We will now consider the conditions of plant life. Heat, light, and moisture are the principal necessaries, with of course air and certain earthy matter. Some plants, like some few animals, live in darkness, such as truffles and fungi, as do cave-fish and bats. But this is the exception, and the sense in which plants (or animals) can exist without light is a very restricted one, and only to be sustained at the expense of[Pg 660] the plant material, which must originally have been derived by the action of light. Light, therefore, is the great “producer.” It gives life to plants upon which animals feed, and therefore light is in one sense the beginning of all things. We can now understand why light must have been created first.
Many interesting experiments can be made to observe the effect of darkness and different coloured light (transmitted through coloured glasses) upon plants; and it will be observed that although the leaves may not develop the natural green tint, the flowers will exhibit their usual colour. One effect of light upon plants is to make them green.
We all admire the beautiful green of the spring leaves, and the freshness of the colours of the trees and grass. But if we pluck up a plant its root is not green. Why then is the cleaned root not as green as the upper portion?—Because of the absence of light. There is a substance called Chlorophyl which, when acted upon by light, becomes green. This is contained in plants, and when the daylight falls upon it the substance turns green. So, as we said above, plants are not green when kept in the dark. Celery is a common instance. Heat, of course, has much to do with the activity or vitality of plants, and the range extends from just above freezing point to 122° Fahr. We find tiny plants blossoming in Alpine regions close to the snow, and others in full life in the tropics, protected from the fierce rays by scaly coverings and huge leaves. In the northern regions buds appear as soon as the surface warmth is felt, and even when no heat can yet penetrate to the roots. Thus we see that Nature fits the animal and the plant to the localities in which they live, and they exist interdependently. Some can defy cold, others flourish in drought; some love moisture, others live in great heat encased in prickly armour.

With this introduction to biology we may now pass on to speak of the seeds and germination of plants, which we divide into the flowering and non-flowering species. We suppose that the appearance of various organs of plants are familiar to our readers, and the root, the stem, the leaves, and the flower itself, as well as the seeds, are well known, and their uses understood generally.
Now if we compare a mineral—say a crystal of quartz—with a plant, we find the crystal uniform, consisting of small particles of quartz throughout, and it appears an aggregation from outside of these particles in a particular form. It cannot grow from within. But a plant can; and it is very different in structure and appearance. It receives nourishment from outside also, but it assimilates the materials, which are not the same as those we meet with in the plant itself. The mineral, on the contrary, is essentially the same throughout; it can only grow by aggregation of atoms like itself. A plant, therefore, like an animal, must have organs within it, and must be capable of change in itself; it has powers of reproduction, and in some few instances of locomotion; it can eat flies, and assimilate them as an animal does.
A plant, therefore, is an organized body without external voluntary movement; and hereby it is essentially distinct from an animal, with which, in organization, it is closely connected. The simplest form of the animal as of the plant, is that of a minute vesicle or cell, containing a fluid in which are some granular substances. At this stage it could not be distinguished from the simplest plant, if it had not the faculty of voluntary movement—the power of changing its place. The animal has a locomotive power. Sometimes, indeed, it is a very limited sphere to which it is confined; yet it may change its place for another more conducive to the exigencies of its being.
It is sufficient for the present to have given the most general characteristics by which plants are distinguished from the other objects that, with them, compose the great kingdom of Nature. A precise and clear apprehension of their varied forms and wonderful phenomena can only be obtained by a careful analysis of the nature and structure of the subjects of the vegetable kingdom.
The cell is the fundamental or elementary organ of plants, and the knowledge of its metamorphoses and functions constitutes the foundation of botany. We must therefore first consider the simple organs of plants.
Structure of Plants.
It will be necessary for the reader to gain some little knowledge of the tissues and cells of plants before he proceeds to examine the organs of development, and a microscopic examination will soon disclose the few simple tissues which are termed cells and vessels. These exist in all plants of whatever nature. Plants are aggregations of cells, “every one of which has its little particle of protoplasm enclosed by a casing of the substance called cellulose, a non-nitrogenous substance nearly allied in chemical composition to starch.”35 The tissues are “cellular” and “vascular” respectively.
The cells have an outer sac or covering which is transparent, and this cover is the cellulose above mentioned. It contains (1) the protoplasm, a[Pg 662] kind of jelly-like substance (which holds the proteine or basis of life); (2) water or cell-sap; (3) the nucleus; and (4) chlorophyl. This protoplasm is apparent in both plants and animals. The cells containing these various substances—in which we find oxygen, hydrogen, nitrogen, sulphur, and carbon, with phosphorus perhaps—are divided to form new cells, and so on with most astonishing rapidity, amounting in some instances to millions in a day, and a case of this nature will readily be recognized in the mushroom.

Fig. 739.—Plant cells.
Cellular tissue is composed of these cells, and vascular tissue is composed of vessels or tubes like coiled springs, which are cells without divisions or partitions. These tissues will be referred to farther on as dotted ducts or tubes.

In most of the spongy parts of plants, as in the pulp of fruits and pith of elder, the cells preserve the globular or oval shape represented in fig. 739 A. But the cells, in consequence of that mutual pressure, more frequently assume the form of a polygon (fig. 739 B), the section of which is generally hexagonal. The cellular tissue may generally be compared to the bubbles produced by blowing through a straw or tobacco-pipe into soap and water; or it may be illustrated by placing balls of moist clay together, and then pressing them more or less strongly. In this manner every individual ball assumes a polygonal shape corresponding to the form of the cells represented in fig. 739 C, and which disposition is, in many plants, preserved with the utmost regularity. Such cells as are, with tolerable equality, extended in all directions, are named parenchyma, and of these are composed the tuberous parts of plants, as the potato, dahlia-roots, etc., and especially the soft, spongy parts of the pith, bark, leaves, etc. We frequently, however, meet with cells which are extended longitudinally, and pointed at both extremities, as in fig. 740. The sections of these cells, which are compactly arranged, have the appearance of a hexagon. They are termed woody cells, or woody tissue (prosenchyma), and constitute the chief portions of the more solid parts of plants, as the ligneous parts of trees, shrubs, etc. Very long, flexible cells, as those which constitute the fibres of flax and hemp, are called bast-cells, and appear under the microscope as round threads of uniform thickness, whereas the fibres of cotton wool, which rarely exceed one or two inches in length, when magnified, present the appearance of flattish bands with somewhat rounded margins. By these marks, the union of flax and cotton in the same web or piece of cloth may be detected.
Occasionally the cells assume very abnormal shapes, as the stellate or star-formed cells. These are described as irregular cells.

As every plant, whether small or great, is only an aggregate of a great number of cells, so, also, the life of a plant is nothing else but the sum of the activities of all the cells of which it is composed. The special province of the cells is to receive from the soil or atmosphere the water necessary for the various vegetative purposes, together with the nutritious materials dissolved in the watery and aerial fluids, and to circulate them through the whole body of the plant. The circulation within a plant is not carried on through the agency of tubular channels, but only by the passage of sap in all directions from one cell to another.
Since the cells have no openings, it is somewhat difficult to understand in what manner the fluid can enter into the plant from without, and by what means it can inwardly pass from cell to cell. This phenomenon, however, is dependent on the peculiar quality both of vegetable and animal membranes and fibres—viz., that they are permeable by many fluids, without being dissolved by them. Experiments show that this permeative action is carried on in accordance with definite laws. When two fluids of unequal densities—as, for example, an aqueous solution of sugar and mere water—are separated from each other by a diaphragm of pig’s bladder, we perceive a constant tendency on both sides to restore the equilibrium in the density of the two fluids. A portion of the water penetrates the bladder, mixing with the solution, and a portion of the latter finds its way to the former by the same medium. In this experiment one important fact is to be observed—viz., that the lighter fluid always passes through the separating medium more rapidly to the denser than vice versâ; consequently, in this experiment more of the water passes through the bladder to the saccharine solution than of the latter to the water. This permeative capability of the tissue of vegetables and animals is called endosmose.
The cells both circulate the sap and alter its condition, so we find differing substances in the same plant. The cell as described creates new cells, and the force with which the sap rises is rather greater than the pressure of the atmosphere.
The vascular, or fibrous tissues, are illustrated in the margin (fig. 741). They usually contain air. Some plants have no vascular tissue, and are termed cellular plants—such as mushrooms, fungi, mosses, and seaweeds. Many contain both tissues, and these are the more highly developed kinds.

Sometimes we find a milky juice in plants. This is called latex; and caoutchouc is always present in it. This juice is contained in tiny tubular vessels, which have their origin in the new cellular tissue of the lactiferous plants.

The tissue of the cuticle, or epidermis, which externally covers all parts of the plant while they remain green, is of a peculiar nature, and demands special consideration. It is formed of flat tubular cells, very much compressed, and in close contact, with the exception of some parts where the stomata, or mouths, are placed. In fig. 742 a section of the leaf is represented, the large transparent empty cells of the epidermis, and above these the parenchymatous cells of the leaf filled with greenish-coloured granules. In four places (fig. 743) stomata (s s s s) are seen, which have their openings surrounded by parenchymatous cells disposed in semilunar forms. Under each stoma (mouth) there is a hollow space which is connected with the intercellular passages of the leaf. These stomata, represented in fig. 743, are so numerous on the under side of the leaf, that hundreds have been counted in the space of a square line. Through these minute organs an intimate connection exists between the interior of the plant and the external air.
The epidermal cells not unfrequently exhibit very abnormal formations. When much extended in length they appear as hairs which are frequently branched, and in many plants they contain an irritating sap (in the nettle, for example). Bristles, prickles, glands, warts, and especially the substance which forms the well-known cork, are all due to the metamorphosis of this exterior integument.
Flowering Plants.
 :
:

Flowering plants have certain distinct features which cannot be mistaken, for they grow well above ground, and can easily be examined. There are a hundred-thousand different species of flowering plants, and a visitor to Kew can study them there. Any child can tell a flower when he sees it, but a flowering plant is no more restricted in Botany to actual bright blossoming plants, than the term rock in Geology means a mass of stone only. Flowering plants may be either very gorgeous or very simple; and so long as they contain a reproductive apparatus they are flowering plants. The rose is a flowering plant, but the oak is equally one. The beech tree and the primrose are classed under the same heading.


Flowering plants must possess stamens and pistils, which bring forth seeds which contain an embryo, and the germination of seeds can be easily perceived by any one who will take the trouble to soak them (say “scarlet runners”) in warm water, and keep them warm in moist flannel. The process may then be examined at leisure.
We need hardly insist, after what we have said, upon the necessity for some air and light, or remind the reader that he must not keep the seeds in a close, dark place, though light is not so necessary at first as air. The embryo connects the “cotyledons” or halves of the seed, and this develops into a tiny rootlet or “radicle,” and upwards into the stem, the commencement of which is known in botany as a “plumule.” The rootlet seeks nourishment from the ground. The albumen secreted in the cotyledons feeds the embryo, until (in some cases) it is exhausted and they die away. In other cases they grow up and obtain food for the young plant in the air. Some plants have (like wheat) only one seed-leaf, or cotyledon; and these kinds are called monocotyledons, or endogens, in which the growth is upright. The others are called dicotyledons, or exogens.


So far now, perhaps, you may understand that the outer covering of the seed is called the testa; the opening which may be perceived in the ordinary bean near the dark spot is the micropyle, or little gate; that the halves of the covering are termed cotyledons, or cups, and that the embryo sprouts upwards and downwards, the upper part of the stem being the plumule, and the lower portion the radicle. Even if the seed be put micropyle upwards into the ground, or between layers of flannel, to germinate, you will find that the radicle will always curve downwards.


The root then being displayed, it pushes its way into the ground to seek for nourishment, and when the proper moisture has been admitted to the seedling, which has been reposing in the cotyledons all the time, it sprouts up rapidly. The root and its fibrous extremities have been pushing and insinuating themselves into and through the ground, and by small knobs or suckers known as spongioles, the rootlets or fibrous parts of the root pick up sustenance for[Pg 666] the plant, and it is then carried by tubes to the root, and so on throughout the plant, and with air ducts serve to keep the plant alive.
The stem emanates from the plumule, and in a short time little knots develop upon it, which are the incipient leaves. The knots are divided into nodes and internodes, because they appear on different sides of the stem and intermediate, so as to alternate with each other, and are really buds. The issues unite also into leaf-stalks or petioles, and extend into the leaf-frame or skeleton as we see it when the leaf has decayed. So thus we have an upward and a descending growth, which respectively constitute the stem and root of a flowering plant.

Some trees have roots growing from the stem, as in the banyan tree, and roots can produce stems as well as the latter can form roots. The uses of roots are so well understood that we need not particularize them. In many trees we find what are termed lenticellæ, like holes in the bark. These fissures will put forth roots under favourable circumstances. These stem roots are called adventitious, and by taking “cuttings” from plants we make good use of them for propagation.

But there are underground stems as well as those which flourish and climb above it. “Bulbs” and “tubers” are common instances of these underground stems, or “rhizoma,” which are horizontal. The ordinary stems[Pg 667] are termed “aerial” stems to distinguish them from the earthy and subterranean. The aerial roots of ivy are only used for support, and are not its proper roots, though some parasitic plants strike into the trees and are nourished by them.
The Stem.

The stem is that portion of the plant-axis which grows upwards or above ground, and may be, as we have just read, subterranean. As the great function of the root is to procure sustenance for the plant, the stem assists in carrying the nourishment through the branches and leaves. We shall find two forms of stem—the underground, or root-stock, and the stem proper. There are in these two former several varieties as under:—
1. The Bulb, which is a short globular stem surrounded by thick leaves, and producing buds—as, for example, the onion.

2. The Tuber, similar to the foregoing in shape, having no leaves, however; the potato is an instance.
3. The Rhizome (root-stock), like a root only producing buds, which roots do not. The iris will serve as an example.
The varieties of the stem-proper are:—
(1) Filiform, or thread-like, simple, or branched, as in mosses.

(2) The culno, a thin, hollow, and frequently-jointed stem.
(3) The palm or simple stem, seen in tree-ferns and palms. It is marked by the scars of dropped leaves.
(4) The stalk, very common, of a green hue, and its life is limited to a twelve-month as a rule. The so-called “stem” of the hyacinth is not a stem, it is a stalk, or flower-stalk, pushed forth for a temporary purpose.
(5) The ligneous stem is the perfected kind, and an example will be apparent in every tree.
The duration of the stem of a plant is usually the same as of the plant—so we have annuals, biennials, and perennials. The substance of the stem determines its character, so we may have it solid, or soft, hollow, tubular, flexible, rigid, or a tough stem. There are fibrous, herbaceous, and juicy stems. They may be directed uprightly, straight, procumbently, arched, or creeping, above, or underground, climbing, clinging, floating, or twining.
There are many plants with little or no stem deserving the name, as in the onion; and we must all remember when studying botany that it is not the place where a portion of a plant may be found that constitutes it a root or a stem. The form and structure should be studied, and its purpose in creation. So stems may be underground and roots above it. The root and stem, briefly treated of in the foregoing paragraphs, have certain points of resemblance, inasmuch as both consist of a main or trunk line, so to speak, from which branches diverge as “rootlets” and “twigs”; and how beautiful the latter are any one can see in a good photograph of a wintry landscape. But stems have nodes and internodes, and roots have not, and this is the great and apparent difference.
The covering of plant-stems is varied, and many instances of such clothing will occur. We have woolly stems and hairy stems, which develop into thorny ones—for thorns are only strong hairs. Spines and stings and prickles defend the stems, and keep rude hands from meddling. We will now cut the stem and see what it is composed of, and how it looks inside. We have only to cut it across and again perpendicularly to find out a great deal about the interior structure of the stems of branching plants (exogens).
The elder, from which the whistle of our boyish days is fashioned with a penknife, will serve any lad for an illustration. Inside we find what is called “pith,” which is cellular tissue. Round this is fibre, and outside is a skin, or the plant-cuticle. We may remark that the tissues of flowering plants are characteristic of the monocotyledonous and the dicotyledonous plants. Of the former we append an illustration,—a section of palm-stem,—and we find bundles of vascular tissue dispersed apparently at random amongst the cellular tissue of the parenchyma, or cellular tissue. These stems do not grow by the increase of the existing vascular tissue, but by their new production at the circumference, and so they grow in both directions, laterally and uprightly. These plants belong to the Endogens, and if Indian corn be grown we shall have full opportunity to study the formation. In cutting a fern stem we are familiar with the “oak” pattern of the matter it contains. We have few specimens of endogens in England.
The dicotyledonous stems are common to our trees and most plants, and may therefore be considered with advantage. The stem consists of the vascular tissue called “pith,” and we give an illustration of the cells magnified very considerably. The arrow indicates the outward direction (fig. 757).

We here perceive the vascular bundle proper surrounded by a very large-celled tissue, aa′bef. The almost square cells, aa′, form the epidermis on which follows the less dense cellular tissue of the bark. The latter[Pg 669] surrounds a half-moon-shaped bundle of bast-cells, c, which are separated in the direction towards the interior, by a layer of cambium, dd′d″, from the bundles of vascular tissue, consisting of vessels and longitudinal cells. The latter tissues may be distinguished in the transverse section by the thicker walls, gg, and by their greater breadth, hh. It is further to be remarked that the cambium transparent tissue, dd″, appears on both sides of the bundles of vascular tissue, and extends to the next bundle, and thus presents an uninterrupted circle throughout the entire circumference of the stem.

On examining the section of a one-year-old dicotyledonous stem, magnified six times, as in fig. 758, we perceive several parts clearly distinguishable from each other, corresponding with the arrangement of the bundles of vascular tissue.
Enclosed by the epidermis, a, is a large-celled tissue, b f and m, in which a number of vascular bundles form a circle. In each of these we notice that the outer portion, consisting of bast-shell, c, is separated by the cambium, d, from the inner woody portion, e. The cambium forms a closed circle which penetrates through all the vascular bundles.
In the course of the further development of the stem, the parts, a b c, constitute the bark, the vascular bundles, e, the wood, and the cellular tissue, f, its pith. The tissues, m, penetrating between the vascular bundles, are called the medullary rays. The cambium is to be regarded as the most important part, since it is the source of new bundles of vascular tissue which year by year increase the circumference of the stem.

The growth of a dicotyledonous stem is continued by the formation of a new circle of vascular bundles on the circumference of the stem in the second year. Each new bundle, as has already been shown, is produced in the cambium, and consequently is deposited between the wood and inner bark.
Thus every year a new layer is deposited between the previous formation and the bark; and a section will exhibit these concentric rings of wood[Pg 670] obviously distinct from each other; and as one year is requisite for the formation of a single layer of wood, these depositions are named annual layers or rings. In fig. 759 we have a representation of a stem three years old, and one of five years of age.
The number of rings in the stem do not invariably agree with the number of years the tree has been growing, but it may be accepted as a rule.
The stem is the medium of communication between the roots and leaves at first; but after a year this important duty is deputed to the cambium layers of new woody tissue, etc., and as time goes on the living power has accumulated immediately under the bark. So although the tree be quite hollow it will live. The interior has been closed up by deposition of wood and has decayed; but the life functions being relegated to the bark, the old tree lives on. If we remove the rind all round a tree it will die.
The Leaves.

When in the spring the young leaves appear upon the trees, and as summer advances they become fully developed, we are all grateful for the beautifully varied tints of green, and for the shade we can so fully enjoy. The study of leaves is a most interesting and instructive one, and nobody should omit to examine them. Their forms are infinite, or, at any rate, countless; their size as varied as their forms. Many attributes of the leaf will occur to every reader, and we will briefly describe these essential organs of plants. Air and light are necessary to the development of leaves, and their principal use is to present a surface to the food material which the plant absorbs. They breathe, as it were, and absorb the carbonic acid from the atmosphere. These functions are called “assimilation,” “transpiration,” and “respiration,” which we will detail by-and-by.

Leaves are distinguished according to position and duration. Some leaves have very simple forms, others are compound, so to speak. Some are plain and rounded, others are toothed, like the holly. The skeleton of a leaf is a very interesting study, and it will show the beautiful structure of these common objects. The delicate lines of the green leaf are “veins,” or sap-vessels, which convey the necessary nourishment. The leaves are called the “embryonic” (seed-like), the radicle, or root-leaf, the stalk-leaf, and the stipules, which grow at the base of stem-leaves, and the floral leaves, which bear the flowers or fruit buds.[Pg 671] Leaves which are developed at the end of a chief axis are termed blossoms. Of course it must be understood that all the different kinds of leaves do not occur upon the same plant. The leaf may be accepted to mean the stem-leaf.

Leaves are folded up in various ways, and the manner in which this is accomplished is termed the vernation of the plant. The leaves of endogens and exogens differ in their veining. The former veins do not touch; there is none of that beautiful interlacing which we find in the exogenous leaves. In the former the veins rise from base to apex, curving as they advance, as in the well-known lily of the valley. This “nervous system” of the leaf is its “venation,” and the veins distributed in the blade or lamina of the leaf are twofold,—as remarked,—ascending in curves, or diverging from a central nerve called the “mid-rib.” These lateral nerves are either parallel or “reticulate”—that is, net-like.

We will now examine the forms of leaves which are regulated by the divergence and extension of the divisions of the mid-rib. Thus we get an orbicular, or peltate leaf; palmate, digitate, and pedate forms also occur, as may be seen in the illustrations, pages 672 and 673, where all the varied shapes can be studied. The leaf consists of a petiole or stalk, and the lamina or blade. The petiole is composed of bundles of vascular tissue; the lamina is formed by their extension, the interstices being filled with cellular tissue. So we perceive that the leaves and stems are composed of similar materials. To defend the tissue a skin, or epidermis, is placed upon the surface of the leaf, and this epidermis is full of breathing holes, or pores, called stomates (compare page 664). There are also cells filled with chlorophyl, which gives the leaf its green tint.

The petiole may be absent in a leaf, and when it is the leaves are termed sessile, or sitting leaves. These leaves sometimes coil round the stem, and are called “amplexicaul,” or stalk embracers. These are simple leaves. Compound leaves are[Pg 672] composed of several blades or laminæ on a stalk, and are seldom sessile. Simple Leaves are almost innumerable in form and variety. Leaves may be equal or unequal, acicular or linear, rounded or oval, cordate or obcordate, reniform or sagittate, perfoliate or connate, crisp, whorled or truncate, retuse, acuminate or mucronate. The margins of simple leaves again are entire, deft, notched, crenated, crenulated, sinuous, or dentated. They are pinnatifid, multifid, or lobed, according to the divisions of the leaf.
Compound leaves are also divided into classes. The pinnate, as the rose-leaf, the clover trefoil. There are “doubly pinnate,” the digitate, as in the horse chestnut. Compound and simple leaves can be readily distinguished by inspection, for the former are “articulated” to the stalk and can be separated, but the simple leaves will be torn, for they are confluent throughout.
Leaves are evergreen or deciduous, accordingly as they retain or shed themselves. The ordinary leaf is deciduous; the fir and the yew and the imported laurel are evergreens. We have very few of these as natives of England, the ivy, yew, and fir being the three most common. Sometimes a plant peculiar to Killarney, and known as the arbutus, is included in the list. But the Scotch fir and the yew are distinctly native evergreens.
The detailed characteristics of leaves must be passed over until we come to the fly-catching leaves—such as Venus’ fly-trap, the droseras, and nepenthes, which appear to catch and devour insects for food. The Venus’ fly-trap may be examined, and we shall find the leaves covered with tiny and very sensitive hairs. Often a fly happens to alight upon the leaf, which is extended in a most innocent manner (see illustration). As soon as the fly settles the leaves close,[Pg 673] and the digits lock tightly together, thus preventing the escape of the prey. The droseras, sarracenias, and nepenthes also kill their food. The sarracenias form curious cups, into which insects are enticed in search of fluid, and then, as in the case of the house-haunting cockroach, they cannot get out again. The nepenthes have a cup and lid for insect-catching, and within the cup a liquid is secreted.
We will close this portion of our subject with a quotation from a recent article upon botany referring to leaf arrangement. The writer says:—



“Efforts have been made to determine the laws to which these various modes of leaf-arrangement may be referable. The result is found in the doctrine of ‘Phyllotaxy,’ as it is called, the fundamental principle of the whole being that Nature, in the disposition of the leaves upon the stem, works upon precisely the same idea as that which is set forth so distinctly and elegantly in the common pine-cone; and, on a minor scale, in the beautiful cone of the female hop; not to mention the quasi-cones of many species of tropical palm, such as the Sagus and the Mauritia; nor to mention either, the very delicate repetition of the whole series in the florets of the Rudbeckia and the ripening fruits of Chaucer’s daisy. In every one of the flower and fruit arrangements mentioned, the idea is the spiral,—the same sweet old fashion which we have had in the twining stems of the convolvulus, the woodbine, and the scarlet bean; which comes out again in many a sea-shell, and in human ringlets; and this idea, according to ‘Phyllotaxy,’ governs the position of the leaves. Following alternate leaves up the stem, their sequence is clearly spiral. Through the non-development of internodes, they are brought closer and closer together; and even when the entire mass of foliage is concentrated and condensed into the rosulate form, as in the houseleek and the Echeverias, the spiral prototype is still distinguishable. The whole matter has been reduced to one of[Pg 674] arithmetical exactitude; and for those who love calculations and “fractions,” the determination of the spirals, their continuity and intermixture, supplies abundance of curious entertainment. All three modes of leaf-arrangement are found in certain herbaceous plants, none disclosing this particular kind of playfulness more plainly than the common pyramidal Loosestrife, Lysimachia vulgaris, and the purple Lythrum of the waterside, in each of which very handsome wild flowers, alternate, opposite, and whorled leaves may be found in near neighbourhood. Alternate and opposite leaves are also met with, side by side, in various species of Myrtaceæ; and imperfectly, upon young shoots of the common ash-tree. The rule is, nevertheless, that there shall be uniformity, and in many of the largest natural orders the rule is never broken. In the Rosaceæ the stem leaves are invariably alternate; in the Gentianaceæ they are invariably opposite.”


CHAPTER LII.
FLOWERING PLANTS.
ORGANS OF INCREASE AND REPRODUCTION—THE FLOWER—THE CALYX—THE COROLLA—THE STAMEN—THE PISTIL.
Some of the simplest plants are propagated by spores, which are detached, and fall upon the ground to vegetate; but in the case of the higher orders the reproduction of species is a much more elaborate process, and is carried on by means of certain organs called flowers. Small buds, or ovules, are formed, which develop into seed. Plants also produce buds, which grow upon various parts of it, and are capable of reproducing their species. We will first speak of Flowers.
Flowers are not only the lovely blossoms we cut and place in our rooms, but the reproductive organs of plants which may be very plain and simple or gorgeous and fragrant, and in all probability the so-called flowers are few in comparison to the unrecognized flowers. Trees and bushes flower equally with the rose and the pink and carnation. Vegetables flower as well as the lily, though we do not recognize it so well. Let us now examine the “flower.”
Flowers may consist of four parts, but it is not absolutely necessary that they should contain more than two. The four portions of a complete flower are—
- The Calyx.
- The Corolla.
- The Stamen.
- The Pistil.
The two last mentioned are essential. The four organs are placed around a pedicel or peduncle (flower stalk), and are known as floral whorls.
The Calyx is the outermost whorl of all when all exist. The portions of the calyx are known as sepals.
The Corolla is usually the showy portion—the attraction of the flower. The pieces of the corolla are called petals. The sweet fluids of the plant are here concealed.
These parts—the calyx and corolla—are known as the floral envelopes, or “perianth.” The tulip has one whorl only, and it is called the envelope.
The calyx sometimes falls before the flower is full blown, as in the poppy. Its lower portion is the “throat,” and the shape of the organ varies, as will be seen by the illustrations.

| 1. Tubular. | 2. Clavate, or club-shaped. | 3. Tubinate, or top-shaped. |
| 4. Campanulate, or bell-shaped. | 5. Funnel-shaped. | 6. Urceolate, or urn-shaped. |
| 7. Globular. |
The sepals are usually three to five in number. The poppy has two, and the well-known wall-flower four free—that is, disunited—sepals. The primrose possesses five. The calyx is the outside rim of all, and we may thus remember it, because its sepals alternate with the petals of the corolla. The petals may be formed cup-fashion, as in the lily of the valley, and here we have these sepals and petals in groups of three each.




The petals differ from ordinary leaves, and in them we find all the beautiful tints and the odour we imbibe from blossoms. The forms of corolla correspond to those of the calyx, and are called by the same names. But when corollas are absent the petals of course cannot provide the necessary colours for the flower. Then the calyx is gifted, and the sepals are brilliant. Thus Nature provides for everything.
Corollas are found with five or ten petals, and sometimes with three, six, and nine—the numbers always doubling or adding the original number. There may be four petals or eight, as in the “tetramerous” corolla (fig. 771). Instances of others are illustrated, and a plant whose petals, sepals, and stamens are numerically equal, or are multiples of each other, are termed “symmetrical.” The “regular” flower does not vary much, as the petals are of the same size and shape, but there are many “irregular” flowers—as the pea—in which portions of the calyx or corolla are of different shapes. The “labiate” and the “campanulate” are illustrated in figs. 774, 775, including the convolvulus and the snap-dragon. These are but a few examples of an almost endless diversity. The “regular” flowers—exemplified in the buttercup and convolvulus—always present the same figure to the observer.


To the petals the beautifully-varied colours of plants are due, and though it is not possible to enter upon the subject here, we may conclude that the various beauties of the colours of flowers are owing to light and air acting upon the various “colouring matters” contained in the plant. Seeds planted in a dark cellar will spring up pale; admit light, and they will become green, for light thus acts upon the chlorophyl. But the flowers of the plant are not so dependent upon light, as can easily be proved. Many interesting experiments have been made upon flowers by acids and gases.36
The Stamens are the next in order for our consideration. They are found within the petals (or the calyx if no petals be present). Stamens vary very much in different plants both in number and general features—but, as in the case of petals, they keep, as a rule, to certain numbers and doubles of them. The stamen consists of two portions—a lower, thread-like part called the filament, and an oblong bag or head, termed the anther. This contains a powdery matter called pollen, and is the essential part of the stamen. The filament, which corresponds to the petiole of the leaf, may be absent, in which case the anther is called sessile. A lily will show the stamens perfectly, the anther being prominent in many other plants also, such as daffodils and fuchsias.
The stamens are very important organs with regard to the classification of plants—for number, length, and position, whether free or united, are all characteristic features. The length of filaments is always the same in the same kind of plant, and therefore is a very palpable test.
The anther contains the pollen, a powdery matter, usually yellow-coloured, but sometimes also red, brown, violet, or green-coloured. Pollen-grains vary from 1/20 to 1/300 of a line in diameter. Under a powerful microscope they appear as ellipsoidal, or sometimes spherical, triangular, polyhedral vesicles, filled with a granular semi-fluid matter. To effect fecundation, the pollen-grains must come into contact with a certain part of the plant which is intended to receive them, and which is called the ovule, and is found in the fourth or innermost verticil of the flower, the pistil. Of the further development of the ovule, we shall have occasion to speak in the paragraph treating of the seed.
At the proper time the anther opens and discharges its contents, the pollen-grains, some of which reach the place of their destination. The position of the stamens to the pistil is usually such that the latter can readily[Pg 678] receive the pollen-grains. In many plants, however, the stamens are too short to reach the pistils; or the two essential organs of reproduction are in separate flowers, or even on different plants. In such cases, the conveyance of the pollen from the anthers to the pistils is effected by the agency of the wind, or by that of insects, and more particularly by the bee. If the anthers are removed from the flower previously to their opening, no fruit is produced.
Varieties of flowers and fruits are produced artificially, by shaking the pollen of one plant upon the flowers of another, deprived of the stamens. Many esteemed sorts of stock-gilliflowers and pinks have been produced in this way.
The pistil constitutes the fourth and innermost whorl, and occupies accordingly the centre of the flower and the apex of the axis, whose growth is terminated with the production of the fruit.

The pistil also is formed by one or several modified leaves, called carpels, in this part of the flower, and which exhibit a more marked resemblance in colour and structure to the ordinary leaves than the stamens and petals do. The formation of the pistil from the leaf may be considered to proceed in this manner: that the edges of the leaf are folded inwards and unite, whilst the mid-rib is prolonged upwards (fig. 776A). The place where the margins of the folded leaves are united is called suture or seam (ventral suture, in contradistinction to the mid-rib, which is called the dorsal suture); and it is here that the seed-buds or ovules are developed.
The pistil consists of two parts—viz., the ovary or germen, which contains the ovules or young seeds, a, and the stigma, b, either placed upon the ovary, or upon the style, or stalk, which is between the stigma and the ovary.
A pistil may be of one carpel (simple), or of more than one (compound). The carpels or the carpellary leaves are the “ovaries.”
The pistil is a very important test for the classification of plants; some trees have no pistils, and the ovules are consequently naked. Such plants are called gymnospermæ. The coniferæ (firs and pines) are thus recognizable, and the position of the ovule is very much that of the ordinary bud.

CHAPTER LIII.
FLOWERING PLANTS (continued).
THE FLORAL AXIS—INFLORESCENCE—FRUIT—SEED—NUTRITION OF PLANTS—ABSORPTION OF CONSTITUENTS.
There are certain arrangements and mutual relations of the various portions of the flowers which we have mentioned that it is useful to consider. The floral axis refers to the position of the verticils, and inflorescence signifies the arrangement of the flowers on the stem. Flowers which possess both stamens and pistil are hermaphrodite; those with only stamens are male; those with the pistil female flowers. If both organs be absent the flower is neutral.
Plants bearing flowers in clusters form several distinct groups, to which appropriate terms are applied indicative of their respective form of flora arrangement.

In the examination of this kind of inflorescence (indefinite or axillary inflorescence), the first object of remark is the general or primary peduncle,[Pg 680] termed rachis, and which bears numerous leaflets called bracteoles or bractlets, from whose axils arise the pedicellate or sessile flowers. The lower bracts often produce no flower-buds in their axils, and form instead a whorl surrounding the heads of flowers on the primary axis, and which is called involucre (as in the sun-flower, for instance).



The different varieties of axillary inflorescence are determined principally by the elongation or depression of the axis, the presence or absence of stalks to the flowers, and the form and nature of the bracts. We distinguish—


1. (1) The spike (fig. 777). In this form of inflorescence, sessile or short-stalked flowers are arranged along the rachis in the axils of the bracts; the spike is said to be compound when small spikes or spikelets arise again from the bracts of the secondary axis. (2) The catkin or[Pg 681] amentum (fig. 777 [2]); a spike, usually pendulous, which falls off, rachis and all, by an articulation, as in the willow or hazel. 3. The spadix, a thick fleshy spike (fig. 777 [3]); examples, arum and calamus. 4. The cone, a fruit-bearing spike, covered with scales (fig. 777 [4]); examples, the coniferæ. 5. The raceme or cluster, a spike with the flowers on longer pedicels (fig. 778); examples, the currant. 6. The panicle, a branching raceme (fig. 779, Yucca gloriosa). 7. The thyrsus, a dense panicle, with longer peduncles in the middle than at the extremities; example, lilac. 8. The corymb, a raceme, in which the lower flower stalks are elongated and raised to nearly a level with the upper (fig. 780)—example, cerasus mahaleb. 9. The compound or branching corymb, a corymb in which the secondary axis again sub-divides; example, Pyrus terminalis. 10. The umbel: in this form the primary axis is greatly depressed, and the peduncles arise from a common point, and spread out like radii of nearly equal length, a whorl of bracts (involucre) surrounding the common base. In the compound umbel (fig. 781), Daucus carota, the secondary axis ends in small umbels surrounded by bracts, which is termed an involucel. This is observable in the umbelliferous plants—carrot, parsley, hemlock, etc.

A very peculiar kind of inflorescence, which characterises the great family of the compositæ, is illustrated by fig. 783. We see here the enlarged floral axis or receptacle, a, surrounded by several whorls or bracts, b b, which constitute a general involucre; the membranous bracts, (paleæ), b´ b´, seen in the receptacle, bear in their axils the sessile florets, c and d, which either have a calyx, e e, or not. The florets on the receptacle are either all of them tubular (d) or ligulate (tongue or strap-shaped); florets (c) are associated with the tubular ones. The receptacle is not always flat, but frequently presents a convex, globular, conical, concave, etc., shape.
In the absence of paleæ the receptacle is said to be naked. The florets at the margin, or circumference, are termed marginal flowers, or flowers of the ray; the florets in the disc (centre), central flowers, or flowers of the disc.
Some plants bear male and female flowers on the same stem. These are termed monæcious plants. The oak is an instance. The diæcious plants are those which bear stamens and pistil, or separately, on different plants, like willows. We will now glance at the functions of the stamens and pistil. The ovule has been mentioned as a tiny body in the ovary, and it consists of a nucleus, and cellular tissue surround it, leaving a small hole called the micropyle, into which the pollen tube enters after passing through the ovary. As in the animal creation, the unions of different families succeed best; no close relationship will fertilize so well as with other flowers.

Fertilization is accomplished in two ways; (1) by the action of the wind, by which the pollen is carried away to other plants; and (2) by means of insects—the bee particularly. These flowers have distinctive qualities relatively. In the case of the pine the pollen is powdery; so those plants which are thus fertilized are the diæcious species, which include the poplar, the oak, and the birch, as well as the pines. These are all wind-carried pollen plants. The nettle is illustrated here with male and female flowers.

Plants fertilized by insects are visited by them, and they carry away upon their heads, or bodies, the pollen, which is then thrust into the stigma by the insect; or perhaps birds may carry the pollen in the same way after sipping the nectar, and thus playing an unconscious, but most important, part in the economy of nature.

We always find the ovule at the termination of an axis; it is unable to form a seed alone. The pollen grains must fertilize it, and in consequence many ovules come to nought. The ovule is produced in the pistil, which, as before stated consists essentially of two parts—the ovary and the stigma; the latter secretes a fluid to hold the pollen. We annex the representation of a highly-magnified pistil (vertical section, fig. 786a). The pollen grains are indicated by d, attached to stigma, c, projecting through the style, b, into the ovary, a, and passing through the ovules.
With the transmission of the pollen to the ovary of the pistil, the functions of the anther and stigma terminate; accordingly these parts of the flower rapidly wither and decay after fertilization. The filaments, the style, and the petals speedily participate in the decay, but the sepals remain sometimes persistent in an altered form. The ovary and its contents alone proceed in their further development, and undergo material changes, in which, however, the bracts and the calyx often participate.



The fully developed and matured ovule, the seed, is, of course, regarded as the essential part of the fruit; the enlarged ovary forms the pericarp, enclosing the seed. The form of the pericarp[Pg 683] determines the external appearance of the denomination of the fruit. The structure of the fruit, and the arrangement of its parts depends in a great measure upon the number and position of the carpellary leaves in the pistil, and the manner and extent of their union, and the extent to which their edges are folded inwards.


The carpellary leaves occupy the summit of the floral axis. The axis terminates either in one single carpel, in which case the ovary is one-celled, or unilocular; or the axis is surrounded by several carpels, in which case the manner of their union determines the number of cells in the ovary.
The Fruit.



The carpels are the chief agents in the formation of the fruit, and they form the endocarp (core), and sometimes the whole pericarp, or seed-vessel. Upon the nature of the various parts and the changes they undergo during the ripening of the seeds[Pg 684] the nature of the fruit depends. The fruits are classified, some being the produce of a single carpel, others of several united carpels.


Fruit, in botany, is by no means limited to the juicy products of trees or plants which are so refreshing in the summer weather, and so acceptable in any form. In plant life the herb yielding seed produces a fruit equally with the orange or the apple. The fruit is the outcome of the varied processes of the plant. We may trace the plant from its tiny, sometimes very minute seed, through stem to flower and seed again. “In the final struggle, even when life is hopeless, and starvation, in consequence of drought, is imminent—when all is hopeless and barren, the plant will make an effort to produce its fruit and flower.” This is a very touching and interesting fact in nature—this last attempt to beautify the earth and to propagate its species for the use of man.

Fruit, then, is not limited to the market and the stall.
This statement scarcely needs proof; but if we consider for a moment the number of “wild” fruits—the parents, probably, of our table-fruits—we find many we cannot eat. In short, out of the hundred thousand plants which bear flowers scarce one two-hundredth part serve us as producers of edible fruits.


The fruit is the result of the flower, and if any objection be made by readers on the part of the common fig, it will be found that this appreciated fruit really consists of male and female flowers that are fertilized by the action of minute insects, which enter and depart (sometimes they[Pg 685] die, and are found dead and black in the figs). No blossom is perceived on the tree, because within the green sac the so-called “seeds” (really the fruits) are developing. A fig is a sac full of fruits.


The legume or pod is formed of a single carpel bearing seeds. We annex illustrations of the pod. The covering is called the pericarp, and the parts when opened separate into valves. Dehiscent fruits shed their seeds, indehiscent fruits do not; they lie within the seed-vessel, like the acorns and nuts. These are dry fruits, but there are others of a soft nature, such as apples or gooseberries.
Fruits are variously named, and underneath will be found a list. We have the aggregate, like the mulberry, etc.; the dehiscent fruit of one carpel like the pea, etc.; the simple fruits as cherry, nettle, wheat, etc. The dandelion fruit is often a precious object in children’s estimation, as it is blown away to ascertain the time. There are indehiscent fruits with many carpels,—the common buttercup, for instance, and the strawberry. A list is added.





a. Fruits which are the Produce of a Solitary Carpel.
1. The gymnospermous fruit, where the seed lies naked in the axils of the ligneous bracts, as in the cone of the fir and spruce tribe.
2. The legume or pod, which is formed of a solitary carpel bearing seeds on the ventral suture. It characterises the pea and bean tribe (leguminosæ).
3. The follicle is a mature carpel containing several seeds, and opening by the ventral suture. There are usually several follicles aggregated together; examples, larkspur, monkshood, evergreen.
b. Fruits which are the Produce of Several Carpels United.
4. The capsule consists of two or more carpels, either simply later[Pg 686]ally united (one-celled or unilocular capsule), or folded inwards towards the axis, but without reaching it (spuriously multilocular capsule), or uniting with the axis (bilocular, trilocular, multilocular capsule). Examples of capsular fruit—mignonette, balsam, violet, poppy, etc.


5. The siliqua or long pod is formed of two carpels, and longitudinally divided into two parts by a spurious dissepiment called the replum; examples—cabbages, stock, wallflower, etc. The silicula is a broad and short pod; examples—Iberis, shepherd’s-purse, etc.
6. The cariopse (caryopsis, having the appearance of a nut), is a monospermous or one-seeded fruit, with an indehiscent membranous pericarp, closely investing the seed or incorporated with it; examples—rye, wheat, and other grains.

7. The achænium is a dry, monospermous, indehiscent fruit with one seed; examples—cashew, ranunculus, strawberry, etc.
8. The nut or glans is a one-celled, indehiscent fruit, with a hardened coriaceous or ligneous pericarp; examples—hazel-nut, acorn, etc. The nucula, or little nut, is a cariopse, with a solid coriaceous pericarp; examples—buckwheat hemp, etc.
9. The berry (bacca) is a pulpy, succulent fruit, with soft rind; examples—the gooseberry and the currant. The pepo or peponida (pumpkin), illustrated by the fruit of the gourd and melon, and the hesperidium, illustrated by the fruit of the orange and lemon, are modifications of the berry.
10. The drupe (drupæ, unripe olives); the mesocarp is generally pulpy and succulent, the endocarp hard; examples—the cherry, the peach, the plum, etc.
11. The pome (pomum, or apple); the outer parts of the pericarp form a thick cellular, eatable mass; the endocarp (core) is scaly or horny, and encloses the seeds within separate cells; examples—the apple, pear, etc.


Fruits consisting of the floral envelopes and the ovaries of several flowers united into one, are termed multiple or anthocarpous; the sorosis (cluster-fruit: example—the pine-apple, the breadfruit, the mulberry), the sycosis (fig-fruit), and the strobilus (fir-cone), form varieties of the anthocarpous or multiple fruit.
Non-Flowering Plants.
The cryptogamia or acrogens is the botanical term for these plants,[Pg 687] of which we must be very brief in our description,—not that the subject is not worthy of a much larger space than we can devote to it, but our pages are not elastic.


There are numbers of plants without pistils or stamens properly so called. They are hidden from human observation—buried out of sight; and in the fern, moss, and other primitive plants they are thus hidden. There are several families of the cryptogamia, but two main sections include them all—viz., the cormogens and thallogens. These are sometimes known as cormophytes and thallophytes, but the former will be our terms, and they include the ferns, algæ, lichens, and mosses, with many other families, which we do not propose to examine in this summary sketch. The microscope will here be a great aid if not always absolutely necessary for any close investigation.
We are all familiar with the appearance of ferns, and we may commence with a few observations concerning them. They are an extensive family and very beautiful, some of the tropical species being particularly noticeable for elegance. We are here mostly concerned with the development of the plant. The polypod ferns fructify under the leaves or “fronds,” which open from a ball. The seed-cases or sorri are situated at the back of the fronds in brown spots, and when examined they will be found to be collections of capsules like tiny cases. There is a kind of band at the upper part which at the proper time is extended, and tearing open the capsule releases the seeds. These seeds or “spores” are very minute, and not properly seeds but buds, every one of which can generate seeds. So if we try to grasp in imagination the generating powers of a few fern fronds, we shall miserably fail in the attempt.


Some ferns have the “spores” upon the summit of the frond. The osmundas belong to this family, and are known to all as the “flowering fern,” a contradiction palpable enough under the circumstances. The beautiful dust upon some ferns has been mistaken for “spores” by many people, but it is merely a natural ornament of the plant. The venation and vernation of ferns are very curious, but in the determination of ferns the only sure way is to consider the sorri and the venation.[Pg 688] The differences that puzzle may be little or great, but when the sorri have been examined all doubts will be set aside.
There are about three thousand varieties of ferns known, and we give a few illustrations of them, although any detailed description is out of the question, for we have to mention the beautiful mosses of which there are in Britain more than five hundred different species, all extremely beautiful, perfectly innocuous, and even beneficial.
The Mosses and Algæ.


These plants are extremely lowly in the score of creation, and also in stature. Very few mosses attain any elevation, only the “sporangia” shoot up, and the plants are very delicately formed, the leaves being all of the same pattern. They are common in damp situations, and thrive in woods, streams, and banks. The Fontinalis is a river moss, while the Hypnum is found in hedges. The Lycopodiaceæ or the club-moss family is intermediate between ferns and mosses. They are found in warm, moist climates, and contain a sort of brimstone. They grow well with ferns under glass.
The Musci or moss-family proper are useful in various ways. We have also the liverworts, which bear some resemblance to lichens. They grow between stones near water, or in damp situations. There are two distinct families, both beautiful when examined, and are named Marchantiaceæ, and Jungeramanniaceæ, or scale moss.


The Thallogens or Thallogenæ include algæ, lichens, and fungi, which are the lowest of the plants, and all very much alike. The algæ are termed “protophytes,” and consist of living cells propagating by subdivision, or union. The thallogens have therefore no distinct axes, leaves, or stomata.
The algæ are thus simply cellular plants found in salt or fresh water, hot and cold. They sometimes appear as “slime.” Some contain silicia, and are termed Diatomaceæ, and these propagate by subdivision, and when[Pg 689] they die their shelly covering remains, and we find the shells or cases in all earthy formations. These diatomaceæ have been raised from the beds of oceans, and Atlantic soundings have revealed their presence,—as mud, when examined, proves to be these remains of vegetable shells. Thus the infinitely little in the animal and vegetable worlds meet at the bottom of the sea, as well as on dry land.
There are marine and fresh-water algæ—the former familiar to us as seaweeds which possess air-bladders that children love to explode, and which assist the algæ to float. They attach themselves to rocks, generally at the base; the lovely colours of seaweeds are well known. They will be recognized under the name of “tangle” (fucus), which, when burned, gives kelp and barilla, which is full of iodide and sodium. The Sargasso Sea is composed of miles of algæ which live in the open ocean. The Carrageen or Irish moss is very nutritious and useful in consumptive cases. Indeed, all algæ, if not absolutely useful, are certainly not deleterious. The “bladder-wrack” was formerly useful for the production of soda.


“The life-history of one of these uni-cellular plants in its most simple form, can scarcely be better exemplified than in the Palmogeœa macrococca, one of those humble forms of vegetation which spreads itself as a green slime over damp stones, walls, etc. When this slime is examined with a microscope, it is found to consist of a multitude of green cells, each surrounded by a gelatinous envelope; the cell which does not seem to have any distinct membranous wall is filled with granular particles of a green colour, and a ‘nucleus’ may sometimes be distinguished through the midst of these. When treated with tincture of iodine, however, the green contents of the cell are turned to a brownish hue, and a dark-brown nucleus is distinctly shown. Other cells are seen, which are considerably elongated, some of them beginning to present a sort of hour-glass contraction across the middle; in these is commencing that curious multiplication by duplicative subdivision which is the mode in which increase nearly always takes place throughout the vegetable kingdom.”37
Lichens are numerous, and may be found upon the bark of trees in dry forms of grey and yellow growth, and on walls and old stones in our graveyards. On the hills we find them growing upon the granite, and it would appear that they prefer stone to any other holding ground. The Arctic[Pg 690] lichens form the principal food of the useful reindeer, and “Iceland moss” is represented as wholesome for man. Lichen is derived from the Greek term for “wart.”
The Fungi are very important, and with them we will close our summary. They include the favourite mushrooms and poisonous toad-stools, with many other “fungous growths,” from the “mould” on the jam pot to the mushroom.

Some of these fungi are peculiar to the substances upon which they exist, and are in numerous instances destructive. The microscopic fungus Puccinea graminis is the parasite which fixes itself to corn, and produces the disease known as mildew, and the Uredo segetum (another microscopic fungus) causes the “smut”; the “bunt” is caused by the Uredo fœtida, and the “spur” or “ergot,” which attacks rye, is caused by the Acinula clavis. These fungi completely destroy the grain of corn in which they form, and propagate in the most rapid manner; the ergot is moreover a dangerous poison to those who eat the bread made of rye infected by it. The truffle is a kind of underground fungus, and is esteemed a dainty. Mushrooms are also fungi, and several species are sufficiently wholesome; these are the field mushroom and the fairy-ring mushroom.
Any organic substance will shortly become covered with this “mould” or mildew. The air is so full of the germs of animal and vegetable life that, as it penetrates everywhere, the smallest supply must contain some germs; and these, under a powerful microscope, present most beautiful forms and colours. We annex (fig. 822) some of these forms highly magnified. They are deposited by the air, and the substance into which they happen to fall determines the kind of life which is to inhabit it. A few of these spores only come to maturity.
We again take the liberty to quote Dr. Carpenter on this subject. He says:—
“There are scarcely any microscopic objects more beautiful than some of those forms of mould or mildew which are so commonly found growing upon the surface of jams and preserves, especially when they are viewed with a low magnifying power and by reflected light; for they present themselves as a forest of stems and branches of extremely varied and elegant forms,[Pg 691] loaded with fruit of singular delicacy of conformation, all glistening brightly on a dark ground.
“The universality of the appearance of these simple forms of fungi upon all spots favourable to their development, has given rise to the belief that they are spontaneously produced by decaying substances, but there is no occasion for this mode of accounting for it, since the extraordinary means adopted by nature for the production and diffusion of the germs of these plants adequately suffices to explain the facts of the case.
“The number of sporules which any one fungus may develop is almost incalculable; a single individual of the “puff-ball” tribe has been computed to send forth no fewer than ten millions. And their minuteness is such that they are scattered through the air in the finest possible dust, so that it is difficult to conceive of a place from which they should be excluded.”


Pure water exposed to the air does not afford nourishment to the germs which fall into it, till a sufficient number of them shall have been deposited to form a food for those which come after them; but if we mix with the water any soluble vegetable or animal matter, in a short time the microscope will detect the growth of the germs that are being deposited, for where nourishment is, there only can they be developed. These germs are capable of existing for an indefinite period, either floating in the water, or blown about by the air, and have been detected hundreds of miles from land; the rigging and sails of ships far away from shore are often covered with what sailors suppose to be sand blown from the land, but which are organic substances, either vegetable or animal. According to Humboldt, the Red Sea has derived its name from the fact that at certain seasons the surface of the water has a reddish appearance, and this (as he says) he was fortunate enough to observe, which colour he found to be due to myriads of red fungi, which had formed on the surface. The seeds of some plants are furnished with minute wings or plumes, which cause them to be borne on the air or floated on the water (fig. 824), to fertilise some barren spot, perhaps a coral reef, which has at length reached the surface of the water, and which ascends no higher, for the little creatures which built it are aquatic, and cannot live exposed to the air; this coral reef now becomes a receptacle for seaweed and fungi, which float on the surface of the ocean[Pg 692] are washed on to the reef, die, decay, and leave behind a thin layer of mould, which process being repeated again and again, forms an elevated edge to the reef, enclosing a lake, or “lagoon” as it is called, the waters of which evaporate, and the space is filled up in the same way as the edge was formed, together with the excrements of birds, etc., forming layer after layer of mould, and the surface becomes fit for the growth of larger seeds, as the cocoa-nut, banana, etc., which are drifted on to it by the waves; in this way a coral reef becomes an island fit to be inhabited by man and other animals.
It is impossible for any person not accustomed to observe the manner of the propagation of the fungi, to understand a written description, for the fructification of these plants are very varied in the manner of the development of the spores. They are not generally hurtful, but much caution should be observed in the matter of the mushroom, which may be distinguished by the pale pink and black of the under part. There are many poisonous fungi, but the greater number are harmless, though they are not intended for food. They simply clear away the decaying growths, and act as safety-valves to Nature by carrying away what is not required, to give it to the air again to be renewed into life.
The vegetable kingdom forms the link between the minerals and the animals. The vegetable derives food and nourishment from water, carbonic acid, and ammonia, which are, as we already know, made up of certain elements, and thus supply us all with food. They give out oxygen for the use of animals, and are thus, in another sense, the source of life. The growth of a plant is very interesting, and we may conclude by following it.
The seed is sown, and the cells of the “cellular tissue” become developed, passing some upwards, some downwards, to form a radicle or plumule, as explained. The latter carries up the cotyledon, which begins to decompose carbonic acid from the atmosphere, and fixing the carbon as woody fibre. The leaves are then formed and more fibres, and so on for every leaf; thus the number of woody fibres which form the trunk of a tree is in proportion to the number of leaves which that tree has borne, from which we come to the conclusion that the size of the trunk of a tree is the sum of all its branches. While all this is going on, the cellular tissue of the downward part or radicle also becomes developed and divides out into roots, on the surface and at the extremities of which are minute cellular bodies called “spongioles” (from their power of absorbing moisture), which take up the fluid of the earth which surrounds them; this moisture ascends through the vessels of the plant till it arrives at the surface of the leaves, where it is exposed to the action of light and sunshine. The ascent of the moisture of the earth was first correctly explained by Du Trochet, and is owing to a peculiar power which he discovered, and which is called “Endosmose”; this consists in the tendency which a fluid has to penetrate a membrane on the other side of which is a fluid of greater density than itself. This may be seen by the following experiment: obtain a piece of glass tubing about a foot long, having the end blown out into the form of a bell, as in fig. 825, tie[Pg 693] a piece of bladder over the expanded end and fill it partly with syrup or gum-water, so that this shall rise in the stalk about an inch; place this in a glass of water with the bladder downwards, and the fluid will be seen slowly to rise in the stalk, so that in perhaps an hour it will rise to the top. This apparatus resembles one of the spongioles at the extremity of the fibre of a root.

The rain falling through the air carries with it a certain amount of carbonic acid and ammonia, which the air always contains, and it is the whole source of the nitrogen which forms a very important part of the bodies of plants and animals. When the rain arrives at the surface of the earth, it sinks down into it and carries with it all soluble vegetable or animal matter which it meets with, together with any soluble earthy matter which may exist in the soil; this forms the sap of the tree. When it arrives at the surface of the leaf, the watery part of it combines with the carbonic acid of the air (through the influence of light), and appropriating its carbon, gives out the oxygen; this is the true respiration of plants, and is exactly the reverse of what takes place during the respiration of animals, in which case oxygen is absorbed and carbonic acid given off. The carbon thus retained by the plant combines with the elements of the water to form the solid green substance called chlorophyl, which is the basis of all the tissues of the plant; the ammonia is also decomposed, and its nitrogen combining with the oxygen and hydrogen of the water, and the carbon of the carbonic acid forms those compounds which constitute the most nourishing parts of vegetables, such as albumen, gluten, etc., and of which all the animal tissues are built up, for the production of these organic substances takes place in the vegetable only, animals simply appropriating them for their food. The sap which reaches the leaf is not all converted into chlorophyl, but also into those peculiar juices which are found in plants, some of which contain sugar, some gum, others (as the pine tribe) turpentine, and in the laurel tribe camphor, all of which are substances containing much carbon; moreover the solid wood and bark are deposited from these juices as they descend from the leaf after having been acted on by light (or the actinic power associated with it). Now, as the water, ammonia, and carbonic acid which descend with the rain are from the air, and as the vegetable is formed wholly by their absorption, it may be fairly said that the vegetable kingdom (and therefore the animal) feeds upon the air, and that the trees do not grow out of the earth, but into it.

Classification of Plants.
For the groundwork of the system of classification which universally obtains at present, we are indebted to Linnæus, a Swede, born in 1707. In his classification of plants, Linnæus followed two different methods. In the one, he based his division of plants in classes and orders, upon certain peculiarities in the floral organs. This system, being thus founded on characters taken from certain parts of the plant only, without reference to others, and having something artificial in it, has for that reason been termed the artificial system, but it is now more generally known as the Linnæan system. In the other method, he arranged the plants according to certain general resemblances and affinities, in natural orders or families. This system, which is known as the natural system, has subsequently been much improved.
We use the term species, to designate a number of individual plants, which, in all essential and unvarying characters, resemble each other more closely than they do any other plant; the term genus or kind, to designate an assemblage of nearly allied species, agreeing with one another in general structure and appearance more closely than they do with any other species. Here, too, it must be obvious, that while all parts of the plant may furnish specific characters, the character of the genera are taken exclusively from the parts of fructification.
In the name of a plant both the genus and the species are given. The name designating the genus is called the generic name of the plant, the one designating the species, the specific or trivial name. Thus, for instance, we have the genus Viola, which includes the species Viola odorata, sweet violet; Viola canina, dog violet; Viola tricolor, heart’s-ease.
It is necessary to give the Latin names of plants, as the common name differs, not only in different countries, but even in different parts of the same country.
An assemblage or group of allied genera, agreeing in their general characters, though differing in their special conformation, is called an order or family of plants.
The sunflower, the daisy, the aster, and the dahlia, are, for example, plants of different genera, but which, all of them, belong to the same order or family.
All plants are divided into three primary classes—viz., Dicotyledons, Monocotyledons, and Acotyledons, as has been stated already.
A proper degree of familiarity with the systematic classification of plants is of the very highest importance to the student. A successful pursuit of this branch of the botanical science presupposes a thorough knowledge of the structure and physiology of plants, and requires, moreover, the aid of attentive observation, and also some diligence in collecting and arranging plants.
The Artificial or Linnæan System of Classification.
In this system plants are divided into twenty-four classes; twenty-three of these contain the Dicotyledons and Monocotyledons indiscriminately; the twenty-fourth class contains the Acotyledons.
The first twenty-three classes are founded on the number, position, relative lengths, and connection of the stamens. The twenty-fourth comprises the plants with inconspicuous flowers. Every class is subdivided again into several orders. This division depends, in the first thirteen classes, on the number of the styles; in classes XIV. and XV. on the nature of the fruit; in classes XVI. to XVIII. and XX. to XXII. on the number of stamens; in classes XIX. and XXIII. on the perfection of the flower. In class XXIV. the orders are formed according to natural affinities.
Tabular View of the Linnæan System of Classification.
| A.—Flowers Present (Phanerogamia). | |||||
| I. Stamens and pistil in every flower (hermaphrodite). | |||||
| 1. Stamens free. | |||||
| a. Stamens of equal length, or not differing in definite proportions. | |||||
| Number of Stamens. | |||||
| 1 | Class | 1. Monandria. | |||
| 2 | “ | 2. Diandria. | |||
| 3 | “ | 3. Triandria. | |||
| 4 | “ | 4. Tetrandria. | |||
| 5 | “ | 5. Pentandria. | |||
| 6 | “ | 6. Hexandria. | |||
| 7 | “ | 7. Heptandria. | |||
| 8 | “ | 8. Octandria. | |||
| 9 | “ | 9. Enneandria. | |||
| 10 | “ | 10. Decandria. | |||
| 11-19 | “ | 11. Dodecandria. | |||
| 20 or more | inserted on calyx | “ | 12. Icosandria. | ||
| inserted on receptacle | “ | 13. Polyandria. | |||
| b. Stamens of different lengths, two long and two short | “ | 14. Didynamia. | |||
| Stamens of different lengths, four long and two short | “ | 15. Tetradynamia | |||
| 2. Stamens united by filaments in one bundle | “ | 16. Monadelphia. | |||
| Stamens united by filaments in two bundles | “ | 17. Diadelphia. | |||
| Stamens united by filaments in more than two bundles | “ | 18. Polyadelphia. | |||
| Stamens united by anthers (compound flowers) | “ | 19. Syngenesia. | |||
| Stamens united with pistil on a column | “ | 20. Gynandria. | |||
| II. Stamens and pistil in different flowers (unisexual) on the | |||||
| same plant | “ | 21. Monœcia. | |||
| on different plants | “ | 22. Diœcia. | |||
| III. Stamens and pistil in the same or in different flowers, on the same or on different plants |
“ | 23. Polygamia. | |||
| B.—Flowers Absent | “ | 24. Cryptogamia | |||
Tabular View of Classes and Orders.
| Classes. | Orders. | Examples. | |
|---|---|---|---|
| I.—Monandria | Monogynia | one style | Hippuris. |
| One stamen. | Digynia | two styles | Callitriche. |
| II.—Diandria | Monogynia | one style | Syringa. |
| Two stamens. | Digynia | two styles | Anthoxanthum. |
| Trigynia | three do. | ||
| III.—Triandria | Monogynia | one style | Iris. |
| Three stamens. | Digynia | two styles | Hordeum. |
| Trigynia | three do. | Holosteum. | |
| IV.—Tetrandria | Monogynia | one style | Scabiosa. |
| Four stamens. | Digynia | two styles | Gentiana. |
| Trigynia | three do. | ||
| V.—Pentandria | Monogynia | one style | Borago. |
| Five stamens. | Digynia | two styles | Fœniculum. |
| Trigynia | three do. | Sambucus. | |
| Tetragynia | four do. | Parnassia. | |
| Pentagynia | five do. | Linum. | |
| Polygynia | six and more do. | Myosurus. | |
| VI.—Hexandria | Monogynia | one style | Lilium. |
| Six stamens. | Digynia | two styles | Oxyria. |
| Trigynia | three do. | Rumex. | |
| Tetragynia | four do. | Alisma. | |
| Polygynia | many do. | ||
| VII.—Heptandria | Monogynia | one style | Trientalis. |
| Seven stamens. | Digynia | two styles | |
| Trigynia | three do. | ||
| Heptagynia | seven do. | ||
| VIII.—Octandria | Monogynia | one style | Daphne. |
| Eight stamens. | Digynia | two styles | Chrysosplenium. |
| Trigynia | three do. | Polygonum. | |
| Tetragynia | four do. | Paris. | |
| IX.—Enneandria | Monogynia | one style | |
| Nine stamens. | Trigynia | three styles | |
| Hexagynia | six do. | Butomus. | |
| X.—Decandria | Monogynia | one style | Pyrola. |
| Ten stamens. | Digynia | two styles | Dianthus. |
| Trigynia | three do. | Silene. | |
| Pentagynia | five do. | Lychnis. | |
| Decagynia | ten | do. | |
| XI.—Dodecandria | Monogynia | one style | Lythrum. |
| Twelve to nineteen stamens. | Digynia | two styles | Agrimonia. |
| Trigynia | three do. | Reseda. | |
| Pentagynia | five do. | ||
| Dodecagynia | twelve do. | Sempervivum.[Pg 697] | |
| XII.—Icosandria | Monogynia | one style | Prunus. |
| Twenty or more stamens inserted on the calyx. | Digynia | two styles | Cratægus. |
| Trigynia | three do. | Sorbus. | |
| Pentagynia | five do. | ||
| Polygynia | many do. | Rosa. | |
| XIII.—Polyandria | Monogynia | one style | Papaver. |
| Many stamens inserted on the receptacle. | Digynia | two styles | Pæonia. |
| Trigynia | three do. | Aconitum. | |
| Tetragynia | four do. | ||
| Pentagynia | five do. | Nigella. | |
| Hexagynia | six | do. | |
| Polygynia | many do. | Ranunculus. | |
| XIV.—Didynamia | Gymnospermia | four naked seeds | Lavandula. |
| Two long and two short stamens. Labiate and Personate Flowers. | Angiospermia | seeds in capsules | Linaria. |
| XV.—Tetradynamia | Siliculosa | broad and short pod (silicula), and style | Capsella. |
| Four long and two short stamens. Cruciferous Flowers. | Siliquosa | long pod (siliqua); stigma sessile | Brassica. |
| XVI.—Monadelphia | Pentandria | five stamens | Erodium. |
| Stamens united in one bundle. | Enneandria | nine do. | |
| Decandria | ten do. | Geranium. | |
| Dodecandria | 11-19 do. | Malva. | |
| Polyandria | many do. | ||
| XVII.—Diadelphia | Pentandria | five stamens (two above and three below.) | |
| Stamens united in two bundles (one generally containing nine enclosed in a tube, and one free). Papilionaceæ. | |||
| Hexandria | six stamens (three right, three left, or three above and three below.) | Fumaria. | |
| Octandria | eight stamens (four above and four below, all united at the base.) | Polygala. | |
| Decandria | ten stamens (one above and nine below, united in a cleft tube surrounding the ovary.) | Pisum, Trifolium, Genista. | |
| XVIII.—Polyadelphia | Pentandria | five bundles (each bundle bearing five anthers = 25 stamens.) | |
| Stamens united in more than two bundles. | Dodecandria | twelve stamens (each bundle bearing three anthers = 36 stamens.) | |
| Icosandria | many stamens in bundles, inserted on the calyx (20 stamens in bundles bearing an unequal number of anthers.) | Citrus. | |
| Polyandria | many stamens in three, five, and nine bundles, inserted on the receptacle. | Hypericum.[Pg 698] | |
| XIX.—Syngenesia | Polygamia æqualia, florets all hermaphrodite. | Lactuca. | |
| Five stamens, filaments free, anthers united, flower monopetalous, florets united on a disc. Compositæ. In the first four orders only a common calyx. |
|||
| Polygamia superflua, florets of the disc hermaphrodite, those of the ray pistilliferous and fertile. | Aster. | ||
| Polygamia frustranea, florets of the disc hermaphrodite, those of the ray neutral. | Helianthus. | ||
| Polygamia necessaria, florets of the disc staminiferous, of the ray pistilliferous | Calendula. | ||
| Polygamia segregata, a common calyx including all the florets, and a separate involucre for each. | Echinops. | ||
| Monogamia, anthers united, flowers not compound. | |||
| XX.—Gynandria | Diandria | two anthers | Orchis. |
| Stamens and pistil united. | Triandria | three do. | |
| Tetrandria | four do. | ||
| Pentandria | five do. | ||
| Hexandria | six do. | Aristolochia. | |
| Decandria | ten do. | ||
| Dodecandria | 11-19 do. | ||
| Polyandria | twenty or more do. | ||
| XXI.—Monœcia | Monandria | one stamen | Arum. |
| Stamens and pistils in different flowers on the same plant. | Diandria | two stamens | Lemna. |
| Triandria | three do. | Carex. | |
| Tetrandria | four do. | Urtica. | |
| Pentandria | five do. | Amaranthus. | |
| Hexandria | six do. | ||
| Heptandria | seven do. | ||
| Polyandria | more than seven do. | Quercus. | |
| Monadelphia | stamens united | Pinus. | |
| Syngenesia | stamens united by their anthers. | ||
| Gynandria | stamens and styles united | ||
| XXII.—Diœcia | Monandria | one stamen | Salix. |
| Stamens and pistils in different flowers on different plants. | Diandria | two stamens | |
| Triandria | three do. | Ficus. | |
| Tetrandria | four do. | Viscum. | |
| Pentandria | five do. | Cannabis. | |
| Hexandria | six do. | Loranthus. | |
| Octandria | eight do. | Populus. | |
| Enneandria | nine do. | Laurus. | |
| Decandria | ten do. | ||
| Dodecandria | 11-19 do. | Stratiotes. | |
| Polyandria | many | do. | |
| Monadelphia | stamens united in one bundle. | Juniperus. | |
| Syngenesia | stamens united by | the anthers. | |
| Gynandria | stamens and styles united.[Pg 699] | united. | |
| XXIII.—Polygamia | Monœcia, hermaphrodite, staminiferous, and pistilliferous flowers on the | same plant. | Acer. |
| Stamens and pistil in the same, or in different flowers, on the same or on different plants. | |||
| Diœcia | on two plants | Fraxinus. | |
| Triœcia | on three plants | ||
| XXIV.—Cryptogamia | Filices | Ferns | Aspidium. |
| Organs of fructification concealed (flowers inconspicuous). | Musci | Mosses | Spagnum. |
| Hepaticæ | Liverworts | Marchantia. | |
| Lichenes | Lichens | Cetraria. | |
| Algæ | Seaweeds | Fucus. | |
| Fungi | Mushrooms | Agaricus. | |
With all its imperfections, the artificial system has this advantage, that the character on which it is founded is sufficiently conspicuous (that is, of course, with the plants in full flower) to render it generally easy to ascertain the class and order of a plant. At all events, it may serve as a useful artificial key, and as such may be combined advantageously with the natural system.
114. Natural System (Jussieu’s).
| Classes. | ||||||
| I. | Acotyledons | 1st | Class. | |||
| II. | Monocotyledons | |||||
| Mono-hypogynæ (stamens hypogynous) | 2nd | ” | ||||
| Mono-perigynæ (stamens perigynous) | 3rd | ” | ||||
| Mono-epigynæ (stamens epigynous) | 4th | ” | ||||
| III. | Dicotyledons. | |||||
| Monoclines, flowers hermaphrodite. | ||||||
| Apetalæ (no petals) | ||||||
| Epistamineæ (stamens epigynous) | 5th | ” | ||||
| Peristamineæ (stamens perigynous) | 6th | ” | ||||
| Hypostamineæ (stamens hypogynous) | 7th | ” | ||||
| Monopetalæ (petals united). | ||||||
| Hypocorollæ (corolla hypogynous) | 8th | ” | ||||
| Pericorollæ (corolla perigynous) | 9th | ” | ||||
| Epicorollæ (corolla epigynous) | Synantheræ (anthers united) | 10th | ” | |||
| Chorisantheræ (anthers free) | 11th | ” | ||||
| Polypetalæ (petals distinct) | ||||||
| Epipetalæ (petals epigynous) | 12th | ” | ||||
| Peripetalæ (petals perigynous) | 13th | ” | ||||
| Hypopetalæ (petals hypogynous) | 14th | ” | ||||
| Diclines, flowers unisexual, or without a perianth. | 15th | ” | ||||
This system, being likewise founded partly on individual organs, is also, to a certain extent, artificial; and, strictly speaking, every natural method of botanic classification must partake more or less of an artificial character, as many orders of plants merge so insensibly into others that their respective limits cannot be accurately or rigorously defined.
CHAPTER LIV.
ZOOLOGY.
CLASSIFICATION OF ANIMALS—VERTEBRATES AND INVERTEBRATES—PROTOZOA—HYDROZOA—ACTINOZOA.
Zoology treats of life—of organized beings which are capable of voluntary motion. Plants exist, animals live and move. Both are organic beings, but the latter possess the faculty of will and spontaneous movement. The animal can leave a place and enjoy other surroundings, the plant cannot. We have already crossed the borderland which connects the plant and the animal. We have seen plants almost animals. We could commence this section with animals which are almost plants, so closely do the divisions approach each other. Zoology is the science of the knowledge of animals as Botany is of the knowledge of plants.

Where there is vegetation there are animals, not quadrupeds or bipeds necessarily, but numbers of small, it may be invisible, creatures which exist upon the vegetable kingdom—the algæ and minute creations of globules and cells, the infusoria already mentioned, the corals, etc. And in the “protozoa,” or first specimens of animal life, we have a similarity to the vegetable kingdom; we then get by gradual steps to other more perfect beings, each after his kind, till we arrive at the most perfect animal—Man.
Animals are divided into two families, the Invertebrate and the Vertebrate. The former has no spine nor skeleton; the latter has both. These again are divided into sub-families, classes, and orders, as follows.
Man is an animal—but what is an animal? We can scarcely tell in a few words. Linnæus defined the difference between the animal and the plant, for the former, said he, live, grow, and feel, while the latter live and grow. We have protozoa in the animal kingdom consisting of a single cell[Pg 701] or blood corpuscle, some others without mouths or digestive organs, some have no head; some, as in the tape-worm, only a so-called head, with suckers or attachments, after which it develops joints, which are at first imperfect, but gradually mature as they are pushed farther away by new-issuing joints.
Animals, therefore, do not all possess organs, nor is there any common organ by which all animals can be classed. The indispensable in one is absent in another, and while our mouths and digestive apparatus are all important, in other animals suckers and no digestive apparatus at all is quite sufficient. Some have one mouth, some several; some have mouths and a proboscis to assist them, some only the trunk and no mouth—so called—at all, as in some insects.

The organisms which could not be distinguished from vegetables were termed zoophytes, or plant animals, and, were space available, a comparison might be instituted between the extremes of growth of the animals and plants, from the largest whales to the tiny microscopic protozoa, and from the mould upon jam to the gigantic trees of California, one leaf of which it is said will shelter twenty men from rain.
Cuvier spent many years in perfecting his systematic arrangements of animals, and this classification, though many rearrangements have been made as modern discovery progressed, may be regarded as the fundamental system of all. Professor Agassiz adopted it with modifications. Professor Nicholson has made a somewhat different arrangement, but essentially there will be found but slight difference between them. We append both these arrangements for comparison:—
| Agassiz-Cuvier. | ||
|---|---|---|
| INVERTEBRATA. | ||
| Branch I.—Radiata. | ||
| Class I.—Polypi | 2 orders | Including actinoids and halcyonoids. |
| Class II.—Acalephs | 3 orders | hydroids, discophoræ, ctenophoræ. |
| Class III.—Echinoderms | 4 orders | crinoids, asteroids, echinoids. |
| Branch II.—Mollusca. | ||
| Class I.—Acephala | 4 orders | bryoza, brachiopods, tunicata, and lamellibranchiata. |
| Class II.—Gasteropoda | 3 orders | pipteropoda, heteropoda, and gasteropoda (proper). |
| Class III.—Cephalopoda | 2 orders | tetrabranchiata, and dibranchiata.[Pg 702] |
| Branch III.—Articulata. | ||
| Class I.—Worms | 3 orders | trematods (including leeches, etc.), nematoids, and annelides. |
| Class II.—Crustacea | 4 orders | rotifera, crinopods, tetradecapods, and decapods. |
| Class III.—Insects | 3 orders | myriapods, arachnoids, and insects proper. |
| Branch IV.—Vertebrata. | ||
| Class I.—Myzontes | 2 orders | myxinoids and cyclostomes. |
| Class II.—Fishes proper. | ||
| Class III.—Ganoids | 3 orders | cælacanths, axipenseroids, and sauroids. |
| Class IV.—Selachiens | 3 orders | chimæræ, galeodes, and batides. |
| Class V.—Amphibians | 3 orders | cæciliæ, ichthyodi, and anoura. |
| Class VI.—Reptiles | 4 orders | serpents, saurii, rhizodontes, and testudinata. |
| Class VII.—Birds | 4 orders | natatores, grallæ, rasores, and incessores. |
| Class VIII.—Mammalia | 3 orders | marsupiaia, herbivora, and carnivora. |
In the vertebrated animals the blood is red in consequence of the minute cells (corpuscles) which contain the colouring matter. In invertebrate animals these red cells are absent, and so the animals are white-blooded. Some animals, again, are cold-blooded like the fish; birds and mammalia have warm blood. It is worthy of remark that the higher we advance in the scale the fewer the offspring of the animal. The animalcules multiply at the rate of many billions a day, and even one codfish is stated to contain more than nine millions of eggs. A mackerel will produce 500,000; and so on, as we rise, we find mammals with seldom more than ten young at a time, down to one single offspring.
We could fill pages with the account of the differences existing between animals created for such different purposes and fitted to inhabit different climates, their mode of feeding and catching prey. The manner of bringing forth and rearing the young, and the temperament and temper of the animal creation would fill a volume, but we cannot now stay to examine these various characteristics. The following is the arrangement now usually adopted:—
| Nicholson. | |
|---|---|
| INVERTEBRATES. | |
| Protozoa. | |
| The lowest forms of animal life—microscopic animals. | |
| Gregarinida | Cell forms; worm-like. |
| Rhizopoda | Amebæ, foraminifera, radiolaria, sponges. |
| Infusoria. | Suctoria, ciliata, etc. |
| Cælenterata (The Old Radiata). | |
| HYDROZOA. | |
| Intermediary, having a mouth and receptacle separated by no alimentary canal. | |
| Polypes and Zoophytes, Actinozoa. |
Medusæ, millipores, corals, sea-anemones, tubipora, siphonophera, etc.[Pg 703] |
| Echinodermata. | |
| Star-fishes, sea-urchins, sea-cucumbers, and crinoids. | |
| Annulosa. | |
| Entozoa | Tape-worms, etc. |
| Rotifera | Wheel-Animalculæ. |
| Annelida | Worms, leeches. |
| Cerripida | Barnacles. |
| Crustacea | Shell-fish. |
| Insecta | Various insects. |
| Arachnida | Spiders, scorpions, etc. |
| Mollusca. | |
| MULLOSCOIDA—POLYZOA. | |
| Acephala of headless pupa. | Encephala with head. |
| Tunicata | Pteropoda. |
| Brachiopoda | Gasteropoda (univalves). |
| Lamellibranchiata (bivalves). | Cephalopoda, cuttle-fish, etc. |
| VERTEBRATA. | |
| Ichthyopsida. | |
| Class I.—Fishes | Various orders. |
| Class II.—Amphibia | Frogs, toads, salamanders, etc. |
| Sauropsida. | |
| Class III.—Reptilia | Tortoises, smaller snakes, lizards, etc. |
| Class IV.—Birds | Various orders. |
| Mammalia. | |
| Class I.—Non-Placental | Marsupials. |
| Class II.—Placental | Edentata, cetacea, ungulata, quadrumana, bimana, etc. |
We will adopt the latter order as being the more modern, and endeavour to make the various classes of the invertebrates clear to the mind, if we cannot present them to the vision, of the reader.
In our sketch of Botany we remarked upon the similarity existing between the cells of plants and animals, and although there are, of course, differences, there are many points of resemblance in these cells.
Plants have their lowest representatives called Protophytes. Animals which correspond to this class are termed Protozoa, from the Greek, proton, first, and zoön, animal. The former are, as already mentioned, seen amongst the algæ, consisting of simple cells, and protozoa cannot easily be distinguished from them except in the matter of nutriment, for some protozoa have no mouth except in the infusoria class. The cells are very much alike, and Dr. Carpenter sums them up briefly as follows:—
“The animal cell, in its most complete form, is comparable in most parts[Pg 704] of its structure to that of the plant, but differs from it in the entire absence of the ‘cellulose wall’ or of anything that represents it, the cell-contents being enclosed in only a single limitary membrane, the chemical composition of which, being albuminous, indicates its correspondence with the primordial utricle. In its young state it seems always to contain a semi-fluid plasma, which is essentially the same as the protoplasm of the plant, save that it does not include chlorophyl granules, and this may either continue to occupy its cavity (which is the case in cells whose entire energy is directed to growth and multiplication), or may give place, either wholly or in part, to the special product which it may be the function of the cell to prepare. Like the vegetable cell, that of animals very commonly multiplies by duplicative subdivision, it also (especially among protozoa) may give origin to new cells by the breaking up of its contents into several particles.”

| a, Cyclops Quadracornis. | f, Ambœba princeps. |
| b, Anguillula. Fluviatillis. | g, Acineta mystacina. |
| c, Actinophrys. Sol. | h, Oxytrycha. |
| d, Coleps Hirtus. | i, Triophthalamus dorsalis. |
| e, Vorticella. | j, Polyarthra. |
The protozoa are microscopic creatures consisting of one or more cells, and are infinitely little, thousands existing in a drop of water. They have no distinction of sexes, and their generation takes place by subdivision or blending of cells. The infusoria are the highest of the protozoa, and were formerly included amongst the radiata. Their numbers are infinite, and in a drop of water (see fig. 828) some very interesting specimens will be found. These infusoria are merely sarcode, or a jelly-like substance, and some have cilia, or hairy appendages, with which they agitate the water and cause a kind of current which brings them food. It is this partaking of food which has served to divide the lowest animal from the lowest vegetable[Pg 705] creations. There is no progressive increase of development from the lowest plant to the highest animal. The animal begins by himself, as it were, as the plant, and both grow up in different directions. The protozoa exist upon organic substances, while plants absorb inorganic substances and assimilate them.
The Gregarinidæ are very tiny cells, and though microscopically minute, they sometimes develop into worm-like or elongated oval bodies. They inhabit the intestines of crustacea, worms, and cockroaches, as well as of higher animals. They are capable of certain motion, but are not furnished even with the “false feet” (pseudo podia) of the rhizopoda, the next animal in these very low scales of creation.
Of the Rhizopoda the Amebæ are very interesting, and we find them in our veins as well as in the stagnant green water of the pond. They are simply sarcode or jelly, and, as the name implies, the amebæ can change their appearance (amoibos, changing). They possess a kind of crawling, progressive motion, and under the microscope will be perceived to develop a tiny bud, as it were, which is the “false foot” that assists its progress. These amebæ are in our blood moving about, and are always altering their form, and when warm they move more quickly in the red blood corpuscles or cells, but excessive heat will kill them.
These curious creatures feed by the foot they protrude; and by drawing in the “process” as it is termed, they can collect within themselves the nourishment they require. Of course they have no mouth, and if we can conceive a creature of this kind which thrusts out from a jelly-bag a tiny lump, and pulls it in again at any time and place it likes, we have an idea of an ameba.
The pond ameba is somewhat different from the others, inasmuch as it possesses an outer and inner portion or layer which are different in density. There is what is termed a contractile vesicle which “beats” as a heart beats, but this is very primitive. There is really no structure whatever in these rhizopoda, and, as we have seen, their shape is always undergoing change. The outer and inner layers of the amebæ are called “the ectosarc” and “endosarc” respectively; the latter contains the darker portion—the nucleus.
The Foraminifera have already been mentioned in the chapters on Geology. We find these minute creatures must have had a great deal to do with the building up of rocks, as they have the power to make tiny coverings for themselves, which have been built into rocks by the addition of sandy particles, and consolidated by pressure. Here we have a most wonderful instance of the tiniest creatures producing the greatest masses of the earth. The body is merely sarcode, the shell is carbonate of lime. The foraminifera produce false feet in abundance, which surround the cell like fine hairs or rays. They live in the sea, and when they die the shells descend upon the ocean floor, where they undergo many changes and become converted into rock. The ooze of the great oceans is composed[Pg 706] of these shells, and is practically a chalky deposit; the shells are being built up as in former ages with the curious nummulites of the Eocene formation, which are amongst the most interesting of fossils.
Sponges. We must go on at once to the Sponges, which form such an interesting subject as they are so familiar to us all. Sponge is not often regarded by the public as an animal, and though perhaps authorities may not have yet concluded in what category they should be placed, we may consider them here according to the list.
We find the spongida both in fresh and salt water, and they have given rise to much discussion as to whether they should be classed as animals at all. But that question having been finally settled, we can proceed to examine a sponge in its native state, and we shall find both skeleton and “flesh.”
The skeleton is hard and composed of needles of “tiny” texture. The flesh is “sarcode,” and the animal possesses no mouth, but is full of holes (pores) and canals through which the water is continually distributed. The outer layer of the sponge is formed of ultimate components of the living substance of the sponge (like the amebæ we have been considering). Each contains a nucleus, and when joined together form the outer layer of the body. Beneath is a wide cavity communicating with the exterior by means of minute holes, and filled with water. The cavity separates the superficial layer from the deeper substance, which is of the same character. In the water passages of the sponge are cilia which induce a cement, and the interior canals develop into chambers lined with sponge particles, and the water carries particles to the sponge, which represents a kind of sub-aqueous city, where the people are arranged about the streets and roads in such a manner that each can easily appropriate his food from the water as it passes along.38

Sponge, then, is a mass of living organisms—tiny living creatures capable of feeding and of movement, resembling amebæ or perhaps infusoria, with cilia, to enable them to obtain nourishment by a kind of inhalation or respiration. They are reproductive by sexual and a-sexual processes which produce spongellæ. The living sponge is a beautifully coloured animal, and grows upon almost any solid foundation; and in the autumn the parent sponge displays a number of yellow dots or “gemmules,” which are the young. These are soon cast off and left to shift for themselves, and seek their fortunes, helpless as they appear, in the wide and stormy sea. At last they find a resting-place, and fix themselves for ever, growing up and reproducing their species until they are carried off to be sold and used in civilized countries for domestic purposes.
We must leave these curious animalculæ and glance at the Infusoria,[Pg 707] which constitute a higher branch, but microscopic and universal, and include those called Flagellate, Ciliate, and Tentaculate. The first have whip-like cilia, or feelers, or filaments, which are ever in motion to cause a movement of the water and carry food to the animal. You will find plenty of infusoria in any stagnant water, and when placed under the microscope a mouth may be perceived, but no stomach, nor any apparent receptacle for food, which appears to enter at once into the body substance. The other kinds capture their food by seizure by the tentacles, or by agitating the cilia, like the flagellata, and thus whipping the nourishment towards the mouth, as children will draw in a toy boat to land by agitating the water in the given direction. These cilia, or hairs, serve for organs of locomotion as well as of capture. These creatures are called Infusoria, because they exist in vegetable “infusions” exposed to the atmosphere.

Decaying vegetable or animal substances, such as the leaves of trees, grass, a piece of flesh, etc., affused with water and exposed to air and warmth, will speedily, upon microscopic examination, be found peopled with numbers of most active minute creatures of the most varied forms. These animalcules are found also in the stagnant pools around our cities, in the waters of rivers, harbours, and lakes, and even in the ocean.
In reference to the origin of these animalcules, the view was long entertained that they were generated spontaneously, that the decaying vegetable and animal substances were decomposed and resolved into these simple beings. More accurate experiments have shown, however, that the infusoria are produced from ova, or germs, which are probably carried about in the dried-up state, in the form of minute particles of dust,39 ready to develop themselves in any spot which may afford them the requisite moisture and nutriment. In this respect they[Pg 708] resemble the microscopic fungi, whose germs are diffused in the same way. When once they have obtained the means of development, they multiply with incredible celerity. If the decaying vegetable or animal substances be carefully excluded from contact with the air, or if the air be heated before it is admitted to them, no infusoria will appear. They are rarely developed on mountains of a certain height, where the atmosphere is free from foreign bodies.

Though these animalcules are so exceedingly minute, yet the forms exhibited by them are extremely various, and some of them present also considerable variety in the forms assumed by the same individual under different circumstances. In many species the soft body is enclosed in a firm integument, strengthened by a deposit of siliceous matter; these envelopes, which are often preserved after the death of the animals, are termed the shields, and the animalcules encased in them are called loricated infusoria. The remarkable discovery has been made that large distinct beds of former formations are entirely made up of the accumulated remains of these animalcules.
We arrive at the Hydrozoa after leaving the Infusoria, and find ourselves in the sea, and far from land, where it will be difficult for us to ascertain the characteristics of these interesting animals. But fortunately we can obtain much nearer home, and occasionally in a private aquarium, a specimen of the hydrozoa which will serve our purpose, as it has served before to introduce readers to the study of these water-polypes, some of which are so like plants that they are frequently mistaken for them.
The hydrozoa present a “definite histological structure,” says Professor Huxley; “the body always exhibits a separation into at least two distinct layers of tissue, an outer and an inner.” The Hydras, or fresh-water polypes, which may be found in nearly every pond adhering to the duckweed, appears like tubes, and if touched will curl up into tiny knobs. But if let alone they will adhere to a glass by their single foot, or sucker, which can be moved at pleasure.

The foot, or sucker, is continued to a slender cylindrical stalk, from the end of which radiate a number of tentacles, or “feelers,” growing around the mouth, and serving to convey or attract food to the animal which is, so to speak, all stomach. There is no breathing apparatus, and what food it cannot digest is expelled from the mouth. The peculiarity which has given the hydra its name is, that no matter into how many pieces you cut this polype, the parts cut off will all develop into little polypes perfect[Pg 709] as their parent.40 But germination is carried on naturally by buds thrown out, and cast (by “gemmation”), or by the ordinary sexual production of ova.
The outer and inner skins of the hydra are called the ectoderm and endoderm, and the animal is quite capable of locomotion, walking, or rather moving, backwards, by raising and planting its sucker or foot, and by swimming. The prey is captured by the tentacles and by the darting out of tiny spears from the cells or “thread cells” which contain them on the surface of the body. The well-known “Portuguese man-of-war,” an ocean polype, has these “harpoons” greatly developed, and can inflict serious pain as of many stinging nettles; the sensation is exceedingly painful, and lasts some time.

The Medusidæ are known to the seaside visitor as the jelly-fish, and the other Acalephæ, the “hidden-eyed” medusæ, include the Portuguese man-of-war mentioned above, and many other umbrella-like animals. They have received the name of medusæ from Medusa, whose long, snaky locks the tentacles of the animals are supposed to be like. Some of these “floating umbrellas” are very dangerous, and will inflict severe stings upon any one in their vicinity. The tentacles or filaments extend for a long distance, and bathers should be cautious. We have often watched them, and they are beautiful to contemplate particularly at night, and in Kingstown Harbour, near Dublin, many exceedingly fine specimens have been obtained. The pulsation of the “umbrella” or bell, enables the animal to swim, and the even undulations of this beautiful covering are apparently caused by nervous contractions.
The jelly-fish have no resemblance to “fish,” and scarcely appear to exist; they are of no use to man, and when removed from the water dwindle by little and little to a tiny film and nothing more—they dissolve into air and water. Cases have been known and tales told of how farmers collected hundreds of these jelly-fish for manure, and when the cart reached the field, to the man’s astonishment, nothing was left but what appeared cobweb in the place of the load of fish.
The Cyclippe is a very common specimen, and moves by means of its cilia; Cestum Veneris—the zone or girdle of Venus—is another curious example. It appears like a glass ribbon about five inches wide and perhaps four or five feet long. The cilia when in motion are very brilliant in[Pg 710] colouring, and the creature undulates through the water in a remarkable manner.
The luminosity of the medusæ is clearly perceived, the so-called phosphorescence being due chiefly to the minute jelly-fish which abound near the surface of the sea. It appears impossible, for most, at any rate, if not all, these medusæ to sink beneath the surface, for they can be found in hundreds cast ashore, melting away into film. We might imagine that they would be provided with some means of sinking themselves, but being apparently only air and water, it is necessary for them to remain upon the surface to exist at all.

The term Acalephæ, by which they are known, means “stinging” fish or sea-nettles, the Greek word meaning nettle.
The Actinozoa comprise corals and the popular sea anemones (actinidæ). They resemble the hydrozoa in possessing tentacles, and also the two inner and outer tissues of the body. But they differ from the hydrozoa in their interior arrangement in the possession of a kind of stomach between the “body cavity” and the mouth which the hydrozoa do not possess. The appearance of the sea anemone is well known. It fixes itself by the flat base and hangs out its tentacles to obtain food. When we touch an anemone with a stick we perceive how it contracts itself, but there is no nervous system nor any respiration. The reproduction of its species is carried on within, not as in other animals, like the hydra, by exterior budding.

The corals belong to the same class as the sea anemones, and are called zoanthidæ. We have already in previous portions of this volume mentioned the “coral” building polypes, but we may again describe them here. We have the black coral or antipathidæ, which live in masses and are[Pg 711] united by a stem. They grow upon this fleshy trunk and cover it in time “just as a trunk of a tree is covered by the bark.” This stem is called a cænosarc, which secretes the coral, or skeleton. The madrepores are the greatest producers of the coral of commerce.

“If we examine a simple coral of this group,” says Professor Nicholson, “we find that we have to deal with an animal in all important respects identical with an ordinary sea anemone, but having a more or less complicated skeleton developed in its interior.” This skeleton is the corallum, and it is composed, as most people are aware, of calcareous matter deposited within the polype itself; in the former case the development or formation is exterior to the polype. A single polype will thus secrete a deposit, and a colony of them produce a compound skeleton, and as they throw out buds or young polypes, the manufacture of skeletons goes on by secretion.
The Tubipores are like pipes, and the coral has been termed the “organ-pipe.” It is formed cylindrically and joined externally. As under Geology we have examined the question of coral reefs, we need not here recapitulate the descriptions given in that section.

Doctor Bariel writes of these animals as follows:—“By far the greater part of the Zoanthoid polypes, as they grow, deposit in the cellular substance of the flesh of their back an immense quantity of calcareous matter which enlarges as the animal increases in size, and, in fact, fills up those portions of the substance of the animal, which by the growth of new parts are no longer wanted for its nourishment, and in this manner they form a hard and strong case, amongst the folds of which they contract themselves so as to be protected from external injury, and by the same means they form for themselves a permanent attachment which prevents their being tossed about by every wave of the element in which they live. The stony substances so formed are called corals, and their mode of formation causes them exactly to represent the animal which secretes them. The upper surface is always furnished with radiating plates, the remains of the calcareous particles which are deposited in the longitudinal folds of the stomach.”

CHAPTER LV.
ECHINODERMATA—ANNULOSA—ENTOZOA—INSECTA.
SEA-URCHINS—STAR-FISHES—FEATHERY STARS—SEA-CUCUMBERS—WORMS—LEECHES—ROTIFERS—TAPE WORMS—INSECTS.
The Echinodermata or spiny-skinned, are most commonly represented by the sea-urchins and star-fishes of our coasts. In some of the classes locomotion is performed by means of these spines or prickles, which serve as legs. In others, movement is carried on by suckers and tubes as in the star-fishes, these tubes being also the means whereby the animal obtains its food.

They have a digestive system, and possess a curiously horny skin even when spines are absent. The mouth is in the centre. We give an illustration of the sea-urchin, and of a section of a spine, which is a beautiful object when seen under the microscope, for these spines can be made quite transparent when cut across and ground. The shelly covering is porous, and as the animal grows the shell is added to at the edges. Underneath will be found the mouth, which has teeth fitted for devouring the small crustacea. These sea-urchins abound, and their porous shells may be picked up frequently after a storm.
The star-fishes are well known to all searchers amongst the rocks and those who study the shore, and are often taken home for an aquarium. They are very voracious, however, and when one is examined in a glass of sea-water, the observer will detect many suckers protruding from each of the rays. It is by means of these suckers, which are put forth from innumerable little holes called “ambulacral apertures,” that the star-fish makes his way up the rocks and along the ocean bed. The stomach of the star-fish is extensive, and situated in the centre of the rays wherein is a digestive apparatus. The rays are composed of detached but beautifully[Pg 713] fitted pieces, so united as to be flexible, and around the mouth and in strong frame-work. The star-fish has no teeth, but manages to dispose of a vast quantity of matter, which if left alone would be injurious in decay.
Thus Nature has provided a shore scavenger to devour what would be harmful, just as the vulture on land eats the carrion. Besides this kind of refuse food, the star-fish eats small crustaceans, and oysters fall victims to him. By embracing the shell the star-fish manages to insert itself, and if it cannot bring the oyster out to its mouth, it will quietly turn out its mouth into the oyster-shell, and save the bivalve any trouble in the matter. Some writers declare that the star-fish stupefies or poisons its victim, and then the shell opens. These asteroidea can reproduce a ray that has been injured or cut off, or they can break themselves to pieces if caught.

The brittle stars and feather stars appertain to the order of the Ophiuroida or “serpent-armed,” because the rays are more flexible and thin than the common star-fish. But they differ very much from the star-fish in the arrangement, as well as in the shape of their arms. The former possesses rays which form an appendage of the stomach and enclose it. In the brittle stars the rays are limbs, and could be detached without taking the life of the animal, except in so far as to deprive it of means to obtain its food. The body is quite independent of the rays, the mouth occupying the centre, and is surrounded by minute suckers. The stars are much more flexible than the star-fishes, their rays are longer, and serve either as feet, fins, tentacles, or arms.
The crinoids also belong to the Echinodermata, and resemble plants more than star-fish. They are fixed upon a stalk like a flower, growing upright from the sea-bottom, and the body is called a calyx, which is composed of a ventral and dorsal surface. The arms branch out from the calyx, just as a small tree does, and if we can imagine one of the last planted trees on the Thames embankment reduced to half a finger’s length or less, we have a sort of idea of the crinoid “in the rough.”
A polype supported on a stem branching out in feathery, grassy-looking arms represents the Encrinites, the remains of which are found as fossils. The arms of the crinoids are subdivided, and quite a flowery crown may in time result. The animal obtains its food by the motion of cilia. The stem and the branches are jointed, as it were, and capable of flexible movement in any direction. The crinoids remain stationary during their lives.
The care taken by the star-fish of its young is remarkable. It carries the eggs about in its suckers and with great caution. The young remain attached to the mother until they are able to go about alone, and then the[Pg 714] physical attachments die off, and the asteroidea goes forth to seek its fortune in the sea.
The echinus, already mentioned, is a most elaborately constructed animal; the plates being secreted from the soft parts are ever being renewed as the animal gets older and larger. The whole subject is well worth a long independent study, of which it is here impossible for us to give the results.
The sea-cucumbers are more like the familiar garden slug than any other animal, and are surmounted by a fringe round the mouth which looks like leaves. The surface is moist, and has no horny covering like the “urchin,” or star fish, but the suckers are present and are used for locomotion. The tentacles round the mouth serve as prehensile organs. The “alimentary canal” is most curiously curved, and of great length, and the animal can turn itself “inside out” with great facility if alarmed. It possesses a kind of breathing apparatus, and may be classed as the most highly organized of all the Echinodermata. These cucumbers are much esteemed by the Chinese, and “trepang,” as they are called, are caught by thousands in Australian waters.
Annulosa.
The worm-like animals are divided into sections, which include intestinal worms, entozoa, annelida, and crustacea, with the worms, spiders, and insects classed in each section. We may at once perceive what a very extensive division the Annulosa is, and we must devote some space to it.

The Rotifers, or “wheel animalculæ,” are included in this class; they stand almost alone, and certainly invisible to the naked eye. They are very curious animals, as will be seen from the accompanying illustration. The motion of the cilia around the mouth gives the whirling movement from which their name is derived (fig. 841).
The Annelides, or worms, include earth-worms, water-worms, leeches, etc. The appearance of the earth-worm is so common that few people comparatively studied it until Mr. Darwin’s book took the amateur reader by surprise and delighted him, and to that volume we must refer our readers for details of these very interesting animals, termed annelides because of the rings appearing upon their bodies.
The common leech is well known in medicine. It is curiously enough[Pg 715] an inhabitant of ponds and lakes, and in such conditions has no opportunities for tasting the warm blood for which it develops such a liking when opportunity offers. This is really a remarkable fact, that the animal should be placed in a position naturally in which its most natural tendencies should remain unsatisfied.
The progression of the leech is performed by undulating movements and the prehensile action of the suckers—head and tail. The eyes are ten in number, near the mouth and at the top of the head. The mouth is furnished with numerous tri-radiate teeth, but in some leeches they are not sharp, as in the “medicinal” variety. It is known that both sexes are represented in every leech, but they are not self-reproductive.
The earth-worm, so familiar to all, has been lately raised into importance. It lives in clay, and bores its way through the ground. It feeds upon organic matter contained in the earth, and when it has assimilated the nourishing particles, it ejects the remainder in small heaps of soft dirt, which are visible after rain particularly. The worm, by its burrowing, turns up the land, and vastly increases its fertility.

The earth-worm in its outer structure resembles the leech, but, as any one will at once perceive, the worm is not furnished with suckers by which it can assist itself to move. Instead of these rounded terminals the worm is finely pointed, and thus capable of boring its way through the earth. Progression is accomplished by moving first the head portion and then the next, so that a regular series of movements is necessary. The minute spines or bristles of the worm prevent its body being retracted by muscular effort.
The vital organs are rather forward of the centre of the body, and so if a worm be cut behind them it will survive and reproduce a tail. But the portion cut off will not be found alive, nor is it capable of forming a new perfect worm as generally supposed.
There are many other orders of worms which we can only indicate—viz., the Tubicolæ which surround themselves with a hard case; the Errantia, or sea-worms, sand-worms, etc., like the lobworm used for bait, and the naiads of our fresh-water ponds, all of which are suited to the aquatic life they lead. Indeed, of all the annelides, the earth-worm is the only specimen that is suited for living upon land. As regards the last mentioned, we may add that worms do not prey upon dead bodies as is so generally imagined. They are vegetable feeders, and do not burrow very deeply.
The transparent condition of the Rotifers renders them easy of observation under the microscope, and we find a nervous system, intestines, and a developed stomach. They are fresh-water inhabitants.
The Entozoa or “intestinal” worms claim a brief notice at our hands. The entozoa are those beings which inhabit, as parasites, the intestines and other parts of animals. Their history is still obscure, but there seems to be about twenty varieties of these creatures, and a great number of animals have their peculiar entozoa. The best known in the human subject are the “Ascaris” or thread-worm, the “Lumbricus Teres” or long-worm, and the “Tænia” or tape-worm; this last is jointed, and grows to several yards in length.
The development of these Tænia is one of the most curious performances of nature. Each of the joints shown in the illustration below (fig. 842) is a perfected and mature proglottis, containing the ova or eggs, which can only be brought to perfection when swallowed by a warm-blooded animal (not the same from which they emanated). The head within the embryo then holds to the tissues and penetrates to the alimentary canal, where only it can redevelop joints from the so-called head, which has no organs and merely pushes out immature joints which are continued, and they become more mature the farther they are pushed out by the new ones. The “measles” of the pig are produced by the ova of these worms.

Myriapoda.
The “many-footed” annulosa include the centipedes and millipedes, and may be regarded as a connecting link between the worms and the insects. The heads of these animals are distinct from the body.
The millipedes can be any day found under a large stone in a field which has not been tilled, or any place where a stone has been suffered to remain for some time undisturbed. These specimens are of the pill-millipede order, because they roll themselves up into a ball when disturbed. The myriapods of this country are not of large dimensions, but in tropical climates they attain a great size. The giant centipede has been found in South America more than a foot long, and is capable of inflicting severe wounds, its tenacity being extraordinary and equalling that of the bull-dog when once it has gripped its enemy.
The myriapods have no wings; they possess antennæ, and numerous,[Pg 717] never less than eighteen, feet,—frequently twenty pairs, but never a thousand, much less “ten thousand” feet, as the class name indicates. They are provided with strong forceps or “foot-jaws,” which supply a poison for killing their enemies. The millipedes and centipedes are known scientifically as Iulidæ and Scolopendridæ respectively, and in most points of internal arrangement resemble insects, such as breathing by spiracles or (stomates), and trachæ or tubes. Some of the centipedes possess electric qualities, and can administer a shock to an opponent.
Insecta.
Insects inhabit the world around us in myriad forms in air and earth and water. Some exist for a very brief space in the air; others live under water, or in trees, or in the ground; some burrow and hide in chinks of rocks and under stones. The numbers are countless, and all have some function to perform as palpably as the busy honey-bee, or as mysteriously as the giddy, careless butterfly.

Insects are divided into three distinct parts,—viz., the head, the thorax, and the abdomen, and each of these parts has a pair of legs attached to it, as will be perceived from the accompanying diagram. Along the body are tubes called trachæ,—for insects do not breathe by lungs,—by which the air is carried into the system of the insect, by the “spiracles” or openings of fine network, to prevent dust entering the air-passages. The head is joined to the body by a constricted neck, the part of the body to which it is joined is called the thorax, and to this is added the posterior part or abdomen; this[Pg 718] part is extremely various in form in different insects; in some it is round and full, in others long and extended. The antennæ arise from the head, and are generally composed of eleven pieces variously disposed; these wonderful organs are possessed of great sensibility, and they certainly serve to convey information to the insect, of the nature of one of the special senses; it was formerly thought to be simply that of touch very much refined, or of smell, but it is now generally considered to be that of hearing, or a modification of it. The forms of the antennæ are very various; fig. 845 represents that of the cockchafer (Melolontha vulgaris). The legs proceed from the thorax as do the wings, the abdomen giving rise to none of the extremities; the feet of insects are all pretty much upon the same model, some being more developed than others, they have a pair of hooks or claws for catching and clinging to rough surfaces, and a pair of cushions or pads, covered in some cases with suckers.


The foot of the common house-fly is most beautifully fitted for its progression and support. We have often wondered how the fly manages to support itself back downwards on the ceiling, or walk up glass. We give a cut of the fly’s foot (fig. 846).
The eyes of insects are also marvellous. There are only two, but each one is composed of numerous cells (ocelli), and look like a honey-comb. (See illustration, fig. 847.)


Insects swarm in innumerable companies, and no one who has not seen the locusts descending upon the earth can form more than a faint idea of the devastation they occasion in an incredibly short time. These, as well as thousands of other insects, exist in myriads, and we must content ourselves,[Pg 719] on this occasion, by merely noting the different orders and their characteristics, after we have mentioned some of the attributes common to all.
The term “insect” means cut into or divided, and so the insecta are divided, as already mentioned, into three parts,—head, thorax, and abdomen,—the thorax being subdivided into three rings, pro-thorax, meso-thorax, and meta-thorax—beginning, middle, and end. All insects have six legs, and usually two or four wings, though some have no wings at all. The legs are united to the thorax, the antennæ and eyes to the head. The abdomen contains the important sexual organs, a sting or defensive weapon, and in females the egg chamber.
Insects breathe by tubes in the sides, and consume a great quantity of air. Their powers of flying and leaping are too familiar to need dwelling upon. The wings display beautiful colours like those observable in the soap-bubble, others are covered with scales or hairs. The mouths vary very much with the species, as the manner of obtaining food is by suction or gnawing. The blood of insects is pale and thin.
The various transformations which insects undergo are always a subject of interest for the young student. The ugly forms which develop in beautiful creations are more astonishing than the change of the “ugly duckling” into the graceful swan.


Insects come to maturity only after undergoing successive changes from the egg to the perfect animal. The eggs (some of which are very beautiful) are first deposited in some safe place, either attached to a leaf or tied up in a small bundle by silken threads spun by the parent insect, and in some nutritious substance, so that when it comes to life it may at once have food; this is sometimes in manure, sometimes in flesh, and sometimes under the skin of a living animal (few are exempt from this infliction), where they remain for a time and then come forth as maggots, caterpillars, etc.; in this state they are called larvæ,—these are generally active creatures and eat most voraciously, which seems to be the principal act of this state of their existence. These larvæ frequently change their skins as they grow, and at last they assume the next stage of their life, the pupa or chrysalis state, which is one generally of complete inactivity; many of these larvæ weave themselves a covering of a sort of silk, to defend them while in the pupa state,—such as the silkworm, whose covering (cocoon) is the source of all the silk of commerce,—others merely place themselves in a situation of security. The pupa remains dormant for a certain time, and then becomes the imago or perfect insect (the last state of its existence), such as a moth, a butterfly, a beetle, etc. These are of different sexes, and in due time produce a batch[Pg 720] of eggs and then die; these eggs are often incredible in numbers, amounting to many thousands—but few escape the watchful eyes of other insects and of birds who feed upon them.
But there are some of the insecta which do not undergo metamorphosis; the Aptera or wingless insects include these, as the flea and such parasites which bore into other animals, and deposit their eggs within them.

Insects have very little means for making themselves audible, at least so far as can be ascertained. The humming of bees and flies and other insects are, of course, not intended to represent the voice. The cricket’s “chirp,” as people commonly imagine, but the sound is attributable to the rubbing together of the wings or wing-cases, as is the noise produced by the field-cricket. There is a very peculiar sound attributable to the “Death-Watch,” a ticking, and to nervous people terrible warning of dissolution. It may reassure some one, perhaps, to know that this “unearthly sound” is caused simply by the insect beating its head against a piece of wood to attract its mate, as the female glow-worm lights her lamp to guide her lord to her bower.
The Insecta may simply be divided into nine orders:—
| 1 Coleoptera. | Beetle tribe. | Case-winged. |
| 2 Orthoptera. | Locusts, crickets, etc. | Straight-winged. |
| 3 Neuroptera. | Dragon-flies, etc. | Nerve-winged. |
| 4 Hymenoptera. | Bees, ants, wasps, etc. | Membrane-winged. |
| 5 Strepsiptera. | Parasites of the foregoing. | Twisted-winged. |
| 6 Lepidoptera. | Moths and butterflies. | Scale-winged. |
| 7 Hemiptera. | Bugs, water-boatmen. | Half-winged. |
| 8 Diptera. | House-fly, gnat. | Two-winged. |
| 9 Apraniptera. | Fleas, “chigos.” | Wingless. |
| (Of these the metamorphoses of 1, 3, 4, 6, and 8 are complete). | ||

The Coleoptera are well represented in England as beetles. They have four wings, but the outer pair serve as coverings to the inner ones. They are termed Elytra, and are horny in texture. These beetles are short-lived, but useful as scavengers, and serve to manure the ground by burying objectionable matter. The larvæ of beetles eat tremendously. The stag-beetle is a formidable-looking animal, and the lady-bird is well known as an enemy to the aphides on our rose trees. The tiger-beetle, cockchafer, and various water-beetles belong to[Pg 721] this family. The scarabee, or sacred Egyptian beetle, also will be found classed with the coleoptera. Many of these beetles are excellent scavengers, and some called burying beetles remove the soil underneath the carcases of birds and other small dead animals, letting them fall down below the ground level; the beetles then lay their eggs in the body, so that sustenance may be at hand for the young when hatched.
The Orthoptera include our cockroaches, miscalled “black beetles,” the locusts, crickets, etc. The ravages of the locust are well known. The larvæ of the orthoptera has no wings, but otherwise is very like the grown insect. They change their skins frequently before they become perfect insects.
Passing the “nerve-winged” dragon-flies and caddis, whose larvæ case is so familiar and useful as bait, we come to the very important and interesting order of Hymenoptera, with four membranous wings. In this rank we find bees, wasps, and ants, the first and last named being proverbial for industry and examples of almost superhuman reasoning powers, and a similitude to man’s arrangements in labour and house-building marvellous to contemplate. A study of the habits of ants, bees, and wasps will reveal a state of society existing amongst them which more nearly resembles man in feelings and habits, for these insects possess means of oral communication.

Fig. 852.—Honey-lapping apparatus of wild sea-bee (Halictus), (a, magnified; a b, more highly magnified).
All these insects are armed with a sting, or other offensive weapon. The ant possesses the “formic” acid, which derives its name from the possessor. The destructive white ants will eat away a wooden house very quickly, sapping and mining it in all directions till it is a mere skeleton. The habits of bees are so well known and have been so often described that we need not detail them. The manner in which the ants “milk” the aphides is curious and interesting.

The Strepsiptera order includes very few species, so we may pass quickly to the Lepidoptera, the butterflies and moths, whose beautiful colourings and markings have attracted us all from childhood. There are about 12,000 species of the lepidoptera, and they are divided into “moths” and “butterflies,” the former being seen in twilight, or darkness, the latter in sunlight. They can readily be distinguished by the antennæ, those of[Pg 722] the butterfly being tipped, or knobbed. The silkworm belongs to this family. These insects undergo complete metamorphosis. The remaining two orders of insects include the house-flies and gnats; and the flea, and jigger, or chigo, which penetrates the skin and lays its eggs in the flesh, causing thereby dangerous inflammation.
Crustacea.

This class includes a number of familiar animals such as the barnacle, the crab, the lobster, shrimp, etc.; and curious as it may appear are closely related to our spiders. Their cases or coverings are all articulated or disposed in distinct segments. They breathe through gills or by tubes, and possess legs, or appendages for walking, eating, or guidance. They are generally marine creatures.
The shell of the crustacea is composed largely of lime, and of course becomes very hard in time. It is formed from the skin. The body, like that of an insect, is composed of head, thorax, and abdomen, divided into twenty-one segments, of which seven occupy the head, seven the thorax, and the remainder the abdomen. Twenty segments are furnished with legs, or feelers, or claws—a pair to a segment. The lobster or crayfish will give excellent examples of the anatomy of the macrura or lobster kind of crustacea. The heart is situated in the back.
The following table given by Professor Nicholson will explain the “segments and appendages” of the lobster:—
| 1st | Segment, | Eyes. | |
| 2nd | “ | Lesser antennæ | |
| 3rd | “ | Greater antennæ. | |
| Head | 4th | “ | Pair of biting jaws. |
| 5th | “ | First pair of chewing jaws. | |
| 6th | “ | Second pair of chewing jaws. | |
| 7th | “ | First pair of foot jaws. | |
| 8th | “ | Second pair of foot jaws. | |
| 9th | “ | Third pair of foot jaws. | |
| 10th | “ | First pair of legs (claws). | |
| Thorax | 11th | “ | Second pair of legs (small claws). |
| 12th | “ | Third pair of legs (small claws). | |
| 13th | “ | Fourth pair of legs. | |
| 14th | “ | Fifth pair of legs. | |
| 15th | “ | Ground appendages. | |
| 16th | “ | Swimmerets. | |
| 17th | “ | Swimmerets. | |
| Abdomen | 18th | “ | Swimmerets. |
| 19th | “ | Swimmerets. | |
| 20th | “ | Large swimmerets. | |
| 21st | “ | No appendages (tail fin). |
The tail is, as may be supposed, the great aid to locomotion in the lobster family, and they can swim backwards with great rapidity by its assistance. Lobsters shed their claws when alarmed, and are easily caught by a glittering bait.
The hermit crabs are interesting creatures, but do not possess the horny coat of the crab or lobster. They are therefore compelled to inhabit an empty shell, into which they thrust themselves, holding to the bottom of it by their tail, while a large claw guards the entrance. When the animal gets too big for his house he moves to another, leaving the old home for another hermit of the shore.
The crabs have no developed tails, and are therefore called brachyura—“short-tailed,” and they are walking creatures. There are king crabs, land crabs, and the common swimming crab. These animals can shed their shells as other crustaceans, and a curious fact is they shed them whole. How the claws come out must remain more or less a mystery. Réaumur investigated the action of the crayfish, and noticed that as the casting time approached the crustacea retired to some hiding-place and remained without eating. The shell becomes gradually loosened, and at last by putting its feet against a stone and pushing backwards the animal jerks himself away. It must be a painful operation, for the mill-like teeth of the stomach are also rejected, and the joints do not give way. After a while a new shell appears, and is cast in due time as before.
The eyes of the crustacea are situated in front, and are composed like the insects, or are simple, like spiders. They possess a sense of hearing evidently. The eggs of the lobster are carried by the female, and they are termed the “coral” in consequence of their red and beadlike appearance. Our space will not admit of our saying much more concerning the interesting crustacea, though the barnacles, so well known by sight by all dwellers at the sea, and called Cirripedia, which fix themselves to rocks and ships, deserve notice. The young are capable of movement, and this fact was first discovered in 1830. It resembled a mussel, but when kept in sea-water it adhered to the vessel which retained it. The cirripedia are so called from the cirri or arms which they possess, and by which they are enabled to entangle or catch their food, as in a net. They hold themselves by a “foot stalk.” The goose-mussel, or barnacle, is very common, but must not be confounded with the limpet.
Dr. Baird gives the following description of them:—“The cirripeds are articulated animals contained within a hard covering composed of several pieces and consisting of calcified chitine. The body of the animal is enclosed in a sac lined with the most delicate membrane of chitine, which in one group is prolonged into a peduncle and contains the ova; the body is distinctly articulated and placed with the back downwards.
Arachnida—Spiders.

There are many families of arachnida besides the well-known garden[Pg 724] and house spiders. The sea spiders, though classed with the arachnida, are sometimes placed amongst the crustacea. We have the “tick” and the cheese-mite and the scorpions; all of which belong to the spider family. But the true spiders are known by the joining of the two upper segments, the thorax and head being united (cephalo-thorax). The pretty and marvellous webs are spun from abdominal glands through small apertures. The fluid hardens in its passage sufficiently to be woven into threads to resist the struggles of the captured prey. The forms of these webs vary, but some spiders do not catch their victims in the net; they pounce upon them cat fashion. The large house spider is well known to all. The garden spider is seen in the illustration (fig. 855) with the scorpion. The habits of spiders will be found a very interesting study, and many volumes have been devoted to them. The water spider is a frequent inmate of an aquarium, and the bubble of air he takes down with him to breathe serves as a means of living while he is seeking his aquatic prey.
We will close our rapid survey of the invertebrate animals with a glance at the Mollusca, which are divided into six classes (see page 703). The first is the Tunicata, which have no shell or hard covering, and come under the denomination of molluscoids, and belong to a lower order. The true mollusca include the Brachiopoda, which have a pair of shells. They are called “arm-footed” because a long cord or tendon passes through one of the shells, and fixes the mollusc to the rock. The Lingula of this class have been discovered in very old formations such as the Devonian period, and indeed appear to have been amongst the first created animals.

The Lamellibranchiata include the oyster, cockle, mussel, etc. They are well known, and scarcely need description. The Pteropoda have no shell. The Gasteropoda are very numerous, and periwinkles, whelks, snails, etc., belong to this class. They progress by a muscular “mantle,” which is extended and contracted. The “horns” have eyes at the[Pg 725] extremities. When they retire into their “houses” they can close the door by a kind of lid called the “operculum.”
The Cephalopods include the nautilus and the cuttle fish, the terrible squid, or octopus, etc. Wonderful tales are told of the tenacity and ferocity of the “Poulpes,” and no doubt in long-past ages these animals attained a gigantic growth. They are very unpleasant enemies, and the cold, slimy grasp of the long tentacles is apt to give one the “horrors,” while the terrible head and beak fill one with dismay. The poulpes are very formidable opponents, and discretion will certainly be the better part of valour when they appear in our vicinity.
We must here close our sketch of the Invertebrates, and we regret that the limits of our volume will not permit us to continue this interesting subject, nor can we find space, at present, for even the barest description of the Vertebrate animals.

CHAPTER LVI.
THE ANALYSIS OF CHANCE AND MATHEMATICAL GAMES.
MAGIC SQUARES—THE SIXTEEN PUZZLE—SOLITAIRE—EQUIVALENTS.
We will now proceed to draw our readers’ attention to several experiments very famous at a former period, but which our own generation has completely overlooked. We refer to the Analysis of Chance, a science still known under the title of Calculation of Probabilities, formerly cultivated with so much ardour, but to-day almost fallen into oblivion.
Originating in the caprice of the clever Chevalier de Méré, who in 1654 suggested the game to Pascal, the analysis of chance has given rise to investigations of an entirely novel kind, and attempts have been made to measure the mathematical degree of credence to be given to simple conjectures. We will first recapitulate the principles laid down by Laplace on this subject. We know that of a certain number of events, one only can happen, but nothing leads us to the belief that one will happen more than the other. The theory of chance consists in reducing all the events of the same kind to a certain number of equally possible cases, such, that is to say, that we are equally undecided about, and to determine the number of cases favourable to the event, whose probability we are seeking. The ratio of this number to that of all possible cases is the measure of this probability, which is thus a fraction, the numerator of which is the number of favourable cases, and the denominator the number of all possible cases. When all the cases are favourable to an event, its probability changes to certainty, and it is then expressed by the unit. Probabilities increase or diminish by their mutual combination; if the events are independent of each other, the probability of the existence of their whole is the product of their particular probabilities. Thus the probability of throwing an ace with one dice being 1/6, that of throwing two aces with two dice is 1/36. Each of the sides of one dice combining with the six sides of the other, there are thirty-six possible cases, among which one only gives the two aces. When two events depend on each other, the probability of the double event is the product of the probability of the first event by the probability that, that event having occurred, the other will occur. This rule helps us to study the influence of past events on the probability of future events. If we calculate á priori the probability of the event that has occurred and an event composed of this[Pg 727] and another expected event, the second probability divided by the first, will be the probability of the expected event, inferred from the observed event.
The probability of events serves to determine the hope or fear of persons interested in their existence. The word hope here expresses the advantage which someone expects in suppositions which are only probable. This advantage in the theory of chances is the product of the hoped-for sum by the probability of obtaining it; it is the partial sum which should arise when one does not wish to run the risks of the event, supposing that the apportionment corresponds to the probabilities. This apportionment is only equitable when we abstract from it all foreign circumstances; because an equal degree of probability gives an equal title to the hoped-for sum. This advantage is called mathematical hope. Nevertheless, the rigorous application of this principle may lead to an inadmissible consequence. Let us see what Laplace says. Paul plays at heads and tails, on the understanding that he receives two shillings if he succeeds at the first throw, four shillings if he succeeds at the second, eight at the third, and so on. His stake on the game, according to calculation, must be equal to the number of throws; so that if the game continues indefinitely, the stake also continues indefinitely. Yet, no reasonable man would venture on this game even a moderate sum, £2 for example. Whence, therefore, comes this difference between the result of the calculation, and the indication of common-sense? We soon perceive that it proceeds from the fact, that the moral advantage which a benefit procures for us is not proportional to this advantage, and that it depends on a thousand circumstances, often very difficult to define, but the chief and most important of which is chance. In fact, it is evident that a shilling has much greater value for one who has but a hundred than for a millionaire. We must, therefore, distinguish in the hoped-for good between its absolute and its relative value; the latter regulates itself according to the motives which cause it to be desired, while the former is independent. In the absence of a general principle to appreciate this relative value, we give a suggestion of Daniel Bernouilli which has been generally admitted.
The relative value of an extremely small sum is equal to its absolute value, divided by the total advantage of the interested person. On applying the calculus to this principle, it will be found that the moral hope, the growth of chance due to expectations, coincides with the mathematical hope, when chance, considered as a unit, becomes infinite in proportion to the variations it receives from expectations. But when these variations are a sensible portion of the unit, the two hopes may differ very greatly from each other. In the example cited, this rule leads to results conformable to the indications of common-sense. We find, in point of fact, that if Paul’s fortune amounts only to £8, he cannot reasonably stake more than 7s. on the game. At the most equal game, the loss is always, relatively greater than the gain. Supposing, for example, that a person possessing a sum of £4, stakes £2 on a game of heads or tails, his money after placing his stake will be morally reduced to £3 11s. 0d.—that is to say, this latter sum will procure him the[Pg 728] same moral advantage as the condition of his funds after his stake. Whence we draw this conclusion: that the game is disadvantageous, even in the cases where the stake is equal to the product of the sum hoped for by the probability. We may, therefore, form an idea of the immorality of games in which the hoped-for sum is below this product.

Jacques Bernouilli has thus laid down the result of his investigations on the calculation of probabilities. An urn containing white and black balls is placed in front of the spectator, who draws out a ball, ascertaining its colour, and puts it back in the urn. After a sufficient number of draws, the total number of extracted balls divided by the total number of balls[Pg 729] represents a fraction very near to that which has for a numerator the real number of white balls existing in the urn, and for the denominator the total number of balls. In other words, the ratios of the number either of extracted white balls, or the whole of the white balls to the total number, tend to become equal; that is, the probability derived from this experiment approaches indefinitely towards a certainty. The two fractions may differ from each other as little as possible, if we increase the number of draws. From this theorem we deduce several consequences.
1. The relations of natural effects are nearly constant when these effects are considered in a great number.
2. In a series of events indefinitely prolonged, the action of regular and constant causes affects that of irregular causes.
Applications.—The combinations presented by these games have been the subject of former researches regarding probabilities. We will complete our exposition with two more examples.
Two persons, A and B, of equal skill, play together on the understanding that whichever beats the other a certain number of times, shall be considered to have won the game, and shall carry off the stakes. After several throws the players agree to give up without finishing the game; and the point then to be settled, is in what manner the money is to be divided between them. This was one of the problems laid before Pascal by the Chevalier de Méré. The shares of the two players should be proportional to their respective probabilities of winning the game. These probabilities depend on the number of points which each player requires to reach the given number. A’s probabilities are determined by starting with the smallest numbers, and observing that the probability equals the unit, when player A does not lose a point. Thus, supposing A loses but one point, his chance is 1·2, 3·4, 7·8, etc., according as B misses one, two, or three points. Supposing A has missed two points, it will be found that his chance is as 1·4, 1·2, 11·6, etc., according as B has missed one, two, or three points, etc. Or we may suppose that A misses three points, and so on.
We should note, en passant, that this solution has been modified by Daniel Bernouilli, by the consideration of the respective fortune of the players, from which he deduces the idea of moral hope. This solution, famous in the history of science, bears the name of the Petersburgh problem, because it was made known for the first time in the “Memoires de l’Académie de Russie.”
We will now describe the game of the needle. It is a genuine mathematical amusement, and its results, indicated by theory, are certainly calculated to excite astonishment. The game of the needle is an application of the different principles we have laid down.


If we trace on a sheet of paper a series of parallel and equi-distant lines, AA1, BB1, CC1, DD1, and throw down on the paper at hazard a perfectly cylindrical needle, a b, the length of which equals half the distance[Pg 730] between the parallel lines (figs. 858 and 859), we shall discover this curious result. If we throw down the needle a hundred times, it will come in contact with one of the parallel lines a certain number of times. Dividing the number of attempts with the number of successful throws, we obtain as a quotient a number which approaches nearer the value of the ratio between the circumference and the diameter in proportion as we multiply the number of attempts. This ratio, according to the rules of geometry, is a fixed number, the numerical value of which is 3·1415926. After a hundred throws we generally find the exact value up to the two first figures: 3·1. How can this unexpected result be explained? The application of the calculus of probabilities gives the reason of it. The ratio between the successful throws and the number of attempts, is the probability of this successful throw. The calculation endeavours to estimate this probability by enumerating the possible cases and the favourable events. The enumeration of possible cases exacts the application of the principle of compound probabilities. It will be easily seen that it suffices to consider the chances of the needle falling between two parallel lines, AA1 and BB1 (fig. 858), and then to consider what occurs in the interval, m n, equal to the equi-distance. To obtain a successful throw, it is necessary then:—
1. That the middle of the needle should fall between m and l, the centre of m o. 2. That the angle of the needle with m o will be smaller than the angle, m c b. The calculation of all these probabilities and their combination by multiplication, according to the rules of compound probabilities, gives as the final expression of probability the number.
This curious example justifies the theorem of Bernouilli relating to the multiplication of events; there is no limit to the approximation of the result, when the attempts are sufficiently prolonged. When the length of the needle is not exactly half the distance between the parallel lines, the practical rule of the game is as follows: The ratio between the number of throws and the number of successful attempts must be multiplied by double the ratio between the length of the needle and the distance between the parallel lines. In the case cited above, the double of the latter ratio equals the unit. We will give an application to this. A needle two inches long is thrown 10,000 times on a series of parallel lines, two-and-a-half inches apart; the number of successful throws has been found to equal 5000. We[Pg 731] take the ratio 1090/5009, and multiply it by the ratio 1000/636 and the product is 3·1421. The true value is 3·1415. We have an approximation of 6/10000.
The dimensions indicated in this experiment are those which present in a given number of attempts the most chances of obtaining the greatest possible approximation. We will conclude these remarks on games by some observations borrowed from Laplace.
The mind has its illusions like the sense of sight; and just as the sense of touch corrects the latter, reflection and calculation correct the former. The probability founded on an every-day experience, or exaggerated by fear or hope, strikes us as a superior probability, but is only a simple result of calculation.
In a long series of events of the same kind, the mere chances of accident sometimes offer these curious veins of good or bad fortune, which many persons do not hesitate to attribute to a kind of fatality. It often happens in games which depend both on chance and the cleverness of the players, that he who loses, overwhelmed with his want of success, seeks to repair the evil by rash playing, which he would avoid on another occasion; he thus aggravates his own misfortune and prolongs it. It is then, however, that prudence becomes necessary, and that it is desirable to remember that the moral disadvantage attaching to unfavourable chances is increased also by the misfortune itself.41 Mathematical games, formerly so much studied, have recently obtained a new addition in the form of an interesting game, known as the “Boss” puzzle. It has been introduced from America, and consists of a square box, in which are placed sixteen small wooden dice, each bearing a number (fig. 860). No. 16 is taken away, and the others are placed haphazard in the box, as shown in fig. 861. The point is then to move the dice, one by one, into different positions, so that they are at last arranged in their natural order, from one to fifteen; and this must be accomplished by slipping them from square to square without lifting them from the box. If the sixteenth dice is added, the game may be varied, and we may seek another solution of the problem, by arranging the numbers so that the sum of the horizontal, vertical, and diagonal lines gives the number 34. In this form the puzzle is one of the oldest known. It dates from the time of the primitive Egyptians, and has often been investigated during the last few centuries, belonging, as it does, to the category of famous magic squares, the principles of which we will describe. The following is the definition given by Ozanam, of the Academy of Sciences, at Paris, at the end of the seventeenth century. The term magic square is given to a square divided by several small equal or broken squares, containing terms of progression which are placed in such a manner that all those of one row, either across, from top to bottom, or diagonally, make one and the same sum when they are added, or give the same product when multiplied. It is therefore evident from this definition, that there[Pg 732] are two kinds of magic squares, some formed by terms of arithmetical progression, others by terms of geometrical progression. We must also distinguish the equal from the unequal magic squares.


We give here several examples of magic squares with terms of mathematical progression, among them the square of 34, giving one of the solutions to the puzzle just described (fig. 862). We also give an example of a magic square composed of terms of geometrical progression. The double progression for examples 1, 2, 4, 8, 16, 32, 64, 128, 256, as here[Pg 733] arranged (fig. 863), forms such a square that the product obtained by multiplying the three terms of one row, or one diagonal, is 4,096, which is the cube of the mean term 16. The squares have been termed magic, because, according to Ozanam, they were held in great veneration by the Pythagoreans. In the time of alchemy and astrology, certain magic squares were dedicated to the seven planets, and engraved on a metal blade which sympathized with the planet. To give an idea of the combinations to which the study of magic squares lends itself, it is sufficient to add that mathematicians have written whole treatises on the subject. Frénicle de Bessy, one of the most eminent calculators of the seventeenth century, consecrated a part of his life to the study of magic squares. He discovered new rules, and found out the means of varying them in a multitude of ways. Thus for the magic square, the root of which is 4, only sixteen different arrangements were known.

Frénicle de Bessy found 880 new solutions. An important work from the pen of this learned mathematician has been published under the title of “Carrés ou Tables Magiques,” in the “Memoirs de l’Académie Royale des Sciences,” from 1666-1699, vol. v. Amateurs, therefore, who are accused of occupying themselves with a useless game, unworthy the attention of serious minds, will do well to bear in mind the works of Frénicle, and better still, to consult them.

We have so far considered only the first part of the puzzle. We may now examine the problem to which specially it has given rise. We are quite in accord with M. Piarron de Mondesir, who has been so good as to enlighten us upon the subject, which is really much more difficult than it appears.
A French paper once proposed to give a prize of 500 francs to any individual who would solve the following problem:—
Throw the numbers out of the box, replace them at hazard, then in arranging them place them in the following order (A fig. 864).

Now nobody solved this problem, because in nine cases out of ten it is impossible to do so. The first twelve numbers will come correctly into their places, and even 13 can be put in its place without much trouble; but, instead of getting the last row right we shall find it will come out like B, viz., 14, 15, 13, in the large majority of instances. So any case can be solved in one of the two results given above, and we can tell in advance, without displacing a number, in which way the puzzle will eventuate.


Let us give this problem our attention for a few minutes, and we shall not find it difficult.
Take the first example. We will throw the cubes out of the box and put them back in the order shown in fig. 865.
We see now that 1 occupies the place of 11, 11 that of 7, 7 that of 8, 8 that of 6, 6 of 15, 15 of 1. This much is evident without any study. We formulate these figures as follows, beginning with 1 and working from figure to figure till we are led to 1 again, and so on.
1st. Series.—1, 11, 7, 8, 6, 15, 1 (6) even.
Counting the number of different cubes we have 6; and we put (6) in a parenthesis. We call the first series even because 6 is an even number.
We now establish, by the same formula, a second series commencing with 2, and going back to it, thus—
| 2nd Series.—2, 4, 2 | (2) even. |
| 3rd Series.—3, 5, 10, 12, 3 | (4) even. |
| 4th Series.—9, 13, 14, 9 | (3) uneven. |
We have now four series, the total number of points equal 15, as there ought to be, for one cube is absent.
Let us now take another example (see fig. 866), and by working as before we have four series again, viz:—
| 1st Series.—1, 7, 1 | (2) even. |
| 2nd Series.—2, 11, 3, 8, 4, 15, 2 | (6) even. |
| 3rd Series.—5, 12, 13, 5 | (3) uneven. |
| 4th Series.—9, 14, 10, 9 | (3) uneven. |
This gives us only 14 as a total, because 6 has not been touched at all.
And now for the rule, so that we may be able to ascertain in advance, when we have established our series, whether we shall find our puzzle right or wrong at the end. We must put aside all unplaced numbers and take no notice of uneven series. Only the even series must be regarded.
Thus if we do not find 1, or if we find 2, 4, or 6, the problem will come into A as a result. If we find 1, 3, 5, or 7, the case will eventuate as in B (fig. 864). Let us apply the rule to the problems we have worked, and then the reason will be apparent.
In the first we find three even series; the problem will then end as in B diagram (fig. 864), for the number of like series is odd.
In the second we find two even series (pairs); we shall find our problem work out as in diagram A (fig. 864), for the number of like series is even, one pair in each.
We are now in possession of a simple rule, both rapid and infallible, and which will save considerable trouble, as we can always tell beforehand how our puzzle will come out. Any one can test the practicability of the rules for himself, but we may warn the reader that he will never be able to verify every possible instance, for the possible cases are represented by the following sum—
2×3×4×5×6×7×8×9×10×11×12×13×14×15.
That is to say, 1,307,674,368,000 in all.
Solitaire.
This somewhat ancient amusement is well known, and the apparatus consists of a board with holes to receive pegs or cups to receive the balls, as in the illustrations (figs. 867 and 870.) The usual solitaire board contains thirty-seven pegs or balls, but thirty-three can also be played very well. Many scientific people have made quite a study of the game, and have published[Pg 736] papers on the subject. M. Piarron de Mondesir has given two rules which will prove interesting.
The first is called that of equivalents, and supposes the game to be played out to a conclusion; the second, called the ring-game, admits of a calculation being made so that the prospects of success can be gauged beforehand.
The method of play is familiar, so we need not detail it. It is simply “taking” the balls by passing over them in a straight line. The method of “equivalents” consists in replacing one ball with two others, as we will proceed to explain by the diagram (fig. 868).

Suppose we try the 33 game, which consists in filling every hole with the exception of the centre one, and in “taking” all the balls, leaving one solitary in the centre at the last. Suppose an inexperienced player arrives at an impossible solution of five balls in 4, 11, 15, 28, and 30.
To render the problem soluble, and to win his game, I will replace No. 11 by two equivalents, 9 and 10, the ball 28 by two others, 23 and 16, and the ball 30 by 25 and 18. These substitutions will not change the “taking off,” for I can take 10 with 9, 23 with 16, and 25 with 18. But by so doing I substitute for an irreducible solution of five balls a new system of eight (those shown with the line drawn through them in the diagram), which can easily be reduced to the desired conclusion, and the game will be achieved.
There are in reality three terminations possible to the problem—the single ball, the couple, and the tierce; that is, you may have only one left, or two placed diagonally, such as 9-17, 25-29, or a system of three in[Pg 737] a straight line, 9-16-23. By the “equivalents” you can always succeed in solving the problem desired.
We will now point out four transformations which are very easy to effect, and result from the rule of “equivalents.”
1. Replacement of the two balls, situated on the same line and separated by an empty cup, by one put into that cup. Thus I can replace 23 and 25 by a single ball at 24.
2. Suppression of tierces. And by the above movement I suppress the tierce 9-16-23.
3. Correspondent “cases” are two holes situated in the same line and separated by two cups. If two corresponding cups are filled, I can suppress the balls which occupy them. So I can put aside 4 and 23.

4. It is permissible to move a ball into one of the correspondent cups if it be vacant; thus I can put 10 into 29.
These are the four transformations which can be made evident with the rings, without displacing the balls. To do this we need have only seven rings large enough to pass over the balls and to surround the holes in which they rest. Let us take an example.
Solitaire with 33 holes (fig. 869). Final solution of the single ball.
1st Vertical row: 7 and 21 are occupied, and the intermediate hole 14, being empty, I place a ring upon 14.
2nd Vertical row: No. 8 takes 15, and comes into 22; I place a ring on 22.
3rd Vertical row: I suppress the corresponding balls, 4-23 and 16-31, there now only remains 9, so I place a ring on 9.
4th Vertical row: I suppress the correspondents 10-29, put 2 into 17, and I place a ring upon 17.
5th Vertical row: I suppress correspondents 6-25, put 33 into 18, and I place a ring upon 18.
6th Vertical row: No. 12 takes 19 and comes to 26; I place a ring on 26.
7th Vertical row: No. 20 is the only ball; I place a ring on 20.
(It must be understood that these operations should be proceeded with mentally; the balls must not be disturbed.)
We have thus reduced the problem to seven ringed balls, which are 14, 22, 9, 17, 18, 26, and 20 which are indicated on the diagram by the line drawn through each vertically. They are all comprised in the three horizontal rows, 3, 4, 5.

We can now set to work upon these three rows in the same manner as before, considering the rings as balls.
3rd row: We find (and leave) a ring upon 9.
4th row: The two corresponding rings, 17-20, neutralize each other, and we suppress them. We carry 14 to 17, and take 17 with 18, which comes into 16. We leave a ring on 16.
5th row: Carry the ring 26 to 23, take 23 with 22, which comes thus to 24, and we leave a ring on 24.
We now have reduced our problem to three rings, 9, 16, and 24, all in the central square, indicated in the diagram by horizontal bars. It is easy to see that 9 will take 16 and 24 and come into 25, and 25 will remain[Pg 739] alone—as was intended to be done—a single ball upon the board, indicated by the circle around it in the cut.
By playing the “equivalent” method you will always arrive at this result—a single ball in No. 25. It may now be perceived how we cannot only arrive at a satisfactory solution, but by means of the rings ascertain whether we shall succeed in our game without disturbing a single ball. After some experience we may even learn to dispense with the rings altogether.

CHAPTER LVII.
THE MAGIC TOP—THE GYROSCOPE AND SCIENTIFIC GAMES
We will not do our readers the injustice to suppose that they are not familiar with the ordinary top,—the delight of all school-boys and young people,—of which, therefore, we forbear giving any description; but we now desire to give some details of the construction of the wonderful magic top. It is composed of a large disc, with an axis turning on two pivots connected with a circle of iron. When in repose, this plaything exhibits nothing of a remarkable character; it is completely inert, obeying, like all other bodies, the laws of gravity. But when we come to give the disc a movement of rapid rotation, this inert instrument seems to assume a vitality of its own if we attempt to move it; it resists, and seems to thrust back the hand, and executes movements even in a contrary direction. Besides this, it appears to be freed, in a certain measure, from the laws of gravity; if we place it on its pivot, instead of falling, as it would when the disc is motionless, it preserves the upright or inclined position in which we place it, the upper extremity of the axis slowly describing a horizontal circle round the fulcrum of the other extremity.
Few persons are sufficiently familiar with the theory of mechanics to understand these phenomena, and it often happens that such a top purchased to amuse a child becomes an object of wonder and interest to his seniors. We do not pretend here to explain mathematically the reason of the facts before us, but the mechanical principle on which this top is constructed is of such great scientific importance, that we will, in a few words, explain it to our readers. It is sufficient to have a little knowledge of mechanics to be aware that a body in motion, subjected to the action of a force tending to give it a directly contrary motion, will follow a movement in a third direction, which is termed the resultant of the two others; and this resultant approaches nearer to one of the original directions, in proportion as the corresponding movement is more rapid in relation to the other. If, for example, you strike a billiard ball, which is rolling past you, in such a manner that you drive it regularly along in the same direction, it appears only to obey a part of the given impulsion, and continues its course in an oblique direction, the speed with which it commenced rolling combining with the impulsion to produce a resultant movement. If it is rolling very[Pg 741] quickly, and you strike it gently, it will scarcely turn out of its course. If, on the contrary, it is moving slowly, and receives a violent shock, it will run off almost exactly in the direction in which it has been struck.

Now that which occurs in this example of a body tending to two movements at the same time, is also produced when it is a question of movements of rotation, so that if a force acts upon a body in rotation in such a manner as to give it a movement of the same kind round another axis, a third movement will be originated round a third axis, the direction of which will be nearest to that in which the rotation is most rapid. Let us apply this very simple principle to our top, and we shall see that magic has nothing whatever to do with these movements, which at first glance appears so extraordinary. Having set it in motion, we rest it on its pivot, its axis in a horizontal position; we then find that we have two movements before us; first, that which we gave the top ourselves, and secondly, the movement of rotation which occurs round a second axis equally horizontal passing through the fulcrum and perpendicular line to the first. A movement of rotation therefore originates round a third axis placed between the two first, but whilst the real axis of the top, obeying this resultant movement, takes up its new position, the law of gravity continuing to act, displaces and moves it a little further, so that in endeavouring to reach its centre of gravity, it turns round its fulcrum (fig. 871). From this explana[Pg 742]tion, it will be easily seen that the more rapid the movement given to the top,—that due to gravity remaining constant,—the nearer will be the axis of the resultant movement to its real axis, and consequently the slower will be the movement of rotation of the whole round the pivot. Thus this apparently incomprehensible phenomenon is easily explained by gravity, vertical force producing a movement of rotation in a horizontal plane. One can also explain by analogous reasoning, and calculation of passive resistance, why the axis of the top gradually inclines in proportion as the speed of the latter diminishes, and the speed of rotation round the fulcrum increases; why it falls immediately if an obstacle is opposed to the latter movement, and finally, why it produces on the hand which holds it, movements which astonish persons so intensely who behold it for the first time.
The principle we have just described is often enunciated, by saying that every body in rapid rotation rests in its plane, and can only be driven out by a considerable force; this, however, is a defective formula. The principle should be stated in the following manner. A body in rapid rotation tends to remain in its plane; that is, its axis rests parallel with itself, and instead of obeying any force tending to divert its direction, it produces in consequence of the combination of two simultaneous movements, a displacement of the axis, generally much feebler and of a different kind from that which this force exercises on the same body in repose. One of the most charming applications of this theory is due to M. Foucault. The Gyroscope, which bears his name, is a heavy disc, the axis of which is supported by a “Cardan” balance, so that, whatever is the position of the contrivance, it is possible to preserve it in a constant direction. Therefore if the disc is, by means of special mechanism, put in rapid rotation, we may give it all kinds of possible displacement without changing the plane in which the gyroscope moves. Supposing then that its connection with the suspension is fixed in a relatively immovable manner, but attracted by a movement towards the ground, the plane of rotation of the disc will not entirely participate in this movement. It is true, it will be carried into the movement of general removal, but it will remain constantly parallel with itself, and only appears displaced in comparison with the surrounding objects, which obey more completely than itself the movement of the globe’s rotation round its poles. Thus can we demonstrate the movement of our planet. In virtue of the same principle, we see every day passing before our eyes a crowd of phenomena with which we are so familiar that they do not excite our attention. Thus it is because the hoop tends to remain in its plane of rotation that it rolls on without falling or deviating, and for the same reason that tops rotate vertically on their points, or when they are running down, describe a series of concentric circles; and for the same reason again, a juggler is able so easily to hold on the point of a stick a plate which he puts in rapid rotation, etc. It is also owing to this property of rotating bodies that we have been enabled to make use of cylindrical or conical projectiles in artillery. The coiled riflings of the cannon causing the[Pg 743] projectiles to turn round very rapidly, their axis preserves an invariable direction during their whole course, until they finally strike the object at which they are aimed. Without this rotation they would pirouette in an irregular manner in the air, and besides any precision in firing being impossible, the resistance of the air would diminish their range to an enormous extent.
The Gyroscope, an instrument now familiar to most scientific persons, is still a problem of which the solution has not yet been found. It may be called the paradox of mechanics, for although it depends on gravitation, it appears to be entirely indifferent to it.
An American scientist has applied electricity to the gyroscope, so as to make its movements as continuous as possible, and to enable us to study it more at leisure and with better results. The gyroscope is mounted on a pedestal which tapers to a point, and supports the instrument. The bar of the gyroscope on which the electro-magnets are fixed rests upon the top of the pedestal. One of the extremities of the bobbin is fixed to the cavity, when the bar and support join, the other extremity communicates with the bar which joins the nuts of the magnets.
An insulator of hardened caoutchouc is so placed that it just touches the axis of the wheel twice in every revolution of that wheel. Its plane of rotation is at right angles to the magnets, and carries an armature of soft iron which turns very close to the magnet without touching it. The armature is put en rapport with the surface of contact of the cylinder, so that when the armature approaches it is attracted; but immediately afterwards, as it reaches the opposite side, the current is interrupted, and the impulse acquired is sufficient to move the wheel to the spot where the armature can again come under the influence of the magnet.
The magnets, the wheel, and all the parts of the instrument together can move around in any direction. When two or four Bunsen cells are put in connection with the gyroscope, the wheel turns with tremendous rapidity, and by permitting the magnets to work (an operation which requires some little dexterity), the wheel not only sustains itself, but also the magnets and the other subjects which are between it and the extremity of the pedestal—in opposition to the laws of gravitation. The wheel, besides turning rapidly around its axis; revolves slowly around the point of the column in the same direction taken by the lower part of the wheel.
When attaching the arms and counter-poise of the machine, so that the wheel and the magnets may balance themselves exactly on the pointed pedestal, the machine remains stationary. But if we give any preponderance to the wheel and magnets the rotation of the apparatus is in a direction opposite to that which would result from turning the upper part of the wheel.
The gyroscope illustrates the persistence with which a body that submits to rotation maintains itself in the plane of its rotation, notwithstanding the force of gravitation. It also shows the result of the combined action of two forces tending to produce rotation around two separate axes, which are, however, situated in the same plane.
The rotation of the wheel round its axis is produced in the present case by the electro-magnet; and the tendency of the wheel to fall, or to turn in a vertical plane parallel to its axis, results in the rotation of the entire instrument upon a new axis, which coincides with the pointed pedestal.
The American Money-Box.
During a recent visit to London, as I was one day walking in the Crystal Palace, my attention was attracted by a curious money-box, surmounted by a pictorial representation of one of the London streets. The carriages, horses, and pedestrians were represented by figures cut out of cardboard, arranged in a groove. A large placard bore this inscription: “Notice to visitors: Throw a penny in the money-box; and the figures will perform.”
I at once responded to this invitation, and immediately beheld the little tableaux become moving and life-like; the cabs rolled along, and the passers-by walked up and down the street. A number of visitors followed my example, and there is no doubt the money-box was full at the end of the day. This ingenious contrivance for obtaining money in so easy a manner, and without having recourse to a “show-man,” appeared to me worthy of investigation and description.
The Scientific American (New York) has recently given an explanation of this curious contrivance, and we will here quote what has been published on the subject.
“Among the inventions intended to obtain contributions of money from the visitors at the Philadelphia Exhibition,” says the American writer, “we will describe the singular money-boxes placed in the salons of the principal hotels and the galleries of the exhibition, etc. These contrivances all consisted of a case or box, with a glass front, through which can be seen a landscape in miniature, with trees, houses, figures, etc., all cut out of cardboard, and painted with great nicety. On the box was a label requesting the visitor to drop a coin into it and await the result of the contribution. When the penny has fallen in it puts in motion some hidden machinery, and then we see the people in the miniature landscape all in motion, riding or walking or hunting, as the case may be.”
Another box is even more successful, for it places in the hands of the contributor a photograph of some celebrated person. But to obtain the photograph we must contribute six pennies. The carte will not come out if we do not put in the proper coins, and the apparatus is perfectly fair and honest.
The illustration, fig. 872, shows the apparatus, which is very simple. On the left the ordinary box is seen, on the right there is a longitudinal section of it.
At the top of the lower portion, where the money is received in, is a hollow support, A, which sustains the box in which the photographs are[Pg 745] placed upon an inclined plane, and resting against the glass. The pieces of money, in falling, strike the extremity of a vertical balance, which immediately turns a toothed wheel, C. This wheel has as many teeth as there are pieces of money necessary to purchase the photograph or carte de visite. Upon the escapement wheel is a ratchet arrangement, D, the shaft being moved by a cord rolled around it and attached to a spring, E. A bolt, F, moved by a spring, is kept constantly pressed against the “snail,” D.

Thus at each revolution, as the parts of the machinery are animated by the same movement, the bolt is withdrawn sufficiently to permit a carte to fall, and then the card next following will be ready resting upon the bolt. The photographs being placed upon an inclined plane, are pushed forward by a movable frame, G, which has a roller at the base. So as one card falls out another is immediately replaced close to the glass.
We have remarked that the wheel has six teeth, so that as one piece of money dropped in moves it one-sixth of its revolution, six pieces will be necessary to produce the card. Of course wheels can be made with one or more teeth, and the payment may be varied for valuable objects at the desire of the possessor.
The invention is not only a plaything. It can be made useful in the distribution of pamphlets, or newspapers, which can be introduced into the[Pg 746] box folded uniformly. They can also be used in omnibuses or tram-cars, and tickets may be given by the machine on payment of the proper sum of money.
We will close this chapter with an illustration of a spiral bottle, which can be done in the manner now to be described, so that the bottle will actually become a glass spring.
Take a mixture of 180 grammes of lampblack, 60 grammes of gum arabic, 23 grammes of adraganth, and 23 grammes of benzoin. Make these ingredients into a paste by the addition of water, and fashion a pencil of the charcoal thus obtained. This pencil, when heated, will cut the glass wherever it is applied.
The process is commenced by scraping the bottle with a file and following the instrument with the red-hot pencil. Wherever the hot pencil is applied, the glass will be cut as shown in the illustration herewith. It will be necessary to blow upon the heated pencil to maintain the incandescence as long as possible. The bottle as cut and representations of the instruments are given in the cut (fig. 873).

CHAPTER LVIII.
SCIENTIFIC OBJECTS FOR THE HOUSEHOLD.

At the beginning of the seventeenth century there was at Lyons a very remarkable mansion built by a man named Nicholas Grollier de Servière. This house was filled with all the most remarkable curiosities and inventions of the period. The owner belonged to an ancient family. His great-uncle, Jean Grollier, had amassed a magnificent library, the best in France. His father was also a celebrated adherent of Henry IV., and M. Servière himself[Pg 748] had inherited much scientific taste and intelligence from his ancestors. His house was full of curiosities, ingenious machines, and mysterious clocks, concerning some of which things we shall have something to say in this chapter.
M. de Servière’s ingenuity was first apparent in the circular reading desk, or wheel-desk, on which he put all the books he was likely to require within a certain time. He seated himself by this revolving desk, and then was enabled to read any book or paper he desired by merely turning the wheel with his hands and thus bringing it under his vision. In these days it is equally possible to collect useful articles either of an electric nature or otherwise. We have already described the electric pen and the writing machine, with some other things which might be included in our list of domestic appliances, but the Chromograph has not been yet illustrated.

The Chromograph.
When we have written with a certain well-known violet “ink” upon a sheet of paper and applied it to a soft gelatinous surface and rubbed it a few times, we shall obtain an impression of the writing on the gelatine. By pressing blank sheets of paper upon this we may pull off quite a number of copies of our letter or circular. This practice is now so well known that it is scarcely[Pg 749] necessary to detail it. The layer of gelatine is made up as follows, and any of the recipes will suffice.
1. Gelatine 100 grammes, water 375 grammes, glycerine 375 grammes, kaolin 50 grammes. (Lebaigueé.)
2. Gelatine 100 grammes, dextrine 100 grammes, glycerine 1000 grammes, sulphate of baryta q.s. (W. Wartha.)
3. Gelatine 100 grammes, glycerine 1,200 grammes, bouillie de sulphate de baryta, strained, 500 cubic centimètres. (W. Wartha.)
4. Gelatine 1 gramme, glycerine à 30° 4 grammes, water 2 grammes. (Kwaysser and Husak.)

The “mixture” is shaken until it cools to the point of thickening, and then poured into a zinc vessel. The kaolin or the sulphate of baryta makes the composition white. It can be treated again with gelatine and molasses employed for printing rollers. When the proofs have been taken from the frame the surface may be rubbed with a damp sponge, and then it will be ready for use again immediately. The introduction of dextrine facilitates the cleansing of the surface plate.
The Campylometer.42
This instrument, constructed by Lieutenant Gaumet, is very easily[Pg 750] carried in the pocket, and by a very simple process gives (1) the length of any line, straight or curved, traced on a map or plan; (2) the actual length corresponding to a “graphical” length on maps of the scale of 1/80000 or 1/100000, or on maps which are multiples of these numbers.
The instrument consists of a toothed disc, the circumference of which is dentated exactly in five centimètres. The faces of this disc each carry a system of divisions; one is divided into four parts, the other into five. The circumference of the disc (5 centimètres) corresponds to the 4 kilomètres of the scale of 1/80000, and to 5 kilomètres of that of 1/100000. The division 1/40 of the disc in the former scale measures 100 mètres, and is in it the same as 1/50 of the other scale.

The toothed disc moves upon a micro-metric screw, the markings of which are 0·0015 of a mètre, and a small “rule” or “reglet” carries equal graduations, as the screw representing lengths so follow:—
| 1. | 5, 10, 15, 20 | 50 centi. | according to metric scale. |
| 2. | 5, 10, 15, 20 | 50 kil. | scale 1/100000; |
| 3. | 4, 8, 12, 16 | 40 kil. | 1/80000; |
The micro-metric screw is fixed in a frame so made as to form a kind of indicator or guide at one side.
To make use of the campylometer, bring the zero of the disc opposite the zero of the rule (reglet), then place the instrument on the map in a perpendicular position; the point will serve as guide, and move the disc upon the line, whether direct or sinuous, of which you wish to ascertain the length.
When this has been done, note the last graduation of the “reglet” beyond which the disc has stopped, add to the value of this graduation the[Pg 751] complementary length shown by the division of the disc which is opposite the “reglet.” To find the length of a material line we must add to the number of centimètres shown by the upper graduation the complement in millimètres furnished by the division to the 1/50th.
For example, suppose we read 20 upon the upper scale, 35 the division to the 1/50 opposite the “reglet”; the length obtained is 20 centimètres plus 35 millimètres, or 0·235 mètres. If we are measuring upon a map on the 1/100000 scale, the upper graduations represent kilomètres, the complementary divisions on the 1/50 scale hundredths of mètres.
For example, suppose again 20 be the superior graduation, 35 the division to the 1/50 of the disc as before; the distance measured is 20 kilomètres plus 3,500 mètres, or 23,500 mètres.
On the map the lower graduation of the “reglet” is used. For instance, if 12 be the upper graduation of the division to 1/40 of the distance opposite to the “reglet,” the distance measured will be 12,700 mètres.
The campylometer has been specially constructed for maps on the 1/80000 and 1/100000 scales, and calculations can be made easily for any maps whose scales are multiples or sub-multiples of these. But the instrument will serve equally well for all maps or plans of which the numerical scale is known. We must multiply the length of the line expressed in millimètres by the denominator of the scale divided by 1,000.
So upon an English map to the 1/63360, a length of 155 millimètres corresponds to a “natural” length of 63,360 multiplied by 155, or 9820·80 mètres.
Thus we perceive that the employment of the campylometer does not necessitate the tracing of a graphic scale, but only the knowledge of the numerical scale. When the former only is known, the campylometer may be used in the following manner:—
Having traced with the disc the line you wish to measure, carry the instrument to the zero of the scale and let it run inversely the length of that scale, until the zero of the disc returns opposite to the zero of the “reglet.” The point at which the disc is stopped on the scale indicates the length of the line measured upon the map. If the scale be smaller than the line measured, repeat the operation as many times as may be necessary.
If it is desirable to ascertain upon a map of a scale of 1/20000 the distance represented by 1,200 mètres, we have only to place the toothed disc so that its position marks four times the required distance—that is, 4,800 mètres on the map of 1/80000 (for 4 times 20 = 80). Then move the disc in the given direction until the zero returns opposite the zero of the “reglet”; this limit will mark the extremity of the length required.
Explanations are not easy upon paper, but the instrument is found very easy in actual use. It is employed by the military staff for calculating distances of any kind, curves or straight lines. On the march, or even on horseback, the campylometer can be employed.
Mysterious Clocks.
The clocks represented in the two following illustrations (figs. 878 and 879), are well worthy of being placed in the house of any amateur of science. They are made of transparent crystal, and though all mechanism is cleverly concealed they keep capital time. The former clock (fig. 878) is the invention of Robert Houdin, and consists of two crystal discs superposed and enclosed in the same frame. One carries the usual numerals, the other moves upon its centre with the minute hand attached, and its rotation induces by the ordinary method the movement of the hour hand. The requisite motion is transmitted to the dial by gear disposed along the circumference and hidden within the metallic frame, and is itself put in motion by clockwork, enclosed in the pedestal of the timepiece.

M. Cadot, in his clock (fig. 879), retains the plates, but adopts the rectangular form, so as to preclude all idea of rotation, and to puzzle those who are acquainted with the working of Houdin’s clock. The minute hand cannot, in this instance, be fixed to the second glass plate, it preserves its independence. This movable plate has only a very slight angular movement around its centre, which oscillation or “play” is permitted in the interior of the rectangular dial. A little spring movement, hidden in the central nut of the “hand,” provides in progressive rotation the oscillation of the transparent plate, which cannot be perceived to move.
To produce this “balance” motion the plate is supported upon a bar in the lower part of the metal frame. After the direct oscillation of which we have spoken, a little spring puts the machinery back. The direct displacement is produced by a vertical piston which raises the end of the bar. This piston rests upon a bent lever communicating with a wheel with thirty triangular teeth. Finally this wheel turns upon its axis once in an hour by a clockwork arrangement in the pedestal of the clock. Each tooth takes two minutes to pass, and the movement is communicated to the minute hand, which thus goes round the dial in the hour. The hour hand is con[Pg 753]trolled by a delicate arrangement hidden in the base. The illustration and notes will explain the working.

M. Henri Robert has also invented a very interesting clock, and one calculated to excite much curiosity (fig. 881).

We can see nothing but a crystal dial, perfectly transparent, upon the surface of which two “hands” move, as upon an ordinary clock face. There is no machinery visible, and electricity may be credited with the motive power, because the dial is suspended by two wires. But they will soon be perceived not to be connected with the hands, and all search for the mechanism will be fruitless.
The hands, moreover, turn backwards or forwards, and may be moved by a treacherous finger, but will always return as by a balanced motion to their position, not the hour which they were at, but to the time which it actually is. They will take their proper place notwithstanding all efforts to the contrary, and will then, if let alone, indicate the time as steadily as ever.

The hands of this very mysterious timepiece carry their own motive power, and consist of unequally balanced levers, so to speak, in which the clockwork arrangement is intended to disturb the equilibrium. This property is employed to indicate the hour and the minute, as we will attempt to show.
The minute hand is the balance, and it is very exactly poised. In the round box fitted to the end of this hand a plate of platinum is displaced by clockwork. The centre of gravity being displaced every instant by the revolution of the weight which goes round once in an hour, the minute[Pg 755] hand is forced to follow, and carries the hour hand with it. By the hidden arrangements the hands are dependent one upon the other, but remain independent in movement. If they be moved backwards or forwards they will return automatically to their respective places, and if turned quickly round the minute hand will return to the proper minute, and the hour hand to the hour.
The mechanism is simple and ingenious; the principle, however, is not absolutely novel, and before M. Robert applied it many attempts had been made to move indicators by the machinery they themselves contained. But M. Robert has succeeded in adapting the idea beneficially and usefully, giving it a practical as well as an elegant shape.
A New Calculating Dial.


The small instrument herewith illustrated (figs. 882 and 883) is very serviceable for calculators, and its size adapts it for the waistcoat pocket. It can be used to calculate by addition, subtraction, multiplication, and division. Logarithms can be found, and the powers and roots of numbers—even trigonometrical calculations may be made by its aid. We need not go into any details regarding the principle of the little “circle.” Such explanations are only wearying and unsatisfactory at best. The principle is, simply stated, the theorem that the logarithm of the product of two numbers is equal to the sum of their logs. The size of the dial will of course regulate the length of the calculation. The instrument depicted permits of calculation to three figures with exactitude. M. Boucher, the inventor, hopes to succeed[Pg 756] in perfecting an instrument of small size which will combine all desiderata, and calculate to high powers.
The Pedometer.
We all know how useful it is to be able to calculate distances approximately when upon an excursion or walking tour, and much trouble is taken by many tourists to ascertain the number of miles they may have walked in a certain time. The rapid success which the Pedometer has gained is a testimony to the need it has adapted itself to fill.
The pedometer is much like an ordinary watch in appearance and size. We perceive a dial with figures and spaces to show the number of paces walked. The cut represents the mechanism, which is exceedingly simple.

In the fig. 884, B is a counter-poise at the extremity of a lever, which oscillates around an axis, A. A screw, V, serves to limit the extent of these oscillations, and a spring which acts upon the counter-poise holds the latter to the upper end. The apparatus is completed by a movement which counts the number of oscillations of the lever.
So much being understood, it will be presumed that if we give to the instrument an “up-and-down” movement, the spring which holds the counter-poise, B, being too weak to compensate the force of inertion of the latter, it gives way and presses against the screw, V. When the opposite movement takes place the counter-poise is at the end of its course, and so on. Thus during a walk each step produces an oscillation which the counter registers.
In the hands of a careful observer, such a pedometer is capable of registering exact results, and the number of paces being counted, a very good idea of the number of yards and miles passed over can be arrived at.

CHAPTER LIX.
SCIENCE AND DOMESTIC ECONOMY.
All branches of applied science are capable of giving us important hints and rendering us great service in all the conditions of our daily life, and as we have at various times throughout this volume mentioned useful domestic inventions applicable for use by means of water, air, etc., we may describe some more particularly relating to the inside of the house, and the science of domestic economy.

Sometimes during the winter we may feel it very difficult, if not impossible, to keep the room warm. This we can do, however, by means of double windows.
Why is it that the double window as used in Russia keeps out the cold so well? Is it because the room is defended against frost by two windows instead of there being only one to resist it?—Not entirely. Such an explanation is not sufficient. If one be protected against the exterior cold, it is, thanks to the mass of air which is imprisoned, between the two windows. Extraordinary as it may appear, the air is a very bad conductor of heat, and forms the best insulator that one can find. The heat of the[Pg 758] apartment is then perfectly retained by means of the air between the double windows.
In the same way the double window is not less useful during the summer, for it prevents the entrance of the heated air into the house. The double window may therefore be compared to the bournous of the Arab and the cloak of the Spaniard, which preserves from heat as well as guards against cold.
The double windows also perform another service. The glasses form a hot-house. The sun heats the air which is enclosed, and thus between the panes ferns and even vines will flourish. The windows are very easy to make, and in the event of any reader desiring to construct one or more, we give the dimensions. (See fig. 885.)
T T, is the exterior frame of the window. The two panes are mounted on a frame of wood, and are represented by A A´ and B B´ The sashes are represented apart, P and P´ are the shutters of sheet iron, which, if the walls be not so thick as represented, can be replaced by a spring-blind, which descends between the windows.
Sewing Machine worked by a Dog.

Animals have been employed for all time to draw carriages and the plough, etc. But these animal “motors” are usually employed under defective conditions, and therefore without full profit. The inert mass of the animals remains quite unutilized, his force only is employed, and there are many objections on the score of humanity, as well as from a mechanical standpoint, and great muscular tension with suffering may be inflicted upon an animal which is continually mounting a wheel or such contrivance for raising water. There was in the Paris Exhibition a threshing machine put in motion by a horse walking upon a pair of rollers which constituted an “endless” way, and we will now briefly describe a machine which utilizes animal force and weight. It is the invention of M. Richard of Paris, who has made many mechanical apparatus for industrial purposes.
The principle of the invention (fig. 886) consists in the animal utilizing all the force resulting from his dead-weight. A small box contains the dog very easily. In the illustration we see the dog at rest, and in that case he maintains his centre of gravity and exercises no force upon the wheel. But when the box is inclined, the mere weight of the animal is sufficient merely to turn the wheel in the direction of the arrows. The dog, finding himself sliding away, naturally endeavours to move forward, and the rotation of the wheel is continued; the best results are obtained when the body is placed entirely upon the descending line, and this result is owing only to the weight of the animal.
There is a resting-place, just above and outside the “endless” way traversed by the dog. A basin with water is also provided for the animal.

M. Robert was let to this discovery in the following way:—He employs a large number of sewing-machine hands, and finding that the working of the machines had an injurious effect upon the health of the workers, he determined to substitute, in part, other labour for that of female hands. He then thought out his “quadrupedal motors,” which are worked by intelligent dogs. There is very little trouble or expense connected with the working, so a great saving is effected, as the dogs cost little, and are cheaply fed. The result is that M. Robert has four heavy machines occasionally at work, which are kept in motion by dogs at a very small expense.
A Clock-Lamp.
The illustration (fig. 887) represents an ingenious arrangement, which, by means of combustion of oil in a lamp, indicates the hour of the night. The design explains itself. Two vertical tubes are fixed above the reservoir of oil. The left tube contains oil, and is marked with the hours; the right tube burns the oil as a lamp.
The apparatus is so constructed by the inventor, M. H. Behn, that a certain quantity of oil is consumed exactly in one hour between two gradua[Pg 760]tions of the hour-tube. A reflector placed beside the lamp enables one to see the time by night very plainly.
An “Alarum” Lamp.

The apparatus represented below (fig. 888) is an ordinary “alarum” lamp. It is surmounted by a petroleum lamp, which carries a burner that remains lighted all night, and which serves as a night-light. The “alarum” carries an index, represented by the dotted lines in the illustration, and the hands are fixed (with the index) to the hour you wish to rise in the morning. The index is fitted with an arrangement which lets loose a vertical bar represented on the right of the figure. This bar is held by a spring, and carries a toothed rack which acts upon and raises the wick. At the proper time the bar is loosed, and the lamp-wick is raised, diffusing a strong and sudden light through the apartment. This illumination, in concert with an alarum-bell, generally succeeds in awaking the heaviest sleeper.
A Good Petroleum Lamp.
This lamp (fig. 889) burns gazoline without the least odour or danger of explosion. It will serve equally well for petroleum or naphtha. The gazoline used ought to be 660 grammes weight to the litre.

The central portion of the lamp under consideration has an orifice, A B, which extends through the upper part, and by which the air is admitted to the centre of the flame. Two vertical plates divide the air-current into four portions. The chimney-rest, or gallery, forms with the glass three concentric envelopes, so arranged in stages that the air, when it reaches the plates, may be more and more carried under the flame. The orifices, a b, carefully regulated, give access to the exterior air. Including the central one, there are four currents of air, of which three strike against the flame. These are very excellent conditions for obtaining perfect combustion, and, consequently, there is an entire absence of smell and smoke, while the light is very powerful.
We may add that any glass will be found suitable to this lamp, and that, in consequence of the separation of the hot air by the currents mentioned, all danger of the glasses breaking from over-heating is avoided. In pro[Pg 762]vincial districts, where lamp-glasses are not plentiful, this characteristic will be appreciated. The lamp can only be filled when it is extinguished, and thus the chances of explosion are practically obviated. A burner of twelve lines will give double the light of a moderator of the same capacity, and cost only a penny or less per hour. The light is perfectly still and clear.
A New Tap.
This new tap is the invention of M. Guyonnet, a Frenchman. The illustration (fig. 890) gives a very good idea of its construction, and it permits the gradual release of the liquid without any of the sudden rush which ordinary taps, or “bungs,” are apt to do. The plug is covered with indiarubber, and follows a double curve, which reduces the force of the liquid, and the indiarubber removes any incrustation from the bung hole into which it may be fitted, and closes the aperture effectively without force.

In order to guard against a contingency, which, however, is an unlikely one, the “envelope” (casing) has been made in two pieces, one of which can never be displaced; the head only can be moved, and it is easily detached. The plug adapts itself to the aperture as a button to the buttonhole, and only costs about three halfpence (15 centimes). Ice has no effect upon the aperture of the barrel, thanks to the indiarubber covering of the plug. So, altogether, such a tap will be found useful and very cheap.
The Trapeze and Swing.
We may here notice the simple trapeze and swing for children, which can be easily fitted up in any house between two rooms. The advantages of gymnastics for the young are incontestable, but practically there are difficulties in the way, particularly for those living in towns, but a skilful[Pg 763] American has solved the problem in an ingenious way. He has found means to suspend the trapeze and a swing between the doorposts of a room without nails or any unsightly wood supports. The trapeze is simply suspended as represented in the accompanying illustrations.


The bar, B (see fig. 892), is of wood, terminating in screws enclosed in the grooves of the wood, at the extremity of which indiarubber discs are fixed (C and C´). When the bar is placed between the side posts of the[Pg 764] open door and with the indiarubber in contact with the sides, the bar, B, is vigorously screwed in the direction of the arrow, and this motion is transmitted to the indiarubber discs which press against the door, and the apparatus remains fixed. The trapeze cords, or the swing ropes, can be fastened to the bar with hooks, as shown in the illustration, and the solidity and safety of the bar may be tested by putting heavy weights upon the ropes before venturing upon the swing, or trapeze. Even violent exercises may be indulged in without any fear of falling if the bar be firmly screwed against the sides of the door.
Simple Toys.
The accompanying illustration shows us a circlet of paper, very thin, fastened upon a frame, with paper wings fixed to the radii. This “screw” fashioned wings and the circlet can be kept up in the air by means of a hand screen. The effect will be observable in the rapid revolution of the little paper wheel, which must be very light and thin. (See fig. 893.)

There are many toys which can be controlled by the use of indiarubber springs. The bicyclist in the cut (fig. 894) is an instance in point. He[Pg 765] turns around a pivot, and the tension of the spring keeps the machine in its place.

The swimming-fish (fig. 895) is moved by an indiarubber spring, much as the drawing-room kite is elevated in the air. The spring of indiarubber is twisted to make the fish swim, and the caoutchouc is adapted to a toothed wheel which has a clock-work motion that gives the tail a motion sideways and round, acting like a propeller, and thus the fish swims.

It is perhaps as well to say how these fish are managed, because then children will not break them, when they have been purchased, to see what is inside. Very young students are very fond of analyses of this nature, but synthesis, or putting together, is a far superior occupation in these circumstances to analysis, and to put together more lawful than to pull asunder.
Tree-felling by Steam.
The machine constructed a few years ago by Messrs. Ransome, and which was tried at Roupell Park, near London, seems to combine all the desiderata in the matter of mechanical tree-felling. Many experiments have been previously made by people to cut down trees by means of steam machinery, but none of them included all the conditions necessary for success. The Ransome Machine cut down four large trees in forty minutes.

The apparatus, as shown in the illustration, is not unlike, in appearance, the perforating machines employed in boring rocks, in which the drill is[Pg 767] replaced by a saw. The cylinder is small, and works at high pressure; a piston moves the saw in a guide-frame. The machine is firmly fixed against the tree, and the support is fastened by a chain.
A rack arrangement provides for the turning of the machine as the saw continues to cut its way through the trunk of the tree.
The weight is not excessive, and the necessary steam is supplied by a portable furnace and boiler, which communicates with the saw-motion by a flexible tube. The saw can cut through a horizontal as well as through a perpendicular trunk—thus timber can be rapidly cut up.
Another ingenious sawing machine is that invented by Mr. W. W. Giles, of Chicago, United States, America. This apparatus is about eight feet long, and one extremity is fixed to the trunk of the tree to be operated on.

The operator sits upon a ledge or saddle at the opposite end, and putting his feet upon the treadles, pushes them and the saw forward; this movement is assisted by the weight of the hands on the lever. The saw, under these circumstances, cuts into the wood with great force, and when the operator pushes the lever forward he brings the force of his legs to bear at the same time, and carries the saw back again. So feet, hands, dead weight with the saw itself, combine at once upon the tree, and the[Pg 768] blade quickly does its work. The saw is three feet long and is very easily manipulated.
A Way of Preserving Grapes.
Remarkable progress has been made of late years in the conservation of various articles of food, and we may here speak of the preservation of the grape.
We will first mention M. R. Charmoux’s method, which is called the “Fresh Grape” system. The portion of the building used for the business is on the first floor, as nearly as possible in the centre of the building, so as to be guarded from damp. Two windows are sufficient for all purposes, one to the north, and one to the south. They may be merely kept shut on ordinary occasions, but when frost comes they must be draped and “packed” with nets filled with moss or dried seaweed. The principal one of the windows is to admit of the cleansing of the room and for the admission of air in the summer time, when there are not many grapes left.

In winter the apartment may be warmed by hot air, and if this cannot be managed the ordinary means must be resorted to to keep up the temperature. The upper clusters of grapes should first be picked, for shade conduces to longevity of the fruit, and the 20th October is about the time to commence. A fine day should be chosen; a cloudy day will suit provided there is no dew or dampness in the air.
The finest bunches are cut first, and care must be taken to separate them at the end of the stalk, having three “eyes” under the grape and two above it. The leaves should be at once cut off, and the grapes put with[Pg 769] great caution into boxes or baskets to be taken to the preserving house, where each stalk is plunged into a phial holding about 125 grammes of water, into which, two or three days previously, a teaspoonful of wood charcoal has been put.

The phials are suspended as shown in the accompanying illustration (fig. 899), and then certain precautions must be observed: they must not be disturbed, nor must any draught be admitted, as the temperature must not descend below 1° to 2° cent. There is no necessity to change the water in the bottles; very little will evaporate between November and May, when the process ought to be finished, but the phials must neither be corked nor concealed.

In the dry process the same house can be used, and stagings are employed. These frames are furnished with grooved boxes inclined towards each other, and lined with very dry fern-leaves or straw (fig. 900). Some days after the phials have been filled cut the grapes successively at the first time, which generally begins about the 6th to the 12th of November. The grapes are then put in baskets and carefully carried to the preserving room, where they are ranged in the boxes so as not to touch. Each box contains about six kilogrammes of grapes.
All the time of the conservation process care must be taken to eradicate all grapes which change colour or alter in any way. If dampness be feared have a lighted stove in the room for a time. Grapes are also preserved en espalier, but not so well. Sometimes a mouldy smell will be perceived in the room; to prevent this ventilators should be placed in the ceiling, which must, however, never be opened until the mouldy smell renders such a proceeding absolutely necessary.

CHAPTER LX.
SOME CURIOUS MODES OF TRANSIT.
We have already noticed some novel means of locomotion in the water and in the air, and now a few of the means whereby locomotion is attained as a recreation or as an exhibition may be mentioned.

For instance, here is a very curious vehicle, and the explanation of it we give in the words of the anonymous inventor:—
“My vehicle will carry four people without counting the driver. It is strong, easy to draw, and can turn in a horse’s length. The driver completely controls the animal, and no dust is thrown up to inconvenience the sitters, for by the time it rises the car is well in advance of it. It is cheap; the harness is simple and safe. The horse is sheltered from heat and rain and flies. If he should fall, there is no more than ordinary danger to life and limb than if he fell in a carriage; and, last of all, no very showy animal is needed, so long as his wind is sound, and his legs and tail respectable. Travellers in this “trap” can sit in any position, back to back, or face to face, two and two. The weight is all near the collar, and the animal is under control most perfectly.

“The estimated cost is £40; the horse about £40, or less; harness[Pg 771] (say), £7, which contrasts favourably with the expenses of an ordinary one horse vehicle.”
Endless Rails.
These adjuncts to locomotion can be adapted to any kind of vehicle, and are in pieces about two feet long, articulated, and resting upon a base to give the necessary stability. The endless rail entirely envelopes the wheels all along the train, and the right and left rails are quite independent of each other, and as the vehicles advance the rails are put down and raised again when the carriages have passed. In front there are two distributing wheels governed by the tractive power, so that as the engine, or the animal drawing the train turns aside, the rails are still laid down parallel as before, but the hind wheels will not permit of very sharp curves.
There are wheels also at the rear of the train, and as on curves one wheel will pass over more rail than another, and in the hinder wheels a differential arrangement is used, and when one goes back the other advances as much, and so the relative distance is kept up, for the rail does not alter in length at all. The wheels have double flanges to retain them on the line.

The system, considered from a mechanical point of view, gives striking results, and very little effort is required to put the train in motion. The resistance is very small, and much greater weights can, of course, be transported upon the endless rail than upon the ordinary road.
The experiment has been tried in the Tuilleries Gardens in Paris. Three carriages filled with children are drawn by two goats without any fatigue, and in the ordinary goat carriages at least twelve of the animals would be necessary—that is, four to each carriage. The economy of this mode of transport is therefore incontestable. The usual rate is about three-and-a-half to four miles an hour, so it is not adapted for travellers, but for merchandise.
The system might be applied to numerous vehicles on all kinds of roads for horses and oxen, in mines and factories, and in colonial plantations. M. Ader, the inventor, intended the system to be applied in the Landes, where the rails would lie close upon the sandy soil, and the expense of “metalling” roads would be entirely done away with. The adoption of the endless rail method of conveyance would prove a fortune to the Landes, where[Pg 772] pine forests abound, and the wood and resin which is lost for want of transport could be removed and sold to advantage.
The endless rail may also be used upon the ordinary road in places where the highways are out of repair.

The Smallest Steamboat in the World.
The picture (fig. 904) shows us the Nina, the tiniest steamer afloat. The keel is somewhat over twelve feet in length, and about three feet wide,[Pg 773] the depth of water ten inches. A speed of about five-and-a-half miles an hour can be obtained with a pressure of one hundred pounds. It is a twin-screw “ship” with propellers of three blades. The Nina was built on the lines of the Nautilus, of cedar and oak, and coppered. It is stated to be a marvel of solidity and lightness. The chimney is movable, and can be lowered at pleasure if a bridge be too low. There is ample room for provisions for the occupant in a frame which can be attached to the sides or fixed astern. The boat is easily carried in sections, and can be transported easily from place to place.
The weights of the various portions are as follows:—The hull 90 lb., boiler 80 lb., engine 25 lb., machinery 20 lb.; total, 215 lb. Forty pounds of good charcoal can be packed into the sides of the boat in racks. The rudder can be so connected by wires that the feet will perform the function of steering, thus leaving the hands free to attend to the engine, so the occupant is perfectly at liberty to go where and how he pleases.

For river navigation or calm sea-steaming the Nina is admirably adapted, and any one who can be stoker, steersman, and engineer, as well as passenger and crew, will enjoy a trip in such a boat. Such a steamer costs about £250, but it might be less. It may be added that the Nina has uniformly behaved well, and was built by Fordham of New York.
A Mechanical Carriage.
A distinguished savant of the seventeenth century, Ozanam by name, a member of the Academy of Science, gave in 1693 a curious description of a mechanical carriage, which may perhaps be regarded as the parent of the velocipede and the bicycle. We here reproduce the engravings from Ozanam’s work and his words.
“Some years ago,” wrote the philosopher in 1693, “there may have been seen in Paris a chaise,” as in the picture, “and which a servant, by[Pg 774] pressing alternately upon treadles” (as in the detail), “caused to progress by turning two small wheels hidden in a frame between the hinder pair of wheels of the chaise. The description I give as I received it from M. Richard, the doctor of Rochelle.
“A A is a roller attached to the box behind the vehicle, B is a pulley, over which the cord that works with the treadles passes; C and D are the treadles, with pedals, F F. The wheels, H H, being thus put in motion, the large wheels are moved, and when the hind wheels move forward, the foremost ones must advance also, and the sitter has only to guide the machine by the reins he holds attached to the guiding axle.”

The End.[Pg 775]
INDEX.
- Aberration, Chromatic, 104.
- of sphericity, 105.
- Absorption of light, 95.
- Acid, Acetic, 411.
- Citric, 414.
- Formic, 415.
- Lactic, 415.
- Malic, 414.
- Oxalic, 414.
- Tannic, 414.
- Tartaric, 414.
- Acoustics, Instruments for, 180.
- The science of, 166.
- Actinozoa, The, 710.
- Action and reaction, 35.
- Catalytic, 328.
- Electro-chemical, 220.
- Adhesion of fluids, 25.
- Aerolites, Meteorites or, 493.
- Age, The great ice, 595.
- Agricultural, Science in, 7.
- Air, Composition of, 340.
- Composition of the, 45.
- As motive power, 57.
- Experiments with, 45.
- Movement by heat, 82.
- Pressure of, in bodies, 292.
- on mountains, 55.
- the, 45.
- Science in open, 6.
- Weight of the, 50.
- pump, Experiments, 45.
- Description, 51.
- Sprengel’s, 51.
- Alarum lamp, A new, 760.
- Albumen, 422.
- Alchemists, Celebrated, 336.
- Alchemy, 336.
- Alcoholic thermometers, 80.
- Alcohol, 419.
- Alembic, The, 357.
- Algæ, Mosses and, 688.
- Alkali, Definition of an, 310.
- Alphabets, Telegraphic, 238, 241.
- Alps, Electric clouds in the, 291.
- Alum, 440.
- Aluminum, 393, 439.
- Amber, 421.
- Amebæ, The, 705.
- Ammonia, Uses of, 361.
- Ammonite, 18.
- Ammonium, 393, 437.
- never found, 365.
- Amorphous crystals, 431.
- Anæsthetic, A new, 13.
- Analysis of chance, 726.
- Spectrum, 145.
- Anamorphoses, 135.
- Anatomy of the eye, 102.
- Anemones, Sea, 710.
- Angles, how to measure, 474.
- Animal electricity, 283.
- Animals, Classifications of, 701.
- Vertebrate, etc., 700.
- Annelidæ, The, 714.
- Annulosa, The, 714.
- Anthelion, An, 300.
- Antimony, Uses of, 404, 446.
- Apparatus for Botanists, 17.
- Geologists, 17.
- Mineralogists, 17.
- Appliances, Astronomical, 557.
- Aqua regia, 325.
- Aquarium, A home-made, 9.
- Aquarius constellation, 540.
- Aquatic experiments, 9.
- Arachnida, The, 723.
- Arc, Voltaic, 223.
- Archimedes, Principle of, 68.
- Story of, 68.
- Areometer, Use of the, 27.
- Aries, Constellation, 536.
- Arsenic, 386, 446.
- Artesian wells, 604.
- Ascents, Celebrated balloon, 301.
- Ascent, Gay-Lussac’s, 298.
- Astatic galvanometer, The, 227.
- Asteroids, The, 527.
- Astræa, Discovery of, 528.
- Astronomers, Celebrated, 468.
- Astrology, Early practice of, 467.
- Astronomy, Definition of, 466.
- History of, 466.
- Terms used in, 471.
- Atmosphere, Composition of, 340.
- the same, 628.
- Atmospheric boat, The, 452.
- electricity, 283.
- Atom, Definition of an, 309.
- Atomic or combining weight, 309.
- theory, The, 309.
- Attraction, Capillary, 25, 64.
- Chemical, 25.
- Molecular, 65.
- of cohesion, 24.
- Audiphone, The, 185.
- Uses of the, 185.
- Augites, 439.
- Aurora borealis, Cause of, 646.
- Autophone, Principle of, 184.
- Use of the, 183.
- Axis, Floral, 679.
- Azimuth compass, The, 260.
- Azote, 359.
- Balance, Chemists’, 26.
- Hydrostatic, 26.
- Laws of, 25.
- Balard, Experiments of, 27.
- Ballooning, Sensational, 302.
- Balloons, Accidents to, 297.
- Early ascents in, 296.
- Endeavours to steer, 306.
- Filling, 305.
- Principle of, 305.
- Band, A phantom, 196.
- Barium, 393.
- Barometer, Aneroid, The, 53.
- Glycerine, The, 54.
- Pascal’s, 52.
- Weather forecasts, 652.
- Barometers, Various, 53.
- Barytes, 393, 438.
- Bases, Definitions of, 310, 415.
- Batteries, Different galvanic, 222.
- Battery, electric, Description, 208.
- Beaches, Mirage on, 18.
- Bear, The Great, 542.
- Bell, diving, The, described, 56.
- Bernard Palissy, Saying of, 1.
- Bessemer process, The, 399.
- Bicyclist, A toy, 765.
- Binocular vision, 141.
- Biology, Meaning of, 658.
- Bird, M. Tatin’s artificial, 451.
- Birds, Mechanical, 449.
- Blue John, 395.
- Lias, The, 586.
- Boat, Atmospheric, 452.
- Bores, or tidal waves, 613.
- Boron, 386.
- Mineral nature of, 435.
- “Boss” puzzle, The, 731.
- Botanists, Apparatus for, 17.
- Botany, Introduction to, 657.
- Boxes, Scientific money, 745.
- Breezes, Sea and land, 630.
- British Isles, Date of the, 593.
- Bromine, where found, 367.
- Bronze Age, The, 598.
- Bulb, What is a, 667.
- Wollaston’s, 91.
- Bullets formed by electricity, 264.
- Bunter formation, The, 585.
- Buoyancy of water, The, 67.
- Burglar-detector, A new, 195.
- Butterflies, Capture of, 16.
- Cabinets, Optical, 98.
- Cadot’s clock, 752.
- Cæsum, 393.
- Calamine, 403.
- Calcium, 393, 437.
- Calculation, Machine for, 755.
- Caloric, Theory of, 72.
- Calyx, The, 675.
- Cambrian system, 575.
- Camera obscura, The, 140.
- photographic, The, 151.
- Camphor, 421. [Pg 776]
- Campylometer, Construction, 750.
- Use of the, 749.
- Cancer, Constellation, 538.
- Candle, The burning of, 155.
- Capillarity, 25.
- Description of, 64, 25.
- Capillary attraction, 64, 25.
- Capricornus, Constellation, 539.
- Carbon, Importance of, 368.
- Mineral nature of, 435.
- Carbonic acid, 343.
- Danger of, 374.
- Carboniferous formation, The, 578.
- Carbonization, Slow, 423.
- Card, to perforate by electricity, 215.
- Caseine, 422.
- Castelli, Experiment of, 78.
- Catalepsy, How to induce, 12.
- in fowls, 12.
- Cataleptic fowl, The, 12.
- Cell, A botanical, 661.
- Cells, Animal, 704.
- Plant, 661.
- Cellular tissues, 661.
- Cementation, 398.
- Centre of Gravity, 25.
- magnitude, 34.
- parallel forces, 34.
- Centrifugal force, 43.
- Cephalopods, 725.
- Ceres, Discovery of, 528.
- Chalk, Fossils of the, 589.
- Chance, Analysis of, 726.
- Chemical attraction, 25.
- Chemistry, Early history of, 336.
- Introduction to, 307.
- Organic, 410.
- Sleight of hand and, 335.
- The science of, 22.
- without a laboratory, 313.
- Children,, Simply-made toys for, 764.
- Trapeze and swing for, 763.
- Chladni’s figures, 195.
- Chlorine, 366.
- Uses of, 367.
- Chloroform, Use of, 420.
- Chlorophane, 333.
- Chlorophyl, Definition of, 660.
- Chromatic aberration, 104.
- Chromosphere, The sun’s, 499.
- Chromium, 404, 446.
- Chromograph, The, 748.
- Chronograph, The, 478.
- Chronometers, Solar, Use of, 563.
- Circles, Optical illusions with, 131.
- Circulating fountain, The, 454.
- Cirripeds, The, 723.
- Classification of animals, 701.
- plants, 694.
- Clay, Uses of, 321.
- Cleavage attribute of minerals, 432.
- Clepsydra, The, 479.
- Climate, Differences in, 653.
- Meaning of the term, 652.
- Climatology, 651.
- Clock, A cosmographical, 559.
- Cadot’s, 752.
- Houdin’s, 752.
- Roberts’, 753.
- Clock-lamp, A, 759.
- Clocks, Ancient, 479.
- Mysterious, 752.
- Watches and, 479.
- Clouds, Causes of, 634.
- Classification of, 635.
- Electricity in, 287.
- Vapour and, 634.
- Coal, Formation of, 375.
- Coal found in basins, 581.
- measures, Animal life of, 578.
- period, Plants of the, 80.
- Cobalt, Nickle and, 401, 445.
- Cock, A cataleptic, 12.
- Cohesion attribute of minerals, 431.
- Attraction of, 24.
- Coke ovens, 370.
- Coleoptera, The, 720.
- Collection of insects, 8.
- Colouring of flowers, Artificial, 329.
- Colours, Star, 548.
- Coma, 416.
- Combustion, 345.
- Comets, Celebrated, 492.
- distinguished by, 491.
- Commutator, The, 236.
- Compass, Azumith, The, 260.
- Invention of the, 259.
- Mariners’, To make, 201.
- Ordinary form of the, 259.
- Compensation in optics, 132.
- Composition of the atmosphere, 340.
- Conduction of electricity, 202.
- Conductors, electric, List of, 210.
- Heat, 89.
- Constellations, Northern, 541.
- Southern, 543.
- The chief, 536.
- Copper, 401, 445.
- Coral insect, The, 620.
- islands, 619.
- Corals, 710.
- Cords, Knots, and puzzles, 775.
- Corolla, The, 675.
- Cost of light, 101.
- Crabs, 723.
- Hermit, 723.
- Crust, The earth’s, 566.
- Crustacea, The, 722.
- Crystallization, Instantaneous, 319.
- Crystallography, 424.
- The study of, 427.
- Crystals, Definition of term, 426.
- Forms of, 427.
- Systems of, 427, et. seq.
- Cucumbers, Sea, 714.
- Cups, Volta’s crown of, 220.
- Curiosity, The age of, 8.
- Currents, Air, winds, and, 629.
- Curves, Various sound, 176.
- Cyanogen, 378.
- Daguerreotypes described, 152.
- Dark spot, The, 134.
- Dazzling top, The, 128.
- Dead Sea, Drowning in the, 67.
- Decomposition, 423.
- Definition of physics, 22.
- Definitions, Scientific, 4.
- Density, Laws about, 24.
- Despatch, The pneumatic, 57.
- Devonian system, 576.
- Dew, Hail and, 641.
- Diamonds, Cutting of, 369.
- Dip, Magnetic, 256.
- Discharges, Electric, 214.
- Discoveries, Astronomical, 468.
- Discs, Rotating use of, 108.
- Distances, Measurement of, 482.
- Distillation, Sublimation and, 86.
- Dogs, New work for, 758.
- Double stars, List of, 547.
- Dress, Boyton’s swimming, 460.
- Drops, Prince Rupert’s, 81.
- Drummond light, The, 160.
- Dunes, History of the, 615.
- Dyes, Hair, 326.
- Ear, Anatomy of the, 166.
- Earth, Constitution of the, 568.
- Crust of the, 566.
- Facts about the, 508.
- Formation of the, 566.
- Form of the, 504.
- Latitude and longitude of, 504.
- Motion of the, 504.
- Rate of motion of the, 504.
- Stoppage of the, 507.
- Track of the, 506.
- Earthquakes, Motion of, 623.
- Volcanoes and, 620.
- Ebullition, 83.
- Temperature for, 83.
- Echo, Causes of, 171.
- Definition of an, 171.
- Eclipses, Causes of, 518.
- Lunar, 519.
- Solar, 519.
- Ecliptic, The, 497.
- Egg, electric, The, 214.
- Elasticity, Motion by, 36.
- Electric egg, The, 214.
- light, How to produce, 265.
- machine, To make an, 207.
- pen, The, 248.
- toys, 279.
- Electricity a mystery, 197.
- Animal and other, 282.
- Conduction of, 202.
- decomposes water, 226.
- Derivation of, 197.
- Domestic lighting by, 271.
- in clouds, 287.
- in medicine, 230.
- Negative and positive, 203.
- Novel applications of, 250.
- not to be played with, 205.
- Static and dynamic, 209.
- Velocity of, 212.
- Electro-magnetism, 255, 260.
- Electro-motograph, The, 262.
- Electroplating, 227.
- Electrotyping, 229.
- Electrodes, Poles or, 221.
- Electrolysis, 226.
- Electrometer, Torsion, The, 209.
- Electrophorus, How to make, 198.
- Peiffer’s, 279.
- Electroscope, To make an, 206.
- Elements, Definition of the, 307.
- Electrical relation, 410.
- Phial of the four, 47.
- Table of the, 308.
- Emulsion process, The, 153.
- Encrinites, The, 713.
- Endless rails, Use of, 771.
- Endogens, Enogens and, 665.
- Endosmose, 663, 692.
- Energy changed into heat, 91.
- Entozoa, The, 716.
- Eocene formation, The, 591.
- Epidermis of plants, 664.
- Epsom salts, 395.
- Equator, Magnetic, 256.
- Equilibrium, Laws of, 28.
- Equatorial, The, 478.
- Equinoctial, The, 495.
- Equinoxes, Precession of the, 497.
- Solstices and, 496.
- Eruption, Signs of an, 621.
- Estimation, ocular, Illusions of, 116.
- Ether, 419.
- Stillness of, 168.
- The nature of, 93.
- Eudrometer, Use of the, 353.
- Europe, Geological date of, 593. [Pg 777]
- Eusthenes, Experiment by, 38.
- Evaporation defined, 83.
- Laws of, 84.
- Exogens, Endogens and, 665.
- Experiments, Some of Edison’s, 269.
- Eye, Accommodation in the, 103.
- Light in the, 142.
- The, an optical instrument, 102.
- Faculae, what they are, 498.
- Fata Morgana, The, 649.
- Felspars, 442.
- Fertilization of plants, 682.
- Fibrine, 422.
- Figures, Chladni’s, 195.
- Fiords, Norwegian, 615.
- Fire, Green, 393.
- Red, 395.
- Fish, A fossil, 577.
- Electric, 284.
- Magic, 281.
- New swimming toy, 765.
- Star, 713.
- Fishes, how they breathe, 358.
- Fixed stars, The, 535.
- Flames, Sensitive, 195.
- Singing, 195.
- Flowers, artificial, Colouring of, 329.
- what are they, 675.
- Fluorine, 368.
- Flying, Earliest attempts at, 294.
- Foraminifera, The, 705.
- Force, Centrifugal, 43.
- Definition of a, 4.
- Forces, Natural, 22.
- Parallel centre of, 34.
- Formation, Carboniferous, 578.
- Eocene, 591.
- Jurassic, 586.
- Lias, 586.
- Maestricht, 590.
- Miocene, 593.
- Oolite, 586.
- Permian, 582.
- Trias, 585.
- Wealden, 588.
- Fountain, Circulating, 453.
- Fracture, attribute of minerals, 433.
- Franklin, Experiments of, 205.
- Fraunhofer, Discovery of, 143.
- Freezing machinery, 363.
- mixtures, 89.
- Friction, Definition of, 40.
- Inertia and, 35, et sq.
- Frogs, Electrified, 217.
- Tree, 11.
- Fruit, Definition of, 684.
- How formed, 683.
- Fruits produced by one carpel, 685.
- several, 685.
- Fulgarites, 644.
- Fungi, 690.
- Destructive, 690.
- Edible, 691.
- Propagation of the, 692.
- Fusee, The, 481.
- Fusion, Definition of, 88.
- Future ages, The, 599.
- Galaxy, The, 553.
- Galena, Use of, 401.
- Galileo, Tube of, 148.
- Galleries, Whispering, 172.
- Galvani, defeated by Volta, 218.
- Discovery of, 217.
- Galvanometer, Astatic, 227.
- Pungent, 227.
- , Use of the, 223.
- Galvanoscope, The, 227.
- Game, The needle, 729.
- Games, Mathematical, 726.
- Garnets, Mineral nature of, 442.
- Gas, Coal, 375.
- companies’ profits, 377.
- Definition of, 4.
- harmonicon, The, 351.
- Laughing, 361.
- Marsh, 347.
- Gases, Liquids and, 44.
- Gauges, Rain, 638.
- Gazogene, Use of the, 373.
- Gemini, Constellation, 537.
- Gems, The precious, 443.
- Generation of heat, 77.
- Generator, gramme, The, 268.
- Geography, Geology and, 564.
- Physical, 601.
- Sources of, 603.
- Geologists, Apparatus for, 17.
- Geology, what it teaches, 565.
- Germany, experiment in, 13.
- Geysers, The, 605.
- Theory of the, 84.
- Ghost, Pepper’s, 138.
- stories, 161.
- Ghosts, Explanations about, 161.
- substantial, 142.
- Gilding, Processes of, 407.
- Glacial period, Cause of the, 595.
- The, 595.
- Glaciers, Ice-rivers and, 606.
- Glass, Facts about, 384.
- perforated by electricity, 215.
- Glauber’s salt, 393.
- Globe, Motion of the, 504.
- Spherical form of the, 504.
- Globes, terrestrial, Use of, 562.
- Gold, Nuggets of, 407, 447.
- resists acid, 325.
- the king of metals, 325.
- Goniometer, Use of the, 431.
- Gramme generator, The, 268.
- Grapes, method of preserving, 768.
- Grapes, Room for preserving, 768.
- Graphite, Plumbago or, 370.
- Gravitation, Force of, 4, 486.
- Laws of, 2.
- Gravity, Centre of, 25.
- less in the air, 24.
- same in all bodies, 24.
- Green fire, 393.
- Grit, Millstone, 581.
- Grotto del Cave, The, 374.
- Gulf Stream, The, 618.
- Gum, 418.
- Gymnotus, Electricity of the, 284.
- Gyroscope, Principle of the, 277.
- The, 742.
- The electric, 743.
- Hail, Dew and, 641.
- Halos, Lunar, 648.
- Harmonograph, Construction, 175.
- Havre, Mirage at, 19.
- Heat, a series of vibrations, 74.
- Absorption of, 75.
- Conduction of, 89.
- Definition of, 72.
- Development of, 77.
- Expansion by, 81, 82.
- Generation of, 77.
- How to study, 75.
- Latent, 89.
- light and, Connection of, 94.
- Mechanical equivalents, 74.
- Material theory of, 72.
- produces changes of state, 89.
- Radiant, 90.
- Reflection and refraction, 92.
- Science of, 72.
- Sources of, 77.
- Specific, 88.
- spectrum, The, 146.
- the movement of particles, 91.
- Theory of, 72.
- History, Natural, 4.
- Holland, Sailing on land in, 463.
- Home-made aquarium, A, 9.
- Hope, Mathematical, 727.
- Moral, 727.
- Horn, Alexander’s, 183.
- Hornblend, 439.
- Horoscopes, Early study of, 467.
- Horses, Electric government of, 250.
- Houdin’s clock, 752.
- Household, Scientific objects for, 747.
- Hydraulic Lift, The, 71.
- press, The, 61.
- Hydraulics, 70.
- Hydrogen, Apparatus for, 322.
- Bubbles of, 351.
- How to generate, 350.
- Hydrometers, Table of, 420.
- Hydrophilus, The, 10.
- Hydrostatics, Principles of, 61.
- Hydrozoa, The, 708.
- Hymenoptera, The, 721.
- Hypnotism, 13.
- Ice, How to freeze, 76.
- The age of, 595.
- Ice-rivers, Glaciers and, 606.
- Ice-yachts, Canadian, 463.
- Iceland, Geysers in, 605.
- Igneous rocks, 571.
- Illusions, Optical, 116.
- More about, 129.
- Images, Accidental, 112.
- Implements, Neolithic, 598.
- Palæolithic, 598.
- Inclination, Magnetic, 256.
- Indicator, Use of the celestial, 558.
- Inertia, Definition of, 5.
- Experiments in, 37.
- Friction and, 35, et sq.
- Laws of, 35.
- Inflorescence, 679.
- Varieties of, 680.
- Infusoria, Divisions of the, 707.
- How to capture, 15.
- Origin of, 707.
- Study of, 7.
- Inks, how made, 414.
- Insects, 717.
- Anatomy of, 717.
- Collection of, 8.
- Eyes of, 718.
- Feet of, 718.
- Orders of, 720.
- Palace for, 10.
- Preservation of, 8.
- Transformations of, 719.
- Insulators, electric, List of, 210.
- Integrator, Boys’ mechanical, 264.
- Intensity of sound, 171.
- Iodine, 368.
- Iron age, The, 598.
- Bar, 397.
- Mineral nature of, 443.
- Ores of, 444.
- Pig or cast, 397.
- Pyrophoric, 322.
- unites with oxygen, 321.
- whence obtained, 396. [Pg 778]
- Irradiation, Laws of, 106.
- Islands, Coralline, 619.
- Isoclinic lines, 257.
- Isodynamic lines, 257.
- Isogenic lines, 257.
- Jar, Leyden, Home-made, 199.
- Jardin, The, near Chamouni, 607.
- Jelly-fish, 709.
- Jersey, Mirage in, 19.
- Juggling, Balance experiments, 31.
- Juno, Discovery of, 528.
- Jupiter, Appearance of, 530.
- Moons of, 529.
- The planet, 528.
- Jurassic formation, The, 586.
- Keuper formation, The, 585.
- Kinetic theory, The, 72.
- Kite, A new, 448.
- Franklin’s, 286.
- Knots and cords, Puzzle of, 775.
- Laboratory, Chemistry without, 313.
- Lactoscope, The, 157.
- Ladd, Lontin and, 275.
- Lakes, 627.
- Lamp, A good petroleum, 761.
- A new alarum, 760.
- Dobereiner’s, 408.
- Gay-Lussac’s, 327.
- The Edison, 269.
- The safety, 347.
- The Swan, 271.
- Land, Sailing on, 463.
- Water and, 603.
- Lantern, Magic, 158.
- Lapis-lazuli, 442.
- Latent heat, 89.
- Latex, what it is, 663.
- Latitude, Longitude and, 505.
- Laughing gas, 361.
- Laurentian system, The, 573.
- Lead, 401, 446.
- Crystallization of, 323.
- Leaning, Laws concerning, 33.
- towers, Laws of, 33.
- Leaves, Anatomy of, 671.
- Arrangement of, 673.
- The, 670.
- Varieties of, 671.
- Various, 150.
- Leech, The, 714.
- Lenses, Description of various, 150.
- Leo, Constellation, 538.
- Lepidoptera, The, 721.
- Leyden jar, To make a, 199.
- Lias, The, 586.
- Libra, Constellation, 539.
- Lichens, 689.
- Lift, Hydraulic, 71.
- Light, a vibratory motion, 93.
- Absorption of, 95.
- and its sources, 93.
- Cost of, 101.
- Decomposition of, 143.
- Definition of, 93.
- Lightning, Different kinds of, 289.
- Light distributed in rays, 94.
- electric, How to produce, 265.
- First discovery of, 221.
- heat and, Connection of, 94.
- in the eye, 142.
- of an electric spark, 119.
- oxy-hydrogen, The, 160.
- Polarization of, 155.
- producer of life, 660.
- Reflection of, 95.
- Refraction of, 96.
- Velocity of, 94.
- what made up of, 143.
- Zodiacal, 500.
- Lightning, Forked and sheet, 289.
- Colour of, 288.
- Lights, Bengal, how made, 404.
- Comparison of, 99.
- Lime, Salts of, 393, 437.
- Lines, Isoclinic, 257.
- Isodynamic, 257.
- Isogonic, 257.
- Isothermal, 653.
- oblique, Influence of, 121.
- Linnæan system, The, 695.
- Liquids, Definition of, 4.
- Displacement of, 69.
- Gases and, 44.
- Lithium, 393.
- Longitude, Latitude and, 505.
- Lontin, Ladd and, 275.
- Ludion, The, 57.
- Luminous paint, 160.
- surfaces, Laws of, 107.
- Machine, electric, To make an, 207.
- Tree-felling, 767.
- Writing, 246.
- Machines, Electro-magnetic, 272.
- Maestricht formation, The, 590.
- Magic squares, 732.
- top, The, 740.
- Magnesian limestone, The, 583.
- Magnesium, 395, 439.
- Magnet, A natural, 231.
- Definition of a, 231.
- Magnetic dip, The, 256.
- inclination, 256.
- Magnetism, Electro, 255.
- Terrestrial, 645.
- Magnetization, 232.
- Magnets in ancient times, 254.
- Magnitude, Centre of, 34.
- Man, cave, The, 598.
- during the Glacial Period, 597.
- prehistoric, 597.
- river-drift, The, 598.
- Manganese, 400, 445.
- Mars, Moons round, 526.
- The planet, 523.
- Mathematical games, 726.
- Matter, Definition of, 4.
- Medullary rays, The, 669.
- Medusæ, The, 709.
- Phosphorescence of, 740.
- Megaphone, Mr. Edison’s, 183.
- Membrane tympani, The, 166.
- Menagerie for insects, 10.
- Menisques in a barometer, 65.
- Mercury, All about, 521.
- Fulminating, 420.
- Uses of, 405, 446.
- Mesozoic period, The, 584.
- Metals, Characteristics of, 388.
- Classification of, 389, 409.
- Common and precious, 320.
- in the spectroscope, 146.
- Noble, 405.
- Specific gravity of, 389.
- what they are, 388.
- Meteorites, aerolites, or, 493.
- Meteorology, 628.
- Phenomena of, 20.
- Meteors, what are they? 490.
- Mica, 443.
- Microscope, Invention of the, 149.
- periscopic, The, 150.
- The spectrum, 147.
- Microscopes, Reflecting, 150.
- Milk, Constituents of, 422.
- Sugar of, 423.
- Milky way, The, 553.
- Millstone grit, 581.
- Mineralogists, Apparatus for, 17.
- Mineralogy, Crystallography, 424.
- Mineral waters, 372.
- Minerals, Amorphous, 431.
- Classification of, 424, 425.
- Definition of the term, 424.
- Synoptical table of the, 435.
- Miocene formation, The, 593.
- Mirage at Havre, 19.
- Cause of, 649.
- in Jersey, 19.
- on beaches, 18.
- Mirrors, Remarks on, 95.
- Mistral, The, 631.
- Mixtures, Freezing, 89.
- Molecule, Definition of a, 309.
- Molluscs, 724.
- Money-boxes, Scientific, 745.
- Montgolfier, Discovery of, 2.
- Early balloons of, 295.
- Monsoon, The, 630.
- Moon, Description of the, 510.
- Eclipses of the, 519.
- Influences of on weather, 652.
- its influence on the tides, 517.
- Motion of the, 513.
- Phases of the, 515.
- Rate of progression of the, 513.
- Superstitions concerning, 510, 513.
- Surface of the, 511.
- Planetary, 489.
- Morphine, 416.
- Morse system, The, 241.
- Morse’s telegraph, 233.
- Mosses, Algæ and, 688.
- Motion, Causes of, 40.
- Definition of, 40.
- Perpetual, 41.
- Mould, Vegetable, 690.
- Mountain strata, Contortion of, 625.
- What is a, 624.
- Mountains, Causes of, 624.
- Slopes of, 625.
- Movements, Synthesis of, 124.
- Multiplier, First use of the, 232.
- Mural circle, The, 478.
- Musical pitch, 193.
- Muslin, Incombustible, 313.
- Myriapoda, The, 716.
- Natural History, 4.
- Philosophy, 4.
- system, The, 699.
- Nature, Balance of, 617.
- Forces of, 22.
- Need for knowing about, 3.
- Nothing mute in, 21.
- Smooth polish of, 14.
- Phenomena of, 3.
- what it is, 2.
- Near-sightedness, 140.
- Nebulæ, 551.
- Needle, Game of the, 729.
- The magnetic, 231.
- machine, The, 238.
- Negative and positive electricity, 202.
- Neptune, The planet, 534.
- Nichol’s prism, 156.
- Nicholson’s classes of plants, 702.
- Nickel, cobalt and, 401, 445.
- Nicotine, 416. [Pg 779]
- Nina, The, 773.
- Nitrogen, 359.
- Compounds of, 359.
- Monoxide, 361.
- Nitrogenous substances, 422.
- Nodal points, The, 194.
- Nodes of sound waves, 169.
- Noise distinguished from sound, 167.
- Nomenclature, Astronomical, 471.
- Normandy, A trip in, 6.
- Object, A natural, 3.
- Oils, Fats and, 421.
- “Old Red” a fresh-water deposit, 577.
- Oolite formation, The, 586.
- Opium, 416.
- Optical cabinets, 98.
- Optics, The science of, 93.
- Organic chemistry, 410.
- Orion constellation, 544.
- Orthoptera, The, 721.
- Oxidation, 349.
- Oxygen, Discovery of, 348.
- consumed by breathing, 342.
- How to obtain, 348.
- Oysters, Light from shells of, 160.
- Ozone, Use of, 344.
- Paint, Luminous, 160.
- Palace, Insects, 10.
- Palæozoic systems, 573.
- Pallas, Discovery of, 528.
- Paper wheel toy, 764.
- Parachutes, Descents by, 304.
- Parallax, Explanation of, 484.
- Illustrations of, 483.
- Use of, 485.
- Para-magnetic and dia-magnetic, 258.
- Paraselenæ, Cause of, 648.
- Paris, Great snowfall in, 20.
- Pedometer, The, 756.
- Peiffer’s electrophorus, 279.
- Pen, electric, The, 248.
- Pencil, Edison’s Pneumatic, 454.
- Pendulum, Description of the, 42.
- The, 481.
- Variations in the, 42.
- Period, The Glacial, 595.
- Permian formation, The, 582.
- Fauna of, 582.
- Phantom band, A, 196.
- Pharaoh’s serpents, 315.
- Phases of the Moon, 515.
- Phenakistoscope, The, 110, 121.
- Phenomena, Atmospheric, 642.
- Chemical, 22.
- Meteorological, 20.
- Nature, 3.
- of contrast, 112, 113.
- Physical, 22.
- Phial of the four elements, 47.
- Philosophy, Natural, 4.
- Phonograph, Edison’s, 190.
- Phosphorescence, 331.
- Phosphorus, Bologna, 333.
- how obtained, 381.
- Photography, Camera for, 151.
- Instantaneous, 153.
- Photometers, 101.
- Photometry, 101.
- Photophone, The, 155.
- Photosphere, The, 499.
- Phraseology, Chemical, 338.
- Physics, Meaning of, 22.
- Mechanical, 31.
- Pile, A microscopic, 200.
- hermetic, The, 283.
- Volta’s first, 219.
- Zamboni, 221.
- Pins, scarf, Electrical, 281.
- Pisces, Constellation, 540.
- Pistil, The, 678.
- Pistils, Use of, 665.
- Pitch, Musical, 193.
- Plains, 626.
- Planet, The giant, 528.
- Planets, Comparative sizes of, 487.
- List of the, 487.
- Minor, 489, 527.
- Moons of the, 489.
- Plant, Definition of a, 661.
- Plants, Classification of, 694.
- Flowering, 664.
- Growth of, 665.
- Monœcious, 681.
- Non-flowering, 686.
- Similarity of, to animals, 658.
- Structure of, 661.
- Plateaus, Tablelands or, 626.
- Plating, Electro, 227.
- Platinum, All about, 327.
- Uses of, 408, 447.
- Plumbago, Graphite or, 370.
- Plutonic rocks, The, 601.
- Pneumatic despatch, The, 57.
- Polaris, The star, 542.
- Polarization of light, 155.
- Polarizer, Use of a, 156.
- Poles, Electrodes or, 221.
- Pompeii, Paintings at, 121.
- Porcelain, Manufacture of, 441.
- Porosity, Definition of, 5.
- Positive and negative electricity, 202.
- Portuguese man-of-war, The, 709.
- Potassium, 390, 437.
- Compounds of, 391.
- Praxinoscope, The, 110, 123.
- theatre, The, 126.
- Prehistoric man, 597.
- Preservation of insects, 8.
- Press, Hydraulic, 61.
- Pressure, Fluid application of, 63.
- on the ocean bed, 616.
- Prism, Nichols’, 156.
- Probabilities, Science of, 726.
- Protoplasm, Definition of, 659.
- Protozoa, Definition of, 704.
- Protractor, Use of the, 475.
- Pump, The common, 57.
- Punctum cæcum, The, 134.
- Puzzle, The “Boss,” 731.
- Pyrites, Crystallized, 18.
- Iron, 444.
- Pyrometer, The, 91.
- Quadrant, Use of the simple, 476.
- Quarry, Derivation of the term, 427.
- Quartz, Varieties of, 436.
- Quicksilver. See Mercury.
- Quinine, 416.
- Radiant heat, 90.
- Rain, Causes of, 637.
- Distribution of, 637.
- Measurement of, 638.
- water, The, 71.
- River-beds, Slope of, 626.
- Rainbow, The, 647.
- Rays, Medullar, 669.
- Reaction, Action and, 35.
- Recreation, Science and, 1.
- Red fire, 395.
- Reflection of heat, 92.
- light, 95.
- sound, 171.
- Refraction of heat, 92.
- Reaction of, light, 96.
- sound, 171.
- Refractions, Table of, 479.
- Reptiles, The age of, 585.
- Repulsion in air-particles, 48.
- Ruins, 421.
- Rest, No absolute, 40.
- Rhizome, Definition of, 667.
- Rhone, Colours of the, 570.
- Robert’s clock, 753.
- Robin’s spectres, 138.
- Rocks, Acidic, 602.
- Basic, 602.
- Igneous, 571, 601.
- Plutonic, 601.
- Sedimentary, 570.
- Volcanic, 601.
- Roots, Various, 666.
- Rubidium, 393.
- Sagittarius, Constellation, 539.
- Sailing on railroads, 465.
- Salt, Glauber’s, 393.
- Epsom, 395.
- what meant by in chemistry, 311.
- Sandstone, Old Red, 576.
- Upper Red, 585.
- Sassoline, Boron or, 435.
- Satellites, Planetary, 489.
- Saturn, Rings of, 532.
- Satellites of, 532.
- The planet, 532.
- Tree of, 323.
- Sawing, Machine for, 767.
- Scale, diagonal, Use of the, 477.
- Scarf-pins, Electrical, 281.
- Scavengers, Nature’s, 713.
- Scenograph, Description, 153.
- Scheele, Apparatus used by, 28.
- Science and Recreation, 1.
- Definitions of, 1-5.
- Domestic economy and, 757.
- in the open air, 6.
- Scorpio, Constellation, 539.
- Sea, At the bottom of the, 615.
- Saltness of the, 610.
- The, 610.
- anemones, 710.
- bed, Irregularity of the, 617.
- cucumbers, 714.
- urchins, 712.
- water, Buoyancy of, 67.
- Composition of, 610.
- Sealing-wax, Experiments with, 197.
- Seasons, Recurrence of the, 507.
- Sedimentary rocks, 570.
- Selenium, 386.
- Mineral nature of, 435.
- Selenography, 510 et sq.
- Semaphore, The, 232.
- Serpents, Pharaoh’s, 315.
- Sewing-machines, Motive power, 758.
- Shadows, comic, 158.
- Shot, how made, 403.
- Signalling, 183.
- Silicon, Silica and, 383, 436.
- Silurian system, 575.
- Silver dissolved by nitric acid, 326.
- how obtained, 406, 447.
- Uses of, 406.
- Simoon, The, 631.
- Sky, How to read the, 555.
- why blue, 647.
- Sleet, Cause of, 640.
- Sleight of hand, Chemistry and, 335.
- Smelting, Melting and, 396.
- Snow, Causes of, 639.
- Great falls of, 20. [Pg 780]
- what it is, 639.
- Soap, how made, 391.
- Soap-bubbles, Notes on, 98.
- Sodium, 392, 437.
- Experiments with, 317.
- Solar chronometers, 563.
- spectrum, The, 143.
- Solid, Definition of, 4.
- Solitaire, explanation of puzzles, 736.
- The game of, 735.
- Solstices, Equinoxes and, 496.
- Sound impossible without air, 163.
- Intensity of, 171.
- Reflection of, 171.
- Refraction of, 171.
- transmitted by solids, 174.
- Velocity of, 169.
- Velocity of, varies, 170.
- what it is, 167.
- whence it arises, 167.
- Sound-waves, Nodes of, 169.
- to see, 173.
- Sounds, musical and unmusical, 167.
- Sources of heat, 77.
- Space, what it is, 4.
- Spar, Derbyshire, 395.
- Spark, Electric duration of, 213.
- Light of an electric, 119.
- Speaking tubes, 172.
- Specific gravity, 68.
- Huxley’s definition of, 70.
- of metals, 389.
- Specific heat, 88.
- Spectacles, Different glasses for, 150.
- Spectra, Composition of, 147.
- ocular, 143.
- Spectral illusions, 161.
- Spectre, a visible, 161.
- of the Brocken, The, 650.
- Spectres, Impalpable, 126.
- M. Robin’s, 138.
- Spectroscope, Discovery of the, 145.
- Uses of the, 145.
- Spectroscopy, Science of, 145.
- Spectrum analysis, 145.
- heat, 146.
- solar, 143.
- Sphericity, Aberration of, 105.
- Spider tribe, The, 723.
- Sponges, Nature of, 706.
- Reproduction of, 706.
- Spots, Sun, 498.
- Springs, Causes of, 604.
- Squares, Magic, 731.
- Stamens, The, 677.
- Uses of, 665.
- Starch, Notes about, 417.
- Star, pole, The, 494.
- Star-fish, 713.
- Stars, Clusters of, 551.
- Colours of the, 548.
- Distance of the, 544.
- Double and multiple, 546.
- Falling, 490.
- Fixed, 535.
- Lost, 550.
- Magnitude of the, 554.
- Motions of, 535.
- New, 550.
- Number of the, 536.
- Radiating form of, 105.
- Showers of, 491.
- State, Changes of, produced by heat, 89.
- Static electricity, 209.
- Steam, Definition of, 91.
- Tree-felling by, 766.
- Steamer, The smallest, 773.
- Stem, Parts of the, 667.
- The, 667.
- Varieties of the, 667.
- Stems, Tree, 668.
- Stereoscope, Principle of the, 141.
- Reflecting, 141.
- Refracting, The, 141.
- Stone, Pudding, 568.
- Stories, Ghost, 161.
- Strata, List of geological, 573.
- Strepsiptera, The, 721.
- Strings, Vibration of, 170.
- Strontium, 395, 438.
- Strontium, Luminous sulphates, 333.
- Structure of plants, 661.
- Strychnine, 416.
- Sublimation and distillation, 86.
- Substances, Indifferent, 417.
- Substances, Nitrogenous, 422.
- Sucker, The school-boy’s, 48.
- Sugar, Refining of, 418.
- Sulphur, Mineral, 435.
- Uses of, 379.
- Sun, Density of the, 503.
- Distance of the, 503.
- Eclipses of the, 519.
- Form of the, 498.
- Motion of the, 496.
- Power of the, 503.
- Spots on the, 498.
- Volume of the, 503.
- Suns, mock, Cause of, 648.
- Sunset, Colours of the, 655.
- Surfaces, luminous, Laws of, 107.
- Swan lamps, The, 271.
- Swimming, New apparatus for, 458.
- Swing, Simple child’s, 763.
- Symbols, Chemical table of, 308.
- Synthesis of movements, 125.
- Syphon recorder, Thomson’s, 244.
- Syren, The, 194.
- Syringes, An effect of atmospheric pressure, 63.
- System, Cambrian, 575.
- Coal, 578.
- Devonian, 576.
- Laurentian, 573.
- Silurian, 575.
- The Solar, 487.
- Systems, Palæozoic, 573.
- Tablelands, Plateaus or, 626.
- Tadpoles in aquaria, 10.
- Talking head, How to work, 135.
- Tangent galvanometer, The, 227.
- Tanning, 414.
- Tanning, Process of, 414.
- Tap, A new kind of, 762.
- Tape-worms, 716.
- Tar, Uses of, 378.
- Taurus, Constellation, 537.
- Telegraph, Automatic, 243.
- electric, Discovery of, 232.
- Ordinary form of, 234.
- Telegraphic system, New, 244.
- Telegraphs, Early, 232.
- Telegraphy, Practical, 239.
- Submarine, 243.
- Telephone, Description of the, 186.
- Invention of the, 186.
- Telescope, Achromatic, 149.
- Description of the, 147.
- Divided, explained, 135.
- Introduction of the, 469.
- reflector, The, 149.
- Telescopes, 149.
- Tellurium, 386.
- Terminations, Chemical, 337.
- Tertiary period, The, 591.
- Thaumatrope, The, 110, 121.
- Theatre, The praxinoscope, 126.
- Theory, atomic, The, 309.
- Thermo-dynamics, Definition of, 73.
- Thermometer, How to make a, 79.
- Invention of the, 78.
- Thermometers, Alcoholic, 80.
- Thunder, Causes of, 291.
- Thunderstorms, Precautions, 283.
- Tides, Ebb and flow of, 612.
- Influence of the moon, 517.
- Science of the, 614.
- Time, Ancient measurements of, 479.
- Equation of, 482.
- Sidereal, 478.
- Tin, Crystallization of, 324.
- Uses of, 403, 446.
- Tissues, Cellular and vascular, 661.
- Top, The dazzling, 128.
- The magic, 740.
- Topophone, Description of the, 180.
- Invention of the, 180.
- Tops, Chromatic, 109.
- in optical physiology, 108.
- Torpedo, Electricity of the, 285.
- Torsion electrometer, The, 209.
- Towers, leaning, Laws of, 33.
- Toys, Electric, 279.
- Simple, 764.
- Tramways, Electric, 272.
- Transit, Curious modes of, 770.
- instrument, How to use, 477.
- Trapeze, Simple home-made, 762.
- Tree-felling, Steam power for, 766.
- frogs, 11.
- Trias, The, 585.
- Upper and lower, 585.
- Trolly-sailing, 465.
- Trumpets, Speaking, 172.
- Tube, Galileo’s, 148.
- Tube well, The, 455.
- Tuber, Definition of the, 667.
- Tubes, Speaking, 172.
- Tuning-fork, The, 193.
- Type casting, 405.
- metal, 404.
- Union, Chemical, involves heat, 311.
- Uranus, The planet, 533.
- Vacuum, Torricellian, 51.
- Vanessa algina, 16.
- Vapour, Clouds and, 634.
- what it is, 629.
- Variations of the compass, 257.
- Varnishes, 421.
- Vascular tissues, 661.
- Vehicle, A new two-wheeled, 770.
- Velocipede, New water, 461.
- Velocipedes, Ancient, 775.
- Velocity, Acceleration of, 41.
- Definition of, 23.
- Facts about, 23.
- of Electricity, 212.
- of light, 94.
- Retarded, 41.
- Ventilation, Notes on, 344.
- Venus, The planet, 522.
- Vessels, connected, Laws of, 62.
- Vesta, Discovery of, 528.
- Views, Dissolving, 160.
- Vinegar, how prepared, 418.
- Virgo, Constellation, 538.
- Vision, Binocular, 141.
- Definition of, 103.
- Field of, 140.
- The eye and, 140. [Pg 781]
- Vivaria, 16.
- Volcanic rocks, The, 601.
- Volcanoes, Earthquakes and, 620.
- Formation of new, 623.
- Number of, 621.
- Voltaic arc, The, 223.
- Volume, Weight and, 59.
- Waste, none in nature, 341.
- Watches, Clocks and, 480.
- Water a compound body, 353.
- a form of matter, 59.
- Action of, in Geography, 608.
- All about, 59.
- as ice, 355.
- as steam, 355.
- Buoyancy of, 67.
- Chemistry of, 352.
- decomposed by electricity, 226.
- Distillation of, 356.
- Effects of heat on, 82.
- Evaporation of, 7.
- freezing by evaporation, 85.
- Fresh, in the sea, 611.
- hot, grows lighter, 81.
- Land and, 603.
- Mineral, 372.
- Petrification of, 357.
- Pressure of, 60.
- Sea, composition of, 610.
- Spring, 353.
- sustained by air, 59.
- The force of, 60.
- the unit of specific gravity, 70.
- Water-press, The, 61.
- Water-ram, The, 71.
- Waterspout, Cause of the, 643.
- Waterspouts, How to destroy, 643.
- Water-wheels, 71.
- Waves, Height of the, 613.
- Hurricane, 613.
- Movement of the, 612.
- Standing and progressive, 169.
- Tidal, 613.
- Way, Milky, 553.
- Wealden formations, The, 588.
- Fauna of, 589.
- Flora of, 589.
- Weather, Danger of forecasting, 655.
- forecasts, 651.
- indications, 656.
- Rules for prophesying, 656.
- Weather-glass, The, 53.
- Weight, Combining or atomic, 309.
- Definition of, 22.
- Well tube, The, 455.
- Wells, Artesian, 604.
- Gas, 606.
- Instantaneous, 457.
- Oil, 606.
- Wheatstone’s telegraph, 242.
- Whispering galleries, 172.
- Wind, Pressure of the, 632.
- Use of the, 633.
- Wind, Velocity of the, 630.
- Windows, Double, 757.
- Winds, Air currents and, 629.
- Cause of, 629.
- List of local, 631.
- Trade, 630.
- Wine, Spirits of, 418.
- Wire-drawing, 398.
- Wollaston’s bulb, 91.
- World, Study of the, 1.
- Worms, The, 714.
- Writing machine, The, 246.
- Wings, Best form for, 450.
- Yachts, Canadian ice, 463.
- Double sailing, 462.
- Yellow spot, The, 140.
- Zamboni pile, 221.
- Zeolites, 440.
- Zinc, Use of, 403, 446.
- Zodiac, Signs of the, 471.
- Zodiacal light, The, 500.
- Zoology, Definition of, 700.
- Zootrope, The, 121.

FOOTNOTES:
“When a siphon of seltzer water has been opened some little time, and the equilibrium of tension is nearly established between the escaped gas and the dissolved gas, a vertical stream of bubbles is seen to rise from the bottom of the apparatus, which present a very clear example of the law of ascension of bubbles; that is to say (putting out of the question the expansion of the bubbles in their passage upwards), it is an inverse representation of the law of gravity affecting falling bodies. The bubbles, in fact, detach themselves from their starting point with perfect regularity; and as the interval varies in one file from another, we have before us a multiplied representation of that terrible law which Attwood’s machine made such a bugbear to the commercial world. I believe it is possible, by counting the number of bubbles that detach themselves in a second, in each file, and the number which the whole stream contains at a given instant, to carry the verification further; but I must confess that I have not done so myself.”
“Panuræ then took two glasses of the same size, filled them with water, and put one on one stool, and the other on another, about five feet apart, and placed the staff of a javelin about five-and-a-half feet long across, so that the ends of the staff just touched the brim of the glasses. That done, he took a stout piece of wood, and said to the others: “Gentlemen, this is how we shall conquer our enemies; for in the same way that I shall break this staff between these two glasses, without the glasses being broken or injured, or spilling a single drop of water, so shall we break the head of our Dipsodes, without any injury to ourselves, and without getting wounded. But that you may not think there is magic in it, you, Eusthenes, strike with this stick as hard as you can in the centre.” This Eusthenes did, and the staff broke in two pieces, without a drop of water being spilt.
Leaf Shapes from the illustration on page 672
Lanceolate (Privet).
Ovate (Fuchsia fulgens).
Oblong (Primrose).
Cordate (White Bryony).
Palmate (vine).
II. Depending on Margin and Arrangement.
Serrate (Rose).
Biserrate (Elm).
Crenate (Betony).
Entire (Lilac).
Digitate (Lupin).
Pinnate (Vetch).
Bipinnate (Acacia).
Pinnatifid (Crepis).
Ternate (Clover).
Biternate (Columbine).
III. Depending on Point.
Obtuse (Dock).
Mucronate (Holly).
Retuce (Snowball).
Emarginate (Bladder Senna).
Moon Features
Table of the features illustrated in Figure 565, page 514
A Mare Crisium.
B Palus Somnii.
C Mare Serenitatis.
D Mare Tranquillitatis.
E Mare Fœcunditatis.
F Mare Nectaris.
G Sinus Medii.
H Mare Vaporum.
I Lacus Mortis.
J Mare Frigoris.
K Mare Imbrium.
L Oceanus Procellarum.
M Mare Humorum.
N Mare Nubium.
O Sinus Iridium.
a Apennine Mts.
b Caucasus.
c Carpathians.
d Pyrenees.
e Altai Mts.
f Riphaen Mts.
g Doerfel Mts.
h Leibnitz Mts.
i Corderillas.
j D’Alembert Mts.
k Taurus Mts.
l Hæmus Mts.
m Alps.
1 Clavius.
2 Maginus.
3 Maurolycus.
4 Stöfler.
5 Tycho.
6 Longomontanus.
7 Wilhelm I.
8 Schiller.
9 Schickhardt.
10 Hainzel.
11 Furnerius.
12 Metius.
13 Fabricius.
14 Riccius.
15 Piccolomini.
16 Zagut.
17 Apianus.
18 Walter.
19 Hell.
20 Pitatus.
21 Hesiodus.
22 Capuanus.
23 Ramsden.
24 Vieta.
25 Peravius.
25 Vendelinus.
27 Langrenus.
28 Fracastorius.
29 Theophilus.
30 Cyrillus.
31 Catharina.
32 Sacrobosco.
33 Almanon.
34 Albufeda.
35 Albategnius.
36 Hipparchus.
37 Ptolemy.
38 Alphonsus.
39 Purbach.
40 Regiomontanus.
41 Thebit.
42 Arzachel.
43 Bullialdus.
44 Lalande.
45 Mösting.
46 Herschel.
47 Gassendi.
48 Mersenius.
49 Sirsalis.
50 Grimaldi.
51 Riccioli.
52 Hevelius.
53 Condorcet.
54 Taruntius.
55 Proclus.
56 Cleomedes.
57 Romer.
58 Posidonius.
59 Plinius.
60 Julius Cæsar.
61 Manilius.
62 Godin.
63 Agrippa.
64 Triesnecker.
65 Bode.
66 Gambart.
67 Eratosthenes.
68 Copernicus.
69 Reinhold.
70 Landsberg.
71 Encke.
72 Kepler.
73 Marius.
74 Archimedes.
75 Timocharis.
76 Euler.
77 Aristarchus.
78 Herodotus.
79 Struve.
80 Messala.
81 Mare Humboldtanius.
82 Atlas.
83 Hercules.
84 Endymion.
85 Eudoxus.
86 Aristoteles.
87 Linne.
88 Autolycus.
89 Aristillus.
90 Cassini.
91 Plato.
92 Helicon.
93 Pythagoras.


