.
Ο νόμος του Χουκ ή νόμος της ελαστικότητας περιγράφει την ελαστικότητα ενός υλικού ή συστήματος, όταν αυτό παραμορφώνεται υπό την επίδραση εξωτερικής δύναμης. Φέρει το όνομα του Άγγλου φυσικού Ρόμπερτ Χουκ που εξήγαγε πειραματικά αυτόν τον νόμο. Σύμφωνα με τον νόμο του Χουκ, η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που ασκείται στο ελατήριο. Με άλλα λόγια:
F=kx \ \ \
όπου :
F είναι η δύναμη που ασκείται στο ελατήριο
k η σταθερά του εκάστοτε ελατηρίου και
x η επιμήκυνση του ελατηρίου (η μετατόπιση από τη θέση φυσικού μήκους)
Για την έκφραση του Νόμου του Χουκ στις τρεις διαστάσεις δείτε Θεωρία ελαστικότητας.
Η δυναμική ενέργεια U του ελατηρίου δίνεται από τον τύπο:
U={1\over2}kx^2
Σταθερά ελατηρίου
Η σταθερά ελατηρίου, γνωστή και σαν σταθερά του Χουκ, εκφράζει τη σκληρότητα ενός ελατηρίου και εξαρτάται από:
- το μήκος του ελατηρίου,
- το πάχος του σύρματος του ελατηρίου,
- το άνοιγμα (διάμετρο) των σπειρών του ελατηρίου,
- το υλικό και τη θερμοκρασία του σύρματος του ελατηρίου και
- την απόσταση μεταξύ των σπειρών («βήμα») του ελατηρίου
Μονάδα μέτρησης της σταθεράς ελατηρίου στο Διεθνές Σύστημα (SI) είναι το Νιούτον/Μέτρο (N/m).
Νόμος του Χουκ στη θεωρητική μηχανική
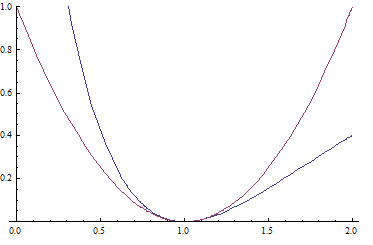
Προσέγγιση του δυναμικού (1-e-(x-1))2 (μπλε) με το αρμονικό δυναμικό (x-1)2 (κόκκινο) γύρω από το σημείο ισορροπίας x=1.
Ο νόμος του Χουκ δεν ισχύει μόνο για μηχανικά ελατήρια. Αντιθέτως, ο συγκεκριμένος νόμος δύναμης ισχύει στις περιοχές ευσταθούς ισορροπίας οποιουδήποτε δυναμικού.
Απόδειξη:
Έστω μονοδιάστατο δυναμικό V(x), το οποίο παρουσιάζει τοπικό ελάχιστο σε κάποιο σημείο x0 που ανήκει στο πεδίο ορισμού του. Αναπτύσσοντας το δυναμικό σε δυναμοσειρά γύρω από το x0:
V(x)=V(x_0)+V'(x_0)x+\frac{1}{2}V''(x_0)x^2+...
Στη γειτονιά του σημείου x0 το δυναμικό μπορεί να προσεγγιστεί από τους πρώτους όρους του αναπτύγματος, ήτοι
V(x)\approx V(x_0)+V'(x_0)x+\frac{1}{2}V''(x_0)x^2
Επιλέγοντας σύστημα αναφοράς έτσι ώστε V(x0)=0 και x0=0 (κάτι που μπορούμε πάντα να κάνουμε με κατάλληλη επιλογή των αξόνων αναφοράς), η παραπάνω έκφραση απλοποιείται περαιτέρω αναγνωρίζοντας επίσης το γεγονός ότι V’(x0)=0 (η V(x0) παρουσιάζει ακρότατο στο σημείο αυτό). Συγκεκριμένα,
V(x)\approx \frac{1}{2}V''(0)x^2=\frac{1}{2}kx^2, \ k=V''(0)
Η αντίστοιχη δύναμη που προκαλεί το παραπάνω δυναμικό ισούται με
F=-\frac{dV}{dx}=-kx
που είναι ακριβώς ο νόμος του Χουκ με k=V”(0). Συνεπώς, ο νόμος του Χουκ είναι εντελώς γενικός και ισχύει για κίνηση κοντά σε οποιοδήποτε σημείο ευσταθούς ισορροπίας τυχαίου δυναμικού V(x). Υπό το φως της παραπάνω μαθηματικής ανάλυσης, η «σταθερά ελατηρίου» k αποκτά καθαρά μαθηματικό χαρακτήρα, ενώ η τιμή του εξαρτάται από την ακριβή μορφή του δυναμικού.
Πηγές
Καίσαρ Δ. Αλεξόπουλος Φυσική. Τ. Α΄ Μηχανική, Αθήνα, 1971
Κανάρης Χ. Τσίγκανος (2004). Εισαγωγή στη Θεωρητική Μηχανική. Εκδόσεις Σταμούλη.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

