Uniform acceleration
See also: Torricelli's equation
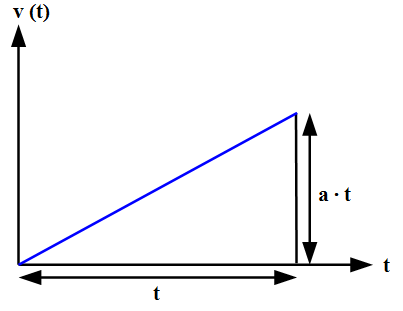
Calculation of the speed difference for a uniform acceleration (Source: Information about this image)
Uniform or constant acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.
A frequently cited example of uniform acceleration is that of an object in free fall in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field strength g (also called acceleration due to gravity). By Newton's Second Law the force {\displaystyle \mathbf {F_{g}} } acting on a body is given by:
{\displaystyle \mathbf {F_{g}} =m\mathbf {g} .}
Because of the simple analytic properties of the case of constant acceleration, there are simple formulas relating the displacement, initial and time-dependent velocities, and acceleration to the time elapsed:[10]
{\displaystyle {\begin{aligned}\mathbf {s} (t)&=\mathbf {s} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}=\mathbf {s} _{0}+{\tfrac {1}{2}}\left(\mathbf {v} _{0}+\mathbf {v} (t)\right)t\\\mathbf {v} (t)&=\mathbf {v} _{0}+\mathbf {a} t\\{v^{2}}(t)&={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}],\end{aligned}}}
where
t is the elapsed time,
\mathbf {s} _{0} is the initial displacement from the origin,
) {\displaystyle \mathbf {s} (t)} is the displacement from the origin at time t t,
\mathbf {v} _{0} is the initial velocity,
\mathbf {v} (t) is the velocity at time t t, and
\mathbf {a} is the uniform rate of acceleration.
In particular, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, which describes, e.g., the trajectory of a projectile in vacuum near the surface of Earth.
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

