In superconductivity, a type-II superconductor is a superconductor which exhibits an intermediate phase of mixed ordinary and superconducting properties at intermediate temperature and fields above the superconducting phases. It also features the formation of magnetic field vortices with an applied external magnetic field. This occurs above a certain critical field strength Hc1. The vortex density increases with increasing field strength. At a higher critical field Hc2, superconductivity is destroyed. Type-II superconductors do not exhibit a complete Meissner effect. [2]
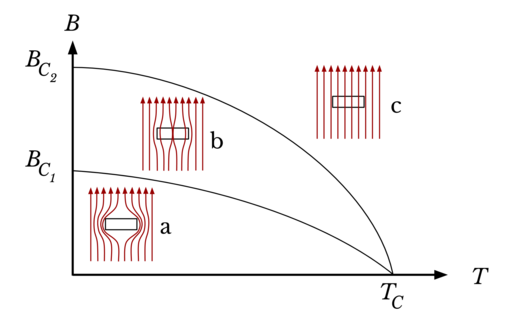
Superconductive behavior under varying magnetic field and temperature. The graph shows magnetic flux B as a function of absolute temperature T. Critical magnetic flux densities BC1 and BC2 and the critical temperature TC are labeled. In the lower region of this graph, both Type-I and Type-II superconductors display the Meissner effect (a). A mixed state (b), in which some field lines are captured in magnetic field vortices, occurs only in Type-II superconductors within a limited region of the graph. Beyond this region, the superconductive property breaks down, and the material behaves as a normal conductor (c).
History
In 1935, Rjabinin and Shubnikov[3][4] experimentally discovered the Type-II superconductors. In 1950, the theory of the two types of superconductors was further developed by Lev Landau and Vitaly Ginzburg in their paper on Ginzburg–Landau theory.[5] In their argument, a type-I superconductor had positive free energy of the superconductor-normal metal boundary. Ginzburg and Landau pointed out the possibility of type-II superconductors that should form inhomogeneous state in strong magnetic fields. However, at that time, all known superconductors were type-I, and they commented that there was no experimental motivation to consider precise structure of type-II superconducting state. The theory for the behavior of the Type-II superconducting state in magnetic field was greatly improved by Alexei Alexeyevich Abrikosov, who was elaborating on the ideas by Lars Onsager and Richard Feynman of quantum vortices in superfluids. Quantum vortex solution in a superconductor is also very closely related to Fritz London's work on magnetic flux quantization in superconductors. The Nobel Prize in Physics was awarded for the theory of Type-II superconductivity in 2003.[6]
Vortex state
Ginzburg–Landau theory defines two parameters: The superconducting coherence length and the London magnetic field penetration depth. In a type-II superconductor, the coherence length is smaller than the penetration depth. This leads to negative energy of the interface between superconducting and normal phases. The existence of the negative interface energy was known since the mid-1930s from the early works by the London brothers. A negative interface energy suggests that the system should be unstable against maximizing the number of such interfaces, which was not observed in first experiments on superconductors, before the experiments of Shubnikov in 1936 where two critical fields were found. In 1952 observation of type-II superconductivity was also reported by Zavaritskii. As was later discussed by A. A. Abrikosov, these interfaces manifest as lines of magnetic flux passing through the material, turning a region of the superconductor normal. This normal region is separated from the rest of the superconductor by a circulating supercurrent. In analogy with fluid dynamics, the swirling supercurrent creates what is known as a vortex, or an Abrikosov vortex, after Alexei Alexeyevich Abrikosov. In the limit of very short coherence length the vortex solution is identical to London's fluxoid, where vortex core is approximated by sharp cutoff rather than gradually vanishing of superconducting condensate near the vortex center. Abrikosov found that the vortices arrange themselves into a regular array known as a vortex lattice.[6]
Flux pinning
In the vortex state, a phenomenon known as flux pinning, where a superconductor is pinned in space above a magnet, becomes possible. This is not possible with type-I superconductors, since they cannot be penetrated by magnetic fields.[7] Since the superconductor is pinned above the magnet away from any surfaces, there is the potential for a frictionless joint. The worth of flux pinning is seen through many implementations such as lifts, frictionless joints, and transportation. The thinner the superconducting layer, the stronger the pinning that occurs when exposed to magnetic fields.
Materials
Type-II superconductors are usually made of metal alloys or complex oxide ceramics. All high temperature superconductors are type-II superconductors. While most elemental superconductors are type-I, niobium, vanadium, and technetium are elemental type-II superconductors. Boron-doped diamond and silicon are also type-II superconductors. Metal alloy superconductors also exhibit type-II behavior (e.g. niobium-titanium and niobium-tin).
Other type-II examples are the cuprate-perovskite ceramic materials which have achieved the highest superconducting critical temperatures. These include La1.85Ba0.15CuO4, BSCCO, and YBCO (Yttrium-Barium-Copper-Oxide), which is famous as the first material to achieve superconductivity above the boiling point of liquid nitrogen (77 K). Due to strong vortex pinning, the cuprates are close to ideally hard superconductors.
Important uses
Strong superconducting electromagnets (used in MRI scanners, NMR machines, and particle accelerators) often use coils wound of niobium-titanium wires or, for higher fields, niobium-tin wires. These materials are type-II superconductors with substantial upper critical field Hc2, and in contrast to, for example, the cuprate superconductors with even higher Hc2, they can be properly machined into wires.
See also
Type-I superconductor – Type of superconductor with a single critical magnetic field
Ideally hard superconductor
Conventional superconductor – Materials that display superconductivity as described by BCS theory or its extensions
Covalent superconductor – Superconducting materials where the atoms are linked by covalent bonds
List of superconductors
Superconductor classification – Different types of superconductors
Technological applications of superconductivity
Timeline of low-temperature technology – aspect of history
Type-1.5 superconductor – Multicomponent superconductors characterized by two or more coherence lengths
Unconventional superconductor – Superconductive materials not explained by existing established theories
References
Wells, Frederick S.; Pan, Alexey V.; Wang, X. Renshaw; Fedoseev, Sergey A.; Hilgenkamp, Hans (2015). "Analysis of low-field isotropic vortex glass containing vortex groups in YBa2Cu3O7−x thin films visualized by scanning SQUID microscopy". Scientific Reports. 5: 8677. arXiv:1807.06746. Bibcode:2015NatSR...5E8677W. doi:10.1038/srep08677. PMC 4345321. PMID 25728772.
Tinkham, M. (1996). Introduction to Superconductivity, Second Edition. New York, NY: McGraw-Hill. ISBN 0486435032.
Rjabinin, J. N. and Schubnikow, L.W. (1935) "Magnetic properties and critical currents of superconducting alloys", Physikalische Zeitschrift der Sowjetunion, vol. 7, no.1, pp. 122–125.
Rjabinin, J. N.; Shubnikow, L. W. (1935). "Magnetic Properties and Critical Currents of Supra-conducting Alloys". Nature. 135 (3415): 581. Bibcode:1935Natur.135..581R. doi:10.1038/135581a0.
Ginzburg, V.L. and Landau, L.D. (1950) Zh. Eksp. Teor. Fiz. 20, 1064
A. A. Abrikosov, "Type II superconductors and the vortex lattice", Nobel Lecture, December 8, 2003
Rosen, J., Ph.D., & Quinn, L. "Superconductivity". In K. Cullen (ed.), Encyclopedia of physical science.
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License