Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a reference plane and the orbital plane or axis of direction of the orbiting object.
For a satellite orbiting the Earth directly above the equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°.
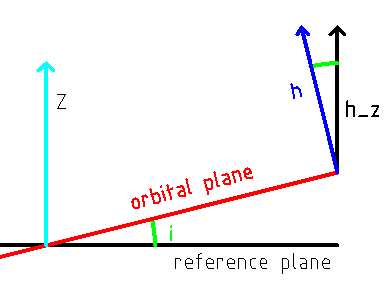
Fig. 1: One view of inclination i (green) and other orbital parameters
Orbits
The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degrees. For a satellite orbiting a planet, the plane of reference is usually the plane containing the planet's equator. For planets in the Solar System, the plane of reference is usually the ecliptic, the plane in which the Earth orbits the Sun.[1][2] This reference plane is most practical for Earth-based observers. Therefore, Earth's inclination is, by definition, zero.
Inclination can instead be measured with respect to another plane, such as the Sun's equator or the invariable plane (the plane that represents the angular momentum of the Solar System, approximately the orbital plane of Jupiter).
Natural and artificial satellites
The inclination of orbits of natural or artificial satellites is measured relative to the equatorial plane of the body they orbit, if they orbit sufficiently closely. The equatorial plane is the plane perpendicular to the axis of rotation of the central body.
An inclination of 30° could also be described using an angle of 150°. The convention is that the normal orbit is prograde, an orbit in the same direction as the planet rotates. Inclinations greater than 90° describe retrograde orbits. Thus:
An inclination of 0° means the orbiting body has a prograde orbit in the planet's equatorial plane.
An inclination greater than 0° and less than 90° also describes a prograde orbit.
An inclination of 63.4° is often called a critical inclination, when describing artificial satellites orbiting the Earth, because they have zero apogee drift.[3]
An inclination of exactly 90° is a polar orbit, in which the spacecraft passes over the poles of the planet.
An inclination greater than 90° and less than 180° is a retrograde orbit.
An inclination of exactly 180° is a retrograde equatorial orbit.
For impact-generated moons of terrestrial planets not too far from their star, with a large planet–moon distance, the orbital planes of moons tend to be aligned with the planet's orbit around the star due to tides from the star, but if the planet–moon distance is small, it may be inclined. For gas giants, the orbits of moons tend to be aligned with the giant planet's equator, because these formed in circumplanetary disks.[4] Strictly speaking, this applies only to regular satellites. Captured bodies on distant orbits vary widely in their inclinations, while captured bodies in relatively close orbits tend to have low inclinations owing to tidal effects and perturbations by large regular satellites.
Exoplanets and multiple star systems
The inclination of exoplanets or members of multiple stars is the angle of the plane of the orbit relative to the plane perpendicular to the line of sight from Earth to the object.
An inclination of 0° is a face-on orbit, meaning the plane of the exoplanet's orbit is perpendicular to the line of sight with Earth.
An inclination of 90° is an edge-on orbit, meaning the plane of the exoplanet's orbit is parallel to the line of sight with Earth.
Since the word "inclination" is used in exoplanet studies for this line-of-sight inclination, the angle between the planet's orbit and the star's rotation must use a different word and is termed the "spin-orbit angle" or "spin-orbit alignment". In most cases the orientation of the star's rotational axis is unknown.
Because the radial-velocity method more easily finds planets with orbits closer to edge-on, most exoplanets found by this method have inclinations between 45° and 135°, although in most cases the inclination is not known. Consequently, most exoplanets found by radial velocity have true masses no more than 40% greater than their minimum masses. If the orbit is almost face-on, especially for superjovians detected by radial velocity, then those objects may actually be brown dwarfs or even red dwarfs. One particular example is HD 33636 B, which has true mass 142 MJ, corresponding to an M6V star, while its minimum mass was 9.28 MJ.
If the orbit is almost edge-on, then the planet can be seen transiting its star.
Calculation
Components of the calculation of the orbital inclination from the momentum vector
In astrodynamics, the inclination i {\displaystyle i} i can be computed from the orbital momentum vector h {\displaystyle h} h (or any vector perpendicular to the orbital plane) as
\( {\displaystyle i=\arccos {h_{z} \over \left|h\right|}} \)
where \( {\displaystyle h_{z}} \) is the z-component of h.
Mutual inclination of two orbits may be calculated from their inclinations to another plane using cosine rule for angles.
Observations and theories
Most planetary orbits in the Solar System have relatively small inclinations, both in relation to each other and to the Sun's equator:
| Inclination to | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Body | Ecliptic | Sun's equator | Invariable plane[5] | ||||||||
| Terre- strials |
Mercury | 7.01° | 3.38° | 6.34° | |||||||
| Venus | 3.39° | 3.86° | 2.19° | ||||||||
| Earth | 0 | 7.155° | 1.57° | ||||||||
| Mars | 1.85° | 5.65° | 1.67° | ||||||||
| Gas giants |
Jupiter | 1.31° | 6.09° | 0.32° | |||||||
| Saturn | 2.49° | 5.51° | 0.93° | ||||||||
| Uranus | 0.77° | 6.48° | 1.02° | ||||||||
| Neptune | 1.77° | 6.43° | 0.72° | ||||||||
| Minor planets |
Pluto | 17.14° | 11.88° | 15.55° | |||||||
| Ceres | 10.59° | — | 9.20° | ||||||||
| Pallas | 34.83° | — | 34.21° | ||||||||
| Vesta | 5.58° | — | 7.13° | ||||||||
On the other hand, the dwarf planets Pluto and Eris have inclinations to the ecliptic of 17° and 44° respectively, and the large asteroid Pallas is inclined at 34°.
In 1966, Peter Goldreich published a classic paper on the evolution of the moon's orbit and on the orbits of other moons in the solar system.[6] He showed that, for each planet, there is a distance such that moons closer to the planet than that distance maintain an almost constant orbital inclination with respect to the planet's equator (with an orbital precession mostly due to the tidal influence of the planet), whereas moons farther away maintain an almost constant orbital inclination with respect to the ecliptic (with precession due mostly to the tidal influence of the sun). The moons in the first category, with the exception of Neptune's moon Triton, orbit near the equatorial plane. He concluded that these moons formed from equatorial accretion disks. But he found that our moon, although it was once inside the critical distance from the earth, never had an equatorial orbit as would be expected from various scenarios for its origin. This is called the lunar inclination problem, to which various solutions have since been proposed.[7]
Other meaning
For planets and other rotating celestial bodies, the angle of the equatorial plane relative to the orbital plane — such as the tilt of the Earth's poles toward or away from the Sun — is sometimes also called inclination, but less ambiguous terms are axial tilt or obliquity.
See also
Altitude (astronomy)
Axial tilt
Azimuth
Beta angle
Kepler orbits
Kozai effect
Orbital inclination change
Space Shuttle Columbia disaster: Possible emergency procedures
References
Chobotov, Vladimir A. (2002). Orbital Mechanics (3rd ed.). AIAA. pp. 28–30. ISBN 1-56347-537-5.
McBride, Neil; Bland, Philip A.; Gilmour, Iain (2004). An Introduction to the Solar System. Cambridge University Press. p. 248. ISBN 0-521-54620-6.
Arctic Communications System Utilizing Satellites in Highly Elliptical Orbits, Lars Løge – Section 3.1, Page 17
Moon formation and orbital evolution in extrasolar planetary systems-A literature review, K Lewis – EPJ Web of Conferences, 2011 – epj-conferences.org
Heider, K.P. (3 April 2009). "The Mean Plane (Invariable plane) of the Solar System passing through the barycenter". Archived from the original on 3 June 2013. Retrieved 10 April 2009. produced using Vitagliano, Aldo. "Solex 10" (computer program).
Peter Goldreich (Nov 1966). "History of the Lunar Orbit". Reviews of Geophysics. 4 (4): 411. Bibcode:1966RvGSP...4..411G. doi:10.1029/RG004i004p00411. Termed "classic" by Jihad Touma & Jack Wisdom (Nov 1994). "Evolution of the Earth-Moon system". The Astronomical Journal. 108: 1943. Bibcode:1994AJ....108.1943T. doi:10.1086/117209.
Kaveh Pahlevan & Alessandro Morbidelli (Nov 26, 2015). "Collisionless encounters and the origin of the lunar inclination". Nature. 527 (7579): 492–494. arXiv:1603.06515. Bibcode:2015Natur.527..492P. doi:10.1038/nature16137. PMID 26607544.
vte
Gravitational orbits
Types
General
Box Capture Circular Elliptical / Highly elliptical Escape Horseshoe Hyperbolic trajectory Inclined / Non-inclined Lagrange point Osculating Parabolic trajectory Parking Prograde / Retrograde Synchronous
semi sub Transfer orbit
Geocentric
Geosynchronous
Geostationary Geostationary transfer Graveyard High Earth Low Earth Medium Earth Molniya Near-equatorial Orbit of the Moon Polar Sun-synchronous Tundra
About
other points
Mars
Areocentric Areosynchronous Areostationary Lagrange points
Distant retrograde Halo Lissajous Lunar Sun
Heliocentric
Earth's orbit Heliosynchronous
Parameters
ShapeSize
e Eccentricity a Semi-major axis b Semi-minor axis Q, q Apsides
Orientation
i Inclination Ω Longitude of the ascending node ω Argument of periapsis ϖ Longitude of the periapsis
Position
M Mean anomaly ν, θ, f True anomaly E Eccentric anomaly L Mean longitude l True longitude
Variation
T Orbital period n Mean motion v Orbital speed t0 Epoch
Maneuvers
Bi-elliptic transfer Collision avoidance (spacecraft) Delta-v Delta-v budget Gravity assist Gravity turn Hohmann transfer Inclination change Low energy transfer Oberth effect Phasing Rocket equation Rendezvous Transposition, docking, and extraction
Orbital
mechanics
Celestial coordinate system Characteristic energy Escape velocity Ephemeris Equatorial coordinate system Ground track Hill sphere Interplanetary Transport Network Kepler's laws of planetary motion Lagrangian point n-body problem Orbit equation Orbital state vectors Perturbation Retrograde motion Specific orbital energy Specific relative angular momentum Two-line elements
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License