.
Στη γεωμετρία, κατηγοριοποιούμε τις σχετικές ή αμοιβαίες θέσεις δύο γεωμετρικών σχημάτων ανάλογα με συγκεκριμένα κριτήρια. Το πρωταρχικό κριτήριο είναι το πλήθος των κοινών σημείων τους σε κάθε θέση. Δευτερεύοντα κριτήρια βασίζονται συνήθως αφενός στην ποιότητα των κοινών σημείων (επαφές, τομές, ταυτίσεις…) και αφετέρου στη θέση των μη κοινών σημείων.
Ενδεικτικά κριτήρια κατηγοριοποίησης
Ας είναι Σ και Ρ δύο σχήματα με αδιάφορο πλήθος κοινών σημείων. Διακρίνουμε δύο σχετικές θέσεις τους με βάση τις εξής περιπτώσεις:
- Υπάρχει ευθεία (ή επίπεδο για τη χωρογεωμετρία), ανάμεσα στα Σ, Ρ, δηλαδή υπάρχει ευθεία ε τέτοια ώστε τα Σ και Ρ να βρίσκονται (ολόκληρα) σε διαφορετικά ημιεπίπεδα της ε.
- Δεν υπάρχει ευθεία ανάμεσα στα Σ, Ρ· στην περίπτωση αυτή μπορούμε (όχι αυστηρά) να χαρακτηρίσουμε το σύστημα των δύο σχημάτων ως «συναφές» ή «συνεκτικό».
Η διάκριση σε σχετικές θέσεις μπορεί να περιληφθεί στα εξής τρία κριτήρια, τα οποία εφαρμόζονται διαδοχικά:
- Κριτήριο ποσότητας κοινών σημείων: Δύο σχετικές θέσεις των Σ και Ρ διαφέρουν, όταν το πλήθος των κοινών σημείων των Σ και Ρ διαφέρει από θέση σε θέση.
- Κριτήριο ποιότητας κοινών σημείων: Δύο σχετικές θέσεις των Σ και Ρ με το ίδιο πλήθος κοινών σημείων διαφέρουν, όταν τα κοινά σημεία των Σ και Ρ εμφανίζουν ποιοτικές διαφορές από θέση σε θέση.
- Κριτήριο «συνάφειας»: Δύο σχετικές θέσεις των Σ και Ρ με ίδιο πλήθος κοινών σημείων αντίστοιχης ποιότητας, διαφέρουν όταν το σύστημα των Σ και Ρ είναι «συναφές» στη μία θέση και μη «συναφές» στην άλλη.
Σχετικές θέσεις σημείου και ευθείας
Ένα σημείο μπορεί να
- κείτεται πάνω σε μια ευθεία (ένα κοινό σημείο)
- κείτεται έξω από μια ευθεία (κανένα κοινό σημείο)
Σχετικές θέσεις σημείου και κύκλου
Ένα σημείο μπορεί να
- κείτεται πάνω σε έναν κύκλο (ένα κοινό σημείο)
- κείτεται έξω από έναν κύκλο (κανένα κοινό σημείο, μη «συνάφεια»)
- κείτεται μέσα σε έναν κύκλο (κανένα κοινό σημείο, «συνάφεια»)
Σχετικές θέσεις ευθειών
Στην ευκλείδεια γεωμετρία δύο ευθείες μπορούν να
- ταυτίζονται (άπειρα κοινά σημεία)
- τέμνονται (ένα κοινό σημείο)
- είναι παράλληλες (κανένα κοινό σημείο και συνεπίπεδες)
- είναι ασύμβατες (κανένα κοινό σημείο ούτε συνεπίπεδες)
Σχετικές θέσεις ευθείας και κύκλου
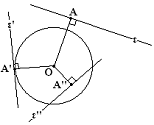
Σχετικές θέσεις ευθείας και κύκλου στο ευκλείδειο επίπεδο.
Στην ευκλείδεια επιπεδομετρία, μία ευθεία μπορεί να
- κείτεται έξω από έναν κύκλο (κανένα κοινό σημείο)
- εφάπτεται σε έναν κύκλο (ένα κοινό σημείο)
- τέμνει έναν κύκλο (δύο κοινά σημεία)
Κριτήριο για τη σχετική θέση ευθείας-κύκλου αποτελεί η απόσταση της ευθείας από τον κύκλο: αν είναι μεγαλύτερη από, ίση με ή μικρότερη από την ακτίνα τότε η ευθεία είναι εξωτερική, εφαπτόμενη ή τέμνουσα του κύκλου αντίστοιχα.
Σχετικές θέσεις κύκλων
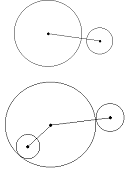
Επάνω: Δύο κύκλοι εξωτερικοί ο ένας του άλλου. Κάτω: Εξωτερική και εσωτερική επαφή κύκλων.
Στα πλαίσια της ευκλείδειας επιπεδομετρίας, δύο κύκλοι μπορούν να
- ταυτίζονται (άπειρα κοινά σημεία)
- τέμνονται (δύο κοινά σημεία)
- εφάπτονται εξωτερικά (ένα κοινό σημείο, μη «συνάφεια»)
- εφάπτονται εσωτερικά (ένα κοινό σημείο, «συνάφεια»)
- κείτονται ο ένας έξω από τον άλλο (κανένα κοινό σημείο, μη «συνάφεια»)
- κείτονται ο ένας μέσα στον άλλο (κανένα κοινό σημείο, «συνάφεια»)
Εξωτερικοί σύνδεσμοι
Σχετικές θέσεις διανυσμάτων από τον ιστότοπο PlanetMath (στα Αγγλικά).
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

