.
Στα μαθηματικά και τη φυσική, ένα σφαιρικό σύστημα συντεταγμένων είναι ένα σύστημα αναφοράς για τριδιάστατο χώρο όπου η θέση ενός σημείου προσδιορίζεται από τρεις αριθμούς: την ακτινική απόσταση του σημείου από ένα σταθερό σημείο αναφοράς (το κέντρο τον αξόνων Ο), την πολική γωνία που μετράται από τη σταθερή κατεύθυνση του ζενίθ (άξονας z), και το αζιμούθιο η γωνία της προβολής του σημείου στο επίπεδο, από κάποια σταθερή κατεύθυνση στο επίπεδο (άξονας x).
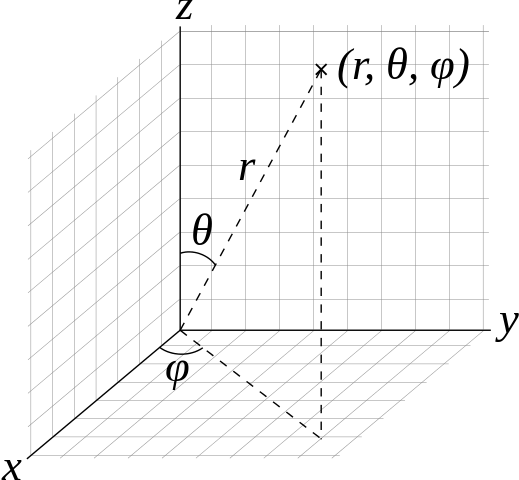
Σφαιρικές συντεταγμένες (r, θ, φ) όπως χρησιμοποιούνται συνήθως στη φυσική: ακτινική απόσταση r, πολική γωνία θ και αζιμούθιο φ. Το γράμμα ρ πολλές φορές χρησιμοποιείται αντί για το r.
Η ακτινική απόσταση συνήθως καλείτε και απλά ακτίνα ή ακτινική συντεταγμένη. Η πολική γωνία καλείται και ζενίθια γωνία ή ζενίθια απόσταση.
Σφαιρικές συντεταγμένες (r, θ, φ) όπως χρησιμοποιούνται συνήθως στα μαθηματικά: ακτινική απόσταση r, πολική γωνία φ και αζιμούθιο θ. Οι έννοιες των θ και φ είναι αλλαγμένες σε σχέση με τις αντίστοιχες που χρησιμοποιούνται στη φυσική.
Η χρήση των συμβόλων σε σχέση και η σειρά των συντεταγμένων διαφέρει μεταξύ των πηγών. Το σύστημα που συνήθως εμφανίζεται στη φυσική είναι (r, θ, φ) για ακτινική απόσταση, πολική γωνία και αζιμούθιο αντίστοιχα, ενώ το σύστημα που εμφανίζεται κυρίως στα μαθηματικά συγγράμματα είναι (r, θ, φ) για ακτινική απόσταση, αζιμούθιο και πολική γωνία αντίστοιχα. Και στα δύο συστήματα το γράμμα ρ συναντάται συχνά αντί για το r. Διαφορετικές χρήσεις επίσης συναντώνται, όποτε χρειάζεται ιδιαίτερη προσοχή για το ποιο σύστημα χρησιμοποιείται.
Διαφορετικά συστήματα που χρησιμοποιούνται για τις σφαιρικές συντεταγμένες, είναι οι γεωγραφικές συντεταγμένες και οι ουράνιες συντεταγμένες.
Το σφαιρικό σύστημα συντεταγμένων είναι γενίκευση του διδιάστατου πολικού συστήματος συντεταγμένων. Μπορεί να επεκταθεί και σε περισσότερες χωρικές διαστάσεις στη γεωμετρία της υπερσφαίρας.
Σχέση με τις καρτεσιανές συντεταγμένες
Οι καρτεσιανές συντεταγμένες προκύπτουν από τις σφαιρικές συντεταγμένες (με τη σύμβαση ακτίνα r, πολική γωνία θ, αζιμούθιο φ), και με πεδία ορισμού r ∈ [0, ∞), θ ∈ [0, π], φ ∈ [0, 2π), από τους ακόλουθους τύπους:
x=r \, \sin\theta \, \cos\varphi
y=r \, \sin\theta \, \sin\varphi
z=r \, \cos\theta
Οι σφαιρικές συντεταγμένες (σύμφωνα με τη σύμβαση για ακτίνα r, πολική γωνία θ, αζιμούθιο φ) του σημείου αντίστοιχα προκύπτουν από τις καρτεσιανές συντεταγμένες(x, y, z) από τους τύπους:
r=\sqrt{x^2 + y^2 + z^2}
\theta = \operatorname{arccos}\left(\frac{z}{\sqrt{x^2 + y^2 + z^2}}\right)
\varphi = \operatorname{atan2}(y, x) = \begin{cases} \arctan(\frac y x) & ,\gamma\iota\alpha\; x > 0, \\ \sgn(y)\frac \pi 2 & ,\gamma\iota\alpha\; x = 0, \\ \arctan(\frac y x) + \pi & ,\gamma\iota\alpha\; x < 0 \land y \geq 0, \\ \arctan(\frac y x) - \pi & ,\gamma\iota\alpha\; x < 0 \land y < 0. \end{cases}
Ενδεικτική Βιβλιογραφία
Γ. Γεωργανοπουλος, Δ. Παπαδόπουλος, Γ. Τσαγκας (2002). Στοιχεία Διανυσματικής Ανάλυσης, Διανυσματικού Λογισμού, Αναλυτικής Γεωμετρίας. Θεσσαλονίκη: Εκδόσεις Αϊβάζης, σελ. 91.
Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill, σελ. 174–175. ASIN B0000CKZX7. LCCN 59014456.
Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag, σελ. 95–96. LCCN 67025285.
Moon P, Spencer DE (1988). «Spherical Coordinates (r, θ, ψ)». Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print έκδοση). New York: Springer-Verlag, σελ. 24–27 (Table 1.05). ISBN 978-0-387-18430-2.
Στο λήμμα αυτό έχει ενσωματωθεί κείμενο από το λήμμα Spherical coordinate system της Αγγλικής Βικιπαίδειας, η οποία διανέμεται υπό την GNU FDL και την CC-BY-SA 3.0. (ιστορικό/συντάκτες).
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License


