.
Το πεντάγραμμα (γνωστό και ως η πεντάλφα) είναι ένα γεωμετρικό αστεροειδές σχήμα πέντε σημείων που κατασκευάζεται με πέντε συνεχόμενες μολυβιές.
Η λέξη πεντάγραμμα συνδυάζει το αριθμητικό πρόθεμα πέντε- με το επίθεμα -γραμμή.[1] Προέρχεται από την αρχαία ελληνική λέξη πεντάγραμμον που είναι το ουδέτερο του επιθέτου πεντάγραμμος.[2] Η λέξη πεντάλφα αναβιώθηκε τον 17ο αιώνα από την μετα-κλασσική ελληνική ονομασία του σχήματος, που κατασκευάζεται επίσης από πέντε -άλφα.[3]
Γεωμετρία
Το πεντάγραμμα είναι το απλούστερο κανονικό αστεροειδές πολύγωνο. Το πεντάγραμμα περιέχει δέκα σημεία (τα πέντε σημεία του αστεριού και οι πέντε κορυφές του εσωτερικού πενταγώνου) και δεκαπέντε ευθύγραμμα τμήματα. Εκπροσωπείται από το σύμβολο Schläfli {5/2}. Όπως ένα κανονικό πεντάγωνο ή ένα κανονικό πεντάγωνο με ένα πεντάγραμμα κατασκευασμένο μέσα σε αυτό, έτσι και το κανονικό πεντάγραμμα έχει διεδρική συμμετρία (D5) τάξης 10.
Χρυσή τομή
Ένα κανονικό πεντάγραμμα χρωματισμένο ώστε να γίνει διάκριση των ευθυγράμμων τμημάτων του που έχουν διαφορετικά μήκη. Τα τέσσερα μήκη είναι σε χρυσή αναλογία μεταξύ τους
Φράκταλ πενταγράμμου που κατασκευάζεται με έναν βρόγχο επανάληψης διανυσμάτων
Η χρυσή τομή, φ = (1 + √5) / 2 ≈ 1.618, ικανοποιεί:
\( \varphi=1+2\sin(\pi/10)=1+2\sin 18^\circ\, \)
\( \varphi=1/(2\sin(\pi/10))=1/(2\sin 18^\circ)\, \)
\( \varphi=2\cos(\pi/5)=2\cos 36^\circ\, \)
Διαδραματίζει έτσι σημαντικό ρόλο στα κανονικά πεντάγωνα και τα πενταγράμματα. Ο λόγος κάθε ευθύγραμμου τμήματος που εμφανίζεται σε αυτή ως προς το αμέσως βραχύτερό του σε μήκος ισούται με τη χρυσή τομή, φ. Επίσης, ο λόγος του μήκους του βραχύτερου τμήματος προς το τμήμα που οριοθετείται από τις δύο τεμνόμενες ακμές (μια πλευρά του πενταγώνου στο κέντρο του πενταγράμμου) είναι φ (βλ. την τετράχρωμη εικόνα δεξιά):
\( \frac{\mathrm{red}}{\mathrm{green}} = \frac{\mathrm{green}}{\mathrm{blue}} = \frac{\mathrm{blue}}{\mathrm{magenta}} = \varphi. \)
Το πεντάγραμμα περιλαμβάνει δέκα ισοσκελή τρίγωνα: πέντε οξυγώνια και πέντε αμβλυγώνια ισοσκελή τρίγωνα. Σε όλα αυτά, η αναλογία της μεγαλύτερης πλευράς προς την μικρότερη πλευρά είναι φ. Τα οξυγώνια ισοσκελή τρίγωνα είναι χρυσά τρίγωνα. Το αμβλυγώνιο ισοσκελές τρίγωνο που επισημαίνονται μέσω των χρωματιστών γραμμών στην εικόνα είναι ένας χρυσός γνώμονας.
Τριγωνομετρικές τιμές
\( \sin \frac{\pi}{10} = \sin 18^\circ = \frac{\sqrt 5 - 1}{4}=\frac{\varphi-1}{2}=\frac{1}{2\varphi} \)
\( \cos \frac{\pi}{10} = \cos 18^\circ = \frac{\sqrt{2(5 + \sqrt 5)}}{4} \)
\( \tan \frac{\pi}{10} = \tan 18^\circ = \frac{\sqrt{5(5 - 2 \sqrt 5)}}{5} \)
\( \cot \frac{\pi}{10} = \cot 18^\circ = \sqrt{5 + 2 \sqrt 5} \)
\( \sin \frac{\pi}{5} = \sin 36^\circ = \frac{\sqrt{2(5 - \sqrt 5)} }{4} \)
\( \cos \frac{\pi}{5} = \cos 36^\circ = \frac{\sqrt 5+1}{4} = \frac{\varphi}{2} \)
\( \tan \frac{\pi}{5} = \tan 36^\circ = \sqrt{5 - 2\sqrt 5} \)
\( \cot \frac{\pi}{5} = \cot 36^\circ = \frac{ \sqrt{5(5 + 2\sqrt 5)}}{5} \)
Ως αποτέλεσμα, σε ένα ισοσκελές τρίγωνο με μία ή δύο γωνίες 36°, το μεγαλύτερο από τα δύο μήκη πλευράς είναι φ φορές μεγαλύτερο από εκείνο του βραχύτερου των δύο, τόσο στην περίπτωση του οξυγώνιου τριγώνου, όσο και στην περίπτωση του αμβλυγώνιου τριγώνου.
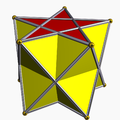
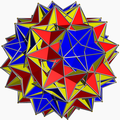
Τρισδιάστατα σχήματα
Αρκετα πολύεδρα έχουν ενσωματωμένα πενταγράμματα:
-
Πενταγραμμικό πρίσμα
-
Πενταγραμμικό αντιπρίσμα
-
Πενταγραμμικό σταυρωτό-αντιπρίσμα
-
Μικρό αστρώδες δωδεκάεδρο
-
Μεγάλο αστρώδες δωδεκάεδρο
-
Μεγάλο εικοσιδωδεκάεδρο
-
Μικρό διτρίγωνο εικοσιδωδεκάεδρο
-
Δωδεκαδωδεκάεδρο
-
Κολοβό δωδεκαδωδεκάεδρο
-
Μικρό κολοβό εικοσεικοσιδωδεκάεδρο
-
Μικρό ρετροκολοβό εικοσεικοσιδωδεκάεδρο
-
Μεγάλο ρετροκολοβό εικοσιδωδεκάεδρο
-
Μεγάλο διρομβεικοσιδωδεκάεδρο
-
16ο αστρώδες του εικοσιδωδεκάεδρου
Υψηλότερες διαστάσεις
Οι ορθογώνιες προβολές πολυτόπων υψηλότερων διαστάσεων μπορούν επίσης να δημιουργήσουν πανταγραμμικά σχήματα:
| 4D | 5D | ||
|---|---|---|---|
 Το κανονικό πεντάχωρο έχει 5 κορυφές και 10 ακμές. |
 Το ανορθωμένο πεντάχωρο έχει 10 κορυφές και 30 ακμές. |
 Το ανορθωμένο εξάτερο έχει 15 κορυφές, που στην ορθογώνια προβολή φαίνονται ως 3 ένθετα πεντάγραμμα. |
 Το δις ανορθωμένο εξάτερο έχει 20 κορυφές, που στην ορθογώνια προβολή φαίνονται ως 4 επικαλυπτόμενα πεντάγραμμα. |
Και τα δέκα Schläfli–Hess τετραδιάστατα πολύτοπα είτε έχουν πανταγραμμικές έδρες ή αποτελούνται από στοιχεία σε σχήμα κορυφής.
Παραπομπές
Liddell, Henry George; Scott, Robert. «A Greek-English Lexicon: γραμμή». Perseus.
Liddell, Henry George; Scott, Robert. «A Greek-English Lexicon: πεντάγραμμον». Perseus.
Liddell, Henry George; Scott, Robert. «A Greek-English Lexicon: άλφα». Perseus.
Βιβλιογραφία
Arakelian, Hrant (2014). The History of the Pentagram, Ch. 6 in Mathematics and History of the Golden Section, p. 207-270, Logos, 404 p. ISBN 978-5-98704-663-0 (rus.).
Grünbaum, Branko; Shephard, Geoffrey Colin (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 978-0-7167-1193-3.
Grünbaum, Branko (1994). «Polyhedra with Hollow Faces». Polytopes: Abstract, Convex and Computational. NATO ASI Series C: Mathematical and Physical Sciences. 440. Dordrecht: Springer Netherlands, σελ. 43–70. doi:10.1007/978-94-011-0924-6_3. ISBN 978-94-010-4398-4.
John Horton Conway, Heidi Burgiel, Chaim Goodman-Strass, (2008). The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)
Εξωτερικοί σύνδεσμοι
Weisstein, Eric W., "Pentagram" από το MathWorld.
The Pythagorean Pentacle from the Biblioteca Arcana.
In-depth analysis of the Golden Ratio
The pentagram and Freemasonry
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License
