.
Αυτό το άρθρο αφορά τον όρο που χρησιμοποιείται στο λογισμό.Για μια λιγότερο τεχνική επισκόπηση του θέματος, δείτε διαφορικός λογισμός. Για άλλες χρήσεις, δείτε Παράγωγος (αποσαφήνιση).
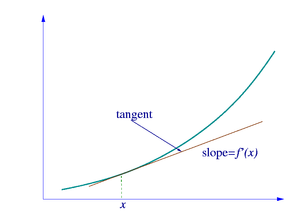
Το γράφημα μιας συνάρτησης, με μαύρο χρώμα, και η εφαπτομένη της συνάρτησης, με κόκκινο χρώμα. Η κλίση της εφαπτόμενης γραμμής είναι ίση με την παράγωγο της συνάρτησης στο υποδεικνυόμενο σημείο.
Η παράγωγος μιας συνάρτησης με πραγματική μεταβλητή είναι ένα μέτρο που εκφράζει τη μεταβολή της τιμής της συνάρτησης (μια συνάρτηση ή εξαρτημένη μεταβλητή) η οποία προσδιορίζεται από μια άλλη ποσότητα (η ανεξάρτητη μεταβλητή). Είναι ένα θεμελιώδες εργαλείο του λογισμού. Για παράδειγμα, η παράγωγος της θέσης ενός κινητού αντικειμένου σε σχέση με το χρόνο είναι η ταχύτητα του αντικειμένου: η οποία μετρά πόσο γρήγορα αλλάζει η θέση του αντικειμένου όταν ο χρόνος προχωρήσει.Η παράγωγος μετρά τον στιγμιαίο ρυθμό μεταβολής της συνάρτησης, όπως διακρίνεται από τον μέσο ρυθμό μεταβολής, και ορίζεται ως το όριο του ρυθμού μεταβολής της συνάρτησης όπου το μήκος του διαστήματος που ορίζεται ο μέσος όρος τείνει στο μηδέν.
Η παράγωγος μιας συνάρτησης με επιλεγμένη τιμή εισόδου περιγράφει την καλύτερη γραμμική προσέγγιση της συνάρτησης κοντά σε αυτή τιμή εισόδου.H παράγωγος σε ένα σημείο της συνάρτησης μιας μεταβλητής είναι η κλίση της εφαπτόμενης γραμμής στην γραφική παράσταση της συνάρτησης στο σημείο αυτό.

Το γράφημα μιας συνάρτησης, με μαύρο χρώμα, και η εφαπτομένη της συνάρτησης, με κόκκινο χρώμα. Η κλίση της εφαπτόμενης γραμμής είναι ίση με την παράγωγο της συνάρτησης στο υποδεικνυόμενο σημείο.
Η έννοια της παραγώγου μπορεί να γενικευθεί σε συναρτήσεις πολλών πραγματικών μεταβλητών. Η παράγωγος μιας συνάρτησης πολλών μεταβλητών είναι ένας γραμμικός μετασχηματισμός που ονομάζεται διαφορικός πίνακας. Η αναπαράσταση του πίνακα είναι ένας Ιακωβιανός πίνακας, ο οποίος μειώνει την κλίση του διανύσματος στην περίπτωση πραγματικής συνάρτησης πολλών μεταβλητών.
Η διαδικασία εύρεσης της παραγώγου ονομάζεται παραγώγιση. Η αντίστροφη διαδικασία ονομάζεται αντιπαραγώγιση. Το Θεμελίωδες Θεώρημα του λογισμού αναφέρει ότι η αντιπαραγώγιση είναι το ίδιο με το ολοκλήρωμα. Παραγώγιση και ολοκλήρωση αποτελούν δυο βασικές λειτουργίες στο λογισμό.[1]
Παραγώγιση και παράγωγος
Η παραγώγιση είναι η μέθοδος για τον υπολογισμό της παραγώγου. Η παράγωγος μιας συνάρτησης f(x) με μεταβλητή x είναι ένα μέγεθος βαθμού με το οποίο η τιμή της συνάρτησης αλλάζει σε σχέση με τη μεταβολή της μεταβλητής. Αυτό ονομάζεται παράγωγος της f στο x. Αν το x και το y είναι πραγματικοί αριθμοί, και αν σχεδιαστεί η γραφική παράσταση της f συναρτήσει του x, η παράγωγος είναι η κλίση του γραφήματος σε κάθε σημείο.
Η απλούστερη περίπτωση, εκτός από την περίπτωση της σταθερής συνάρτησης, είναι όταν το y είναι γραμμική συνάρτηση του x, που σημαίνει ότι το γράφημα του y συναρτήσει του x είναι ευθεία γραμμή. Στην περίπτωση αυτή, y=f(x)=mx + b, για πραγματικούς αριθμούς m και b, και η κλίση m δίνεται από τη σχέση
\( m=\frac{\text{change in } y}{\text{change in } x} = \frac{\Delta y}{\Delta x}, \)
όπου το σύμβολο Δ (Δέλτα) είναι συντομογραφία της "μεταβολής". Ο τύπος αυτός ισχύει αφού
y + Δy = f(x + Δx) = m (x + Δx) + b = m x + m Δx + b = y + m Δx.
και από αυτό έχουμε ότι Δy=m Δx.
Αυτό δίνει ακριβή τιμή για την κλίση μιας γραμμής. Αν η συνάρτηση f δεν είναι γραμμική (δηλαδή η γραφική της παράσταση δεν είναι ευθεία) τότε η αλλαγή του y σε σχέση με την αλλαγή του x ποικίλει: η παραγώγιση είναι μια μέθοδος της ακριβούς τιμής του βαθμού αλλαγής για οποιοδήποτε δοθέν τιμή του x.
Η ιδέα που απεικονίζεται στα Σχήματα 1 έως 3, είναι να υπολογιστεί ο βαθμός της μεταβολής ως η οριακή τιμή του λόγου Δy/Δx καθώς το Δx γίνεται άπειρα μικρό.
Σημειογραφία
Δυο ξεχωριστές σημειογραφίες που χρησιμοποιούνται συνήθως για την παράγωγο, η μια απορρέει από τον Leibniz και η άλλη από τον Joseph Louis Lagrange.
Στη σημειογραφία του Leibniz, μια απειροελάχιστη αλλαγή στο x συμβολίζεται με dx, και η παράγωγος του y σε συνάρτηση με το x γράφεται
\( \frac{dy}{dx} \,\! \)
συμβολίζοντας τον λόγο των δυο απειροελάχιστα μικρών ποσοτήτων.(Η παραπάνω έκφραση διαβάζεται ως "η παράγωγος του y σε συνάρτηση με το x", "dy από dx", ή "dy πέρα dx". Η προφορική μορφή "dy dx" συχνά χρησιμοποιείται conversationally, αλλά μπορεί να οδηγήσει σε σύγχυση.)
Στη σημειογραφία του Lagrange, η παράγωγος της συνάρτησης f(x) σε συνάρτηση με το x συμβολίζεται f '(x) (διαβάζεται "f τόνος του x") ή fx'(x) (διαβάζεται "f τόνος x του x"), σε περίπτωση ασάφειας συνεπάγεται η παράγωγος της μεταβλητής. Η σημειογραφία του Lagrange μερικές φορές αποδίδεται λανθασμένα στον Newton.
Ορισμός μέσω διηρημένων διαφορών
Η πιο συνηθισμένη προσέγγιση για τον σαφή ορισμό αυτής της διαισθητικής ιδέας, είναι να ορίσουμε την παράγωγο ως το όριο της διαφοράς πηλίκο των πραγματικών αριθμών.[2] Αυτή η προσέγγιση περιγράφεται παρακάτω.
Έστω μια πραγματική συνάρτηση f συναρτήσει ενός πραγματικού αριθμού a που ορίζεται σε ένα ανοιχτό διάστημα.Στην κλασική γεωμετρία, η εφαπτομένη γραμμή του γραφήματος της συνάρτησης f στο a είναι η μοναδική γραμμή που περνά από το σημείο (a,f(a)) και δεν συναντά το γράφημα της f εγκάρσια, που σημαίνει ότι η γραμμή δεν περνά μέσα από το γράφημα. Η παράγωγος του y σε σχέση με το x στο σημείο a, γεωμετρικά είναι η κλίση της εφαπτόμενης γραμμής στο γράφημα της f στο σημείο (a,f(a)).Η κλίση της εφαπτομένης είναι πολύ κοντά στην κλίση της γραμμής που περνάει από το (a,f(a)) και από ένα κοντινό σημείο σε αυτό (δηλαδή στο(a,f(a))) του γραφήματος, για παράδειγμα το (a+h,f(a+h)).Αυτή η γραμμή ονομάζεται τέμνουσα.Όσο η τιμή του h είναι πιο κοντά στο μηδέν δίνει καλύτερη προσέγγιση στην κλίση της εφαπτόμενης γραμμής, και οι μικρότερες τιμές (κατά απόλυτη τιμή) του h, γενικά, δίνουν καλύτερη προσέγγιση.Η κλίση m της τέμνουσας είναι η διαφορά μεταξύ των τιμών της y διαιρούμενη με τη διαφορά των τιμών του x, δηλαδή,
\( m = \frac{\Delta f(a)}{\Delta a} = \frac{f(a+h)-f(a)}{(a+h)-(a)} = \frac{f(a+h)-f(a)}{h}. \)
Αυτή η έκφραση είναι η διηρημένη διαφορά του Newton. Περνώντας από μια προσέγγιση σε μια ακριβή απάντηση επιτυγχάνεται με τη χρήση του ορίου.Γεωμετρικά το όριο της τέμνουσας είναι η εφαπτομένη.Ως εκ τούτου, το όριο της διηρημένης διαφοράς ως προς το h το οποίο τείνει στο μηδέν, αν υπάρχει, πρέπει να αντιπροσωπεύει την κλίση της εφαπτομένης στο σημείο (a,f(a)).Το όριο αυτό ορίζεται να είναι η παράγωγος της f στο a:
\( f'(a) = \lim_{h \to 0}\frac{f(a+h)-f(a)}{h} \)
Όταν το όριο υπάρχει, η f ονομάζεται παραγωγίσιμη στο a. Εδώ το f '(a) είναι ένας από τους κοινούς συμβολισμούς για την παράγωγο.
Ισοδύναμα, η παράγωγος ικανοποιεί την ιδιότητα
\( \lim_{h\to 0}{f(a+h)-f(a) - f'(a)\cdot h\over h} = 0, \)
η οποία έχει την ερμηνεία (δείτε Σχήμα 1) ότι η εφαπτομένη της f στο a δίνει την καλύτερη γραμμικήπροσέγγιση.
\( f(a+h) \approx f(a) + f'(a)h \)
της f στο a (π.χ. για μικρές τιμές του h).Η ερμηνεία αυτή είναι η πιο εύκολη για γενίκευση.
Αντικαθιστώντας με 0 το h στη διηρημένη διαφορά θα είχαμε διαίρεση με το μηδέν, έτσι η κλίση της εφαπτομένης δε μπορεί να βρεθεί άμεσα χρησιμοποιώντας αυτή τη μέθοδο.Αντί αυτού, ορίζεται η Q(h) ως η διηρημένη διαφορά συναρτήσει του h:
\( Q(h) = \frac{f(a + h) - f(a)}{h}. \)
Q(h) είναι η κλίση της τέμνουσας μεταξύ (a,f(a)) και (a+h,f(a+h)). Aν f είναι συνεχής συνάρτηση,πράγμα που σημαίνει ότι η γραφική της παράσταση δεν διακόπτεται και δεν έχει κενά, τότε και η Q είναι συνεχής συνάρτηση μακριά από το h=0. Αν το όριο \textstyle\lim_{h\to 0} Q(h) υπάρχει, που σημαίνει ότι υπάρχει τρόπος επιλογής τιμής για το Q(0) επομένως Q είναι συνεχής συνάρτηση, τότε η συνάρτηση f είναι παραγωγίσιμη στο a και η παράγωγός της ισούται με το Q(0).
Στην πράξη, η ύπαρξη μιας συνεχούς επέκτασης της διηρημένης διαφοράς Q(h) στο h=0 προκύπτει από την αλλαγή του αριθμητή ώστε να απαλειφθεί το h του παρονομαστή. Τέτοιοι χειρισμοί μπορεί να κάνουν την οριακή τιμή της Q ξεκάθαρη για μικρές τιμές του h ακόμη και αν η Q δεν ορίζεται στο h=0. Αυτή η διαδικασία μπορεί να είναι τεράστια και κουραστική για πολύπλοκες συναρτήσεις, και γίνονται πολλές συντομεύσεις για να απλοποιηθεί η διαδικασία.
Παράδειγμα
Η συνάρτηση τετραγωνισμού f(x)=x2 είναι παραγωγίσιμη στο x=3, και η παράγωγός της (στο x=3) είναι ίση με 6. Το αποτέλεσμα αυτό βγαίνει με τον υπολογισμό του ορίου, με το h να τείνει στο μηδέν της διαφοράς πηλίκο \( f(3):f'(3)= \lim_{h\to 0}\frac{f(3+h)-f(3)}{h} = \lim_{h\to 0}\frac{(3+h)^2 - 3^2}{h} = \lim_{h\to 0}\frac{9 + 6h + h^2 - 9}{h} = \lim_{h\to 0}\frac{6h + h^2}{h} = \lim_{h\to 0}{(6 + h)}. \)
Η τελευταία σχέση δείχνει ότι η διηρημένη διαφορά ισούται με 6 + h όταν το h είναι διάφορο του μηδενός και είναι απροσδιόριστο όταν h=0, λόγω του ορισμού της διηρημένης διαφοράς. Ωστόσο ο ορισμός του ορίου επισημαίνει ότι η διηρημένη διαφορά δε χρειάζεται να προσδιοριστεί όταν h=0.Το όριο είναι το αποτέλεσμα καθώς το h τείνει στο 0, που σημαίνει ότι η τιμή είναι 6 + h καθώς το h τείνει να γίνει αρκετά μικρό:
\( \lim_{h\to 0} (6 + h) = 6 + 0 = 6. \)
Η κλίση της γραφικής παράστασης της συνάρτησης τετραγωνισμού στο σημείο (3,9) είναι 6, κι έτσι η παράγωγός της στο x=3 είναι f '(3)=6.
Γενικότερα, με παρόμοιο τρόπο υπολογισμού έχουμε ότι η παράγωγος της τετραγωνικής συνάρτησης στο x=a είναι f′(a) = 2a.
Συνέχεια και παραγωγισιμότητα

Αυτή η συνάρτηση δεν είναι συνεχής στο μαρκαρισμένο σημείο αλλά ούτε και παραγωγίσιμη.
Αν y=f(x) είναι παραγωγίσιμη στο a, τότε η f πρέπει να είναι συνεχής στο a. Για παράδειγμα, επιλέγουμε ένα σημείο a και f μια δίκλαδη συνάρτηση που επιστρέφει την τιμή, ας πούμε 1, για όλα τα x μικρότερα του a, και επιστρέφει μια διαφορετική τιμή, ας πούμε 10, για όλα εκείνα τα x που είναι μικρότερα ή ίσα με το a. Η f δεν έχει παράγωγο στο a. Αν το h είναι αρνητικό, τότε το a + h είναι στο χαμηλό τμήμα του σταδίου, κι έτσι η τέμνουσα γραμμή από το a στο a + h είναι απότομη, και αν το h τείνει στο μηδέν η κλίση τείνει στο άπειρο. Αν το h είναι θετικό, τότε το a + h είναι στο υψηλό τμήμα του σταδίου, κι έτσι η τέμνουσα γραμμή από το a στο a + h έχει μηδενική κλίση.Κατά συνέπεια οι τέμνουσες ευθείες δεν απευθύνονται σε οποιαδήποτε κλίση, καθώς το όριο της διηρημένης διαφοράς δεν υπάρχει.[3]
Ωστόσο, ακόμη και αν μια συνάρτηση είναι συνεχής σε ένα σημείο, μπορεί να μην είναι παραγωγίσιμη στο σημείο αυτό. Για παράδειγμα η συνάρτηση της απολύτου τιμής συναρτήσει του x είναι συνεχής στο x=0, αλλά δεν είναι παραγωγίσιμη εκεί. Αν το h είναι θετικό, η κλίση της τέμνουσας γραμμής από το 0 στο h είναι ένα, ενώ αν το h είναι αρνητικό, τότε η κλίση της τέμνουσας γραμμής από το 0 στο h είναι μείον ένα. Αυτό γραφικά δείχνει μια απότομη στροφή στο σημείο x=0. Ακόμα μια συνάρτηση με ομαλή γραφική παράσταση δεν είναι παραγωγίσιμη σε σημείο όπου η εφαπτομένη είναι κατακόρυφη: Για παράδειγμα, η συνάρτηση y = x1/3 δεν είναι παραγωγίσιμη στο x=0.
Συνοπτικά: για μια συνάρτηση f να έχει παράγωγο είναι αναγκαίο για την συνάρτηση f να είναι συνεχής, αλλά η συνέχεια από μόνη της δεν είναι επαρκής.
Οι περισσότερες συναρτήσεις που εμφανίζονται στην πράξη έχουν παράγωγο σε όλα τα σημεία ή σχεδόν σε όλα τα σημεία. Στην ιστορία του λογισμού, πολλοί μαθηματικοί υπέθεταν ότι οι συνεχείς συναρτήσεις ήταν παραγωγίσιμες στα περισσότερα σημεία. Κάτω από συνθήκες, για παράδειγμα αν η συνάρτηση είναι μονότονη ή συνάρτηση Lipschitz, αυτό αληθεύει.Ωστόσο, το 1872 ο Weierstrass βρήκε το πρώτο παράδειγμα συνάρτησης η οποία είναι συνεχής οπουδήποτε αλλά πουθενά παραγωγίσιμη. Αυτό το παράδειγμα είναι τώρα γνωστό ως συνάρτηση Weierstrass. Το 1931, ο Stefan Banach απέδειξε ότι το σύνολο των συναρτήσεων που έχουν παράγωγο σε κάποιο σημείο είναι ένα σύνολο πρώτης κατηγορίας στον χώρο των συνεχών συναρτήσεων.[4] Αυτό σημαίνει ότι σχεδό καμία συνεχής συνάρτηση έχει παράγωγο σε κάθε σημείο.
Η συνάρτησης της απολύτου τιμής είναι συνεχής παντού, αλλά όχι παραγωγίσιμη στο x = 0, οι εφαπτόμενες δε δίνουν την ίδια τιμή αριστερά και δεξιά.
Η παράγωγος ως συνάρτηση
Έστω f μια συνάρτηση που έχει παράγωγο σε κάθε σημείο του πεδίου ορισμού της. Επειδή κάθε σημείο a έχει μια παράγωγο, υπάρχει μια συνάρτηση που αντιστοιχεί το σημείο a με την παράγωγο της f στο a. Αυτή η συνάρτηση συμβολίζεται f'(x) και ονομάζεται παράγωγος συνάρτηση ή παράγωγος της f. Η παράγωγος της f "μαζεύει" όλες τις παραγώγους της f σε κάθε σημείο του πεδίου ορισμού της f.
Μερικές φορές, η f έχει παράγωγο στα περισσότερα αλλά όχι σε όλα τα σημεία του πεδίου ορισμού της. Η παράγωγος της οποίας η τιμή στο a είναι ίση με f'(a) όταν το f'(a) ορίζεται και οπουδήποτε αλλού δεν ορίζεται, καλείται επίσης παράγωγος της f. Συνεχίζει να είναι συνάρτηση, αλλά το πεδίο ορισμού της είναι γνήσια μικρότερο από το πεδίο ορισμού της f.
Χρησιμοποιώντας αυτή την ιδέα, η παραγώγιση μετατρέπεται σε μια συνάρτηση συναρτήσεων. Η παράγωγος είναι ένας τελεστής του οποίου το πεδίο ορισμού είναι το σύνολο όλων των συναρτήσεων που έχουν παράγωγο σε κάθε σημείο του πεδίου ορισμού τους και το πεδίο τιμών του είναι ένα σύνολο συναρτήσεων. Αν συμβολίσουμε αυτόν τον τελεστή D , τότε το D(f) είναι η συνάρτηση f′(x). Από την στιγμή που το D(f) αποτελεί συνάρτηση, μπορεί να πάρει τιμή στο σημείο a. Από τον ορισμό της παραγώγου ως συνάρτηση: D(f)(a) = f′(a).
Για σύγκριση, θεωρήστε την συνάρτηση f(x) = 2x. H f είναι μια πραγματική συνάρτηση πραγματικής μεταβλητής, που σημαίνει ότι δέχεται σαν είσοδο πραγματικούς αριθμούς και βγάζει σαν έξοδο πραγματικούς αριθμούς.
\( \begin{align} 1 &{}\mapsto 2,\\ 2 &{}\mapsto 4,\\ 3 &{}\mapsto 6. \end{align} \)
Ο τελεστής D, όμως, δεν ορίζεται για συγκεκριμένους αριθμούς, αλλά μόνο για συναρτήσεις:
\( \begin{align} D(x \mapsto 1) &= (x \mapsto 0),\\ D(x \mapsto x) &= (x \mapsto 1),\\ D(x \mapsto x^2) &= (x \mapsto 2\cdot x). \end{align} \)
Επειδή η έξοδος του D είναι συνάρτηση, αυτή μπορεί να πάρει τιμή σε κάποιο σημείο. Για παράδειγμα, όταν το D εφαρμόζεται στην τετραγωνική συνάρτηση,
\( x \mapsto x^2, \)
τότε βγάζει για έξοδο την συνάρτηση
\( x \mapsto 2x , \)
την οποία ονομάζουμε f(x). Αυτή η συνάρτηση της εξόδου, μπορεί να πάρει τιμές f(1)=2 , f(2)=4 κ.ο.κ.
Παράγωγοι μεγαλύτερης τάξης
Έστω f παραγωγίσιμη συνάρτηση και f′(x) η παράγωγός της. Η παράγωγος της f′(x) (αν υπάρχει) γράφεται f′′(x) και ονομάζεται δεύτερη παράγωγος της f. Όμοια, η παράγωγος της δεύτερης παραγώγου, αν υπάρχει, γράφεται f′′′(x) και καλείται τρίτη παράγωγος της f. Συνεχίζοντας αυτή τη διαδικασία, μπορεί κανείς να ορίσει τη ν-οστή παράγωγο αν υπάρχει η (ν-1)-οστή παράγωγος.Αυτές οι επαναλαμβανόμενες παράγωγοι ονομάζονται παράγωγοι μεγαλύτερης τάξης. Η ν-οστή παράγωγος καλείται παράγωγος τάξης ν.
Αν x(t) παριστά τη θέση ενός αντικειμένου κατά το χρόνο t, τότε οι παράγωγοι μεγαλύτερης τάξης του x έχουν φυσικές ερμηνείες. Η δεύτερη παράγωγος του x είναι η παράγωγος του x'(t), η ταχύτητα, και (η δεύτερη παράγωγος) είναι η επιτάχυνση του αντικειμένου. Η τρίτη παράγωγος του x ορίζεται να είναι το τράνταγμα, και η τέταρτη παράγωγος ορίζεται να είναι το τίναγμα.
Μια συνάρτηση f δεν έχει παράγωγο,για παράδειγμα, αν δεν είναι συνεχής. Κατά τον ίδιο τρόπο, ακόμα κι αν η f έχει παράγωγο, μπορεί να μην έχει δεύτερη παράγωγο. Για παράδειγμα, έστω
\( f(x) = \begin{cases} x^2, & \mbox{if }x\ge 0 \\ -x^2, & \mbox{if }x \le 0\end{cases}. \)
Με βασικούς υπολογισμούς, διαπιστώνεται ότι η f είναι παραγωγίσιμη (ή διαφορίσιμη), της οποίας η παράγωγος είναι
\( f'(x) = \begin{cases} 2x, & \mbox{if }x\ge 0 \\ -2x, & \mbox{if }x \le 0\end{cases}. \)
Η f'(x) είναι το διπλάσιο της απόλυτης τιμής του x, και δεν έχει παράγωγο στο 0. Παρόμοια παραδείγματα δείχνουν ότι μια συνάρτηση μπορεί να έχει κ παραγώγους (όπου κ ένας μη αρνητικός ακέραιος αριθμός), αλλά όχι κ+1 τάξης παράγωγο. Μια συνάρτηση που έχει κ παραγώγους, καλείται κ φορές διαφορίσιμη. Επιπλέον, αν η κ-οστή παράγωγος της f είναι συνεχής, τότε η f είναι διαφορικής κλάσης Cκ. (Αυτή είναι μια δυνατότερη συνθήκη από τα να έχει κ παραγώγους. Για παραδείγματα, δείτε τάξη διαφορισιμότητας). Μια συνάρτηση που έχει άπειρα πολλές παραγώγους, λέγεται απείρως παραγωγίσιμη/διαφορίσιμη ή ομαλή.
Στην γραμμή των πραγματικών αριθμών, κάθε πολυωνυμική συνάρτηση είναι απείρως παραγωγίσιμη. Από τους κανόνες της παραγώγισης, προκύπτει ότι αν ένα πολυώνυμο βαθμού n παραγωγιστεί n φορές, τότε καταλήγει σε σταθερή συνάρτηση. Όλες οι υπόλοιπες υπακόλουθες παράγωγοι είναι μηδενικές, δηλαδή υπάρχουν. Έτσι, τα πολυώνυμα είναι ομαλές συναρτήσεις.
Οι παράγωγοι μιας συνάρτησης f σ'ένα σημείο x παρέχουν πολυωνυμικές προσεγγίσεις της συνάρτησης αυτής κοντά στο x. Για παράδειγμα, αν η f είναι δύο φορές παραγωγίσιμη, τότε
\( f(x+h) \approx f(x) + f'(x)h + \tfrac12 f''(x) h^2 \)
με το σκεπτικό ότι
\( \lim_{h\to 0}\frac{f(x+h) - f(x) - f'(x)h - \frac12 f''(x) h^2}{h^2}=0. \)
Αν η f είναι απείρως παραγωγίσιμη, τότε αυτή είναι η αρχή της σειράς Taylor για την f.
Σημείο καμπής
Κύριο άρθρο: σημείο καμπής
Ένα σημείο στο οποίο η δεύτερη παράγωγος έχει διαφορετικό πρόσημο ονομάζεται σημείο καμπής.[5] Σε ένα σημείο καμπής, η δεύτερη παράγωγος μπορεί να είναι μηδενική, όπως στην περίπτωση του σημείου καμπής x=0 της συνάρτησης y=x3, ή μπορεί να αποτύχει να υπάρχει, όπως στην περίπτωση του σημείου καμπής x=0 της συνάρτησης y=x1/3 . Σε ένα σημείο καμπής, η συνάρτηση αλλάζει κυρτότητα από κοίλη σε κυρτή ή αντίστροφα.
Σημειογραφία και συμβολισμός του διαφορικού λογισμού
Κύριο άρθρο : Σημειογραφία και συμβολισμός του διαφορικού λογισμού
Σημειογραφία του Leibniz
Κύριο άρθρο : Σημειογραφία του Leibniz
Η σημειογραφία για τις παραγώγους που παρουσιάστηκε από τον Gottfried Leibniz είναι μία από τις πρώτες. Χρησιμοποιείται ακόμα ευρέως όταν η εξίσωση y=f(x) εκλαμβάνεται ως μια συναρτησιακή σχέση μεταξύ εξαρτημένων και ανεξάρτητων μεταβλητών. Τότε, η πρώτη παράγωγος συμβολίζεται με
\( \frac{dy}{dx},\quad\frac{d f}{dx}(x),\;\;\mathrm{or}\;\; \frac{d}{dx}f(x). \)
Παράγωγοι μεγαλύτερης τάξης εκφράζονται:
\( \frac{d^ny}{dx^n}, \quad\frac{d^nf}{dx^n}(x), \;\;\mathrm{or}\;\; \frac{d^n}{dx^n}f(x) \)
για την n-οστή παράγωγο της y=f(x).
Με την σημειογραφία του Leibniz μπορούμε να εκφράσουμε την παράγωγο της f στο x=α με δύο διαφορετικούς τρόπους:
\( \frac{dy}{dx}\left.{\!\!\frac{}{}}\right|_{x=a} = \frac{dy}{dx}(a). \)
Στον συμβολισμό του Leibniz γίνεται σαφές ως προς πια μεταβλητή γίνεται η παραγώγιση (στον παρονομαστή). Αυτό σχετίζεται ιδιαίτερα με την μερική διαφόριση. Επίσης, με αυτήν την σημειογραφία γίνεται ευκολομνημόνευτος ο κανόνας της αλυσίδας:[6]
\( \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}. \)
Σημειογραφία του Lagrange
Ένας από τους πιο κοινούς σύγχρονους συμβολισμούς για την διαφόριση,και μερικές φορές καλείται ως τονική διαφόριση[7], οφείλεται στον Ζοζέφ Λουί Λαγκράνζ και χρησιμοποιεί τον τόνο έτσι, ώστε η παράγωγος μια συνάρτησης f(x) συμβολίζεται με f'(x) ή απλούστερα f'. Όμοια, η δεύτερη και η τρίτη παράγωγος συμβολίζονται
\( (f')'=f''\, και (f'')'=f'''\,. \)
Εκτός από τον τόνο, μερικοί χρησιμοποιούν τους ρωμαϊκούς αριθμούς, όπως
\( f^{\mathrm{iv}}\, \)
καθώς άλλοι τοποθετούν τον αριθμό της τάξης της παραγώγου σε παρένθεση,όπως για παράδειγμα για την τέταρτη παράγωγο
\( f^{(4)}\, \)
Ο τελευταίος συμβολισμός γενικεύεται δίνοντας το σύμβολο f(n) για την n-οστή παράγωγο της f. Αυτή η σημειογραφία είναι πιο χρήσιμη όταν αναφερόμαστε στην παράγωγο όντας μια συνάρτηση από μόνη της, κάτι για το οποίο η σημειογραφία του Leibniz γίνεται περίπλοκη.
Σημειογραφία του Νεύτωνα
Κατά τον συμβολισμό του Νεύτωνα για την παραγώγιση, τοποθετείται μια τελίτσα πάνω από την συνάρτηση που παριστάνει την παράγωγο. Αν y=f(t), τότε τα
\( \dot{y} and \ddot{y} \)
παριστάνουν, αντίστοιχα, την πρώτη και την δεύτερη παράγωγο της y σε σχέση με την μεταβλητή t. Αυτός ο συμβολισμός χρησιμοποιείται σχεδόν αποκλειστικά για χρονικές παραγώγους, με την έννοια ότι η ανεξάρτητη μεταβλητή της συνάρτησης εκφράζει τον χρόνο. Είναι κάτι κοινό στην Φυσική και σε τομείς των Μαθηματικών που συνδέονται με την Φυσική, όπως οι διαφορικές εξισώσεις. Καθώς ο συμβολισμός αυτός γίνεται πολύ δύσχρηστος για μεγάλες τάξεις παραγώγων, πρακτικά χρειάζονται αρκετά μικρές παράγωγοι.
Διαφορικό και Παράγωγος στο χρόνο
Ο Newton προσπάθησε να εξηγήσει το λογισμό με βάση την έννοια του διαφορικού και της παραγώγου ως προς τον χρόνο,που ακολουθούσαν τις δικές του μαθηματικές εφευρέσεις.Είπε ότι ο ρυθμός παραγωγής είναι η παράγωγος ως προς τον χρόνο ενός στοιχείου,η οποία συμβολίζεται από μια μεταβλητή με μια τελεία από πάνω.Όμοια ο ρυθμός της δεύτερης παραγώγου ως προς τον χρόνο συμβολίζεται με δύο τελείες από πάνω. Αυτοί οι παράγωγοι τείνουν πολύ κοντά στο μηδέν αλλα δεν είναι μηδέν. Αλλά όταν πολλαπλασσιάζουμε δύο παραγώγους της ίδιας τάξης,το αποτέλεσμα αυτό είναι πολύ κοντά στο μηδέν και το θεωρούμε ως μηδέν.Έτσι ο Newton πήρε τις παραγώγους και αντικατέστησε τις μεταβλητές του x με x+\dot{x} και όλες τις μεταβλητές του y με \( y+\dot{y} \) και μετά χρησιμοποίησε τους κανόνες της παραγώγισης για να πάρει την παράγωγο και να βρει ένα αποτέλεσμα για το \( \frac{\dot{y}}{\dot{x}}\,. \) [8]. Για παράδειγμα ,
\( \begin{align} x^2+y^2=1\\ (x+\dot{x})^2+(y+\dot{y})^2=1\\ x^2+2x\dot{x}+\dot{x}^2+y^2+2y\dot{y}+\dot{y}^2=1\\ x^2+2x\dot{x}+y^2+2y\dot{y}=1 \end{align} \)
χρησιμοποιώντας το γεγονός ότι \( x^2+y^2=1 \) μπορούμε να δούμε \( 2x\dot{x}+2y\dot{y}=0 \) και \( \frac{\dot{y}}{\dot{x}}=-\frac{2x}{2y} \) έτσι \( \frac{\dot{y}}{\dot{x}}=-\frac{x}{y}. \)
Ο Νεύτων περιέγραψε μαθηματικές ποσότητες σαν να είναι σε συνεχή κίνηση. Αυτή η κίνηση,είπε,μπορεί να θεωρηθεί ισάξια ενός σημείου που διατρέχει μια καμπύλη. Προσδιόρισε αυτή την ποσότητα και την ονόμασε ''διαφορικό''. Αυτή η ιδέα για το όνομα του γεννήθηκε από τον ρυθμό με τον οποίο αυτές οι ποσότητες αλλάζουν. Ο Newton το ονόμασε στη τελική '' Διαφορικά και παράγωγοι ως προς τον χρόνο'' και το παρουσίασε. Έτσι, αν ένα διαφορικό παριστάνεται από το x, το ονομάζει παράγωγο του χ και όμοια την δεύτερη παράγωγο και συνεχίζει και τους υπόλοιπους συμβολισμούς. Αυτό μπορεί να συσχετιστεί με τον νεότερο συμβολισμό της παραγώγου. Στην σημερινή εποχή, η παράγωγος της μεταβλητής x έχει σχέση με μια ανεξάρτητη μεταβλητή του χρόνου,την t η οποία συμβολίζει το διάνυσμα της ταχύτητας και συμβολίζεται με dx/dt. Με άλλα λόγια η παράγωγος της f(x) ως προς τον χρόνο t είναι dx/dt.
Η στιγμή του διαφορικού
Ο Νεύτων καλεί o τη στιγμή ενός διαφορικού. Η στιγμή ενός διαφορικού παριστάνει το απείρως μικρό κομμάτι στο οποίο ένα στοιχείο αυξάνεται σε ένα μικρό χρονικό διάστημα. Κάποτε επέτρεψε στον εαυτό του να κάνει μια διάρεση μέσω του o ( παρόλα αυτά το o δεν μπορεί να θεωρηθεί ως μηδέν διότι αυτό θα καθιστούσε την διαίρεση αδύνατη). Ο Newton αποφάσισε ότι είναι δικαιολογημένο να απαλείψει όλους τους όρους που περιέχουν το o.
Σημειογραφία του Euler
Στην σημειογραφία του Όιλερ χρησιμοποιείται ένας διαφορικός τελεστής D, ο οποίος εφαρμόζεται σε μια συνάρτηση f δίνοντας την πρώτη παράγωγο Df. Η δεύτερη παράγωγος συμβολίζεται με D2f και η n-οστή παράγωγος με Dnf.
Αν y=f(x) είναι μια εξαρτημένη μεταβλητή, τότε ο δείκτης x γράφεται μαζί με το D διευκρινίζοντας την ανεξάρτητη μεταβλητή x. Έτσι, ο συμβολισμός του Euler είναι
\( D_x y\, ή D_x f(x)\,, \)
αν και αυτός ο δείκτης συχνά παραλείπεται όταν εννοείται, για παράδειγμα όταν αυτή είναι η μόνη μεταβλητή που υπάρχει σε μια έκφραση.
Η σημειογραφία του Όιλερ είναι χρήσιμη στην δήλωση και επίλυση γραμμικών διαφορικών εξισώσεων.
Υπολογίζοντας την παράγωγο
Η παράγωγος μιας συνάρτησης μπορεί, κατά κανόνα, να υπολογιστεί μέσω του ορισμού θεωρώντας τις διηρημένες διαφορές και υπολογίζοντας τα όριά τους. Πρακτικά, από την στιγμή που οι παράγωγοι απλών συναρτήσεων είναι γνωστές, οι παράγωγοι άλλων συναρτήσεων είναι πιο εύκολα υπολογίσιμοι χρησιμοποιώντας κανόνες για την εύρεση της παραγώγου σύνθετων συναρτήσεων μέσω απλούστερων.
Παράγωγοι στοιχειωδών συναρτήσεων
Κύριο άρθρο : Πίνακας των παραγώγων
Τις περισσότερες φορές, ο υπολογισμός μιας παραγώγου απαιτεί την παραγώγιση μερικών κοινών συναρτήσεων. Η παρακάτω μη ολοκληρωμένη λίστα δίνει κάποιες από τις συχνότερα χρησιμοποιούμενες συναρτήσεις και τις παραγώγους τους.
Παράγωγοι δυνάμεων: Αν
\( f(x) = x^a\,, \)
όπου α σταθερός πραγματικός αριθμός, τότε
\( f'(x) = a x^{a-1}\, \)
σε κάθε σημείο όπου ορίζεται η συνάρτηση. Για παράδειγμα, αν α=1/2, τότε
\( f'(x) = \frac{1}{2} x^{-\frac{1}{2}}, \)
και η συνάρτηση ορίζεται μόνο για μη αρνητικά x. Όταν x=0, αυτός ο κανόνας περικλείει τον κανόνα παραγώγισης σταθερής συνάρτησης.
Εκθετικές και λογαριθμικές συναρτήσεις:
\( \frac{d}{dx}e^x = e^x \)
\( \frac{d}{dx}a^x = \ln(a)a^x \)
\( \frac{d}{dx}\ln(x) = 1/x,\qquad x > 0 \)
\( \frac{d}{dx}\log_a(x) = \frac{1}{x\ln(a)} \)
Τριγωνομετρικές συναρτήσεις:
\( \frac{d}{dx}\sin(x) = \cos(x). \)
\( \frac{d}{dx}\cos(x)= -\sin(x). \)
\( \frac{d}{dx}\tan(x)= \sec^2(x). \)
Αντίστροφες τριγωνομετρικές συναρτήσεις:
\( \frac{d}{dx}\arcsin(x) = \frac{1}{\sqrt{1-x^2}}. \)
\( \frac{d}{dx}\arccos(x)= -\frac{1}{\sqrt{1-x^2}}. \)
\( \frac{d}{dx}\arctan(x)= \frac{1}{{1+x^2}}. \)
Κανόνες παραγώγισης
Κύριο άρθρο : Κανόνες Παραγώγισης
Σε πολλές περιπτώσεις, περίπλοκοι υπολογισμοί ορίων με την άμεση εφαρμογή των διηρημένων διαφορών του Νεύτωνα μπορούν να αποφευχθούν με τους κανόνες παραγώγισης. Κάποιοι από τους βασικότερους είναι οι ακόλουθοι.
Κανόνας σταθερής συνάρτησης: αν η f(x) = α είναι σταθερή συνάρτηση και α είναι ένας πραγματικός αριθμός, τότε
\( f'(x) = (a)' = 0 \,. \)
Κανόνας αθροίσματος:
\( (a f(x) + \beta g(x))' = a f'(x) + \beta g'(x) \,, \) για κάθε συνάρτηση f και g και για κάθε πραγματικό αριθμό α και β.
Το ίδιο ισχύει και για περισσότερες από δύο συναρτήσεις.
Κανόνας γινομένου:
\( (f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x) \,, \) για κάθε συνάρτηση f και g.
Το ίδιο ισχύει και για περισσότερες από δύο συναρτήσεις.
Κανόνας πηλίκου:
\( \frac{f(x)}{g(x)}=\frac{f'(x) g(x) - f(x) g'(x)}{g^2(x)} \) , για κάθε συνάρτηση f και g, όπου g(x) \neq 0.
Κανόνας αλυσίδας: εάν f(x) = h(g(x))
\( f'(x) = h'(g(x)) \cdot g'(x) \,. \)
Παράδειγμα υπολογισμού
Η παράγωγος της
\( f(x) = x^4 + \sin (x^2) - \ln(x) e^x + 7\, \)
είναι
\( \begin{align} f'(x) &= 4 x^{(4-1)}+ \frac{d\left(x^2\right)}{dx}\cos (x^2) - \frac{d\left(\ln {x}\right)}{dx} e^x - \ln{x} \frac{d\left(e^x\right)}{dx} + 0 \\ &= 4x^3 + 2x\cos (x^2) - \frac{1}{x} e^x - \ln(x) e^x. \end{align} \)
Εδώ, ο δεύτερος όρος υπολογίστηκε με τον κανόνα της αλυσίδας και ο τρίτος με τον κανόνα του γινομένου. Χρησιμοποιήθηκαν επίσης οι γνωστές παράγωγοι των στοιχειωδών συναρτήσεων x2, x4, sin(x), ln(x) and exp(x) = ex
Παράγωγος σε περισσότερες διαστάσεις
Δείτε επίσης:Διανυσματική συνάρτησηκαι Συναρτήσεις με πολλές μεταβλητές
Παράγωγος διανυσματικής συνάρτησης
Η διανυσματική συνάρτηση y(t) μιας πραγματικής μεταβλητής στέλνει πραγματικούς αριθμούς σε διανύσματα στον διανυσματικό χώρο \( \R^n \) . Μια διανυσματική συνάρτηση y(t)=(y1(t), y2(t), y3(t),...,yn(t)) μπορεί να διασπαστεί στις συνιστώσες συναρτήσεις της y1(t),...,yn(t). Αυτό περιλαμβάνει, για παράδειγμα, παραμετρικές καμπύλες στο \( \R^2\) ή \( \R^3\). Οι συνιστώσες συναρτήσεις είναι πραγματικές συναρτήσεις και έτσι ο παραπάνω ορισμός της παραγώγισης μπορεί να εφαρμοστεί σ'αυτές. Η παράγωγος της y(t) ορίζεται να είναι ένα διάνυσμα,το οποίο λέγεται εφαπτομενικό διάνυσμα, του οποίου οι συντεταγμένες είναι οι παράγωγοι των συνιστωσών συναρτήσεων. Δηλαδή,
\( \mathbf{y}'(t) = (y'_1(t), \ldots, y'_n(t)). \)
Ισοδύναμα,
\( \mathbf{y}'(t)=\lim_{h\to 0}\frac{\mathbf{y}(t+h) - \mathbf{y}(t)}{h},
αν το όριο υπάρχει. Η διαφορά στον αριθμητή είναι διαφορά διανυσμάτων, όχι βαθμωτών. Αν η παράγωγος της y υπάρχει για κάθε τιμή του t, τότε η y′ είναι μια άλλη διανυσματική συνάρτηση.
Αν {e1, e2, e3,...,en} αποτελεί μια βάση του \( \R^n ), τότε η y(t) μπορεί επίσης να γραφτεί y1(t)e1, y2(t)e2, y3(t)e3,...,yn(t)en. Αν θεωρήσουμε ότι η παράγωγος μια διανυσματικής συνάρτησης διατηρεί την γραμμικότητα, τότε η παράγωγος της y(t) είναι
\( y'_1(t)\mathbf{e}_1 + \cdots + y'_n(t)\mathbf{e}_n \)
γιατί κάθε ένα από τα διανύσματα της βάσης είναι σταθερές.
Αυτή η γενίκευση είναι χρήσιμη αν, για παράδειγμα, η y(t) είναι το διάνυσμα θέσης ενός αντικειμένου στην στιγμή t. Τότε η παράγωγος y′(t) εκφράζει την ταχύτητα του αντικειμένου την στιγμή t.
Μερικές παράγωγοι
Κύριο άρθρο: Μερική παράγωγος
Υποθέστε ότι η f είναι μια συνάρτηση που εξαρτάται από παραπάνω από μία μεταβλητές. Για παράδειγμα,
\( f(x, y) = x^2 + x y+ y^2 \,. \)
Η f μπορεί να αναθεωρηθεί ως μια οικογένεια συναρτήσεων μιας μεταβλητής με δείκτες τις άλλες μεταβλητές:
\( f(x,y) = f_x(y) = x^2 + x y+ y^2 \,. \)
Με άλλα λόγια, κάθε τιμή του x «επιλέγει» μια συνάρτηση, που συμβολίζεται fx και είναι συνάρτηση μίας πραγματικής μεταβλητής[9]. Έτσι,
\( x \mapsto f_x,\, \)
\( f_x(y) = x^2 + xy + y^2.\, \)
Από την στιγμή που έχει επιλεγεί μια τιμή για το x, έστω α, τότε η f(x,y) καθορίζει την fα που «στέλνει» το y στο α2+αy+y2.
\( f_a(y) = a^2 + a y+ y^2 \,. \)
Σ'αυτήν την παράσταση, το α είναι σταθερά, και όχι μεταβλητή, έτσι η fα είναι συνάρτηση μόνο μίας πραγματικής μεταβλητής. Συνεπώς, ο ορισμός της παραγώγου μιας συνάρτησης μιας μεταβλητής μπορεί να εφαρμοστεί:
\( f_a'(y) = a + 2y.\, \)
Η παραπάνω διαδικασία μπορεί να γίνει για οποιαδήποτε τιμή του α. Μαζεύοντας τις παραγώγους σε μία συνάρτηση το αποτέλεσμα θα ήταν μια συνάρτηση που εκφράζει την αλλαγή της f στην κατεύθυνση του y:
\( \frac{\part f}{\part y}(x,y) = x + 2y. \)
Αυτή είναι η μερική παράγωγος της f σε σχέση με το y. Εδώ, το ∂ είναι το σύμβολο της μερικής παραγώγου.Για να το ξεχωρίσουμε από το γράμμα d,το ∂ μερικές φορές προφέρεται "der","del" ή "μερική" αντί του "dee".
Γενικά, η μερική παράγωγος μιας συνάρτησης f(x1, x2,...,xn) στην κατεύθυνση του xi στο σημείο (α1, α2,...,αn) ορίζεται ως:
\( \frac{\part f}{\part x_i}(a_1,\ldots,a_n) = \lim_{h \to 0}\frac{f(a_1,\ldots,a_i+h,\ldots,a_n) - f(a_1,\ldots,a_n)}{h}. \)
Στην παραπάνω διηρημένη διαφορά, όλες οι μεταβλητές εκτός της xi διατηρούνται σταθερές. Αυτή η επιλογή σταθερών τιμών προσδιορίζει μια συνάρτηση μίας μεταβλητής
\( f_{a_1,\ldots,a_{i-1},a_{i+1},\ldots,a_n}(x_i) = f(a_1,\ldots,a_{i-1},x_i,a_{i+1},\ldots,a_n) \)
και εξ'ορισμού
\( \frac{df_{a_1,\ldots,a_{i-1},a_{i+1},\ldots,a_n}}{dx_i}(a_1,\ldots,a_n) = \frac{\part f}{\part x_i}(a_1,\ldots,a_n). \)
Με άλλα λόγια, οι διαφορετικές επιλογές της τιμής του α, δίνουν μια οικογένεια συναρτήσεων μίας μεταβλητής, ακριβώς όπως στο παραπάνω παράδειγμα. Αυτή η έκφραση δείχνει επίσης ότι ο υπολογισμός της μερικής παραγώγου περιορίζεται στον υπολογισμό της παραγώγου μιας συνάρτησης μίας μεταβλητής.
Ένα σημαντικό παράδειγμα συνάρτησης πολλών μεταβλητών είναι η περίπτωση της βαθμωτής συνάρτησης f(x1,...xn) σε ένα πεδίο ορισμού στον Ευκλείδιο χώρο \( \R^n \) (π.χ. \( \R^2 \) ή \( \R^3 \)). Σ'αυτήν την περίπτωση, η f έχει μια μερική παράγωγο ∂f/∂xj σε σχέση με κάθε μεταβλητή xj. Στο σημείο α, αυτές οι μερικές παράγωγοι ορίζουν το διάνυσμα:
\( \nabla f(a) = \left(\frac{\partial f}{\partial x_1}(a), \ldots, \frac{\partial f}{\partial x_n}(a)\right). \)
Αυτό το διάνυσμα ονομάζεται ανάδελτα της f στο α. Αν η f είναι διαφορίσιμη σε κάθε σημείο στο πεδίο ορισμού της, τότε το ανάδελτα είναι μια διανυσματική συνάρτηση ∇f που αντιστοιχεί το σημείο α στο διάνυσμα ∇f(α). Κατά συνέπεια, το ανάδελτα προσδιορίζει ένα διανυσματικό πεδίο.
Διανυσματική παράγωγος
Κύριο άρθρο:Διανυσματική παράγωγος
Αν η f είναι μια πραγματική συνάρτηση στο \( \R^n \), τότε η μερική παράγωγος της f εκφράζει ένα μέτρο αλλαγής της στον άξονα της συνισταμένης. Για παράδειγμα, αν η f είναι μια συνάρτηση του x και του y, τότε οι μερικές της παράγωγοι μετράνε την αλλαγή της f στην κατεύθυνση x και στην κατεύθυνση y. Ωστόσο, δεν μετράνε άμεσα την αλλαγή της f σε κάποια άλλη κατεύθυνση, όπως πάνω στην διχοτόμο y=x. Αυτές μετρούνται με την βοήθεια των διανυσματικών παραγώγων. Επιλέξτε ένα διάνυσμα
\( \mathbf{v} = (v_1,\ldots,v_n). \)
Η διανυσματική παράγωγος της f στην κατεύθυνση του v στο σημείο x είναι το όριο
\( D_{\mathbf{v}}{f}(\boldsymbol{x}) = \lim_{h \rightarrow 0}{\frac{f(\boldsymbol{x} + h\mathbf{v}) - f(\boldsymbol{x})}{h}}. \)
Σε μερικές περιπτώσεις ίσως είναι πιο εύκολο να υπολογίσουμε ή να εκτιμήσουμε την διανυσματική παράγωγο αν αλλάξουμε το μέγεθος του διανύσματος. Συχνά αυτό πραγματοποιείται για να μετατραπεί το πρόβλημα στον υπολογισμό μιας διανυσματικής παραγώγου στην κατεύθυνση ενός μοναδιαίου διανύσματος. Για να δούμε πώς δουλεύει αυτό, υποθέτουμε ότι v = λu. Αντικαθιστούμε το h = k/λ στη διαφορά πηλίκο . Το πηλίκο διαφορών γίνεται:
\( \frac{f(\mathbf{x} + (k/\lambda)(\lambda\mathbf{u})) - f(\mathbf{x})}{k/\lambda} = \lambda\cdot\frac{f(\mathbf{x} + k\mathbf{u}) - f(\mathbf{x})}{k}. \)
Έστω λ πραγματικός αριθμός. Η αντικατάσταση του h με h/λ αλλάζει την διηρημένη διαφορά της κατεύθυνσης λv σε λ φορές την διηρημένη διαφορά της κατεύθυνσης v. Συνεπώς, η διανυσματική παράγωγος στην κατεύθυνση λv είναι ίση με λ φορές την διανυσματική παράγωγο στην κατεύθυνση v. Λόγω αυτού, οι διανυσματικές παράγωγοι συνήθως λαμβάνονται μόνο για μοναδιαία διανύσματα v.
Αν όλες οι μερικές παράγωγοι της f υπάρχουν και είναι συνεχείς στο x, τότε προσδιορίζουν την διανυσματική παράγωγο της f στην κατεύθυνση v με τον τύπο:
\( D_{\mathbf{v}}{f}(\boldsymbol{x}) = \sum_{j=1}^n v_j \frac{\partial f}{\partial x_j}. \)
Αυτή είναι μια συνέπεια του ορισμού της ολικής παραγώγου. Ακολούθως, η διανυσματική παράγωγος είναι γραμμική στο v.
Ο ίδιος ορισμός χρησιμοποιείται επίσης όταν η f είναι μια συνάρτηση που λαμβάνει τιμές στο \( \R^m \) . Απλά, εφαρμόζουμε τον παραπάνω ορισμό σε κάθε στοιχείο του διανύσματος. Σ'αυτήν την περίπτωση, η διανυσματική παράγωγος είναι ένα διάνυσμα στο \(\R^m. \)
Ολική παράγωγος, ολικό ή τέλειο διαφορικό και Ιακωβιανός πίνακας
Κύριο άρθρο:Ολική παράγωγος.
Όταν η f είναι μία συνάρτηση ενός ανοικτού υποσυνόλου από το Rn στο Rm, τότε η διανυσματική παράγωγος της f στη διεύθυνση που έχουμε επιλέξει είναι η καλύτερη γραμμική προσέγγιση της f στο σημείο αυτό και στη διεύθυνση αυτή. Αλλά όταν n > 1, η διανυσματική παράγωγος μπορεί να δώσει μια ολοκληρωμένη εικόνα για την συμπεριφορά της f. Η ολική παράγωγος, ονομάζεται και (ολικό) διαφορικό, και δίνει μια ολοκληρωμένη εικόνα παρατηρώντας όλες τις κατευθύνσεις ταυτόχρονα. Αυτός είναι, για κάθε διάνυσμα v με αρχή το a, ο τύπος που αναμένεται για τη γραμμική προσέγγιση:
\( f(\mathbf{a} + \mathbf{v}) \approx f(\mathbf{a}) + f'(\mathbf{a})\mathbf{v}. \)
Ακριβώς όπως η παράγωγος μιας μεταβλητής, η f ′(a) έχει επιλεχθεί έτσι ώστε το λάθος σε αυτήν την προσέγγιση να είναι όσο πιο μικρό γίνεται.
Αν n και m είναι και τα δυο ένα, τότε η παράγωγος f ′(a) είναι ένας αριθμός και η έκφραση f ′(a)v είναι το γινόμενο δυο αριθμών. Αλλά σε μεγαλύτερες διαστάσεις, είναι αδύνατον το f ′(a) να είναι αριθμός. Αν ήταν αριθμός, τότε το f ′(a)v θα μπορούσε να ήταν ένα διάνυσμα του Rn ενώ οι άλλοι όροι θα μπορούσαν να ήταν διανύσματα του Rm, και συνεπώς ο τύπος δε θα είχε νόημα. Για να έχει νόημα ο τύπος της γραμμικής προσέγγισης, το f ′(a) πρέπει να είναι μια συνάρτηση που στέλνει διανύσματα του Rn σε διανύσματα του Rm, και το f ′(a)v πρέπει να δηλώνει αυτή τη συνάρτηση εκτιμώντας το v.
Για να προσδιορίσετε τι είδους συνάρτηση είναι, παρατηρείστε ότι ο τύπος της γραμμικής προσέγγισης μπορεί να ξαναγραφτεί ως εξής
\( f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a}) \approx f'(\mathbf{a})\mathbf{v}. \)
Σημειώστε ότι αν επιλέξουμε άλλο διάνυσμα w, τότε αυτή η προσεγγιστική εξίσωση προσδιορίζει άλλη προσεγγιστική εξίσωση αντικαθιστώντας το v με w. Προσδιορίζει μια τρίτη προσεγγιστική εξίσωση αντικαθιστώντας και στα δυο v με w και το a με a + v. Αφαιρώντας αυτές τις δυο νέες εξισώσεις, παίρνουμε
\( f(\mathbf{a} + \mathbf{v} + \mathbf{w}) - f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a} + \mathbf{w}) + f(\mathbf{a}) \approx f'(\mathbf{a} + \mathbf{v})\mathbf{w} - f'(\mathbf{a})\mathbf{w} \) .
Αν υποθέσουμε ότι το v είναι μικρό και ότι η παράγωγος τείνει συνεχώς στο a, τότε το f ′(a + v) είναι κατά προσέγγιση ίσο με το f ′(a), και συνεπώς το δεξιό μέλος είναι κατά προσέγγιση μηδέν. Το αριστερό μέλος μπορεί να ξανά γραφτεί με ένα διαφορετικό τρόπο χρησιμοποιώντας τον τύπο της γραμμικής προσέγγισης και αντικαθιστώντας το v με v + w. Ο τύπος της γραμμικής προσέγγισης συνεπάγεται:
\( \begin{align} 0 &\approx f(\mathbf{a} + \mathbf{v} + \mathbf{w}) - f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a} + \mathbf{w}) + f(\mathbf{a}) \\ &= (f(\mathbf{a} + \mathbf{v} + \mathbf{w}) - f(\mathbf{a})) - (f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a})) - (f(\mathbf{a} + \mathbf{w}) - f(\mathbf{a})) \\ &\approx f'(\mathbf{a})(\mathbf{v} + \mathbf{w}) - f'(\mathbf{a})\mathbf{v} - f'(\mathbf{a})\mathbf{w}. \end{align} \)
Αυτό υποδηλώνει ότι το f ′(a) είναι ένας γραμμικός μετασχηματισμός από το διανυσματικό χώρο Rn στον διανυσματικό χώρο Rm . Στην πραγματικότητα, είναι πιθανό να κάνετε αυτήν την ακριβή παραγώγιση μετρώντας το λάθος στις προσεγγίσεις. Υποθέστε ότι το λάθος στον τύπο αυτών των γραμμικών προσεγγίσεων φράσεται από ένα σταθερό χρόνο ||v||, όπου η σταθερότητα είναι ανεξάρτητη από το v αλλά εξαρτάται συνεχώς από το a. Τότε, αφού προσθέσουμε έναν κατάλληλο όρο για το λάθος, όλες οι άνω προσεγγιστικές ισότητες μπορούν να αναδιατυπωθούν ως ανισότητες. Συγκεκριμένα,το f ′(a) είναι ένας γραμμικός μετασχηματισμός πάνω σε ένα μικρό λανθασμένο όρο. Στο όριο όπου τα v και w τείνουν στο μηδέν, πρέπει συνεπώς να είναι ένας γραμμικός μετασχηματισμός. Από τότε που ορίσαμε την ολική παράγωγο παίρνοντας ένα όριο όπως το v να πηγαίνει στο μηδέν, το f ′(a) πρέπει να είναι ένας γραμμικός μετασχηματισμός.
Σε μια μεταβλητή,το γεγονός ότι η παράγωγος είναι η καλύτερη γραμμική προσέγγιση γίνεται αντιληπτό από το γεγονός ότι είναι το όριο στα πηλίκα διαφορών. Παρόλα αυτά, τα συνηθισμένα πηλίκα διαφορών δεν ορίζονται σε μεγαλύτερες διαστάσεις διότι συνήθως δεν είναι εύκολο να διαιρέσουμε διανύσματα. Συγκεκριμένα, ο αριθμητής και ο παρανομαστής των πηλίκων διαφορών δεν ανήκουν στον ίδιο διανυσματικό χώρο: Ο αριθμητής βρίσκεται στον χώρο Rm ενώ ο παρανομαστής βρίσκεται στον Rn. Επιπλέον, η παράγωγος είναι ένας γραμμικός μετασχηματισμός, που σημαίνει οτι υπάρχει διαφορετικός τύπος για την μεταβλητή που βρίσκεται τόσο στον αριθμητή όσο και στον παρανομαστή.Για να καταστήσουμε ακριβής την έννοια ότι η f ′(a) είναι η καλύτερη γραμμική προσέγγιση, είναι απαραίτητο να υιοθετήσουμε μια διαφορετική μεθοδολογία για την πρώτης τάξεως παράγωγο για να δούμε σε ποία από αυτά τα προβλήματα απαλείφεται. Άν f : R → R, τότε ο συνηθισμένος προσδιορισμός της παραγώγου χρησιμοποιείται για να προκύψει ότι ηγ παράγωγος της f στο a είναι ο μοναδικός αριθμός f ′(a) τέτοιος ώστε
\( \lim_{h \to 0} \frac{f(a + h) - f(a) - f'(a)h}{h} = 0. \)
Αυτό ισοδυναμεί με
\( \lim_{h \to 0} \frac{|f(a + h) - f(a) - f'(a)h|}{|h|} = 0 \)
επειδή το όριο της συνάρτησης τείνει στο μηδέν αν και μόνο αν το όριο της απόλυτης συνάρτησης τείνει στο μηδέν. Ο τελευταίος τύπος μπορεί να χρησιμοποιηθεί για περισσότερες απο μια μεταβλητές αντικαθιστώντας τις απόλυτες τιμές με τις νόρμες.
Ο προσδιορισμός της ολικής παραγώγου της f στο a προσδιορίζεται κατά μοναδικό τρόπο απο τον γραμμικό μετασχηματισμό f ′(a) : Rn → Rm τέτοιος ώστε
\( \lim_{\mathbf{h}\to 0} \frac{\lVert f(\mathbf{a} + \mathbf{h}) - f(\mathbf{a}) - f'(\mathbf{a})\mathbf{h}\rVert}{\lVert\mathbf{h}\rVert} = 0. \)
Εδώ το h είναι ένα διάνυσμα στον Rn, έτσι η νόρμα στον παρανομαστή ορίζεται στον Rn. Παρόλα αυτά f′(a)h είναι ένα διάνυσμα στον Rm και η νόρμα στον αριθμητή ορίζεται στον Rm . Άν v είναι ένα διάνυσμα που έχει ως αρχή του το a τότε το f ′(a)v καλείται διαφορικό του v απο το f και μερικές φορές συμβολίζεται ως f∗v.
Αν η ολική παράγωγος υπάρχει στο a, τότε όλες οι μερικές παράγωγοι και οι κατευθυνόμενες παράγωγοι της f υπάρχουν στο a, και για όλα τα v, το f ′(a)v είναι η κατευθυνόμενη παράγωγος της f στην κατεύθυνση του v. Αν γράψουμε την f χρησιμοποιώντας συντεταγμένες συναρτήσεις, έτσι ώστε f = (f1, f2, ..., fm), τότε η ολική παράγωγος μπορεί να εκφραστεί χρησιμοποιώντας μερικές παραγώγους σε έναν πίνακα. Αυτός ο πίνακας ονομάζεται Ιακωβιανός πίνακας της f στο a:
\( f'(\mathbf{a}) = \operatorname{Jac}_{\mathbf{a}} = \left(\frac{\partial f_i}{\partial x_j}\right)_{ij}. \)
Η ύπαρξη της ολικής παραγώγου f′(a) είναι αυστηρά πιο ισχυρή από την ύπαρξη όλων των μερικών παραγώγων, αλλά αν οι μερικές παράγωγοι υπάρχουν και είναι συνεχείς, τότε η ολική παράγωγος υπάρχει, δίνεται από την Ιακωβιανή, και εξαρτάται διαρκώς από το a.
Ο ορισμός της ολικής παραγώγου περιλαμβάνει τον ορισμό της παραγώγου μιας μεταβλητής. Αυτό είναι, αν η f είναι μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, τότε η ολική παράγωγος υπάρχει αν και μόνον αν η κοινή παράγωγος υπάρχει. Ο Ιακωβιανός πίνακας περιορίζεται σε έναν 1×1 πίνακα του οποίου η μόνη είσοδος είναι η παράγωγος f′(x). Αυτός ο 1×1 πίνακας ικανοποιεί την ιδιότητα ότι f(a + h) − f(a) − f ′(a)h είναι κατά προσέγγιση μηδέν, με άλλα λόγια \( f(a+h) \approx f(a) + f'(a)h. \)
Εξαρτάται από την αλλαγή των μεταβλητών, αυτή είναι η διατύπωση ότι η συνάρτηση \( x \mapsto f(a) + f'(a)(x-a) \) είναι η καλύτερη γραμμική προσέγγιση της f στο a.
Η ολική παράγωγος μιας συνάρτησης δε δίνει άλλη συνάρτηση με τον ίδιο τρόπο όπως στην περίπτωση της μιας μεταβλητής. Αυτό συμβαίνει επειδή η ολική παράγωγος της πολυμεταβλητής συνάρτησης έχει να καταχωρήσει πολύ περισσότερες πληροφορίες από την παράγωγο της συνάρτησης μιας μεταβλητής. Αντ' αυτού, η ολική παράγωγος δίνει μια συνάρτηση από τη δέσμη εφαπτομένης της πηγής στη δέσμη εφαπτομένη του σκοπού.
Η φυσική αντιστοιχία της δεύτερης, τρίτης,και ανώτερης-τάξης των μερικών παραγώγων δεν είναι ένας γραμμικός μετασχηματισμός, δεν είναι μια συνάρτηση στην εφαπτόμενη δέσμη, και δεν παράγεται παίρνοντας επανειλημμένως την ολική παράγωγο. Η αντιστοιχία μιας ανώτερης-τάξης παραγώγισης, καλείται ως πίδακας, δεν μπορεί να είναι γραμμικός μετασχηματισμός επειδή οι ανώτερες-τάξεις των παραγώγων εκφράζουν διακριτή γεωμετρική πληροφορία, όπως η κοίλη επιφάνεια, η οποία δεν μπορεί να περιγραφεί με όρους των γραμμικών δεδομένων όπως τα διανύσματα. Δεν μπορεί να είναι μια συνάρτηση στη δέσμη εφαπτομένης επειδή η δέσμη εφαπτομένης έχει μόνο χώρο για τη βάση του χώρου και για τις κατευθυνόμενες παραγώγους. Επειδή οι πίδακες αποθηκεύουν ανώτερης-τάξης πληροφορία, παίρνουν ως επιχείρημα επιπλέον συντεταγμένες απεικονίζοντας ανώτερη-τάξη αλλαγών στην κατεύθυνση. Ο χώρος προσδιορίζεται από αυτές τις επιπλέον συντεταγμένες που ονομάζονται δέσμη πίδακα. Η σχέση μεταξύ της ολικής παραγώγου και των μερικών παραγώγων μιας συνάρτησης είναι παρόμοια με τη σχέση μεταξύ της k-οστής τάξης πίδακα μιας συνάρτησης και των μερικών του παραγώγων σε τάξη μικρότεροη ή ίση του k.
Κατ' επανάληψη αν πάρουμε την ολική παράγωγο, αποκτά ανώτερες εκδοχές της παραγώγου Fréchet , ειδικά στον Rp. Η k-οστή τάξη της ολικής παραγώγου ίσως ερμηνευτεί σαν μια απεικόνιση
\( D^k f: \mathbb{R}^n \to L^k(\mathbb{R}^n \times \cdots \times \mathbb{R}^n, \mathbb{R}^m) \)
στην οποία παίρνοντας ένα σημείο x στο Rn και ορίζοντάς το σε έναν παράγοντα του χώρου των k-γραμμικών απεικονίσεων από τον Rn στον Rm – η "καλύτερη" (με σιγουριά ακριβή έννοια) k-γραμμική προσέγγιση της f σε αυτό το σημείο. Αν την γράψουμε ως διαγώνια απεικόνιση Δ, x → (x, x), μία γενικευμένη σειρά Τέιλορ ίσως
προκύψει ως εξής
\( \begin{align} f(\mathbf{x}) & \approx f(\mathbf{a}) + (D f)(\mathbf{x}) + (D^2 f)(\Delta(\mathbf{x-a})) + \cdots\\ & = f(\mathbf{a}) + (D f)(\mathbf{x - a}) + (D^2 f)(\mathbf{x - a}, \mathbf{x - a})+ \cdots\\ & = f(\mathbf{a}) + \sum_i (D f)_i (\mathbf{x-a})^i + \sum_{j, k} (D^2 f)_{j k} (\mathbf{x-a})^j (\mathbf{x-a})^k + \cdots \end{align} \)
όπου η f(a) εξισώνεται με μια σταθερή συνάρτηση, (x − a)i είναι οι συνιστώσες του διανύσματος x − a, και (D f)i και (D2 f)j k είναι οι συνιστώσες των D f και D2 f σαν γραμμικοί μετασχηματισμοί.
Γενικεύσεις
Κύριο άρθρο: Παράγωγος (γενίκευση)
Η έννοια μιας παραγώγου μπορεί να επεκταθεί σε πολλές άλλες λειτουργίες . Το κοινό νήμα είναι ότι η παράγωγος της συνάρτησης σε ένα σημείο χρησιμεύει ως μια γραμμική προσέγγιση της συνάρτησης στο σημείο αυτό.
- Μια σημαντική γενίκευση της παραγώγου έχει να κάνει με σύνθετες συναρτήσεις των σύνθετων μεταβλητών, όπως λειτουργίες από (έναν τομέα) των σύνθετων αριθμών C έως C. Η έννοια της παραγώγου μιας τέτοιας συνάρτησης επιτυγχάνεται με την αντικατάσταση πραγματικών μεταβλητών με σύνθετων μεταβλητών στον ορισμό . Αν ο C ταυτίζεται με το R2 γράφοντας ένα μιγαδικό αριθμό z ως x + iy, τότε μια διαφορική συνάρτηση από C σε C είναι σίγουρα διαφορική ως μία συνάρτηση από τα R2 έως R2 (με την έννοια ότι οι όλες μερικές παραγωγοί του υπάρχουν ), αλλά το αντίστροφο δεν ισχύει γενικά: η σύνθετη παράγωγος υπάρχει μόνον όταν η πραγματική παράγωγος είναι σύνθετη γραμμική και αυτό επιβάλλει σχέσεις μεταξύ των επιμέρους παραγώγων που ονομάζονται εξισώσεις Cauchy Riemann - βλέπε αναλυτικές συναρτήσεις.
- Μια άλλη γενίκευση αφορά συναρτήσεις μεταξύ διαφορικών ή ομαλών πολλαπλών. Διαισθητικά μιλώντας, μια τέτοια πολλαπλότητα M είναι ένας χώρος που μπορεί να προσεγγιστεί κοντά σε κάθε σημείο x από ένα διανυσματικό χώρο που ονομάζεται εφαπτόμενος χώρος του: ως πρωτότυπο παράδειγμα είναι μια ομαλή επιφάνεια στο R3. Η παράγωγος (ή διαφορικό) ενός (διαφορικού) χάρτης f: M → N μεταξύ πολλαπλών, σε ένα σημείο x στο M, τότε είναι ένας γραμμικός χάρτης από το χώρο εφαπτομένης του M στο x στο χώρο εφαπτομένης Ν στο f (x ). Η παραγωγίσιμη συνάρτηση γίνεται χάρτης μεταξύ των δεσμών εφαπτομένης των M και N. Αυτός ο ορισμός είναι θεμελιώδης στη διαφορική γεωμετρία και έχει πολλές χρήσεις - βλέπε pushforward (διαφορικό) και pullback (διαφορική γεωμετρία).
- Η διαφοροποίηση μπορεί επίσης να οριστεί για τους χάρτες μεταξύ απειροδιάστατων διανυσματικών χώρων, όπως Banach χώρους και χώρους Fréchet. Υπάρχει μια γενίκευση τόσο της κατευθυντήριας παραγώγου, που ονομάζεται η παράγωγος Gâteaux, όσο και της διαφορικής, που ονομάζεται παράγωγος Fréchet.
- Μια ανεπάρκεια της κλασικής παραγώγου είναι ότι δεν είναι πάρα πολλές συναρτήσεις διαφορικές. Παρ 'όλα αυτά, υπάρχει ένας τρόπος επέκτασης της έννοιας της παραγώγου έτσι ώστε όλοι οι συνεχείς συναρτήσεις και πολλές άλλες συναρτήσεις μπορούν να διαφοροποιηθούν χρησιμοποιώντας μια έννοια που είναι γνωστή ως η αδύναμη παράγωγος. Η ιδέα είναι να ενσωματωθούν οι συνεχείς συναρτήσεις σε ένα μεγαλύτερο χώρο που λέγεται χώρος των διανομών και το μόνο που απαιτείται ότι μια συνάρτηση είνα διαφορικήι «κατά μέσο όρο».
- Οι ιδιότητες της παραγώγου έχουν εμπνεύσει την εισαγωγή και μελέτη πολλών παρόμοιων αντικειμένων στην άλγεβρα και την τοπολογία - βλέπε, για παράδειγμα, διαφορική άλγεβρα.
- Το διακριτό ισοδύναμο της διαφοροποίησης είναι οι πεπερασμένες διαφορές. Η μελέτη του διαφορικού λογισμού είναι ενωμένη με τον λογισμό των πεπερασμένων διαφορών στο λογισμό κλίμακας χρόνου.
- Επίσης, δείτε αριθμητική παράγωγο.
Ιστορία
Κύριο άρθρο:Ιστορία του Λογισμού
Η δημιουργία του Λογισμού ήταν ένα από τα μεγαλύτερα επιτεύγματα του 1600, αλλά ο εφευρέτης του λογισμού αμφισβητείται ευρέως: Ήταν ο Ισαάκ Νεύτων και ο Γκότφριντ Βίλχελμ Λάιμπνιτς; O Νεύτων και ο Λάιμπνιτς διατύπωσαν αρχικά τον διαφορικό λογισμό που ουσιαστικά κάνει χρήση της έννοιας του απειροελάχιστου, το οποίο αναφέρεται ως ένα απείρως μικρός αριθμός. Εκείνη την εποχή πριν από την μη-τυπική ανάλυση, η έννοια των απειροστών ήταν πολύ ασαφής και ενόχλησε πολλούς μαθηματικούς. Ωστόσο, η έννοια των απειροστών ήταν απαραίτητη για την ανάπτυξη του διαφορικού λογισμού.[10]
Η μέθοδος του Νεύτωνα αφορούσε τη λήψη αναλογιών απειροστών. Οι όροι για την αναλογία η οποία είχε ένα απειροελάχιστο ως παράγοντα αντιμετωπίστηκαν ως μηδέν και έτσι το προϊόν των απειροστών είναι ίσο με μηδέν. Ο ίδιος εξήγησε, «οι όροι που έχουν [ένα απειροελάχιστο] ως παράγοντα θα είναι ισοδύναμοι με τίποτα σε σχέση με τους άλλους. Ως εκ τούτου, τα απαλοίφω ... " Τελικά οι Κωσύ, Weierstrass και Riemann, αναδιαμόρφωσαν το λογισμό όσον αφορά τα όρια και όχι τα απειροστά. Ως εκ τούτου, η ανάγκη για αυτές τις απείρως μικρές (και ανύπαρκτες) ποσότητες εξαλείφθηκε και αντικαταστάθηκε από μια έννοια των ποσοτήτων που είναι «κοντά» σε άλλες. Έτσι, η παράγωγος όσο και το ολοκλήρωμα πρέπει να επαναδιατυπωθούν όσον αφορά τα όρια.[11]
Στο δέκατο ένατο αιώνα, ο Γερμανός μαθηματικός Καρλ Βάιερστρας (Karl Weierstrass) εισήγαγε τη διαδικασία έψιλον-δέλτα, η οποία προέβλεπε μια αυστηρή βάση για το λογισμό και αποθάρρυνε τους μαθητές να χρησιμοποιούν την ιδέα των απειροστών. Στη συνέχεια, το 1960 ο Έιμπραχαμ Ρόμπινσον (Abraham Robinson) βρήκε έναν τρόπο για να παράσχει μια βάση για τα απειροστά και έτσι τα απειροστά έγιναν αποδεκτά. Ο Ρόμπινσον ονόμασε τη διαμόρφωση του μη τυπική ανάλυση . Ο σκοπός αυτού του υλικού είναι να εξηγήσει, να δείξει και να δικαιολογήσει την μη-τυπική σύνθεση ανάλυση των απειροστών.[12]
Δείτε επίσης
Εφαρμογές των παραγώγων
Αυτόματη διαφοροποίηση
Τάξη Διαφορισιμότητας
Κανόνες διαφοροποίησης
Διαφορικό ολοκλήρωμα
Παράγωγος των fractal
Γενικεύσεις της παραγώγου
Παράγωγος Hasse
Ολοκλήρωμα
Γραμμικοποίηση
Πολλαπλασιαστικός αντίστροφος
Αριθμητική παραγώγιση
Radon-Nikodym θεώρημα
Συμμετρική παράγωγος
Σημειώσεις
Ο Διαφορικός Λογισμός,όπως αναφέρεται σε αυτό το άρθρο,είναι μια έννοια με πολύ χρήσιμη ιδιότητα και υπάρχουν πολλές πηγές.Σχεδόν όλο το υλικό για αυτό το άρθρο βρέθηκε από τα in Apostol 1967, Apostol 1969, και Spivak 1994
Spivak 1994,chapter 10
Παρόλα αυτά, είναι πιθανόν να εκλάβουμε την παράγωγο ως κατανομή.Το αποτέλεσμα είναι εννιά φορές το μέτρο του Dirac κεντράροντας το a.
Banach, S. (1931), "Uber die Baire'sche Kategorie gewisser Funktionenmengen",''Studia. Math.'' (3): 174–179.. Cited by Hewitt, E and Stromberg, K (1963), ''Real and abstract analysis'', Springer-Verlag, Theorem 17.8
Apostol 1967, §4.18
Στη επεξεργασία του Λογισμού στην έννοια των ορίων , το ''du'' σύμβολο έχει καταχωρηθεί με πολλές διαφορετικές έννοιες από πολλούς συγγραφείς. Μερικοί συγγραφείς δεν καταχωρούν ένα νόημα στο du συγκεκριμένα, αλλά μόνο σε συνδυασμό ως σύμβολο du/dx. Άλλοι καθορίζουν το dx ως μια ανεξάρτητη μεταβλητή, και προσδιορίζουν το ''du'' από το du =dx·f'(x). Στην ανάλυση το du καθορίζεται ως απειροελάχιστο. Επίσης ερμηνεύεται ως εξωτερικό παράγωγο μια συνάρτησης u. Βλέπε διαφορικές(απειροελάχιστο) για περισσότερες πληροφορίες.
"The Notation of Differentiation". MIT. 1998. Retrieved 24 October 2012.
Burton, D. (2011). Gottfried Leibniz: Συζήτηση για τον Λογισμό. Η Ιστορία των Μαθηματικών: Μια Εισαγωγή (). Νέα Υόρκη, NY: McGraw-Hill.
Αυτό μπορεί να εκφραστεί ως ισομορφία μεταξύ της παραγώμενης μεταβλητής and της συνάρτησης κατασκευής
Watkins, T. (n.d.).Απειροελαχιστικός Λογισμός . Απειροελαχιστικός Λογισμός.Ανακτήθηκε τον Απρίλιο17, 2014, από http://www.sjsu.edu/faculty/watkins/infincalc.htm
Tomforde, M. (n.d.). Η Ιστορία του Λογισμού. Η Ιστορία του Λογισμού. Ανακτήθηκε 17 Απριλίου, 2014, από http://www.uiowa.edu/~c22m025c/history.html
Watkins,T. (n.d). Απειροελάχιστος λογισμός. Απειροελάχιστος λογισμός.Ανακτήθηκε 17 Απριλίου,2014, από http://www.sjsu.edu/facultywatkins/infincalc.htm
Παραπομπές
Εκδόσεις
Anton, Howard; Bivens, Irl; Davis, Stephen (February 2, 2005), Calculus: Early Transcendentals Single and Multivariable (8th έκδοση), New York: Wiley, ISBN 978-0-471-47244-5
Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra, 1 (2nd έκδοση), Wiley, ISBN 978-0-471-00005-1
Apostol, Tom M. (June 1969), Calculus, Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications, 1 (2nd έκδοση), Wiley, ISBN 978-0-471-00007-5
Courant, Richard; John, Fritz (December 22, 1998), Introduction to Calculus and Analysis, Vol. 1, Springer-Verlag, ISBN 978-3-540-65058-4
Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th έκδοση), Brooks Cole, ISBN 978-0-03-029558-4
Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th έκδοση), Houghton Mifflin Company, ISBN 978-0-618-60624-5
Spivak, Michael (September 1994), Calculus (3rd έκδοση), Publish or Perish, ISBN 978-0-914098-89-8
Stewart, James (December 24, 2002), Calculus (5th έκδοση), Brooks Cole, ISBN 978-0-534-39339-7
Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy (Revised, Updated, Expanded έκδοση), New York: St. Martin's Press, ISBN 978-0-312-18548-0
Βιβλία στο Ίντερνετ
Πρότυπο:Sister project links Πρότυπο:Sister project links Πρότυπο:Library resources box
Crowell, Benjamin (2003), Calculus
Garrett, Paul (2004), Notes on First-Year Calculus, University of Minnesota
Hussain, Faraz (2006), Understanding Calculus
Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals
Mauch, Sean (2004), Unabridged Version of Sean's Applied Math Book[νεκρός σύνδεσμος]
Sloughter, Dan (2000), Difference Equations to Differential Equations
Strang, Gilbert (1991), Calculus
Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus
Wikibooks, Calculus
Εξωτερικοί σύνδεσμοι
Hazewinkel, Michiel, επιμ.. (2001), «Derivative», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Khan Academy: Derivative lesson 1[νεκρός σύνδεσμος]
Weisstein, Eric W. "Derivative." From MathWorld
Derivatives of Trigonometric functions, UBC
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License