.

Στη γεωμετρία, το οκτάγραμμα είναι ένα αστεροειδές πολύγωνο οκτώ σημείων.

Η λέξη οκτάγραμμα συνδυάζει το αριθμητικό πρόθεμα οκτώ- με το επίθεμα -γραμμή.[1]

Γεωμετρία

Σε γενικές γραμμές, οκτάγραμμα είναι ένα οποιοδήποτε αυτο-τεμνόμενο οκτάγωνο (πολύγωνο με οκτώ πλευρές).

Το κανονικό οκτάγραμμα, επισημαίνεται με το σύμβολο Schläfli {8/3}, που σημαίνει αστεροειδές με οκτώ πλευρές, οι οποίες συνδέονται σε κάθε τρίτο σημείο.

Ως σχεδόν-περικομμένο τετράγωνο

Βαθύτερες αποκοπές τετραγώνων μπορεί να παράξουν ισογώνιες ενδιάμεσες μορφές αστεροειδών πολυγώνων με κορυφές που ισαπέχουν μεταξύ τους και δύο μήκη πλευρών. Ένα περικομμένο τετράγωνο είναι οκτάγωνο, t{4}={8}, και ένα σχεδόν-περικομμένο τετράγωνο, ανεστραμμένο ως {4/3}, είναι ένα οκτάγραμμα, t{4/3}={8/3}[2]

Το ομοιόμορφο αστεροειδές πολύεδρο, το αστερώδης περικομμένο εξάεδρο, t'{4,3}=t{4/3,3} έχει έδρες οκταγράμματα που κατασκευάζονται από κύβο με τον εξής τρόπο:

Ισογώνιες περικοπές τετραγώνου και κύβου
Κανονικό	Σχεδόν-κανονικό	Ισογώνιο	Σχεδόν-κανονικό
{4}	t{4}={8}		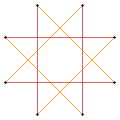t'{4}=t{4/3}={8/3}
Κανονικό	Ομοιόμορφο	Ισογώνιο	Ομοιόμορφο
{4,3}	t{4,3}		t'{4,3}=t{4/3,3}

Παραλλαγές

Όλες οι παραλλαγές έχουν μικρότερη διεδρική συμμετρία, Dih₄:

Κανονικά με περιστροφή 45°		Ισότοξα
Στενό	Πλατύ

Μπορεί να ρυθμιστεί παραλλαγή έτσι ώστε τρεις ακμές να διασταυρώνονται σε ένα μόνο σημείο, όπως στο σύμβολο της λετονικής θεότητας Auseklis (που σημαίνει: φωσφορούχος):

Στο Κοράνιο βρίσκουμε το σύμβολο rubʿ al-ḥizb (που σημαίνει: ένα τεταρτημόριο του μέρους), το οποίο είναι η Unicode γλυφίδα:

۞ (U+06DE)

Ενώσεις αστεροειδούς πολυγώνου

Υπάρχουν δύο κανονικά οκταγραμμικά αστεροειδή σχήματα (ενώσεις) της μορφής {8/k}, το πρώτο είναι κατασκευασμένο ως δύο τετράγωνα {8/2}=2{4}, και το δεύτερο ως τέσσερα εκφυλισμένα δίγωνα, {8/4}=4{2}. Υπάρχουν και άλλες ισογώνιες και ισότοξες ενώσεις, συμπεριλαμβανομένων των ορθογώνιων και των ρομβοειδών μορφών.

Κανονικό		Ισογώνιο		Ισότοξο
a{8}={8/2}=2{4}	{8/4}=4{2}

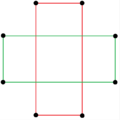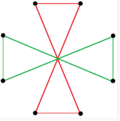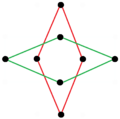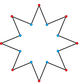
Ένα αστεροειδές οκτάγωνο μπορεί να θεωρηθεί ως κοίλο εξαδεκάγωνο, με εσωτερική διασταυρούμενη γεωμετρία που διαγράφεται. Μπορεί επίσης να αποσυντίθεται με ακτινικές γραμμές.

2{4}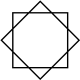
{8/3}

Παραπομπές

Liddell, Henry George; Scott, Robert. «A Greek-English Lexicon: γραμμή». Perseus.

Grünbaum, Branko (1994). Metamorphoses of polygons. The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History.

Βιβλιογραφία

Branko Grünbaum and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
Branko Grünbaum; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
John Horton Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)

Εξωτερικοί σύνδεσμοι

Weisstein, Eric W., "Octagram" από το MathWorld.

Εγκυκλοπαίδεια Μαθηματικών

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

Οκτάγραμμα

.