Μήκος τόξου
Ο καθορισμός του μήκους των αντικανονικών τμημάτων του τόξου ονομάζεται επίσης ευθυγραμμισμός της καμπύλης. Ιστορικά, πολλές μέθοδοι χρησιμοποιήθηκαν για συγκεκριμένες καμπύλες. Η έλευση του απειροστικού λογισμού , οδήγησε σε μια γενική φόρμουλα που παρέχει κλειστού τύπου λύσεις σε ορισμένες περιπτώσεις.
Γενική προσέγγιση
Προσέγγιση κατά πολλαπλά γραμμικά τμήματα
Μια καμπύλη στο επίπεδο μπορεί να προσεγγιστεί από τη σύνδεση ενός πεπερασμένου αριθμό σημείων στην καμπύλη χρησιμοποιώντας τμήματα της γραμμής για να δημιουργήσετε ένα πολυγωνικό μονοπάτι. Δεδομένου ότι είναι εύκολο να υπολογιστεί το μήκος του κάθε γραμμικού τμήματος (χρησιμοποιώντας το Πυθαγόρειο θεώρημα σε Ευκλείδειο χώρο, για παράδειγμα), το συνολικό μήκος της προσέγγισης μπορεί να βρεθεί από την άθροιση των μηκών του κάθε γραμμικού τμήματος? Αυτή η προσέγγιση είναι γνωστή ως η (σωρευτικά) συγχορδιακή απόσταση. [1]
Εάν η καμπύλη δεν είναι ήδη μία πολυγωνική διαδρομή, χρησιμοποιώντας ένα προοδευτικά μεγαλύτερο αριθμό τμημάτων με μικρότερο μήκος θα οδηγήσει σε καλύτερη προσέγγιση. Τα μήκη των διαδοχικών προσεγγίσεων δεν θα μειωθούν και μπορεί να αυξάνεται επ 'αόριστον, αλλά οι ομαλές καμπύλες θα τείνουν σε ένα πεπερασμένο όριο καθώς τα μήκη των τμημάτων μικραίνουν αυθαίρετα.
Για κάποιες καμπύλες υπάρχει ένας μικρότερος αριθμός L ο οποίος είναι ένα άνω όριο του μήκους της κάθε πολυγωνικής προσέγγισης. Αυτές οι καμπύλες ονομάζονται ευθυγραμμίσιμες και ο αριθμός L ορίζεται ως το μήκος του τόξου.
Ορισμός για μια ομαλή καμπύλη
Έστω \( {\displaystyle f:[a,b]\to \mathbb {R} ^{n}} \) να είναι μία συνεχώς διαφορίσιμη λειτουργία. Το μήκος της καμπύλης που ορίζεται από την f {\displaystyle f} f μπορεί να οριστεί ως το όριο του αθροίσματος του μήκους των ευθυγράμμων τμημάτων για μία κανονική διαμέρηση του \( [a,b] \), καθώς ο αριθμός των τμημάτων πλησιάζει στο άπειρο.
Αυτό σημαίνει:
\( {\displaystyle L(f)=\lim _{N\to \infty }\sum _{i=1}^{N}{\bigg |}f(t_{i})-f(t_{i-1}){\bigg |}} \)
όπου \( {\displaystyle i=0,1,\dots ,N.} {\displaystyle i=0,1,\dots ,N.} \)
Ο ορισμός αυτός είναι ισοδύναμος με τον ορισμό του μήκος του τόξου:
\( {\displaystyle \lim _{N\to \infty }\sum _{i=1}^{N}{\bigg |}f(t_{i})-f(t_{i-1}){\bigg |}=\lim _{N\to \infty }\sum _{i=1}^{N}\left|{\frac {f(t_{i})-f(t_{i-1})}{\Delta t}}\right|\Delta t=\int _{a}^{b}{\Big |}f'(t){\Big |}\ dt.} \)
Η παραπάνω ισότητα είναι αληθής, επειδή ο ορισμός της παραγώγου ως όριο σημαίνει ότι υπάρχει μια θετική πραγματική συνάρτηση \( {\displaystyle \delta (\epsilon )} \), των θετικών πραγματικών αριθμών \( \epsilon \), ετσι ώστε \( {\displaystyle \Delta t<\delta (\epsilon )} \). Συνεπάγεται λοιπόν οτι:
\( {\displaystyle \left|{\bigg |}{\frac {f(t_{i})-f(t_{i-1})}{\Delta t}}{\bigg |}-{\Big |}f'(t_{i}){\Big |}\right|<\epsilon .} \)
Αυτό σημαίνει οτι:
\( {\displaystyle \sum _{i=1}^{N}\left|{\frac {f(t_{i})-f(t_{i-1})}{\Delta t}}\right|\Delta t-\sum _{i=1}^{N}{\Big |}f'(t_{i}){\Big |}\Delta t}\)
έχει απόλυτη τιμή μικρότερη απο το γινόμενο \( {\displaystyle \epsilon (b-a)} \) ,για \( {\displaystyle N>(b-a)/\delta (\epsilon ).} \) Αυτό σημαίνει ότι καθώς το \( {\displaystyle N\rightarrow \infty ,} \) στο αριστερό μέρος είναι σχεδόν ισο με το δεξί μερος της ισότητας, που είναι ο ορισμος του Ολοκληρώματος Riemann της \( {\displaystyle |f'(t)|} \) στο διάστημα \( {\displaystyle [a,b].} \) Αυτός ο ορισμός του μήκους τόξου δείχνει ότι το μήκος μιας καμπύλης \( {\displaystyle f:[a,b]\rightarrow \mathbb {R} ^{n}} \) συνεχώς διαφορίσιμη στο \( [a,b] \) είναι πάντα πεπερασμένο. Με άλλα λόγια, η καμπύλη είναι πάντα ευθυγραμμίσιμη.
Ο ορισμός του μήκους τόξου μιάς ομαλής καμπύλης ως το ολοκλήρωμα της νόρμας της παραγώγου είναι ισοδύναμο με τον παρακάτω ορισμό:
\( {\displaystyle L(f)=\sup \sum _{i=1}^{N}{\bigg |}f(t_{i})-f(t_{i-1}){\bigg |}} \)
όπου το supremum υπολογίζεται λαμβάνοντας υπ'οψην όλες τις πιθανές κατατμήσεις \( {\displaystyle a=t_{0}<t_{1}<\dots <t_{N-1}<t_{N}=b} \) του \( {\displaystyle [a,b].} \)[1] Αυτός ο ορισμός ισχύει επίσης αν η \( f \)είναι απλώς συνεχής,και δεν είναι διαφορίσιμη.
Μια καμπύλη μπορεί να παραμετρικοποιηποιηθεί με άπειρους τρόπους. Έστω \( {\displaystyle \varphi :[a,b]\to [c,d]} \) να είναι μια οποιαδήποτε συνεχώς διαφορίσιμη, αμφιμονοσήμαντη (ή επί) συναρτηση. Έστω επίσης, \( {\displaystyle g=f\circ \varphi ^{-1}:[c,d]\to \mathbb {R} ^{n}} \) είναι μία άλλη συνεχώς διαφορίσιμη παραμετρικοποίηση της καμπύλης που αρχικά ορίζεται από \( {\displaystyle f.} \) Το μήκος τόξου της καμπύλης είναι το ίδιο, ανεξάρτητα από την παραμετρικοποίηση που χρησιμοποιείται για τον ορισμό της καμπύλης:
\( {\displaystyle {\begin{aligned}L(f)&=\int _{a}^{b}{\Big |}f'(t){\Big |}\ dt=\int _{a}^{b}{\Big |}g'(\varphi (t))\varphi '(t){\Big |}\ dt\\&=\int _{a}^{b}{\Big |}g'(\varphi (t)){\Big |}\varphi '(t)\ dt\quad {\textrm {since}}\ \varphi \ {\textrm {must}}\ {\textrm {be}}\ {\textrm {non-decreasing}}\\&=\int _{c}^{d}{\Big |}g'(u){\Big |}\ du\quad {\textrm {using}}\ {\textrm {integration}}\ {\textrm {by}}\ {\textrm {substitution}}\\&=L(g).\end{aligned}}} \)
Εύρεση μήκους τόξου με την ενσωμάτωση
Τέταρτο κύκλου
Δείτε επίσης:Διαφορική γεωμετρία των καμπυλών
Εάν μια επίπεδη καμπύλη στο \( {\displaystyle \mathbb {R} ^{2}} \) ορίζεται από την εξίσωση\( y=f(x) \) , όπου f είναι συνεχώς διαφορίσιμη, τότε είναι απλά μια ειδική περίπτωση μιας παραμετρικής εξίσωση όπου \( {\displaystyle x=t} \) και y\( {\displaystyle y=f(t)} \), και το μήκος τόξου είναι ίσο με:
\( {\displaystyle s=\int _{a}^{b}{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}dx.} \)
Καμπύλες με κλειστή μορφή λύσεων για το μήκος τόξου περιλαμβάνουν: την αλυσοειδή, τον κύκλο, την κυκλοειδή,την λογαριθμική σπείρα, την παραβολή,την ημικυβική παραβολή και την ευθεία γραμμή. Η έλλειψη μιας κλειστού τύπου λύσης για το μήκος τόξου ενός ελλειπτικού τόξου οδήγησε στην ανάπτυξη των ελλειπτικών ολοκληρωμάτων.
Αριθμητική ολοκλήρωση
Στις περισσότερες περιπτώσεις, συμπεριλαμβανομένου ακόμη και απλές καμπύλες, δεν υπάρχουν κλείστου τύπου λύσεις για το μήκος του τόξου και η Αριθμητική ολοκλήρωση είναι απαραίτητη.Η Αριθμητική ολοκλήρωση του μήκους τόξου ολοκληρώματος είναι συνήθως πολύ αποτελεσματική. Για παράδειγμα, σκεφτείτε το πρόβλημα της εύρεσης του μήκους ενος τετερτημορίου του κύκλου ενσωματώνοντας το μήκος του τόξου αναπόσπαστο. Το πάνω μισό του κύκλου μπορεί να είναι παραμετροποιημένο ως \( {\displaystyle y={\sqrt {1-x^{2}}}.} \) Το χρονικό διάστημα \( {\displaystyle x\in [-{\sqrt {2}}/2,{\sqrt {2}}/2]} \) αντιστοιχεί στο ένα τέταρτο του κύκλου. Από τότε d\( {\displaystyle dy/dx=-x/{\sqrt {1-x^{2}}}} \) και \( {\displaystyle 1+(dy/dx)^{2}=1/(1-x^{2}),} \) το μήκος του ενος τεταρτημορίου του κύκλου
\( {\displaystyle \int _{-{\sqrt {2}}/2}^{{\sqrt {2}}/2}{\frac {1}{\sqrt {1-x^{2}}}}dx.} \)
Η εκτίμηση του κανόνα 15-σημείο Gauss-Kronrod για αυτό το ολοκλήρωμα της 1.570796326808177 διαφέρει από την πραγματική διάρκεια της \( \ pi / 2 \) από 1.3e-11 και η εκτίμηση του κανόνα 16-σημείο Gaussian τετραγωνισμός 1.570796326794727 διαφέρει από την πραγματική διάρκεια μόνο 1.7e- 13.
Καμπύλη στην επιφάνεια
Έστω \( {\displaystyle \mathbf {x} (u,v)} \) να είναι μια απεικόνιση της επιφάνειας και έστω C ( t ) = ( u ( t ) , v ( t ) ) {\displaystyle \mathbf {C} (t)=(u(t),v(t))} {\displaystyle \mathbf {C} (t)=(u(t),v(t))} να είναι μια καμπύλη σε αυτή την επιφάνεια. Η προς ολοκλήρωση συνάρτηση του ολοκληρώματος του μήκους του τόξου είναι | ( x ∘ C ) ′ ( t ) | . {\displaystyle |(\mathbf {x} \circ \mathbf {C} )'(t)|.} {\displaystyle |(\mathbf {x} \circ \mathbf {C} )'(t)|.} Για τον υπολογισμό των παραγώγων απαιτείται η χρήση του κανόνα της αλυσίδας για τα διανυσματικά πεδία:
\( {\displaystyle D(\mathbf {x} \circ \mathbf {C} )=(\mathbf {x} _{u}\ \mathbf {x} _{v}){\binom {u'}{v'}}=\mathbf {x} _{u}u'+\mathbf {x} _{v}v'.} \)
Το τετράγωνο της νόρμας του διανύσματος είναι \( {\displaystyle (\mathbf {x} _{u}u'+\mathbf {x} _{v}v')\cdot (\mathbf {x} _{u}u'+\mathbf {x} _{v}v')=g_{11}(u')^{2}+2g_{12}u'v'+g_{22}(v')^{2}} \) (που\( {\displaystyle g_{ij}} \(είναι η πρώτη θεμελιώδης μορφή συντελεστή), έτσι ώστε η προς ολοκλήρωση συνάρτηση του ολοκληρώματος του μήκους του τόξου μπορεί να γραφτεί ως \( {\displaystyle {\sqrt {g_{ab}(u^{a})'(u^{b})'}}}\) (όπου \( {\displaystyle u^{1}=u} \) και \( {\displaystyle u^{2}=v}) \).
'Αλλα συστήματα συντεταγμένων
Έστω \( {\displaystyle C(t)=(r(t),\theta (t))} \) να είναι μια καμπύλη εκφρασμένη σε πολικές συντεταγμένες. Η απεικόνιση που μετατρέπει τις πολικές συντεταγμένες σε ορθογώνιες συντεταγμένες είναι η \( {\displaystyle \mathbf {x} (r,\theta )=(r\cos \theta ,r\sin \theta ).} \)
Η προς ολοκλήρωση συνάρτηση του ολοκληρώματος του μήκους τόξου ειναι \( {\displaystyle |(\mathbf {x} \circ \mathbf {C} )'(t)|.} \) Ο κανόνας της αλυσίδας για διανυσματικά πεδία, δείχνει ότι \( {\displaystyle D(\mathbf {x} \circ \mathbf {C} )=\mathbf {x} _{r}r'+\mathbf {x} _{\theta }\theta '.} \) Έτσι το τετράγωνο της προς ολοκλήρωσης συνάρτησης του ολοκληρώματος του μήκους του τόξου είναι:
\( {\displaystyle (\mathbf {x_{r}} \cdot \mathbf {x} _{r})(r')^{2}+2(\mathbf {x} _{r}\cdot \mathbf {x} _{\theta })r'\theta '+(\mathbf {x} _{\theta }\cdot \mathbf {x} _{\theta })(\theta ')^{2}=(r')^{2}+r^{2}(\theta ')^{2}.} \)
Έτσι για μία καμπύλη που εκφράζεται σε πολικές συντεταγμενες, το μήκος τόξου είναι:
\( {\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dr}{dt}}\right)^{2}+r^{2}\left({\frac {d\theta }{dt}}\right)^{2}}}dt=\int _{\theta (t_{1})}^{\theta (t_{2})}{\sqrt {\left({\frac {dr}{d\theta }}\right)^{2}+r^{2}}}d\theta .} \)
Τώρα έστω C(t)=(r(t), θ(t), φ(t)) να είναι μία καμπύλη εκφρασμενη σε σφαιρικές συντεταγμένες όπου θ είναι η πολική γωνία που μετράται απο τον θετικό αξονα z και φ είναι η αζιμουθιακή γωνία. Η απεικόνιση που μετατρέπει τις σφαιρικές συντεταγμένες σε ορθογώνιες συντεταγμένες είναι:
\( {\displaystyle x(r,\theta ,\phi )=(r\sin \theta cos\phi ,rsin\theta sin\phi ,rcos\theta )} \)
Χρησιμοποιώντας τον κανόνα της αλυσίδας και πάλι δείχνουμε ότι \( {\displaystyle D(\mathbf {x} \circ \mathbf {C} )=\mathbf {x} _{r}r'+\mathbf {x} _{\theta }\theta '+\mathbf {x} _{\phi }\phi '.} \) Όλα εσωτερικά γινόμενα \( {\displaystyle \mathbf {x} _{i}\cdot \mathbf {x} _{j}} \) ,όπου\( {\displaystyle j} \) διάφορα του μηδενός, οπότε το τετράγωνο της νόρμας αυτού του διανύσματος είναι:
\( {\displaystyle (\mathbf {x} _{r}\cdot \mathbf {x} _{r})(r'^{2})+(\mathbf {x} _{\theta }\cdot \mathbf {x} _{\theta })(\theta ')^{2}+(\mathbf {x} _{\phi }\cdot \mathbf {x} _{\phi })(\phi ')^{2}=(r')^{2}+r^{2}(\theta ')^{2}+r^{2}\sin ^{2}\theta (\phi ')^{2}.} \)
Έτσι για μία καμπύλη που εκφράζεται σε σφαιρικές συντεταγμένες, το μήκος τόξου είναι:
\( {\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dr}{dt}}\right)^{2}+r^{2}\left({\frac {d\theta }{dt}}\right)^{2}+r^{2}\sin ^{2}\theta \left({\frac {d\phi }{dt}}\right)^{2}}}dt.} \)
Ένας παρόμοιος υπολογισμός μας δείχνει οτι το μήος του τόξου μιας καμπύλης που εκφράζεται σε κυλικδρικές συντεταγμένες είναι:
\( {\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dr}{dt}}\right)^{2}+r^{2}\left({\frac {d\theta }{dt}}\right)^{2}+\left({\frac {dz}{dt}}\right)^{2}}}dt.} \)
Απλές περιπτώσεις
Τόξα των κύκλων
Τα μήκη τόξου συμβολίζονται με s, δεδομένου ότι η λατινική λέξη για το μήκος (ή το μέγεθος) είναι spatium.
Στις παρακάτω γραμμές, r αντιπροσωπεύει την ακτίνα ενός κύκλου, το d είναι η διάμετρος του, το C είναι περιφέρειά του, το s είναι το μήκος ενός τόξου του κύκλου, και θήτα είναι η γωνία η οποία το τόξο υποτείνει στο κέντρο του κύκλου . Οι αποστάσεις r, d, C, και s εκφράζονται στις ίδιες μονάδες.
\( {\displaystyle C=2\pi r} \), η οποία είναι η ίδια ως \( {\displaystyle C=\pi d} \). (Αυτή η εξίσωση είναι ο ορισμός του π {\displaystyle \pi } \pi .)
Αν το τόξο είναι ένα ημικύκλιο, τότε \( {\displaystyle s=\pi r} \).
Αν \( \theta \) είναι σε ακτίνια τότε \( {\displaystyle s=r\theta } \). (Αυτό είναι ο ορισμός της σε ακτίνια).
Αν \( \theta \) είναι σε μοίρες, τότε \( {\displaystyle s={\frac {\pi r\theta }{180}},} \) το οποίο είναι το ίδιο με \( {\displaystyle s={\frac {C\theta }{360}}.} \)
Αν\( \theta \) είναι σε βαθμούς (100 βαθμούς, ή βαθμούς, ή gradians είναι μία ορθή γωνία), τότε \( {\displaystyle s={\frac {\pi r\theta }{200}},} \) το οποίο είναι το ίδιο με \( {\displaystyle s={\frac {C\theta }{400}}.} \)
Αν \( \theta \)είναι σε στροφές (μία στροφή είναι μία πλήρη περιστροφή, ή 360 ° ή 400 βαθμούς, ή 2\( \pi \)ακτίνια), τότε \( {\displaystyle s=C\theta .} \).
Τόξα των μεγάλων κύκλων στη Γη
Κύριο λήμμα: Η απόσταση του Μεγάλου κύκλου
Περαιτέρω πληροφορίες: Geodesics σε ένα ελλειψοειδές
Δύο μονάδες μήκους, το ναυτικό μίλι και ο μετρητής (ή χιλιόμετρα), είχαν αρχικά οριστεί έτσι ώστε τα μήκη των τόξων των μεγάλων κύκλων στην επιφάνεια της Γης να σχετίζονται απλά αριθμητικά με τις γωνίες που υποτείνουν στο κέντρο του. Η απλή εξίσωση s = θ {\displaystyle s=\theta } {\displaystyle s=\theta } ισχύει στις ακόλουθες περιπτώσεις:
αν s είναι σε ναυτικά μίλια, και \( \theta \) είναι σε λεπτά του τόξου (1/60 βαθμού), ή
αν s είναι σε χιλιόμετρα, και \( \theta \)είναι σε βαθμούς Κελσίου (1/100 grad).
Τα μήκη των μονάδων απόστασης που επιλεχτηκαν για να κάνουν την περιφέρεια της Γης είναι ίσο με 40.000 χιλιομέτρων, ή 21.600 ναυτικά μίλια. Αυτοί είναι οι αριθμοί των αντίστοιχων μονάδων γωνίας σε μια πλήρη περιστροφή.
Αυτοί οι ορισμοί του μετρητή και του ναυτικο'ύ μιλίου έχουν αντικατασταθεί από πιο ακριβείς,αλλά οι αρχικοί ορισμοί εξακολουθούν να είναι αρκετά ακριβείς για εννοιολογικούς σκοπούς, καθώς και για ορισμένους υπολογισμούς. Για παράδειγμα,συνεπάγουν ότι ένα χιλιόμετρο είναι ακριβώς 0,54 ναυτικά μίλια. Χρησιμοποιώντας επίσημους σύγχρονους ορισμούς, ένα ναυτικό μίλι είναι ακριβώς 1,852 χιλιομέτρα, το οποίο σημαίνει ότι 1 χιλιόμετρο ≈ 0,53995680 ναυτικά μίλια. Αυτή η μοντέρνα αναλογία διαφέρει από τη μία που υπολογίζεται από τους αρχικούς ορισμούς κατά λιγότερο από 1/10.000.
Μήκος τόξου της παραβολής
Για τον υπολογισμό του μήκους του παραβολικού τόξου, βλέπε Παραβολή § Μήκος ενός τόξου μιας παραβολής.
Ιστορικές μέθοδοι
Υπολογισμός του μήκους ενός τμήματος μιας καμπύλης.
1) μήκος ενός τμήματος μιας καμπύλης f(x) μεταξύ x = a και x = b:
![]()
f(x) και f′(x) συνεχές στο διάστημα [a, b] .
Παράδειγμα, μήκος L (περιφέρεια) ενός κύκλου, x2 + y2 = r2:
![]() ,
,
![]()
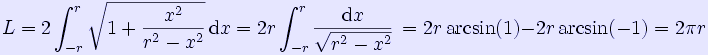
2) μήκος ενός τμήματος μιας καμπύλης με παραμετρική παράσταση
x = X(t) y = Y(t),
![]()
Παράδειγμα, μήκος (περιφέρεια) ενός κύκλου:
![]() ,
, ![]()
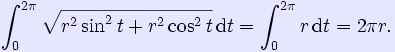
3) μήκος ενός τμήματος μιας καμπύλης με πολικές συντεταγμένες
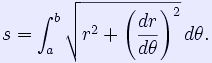
Αρχαιότητα
Για ένα μεγάλο μέρος της ιστορίας των μαθηματικών, ακόμα και οι μεγαλύτεροι στοχαστές θεώρησαν αδύνατο να υπολογιστεί το μήκος του ακανόνιστου τόξου. Παρά το γεγονός ότι ο Αρχιμήδης είχε πρωτοπορήσει έναν τρόπο για την εξεύρεση του χώρου κάτω από μια καμπύλη με την "μέθοδο της εξάντλησης'' του, λίγοι πίστεψαν ότι ήταν ακόμη δυνατό για τις καμπύλες να έχουν σαφή μήκη, όπως και οι ευθείες γραμμές. Ο πρώτος λόγος που καταρρίφθηκε σε αυτόν τον τομέα, όπως συχνά έχει γίνει στο λογισμό, με προσέγγιση. Οι άνθρωποι άρχισαν να εγγράφουν πολύγωνα εντός των καμπυλών και να υπολογίζουν το μήκος των πλευρών για μια κάπως ακριβή μέτρηση του μήκους. Με τη χρήση περισσότερων τμημάτων, και μειώνοντας το μήκος του κάθε τμήματος, ήταν σε θέση να αποκτήσουν μια ολοένα και πιο ακριβή προσέγγιση. Ειδικότερα, με την εγγραφή ένος πολυγώνου πολλών πλευρών σε έναν κύκλο, ήταν σε θέση να βρουν κατά προσέγγιση τιμές του π.
17ος αιώνας
Τον 17ο αιώνα, η μέθοδος της εξάντλησης οδήγησε στην ευθυγράμμιση με γεωμετρικές μεθόδους από αρκετές υπερβατικές καμπύλες: η λογαριθμική σπείρα από Evangelista Torricelli το 1645 (μερικές πηγές λένε John Wallis στα 1650), η κυκλοειδής από τον Christopher Wren το 1658, και η αλυσοειδή από Gottfried Leibniz το 1691.
Το 1659,ο Wallis πιστώνεται την ανακάλυψη του William Neile της πρώτης ευθυγράμμισης μιας μη τετριμμένης αλγεβρικής καμπύλης, την ημικυβική παραβολή.
αναπόσπαστη μορφή
Πριν από την πλήρη επίσημη ανάπτυξη του λογισμού, η βάση για τη σύγχρονη ολοκληρωτική μορφή για το μήκος του τόξου ανακαλύφθηκε ανεξάρτητα από τον Hendrik van Heuraet και τον Pierre de Fermat.
Το 1659 ο van Heuraet δημοσίευσε μια κατασκευή που δείχνει ότι το πρόβλημα του προσδιορισμού μήκους τόξου μπορεί να μετατραπεί σε πρόβλημα του προσδιορισμού της περιοχής κάτω από μια καμπύλη (δηλαδή, αποτελεί αναπόσπαστο). Ως παράδειγμα της μεθόδου του, καθόρισε το μήκος του τόξου μιας ημικυβικής παραβολής, το οποίο απαιτείται για να βρεθεί η περιοχή κάτω από μια παραβολή. Το 1660, ο Fermat δημοσίευσε μια πιο γενική θεωρία που περιέχει το ίδιο αποτέλεσμα στο έργο του De linearum curvarum cum lineis rectis comparatione dissertatio geometrica (Γεωμετρική διατριβή για καμπύλες γραμμές σε σύγκριση με ευθείες γραμμές).
Μορφή ολοκληρώματος
Πριν από την πλήρη επίσημη ανάπτυξη του λογισμού, η βάση για τη σύγχρονη ολοκληρωτική μορφή για τον υπολογισμό του μήκους του τόξου ανακαλύφθηκε από τον Hendrik van Heuraet και Pierre de Fermat.
Το 1659 o Hendrik van Heuraet δημοσίευσε μια κατασκευή που δείχνει ότι το πρόβλημα του προσδιορισμού του μήκους του τόξου μπορεί να μετατραπεί στο πρόβλημα του προσδιορισμού μιας περιοχής κάτω από μια καμπύλη (δηλαδή, αποτελεί ολοκλήρωμα). Ως παράδειγμα της μεθόδου του, καθορίζεται το μήκος του τόξου μιας ημικυβικής παραβολής, το οποίο απαιτείται να βρεθεί η περιοχή κάτω από μια παραβολή. Το 1660, ο Fermat δημοσίευσε μια πιο γενική θεωρία που περιείχε το ίδιο αποτέλεσμα στο έργο του De linearum curvarum cum lineis rectis comparatione dissertatio geometrica (Γεωμετρική διατριβή για καμπύλες γραμμές σε σύγκριση με ευθείες γραμμές).
Βασιζόμενος στο προηγούμενο εργο του για τις εφαπτόμενες,ο Fermat χρησιμοποίησε την καμπύλη:
\( {\displaystyle y=x^{3/2}\,} \)
Του φερμά μέθοδος προσδιορισμού μήκος τόξων
της οποίας η εφαπτόμενη στο x = a είχε μια κλίση
\( {\displaystyle \textstyle {3 \over 2}a^{1/2}} \)
έτσι ώστε η εφαπτόμενη γραμμή να έχει την εξίσωση
\( {\displaystyle y=\textstyle {3 \over 2}{a^{1/2}}(x-a)+f(a).} \)
Στη συνέχεια, αύξησε το a κατά ένα μικρό ποσό σε a + ε, καθιστώντας το τμήμα AC μια σχετικά καλή προσέγγιση για το μήκος της καμπύλης από το Α έως D. Για να βρεί το μήκος του τμήματος AC, χρησιμοποίησε το Πυθαγόρειο θεώρημα:
\( {\displaystyle {\begin{aligned}AC^{2}&{}=AB^{2}+BC^{2}\\&{}=\textstyle \varepsilon ^{2}+{9 \over 4}a\varepsilon ^{2}\\&{}=\textstyle \varepsilon ^{2}\left(1+{9 \over 4}a\right)\end{aligned}}} \)
το οποίο, όταν λυθεί,αποδίδει
\( {\displaystyle AC=\textstyle \varepsilon {\sqrt {1+{9 \over 4}a\ }}.} \)
Για την προσέγγιση του μήκους,ο Fermat θα συνοψίσει μια ακολουθία μικρών τμημάτων.
Καμπύλες με το άπειρο μήκος
Η καμπύλη Koch.
Δείτε επίσης: Ακτογραμμή παράδοξο
Όπως αναφέρθηκε παραπάνω, μερικές καμπύλες είναι μη-ευθυγραμμίσιμες. Δηλαδή, δεν υπάρχει ανώτατο όριο για τα μήκη των πολυγωνικών προσεγγίσεων; το μήκος μπορεί να γίνει αυθαίρετα μεγάλο. Ανεπίσημα, οι εν λόγω καμπύλες λέγεται ότι έχουν άπειρο μήκος. Υπάρχουν συνεχείς καμπύλες επί των οποίων κάθε τόξο (εκτός από ένα μόνο σημείο τόξου) έχει άπειρο μήκος. Ένα παράδειγμα μιας τέτοιας καμπύλης είναι η καμπύλη Koch. Ένα άλλο παράδειγμα μίας καμπύλης με άπειρο μήκος είναι η γραφική παράσταση της συνάρτησης που ορίζεται από την \( {\displaystyle f(x)=x\sin(1/x)} \) για κάθε ανοικτό σύνολο με μηδέν ως έναν από τους οριοθέτες της και \( {\displaystyle f(0)=0} \). Μερικές φορές η Hausdorff διάσταση και το μέτρο Hausdorff χρησιμοποιούνται για την ποσοτικοποίηση του μεγέθους αυτών των καμπυλών.
Γενίκευση σε (ψευδο-) Riemannian Πολλαπλότητες
Έστω M είναι μια (ψευδο) Riemannian πολλαπλότητα, γ: [0, 1] → Μ μια καμπύλη στην Μ και g ένας (ψευδο-) μετρικός
Το μήκος του γ ορίζεται να είναι
\( {\displaystyle \ell (\gamma )=\int _{0}^{1}{\sqrt {\pm g(\gamma '(t),\gamma '(t))}}\,dt,} \)
όπου γ '(t) ∈ Tγ (t) M είναι το διάνυσμα εφαπτομένη της γ σε t. Το πρόσημο της τετραγωνικής ρίζας επιλέγεται μια φορά για μια δεδομένη καμπύλη, για να εξασφαλιστεί ότι η τετραγωνική ρίζα είναι ένας πραγματικός αριθμός. Το θετικό πρόσημο επιλέγεται για καμπύλες χώρου? σε έναν ψευδο-Riemannian συλλέκτη, το αρνητικό πρόσημο μπορεί να επιλεχθεί για καμπύλες χρόνου. Έτσι το μήκος μιας καμπύλης είναι ένα μη αρνητικός πραγματικός αριθμός. Συνήθως δεν υπάρχουν καμπύλες που θεωρούνται εν μέρει χώρου και εν μέρει χρόνου.
Στη θεωρία της σχετικότητας, μήκος τόξου καμπυλών χρόνου (παγκόσμιες γραμμές) είναι ο ιδανικός χρόνος να παρέλθει κατά μήκος της παγκόσμιας γραμμής, και μήκος τόξου μιας καμπύλης χώρου η ιδανική απόσταση κατά μήκος της καμπύλης.
Αναφορές και σημειώσεις
σελ.51 σε Ahlberg & Nilson (1967) Η θεωρία των splines και οι εφαρμογές τους, Academic Press, 1967 [1]
Rudin, Walter (1976). Αρχές της Μαθηματικής Ανάλυσης. McGraw-Hill, Inc. σελ. 137. ISBN 0-07-054235-X.
physics.nist.gov/Pubs/SP811/appenB8.html
CRC Handbook of Chemistry and Physics, σελίδα F-254
John Wallis, Tractatus Duo. Prior, De Cycloide et de Corporibus ανε Genitis. ... (Οξφόρδη, Αγγλία: University Press, 1659), σελίδες 91-96? τα συνοδευτικά στοιχεία εμφανίζονται στη σελίδα 145. Στη σελίδα 91, William Neile αναφέρεται ως "Gulielmus Nelius".
Henricus van Heuraet, "Epistola de transmutatione curvarum linearum σε rectas" (Επιστολή σχετικά με τη μετατροπή των καμπύλων γραμμών σε σωστές [δηλαδή, Επιστολή για τη διόρθωση των καμπυλών]), Renati Des-Cartes Geometria, 2nd ed. (Άμστερνταμ [ "Amstelædami"], (Κάτω Χώρες): Louis & Daniel Elzevir, 1659), σελίδες 517-520.
"M.P.E.A.S." (Ψευδώνυμο του Fermat) De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio γεωμετρικό (Τουλούζη [Tolosæ], Γαλλία: Arnaud Colomer, 1660).
Farouki, Rida T. (1999). Καμπύλες από κίνηση, κίνηση από καμπύλες. Σto P-J. Laurent, Π Sablonniere και Λ Λ Schumaker (επιμ.),Σχεδιασμός Καμπύλης και Επιφάνειας: Saint-Malo 1999, σελ 63-90, Vanderbilt Παν.. Τύπος. ISBN 0-8265-1356-5.
εξωτερικοί σύνδεσμοι
Hazewinkel, Michiel, ed. (2001), "Ευθυγραμμίσιμη καμπύλη», Εγκυκλοπαίδεια των Μαθηματικών, Springer, ISBN 978-1-55608-010-4
Μαθηματικά Πριν τον Λογισμό
Η Ιστορία της καμπυλότητας
Weisstein, Eric W., "Μήκος τόξου», MathWorld.
Το μήκος του τόξου του Ed Pegg, Jr., The Wolfram Δημοσιεύσεις Έργου, 2007.
Οδηγός Σπουδών Λογισμού - Μήκος τόξου (Διόρθωση)
Δείκτης Διάσημων Καμπυλών - αρχειο Η MacTutor Ιστορία των Μαθηματικών
Προσέγγιση μήκους τόξου από το Τσαντ Pierson, Josh Fritz, και η Angela Sharp,Δημοσιεύσεις έργου το Wolfram.
Μήκος μιας Καμπύλης-Πειραμα Απεικονίζει αριθμητική λύση εξεύρεσης μήκους μιας καμπύλης.
Εξωτερικοί σύνδεσμοι
Commons logo
Τα Wikimedia Commons έχουν πολυμέσα σχετικά με το θέμα
Μήκος τόξου
Hazewinkel, Michiel, επιμ.. (2001), «Rectifiable curve», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Τα Μαθηματικά Πριν Από Το Λογισμό
Η Ιστορία της Καμπυλότητας
Weisstein, Eric W., "Arc Length" από το MathWorld.
Μήκος τόξου από Ed Pegg, Jr., Η Wolfram Διαδηλώσεις Έργου, 2007.
Λογισμός Οδηγός Σπουδών – Μήκος Τόξων (Διόρθωση)
Διάσημες Καμπύλες Δείκτη Στο MacTutor History of Mathematics archive
Μήκος τόξου Προσέγγιση από το Τσαντ Πίρσον, ο Τζος Fritz, και η Sharp, Η Wolfram Διαδηλώσεις του Έργου.
Μήκος της Καμπύλης Πείραμα Δείχνει αριθμητική λύση να βρούμε το μήκος της καμπύλης.
Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill, Inc. σελ. 137. ISBN 0-07-054235-X.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

