.
Στα μαθηματικά και την υπολογιστική επιστήμη , η μέθοδος Όιλερ είναι μια πρώτης τάξης αριθμητική διαδικασία για την επίλυση συνήθων διαφορικών εξισώσεων (Σ.Δ.Ε.), με δεδομένη την αρχική τιμή . Είναι η πιο βασική μέθοδος για την ρητή αριθμητικής ολοκλήρωσης των συνήθων διαφορικών εξισώσεων και είναι η απλούστερη Runge-Kutta μέθοδο . Ονομάζεται μέθοδος Όιλερ απο το όνομα του Leonhard Euler, ο οποίος εμφανίζεται στο βιβλίο Institutionum του calculi Integralis (δημοσιεύθηκε 1768-1770).[1]
Η μέθοδος Όιλερ είναι μια πρώτης τάξης μέθοδος, πράγμα που σημαίνει ότι το τοπικό σφάλμα (σφάλμα ανά βήμα) είναι ανάλογο με το τετράγωνο του μεγέθους βήματος, και το παγκόσμιο σφάλμα (σφάλμα σε μια δεδομένη στιγμή) είναι ανάλογο με το μέγεθος του βήματος. Πάσχει επίσης από προβλήματα σταθερότητας. Για τους λόγους αυτούς, η μέθοδος Όιλερ δεν χρησιμοποιείται συχνά στην πράξη. Χρησιμεύει ως βάση για την κατασκευή πιο πολύπλοκων μεθόδων.
Άτυπη γεωμετρική περιγραφή
Εξετάστε το πρόβλημα υπολογισμού του σχήματος μιας άγνωστης καμπύλης που αρχίζει σε ένα δεδομένο σημείο και ικανοποιεί μια δεδομένη διαφορική εξίσωση. Εδώ, μια διαφορική εξίσωση μπορεί να θεωρηθεί ως μια φόρμουλα με την οποία η κλίση της εφαπτομένης γραμμής στην καμπύλη μπορεί να υπολογιστεί σε οποιοδήποτε σημείο επί της καμπύλης, αφού η θέση του εν λόγω σημείου έχει υπολογιστεί.
Η ιδέα είναι ότι, ενώ η καμπύλη είναι άγνωστη αρχικά, με σημείο εκκίνησης, το οποίο συμβολίζουμε με \( A_0 \). είναι γνωστό (δείτε την εικόνα επάνω δεξιά). Στη συνέχεια, από τη διαφορική εξίσωση, η κλίση της καμπύλης στο \( A_0 \). μπορεί να υπολογιστεί, και, έτσι ώστε η εφαπτομένη γραμμή.
Πάρτε ένα μικρό βήμα κατά μήκος αυτής της γραμμής εφαπτομένης μέχρι ένα σημείο \( A_1 \). κατά μήκος .Σ'αυτό το μικρό βήμα, η κλίση δεν αλλάζει πάρα πολύ, οπότε το \( A_ \)1. θα είναι κοντά στην καμπύλη. Αν εμείς υποθέσουμε ότι είναι ακόμα στην καμπύλη, η ίδια συλλογιστική όπως και για το σημείο A_0 ανωτέρω μπορούν να χρησιμοποιηθούν. Μετά από αρκετά στάδια, μια πολυγωνική καμπύλη \( A_0A_1A_2A_3\dots \) υπολογίζεται. Σε γενικές γραμμές, αυτή η καμπύλη δεν αποκλίνει πολύ από την αρχική άγνωστη καμπύλη , και το σφάλμα μεταξύ των δύο καμπυλών μπορεί να γίνει μικρό, αν το μέγεθος του βήματος είναι αρκετά μικρό και το διάστημα του υπολογισμού είναι πεπερασμένο [2].
Διατύπωση της μεθόδου
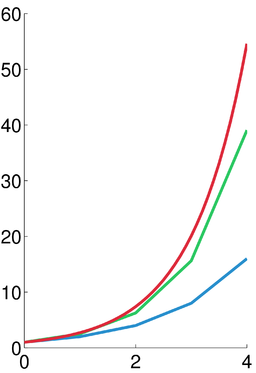
Απεικόνιση της αριθμητικής ολοκλήρωσης για την εξίσωση y'=y, y(0)=1. Το μπλε είναι η μέθοδος του Όιλερ, το πράσινο η μέθοδος ενδιάμεσης τιμής, το κόκκινο η ακριβής λύση \( y=e^t \). Το μέγεθος του βήματος είναι h = 1.0.
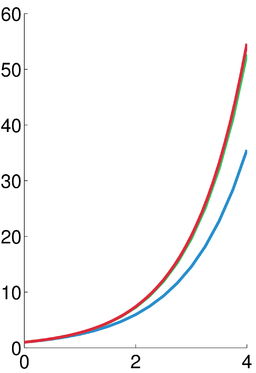
Η ίδια απεικόνιση για h = 0.25. Φαίνεται ότι η μέθοδος ενδιάμεσης τιμής συγκλίνει γρηγορότερα απ’ ότι η μέθοδος του Όιλερ.
Θέλουμε να προσεγγίσουμε την λύση της αρχικής τιμής του προβλήματος
\( y'(t) = f(t,y(t)), \qquad \qquad y(t_0)=y_0, \)
χρησιμοποιώντας τους πρώτους δύο όρους από την επέκταση της σειράς Taylor του y, η οποία παρουσιάζει τη γραμμική προσέγγιση γύρω από το σημείο (t0,y(t0)) . Ένα βήμα της μεθόδου Όιλερ από το tn στο tn+1 = tn + h είναι
\( y_{n+1} = y_n + hf(t_n,y_n). \qquad \qquad \)
Η αξία της \( y_n \) είναι μια προσέγγιση της λύσης του Σ.Δ.Ε. στο χρόνο \( t_n: y_n \approx y(t_n) \) . Η μέθοδος Euler είναι ρητή, δηλαδή η λύση του \( y_{n+1} \) είναι μια ρητή συνάρτηση \( y_i \) για \( i \leq n. \)
Ενώ η μέθοδος του Όιλερ ενσωματώνει πρώτου βαθμού Συνήθεις Διαφορικές Εξισώσεις, κάθε Συνήθης Διαφορική Εξίσωση βαθμού N μπορεί να αναπαρασταθεί ως μία πρώτου βαθμού Συνήθης Διαφορική Εξίσωση:
\( y^{(N)}(t) = f(t, y(t), y'(t), \ldots, y^{(N-1)}(t)) , \)
Παρουσιάζουμε βοηθητικές μεταβλητές \( z_1(t)=y(t), z_2(t)=y'(t),\ldots, z_N(t)=y^{(N-1)}(t) \) και παίρνουμε την αντίστοιχη εξίσωση
\( \mathbf{z}'(t) = \begin{pmatrix} z_1'(t)\\ \vdots\\ z_{N-1}'(t)\\ z_N'(t) \end{pmatrix} = \begin{pmatrix} y'(t)\\ \vdots\\ y^{(N-1)}(t)\\ y^{(N)}(t) \end{pmatrix} = \begin{pmatrix} z_2(t)\\ \vdots\\ z_N(t)\\ f(t,z_1(t),\ldots,z_N(t)) \end{pmatrix} \)
Αυτό είναι ένα πρώτης τάξης σύστημα πρώτου βαθμού στην μεταβλητή \( \mathbf{z}(t) \) και μπορεί να λυθεί εφαρμόζοντας την μέθοδο του Όιλερ ή στην πραγματικότητα, κάθε άλλο σχήμα για πρώτου βαθμού συστήματα.
Παράδειγμα
Δίνεται η διαφορική εξίσωση
\( y'=y, \quad y(0)=1, \)
θα θέλαμε να χρησιμοποιήσουμε τη μέθοδο Όιλερ για την προσέγγιση y(4).[3]
Χρησιμοποιώντας μέγεθος βήματος ίση προς 1 (h = 1)

Απεικόνιση της αριθμητικής ολοκλήρωσης για την εξίσωση y '= y, y (0) = 1. Το μπλε είναι η μέθοδος του Όιλερ, το πράσινο η μέθοδος ενδιάμεσης τιμής, το κόκκινο η ακριβής λύση \ (y = e ^ τ \). Το μέγεθος του βήματος είναι h = 1.0.
Η μέθοδος Όιλερ είναι
\( y_{n+1} = y_n + hf(t_n,y_n). \qquad \qquad
Έτσι, πρώτα θα πρέπει να υπολογίσουμε \( f(t_0, y_0) \) . Στην απλή αυτή διαφορική εξίσωση, η λειτουργία f ορίζεται από f(t,y) = y.Έχουμε
\( f(t_0,y_0) = f(0,1) = 1. \qquad \qquad \)
Κάνοντας το παραπάνω βήμα, έχουμε βρει την κλίση της γραμμής που είναι εφαπτόμενη στην καμπύλη στο σημείο (0,1). Υπενθυμίζουμε ότι η κλίση ορίζεται ως η μεταβολή y διαιρούμενη με τη μεταβολή t, or \( \Delta y/ \Delta t.
Το επόμενο βήμα είναι να πολλαπλασιάσει την ανωτέρω τιμή από το μέγεθος του βήματος h, που παίρνουμε ίση με το ένα εδώ:
\( h \cdot f(y_0) = 1 \cdot 1 = 1. \qquad \qquad \)
Δεδομένου ότι το μέγεθος του βήματος είναι η αλλαγή t, όταν θα πολλαπλασιάσει το μέγεθος του βήματος και την κλίση της εφαπτομένης, έχουμε μια αλλαγή στην y τιμή. Αυτή η τιμή στη συνέχεια προστίθεται στην αρχική y τιμή για να ληφθεί η επόμενη τιμή που θα χρησιμοποιηθεί για υπολογισμούς.
\( y_0 + hf(y_0) = y_1 = 1 + 1 \cdot 1 = 2. \qquad \qquad \)
Τα παραπάνω βήματα θα πρέπει να επαναληφθεί για να βρείτε y_2, y_3 and y_4.
\( \begin{align} y_2 &= y_1 + hf(y_1) = 2 + 1 \cdot 2 = 4, \\ y_3 &= y_2 + hf(y_2) = 4 + 1 \cdot 4 = 8, \\ y_4 &= y_3 + hf(y_3) = 8 + 1 \cdot 8 = 16. \end{align} \)
Λόγω της επαναληπτικής φύσεως αυτού του αλγορίθμου, μπορεί να είναι χρήσιμο να οργανώσει υπολογισμούς σε μορφή γραφήματος, όπως φαίνεται παρακάτω, για να αποφύγουμε λάθη.
| \(n \) | \( y_n\) | \(t_n\) | \( f(t_n,y_n) \) | \(h \) | \( \Delta y\) | \(y_{n+1} \) |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 1 | 2 |
| 1 | 2 | 1 | 2 | 1 | 2 | 4 |
| 2 | 4 | 2 | 4 | 1 | 4 | 8 |
| 3 | 8 | 3 | 8 | 1 | 8 | 16 |
Το συμπέρασμα αυτού του υπολογισμού είναι ότι y_4 = 16 . Η ακριβής λύση της διαφορικής εξίσωσης είναι \( y(t) = e^t , so \( y(4) = e^4 \approx 54.598 . Έτσι, η προσέγγιση της μεθόδου Euler δεν είναι πολύ καλή σε αυτή την περίπτωση. Ωστόσο, όπως δείχνει το σχήμα, η συμπεριφορά του είναι ποιοτικά σωστή.
Χρησιμοποιώντας άλλα μεγέθη βήματος
The same illustration for h = 0.25.
Όπως προτείνεται στην εισαγωγή, η μέθοδος Euler είναι πιο ακριβής εάν το μέγεθος του βήματος h είναι μικρότερο. Ο παρακάτω πίνακας δείχνει το αποτέλεσμα με διαφορετικά μεγέθη βήματος. Η κορυφαία σειρά αντιστοιχεί στο παράδειγμα της προηγούμενης ενότητας, και η δεύτερη σειρά απεικονίζεται στο σχήμα.
| Το μέγεθος του βήματος | αποτέλεσμα της μεθόδου του Όιλερ | σφάλμα |
|---|---|---|
| 1 | 16 | 38.598 |
| 0.25 | 35.53 | 19.07 |
| 0.1 | 45.26 | 9.34 |
| 0.05 | 49.56 | 5.04 |
| 0.025 | 51.98 | 2.62 |
| 0.0125 | 53.26 | 1.34 |
Το σφάλμα που καταγράφονται στην τελευταία στήλη του πίνακα είναι η διαφορά μεταξύ της ακριβούς λύσης στο t = 4 και την προσέγγιση Όιλερ. Στο κάτω μέρος του πίνακα, το μέγεθος βήματος είναι το μισό μέγεθος βήματος στην προηγούμενη σειρά, και το σφάλμα είναι επίσης περίπου το μισό του λάθος στην προηγούμενη σειρά. Αυτό υποδεικνύει ότι το σφάλμα είναι περίπου ανάλογη με το μέγεθος του βήματος, τουλάχιστον για αρκετά μικρές τιμές του μεγέθους βήματος. Αυτό ισχύει σε γενικές γραμμές, επίσης για άλλες εξισώσεις? Δείτε την ενότητα Παγκόσμια Λάθη στην στρογγυλοποίηση για περισσότερες λεπτομέρειες.
Άλλες μέθοδοι, όπως είναι η μέθοδος μέσου σημείου που επίσης, απεικονίζεται στα σχήματα, συμπεριφέρονται πιο ευνοϊκά: το σφάλμα της μεθόδου μέσου σημείου είναι χονδρικά ανάλογη με το τετράγωνο του μεγέθους βήματος. Για το λόγο αυτό, η μέθοδος Όιλερ λέγεται ότι είναι ένα πρώτης τάξης μέθοδος, ενώ η μέθοδος μέσου σημείου είναι δεύτερης τάξης.
Μπορούμε να προεκτείνουμε από τον παραπάνω πίνακα το μέγεθος του βήματος που απαιτείται για να πάρουμε μια απάντηση που είναι σωστή για τα τρία δεκαδικά ψηφία είναι περίπου 0,00001 , πράγμα που σημαίνει ότι χρειαζόμαστε 400.000 βήματα. Αυτός ο μεγάλος αριθμός των βημάτων συνεπάγεται υψηλό υπολογιστικό κόστος. Για το λόγο αυτό, οι άνθρωποι συνήθως χρησιμοποιούν εναλλακτικά , ανώτερης τάξης μεθόδους όπως μεθόδους Runge-Kuttas or γραμμικές μέθοδοι πολλαπλού βήματος, ειδικά αν μια υψηλή ακρίβεια είναι επιθυμητή.[4]
Παραγωγή
Η μέθοδος Όιλερ μπορεί να προκύψει έναν αριθμό τρόπων. Πρώτον, υπάρχει η γεωμετρική περιγραφή που αναφέρονται ανωτέρω.
Μια άλλη δυνατότητα είναι να εξετάσει την επέκταση της συνάρτησης Taylor y around \( t_0 \) :
\( y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2}h^2 y''(t_0) + O(h^3). \)
Η διαφορική εξίσωση δηλώνει ότιy'=f(t,y). Αν αυτό υποκαθίσταται από την επέκταση Taylor και αν αγνοούνται η τετραγωνική και υψηλότερης τάξης οροι, προκυπτει η μέθοδος Όιλερ .[5] Η επέκταση Taylor χρησιμοποιείται παρακάτω για να αναλύσει το σφάλμα της μεθόδου Όιλερ, και μπορεί να επεκταθεί για να παραχθεί η μέθοδος Runge–Kutta.
Μια στενά συνδεδεμένη παραγωγή είναι να αντικαταστήσει προς τα εμπρός διαφορά πεπερασμένων τον τύπο για την παράγωγο,
\( y'(t_0) \approx \frac{y(t_0+h) - y(t_0)}{h} \)
στην διαφορική εξίσωσηy' = f(t,y). Και πάλι, αυτό αποδίδει τη μέθοδο Όιλερ.[6] Ένας παρόμοιος υπολογισμός οδηγεί στον κανόνα και στην αντίστροφη μέθοδο Όιλερ.
Τέλος, μπορεί κανείς να θέσει στην διαφορική εξίσωση από \( t_0 \) σε \( t_0 + h \) και να εφαρμόσει το θεμελιώδες θεώρημα του λογισμού για να:
\( y(t_0+h) - y(t_0) = \int_{t_0}^{t_0+h} f(t,y(t)) \,\mathrm{d}t. \)
Τώρα κατά προσέγγιση το ολοκλήρωμα από την αριστερή ορθογώνια μέθοδο (με μόνο ένα ορθογώνιο):
\( \int_{t_0}^{t_0+h} f(t,y(t)) \,\mathrm{d}t \approx h f(t_0, y(t_0)). \)
Συνδυάζοντας τις δύο εξισώσεις, βρίσκει κανείς και πάλι τη μέθοδο Όιλερ.[7] Αυτή η γραμμή σκέψης μπορεί να συνεχιστεί για να καταλήξουμε σε διάφορα γραμμική μέθοδο πολλαπλών σταδίων
Τοπικό σφάλμα αποκοπής
Το Τοπικό σφάλμα αποκοπής της μεθόδου Euler είναι σφάλμα σε ένα μόνο βήμα. Είναι η διαφορά μεταξύ της αριθμητικής λυσης μετά από ένα βήμα, \( y_1, \) και η ακριβής λύση κατά το χρόνο \( t_1 = t_0+h. \) Η αριθμητική λύση δίνεται από
\( y_1 = y_0 + h f(t_0, y_0). \quad \)
Για την ακριβή λύση, χρησιμοποιούμε την επέκταση Taylor που αναφέρονται στην ενότητα παραγωγή πάνω από:
\( y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2}h^2 y''(t_0) + O(h^3). \)
Η τοπική αποκοπή σφαλμάτων (ΤΑΣ) παρουσιάζεται με τη μέθοδο Euler και δίνεται από τη διαφορά μεταξύ αυτών των εξισώσεων:
\( \mathrm{LTE} = y(t_0 + h) - y_1 = \frac{1}{2} h^2 y''(t_0) + O(h^3). \)
Αυτό το αποτέλεσμα είναι έγκυρο εάν y έχει φραγμένη τρίτη παράγωγο.[8]
Αυτό δείχνει ότι για τις μικρές h, το τοπικό σφάλμα αποκοπής είναι περίπου ανάλογο με \( h^2 \). Αυτό καθιστά τη μέθοδο Όιλερ λιγότερο ακριβή (για μικρά h) από ό, τι άλλων ανώτερης τάξης τεχνικές όπως μέθοδος Runge-Kutta και γραμμική μέθοδο πολλαπλών σταδίων, για την οποία η τοπική αποκοπή σφάλματος είναι αναλογικά σε μια ανώτερη δύναμη του μεγέθους βήματος.
Μια ελαφρώς διαφορετική σύνθεση για την τοπική αποκοπή σφάλματος μπορεί να ληφθεί με χρήση του εντύπου Lagrange για τον όρο υπόλοιπο στα Το θεώρημα Taylor. Εάν y έχει συνεχή δεύτερη παράγωγο, τότε υπάρχει ένα \( \xi \in [t_0,t_0+h] τ \) έτοια ώστε
\( \mathrm{LTE} = y(t_0 + h) - y_1 = \frac{1}{2} h^2 y''(\xi). \) [6]
Στις παραπάνω εκφράσεις για το σφάλμα, η δεύτερη παράγωγος της άγνωστης ακριβής λύση y μπορεί να αντικατασταθεί από μια έκφραση που αφορά την δεξιά πλευρά της διαφορικής εξίσωσης. Πράγματι, όπως προκύπτει από την εξίσωση y'=f(t,y) ότι
\( y''(t_0) = {\partial f\over\partial t}(t_0, y(t_0)) + {\partial f\over\partial y}(t_0, y(t_0)) \, f(t_0, y(t_0)). \) [9]
Παγκόσμιο σφάλμα αποκοπής
Το Παγκόσμιο σφάλμα αποκοπής είναι το σφάλμα σε καθορισμένο χρόνο t, ωστόσο, πρέπει να κάνουν πολλά βήματα οι μέθοδοι για να επιτύχουν αυτό το χρόνο από τον αρχικό χρόνο. Το παγκόσμιο σφάλμα αποκοπής είναι το σωρευτικό αποτέλεσμα του τοπικού σφάλματος αποκοπής που διαπράττονται σε κάθε βήμα.[10] Ο αριθμός των βημάτων προσδιορίζεται εύκολα \( (t-t_0)/h \) , η οποία είναι ανάλογη προς 1/h, και το σφάλμα δεσμεύεται σε κάθε βήμα είναι ανάλογο προς \( h^2 \) (δείτε την προηγούμενη ενότητα).Ετσι, είναι αναμενόμενο ότι το παγκόσμιο σφάλμα αποκοπής θα είναι ανάλογο με h.[11]
Αυτή η διαισθητική λογική μπορεί να γίνει ακριβής. Εάν η λύση y έχει φραγμένη δεύτερη παράγωγο και f είναι Lipschitz συνεχής το δεύτερο επιχείρημά της, τότε το παγκόσμιο σφάλμα αποκοπής (GTE) οριοθετείται από
\( |\text{GTE}| \le \frac{hM}{2L}(e^{L(t-t_0)}-1) \qquad \qquad \)
όπου M είναι ένα άνω όριο για τη δεύτερη παράγωγο y για το δεδομένο χρονικό διάστημα και Lείναι η σταθερά Lipschitz της f.[12]
Η ακριβής μορφή αυτή δεσμεύεται από μικρή πρακτική σημασία, καθώς στις περισσότερες περιπτώσεις η δεσμευμένη είναι πολύ μεγαλύτερη από το πραγματικό σφάλμα στο οποίο υπέπεσε με τη μέθοδο Όιλερ.[13] είναι σημαντικό ότι δείχνει ότι το παγκόσμιο σφάλμα αποκοπής είναι περίπου ανάλογο με το h. Για το λόγο αυτό, η μέθοδος Όιλερ λέγεται ότι είναι πρώτης τάξης.[14]
Αριθμητική σταθερότητα

Λύση της y '= -2.3y υπολογίζεται με τη μέθοδο του Όιλερ με μέγεθος βήματος h = 1 (μπλε τετράγωνα) και h = 0,7 (κόκκινοι κύκλοι). Η μαύρη καμπύλη δείχνει την ακριβή λύση.
Η μέθοδος Όιλερ μπορεί επίσης να είναι αριθμητικη αστάθεια, ειδικά για δυσκολη εξίσωση,πράγμα που σημαίνει ότι η αριθμητική λύση γίνεται πολύ μεγάλη για εξισώσεις, όπου η ακριβής λύση δεν υπαρχει. Αυτό μπορεί να απεικονιστεί χρησιμοποιώντας την γραμμική εξίσωση
\( y' = -2.3y, \qquad y(0) = 1. \)
Η ακριβής λύση είναι \( y(t) = e^{-2.3t} \) ,η οποία τείνει στο μηδέν καθώς t \to \infty. Ωστόσο, εάν η μέθοδος Όιλερ εφαρμόζεται σε αυτή την εξίσωση με το μέγεθος του βήματος h=1,τότε η αριθμητική λύση είναι ποιοτικά λάθος:ταλαντώνεται και μεγαλώνει (βλέπε σχήμα). Αυτό σημαίνει να είναι ασταθής. Εάν χρησιμοποιείται ένα μικρότερο μέγεθος βήματος , για παράδειγμαh=0.7, τότε η αριθμητική λύση τείνει στο μηδέν.
Εάν η μέθοδος Όιλερ εφαρμόζεται στην γραμμική εξίσωση y' = k y, τότε η αριθμητική λύση είναι ασταθής εάν το προϊόνmath>hk</math> είναι εκτός της περιοχής
\( \{ z \in \mathbf{C} \mid |z+1| \le 1 \}, \)
απεικονίζεται στα δεξιά.Η περιοχή αυτή ονομάζεται (γραμμική) περιοχή αστάθειας.[15] Για παραδειγμα, k ισούται με −2.3, ωστόσο αν h=1 τότε hk = -2.3 η οποία είναι έξω από την περιοχή σταθερότητας, και έτσι η αριθμητική λύση είναι ασταθής.
Ο περιορισμός αυτός-μαζί με την αργή σύγκλιση του σφάλματος μεh—σημαίνει ότι η μέθοδος Όιλερ δεν χρησιμοποιείται συχνά, εκτός από ένα απλό παράδειγμα της αριθμητικής ολοκλήρωσης.
Σφάλματα Στρογγυλοποίησης
Η συζήτηση μέχρι τώρα αγνοεί τις συνέπειες των Σφαλμάτων Στρογγυλοποίησης. Στο βήμα n της μεθόδου Όιλερ, το σφάλμα στρογγυλοποίησης είναι περίπου το μέγεθος εyn όπου ε είναι η μηχανή έψιλον. Υποθέτοντας ότι τα σφάλματα στρογγυλοποίησης είναι όλα περίπου το ίδιο μέγεθος, το συνολικό σφάλμα στρογγυλοποίησης στα N βήματα είναι περίπου Nεy0 εάν όλα τα σφάλματα σημεία της είναι στην ίδια κατεύθυνση. Δεδομένου ότι ο αριθμός των βημάτων είναι αντιστρόφως ανάλογος με το μέγεθος του βήματος h, Το συνολικό σφάλμα στρογγυλοποίησης είναι ανάλογο με ε / h. Στην πραγματικότητα, ωστόσο, είναι εξαιρετικά απίθανο όλα τα σφάλματα στρογγυλοποίησης να συγκεντρώνονται προς την ίδια κατεύθυνση. Αν, αντίθετα, υποτίθεται ότι τα σφάλματα στρογγυλοποίησης είναι ανεξάρτητες μεταβλητές στρογγυλοποίησης, τότε το συνολικό σφάλμα στρογγυλοποίησης είναι ανάλογο με \( \varepsilon / \sqrt{h} \) . [16]
Έτσι, για εξαιρετικά μικρές τιμές του μεγέθους του βήματος, το λάθος στην στρογγυλοποίηση θα είναι μικρό, αλλά η επίδραση του σφάλματος στρογγυλοποίησης μπορεί να είναι μεγάλη. Οι περισσότερες από τις επίδρασης του σφάλματος στρογγυλοποίησης μπορούν εύκολα να αποφευχθούν εάν αντιστάθμιση αθροίσεως χρησιμοποιείται στον τύπο για τη μέθοδο Euler.[17]
O ροζ δίσκος δείχνει την περιοχή σταθερότητας για τη μέθοδο Όιλερ
Τροποποιήσεις και επεκτάσεις
Μια απλή τροποποίηση της μεθόδου Όιλερ το οποίο εξαλείφει τα προβλήματα σταθερότητας που εχει σημειωθεί στην προηγούμενη ενότητα είναι η προς τα πίσω μέθοδο Euler:
\( y_{n+1} = y_n + h f(t_{n+1}, y_{n+1}). \)
Αυτό διαφέρει από την (τυπική, ή προς τα εμπρός) μέθοδο Όιλερ στο ότι η συνάρτηση f αξιολογείται στο τελικό σημείο της βαθμίδας, αντί του αρχικού σημείου. Η προς τα πίσω μέθοδος Όιλερ είναι μια έμμεση μέθοδος, πράγμα που σημαίνει ότι η φόρμουλα για την προς τα πίσω μέθοδο Euler έχει \( y_{n+1} \)και στις δύο πλευρές, έτσι ώστε κατά την εφαρμογή της προς τα πίσω μέθοδο Όιλερ έχουμε να λύσουμε μια εξίσωση.Αυτό καθιστά την εφαρμογή πιο δαπανηρή.
Άλλες τροποποιήσεις της μεθόδου Όιλερ που βοηθα με τη σταθερότητα να δώσει την εκθετική μέθοδο Όιλερ ή ημι-έμμεση μέθοδο Όιλερ.
Πιο περίπλοκες μεθόδους μπορεί να επιτύχει μια υψηλότερη τάξη (και με μεγαλύτερη ακρίβεια). Μία δυνατότητα είναι να χρησιμοποιηθούν περισσότερες λειτουργικές αξιολογήσεις. Αυτή απεικονίζεται από την μέθοδο μέσο, η οποία αναφέρεται ήδη σε αυτό το άρθρο:
\( y_{n+1} = y_n + h f \Big( t_n + \tfrac12 h, y_n + \tfrac12 h f(t_n, y_n) \Big). \)
Αυτό οδηγεί στην οικογένεια των Runge–Kutta methods.
Η άλλη δυνατότητα είναι να χρησιμοποιήσετε περισσότερες αξίες του παρελθόντος, όπως φαίνεται και από την Adams-Bashforth μέθοδο:
\( y_{n+1} = y_n + \tfrac32 h f(t_{n}, y_{n}) - \tfrac12 h f(t_{n-1}, y_{n-1}). \)
Αυτό οδηγεί στην οικογένεια της γραμμικής μεθόδου πολλαπλών βημάτων.
Όριο Σφάλματος
Όπως και με άλλες μεθόδους, υπάρχει τρόπος για εμάς να αποφασίσουμε ένα φράγμα σφάλματος για ένα συγκεκριμένο πρόβλημα. Το φράγμα σφάλματος στο συνολικό σφάλμα δίνεται από [18]:
\( |\epsilon_{n+1}| \le \frac{hM}{2L}(e^{L(t-t_0)}-1) \qquad \qquad \)
όπου h είναι το μέγεθος του βήματος, M είναι το άνω όριο στη δεύτερη παράγωγο του y στο δεδομένο διάστημα (το οποίο πρέπει να υπολογιστεί), και L είναι η σταθερά Lipschitz .
Αν το όριο σφάλματος υπολογιστεί, μπορούμε να δούμε, ότι αν είναι επιθυμητό μικρό σφάλμα, το μέγεθος βήματος h πρέπει να είναι πολύ μικρό.
Για παράδειγμα, ας υπολογίσουμε το μέγεθος βήματος που χρειάζεται ώστε η ολική αποκοπή σφάλματος να είναι \( \epsilon_{n+1}=0.01 \), υποθέτοντας ότι η μέγιστη τιμή της δεύτερης παραγώγου είναι M=10, η Lipschitz σταθερά είναι L=1, και t από το μηδέν στο τέσσερα. Χρησιμοποιώντας την συγκεκριμένη εξίσωση, παίρνουμε τα εξής:
\( \frac{2L}{M(e^{L(t-t_0)}-1)}|\epsilon_{n+1}|\le h \qquad \qquad \)
\( \frac{2}{10(e^{(4)}-1)}|0.01|\le h \qquad \qquad \)
\( h \le 0.0037314721 \qquad \qquad \)
Το οποίο σημαίνει ότι το h πρέπει να είναι μικρότερο από το παραπάνω ώστε να έχουμε το επιθυμητό σφάλμα ή μικρότερο , και 4/h, ή θα χρειαστούν περίπου 1072 επαναλήψεις για να γίνει αυτό. Ο τεράστιος αριθμός των βημάτων, και συνεπώς το υψηλό υπολογιστικό κόστος, ενισχύουν την χρήση εναλλακτικών, μεγαλύτερου βαθμού μεθόδων όπως η μέθοδος Runge–Kutta ή γραμμικές μέθοδοι πολλαπλών βημάτων.
Σημειώσεις
Butcher 2003, σελ. 45; Hairer, Nørsett & Wanner 1993, σελ. 35
Atkinson 1989, σελ. 342; Butcher 2003, σελ. 60
See also Atkinson 1989, σελ. 344
Hairer, Nørsett & Wanner 1993, σελ. 40
Atkinson 1989, σελ. 342; Hairer, Nørsett & Wanner 1993, σελ. 36
Atkinson 1989, σελ. 342
Atkinson 1989, σελ. 343
Butcher 2003, σελ. 60
Stoer & Bulirsch 2002, σελ. 474
Atkinson 1989, σελ. 344
Butcher 2003, σελ. 49
Atkinson 1989, σελ. 346; Lakoba 2012, equation (1.16)
Iserles 1996, σελ. 7
Butcher 2003, σελ. 63
Butcher 2003, σελ. 70; Iserles 1996, σελ. 57
Butcher 2003, σελίδες 74–75
Butcher 2003, σελίδες 75–78
Simple Euler method and its modifcations
Πηγές
Ascher, Uri M.; Petzold, Linda Ruth. Computer methods for ordinary differential equations and differential-algebraic equations. 1998. SIAM. ISBN 0898714125
Εξωτερικοί Σύνδεσμοι
Sister project Τo Βικιβιβλίο Calculus έχει μια σελίδα σχετικά με
Euler's Method
Euler's Method for O.D.E.'s
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License


