.
Στη γεωμετρία, ένα καταχρηστικό κανονικό πολύγωνο είναι το κανονικό πολύγωνο που έχει λιγότερες από τρεις πλευρές (ακμές) και λιγότερες από τρεις κορυφές. Ένα καταχρηστικό κανονικό πολύγωνο είναι εκφυλισμένο σε ένα Ευκλείδειο επίπεδο, αλλά μπορεί να κατασκευαστεί πάνω σε μια σφαίρα. Ένα δίγωνο δεν είναι εκφυλισμένο, όταν έχει κατασκευαστεί μεταξύ δύο αντιπόδων σημείων σε έναν κύκλο, ή ως σελήνη σε μια σφαίρα.[1][2]
Μονόγωνο
Στη γεωμετρία ένα μονόγωνο, γνωστό και ως 1-γωνο ή μονόπλευρο, είναι ένας εκφυλισμένος τύπος πολυγώνου με μία πλευρά (ακμή) και μία κορυφή. Επισημαίνεται με το σύμβολο Schläfli {1}[3] και μπορεί να κατασκευαστεί ως ένα εναλλακτικό δίγωνο, h{2}.
Ευκλείδεια γεωμετρία
Στην Ευκλείδεια γεωμετρία ένα μονόγωνο με ευθείες πλευρές είναι αδύνατον να κατασκευαστεί, διότι τα δύο άκρα του πρέπει να συμπίπτουν, σε αντίθεση με οποιοδήποτε άλλο Ευκλείδειο ευθύγραμμο τμήμα. Για το λόγο αυτό, το μονόγωνο είναι καταχρηστικό πολύγωνο στην Ευκλείδεια γεωμετρία.
Σε έναν κύκλο, το μονόγωνο μπορεί να κατασκευαστεί ως μία κορυφή και μία ακμή 360° τόξο με δύο άκρα που μοιράζονται την ίδια κορυφή.
Σφαιρική γεωμετρία
Σε μια σφαίρα το μονόγωνο μπορεί να κατασκευαστεί ως μία κορυφή σε έναν μεγάλο κύκλο (ισημερινός). Αυτό αποτελεί ένα δίεδρο, {1,2}, με δύο ημισφαιρικές μονογωνικές έδρες, οι οποίες μοιράζονται μία ακμή 360° και μία κορυφή. Το διπλό του είναι ένα οσόεδρο, {2,1}, το οποίο έχει δύο αντιπόδες κορυφές στους πόλους, μία σελήνη 360° έδρα, και μία ακμή (μεσημβρινός) μεταξύ των δύο κορυφών.[3] Το αποκεκομμένο μονόγωνο, t{1}, είναι ένα δίγωνο, {2}.
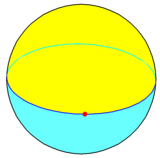 Δίεδρο, {1,2} |
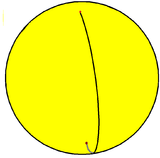 Οσόεδρο, {2,1} |
Στη γεωμετρία, ένα δίγωνο, γνωστό και ως 2-γωνο ή δίπλευρο, είναι ένας τύπος πολυγώνου με δύο πλευρές (ακμές) και δύο κορυφές. Επισημαίνεται με το σύμβολο Schläfli {2}. Η κατασκευή του είναι εκφυλισμένη σε ένα Ευκλείδειο επίπεδο, αλλά το δίγωνο μπορεί να κατασκευαστεί σε μια σφαίρα ως ένα ζεύγος τόξων 180 μοιρών που συνδέουν δύο αντιπόδα σημεία.[2]
Ευκλείδεια γεωμετρία
Στην Ευκλείδεια γεωμετρία ένα δίγωνο είναι κανονικό πολύγωνο, διότι οι δύο πλευρές του είναι ιδίου μήκους και οι δύο γωνίες του είναι ίσες (και οι δύο είναι μηδέν μοιρών).
Μερικοί ορισμοί των πολυγώνων θεωρούν το δίγωνο ως καταχρηστικό πολύγωνο, λόγω του εκφυλισμού του στο Ευκλείδειο επίπεδο.[1]
Σφαιρικές πλακοστρώσεις
Ένα σφαιρικό πολύεδρο μπορεί να περιέχει μη εκφυλισμένα δίγωνα (με μη μηδενικό εσωτερικό εμβαδόν), εάν οι κορυφές τους είναι αντίποδες. Η εσωτερική γωνία της κορυφής του σφαιρικού διγώνου μπορεί να είναι οποιαδήποτε γωνία μεταξύ 0 και 360 μοιρών. Ένα τέτοιο σφαιρικό πολύγωνο μπορεί επίσης να ονομάζεται σφαιρική σελήνη.
Το αποκεκομμένο δίγωνο, t{2} είναι ένα τετράγωνο, {4}. Το εναλλακτικό δίγωνο, h{2} είναι ένα μονόγωνο, {1}.
-
Ένα αντίποδο δίγωνο πάνω σε μια σφαίρα.
-
Έξι αντίποδες δίγωνες έδρες πάνω σε μια οσόεδρη σφαιρική πλακώστρωση.
Πολύεδρα
Ένα δίγωνο θεωρείται εκφυλισμένη έδρα ενός πολύεδρου, διότι δεν έχει γεωμετρικό εμβαδόν και τα άκρα του αλληλοκαλύπτονται, αλλά μερικές φορές μπορεί να έχει χρήσιμη τοπολογική ύπαρξη στον μετασχηματισμό πολυέδρων.
Οποιοδήποτε πολύεδρο μπορεί να τροποποιηθεί τοπολογικά αντικαθιστώντας μια πλευρά του με ένα δίγωνο. Μια τέτοια πράξη προσθέτει μία πλευρά και μία έδρα στο πολύεδρο, αν και το αποτέλεσμα είναι γεωμετρικώς πανομοιότυπο. Αυτή η μετατροπή δεν έχει καμία επίδραση στην χαρακτηριστική Όιλερ (χ = V − E + F).
Μια δίγωνη έδρα μπορεί επίσης να δημιουργηθεί από γεωμετρική κατάρρευση μιας τετράπλευρης έδρας με την μετακίνηση ζεύγων κορυφών έτσι ώστε να συμπίπτουν στο χώρο. Αυτό το δίγωνο μπορεί στη συνέχεια να αντικατασταθεί με μία ενιαία πλευρά. Μια τέτοια πράξη αφαιρεί μία έδρα, δύο κορυφές και τρεις πλευρές, αφήνοντας και πάλι αμετάβλητη την χαρακτηριστική Όιλερ.
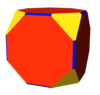
Οι τάξεις πολυέδρων μπορεί να προκύψουν ως εκφυλισμένες μορφές πρωτογενούς πολύεδρου, φέρνοντας ζεύγη ή ομάδες κορυφών σε σύμπτωση. Για παράδειγμα, τα ακόλουθα ομοιόμορφα πολύεδρα με οκταεδρική συμμετρία υπάρχουν ως εκφυλισμένες μορφές του αποκεκομμένου κυβοκτάεδρου (4.6.8):
| Κύβος | Αποκεκομμένος κύβος | Αποκεκομμένο οκτάεδρο | Οκτάεδρο | Κυβοκτάεδρο | Ρομβοειδές κυβοκτάεδρο | Αποκεκομμένο κυβοκτάεδρο |
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
| (2.4)3 | 3.8.2.8 | 2.6.4.6 | (2.3)4 | (3.4)2 | 3.4.4.4 | 4.6.8 |
Σε αυτές τις εικόνες, οι ακμές μεταξύ κόκκινων εδρών στα δύο πρώτα πολύεδρα και των κίτρινων εδρών στο τρίτο και στο τέταρτο μπορεί να θεωρηθούν ως μπλε εκφυλισμένες δίγωνες έδρες {2}. Οι κίτρινες έδρες του κύβου εκφυλίζονται σε σημεία, οι κόκκινες έδρες του οκτάεδρου και οι μπλε έδρες του κυβοκτάεδρου εκφυλίζονται επίσης σε σημεία. Η αρχή αυτή χρησιμοποιείται στην κατασκευή Wythoff.
Δείτε επίσης
Ντεμιυπερκύβος
Παραπομπές
Coxeter, Harold Scott MacDonald (1948). Regular polytopes, Chapter 1, Polygons and Polyhedra, p.4 digon
Coxeter, Harold Scott MacDonald (1948). Regular polytopes, Chapter 1, Polygons and Polyhedra, p.12 digon or lunes, pp.66-67 improper tessellations for p=2.
Coxeter, Harold Scott MacDonald (1969). Introduction to geometry (2η έκδοση), sec 21.3 Regular maps, p.386-388
Βιβλιογραφία
Busemann, Herbert (1955). The geometry of geodesics. New York: Academic Press.
Coxeter, Harold Scott MacDonald (1948). Regular Polytopes (3η έκδοση). Dover Publications Inc.. ISBN 0-486-61480-8.
Ivanov, A. B. (2001). «Digon». Στο: Hazewinkel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Εξωτερικοί σύνδεσμοι
Weisstein, Eric W., "Digon" από το MathWorld.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License
