Καμπύλη του Koch

Helge von Koch , 1904 "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire"

Για την κατασκευή της καμπύλης του Koch ξεκινάμε από ένα ευθύγραμμο τμήμα με μήκος 1 το οποίο χωρίζουμε σε τρία ίσα μέρη και αντικαθιστούμε το μεσαίο τμήμα με δύο άλλα ώστε να σχηματίζουν μαζί με το τμήμα που έχουμε αφαιρέσει ένα ισόπλευρο τρίγωνο

Στη συνέχεια για κάθε πλευρά του σχήματος που προκύπτει επαναλαμβάνουμε την ίδια διαδικασία . Το αποτέλεσμα προσεγγίζει την καμπύλη του Koch. Θα έπρεπε να επαναλάβουμε την ίδια διαδικασία άπειρες φορές

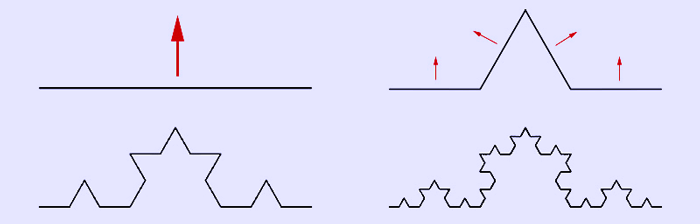
Η καμπύλης του Koch είναι ενα παράδειγμα μια συνεχής αλλα πουθενά διαφορίσιμης καμπύλης.

Διάσταση Hausdorff της "Fraktal" (φράκταλ) καμπύλης του Koch

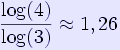
Το μήκος της καμπύλης του Koch είναι άπειρο ενώ η επιφάνεια που περικλείει είναι πεπερασμένη.

Επιφάνεια E = 8/5 E₀( E₀επιφάνεια του ισόπλευρου τριγώνου) λόγω του αθροίσματος της γεωμετρικής σειράς

Χιονονιφάδα του Koch

Παράγεται αν εφαρμόσουμε την διαδικασία για την καμπύλη του Koch σε κάθε πλεύρα ενός ισόπλευρου τριγώνου

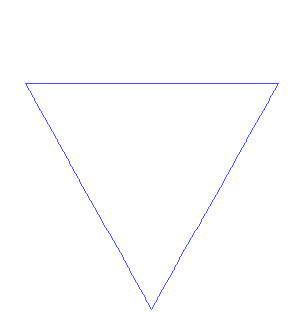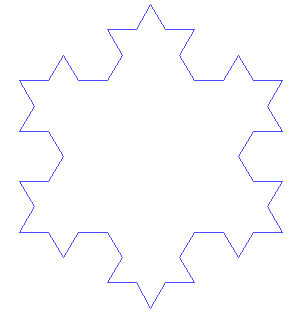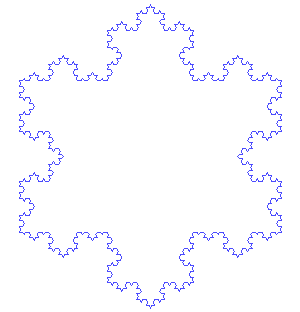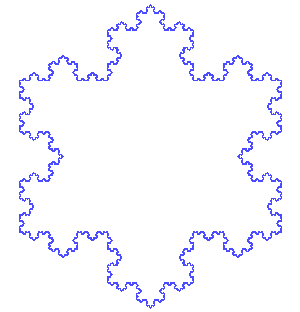
Χιονονιφάδα του Koch

Γραμματόσημο απο την Σουηδία