.

Στη γεωμετρία, το εξάγωνο (από τις ελληνικές λέξεις ἕξ = έξι και γωνία) είναι ένα πολύγωνο σχήμα με έξι πλευρές και έξι κορυφές. Οι εσωτερικές γωνίες οποιουδήποτε εξαγώνου έχουν άθροισμα 720 μοίρες (°).

Κανονικό εξάγωνο

Η κατασκευή βήμα-βήμα ενός κανονικού εξαγώνου με κανόνα και διαβήτη, όπως περιγράφεται από τον Ευκλείδη στα Στοιχεία (βιβλίο 4, πρόταση 15).

Το κανονικό εξάγωνο έχει όλες τις πλευρές του ίσες, και όλες τις εσωτερικές γωνίες του ίσες με 120°. Το κανονικό εξάγωνο έχει 6 περιστροφικές συμμετρίες («περιστροφική συμμετρία τάξεως 6») και 6 κατοπτρικές συμμετρίες (ή έξι γραμμές συμμετρίας), ορίζοντας τη δίεδρη ομάδα D6. Οι μακρύτερες διαγώνιοι ενός κανονικού εξαγώνου, που ενώνουν διαμετρικά αντίθετες κορυφές, έχουν μήκος διπλάσιο από αυτό της κάθε πλευράς του. Από το δεδομένο αυτό έπεται ότι ένα τρίγωνο με τη μία κορυφή του στο κέντρο κανονικού εξαγώνου και τη μία πλευρά του κοινή με μία πλευρά του εξαγώνου είναι ισόπλευρο τρίγωνο, και ότι το κανονικό εξάγωνο μπορεί να διαμερισθεί σε 6 ισόπλευρα τρίγωνα.

Καθώς συμβαίνει και με τα τετράγωνα και τα ισόπλευρα τρίγωνα, τα κανονικά εξάγωνα συναρμόζονται απολύτως, χωρίς κενά μεταξύ τους, ώστε να «πλακοστρώνουν» το επίπεδο (τρία εξάγωνα συναντώνται σε κάθε κορυφή), και έτσι το σχήμα αυτό μπορεί να χρησιμοποιηθεί σε πλακάκια. Για τον ίδιο λόγο, οι μέλισσες κατασκευάζουν τα κελιά στις κερήθρες τους σε σχήμα κανονικών εξαγωνικών πρισμάτων — με το συγκεκριμένο σχήμα χρησιμοποιείται αποδοτικότερα ο διαθέσιμος χώρος και τα υλικά κατασκευής.

Το εμβαδό ενός κανονικού εξαγώνου με μήκος πλευράς α είναι:

\( E = \frac{3 \sqrt{3}}{2}a^2 \simeq 2,59807621135 a^2. \)

Μία άλλη σχέση για το εμβαδό είναι Ε = 1,5αd όπου το μήκος d είναι η απόσταση μεταξύ των παράλληλων πλευρών του (το «ύψος» του εξαγώνου) ή η διάμετρος του εγγεγραμμένου κύκλου. Αν μόνο το d είναι γνωστό, τότε το εμβαδό του εξαγώνου είναι:

\( E = \frac{ \sqrt{3}}{2} d^2 \simeq 0,8660254038 d^2. \)

Η περίμετρος ενός κανονικού εξαγώνου με μήκος πλευράς α είναι 6α, η ακτίνα του περιγεγραμμένου σε αυτό κύκλου α και η διάμετρος του εγγεγραμμένου κύκλου \scriptstyle d\ =\ a\sqrt{3}.

Αν ένα κανονικό εξάγωνο έχει διαδοχικές κορυφές A, B, Γ, Δ, E, Ζ και αν P είναι οποιοδήποτε σημείο του περιγεγραμμένου σε αυτό κύκλου μεταξύ των B και Γ, τότε ισχύει PE + PΖ = PA + PB + PΓ + PΔ.

Κυκλικό εξάγωνο

Κυκλικό εξάγωνο ονομάζεται οποιοδήποτε εξάγωνο εγγεγραμμένο σε κύκλο, με τις πλευρές του εν γένει όλες άνισες μεταξύ τους. Αν οι διαδοχικές πλευρές ενός τέτοιου εξαγώνου έχουν μήκη α, β, γ, δ, ε, ζ, τότε οι τρεις κύριες διαγώνιοί του περνούν από το ίδιο σημείο στο εσωτερικό του αν και μόνο αν αγε = βδζ.[1]
Εξάγωνο εγγεγραμμένο σε κωνική τομή

Το θεώρημα του Πασκάλ (γνωστό και ως Hexagrammum Mysticum Theorem) λέει ότι αν ένα οποιοδήποτε εξάγωνο είναι εγγεγραμμένο σε κωνική τομή και προεκτείνουμε τα ζεύγη των αντίθετων πλευρών του μέχρι που να συναντηθούν, τότε τα τρία αυτά σημεία τομής θα βρίσκονται πάνω στην ίδια ευθεία, τη λεγόμενη «γραμμή Πασκάλ» αυτού του σχήματος.

Εξάγωνο εφαπτόμενο σε κωνική τομή

Αν ABCDEF είναι ένα εξάγωνο που σχηματίζεται από έξι ευθείες εφαπτόμενες σε κωνική τομή, τότε οι τρεις κύριες διαγώνιοί του AD, BE και CF τέμνονται σε ένα σημείο (Θεώρημα του Brianchon).
Συγγενικά σχήματα

Το κανονικό εξάγωνο μπορεί να δημιουργηθεί ως ένα κόλουρο ισόπλευρο τρίγωνο, με σύμβολο Schläfli t{3}. Αυτή η μορφή έχει συμμετρία μόνο D₃. Σε αυτό το σχήμα οι παραμένουσες πλευρές του αρχικού τριγώνου είναι γαλάζιες, ενώ οι νέες είναι κόκκινες.

Το εξάγραμμα μπορεί να δημιουργηθεί με την προέκταση των 6 πλευρών ενός κανονικού εξαγώνου μέχρι που να συναντηθούν σε 6 νέες κορυφές.

Ενα κοίλο εξάγωνο

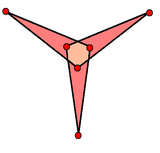Ενα «αυτοτεμνόμενο» εξάγωνο (αστεροειδές πολύγωνο)

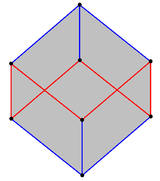Μη επίπεδο κανονικό εξάγωνο αποτελούμενο από τις ακμές ενός κύβου

Πολύγωνα Petrie

Το κανονικό εξάγωνο είναι το πολύγωνο Πέτρι για τα παρακάτω κανονικά και ομοιομορφικά πολύτοπα, που παρατίθενται σε ορθογώνιες προβολές:

(3D)		(5D)
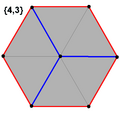κύβος	οκτάεδρο	5-simplex	ανορθωμένο 5-simplex	διανορθωμένο 5-simplex

Πολύεδρα με εξαγωνικές έδρες

Δεν υπάρχει πλατωνικό στερεό με έδρες κανονικά εξάγωνα, επειδή ακριβώς τα εξάγωνα καλύπτουν πλήρως το επίπεδο, μην αφήνοντας «χώρο» για το «δίπλωμά» τους. Τα αρχιμήδεια στερεά με κάποιες έδρες τους εξαγωνικές είναι το κόλουρο τετράεδρο, το κόλουρο οκτάεδρο, το κόλουρο εικοσάεδρο (γνωστό από τη μπάλα του ποδοσφαίρου), το κόλουρο κυβοκτάεδρο και το κόλουρο εικοσιδωδεκάεδρο.

Αρχιμήδεια στερεά
κόλουρο τετράεδρο	κόλουρο οκτάεδρο	κόλουρο εικοσάεδρο	κόλουρο κυβοκτάεδρο	κόλουρο εικοσιδωδεκάεδρο

Υπάρχουν επίσης 9 στερεά Τζόνσον:

τριγωνικός θόλος, επιμηκυμένος τριγωνικός θόλος, γυροεπιμηκυμένος τριγωνικός θόλος, προσαυξημένο εξαγωνικό πρίσμα, παραδιπροσαυξημένο εξαγωνικό πρίσμα, μεταδιπροσαυξημένο εξαγωνικό πρίσμα, τριπροσαυξημένο εξαγωνικό πρίσμα, προσαυξημένο κόλουρο τετράεδρο και τριγωνική σφηνοροτόντα

Πρισμοειδή
εξαγωνικό πρίσμα	εξαγωνικό αντιπρίσμα	εξαγωνική πυραμίδα

Λοιπά συμμετρικά πολύεδρα

Λοιπά συμμετρικά πολύεδρα
κόλουρο τριάκις τετράεδρο	κόλουρο ρομβικό δωδεκάεδρο	κόλουρο ρομβικό τριακοντάεδρο

Κανονικά και ομοιόμορφα μωσαϊκά με εξάγωνα

Το κανονικό εξάγωνο μπορεί να καλύψει το επίπεδο με σύμβολο Schläfli {6,3}, έχοντας 3 εξάγωνα γύρω από κάθε κορυφή.	Μια δεύτερη εξαγωνική κάλυψη του επιπέδου μπορεί να σχηματισθεί ως κόλουρη τριγωνική ή ρομβοειδής κάλυψη, με το ένα από τα τρία εξάγωνα με διαφορετικό χρώμα.	Μια δεύτερη εξαγωνική κάλυψη του επιπέδου γίνεται με 3 χρωματιστά εξάγωνα γύρω από κάθε κορυφή.
Τριεξαγωνική κάλυψη	Τριεξαγωνική κάλυψη
Ρομβοτριεξαγωνική κάλυψη	Κόλουρη τριεξαγωνική κάλυψη

Συναρμολογημένα τμήματα του κατόπτρου του τηλεσκοπίου E-ELT

Συναρμολογημένα τμήματα του κατόπτρου του τηλεσκοπίου E-ELT
Κερήθρα από κυψέλη μελισσών
Τα σχήματα στο καύκαλο μιας χελώνας
Εξαγωνικός σχηματισμός νεφών στη βόρεια πολική περιοχή του πλανήτη Κρόνου, που ανακαλύφθηκε από το Voyager 1 και επιβεβαιώθηκε το 2006 από την αποστολή Cassini
Μικρογραφία μιας νιφάδας χιονιού
Μόριο βενζολίου, το απλούστερο μόριο με εξαγωνικό σχήμα.
Κρυσταλλική δομή ενός μοριακού εξαγώνου που αποτελείται από εξαγωνικούς (αρωματικούς) δακτυλίους και αναφέρθηκε από τον Müllen και τους συνεργάτες του στο περιοδικό Chem. Eur. J., τόμος του 2000, σελίδες 1834-1839.
Φυσικά σχηματισμένες στήλες βασάλτη από την Giant's Causeway στην Ιρλανδία: μεγάλες μάζες βασάλτη πρέπει να κρυώσουν αργά για να δημιουργηθεί ένα τέτοιο σύνολο πολυγωνικών τεμαχίων
Εναέρια άποψη του Φορτ Τζέφερσον στο Εθνικό Πάρκο Dry Tortugas
Το κύριο κάτοπτρο του νέου διαστημικού τηλεσκοπίου James Webb αποτελείται από 18 εξαγωνικά τμήματα.
Η ηπειρωτική Γαλλία έχει ένα χονδρικά εξαγωνικό σχήμα. Στη γαλλική γλώσσα η έκφραση l'Hexagone αναφέρεται στο ευρωπαϊκό έδαφος της Γαλλίας ("metropole") σε αντιδιαστολή με τα υπερπόντια εδάφη της, όπως η Γουαδελούπη, η Μαρτινίκα και η Γαλλική Γουιάνα.
Εξαγωνικός κρύσταλλος χανκσίτη, ενός από τα πολλά ορυκτά που κρυσταλλώνονται στο εξαγωνικό κρύσταλλικό σύστημα
Εξαγωνικός αχυρώνας
Το Hexagon, ένα εξαγωνικό θέατρο στο Ρέντινγκ της Αγγλίας

Δείτε επίσης

Εξάγραμμα: εξάπλευρο άστρο μέσα σε ένα κανονικό εξάγωνο
Εξαγωνικός αριθμός
Εξαγωνικό κρύσταλλικό σύστημα

Σημειώσεις

Cartensen, Jens, "About hexagons", Mathematical Spectrum, τόμος 33(2) (2000-2001), σσ. 37-40.

Εξωτερικοί σύνδεσμοι

Weisstein, Eric W., "Hexagon" από το MathWorld.
Ορισμός και ιδιότητες του εξαγώνου με διαδραστική animation και κατασκευή με κανόνα και διαβήτη.
Το Cassini απεικονίζει παράδοξο εξάγωνο στον Κρόνο
Το παράξενο εξάγωνο του Κρόνου
"Bizarre Hexagon Spotted on Saturn" – από το Space.com (27 Μαρτίου 2007)

Εγκυκλοπαίδεια Μαθηματικών

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License