.
Στα μαθηματικά, η εικασία του Πουανκαρέ (/σwɛn.kɑːˈreɪ/ pwen-kar-AY; γαλλικά: [pwɛkaʁe])[1] είναι ένα θεώρημα σχετικά με το χαρακτηρισμό της 3-σφαίρας, η οποία είναι μια υπερσφαίρα που έχει όρια τη μονάδα μπάλα στον τετραδιάστατο χώρο. Η εικασία δηλώνει:
Κάθε απλώς συνεκτική, κλειστή 3-πολλαπλότητα είναι ομοιμορφική με την 3-σφαίρα.
Για συμπαγείς επιφάνειες δυο διαστάσεων χωρίς φράγμα, αν κάθε βρόχος μπορεί να είναι συνεχώς σφιγμένος σε ένα σημείο, τότε η επιφάνεια είναι τοπολογικά ομοιομορφική σε μια 2-σφαίρα (συνήθως ονομάζεται απλά μια σφαίρα). Η εικασία του Πουανκαρέ, υποστηρίζει ότι το ίδιο ισχύει και για τους τρισδιάστατους χώρους.
Ισοδύναμη μορφή της εικασίας περιλαμβάνει μια πιο χονδροειδή μορφή της ισοδυναμίας όπου ο ομοιομωρφισμός ονομάζεται ομοτοπία ισοδυναμίας: αν μια 3-πολλαπλότητα είναι ομότοπα ισοδύναμη της 3-σφαίρα, τότε είναι αναγκαστικά ομοιομωρφική.
Αρχικά εικάζεται από τον Ανρί Πουανκαρέ, το θεώρημα αφορά ένα χώρο που σε τοπικό επίπεδο μοιάζει με το συνηθισμένο τρισδιάστατο χώρο, αλλά είναι συνδεδεμένος, με πεπερασμένος, και στερείται κάθε φράγματος (μια κλειστή 3-πολλαπλότητα). Η εικασία του Πουανκαρέ, ισχυρίζεται ότι, αν ένας τέτοιο χώρο έχει την επιπλέον ιδιότητα ότι κάθε βρόχος στο χώρο μπορεί να είναι συνεχώς σφιγμένος σε ένα σημείο, τότε είναι αναγκαστικά μια τρισδιάστατη σφαίρα. Οι ανάλογες εικασίες για όλες τις υψηλότερες διαστάσεις είχαν ήδη αποδειχθεί.
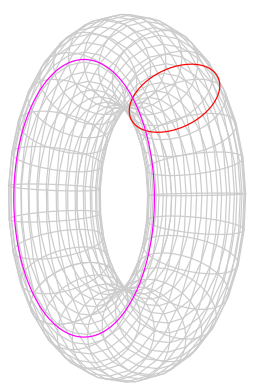
Αντίθετα, κανένας από τους δύο χρωματιστούς βρόχους σε αυτόν τον κυλινδρικό δακτύλιο δεν μπορεί να είναι συνεχώς σφιγμένος σε ένα σημείο. Ένας κυλινδρικός δακτύλιος δεν είναι ομοιομορφικός με μια σφαίρα.
Μετά από σχεδόν ένα αιώνα από την προσπάθεια από μαθηματικούς, ο Γκριγκόρι Πέρελμαν παρουσίασε μια απόδειξη της εικασίας σε τρεις εφημερίδες που διατίθενται το 2002 και το 2003 στο arXiv (ηλεκτρονική εφημερίδα). Η απόδειξη χτισμένη πάνω στο πρόγραμμα του Ρίτσαρντ Χάμιλτον να χρησιμοποιήσετε τη ροή Ricci για να προσπαθήσει να λύσει το πρόβλημα. Ο Χάμιλτον αργότερα εισήγαγε μια τροποποίηση του προτύπου της ροής Ricci, που ονομάζεται ροή Ricci with surgery ώστε να αποκόψει συστηματικά μεμονωμένες περιοχές, καθώς αυτές θα αναπτύσσονται, με ελεγχόμενο τρόπο, αλλά δεν ήταν σε θέση να αποδείξει ότι αυτή τη μέθοδο "συγκλίνει" σε τρεις διαστάσεις.[2] Ο Πέρελμαν ολοκληρώνει αυτό το τμήμα της απόδειξης. Αρκετές ομάδες μαθηματικών επαλήθευσαν ότι η απόδειξη του Πέρελμαν ήταν σωστή.
Η εικασία του Πουανκαρέ, πριν αποδειχθεί, ήταν ένα από τα πιο σημαντικά ανοιχτά ζητήματα στην τοπολογία. Το 2000, πήρε το όνομά ενός εκ των επτά προβλημάτων της χιλιετίας (Millennium Prize Problems), για τα οποία το Μαθηματικό Ινστιτούτο Clay (Clay Mathematics Institute) πρόσφερε 1.000.000 δολάρια βραβείο για την πρώτη σωστή λύση. Το έργο του Πέρελμαν επέζησε αναθεώρηση και επιβεβαιώθηκε το 2006, με αποτέλεσμα να του προσφέρεται ένα Μετάλλιο Φιλντς, το οποίο ο ίδιος αρνήθηκε. Ο Πέρελμαν τιμήθηκε με το Βραβείο Χιλιετίας στις 18 Μαρτίου 2010.[3] Στις 1 Ιουλίου 2010, απέρριψε το βραβείο λέγοντας ότι πίστευε ότι η συμβολή του στο να αποδειχθεί η εικασία του Πουανκαρέ δεν ήταν μεγαλύτερη από αυτή του Χάμιλτον (ο οποίος ήταν ο πρώτος που πρότεινε τη χρήση της ροής Ricci για την λύση).[4][5] από το 2016, η εικασία του Πουανκαρέ, είναι το μόνο λυμένο από τα προβλήματα της Χιλιετίας.
Στις 22 Δεκεμβρίου 2006, το περιοδικό Science τίμησε την απόδειξη της εικασίας του Πουανκαρέ από τον Πέρελμαν ως την επιστημονική "Ανακάλυψη της Χρονιάς", και ήταν η πρώτη φορά που αυτή η τιμή απονεμήθηκε στον τομέα των μαθηματικών.[6]
Ιστορία
Η ερώτηση του Πουανκαρέ
Στις αρχές του 20ου αιώνα, ο Ανρί Πουανκαρέ δούλευε πάνω στα θεμέλια της τοπολογίας—αυτό που αργότερα θα ονομαζόταν "συνδυαστική τοπολογία" και, στη συνέχεια, "αλγεβρική τοπολογία"-, δείχνοντας ιδιαίτερο ενδιαφέρον για τις τοπολογικές ιδιότητες που χαρακτηρίζουν μια σφαίρα.
Το 1900, ο Πουανκαρέ ισχυρίστηκε ότι, η ομολογία, ένα εργαλείο που είχε επινοήσει βασιζόμενος σε προηγούμενη εργασία του Enrico Betti, ήταν αρκετά αξιόπιστη για να πει εάν μια 3-πολλαπλότητα είναι μια 3-σφαίρα. Ωστόσο, σε μια εργασία του το 1904, περιέγραψε ένα αντιπαράδειγμα προς αυτόν του τον ισχυρισμού, ένα χώρο που πλέον ονομάζεται σφαίρα ομολογίας Πουανκαρέ και ορίζεται ως το σύνορο μιας συμπαγούς, απλά συνεκτικής 4-διάστατης πολλαπλότητας. Για να αποδείξει ότι η σφαίρα ομολογίας Πουανκαρέ ήταν διαφορετική από την 3-σφαίρα, ο Πουανκαρέ εισήγαγε μια νέα τοπολογική αναλλοίωτη, τη θεμελιώδη ομάδα και έδειξε ότι η σφαίρα Πουανκαρέ είχε μια θεμελιώδη ομάδα της τάξης 120, ενώ η 3-σφαίρα είχε μια ασήμαντη θεμελιώδη ομάδα. Με αυτό τον τρόπο ήταν σε θέση να συμπεράνει ότι αυτοί οι δύο χώροι ήταν, πράγματι, διαφορετικοί.
Στην ίδια εργασία, ο Πουανκαρέ, αναρωτήθηκε αν μία συνεκτική, συμπαγής, τρισδιάστατη πολλαπλότητα με τις ίδιες ομάδες ομολογίας με αυτές της τρισδιάστατης σφαίρας είναι ομοιομορφική με αυτήν; Η νέα υπόθεση του Πουανκαρέ μπορεί να επαναδιατυπωθεί ως "κάθε βρόχος μπορεί να συρρικνωθεί σε ένα σημείο;"
Η αρχική διατύπωση ήταν η εξής:
"Σκεφτείτε μια συμπαγή 3-διάστατη πολλαπλότητα V χωρίς φράγμα. Είναι δυνατόν, η θεμελιώδης ομάδα της V να είναι ασήμαντη, ακόμα κι αν η V δεν είναι ομομορφική ως προς την 3-διάστατη σφαίρα;"
Ο Πουανκαρέ δεν είχε δηλώσει εάν πίστευε ότι αυτή η πρόσθετη συνθήκη θα χαρακτήριζε την 3-σφαίρα, αλλά παρ ' όλα αυτά, η δήλωση ότι αυτό συμβαίνει είναι γνωστή ως η Εικασία του Πουανκαρέ. Ακολουθεί η τυποποιημένη μορφή της εικασίας:
"Κάθε απλώς συνεκτική 3-πολλαπλότητα είναι τοπολογικά όμοια με την 3-σφαίρα"
Απόπειρες επίλυσης
Για αρκετό καιρό η εικασία ήταν αδιάφορη για την μαθηματική κοινότητα , μέχρι την στιγμή που ο J. H. C. Whitehead αναθέρμανε το ενδιαφέρον για αυτή, όταν στη δεκαετία του 1930 ισχυρίστηκε για πρώτη φορά πως είχε βρει την απόδειξη, την οποία στη συνέχεια απέσυρε. Μέσα από αυτή τη διαδικασία όμως, ανακάλυψε μερικά ενδιαφέροντα παραδείγματα απλά συνδεδεμένων, μη-συμπαγών, 3-πολλαπλοτήτων μη ομομορφισμών στο R3, το πρωτότυπο της οποίας είναι γνωστό ως Πολλαπλότητα Whitehead.
Στη δεκαετία του 1950 και του 1960, διάφοροι μαθηματικοί ισχυρίστηκαν πως βρήκαν την απόδειξη, μόνο για να αποδειχθεί ότι έκαναν λάθος. Σημαντικοί μαθηματικοί όπως ο Bing, ο Haken, ο Moisè, και ο Παπακυριακόπουλος ασχολήθηκαν επίμονα με την εικασία. Το 1958, ο Bing, απέδειξε μια πιο "αδύναμη" εκδοχή της εικασία του Πουανκαρέ: αν κάθε απλώς κλειστή καμπύλη μιας συμπαγούς 3-πολλαπλότητας περιέχεται σε μια 3-σφαίρα, τότε η πολλαπλότητα είναι ομομορφική ως προς την 3-σφαίρα.[7] Επίσης, ο Bing περιέγραψε μερικές από τις παγίδες στην προσπάθειά απόδειξης της εικασία του Πουανκαρέ.[8]
Με την πάροδο του χρόνου, η εικασία απέκτησε τη φήμη ότι είναι ιδιαίτερα δύσκολο να αντιμετωπιστεί. Ο John Milnor σχολίασε ότι μερικές φορές τα σφάλματα σε λανθασμένες αποδείξεις μπορεί να είναι "αρκετά δύσκολο να ανιχνευθούν."[9] Εργασίες σχετικά με την εικασία βοήθησαν στην καλύτερη κατανόηση των 3-πολλαπλοτήτων. Εμπειρογνώμονες στον τομέα ήταν συχνά απρόθυμοι να ανακοινώσουν αποδείξεις, και είχαν την τάση να προβάλουν οποιαδήποτε τέτοια ανακοίνωση με σκεπτικισμό. Τη δεκαετία του 1980 και του 1990 δημοσιεύτηκαν πολλές ψευδείς αποδείξεις (όχι όμως σε εγκεκριμένα περιοδικά).[10][11]
Μια έκθεση του προσπαθεί να αποδείξει την εικασία του Πουανκαρέ μπορεί να βρεθεί στο μη-τεχνικό βιβλίο Το Βραβείο του Πουανκαρέ από τον Γιώργο Szpiro.[12]
Διαστάσεις
Η ταξινόμηση των κλειστών επιφανειών δίνει καταφατική απάντηση στο αντίστοιχο ερώτημα για δύο διαστάσεις. Για διαστάσεις μεγαλύτερες από τρία, εφαρμόζεται η Γενικευμένη εικασία του Πουανκαρέ, η οποία διατυπώνεται ως εξής: είναι μια ομοτοπική ν-σφαίρα ομομορφική ως προς την ν σφαίρα; Μια ισχυρότερη υπόθεση είναι απαραίτητη. Σε τέσσερις και περισσότερες διαστάσεις υπάρχουν απλά συνδεδεμένες, κλειστες πολλαπλότητες που δεν είναι ομοτοπικά ισοδύναμες με μια n-σφαίρα.
Ιστορικά, ενώ η εικασία σε τρεις διαστάσεις φαινόταν λογική, η γενικευμένη εικασία έμοιαζε να είναι ψευδής. Το 1961 ο Stephen Smale σόκαρε τους απανταχού μαθηματικούς αποδεικνύοντας την Γενικευμένη Εικασία του Πουανκαρέ για τέσσερις και παραπάνω διαστάσεις και επέκτεινε τις τεχνικές του για να αποδείξει το θεμελιώδες θεώρημα του συν συνορισμου. Το 1982 ο Μιχαήλ Φρίντμαν απέδειξε την εικασία του Πουανκαρέ σε τέσσερις διαστάσεις. Η εργασία του Φρίντμαν άφησε ανοιχτό το ενδεχόμενο να υπάρχει μια ομαλή 4-πολλαπλότητα, ομομορφική ως προς την 4-σφαίρα, η οποία δεν είναι διαφορομορφική ως προς την 4-σφαίρα. Αυτή, η λεγόμενη ομαλή εικασία του Πουανκαρέ, σε διάσταση 4, παραμένει άλυτη και πιστεύεται ότι η απόδειξή της είναι πολύ δύσκολη. Για παράδειγμα, οι εξωτικές σφαίρες του Milnor δείχνουν ότι η ομαλή Poincaré εικασίες είναι ψευδής σε διάσταση επτά.
Αυτές οι παλαιότερες επιτυχίες σε ανώτερες διαστάσεις άφησαν την περίπτωση των τριών διαστάσεων στο περιθώριο. Η εικασία του Πουανκαρέ ήταν ουσιωδώς αληθινή τόσο σε διάσταση 4 όσο και σε ανώτερες διαστάσεις για πολύ διαφορετικούς λόγους. Στη διάσταση τρία ωστόσο, η εικασία είχε μια αβέβαιη φήμη μέχρι που η εικασία της γεωμετρικοποίησης την έβαλε στο πλαίσιο που διέπει όλες τις 3-πολλαπλότητες. Ο Τζον Μόργκαν έγραψε
" Πιστεύω ότι πριν την δουλειά του Thurston στις υπερβολικές 3-πολλαπλότητες και...την εικασία της γεωμετρικοποίησης δεν υπήρχε ομοφωνία ανάμεσα στους ειδικούς σχετικά με το κατά πόσο η εικασία του Πουανκαρέ είναι αληθής ή όχι. Μετά τον Thurston, άρχισε να φαίνεται πως η εικασία του Πουανκαρέ (και η εικασία της γεωμετρικοποίησης) ήταν αληθείς.[13]
Το πρόγραμμα του Χάμιλτον και η λύση του Πέρελμαν
Διάφορα στάδια της ροής Ricci σε μια δισδιάστατη πολλαπλότητα
Το πρόγραμμα του Χάμιλτον ξεκίνησε το 1982, σε εργασία του, στην οποία εισήγαγε την ροή Ricci σε μια πολλαπλότητα και έδειξε πως αυτή μπορεί να χρησιμοποιηθεί για την απόδειξη ορισμένων περιπτώσεων της εικασίας του Πουανκαρέ.[14] Τα χρόνια που ακολούθησαν επέκτεινε την δουλειά του αλλά δεν κατάφερε να αποδείξει την εικασία. Η πραγματική λύση δεν βρέθηκε μέχρι τη δημοσίευσή της από τον Grigori Perelman.
Στα τέλη του 2002 και 2003 Perelman δημοσίευσε τρεις εργασίες στο arXiv.[15][16][17] Σε αυτές τις εργασίες σκιαγράφησε μια απόδειξη της εικασία του Πουανκαρέ και μιας πιο γενικής εικασίας, της εικασίας της γεωμετρικοποίησης του Thurston, ολοκληρώνοντας έτσι τη ροή Ricci που περιέγραψε νωρίτερα ο Richard Hamilton.
Από το Μάιο έως τον Ιούλιο του 2006, αρκετές ομάδες παρουσίασαν εργασίες που συμπλήρωναν τις λεπτομέρειες στην απόδειξη του Πέρελμαν , ως εξής:
Οι Bruce Kleiner και John W. Lott δημοσίευσαν μια εργασία στο arXiv τον Μάιο του 2006, η οποία συμπλήρωνε την απόδειξη του Πέρελμαν για την εικασία της γεωμετρικοποίησης.[18]
Οι Huai-Dong Cao και Xi-Ping Zhu δημοσίευσαν μια μελέτη στο τεύχος του Ιουνίου του 2006 της Asian Journal of Mathematics με μια έκθεση με την πλήρη απόδειξη της εικασίας του Πουανκαρέ και της εικασίας της γεωμετρικοποίησης.[19] Αρχικά υπονόησαν πως η απόδειξη ήταν δικό τους επίτευγμα, βασιζόμενο στην θεωρία των Χάμιλτον και Πέρελμαν, αργότερα όμως απέσυραν την αρχική έκδοση της εργασίας και δημοσίευσαν μια αναθεωρημένη έκδοση, στην οποία αναφέρονται στην δουλειά τους ως "εκθεση της απόδειξης των Hamilton- Perelman".[20] Επίσης, δημοσίευσαν μια διόρθωση αποκαλύπτοντας ότι ξέχασαν να αναφέρουν σωστά το έργο των Kleiner και Lott που δημοσιεύτηκε το 2003. Στο ίδιο τεύχος/θέμα, η συντακτική επιτροπή του AJM δημοσίευσε μια συγνώμμη γι αυτό που ονομάστηκε "απροσεξία" στην εργασία των Chao-Zhu.
Οι John Morgan και Gang Tian δημοσίευσαν μια εργασία στο arXiv τον Ιούλιο του 2006, η οποία έδωσε μια λεπτομερή απόδειξη της Εικασίας του Πουανκαρέ (που είναι κάπως πιο εύκολο από ό, τι η πλήρης εικασίας της γεωμετρικοποίησης[21] και επεκτάθηκε στο θέμα σε ένα βιβλίο.[22]
Διάφορα στάδια της ροής Ricci σε μια δισδιάστατη πολλαπλότητα
Και οι τρεις ομάδες διαπίστωσαν ότι τα κενά στην εργασία του Perelman ήσσονος σημασίας και θα μπορούσαν να συμπληρωθούν χρησιμοποιώντας δικές του τεχνικές.
Στις 22 αυγούστου, 2006, το ICM που απένειμε στον Perelman το Μετάλλιο Fields για το έργο του σχετικά με την εικασία, αλλά o Perelman αρνήθηκε το μετάλλιο.[23][24][25] O John Morgan μίλησε στο ICM για την εικασία του Πουανκαρέ, στις 24 αυγούστου 2006, δηλώνοντας ότι "το 2003, ο Perelman απέδειξε η Εικασία του Πουανκαρέ."[26]
Τον Δεκέμβριο του 2006, το περιοδικό Science τίμησε την απόδειξη της εικασίας του Πουανκαρέ, ως την πιο σημαντική Ανακάλυψη του Έτους και την χρησιμοποίησε ως εξώφυλλο.
Ricci flow με χειρουργική επέμβαση
Το πρόγραμμα του Χάμιλτον για την απόδειξη της εικασίας του Πουανκαρέ, περιλαμβάνει αρχικά την τοποθέτηση ενός μετρικού Ρίμαν σε άγνωστη απλά συνδεδεμένη κλειστή 3-πολλαπλότητα/τρισδιάστατη πολλαπλότητα. Η ιδέα είναι να προσπαθήσουμε να βελτιώσουμε αυτό το μετρικό* για παράδειγμα, εάν το μετρικό μπορεί να βελτιωθεί αρκετά, έτσι ώστε να έχει σταθερή καμπυλότητα, τότε θα πρέπει να είναι η 3-σφαίρα. Το μετρικό βελτιώνεται μέσω της ακόλουθης ροής Ρίτσι εξίσωσης:
{\displaystyle \partial _{t}g_{ij}=-2R_{ij}}
όπου g είναι το μετρικό και R η Ρίτσι καμπυλότητά του, και αναμένεται ότι καθώς ο χρόνος t αυξάνεται, η πολλαπλότητα γίνεται ευκολότερα κατανοητή. Η ροή Ρίτσι επεκτείνει το αρνητικό μέρος καμπυλότητας της πολλαπλότητας και περιορίζει το θετικό μέρος καμπυλότητας.
Σε ορισμένες περιπτώσεις, ο Χάμιλτον ήταν σε θέση να αποδείξει ότι αυτό ισχύει: για παράδειγμα, έδειξε ότι αν η πολλαπλότητα έχει θετική καμπυλότητα Ρίτσι παντού, τότε τείνει να εξαφανίζεται σε πεπερασμένο χρόνο υπό τη ροή Ρίτσι, χωρίς οποιαδήποτε άλλη ιδιομορφία. (Με άλλα λόγια, η πολλαπλότητα καταρρεει σε ένα σημείο σε πεπερασμένο χρόνο, είναι εύκολο να περιγράψουμε τη δομή λίγο πριν την πολλαπλότητα καταρρεύσει.) Αυτό εύκολα συνεπάγεται την ισχύ της εικασίας του Πουανκαρέ σε περίπτωση θετικής Ρίτσι καμπυλότητα. Ωστόσο, σε γενικές γραμμές οι εξισώσεις ροής Ρίτσι οδηγούν σε ιδιομορφίες του μετρικού μετά από ένα πεπερασμένο χρονικό διάστημα. Ο Πέρελμαν έδειξε πώς να συνεχίσουμε πέρα από αυτές τις ιδιομορφίες: σε πολύ αδρές γραμμές, τέμνει την πολλαπλότητα κατά μήκος αυτών των ιδιομορφιών, χωρίζοντας την πολλαπλότητα σε πολλά κομμάτια, και μετά συνεχίζει με την ροή Ρίτσι σε κάθε ένα από αυτά τα κομμάτια. Αυτή η διαδικασία είναι γνωστή ως Ricci flow με χειρουργική επέμβαση.
Μια ειδική περίπτωση των θεωρημάτων του Πέρελμαν περί της ροής Ρίτσι με χειρουργική επέμβαση δίνεται ως ακολούθως.
Αυτό το αποτέλεσμα συνεπάγεται την εικασία του Πουανκαρέ, επειδή είναι εύκολο να το επαληθεύσουμε για τις δυνατές πολλαπλότητες που αναφέρονται σε αυτό το συμπέρασμα.
Η συνθήκη για τη βασική ομάδα φαίνεται να είναι αναγκαία (και ικανή) για πεπερασμένο χρόνο με εξαφάνιση, και, ειδικότερα, περιλαμβάνει την περίπτωση μηδαμινής βασικής ομάδας. Αυτό είναι ισοδύναμο με το να λέμε ότι η πρώτη διάσπαση της πολλαπλότητας δεν έχει καθόλου άκυκλες συνιστώσες, και αποδεικνύεται ότι είναι ισοδύναμη με την συνθήκη όλα τα γεωμετρικά μέρη της πολλαπλότητας να έχουν γεωμετρίες με βάση τις δύο γεωμετρίες του Θέρστον S2×R και S3. Μελετώντας το όριο της πολλαπλότητας για μεγάλο χρονικό διάστημα, ο Πέρελμαν απέδειξε την εικασία της γεωμετρικοποίησης του Θέρστον για οποιαδήποτε βασική ομάδα: σε μεγάλα διαστήματα η πολλαπλότητα έχει πυκνή-αραιά διάσπαση, της οποίας το πυκνό τμήμα έχει μία δομή υπερβολική, και της οποίας το αραιό τμήμα είναι μια γραφική πολλαπλότητα, αλλά η συγκεκριμένη επικουρική περιπλοκή δεν είναι απαραίτητη για να αποδείξουμε μόνο την εικασία του Πουανκαρέ.[27]
Λύση
Γκριγκόρι Πέρελμαν
Το Νοέμβριο του 2002, ο Ρώσος μαθηματικός Γκριγκόρι Πέρελμαν δημοσιεύτηκε το πρώτο από μια σειρά τριών Ε-prints στο arXiv που περιγράφει μια λύση της εικασίας του Πουανκαρέ. Η απόδειξη του Πέρελμαν χρησιμοποιεί μια τροποποιημένη έκδοση της ροής Ricci πρόγραμμα που αναπτύχθηκε από τον Ρίτσαρντ Χάμιλτον. Τον Αύγουστο του 2006, ο Πέρελμαν απονεμήθηκε, αλλά αρνήθηκε το Μετάλλιο Φιλντς για την απόδειξη του. Στις 18 Μάρτιος 2010, το μαθηματικό Ινστιτούτο Clay (Clay Mathematics Institute) απένειμε στον Πέρελμαν το $1 εκατ. του Βραβείου Χιλιετίας , σε αναγνώριση της απόδειξης.[28] Ο Πέρελμαν απέρριψε και αυτό το βραβείο.[4][29]
Ο Πέρελμαν απέδειξε την εικασία παραμορφώνοντας τη πολλαπλότητα χρησιμοποιώντας τη ροή Ricci (η οποία συμπεριφέρεται παρόμοια με τη εξίσωση θερμότητας που περιγράφει τη διάχυση της θερμότητας μέσω ενός αντικείμενου). Η ροή Ricci συνήθως παραμορφώνει την πολλαπλότητα προς ένα πιο στρογγυλεμένο σχήμα, εκτός από ορισμένες περιπτώσεις, όπου εκτείνεται η πολλαπλότητα εκτός από τον εαυτό της προς αυτό που είναι γνωστό ως μοναδικότητες. Ο Πέρελμαν και ο Χάμιλτον στη συνέχεια, κόβουν την πολλαπλότητα σε μοναδικότητες (μια διαδικασία που ονομάζεται "χειρουργική") προκαλώντας ξεχωριστά κομμάτια που σχηματίσουν μπάλες-σαν σχήματα. Σημαντικά βήματα στην απόδειξη είναι αυτά που δείχνουν πως συμπεριφέρονται οι πολλαπλότητες όταν παραμορφώνονται από τη ροή Ricci, εξετάζοντας τι είδους ιδιομορφίες αναπτύσσονται, τον προσδιορισμό του κατά πόσον αυτή η χειρουργική διαδικασία μπορεί να ολοκληρωθεί και ότι η "επέμβαση" δεν χρειάζεται να επαναλαμβάνεται άπειρες φορές.
Το πρώτο βήμα είναι να παραμορφώνεται η πολλαπλότητα χρησiμοποιώντας της ροή Ricci. H ροή Ricci ορίζεται από τον Ρίτσαρντ Χάμιλτον ως ένας τρόπος παραμόρφωσης συλλεκτών. Η φόρμουλα για την ροής Ricci είναι μια απομίμηση της εξίσωσης θερμότητας η οποία περιγράφει τον τρόπο ροών θερμότητας σε στερεά. Όπως η ροή θερμότητας, έτσι και η ροή Ricci τείνει προς την ομοιόμορφη συμπεριφορά. Σε αντίθεση με τη ροή θερμότητας, η ροή Ricci μπορούσε να τρέξει σε μοναδικότητες και να σταματήσει να λειτουργεί. Μια μοναδικότητα μιας πολλαπλότητας είναι ένα μέρος όπου δεν είναι διαφορίσιμη: σαν μια γωνία ή ένα άνθος ή ένα τσίμπημα. Η ροή Ricci οριζόταν μόνο για τις ομαλά διαφορίσιμες πολλαπλότητες. Ο Χάμιλτον χρησιμοποίησε τη ροή Ricci για να αποδείξει ότι κάποιες συμπαγείς πολλαπλότητες ήταν αμφιδιαφορίσιμες σε σφαίρες και ήλπιζε να την εφαρμόσει για να αποδείξει η Εικασία του Πουανκαρέ. Χρειαζόταν λοιπόν να κατανοήσει τις μοναδικότητες.
Ο Χάμιλτον δημιούργησε μια λίστα με τις πιθανές ανωμαλίες που θα μπορούσαν να σχηματιστούν αλλά ανησυχούσε ότι ορισμένες ιδιομορφίες μπορεί να οδηγούσαν σε δυσκολίες. Ήθελε να κόψει (δημιουργία τομής)την πολλαπλότητα σε μοναδικότητες και επικόλληση στον καλύμματα ( cap = σύμβολο της τομής), και στη συνέχεια, εκτελέστε την ροή Ricci και πάλι, οπότε χρειαζόταν να κατανοήσει τις μοναδικότητες και να δείξει ότι ορισμένα είδη μοναδικοτήτων δεν εμφανίζονται. Ο Πέρελμαν ανακάλυψε ότι οι μοναδικότητες ήταν όλες πολύ απλές: ουσιαστικά ήταν τρισδιάστατοι κύλινδροι φτιαγμένοι από σφαίρες που απλώνονταν κατά μήκος μιας γραμμής. Ένας συνηθισμένος κύλινδρος γίνεται με κύκλους ενωμένους κατά το μήκος μιας γραμμής. Ο Πέρελμαν το απέδειξε αυτό χρησιμοποιώντας κάτι που ονομάζεται "Μειωμένος Όγκος", το οποίο είναι στενά συνδεδεμένο με τις ιδιοτιμές μιας ορισμένης ελλειπτικής εξίσωσης.
Μερικές φορές, μια κατά τα άλλα πολύπλοκη πράξη απλοποιείται σε πολλαπλασιασμό με ένα βαθμωτό (ένας αριθμός). Αυτοί οι αριθμοί ονομάζονται ιδιοτιμές της πράξης. Οι ιδιοτιμές είναι στενά συνδεδεμένες με τις συχνότητες δόνησης και χρησιμοποιούνται στην ανάλυση ενός διάσημου προβλήματος: μπορείς να ακούσεις το σχήμα ενός τυμπάνου;. Ουσιαστικά, μία ιδιοτιμή είναι σαν μία νότα παιγμένη από την πολλαπλότητα. Ο Πέρελμαν απέδειξ ότι αυτή η νότα αγγίζει υψηλότερους τόνους, καθώς η πολλαπλότητα παραμορφώνεται από τη ροή Ρίτσι. Αυτό τον βοήθησε στο να εξαλειφθούν ορισμένες από τις πιο ενοχλητικές ιδιομορφίες που είχαν απασχολήσει τον Χάμιλτον, ιδιαίτερα η λύση που αφορούσε το κυλινδρικό σολιτόνιο, στο οποίο φαινόταν σαν ένα νήμα να εξέχει της πολλαπλότητας δίχως τίποτε από την άλλη πλευρά. Στην ουσία, ο Πέρελμαν έδειξε ότι όλα τα σκέλη αυτά μπορούν να κοπούν και να καλυφθούν και κανένα να μην προεξέχει σε μια πλευρά μόνο.
Ολοκληρώνοντας τη απόδειξη, ο Πέρελμαν λαμβάνει κάθε συμπαγή, απλά συνδεδεμένη, τρισδιάστατη πολλαπλότητα χωρίς όριο και αρχίζει να εφαρμόζει τη ροή Ρίτσι σε αυτή. Αυτό παραμορφώνει την πολλαπλότητα σε κυκλικά κομμάτια με νήματα δράμοντα μεταξύ τους. Τέμνει τα νήματα και συνεχίζει παραμορφώνοντας την πολλαπλότητα μέχρι που τελικά του απομένει μια συλλογή από στρογγυλές τρισδιάστατες σφαίρες. Τότε αναδομεί την αρχική πολλαπλότητα συνδέοντας τις σφαίρες μαζί με τρισδιάστατους κυλίνδρους, τις μεταμορφώνει σε ένα στρογγυλό σχήμα και βλέπει ότι, παρά την αρχική σύγχυση, η πολλαπλότητα ήταν στην πραγματικότητα ομοιομορφική σε μια σφαίρα.
Ένα άμεσο ερώτημα ήταν πώς μπορεί κανείς να είναι σίγουρος ότι δεν υπάρχουν άπειρες το πλήθος αναγκαίες περικοπές; Διαφορετικά, η κοπή μπορεί να συνεχίζεται επ' άπειρον. Ο Πέρελμαν απέδειξε ότι αυτό δεν μπορεί να συμβαίνει, με τη χρήση ελάχιστων επιφανειών στην πολλαπλότητα. Η ελάχιστη επιφάνεια είναι κατ' ουσίαν μία ταινία σαπουνιού. Ο Χάμιλτον είχε δείξει ότι το εμβαδόν της ελάχιστης επιφάνειας μειώνεται καθώς η πολλαπλότητα υποβάλλεται ροή Ρίτσι. Ο Πέρελμαν επαλήθευσε αυτό που συμβαίνει στο εμβαδόν της ελάχιστης επιφάνειας όταν η πολλαπλότητα είναι κομμένη σε φέτες. Απέδειξε ότι, εν τέλει,το εμβαδόν είναι τόσο μικρό ώστε οποιοδήποτε κόψιμο πέρα από αυτό το εμβαδόν είναι τόσο μικρό που μπορεί να κοπεί μόνο σε τρισδιάστατες σφαίρες και όχι σε πιο περίπλοκα κομμάτια. Αυτό περιγράφεται ως μια μάχη με μια λερναία Ύδρα από την Σορμάνι στο βιβλίο του Σπίρο το οποίο αναφέρεται παρακάτω. Αυτό το τελευταίο μέρος της απόδειξης παρουσιάστηκε στην τρίτη και τελευταία εργασία του Πέρελμαν σχετικά με το θέμα.
Το σχήμα του σύμπαντος μέσα από τη εικασία του Πουανκαρέ
Το σύμπαν Φρήντμαν-Λεμέτρ-Ρόμπερτσον-Γουόκερ αντιστοιχεί σε μια χρονικώς εξελισσόμενη ακτίνα του χώρου S3. Υποστηρίζει ότι αν αυτό το σύμπαν τροποποιείται σε M3, στο τέλος η επιτάχυνση μπορεί να παράγει μια μετάπτωση φάσης μετατρέποντας τη M3 σε ένα χώρο σταθερής καμπυλότητας που αντιστοιχεί ακριβώς σε μία φάση ντε Σίτερ σχετική με τον S3. Μια άλλη άποψη είναι ότι από την Είκασία της γεωμετρικοποίησης (μια γενίκευση της εικασίας του Πουανκαρέ) απαιτεί να κατανοήσει όλες τις τοπικά ομοιογενείς γεωμετρίες σε κλειστές τρισδιάστατες πολλαπλότητες, χρησιμοποιώντας ροή Ricci μπορεί κανείς να θεωρήσει ότι η ταξινόμηση Μπιάνκι χρησιμοποιείται για τη μελέτη κοσμολογικών μοντέλων. Αυτό που μπορεί κανείς να προσθέσει σε αυτό το σενάριο είναι ότι μια τέτοια μετάβαση μπορεί να απαιτήσει μια συστροφή, προκειμένου να γίνει ο S3 (ή άλλα κοσμολογικά μοντέλα Μπιάνκι) παραλληλίσιμα.[30]
Παραπομπές
«Poincaré, Jules Henri». The American Heritage Dictionary of the English Language (fourth έκδοση). Boston: Houghton Mifflin Company. 2000. ISBN 0-395-82517-2. Ανακτήθηκε στις 2007-05-05.
Hamilton, Richard S. (1997). «Four-manifolds with positive isotropic curvature». Communications in Analysis and Geometry 5 (1): 1–92. MR 1456308. Zbl 0892.53018.
Clay Mathematics Institute (March 18, 2010). Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman. (PDF) Δελτίο τύπου. Ανακτήθηκε στις November 13, 2015.
«Последнее "нет" доктора Перельмана» (στα Russian). Interfax. July 1, 2010. http://www.interfax.ru/society/txt.asp?id=143603. Ανακτήθηκε στις 5 April 2016.
Ritter, Malcolm (1 July 2010). «Russian mathematician rejects million prize». The Boston Globe.
Mackenzie, Dana (2006-12-22). «The Poincaré Conjecture--Proved». Science (American Association for the Advancement of Science) 314 (5807): 1848–1849. doi:10.1126/science.314.5807.1848. ISSN 0036-8075. PMID 17185565. Αρχειοθετήθηκε στις 2007-01-02.
Bing, RH (1958). «Necessary and sufficient conditions that a 3-manifold be S3». Annals of Mathematics. Second Series 68 (1): 17–37. doi:10.2307/1970041.
Bing, RH (1964). «Some aspects of the topology of 3-manifolds related to the Poincaré conjecture». Lectures on Modern Mathematics. II. New York: Wiley, pp. 93–128.
Milnor, John (2004). «The Poincaré Conjecture 99 Years Later: A Progress Report» (PDF). Ανακτήθηκε στις 2007-05-05.
Taubes, Gary (July 1987). «What happens when hubris meets nemesis». Discover 8: 66–77.
Matthews, Robert (9 April 2002). «$1 million mathematical mystery "solved"». NewScientist.com. Ανακτήθηκε στις 2007-05-05.
Szpiro, George (July 29, 2008). Poincaré's Prize: The Hundred-Year Quest to Solve One of Math's Greatest Puzzles. Plume. ISBN 978-0-452-28964-2.
Morgan, John W., Recent progress on the Poincaré conjecture and the classification of 3-manifolds.
Hamilton, Richard (1982). «Three-manifolds with positive Ricci curvature». Journal of Differential Geometry 17 (2): 255–306. MR 0664497. Zbl 0504.53034.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License