Το δίεδρο είναι τύπος πολύεδρου, από δύο πολυγωνικές έδρες που μοιράζονται το ίδιο σύνολο ακμών. Στον τρισδιάστατο Ευκλείδειο χώρο, είναι εκφυλισμένο όταν οι έδρες του είναι επίπεδες, ενώ στον τρισδιάστατο σφαιρικό χώρο, ένα δίεδρο με επίπεδες έδρες μπορεί να θεωρηθεί ως φακός, ένα τέτοιο παράδειγμα είναι η θεμελιώδης περιοχή ενός χώρου φακού L(p,q).[1]
| Σύνολο κανονικών n-γώνων δίεδρων | |
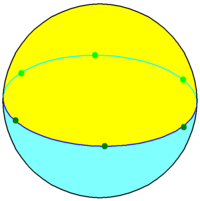 Παράδειγμα εξαγωνικού δίεδρου πάνω σε σφαίρα. |
|
| Τύπος | Κανονικό πολύεδρο ή Σφαιρική πλάκα |
| Έδρες | 2 n-γωνα |
| Ακμές | n |
| Κορυφές | n |
| Διαμόρφωση κορυφής | n.n |
| Σύμβολο Schläfli | {n,2} |
| Σύμβολο Wythoff | 2 | n 2 |
| Διάγραμμα Coxeter | |
| Ομάδα συμμετρίας | Dnh, [2,n], (*22n), τάξη 4n |
| Ομάδα περιστροφής | Dn, [2,n]+, (22n), τάξη 2n |
| Δυϊκό | οσόεδρο |
Συνήθως το κανονικό δίεδρο υπονοεί δύο κανονικά πολυγώνα, αυτό δείχνει και ο συμβολισμός Schläfli {n,2}. Κάθε πολύγωνο γεμίζει ένα ημισφαίριο, με ένα κανονικό n-γωνο πάνω στον ισημερινό που βρίσκεται μεταξύ τους.[2]
Το δυϊκό ενός n-γωνικού δίεδρου είναι το n-γωνικό οσόεδρο, όπου n δίγωνες έδρες μοιράζονται δύο κορυφές.
Ως πολύεδρο
Το δίεδρο μπορεί να θεωρηθεί ως εκφυλισμένο πρίσμα που αποτελείται από δύο (επίπεδα) n-πλευρών πολύγωνα συνδεδεμένα "πλάτη με πλάτη», έτσι ώστε το αντικείμενο που προκύπτει να μην έχει βάθος.
Ως πλάκα πάνω σε σφαίρα
Ως σφαιρική πλάκα, το δίεδρο μπορεί να υπάρχει ως μη εκφυλισμένη μορφή, με δύο n-πλευρών έδρες που καλύπτουν τη σφαίρα, η κάθε έδρα είναι ένα ημισφαίριο, και οι κορυφές βρίσκονται πάνω στον ισημερινό. Ονομάζεται κανονικό όταν οι κορυφές του έχουν ίση απόσταση μεταξύ τους.
Το κανονικό πολύεδρο {2,2} είναι αυτο-διπλό, καθώς είναι τόσο οσόεδρο όσο και δίεδρο.
 |
 |
 |
 |
 |
... |
| Schläfli | {2,2} | {3,2} | {4,2} | {5,2} | {6,2} |
|---|---|---|---|---|---|
| Coxeter | |||||
| Έδρες | 2 {2} | 2 {3} | 2 {4} | 2 {5} | 2 {6} |
| Ακμές και κορυφές |
2 | 3 | 4 | 5 | 6 |
Απειρογωνικό δίεδρο
Στο όριο το δίεδρο γίνεται απειρογωνικό δίεδρο όπως μια δισδιάστατη ψηφοθέτηση:
Δίτοπα
Το κανονικό δίτοπο είναι ένα n-διάστατο ανάλογο ενός διέδρου, με συμβολισμό Schläfli {p, ... q,r,2}. Έχει δύο όψεις, {p, ... q,r}, οι οποίες μοιράζονται όλες τις κορυφογραμμές, {p, ... q} από κοινού.[3]
Παραπομπές
Gausmann, Evelise; Lehoucq, Roland; Luminet, Jean-Pierre; Uzan, Jean-Philippe; Weeks, Jeffrey (2001). «Topological Lensing in Spherical Spaces». Classical and Quantum Gravity 18: 5155–5186. doi:10.1088/0264-9381/18/23/311.
Coxeter, Regular polytopes, σελ. 12
Regular Abstract polytopes, σελ. 158
Πηγές
McMullen, Peter; Schulte, Egon (Δεκέμβριος 2002), Abstract Regular Polytopes (1η έκδοση), Cambridge University Press, ISBN 0-521-81496-0
Coxeter, H.S.M., Regular Polytopes (3η έκδοση), Dover Publications Inc., ISBN 0-486-61480-8
Weisstein, Eric W., "Dihedron" από το MathWorld.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License


