.
Στη γεωμετρία, η διάμεσος ενός τριγώνου είναι ένα ευθύγραμμο τμήμα το οποίο ενώνει μία κορυφή του τριγώνου με το μέσο της απέναντι πλευράς. Κάθε τρίγωνο έχει ακριβώς τρεις διάμεσους: μία από κάθε κορυφή προς την αντίθετη πλευρά. Στην περίπτωση των ισοσκελών και ισόπλευρων τριγώνων, η διάμεσος διχοτομεί οποιαδήποτε γωνία μιας κορυφής, της οποίας οι δύο προσκείμενες πλευρές της είναι ίσες.
Σχέση με το κέντρο βάρους
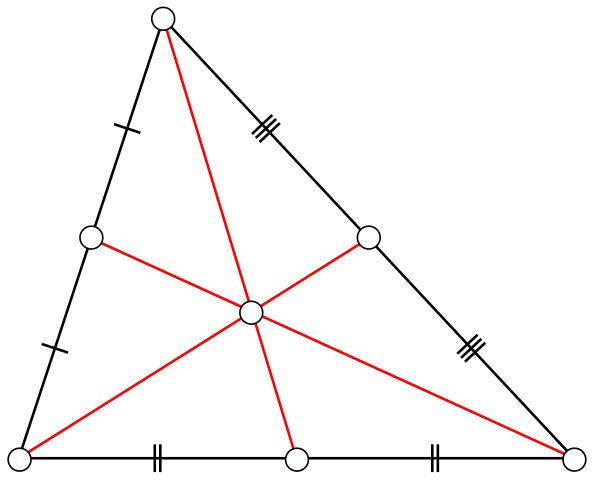
Οι διάμεσοι ενός τριγώνου διέρχονται από το ίδιο σημείο, το κέντρο βάρους του
Κάθε διάμεσος ενός τριγώνου διέρχεται από την τομή των διαμέσων του (βαρύκεντρο) , το οποίο είναι το κέντρο βάρους ενός αντικειμένου ομοιόμορφης πυκνότητας σε σχήμα τριγώνου. Έτσι, το αντικείμενο θα ισορροπεί για κάθε γραμμή που περνά μέσα από το κέντρο βάρους του, συμπεριλαμβανομένης οποιασδήποτε διαμέσου.
Κάθε διάμεσος διαιρεί το εμβαδόν του τριγώνου στο μισό του, εξ ου και το όνομα. (Κάθε άλλη γραμμή που χωρίζει το εμβαδόν του τριγώνου σε δύο ίσα μέρη, δεν περνά από το κέντρο βάρους του.) [1] Οι τρεις διάμεσοι διαιρούν το τρίγωνο σε έξι μικρότερα τρίγωνα ίσων εμβαδών.
Απόδειξη
Θεωρήστε ένα τρίγωνο ABC Έστω D το μέσο της \overline{AB}, E το μέσο της \overline{BC}, F το μέσο της \overline{AC}, \) και O το κέντρο βάρους.
Εξ ορισμού, AD=DB, AF=FC, BE=EC \,. Επομένως [ADO]=[BDO], [AFO]=[CFO], [BEO]=[CEO], και [ABE]=[ACE] \,, όπου [ABC] αντιπροσωπεύει το εμβαδόν του τριγώνου \triangle ABC , αυτό ισχύει διότι σε κάθε περίπτωση τα δύο τρίγωνα έχουν ίσες τις βάσεις τους, έχουν κοινό ύψος από τις βάσεις τους και το εμβαδόν ενός τριγώνου ισούται με το μισό του γινομένου της βάσης του με το αντίστοιχο σε αυτή ύψος.
Άλλες Ιδιότητες
Για κάθε τρίγωνο,[1]
\tfrac{3}{4} (περίμετρος τριγώνου) < άθροισμα διαμέσων < \tfrac{3}{2} (περίμετρος τριγώνου).
Για κάθε τρίγωνο με πλευρές a, b, c και διαμέσους m_a, m_b, m_c, [1]
\tfrac{3}{4}(a^2+b^2+c^2)=m_a^2+m_b^2+m_c^2.
Δείτε επίσης
Διχοτόμος γωνίας
Ύψος
και διάφορα τρίγωνα
Αναφορές
Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp. 86-87.
Εξωτερικοί σύνδεσμοι
Διάμεσοι και Διχοτόμοι ενός Τριγώνου
Διάμεσοι
Area of Median Triangle
Διάμεσοι ενός Τριγώνου Με διαδραστικό animation
Κατασκευάζοντας τη διάμεσο ενός τριγώνου με διαβήτη και ευθεία γραμμή
Weisstein, Eric W., "Διάμεσος τριγώνου" από το MathWorld.
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License


