Δέσμη ινών

Στα μαθηματικά, και ιδιαίτερα στην τοπολογία, μια δέσμη ινών (αγγλ.: fibre bundle) είναι ένας χώρος που είναι τοπικά ένας χώρος με γινόμενο, αλλά γενικά μπορεί να έχει διαφορετική τοπολογική δομή. Συγκεκριμένα, η ομοιότητα ανάμεσα σε ένα χώρο Ε και σε ένα χώρο με γινόμενο B × F ορίζεται χρησιμοποιώντας μια συνεχή επί απεικόνιση

\( {\displaystyle \pi \colon E\to B} \)

η οποία σε μικρές περιοχές του E συμπεριφέρεται ακριβώς όπως μια προβολή από αντίστοιχες περιοχές της Β × F στο Β. Η απεικόνιση π,που ονομάζεται η προβολή ή η βύθιση της δέσμης, θεωρείται ως μέρος της δομής της δέσμης. Ο χώρος E είναι γνωστός ως το συνολικό διάστημα της δέσμης ινών, ο Β ως η βάση του χώρου, και F η ίνα.

Μια κυλινδρική βούρτσα που δείχνει την διαίσθηση πίσω από τον όρο "δέσμες ινών". Αυτή η βούρτσα είναι σαν δέσμες ινών κατά τις οποίες η βάση του χώρου είναι ένας κύλινδρος και οι ίνες (σκληρές τρίχες) είναι τα τμήματα της γραμμής. Η απεικόνιση π:E→B θα παίρνει ένα σημείο για κάθε τρίχα και θα το απεικονίζει στη ρίζα του πάνω κυλίνδρου.

Στην τετριμμένη περίπτωση, ο Ε είναι B × F, και η απεικόνιση π είναι η προβολή του χώρου με γινόμενο στον πρώτο παράγοντα. Αυτό ονομάζεται ασήμαντη δέσμη. Παραδείγματα μη-τετριμμένης δέσμης ινών περιλαμβάνουν τη λωρίδα του Möbius και το μπουκάλι του Klein, καθώς και μη τετριμμένους επικαλυμμένους χώρους. Δέσμες ινών όπως η εφαπτομένη δέσμη από μια πολλαπλότητα και πιο γενικές διανυσματικές δέσμες παίζουν σημαντικό ρόλο στη διαφορική γεωμετρία και τη διαφορική τοπολογία, όπως και οι κύριες δέσμες.

Απεικονίσεις μεταξύ ολικών χώρων από δέσμες ινών που "μετακινούνται" με την προβολή απεικονίσεων είναι γνωστές ως δέσμες απεικονίσεων, και στην κατηγορία των οπτικών δέσμεων δημιουργείται μια κατηγορία με εκτίμησεις αυτών τών απεικονίσεων. Μια δέσμη απεικονίσεων από τη βάση του χώρου,(με την ταυτοτική απεικόνιση ως προβολή) στο Ε ονομάζεται τομή της E. Οι δέσμες ινών μπορεί να είναι εξειδικευμένες σε μια σειρά από μεθόδους, από τους πιο κοινούς οι οποίοι απαιτούν ότι οι μεταβάσεις μεταξύ των τοπικών τετριμμένων μπαλωμάτων βρίσκονται σε μια συγκεκριμένη τοπολογική ομάδα, γνωστή ως η δομή της ομάδας, που ενεργεί για την ίνα F.

Ιστορία

Οι δέσμες ινών έγιναν από μόνες τους αντικείμενο μελέτης κατά την περίοδο 1935-1940. Ο πρώτος γενικός ορισμός εμφανίστηκε στα έργα του Hassler Whitney.[1]

Ο Whitney ήρθε στον γενικό ορισμό μιας δέσμης ινών από την μελέτη του για μια πιο συγκεκριμένη έννοια της σφαιρικής δέσμης,[2] που είναι μια δέσμη ινών της οποίας η ίνα είναι μια σφαίρα αυθαίρετης διάστασης.[3]

Επίσημος ορισμός

Μια δέσμη ινών είναι μια δομή (E, B, π, F), όπου E, B, και F είναι τοπολογικοί χώροι και π : E → B είναι συνεχής και επί ικανοποιώντας μια τοπικά τετριμμένη κατάσταση που περιγράφεται παρακάτω. Ο χώρος B καλείται βάση του χώρου των δεσμών, E ο συνολικός χώρος και F η ίνα. Η απεικόνιση π ονομάζεται η προβολή απεικόνισης (ή δέσμη προβολής). Θα υποθέσουμε στη συνέχεια ότι ο βασικός χώρος Β είναι συνεκτικός.

Απαιτούμε για κάθε x στο E, να υπάρχει μια ανοιχτή περιοχή U ⊂ Β του π(x) (η οποία θα ονομάζεται τετριμμένη περιοχή) έτσι ώστε να υπάρχει ένας ομοιομορφισμός φ: π-1(U) → U × F (όπου U × F είναι ο χώρος με γινόμενο) κατά τέτοιο τρόπο ώστε η π να συμφωνεί με την προβολή πάνω στον πρώτο παράγοντα. Έτσι ώστε στο διάγραμμα που ακολουθεί θα πρέπει να επικοινωνούν:

όπου proj1 : U × F → U είναι η φυσική προβολή και φ : π−1(U) → U × F είναι ένας ομοιομορφισμός. Το σύνολο όλων των {(Ui, φi)} ονομάζεται ένας τοπικός διαμελισμός της δέσμης.

Έτσι, για κάθε p στο Β, η αντίστροφη εικόνα π-1({p}) είναι ομοιομορφική στην F (από τη proj1-1({p}) σαφώς είναι) και ονομάζεται ίνα πάνω στο p. Κάθε δέσμη ινών π : E → B είναι μια ανοιχτή απεικόνιση, καθώς οι προβολές των γινομένων είναι ανοιχτές απεικονίσεις. Ως εκ τούτου,ο B μεταφέρει το τοπολογικό πηλίκο που καθορίζεται από την απεικόνιση π.

Μια δέσμη ινών (E, B, π, F) συχνά συμβολίζεται

\( {\displaystyle F\longrightarrow E\ {\xrightarrow {\,\ \pi \ }}\ B} \)

ώστε, σε αναλογία με μια σύντομη πλήρη ακολουθία, που δείχνει σε ποιο χώρο είναι η ίνα, το συνολικό χώρο και το βασικό χώρο, καθώς και η απεικόνιση από το σύνολο στη βάση του χώρου.

Μια λεία δέσμη ινών είναι μια δέσμη ινών στην κατηγορία των λείων πολλαπλότητων. Έτσι τα Ε, Β, και F απαιτείται να είναι ομαλές πολλαπλότητες και όλες οι παραπάνω συναρτήσεις απαιτείται να είναι ομαλές απεικονίσεις.

Παραδείγματα
Τετριμμένη δέσμη

Έστω E = B × F και έστω π : E → B να είναι η προβολή πάνω στον πρώτο παράγοντα. Τότε ο Ε είναι μια δέσμη ινών ( F) πάνω στο Β. Εδώ ο E είναι όχι μόνο τοπικά ένα γινόμενο, αλλά και γενικά. Κάθε τέτοια δέσμη ινών ονομάζεται μια τετριμμένη δέσμη. Κάθε δέσμη ινών πάνω από ένα συσταλτό CW-σύμπλοκο είναι τετριμμένη.

Μη τετριμμένες δέσμες
Λωρίδα Möbius

Η λωρίδα Möbius είναι μια μη τετριμμένη δέσμη πάνω στον κύκλο.

Ίσως το πιο απλό παράδειγμα από μια μη τετριμμένη δέσμη E είναι η λωρίδα του mobius. Έχει τον κύκλο που τρέχει κατά μήκος του κέντρου της λωρίδας ως μια βάση B και το ευθύγραμμο τμήμα για την ίνα F, έτσι ώστε η λωρίδα του mobius είναι μια δέσμη του τμήματος της γραμμής πάνω από τον κύκλο. Μια γειτονιά U του σημείου x ∈ B είναι ένα τόξο: στην εικόνα, αυτό είναι το μήκος ενός από τα τετράγωνα. Η αντίστροφη εικόνα π − 1 ( U ) {\displaystyle \pi ^{-1}(U)} {\displaystyle \pi ^{-1}(U)} στην εικόνα είναι ένα (κάπως στριμμένο) κομμάτι της ταινίας, τέσσερα τετράγωνα πλάτος και ένα μήκος. Ο ομοιομορφισμός φ απεικονίζει την αντίστροφη εικόνα του U με μια φέτα κυλίνδρου: κυρτή, αλλά όχι στριμμένη.

Η αντίστοιχη τετριμμένη δέσμη B × F θα είναι ένας κύλινδρος, αλλά η λωρίδα του Möbius έχει μια πλήρη "στροφή". Σημειώστε ότι αυτή η στροφή είναι ορατή μόνο γενικά: τοπικά η λωρίδα του Möbius και ο κύλινδρος είναι πανομοιότυπα (κάνοντας μια ενιαία κάθετη περικοπή σε όποιο από τα δυο δίνει το ίδιο διάστημα).

Φιάλη Klein

Μια παρόμοια μη τετριμμένη δέσμη είναι η φιάλη του Klein, η οποία μπορεί να θεωρηθεί ως μια "στριμμένη" κυκλική δέσμη πάνω από έναν άλλο κύκλο. Η αντίστοιχη μη-στριμμένη (τετριμμένη) δέσμη είναι η 2-τόρος, S1 × S1.

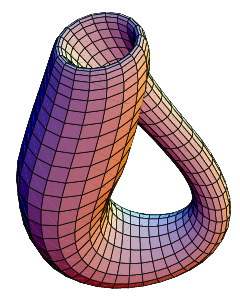
Η φιάλη του Κλάιν βυθίζεται στον τρισδιάστατο χώρο.

Ένας τόρος.

Επικαλυμμένη απεικόνιση

Μια επικαλυμμένη απεικόνιση είναι μια δέσμη ινών έτσι ώστε η δέσμη προβολής να είναι ένας τοπικός ομοιομορφισμός. Επομένως, η ίνα είναι ένας διακριτός χώρος.
Διανυσματικές και κύριες δέσμες

Μια ειδική κατηγορία από δέσμες ινών, που ονομάζονται διανυσματικές δέσμες, είναι εκείνες των οποίων οι ίνες είναι διανυσματικοί χώροι (για να χαρακτηριστεί ως μια διανυσματική δέσμη η δομή της ομάδας της δέσμης — βλ. παρακάτω — θα πρέπει να είναι μια γραμμική ομάδα). Σημαντικά παραδείγματα διανυσματικών δεσμών περιλαμβάνουν την εφαπτόμενη δέσμη και συνεφαπτόμενη δέσμη μιας ομαλής πολλαπλότητας. Από κάθε διανυσματική δέσμη, μπορεί κανείς να κατασκευάσει το πλαίσιο δέσμης των βάσεων, η οποία είναι μια κύρια δέσμη (βλ.παρακάτω).

Μια άλλη ειδική κατηγορία δεσμών ινών, που ονομάζονται κύριες δέσμες, είναι δέσμες των οποίων οι ίνες είναι ελεύθερες και η μεταβατική δράση από μια ομάδα G δίνεται, έτσι ώστε κάθε ίνα να είναι ένας κύριος ομοιογενής χώρος. Η δέσμη συχνά ορίζεται μαζί με την ομάδα αναφερόμενη ως κύρια G-δέσμη. Η ομάδα G είναι επίσης μια δομή της ομάδας της δέσμης. Δίνεται ότι μια αναπαράσταση ρ της G σε ένα διανυσματικό χώρο V, μια διανυσματική δέσμη με ρ(G)⊆Aut(V) ως μια δομή ομάδας μπορεί να κατασκευαστεί, γνωστή και ως προσαρτημένη δέσμη.

Σφαιρικές δέσμες

Μια σφαιρική δέσμη είναι μια δέσμη ινών της οποίας η ίνα είναι μια n-σφαίρα. Δίνεται μια διανυσματική δέσμη Ε με μια μετρική (όπως η εφαπτόμενη δέσμη σε μια πολλαπλότητα Rieman) της οποίας μπορεί κανείς να κατασκευάσει τη σχετική μοναδιαία σφαιρικής δέσμης, για την οποία η ίνα πάνω από ένα σημείο x είναι το σύνολο όλων των μοναδιαίων διανυσμάτων Ex. Όταν η διανυσματική δέσμη είναι η εφαπτόμενη δέσμη T(M), η μοναδιαία σφαιρική δέσμη είναι γνωστή ως η μοναδιαία εφαπτόμενη δέσμη, και συμβολίζεται με UT(M).

Μια σφαιρική δέσμη χαρακτηρίζεται μερικώς από κάθε τάξη του Euler , η οποία είναι βαθμού n+1 συνομολογικής τάξης στο συνολικό χώρο της δέσμης. Στην περίπτωση n=1, η σφαιρική δέσμη ονομάζεται κυκλική δέσμη και η τάξη του Euler είναι ίση με την πρώτη τάξη του Chern , η οποία χαρακτηρίζει τελείως την τοπολογία της δέσμης . Για κάθε n, δεδομένου την τάξη του Euler μίας δέσμης, μπορεί κανείς να υπολογίσει κάθε συνομολογία, χρησιμοποιώντας μια μακρά ακριβή ακολουθία που ονομάζεται ακολουθία Gysin .

Σπειροειδές απεικόνιση

Αν X είναι ένας τοπολογικός χώρος και f:X → X είναι ένας ομοιομορφισμός στη συνέχεια μια σπειροειδής(τοροειδής) απεικόνιση Mf έχει την φυσική δομή μιας δέσμης ινών πάνω από τον κύκλο με την ίνα X. Η τοροειδής απεικόνιση ενός ομοιομορφισμού επιφανειών έχει ιδιαίτερη σημασία στις 3-τοπολογικες πολλαπλότητες.

Χώροι πηλίκο

Αν G είναι μια τοπολογική ομάδα και H είναι μια κλειστή υποομάδα, τότε υπό ορισμένες συνθήκες, ο χώρος πηλίκο G/H , μαζί με την απεικόνιση πηλίκο π : G → G/H είναι μια δεσμη ινών, του οποίου η ίνα είναι ο τοπολογικός χώρος H. Μια ικανή και αναγκαία συνθήκη για να σχηματίζουν τα (G,G/H,π,H) μια δέσμη ινών είναι η απεικόνιση π να δέχεται τοπικές διατομές (Steenrod 1951, §7).

Οι πιο γενικές συνθήκες κάτω από τις οποίες ο απεικόνιση πηλίκο θα δέχεται τοπικές διατομές δεν είναι γνωστές,ωστόσο αν το G είναι μια ομάδα Lie και H μια κλειστή υποομάδα του G (και συνεπώς είναι μια υποομάδα Lie από θεώρημα του Cartan ), τότε η απεικόνιση πηλίκο είναι μια δέσμη ινών. Ένα παράδειγμα είναι η ίνωση του Hopf , S3 → S2 που είναι μια δέσμη ινών πάνω από τη σφαίρα S2 της οποίας το συνολικό διάστημα είναι S3. Από την οπτική των ομάδων Lie , S3 μπορεί να προσδιοριστεί με την ειδική ενιαία ομάδα SU(2). Η αβελιανή υποομάδα διαγώνιων μητρών είναι ισόμορφη με την κυκλική ομάδα U(1), και το πηλίκο SU(2)/U(1) είναι αμφιδιαφορίσιμο με τη σφαίρα.

Πιο γενικά, αν η G είναι οποιαδήποτε τοπολογική ομάδα και H μια κλειστή υποομάδα η οποία συμβαίνει επίσης να είναι μια ομάδα Lie , τότε G → G/H είναι δέσμη ινών.

Τμήματα

Ένα τμήμα (ή διατομή) μιας δέσμης ινών π είναι μια συνεχής απεικόνιση f : B → E τέτοια ώστε π(f(x))=x για όλα τα x στο B. Δεδομένου ότι οι δέσμες γενικά,δεν έχουν σφαιρικά ορισμένα τμήματα, ένας από τους σκοπούς της θεωρίας είναι να λυφθούν υπόψη για την ύπαρξή τους. Η έμφραξη της ύπαρξης ενός τμήματος μπορεί συχνά να μετρηθεί με μια συνομολογική τάξη, η οποία οδηγεί στη θεωρία των χαρακτηριστικών τάξεων στην αλγεβρική τοπολογία.

Το πιο γνωστό παράδειγμα είναι το  θεώρημα της τριχωτής μπάλας, όπου η τάξη του Euler είναι η έμφραξη για την εφαπτομένη δέσμη των 2-σφαιρών  έχοντας ένα πουθενά μηδενιζόμενο τμήμα.

Δομές ομάδων και μεταβατικές συναρτήσεις

Δέσμες ινών συχνά έρχονται με μια ομάδα με συμμετρίες που περιγράφουν τις αντίστοιχες συνθήκες μεταξύ αλληλεπικαλυπτόμενων  τοπικών τετριμένων διαγραμμάτων. Συγκεκριμένα, ας  είναι G μια τοπολογική ομάδα που δρα συνεχώς στον ινοχώρο F στα αριστερά. Τίποτα δεν θα χάσουμε αν χρειαζόμαστε την G να δρα αποτελεσματικά  στην F , ώστε να μπορεί να θεωρηθεί ως μια ομάδα ομοιομορφισμός της F. Ένας G-άτλαντας για τη δέσμη (E, B, d, F) είναι  τοπικά τετριμμένος τέτοιος ώστε για κάθε δύο αλληλεπικαλυπτόμενους χάρτες (U_i, δ_i) και (U_j, δ_j) η συνάρτηση

\( {\displaystyle \varphi _{i}\varphi _{j}^{-1}\colon (U_{i}\cap U_{j})\times F\to (U_{i}\cap U_{j})\times F} \)

που δίνεται από

\( {\displaystyle \varphi _{i}\varphi _{j}^{-1}(x,\xi )=(x,t_{ij}(x)\xi )} \)

όπου t_ij : U_i ∩ U_j → G είναι μια συνεχής απεικόνιση ονομάζεται μεταβατική συνάρτηση. Δύο G-άτλαντες είναι ισοδύναμοι αν η ένωση τους είναι επίσης ένας G-άτλαντας. Μια G-δέσμη είναι μια δέσμη ινών με μια κλάση ισοδυναμίας ίση με  G-άτλαντες. Η ομάδα G ονομάζεται η δομή ομάδας της δέσμης * ο ανάλογος όρος στη φυσική είναι  βαθμίδα ομάδας. Στην ομαλή κατηγορία, G-δέσμη είναι μια ομαλή δέσμη ινών, όπου G είναι μια ομάδα Lie και η αντίστοιχη δράση για την F είναι ομαλή και η μεταβατικές συναρτήσεις είναι όλες ομαλές απεικονίσεις.

Οι μεταβατικές συναρτήσεις t_ij πληρούν τις ακόλουθες προϋποθέσεις

\( {\displaystyle t_{ii}(x)=1\,} \)
\( {\displaystyle t_{ij}(x)=t_{ji}(x)^{-1}\,} \)
\( {\displaystyle t_{ik}(x)=t_{ij}(x)t_{jk}(x).\,} \)

Η τρίτη προϋπόθεση ισχύει για τριπλές αλληλεπικαλύψεις Ui ∩ Uj ∩ Uk και ονομάζεται ομόκυκλη κατάσταση (βλ. συνομολογία του Čech ). Το σημαντικό είναι ότι η μεταβατικές συναρτήσεις προσδιορίζουν την δέσμη ινών (αν συμπεριλάβει κανείς την ομόκυκλη κατάσταση του Čech).

Μια κύρια G-δέσμη είναι μια G-δέσμη, όπου η ίνα F είναι ένας κύριος ομοιογενής χώρος για την αριστερή δράση της G (αντίστοιχα, μπορεί κανείς να προσδιορίσει ότι η δράση της G στην ίνα F είναι ελεύθερη και μεταβατική). Σε αυτή την περίπτωση, είναι συχνά θέμα  ευκολίας να αναγνωρίσεις την F με την G , και έτσι να αποκτήσεις μια (δεξιά) δράση της G στην κύρια δέσμη.

Δέσμη απεικονίσεων

Είναι χρήσιμο να γνωρίζουμε της έννοια του μετασχηματισμού ανάμεσα σε δύο δέσμες ινών. Ας υποθέσουμε ότι M και N είναι βάσεις χώρου, και πE : E → M και πF : F → N είναι δέσμες ινών πάνω στη M και N, αντίστοιχα. Μια δεσμική απεικόνιση (ή δέσμη μορφησμός) αποτελείται από ένα ζευγάρι συνεχών[4] συναρτήσεων

\( {\displaystyle \varphi \colon E\to F,\quad f\colon M\to N} \)

τέτοιων που \( {\displaystyle \pi _{F}\circ \varphi =f\circ \pi _{E}} \). Αυτό είναι, το ακόλουθο διάγραμμα επικοινωνίας:

Για δέσμες ινών με ομάδα δομής G και των οποίων οι συνολικοί χώροι ειναι (δεξιά) G-χώροι (όπως η κύρια δέσμη), δέσμη μορφισμός , απαιτείται επίσης να είναι G-ισαλλοίωτες ίνες. Αυτό σημαίνει ότι \( {\displaystyle \varphi \colon E\to F} \) είναι, επίσης, G-μορφισμός από ένα G-χώρο στον άλλο, δηλαδή, \( {\displaystyle \varphi (xs)=\varphi (x)s} \) για όλα τα \( {\displaystyle x\in E} \) και \( {\displaystyle s\in G} \).

Σε περίπτωση που η βασικοί χώροι M και N συμπίπτουν , τότε, μια δέσμη μορφισμός πάνω στο M από την δέσμη ινών πE : E → M στην πΦ : F → M είναι μια απεικόνιση φ : E → F τέτοια ώστε π E = π F ∘ φ {\displaystyle \pi _{E}=\pi _{F}\circ \varphi } {\displaystyle \pi _{E}=\pi _{F}\circ \varphi }. Αυτό σημαίνει ότι η δεσμική απεικόνιση φ : E → F καλύπτει την ταυτότητα του M. Αυτό σημένει f ≡ i d M {\displaystyle f\equiv {\mathrm {id} }_{M}} {\displaystyle f\equiv {\mathrm {id} }_{M}} , και το διάγραμμα επικοινωνίας είναι

Ας υποθέσουμε ότι και οι δύο πE : E → M και πF : F → M ορίζονται πάνω από την ίδια βάση, το χώρο M. Μια δέσμη ισομορφισμός είναι μια δεσμική απεικόνιση \( {\displaystyle (\varphi ,f)} \)μεταξύ πE : E → M και πF : F → M τέτοια ώστε \( {\displaystyle f\equiv {\mathrm {id} }_{M}} \) και είναι τέτοιες ώστε η φ να είναι επίσης ένας ομοιομορφισμός[5]

Διαφορίσιμες δέσμες ινών

Στην κατηγορία των διαφορίσιμων πολλαπλότητων, δέσμες ινών προκύπτουν φυσικά, από καταβύθισεις από μία πολλαπλότητα στην άλλη. Δεν συνεπάγεται πως κάθε (διαφορίσιμη) κατάδυση ƒ : M → N από διαφορίσιμη πολλαπλότητα M σε άλλη διαφορίσιμη πολλαπλότητα N ,μας δίνει μια διαφορίσιμη δέσμη ινών. Για ένα πράγμα, η απεικόνιση  πρέπει να ειναι επιρριπτική, και (M,N,ƒ) ονομάζεται πολλαπλότητα ινών. Ωστόσο, αυτή η προϋπόθεση δεν είναι αρκετά επαρκής, και υπάρχει μια ποικιλία από επαρκείς προϋποθέσεις σε κοινή χρήση.

Αν M και N είναι συμπαγές και  συνεκτικά, τότε για οποιαδήποτε καταβύθιση f : M → N , συνεπάγεται μια δέσμη ινών, με την έννοια ότι υπάρχει ένας ινοχώρος F αμφιδιαφορίσιμος σε κάθε  ίνα,οπως(E,B,π,F) = (M,N,f,F) είναι μια δέσμη ινών. (Μια επί απεικόνιση  f ακολουθεί  τις παραδοχές που έχουν ήδη δοθεί σε αυτή την περίπτωση.) Γενικότερα, η υπόθεση της πυκνότητας μπορεί να χαλαρώσει εάν η καταβύθιση f : M → N υποτίθεται ότι θα είναι μια επί συνάρτηση γνήσιας απεικόνισης, πράγμα που σημαίνει ότι ƒ⁻¹(K) είναι συμπαγές για κάθε συμπαγές υποσύνολο K του N. Άλλη μια επαρκής προϋπόθεση, λόγω του Ehresmann (1951), είναι ότι αν ƒ : M → N είναι μια επί συνάρτηση καταβύθισης με M και N διαφορίσιμες πολλαπλότητες , όπως ότι η αντίστροφη εικόνα ƒ⁻¹(K) είναι συμπαγές και συνδέονται για όλα τα x ∈ N, τότε ƒ παραδέχεται συμβατή δομή δέσμης ινών  (Michor 2008, §17).

Γενικεύσεις

• Η έννοια της  δέσμης εφαρμόζεται σε πολλές περισσότερες κατηγορίες στα μαθηματικά, * βλ. κύριo ομοιογενή χώρο και κορμό (αλγεβρική γεωμετρία).
• Στην τοπολογία, μια ίνωση είναι μια απεικόνιση π : E → B η οποία έχει ορισμένες ομοτοπικές-θεωρητικές ιδιότητες κοινές με τις δέσμες ινών. Συγκεκριμένα, κάτω από ήπιες τεχνικές υποθέσεις μια δέσμη ινών έχει πάντα την ομοτοπική ανυψωτική ιδιότητα ή ομοτοπική επιστροματική ιδιότητα (βλ. Steenrod (1951, 11.7) για λεπτομέρειες). Αυτή είναι η καθοριστική ιδιότητα μιας ίνωσης.

Παραπομπές

see Steenrod (1951, Preface)
In his early works, Whitney referred to the sphere bundles as the “sphere-spaces”.
Whitney, Hassler (1940). «On the theory of sphere bundles». Proc. Nat. Acad. Sci. 26: 148–153.
Ανάλογα με την κατηγορία των χώρων που συμμετέχουν, οι συναρτήσεις μπορεί να θεωρηθούν ότι έχουν ιδιότητες εκτός από τη συνέχεια. Για παράδειγμα, στην κατηγορία των Διαφορίσιμων πολλαπλότητων, οι συναρτήσεις θεωρείται ότι είναι λείες. Στην κατηγορία των αλγεβρικών πολλαπλότιτων, είναι κανονικός μορφισμός συναρτήσεων.
Ή τουλάχιστον αντιστρέψιμος στην αντίστοιχη κατηγορία? π.χ., μια αμφιδιαφόριση.

Εγκυκλοπαίδεια Μαθηματικών

Κόσμος

Αλφαβητικός κατάλογος

Hellenica World - Scientific Library

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License